Hot-Electron Microwave Noise and Energy Relaxation in (Be)MgZnO/ZnO Heterostructures
Abstract
:1. Introduction
2. Samples and Measurement Techniques
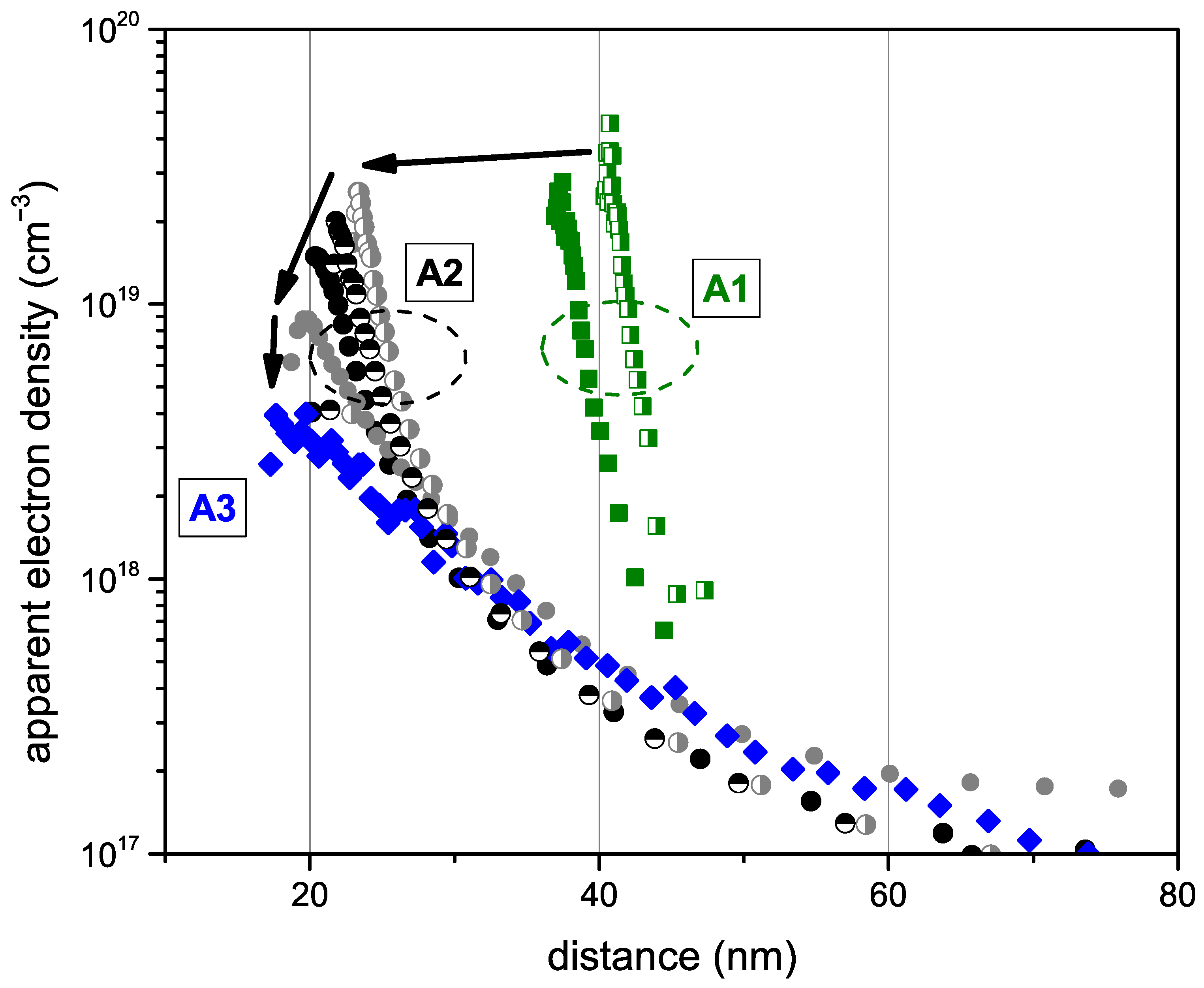
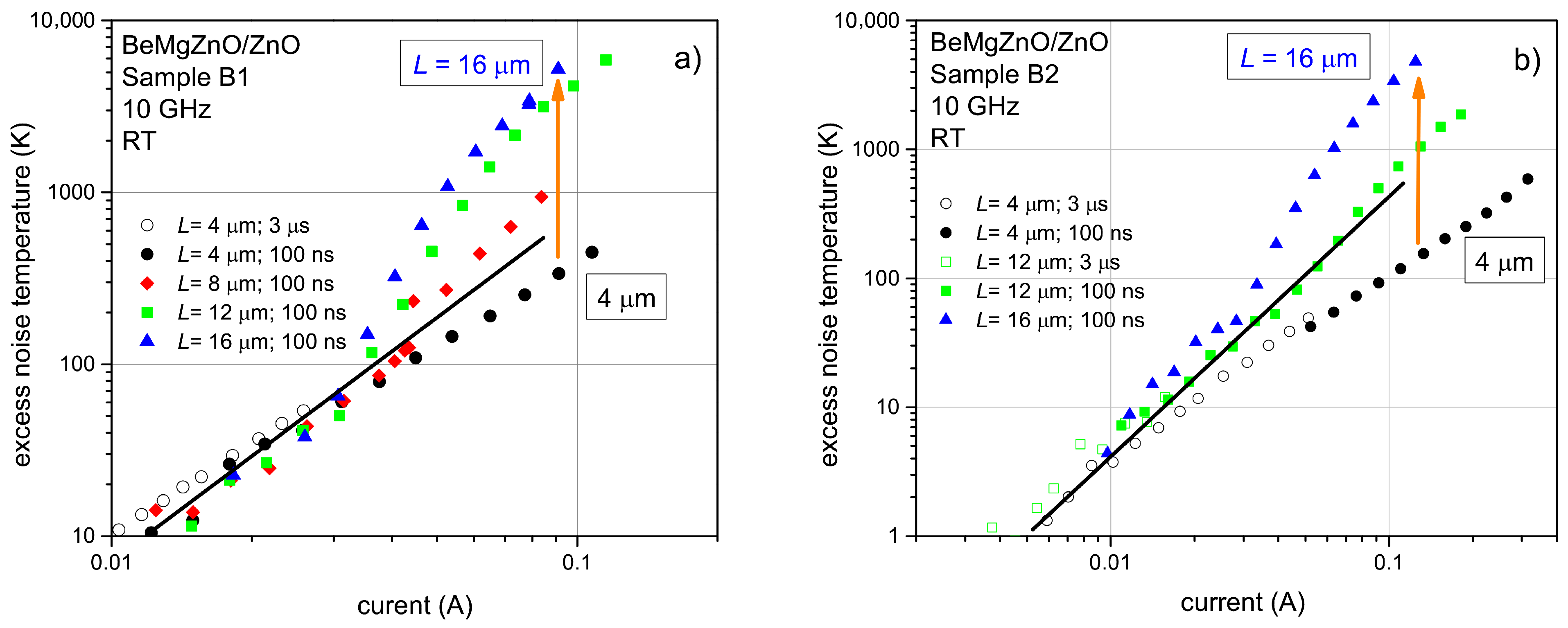
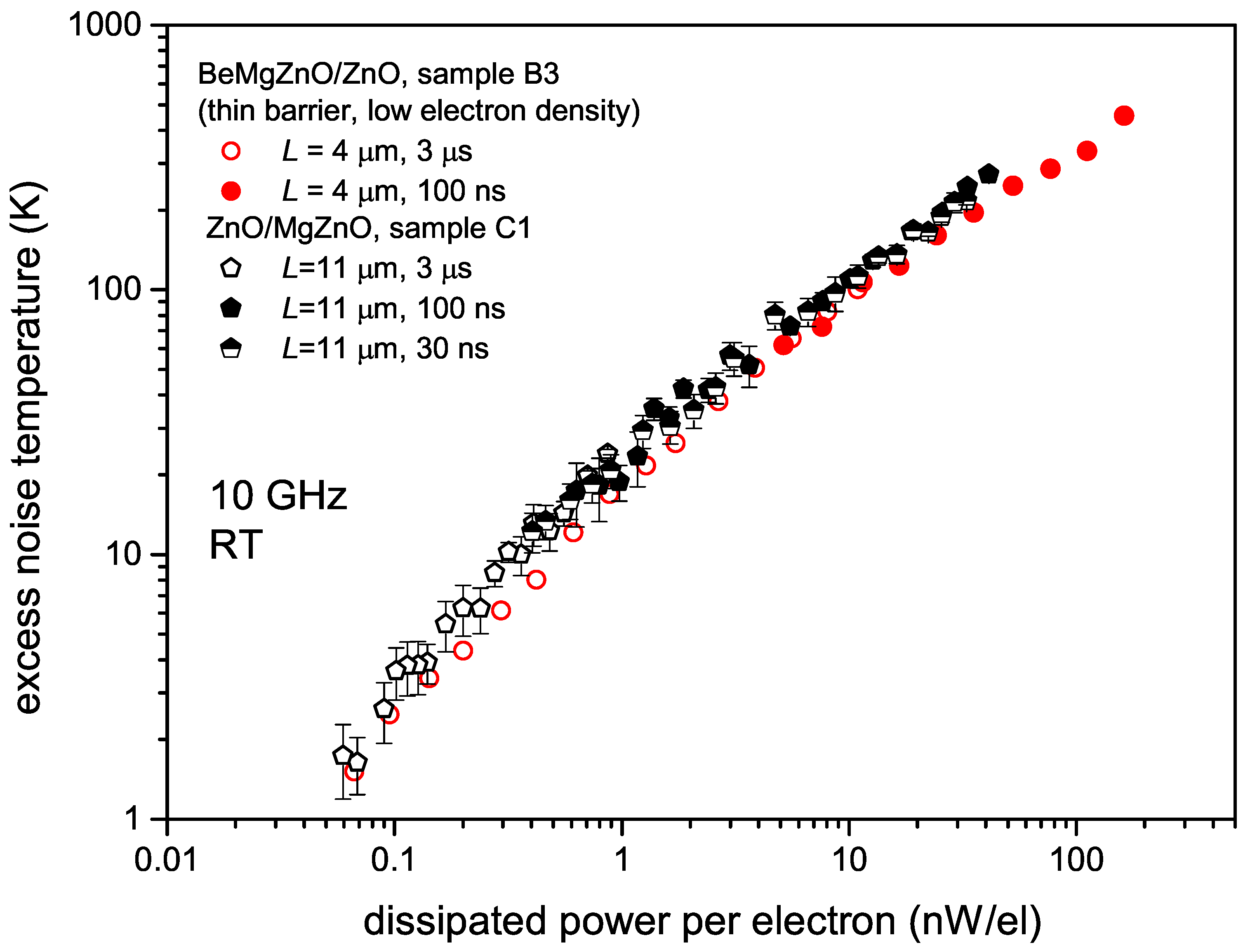
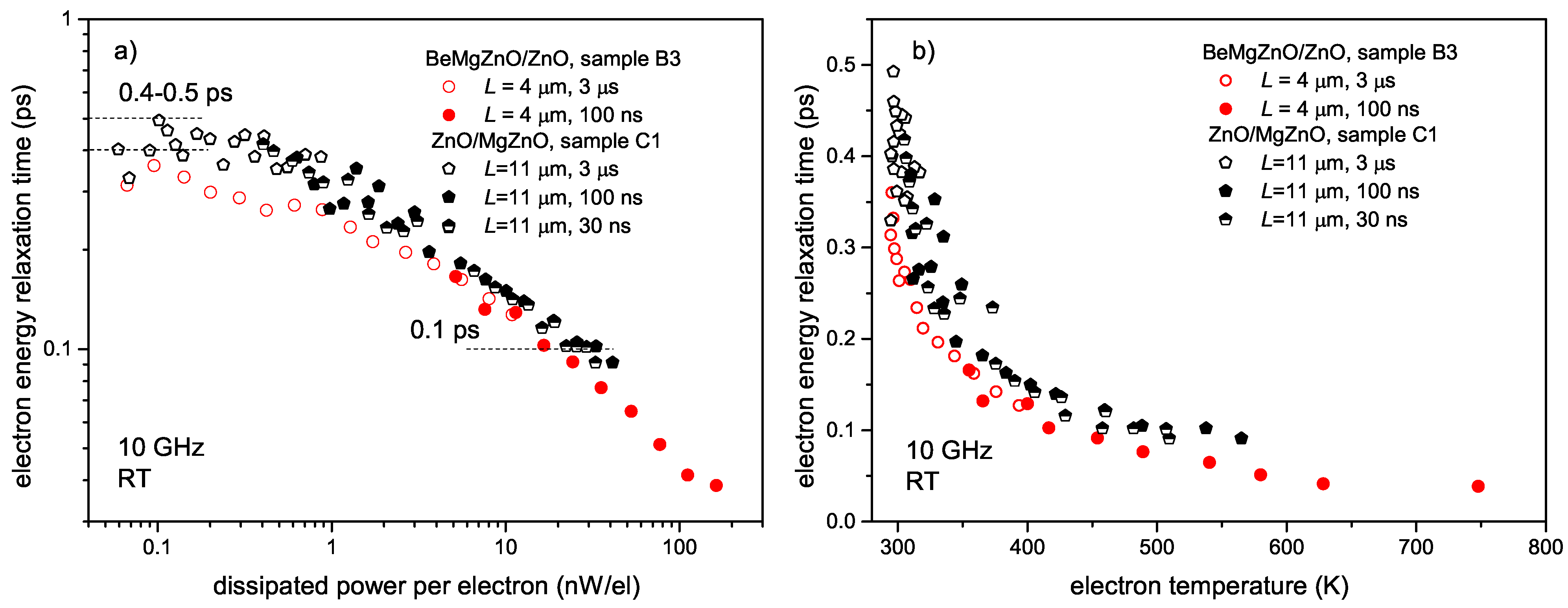
3. Results
4. Discussion
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Albrecht, J.D.; Ruden, P.P.; Limpijumnong, S.; Lambrecht, W.R.L.; Brennan, K.F. High field electron transport properties of bulk ZnO. J. Appl. Phys. 1999, 86, 6864. [Google Scholar] [CrossRef]
- Petti, L.; Münzenrieder, N.; Vogt, C.; Faber, H.; Büthe, L.; Cantarella, G.; Bottacchi, F.; Anthopoulos, T.D.; Tröster, G. Metal Oxide Semiconductor thin-film transistors for flexible electronics. Appl. Phys. Rev. 2016, 3, 021303. [Google Scholar] [CrossRef]
- Hosono, H.; Ueda, K. Transparent Conductive Oxides. In Springer Handbook of Electronic and Photonic Materials; Kasap, P.C.S., Ed.; Springer: Cham, Switzerland, 2017. [Google Scholar] [CrossRef]
- Ellmer, K.; Klein, A.; Rech, B. Transparent Conductive Zinc Oxide: Basics and Applications in Thin Film Solar Cells; Springer: Berlin/Heidelberg, Germany, 2008. [Google Scholar] [CrossRef]
- Mita, A.T.; Ihida, S.; Ségard, B.D.; Cathcart, G.A.; Takahashi, T.; Fujita, H.; Toshiyoshi, H. Review on thin-film transistor technology, its applications, and possible new applications to biological cells. Jpn. J. Appl. Phys. 2016, 55, 04EA08. [Google Scholar] [CrossRef]
- Kumar, A.; Goyal, A.K.; Gupta, N. Review-Thin-Film Transistors (TFTs) for Highly Sensitive Biosensing Applications: A Review. ECS J. Solid State Sci. Technol. 2020, 9, 115022. [Google Scholar] [CrossRef]
- You, H.C.; Wang, C.J. Low-Temperature, Solution-Processed, Transparent Zinc Oxide-Based Thin-Film Transistors for Sensing Various Solvents. Materials 2017, 10, 234. [Google Scholar] [CrossRef] [PubMed]
- Franco, M.A.; Conti, P.P.; Andre, R.S.; Correa, D.S. A review on chemiresistive ZnO gas sensors. Sens. Actuators Rep. 2022, 4, 100100. [Google Scholar] [CrossRef]
- Özgür, Ü.; Avrutin, V.; Morkoç, H. Chapter 16—Zinc Oxide Materials and Devices Grown by Molecular Beam Epitaxy. In Molecular Beam Epitaxy, 2nd ed.; Henini, M., Ed.; Elsevier: Amsterdam, The Netherlands, 2018; pp. 343–375. [Google Scholar] [CrossRef]
- Sasa, S.; Maitani, T.; Furuya, Y.; Amano, T.; Koike, K.; Yano, M.; Inoue, M. Microwave performance of ZnO/ZnMgO heterostructure field effect transistors. Phys. Status Solidi A 2011, 208, 449–452. [Google Scholar] [CrossRef]
- Yabe, T.; Aoki, T.; Higashiyama, Y.; Koike, K.; Sasa, S.; Yano, M.; Gonda, S. Radiation-proof characteristics of ZnO/ZnMgO HFETs. In Proceedings of the 2011 International Meeting for Future of Electron Devices (IMFEDK), Osaka, Japan, 19–20 May 2011. [Google Scholar] [CrossRef]
- Ye, D.; Mei, Z.; Liang, H.; Li, J.; Hou, Y.; Gu, C.; Azarov, A.; Kuznetsov, A.; Hong, W.C.; Lu, Y.; et al. Enhancement-mode ZnO/Mg0.5Zn0.5O HFET on Si. J. Phys. D Appl. Phys. 2014, 47, 255101. [Google Scholar] [CrossRef]
- Bayraktaroglu, B.; Leedy, K.; Neidhard, R. High-Frequency ZnO Thin-Film Transistors on Si Substrates. IEEE Electron. Device Lett. 2009, 30, 946. [Google Scholar] [CrossRef]
- Ding, K.; Ullah, M.B.; Avrutin, V.; Özgür, Ü.; Morkoç, H. Investigation of high density two-dimensional electron gas in Zn-polar BeMgZnO/ZnO heterostructures. Appl. Phys. Lett. 2017, 111, 182101. [Google Scholar] [CrossRef]
- Šermukšnis, E.; Liberis, J.; Matulionis, A. Microwave noise technique for measurement of hot-electron energy relaxation time and hot-phonon lifetime. Lith. J. Phys. 2007, 47, 491. [Google Scholar] [CrossRef]
- Šermukšnis, E.; Liberis, J.; Ramonas, M.; Matulionis, A.; Toporkov, M.; Liu, H.; Avrutin, V.; Özgür, Ü.; H, M. Hot-electron energy relaxation time in Ga-doped ZnO films. J. Appl. Phys. 2015, 117, 065704. [Google Scholar] [CrossRef]
- Yamamoto, A.; Kido, T.; Goto, T.; Chen, Y.; Yao, T.; Kasuya, A. Dynamics of photoexcited carriers in ZnO epitaxial thin films. Appl. Phys. Lett. 1999, 75, 469. [Google Scholar] [CrossRef]
- Li, C.; Feng, D.; Jia, T.; Sun, H.; Li, X.; Xu, S.; Wang, X.; Xu, Z. Ultrafast dynamics in ZnO thin films irradiated by femtosecond lasers. Solid State Commun. 2005, 136, 389. [Google Scholar] [CrossRef]
- Sun, C.K.; Sun, S.Z.; Lin, K.H.; Zhang, K.Y.J.; Liu, H.L.; Liu, S.C.; Wu, J.J. Ultrafast carrier dynamics in ZnO nanorods. Appl. Phys. Lett. 2005, 87, 023106. [Google Scholar] [CrossRef]
- Wen, X.M.; Davis, J.A.; McDonald, D.; Dao, L.V.; Hannaford, P.; Coleman, V.A.; Tan, H.H.; Jagadish, C.; Koike, K.; Sasa, S.; et al. Ultrafast dynamics in ZnO/ZnMgO multiple quantum wells. Nanotechnology 2007, 18, 315403. [Google Scholar] [CrossRef]
- Ou, P.C.; Lin, J.H.; Chang, C.A.; Liu, W.R.; Hsieh, W.F. Thickness effect on ultrafast thermalization of carriers in above-band-gap states in ZnO epitaxial films. J. Phys. D Appl. Phys. 2010, 43, 495103. [Google Scholar] [CrossRef]
- Ou, P.C.; Liu, W.R.; Ton, H.J.; Lin, J.H.; Hsieh, W.F. Ultrafast relaxation and absorption saturation at near exciton resonance in a thin ZnO epilayer. J. Appl. Phys. 2011, 109, 013102. [Google Scholar] [CrossRef]
- Ou, P.C.; Lin, J.H.; Hsieh, W.F. Spectral dependence of transient reflectance in a ZnO epitaxial film at room temperature. Appl. Phys. B 2012, 106, 399. [Google Scholar] [CrossRef]
- Yamamoto, A.; Kido, T.; Goto, T.; Chen, Y.; Yao, T.; Kasuya, A. Time-resolved photoluminescence in ZnO epitaxial thin films studied by up-conversion method. J. Cryst. Growth 2000, 214–215, 308–311. [Google Scholar] [CrossRef]
- Takeda, J.; Jinnouchi, H.; Kurita, S.; Chen, Y.F.; Yao, T. Dynamics of photoexcited high density carriers in ZnO epitaxial thin films. Phys. Stat. Sol. 2002, 229, 877. [Google Scholar] [CrossRef]
- Takeda, J. Femtosecond Dynamics of Photoexcited High Density Carriers in ZnO Epitaxial Thin Films. Nonlinear Opt. 2002, 29, 521. [Google Scholar] [CrossRef]
- Toshine, Y.; Takeda, J.; Ko, H.J.; Yao, T. Conversion of an electron-hole plasma into a high density excitonic state in ZnO epitaxial thin films. Phys. Stat. Sol. 2004, 1, 839. [Google Scholar] [CrossRef]
- Johnson, J.C.; Knutsen, K.P.; Yan, H.; Law, M.; Zhang, Y.; Yang, P.; Saykally, R.J. Ultrafast carrier dynamics in single ZnO nanowire and nanoribbon lasers. Nano Lett. 2004, 4, 197. [Google Scholar] [CrossRef]
- Arai, N.; Takeda, J.; Ko, H.J.; Yao, T. Dynamics of high-density excitons and electron-hole plasma in ZnO epitaxial thin films. J. Lumin. 2006, 119–120, 346. [Google Scholar] [CrossRef]
- Takeda, J.; Arai, N.; Toshine, Y.; Ko, H.J.; Yao, T. Ultrafast dynamics of exciton-exciton and exciton-longitudinal optical-phonon scattering processes in ZnO epitaxial thin films. Jpn. J. Appl. Phys. 2006, 45, 6961. [Google Scholar] [CrossRef]
- Tisdale, W.A.; Muntwiler, M.; Norris, D.J.; Aydil, E.S.; Zhu, X.Y. Electron dynamics at the ZnO (101-0) surface. J. Phys. Chem. 2008, 112, 14682. [Google Scholar] [CrossRef]
- Yang, M.D.; Wu, S.W.; Tong, S.C.; Shu, G.W.; Liu, Y.W.; Shen, J.L.; Lan, S.M.; Wu, C.H.; Huang, Y.H.; Yang, T.N. Hot-electron relaxation in ZnO films. Thin Solid Film. 2011, 519, 3421. [Google Scholar] [CrossRef]
- Ullah, M.B.; Avrutin, V.; Li, S.Q.; Das, S.; Monavarian, M.; Toporkov, M.; Özgür, Ü.; Morkoç, H. Polarity control and residual strain in ZnO epilayers grown by molecular beam epitaxy on (0001) GaN/sapphire. Phys. Status Solidi RRL 2016, 10, 682. [Google Scholar] [CrossRef]
- Ullah, M.B.; Avrutin, V.; Nakagawara, T.; Hafiz, S.; Altuntas, I.; Özgür, Ü.; Morkoç, H. Growth kinetics of O-polar BexMgyZn1-x-yO alloy: Role of Zn to Be and Mg flux ratio as a guide to growth at high temperature. J. Appl. Phys. 2017, 121, 185704. [Google Scholar] [CrossRef]
- Ding, K.; Avrutin, V.; Izyumskaya, N.; Özgür, Ü.; Morkoç, H. Comparative study of BeMgZnO/ZnO heterostructures on c-sapphire and GaN by molecular beam epitaxy. J. Vac. Sci. Technol. A 2020, 38, 023408. [Google Scholar] [CrossRef]
- Keller, S.; Li, H.; Laurent, M.; Hu, Y.; Pfaff, N.; Lu, J.; Brown, D.F.; Fichtenbaum, N.A.; Speck, J.S.; DenBaars, S.P.; et al. Recent progress in metal-organic chemical vapor deposition of (000) N-polar group-III nitrides. Semicond. Sci. Technol. 2014, 29, 113001. [Google Scholar] [CrossRef]
- Ambacher, O.; Smart, J.; Shealy, J.; Weimann, N.; Chu, K.; Murphy, M.; Schaff, W.; Eastman, L.; Dimitrov, R.; Wittmer, L.; et al. Two-dimensional electron gases induced by spontaneous and piezoelectric polarization charges in N- and Ga-face AlGaN/GaN heterostructures. J. Appl. Phys. 1999, 85, 3222–3233. [Google Scholar] [CrossRef]
- Šermukšnis, E.; Liberis, J.; Šimukovič, A.; Matulionis, A.; Ullah, M.B.; Toporkov, M.; Avrutin, V.; Özgür, Ü.; Morkoç, H. Hot-electron noise spectroscopy for HFET channels. In Proceedings of the 2017 International Conference on Noise and Fluctuations (ICNF), Vilnius, Lithuania, 20–23 June 2017; pp. 1–4. [Google Scholar] [CrossRef]
- Ambacher, O.; Majewski, J.; Miskys, C.; Link, A.; Hermann, M.; Eickhoff, M.; Stutzmann, M.; Bernardini, F.; Fiorentini, V.; Tilak, V.; et al. Pyroelectric properties of Al(In)GaN/GaN hetero- and quantum well structures. J. Phys. Condens. Matter 2002, 14, 3399. [Google Scholar] [CrossRef]
- Gonschorek, M.; Carlin, J.F.; Feltin, E.; Py, M.A.; Grandjean, N.; Darakchieva, V.; Monemar, B.; Lorenz, M.; Ramm, G. Two-dimensional electron gas density in Al1-xInxN/AlN/GaN heterostructures (0.03≲x≲0.23). J. Appl. Phys. 2008, 103, 093714. [Google Scholar] [CrossRef]
- Šermukšnis, E.; Jorudas, J.; Šimukovič, A.; Kovalevskij, V.; Kašalynas, I. Self-Heating of Annealed Ti/Al/Ni/Au Contacts to Two-Dimensional Electron Gas in AlGaN/GaN Heterostructures. Appl. Sci. 2022, 12, 11079. [Google Scholar] [CrossRef]
- Šermukšnis, E.; Liberis, J.; Šimukovič, A.; Matulionis, A.; Ding, K.; Avrutin, V.; Özgür, Ü.; Morkoç, H. Self-formation of high-field domain in epitaxial ZnO and its suppression in ZnO/MgZnO heterostructure. Appl. Phys. Lett. 2021, 118, 252102. [Google Scholar] [CrossRef]
- Oh, D.C.; Suzuki, T.; Kim, J.J.; Makino, H.; Hanada, T.; Yao, T.; Ko, H.J. Capacitance-voltage characteristics of ZnO/GaN heterostructures. Appl. Phys. Lett. 2005, 87, 162104. [Google Scholar] [CrossRef]
- Dyson, A.; Ridley, B.K. Negative differential resistance associated with hot phonons. J. Appl. Phys 2012, 112, 063707. [Google Scholar] [CrossRef]
- Matulionis, A. GaN-based two-dimensional channels: Hot-electron fluctuations and dissipation. J. Phys. Condens. Matter 2009, 21, 174203. [Google Scholar] [CrossRef]
- Ridley, B.K. Quantum Processes in Semiconductors; Oxford University Press: Oxford, UK, 2013. [Google Scholar]
- Khurgin, J.; Jena, D. Isotope Engineering of GaN for Boosting Transistor Speeds. In High-Frequency GaN Electronic Devices; Fay, P., Jena, D., Maki, P., Eds.; Springer International Publishing: Cham, Switzerland, 2020; pp. 43–82. [Google Scholar] [CrossRef]
- Leach, J.H.; Wu, M.; Morkoç, H.; Liberis, J.; Šermukšnis, E.; Ramonas, M.; Matulionis, A. Ultrafast decay of hot phonons in an AlGaN/AlN/AlGaN/GaN camelback channel. J. Appl. Phys. 2011, 110, 104504. [Google Scholar] [CrossRef]
- Khurgin, J.; Ding, Y.J.; Jena, D. Hot phonon effect on electron velocity saturation in GaN: A second look. Appl. Phys. Lett. 2007, 91, 252104. [Google Scholar] [CrossRef]
- Khurgin, J.B.; Bajaj, S.; Rajan, S. Elastic scattering by electrons and apparent lifetime of longitudinal optical phonons in gallium nitride. Appl. Phys. Lett. 2015, 107, 262101. [Google Scholar] [CrossRef]
- Zhang, J.Z.; Dyson, A.; Ridley, B.K. Hot electron energy relaxation in lattice-matched InAlN/AlN/GaN heterostructures: The sum rules for electron-phonon interactions and hot-phonon effect. J. Appl. Phys. 2015, 117, 025701. [Google Scholar] [CrossRef]





Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Šermukšnis, E.; Šimukovič, A.; Avrutin, V.; Izyumskaya, N.; Özgür, Ü.; Morkoç, H. Hot-Electron Microwave Noise and Energy Relaxation in (Be)MgZnO/ZnO Heterostructures. Crystals 2024, 14, 75. https://doi.org/10.3390/cryst14010075
Šermukšnis E, Šimukovič A, Avrutin V, Izyumskaya N, Özgür Ü, Morkoç H. Hot-Electron Microwave Noise and Energy Relaxation in (Be)MgZnO/ZnO Heterostructures. Crystals. 2024; 14(1):75. https://doi.org/10.3390/cryst14010075
Chicago/Turabian StyleŠermukšnis, Emilis, Artūr Šimukovič, Vitaliy Avrutin, Natalia Izyumskaya, Ümit Özgür, and Hadis Morkoç. 2024. "Hot-Electron Microwave Noise and Energy Relaxation in (Be)MgZnO/ZnO Heterostructures" Crystals 14, no. 1: 75. https://doi.org/10.3390/cryst14010075
APA StyleŠermukšnis, E., Šimukovič, A., Avrutin, V., Izyumskaya, N., Özgür, Ü., & Morkoç, H. (2024). Hot-Electron Microwave Noise and Energy Relaxation in (Be)MgZnO/ZnO Heterostructures. Crystals, 14(1), 75. https://doi.org/10.3390/cryst14010075





