Thermal Processing Map Study of the GH99 Nickel-Based Superalloy Based on Different Instability Criteria
Abstract
1. Introduction
2. Experimental Materials and Method
3. Result
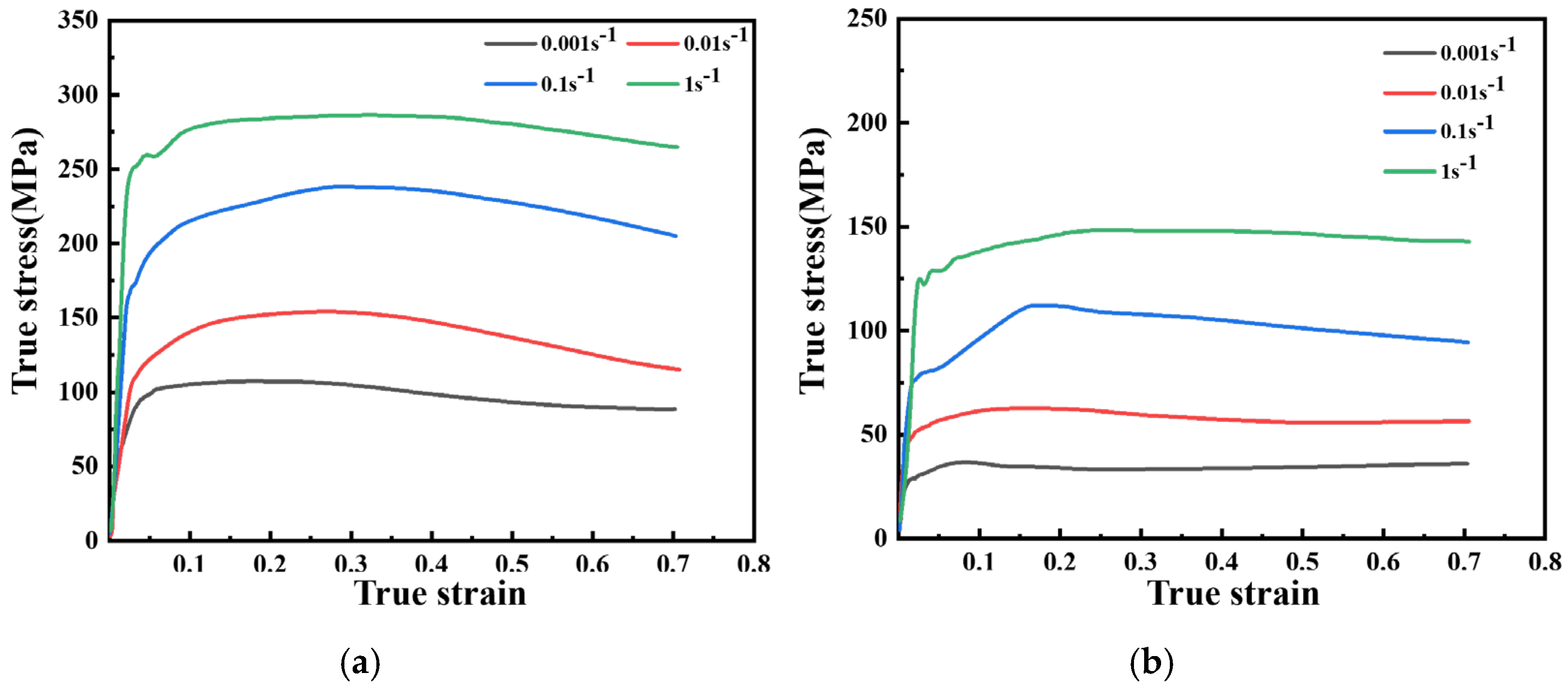
3.1. True Stress-Strain Curve
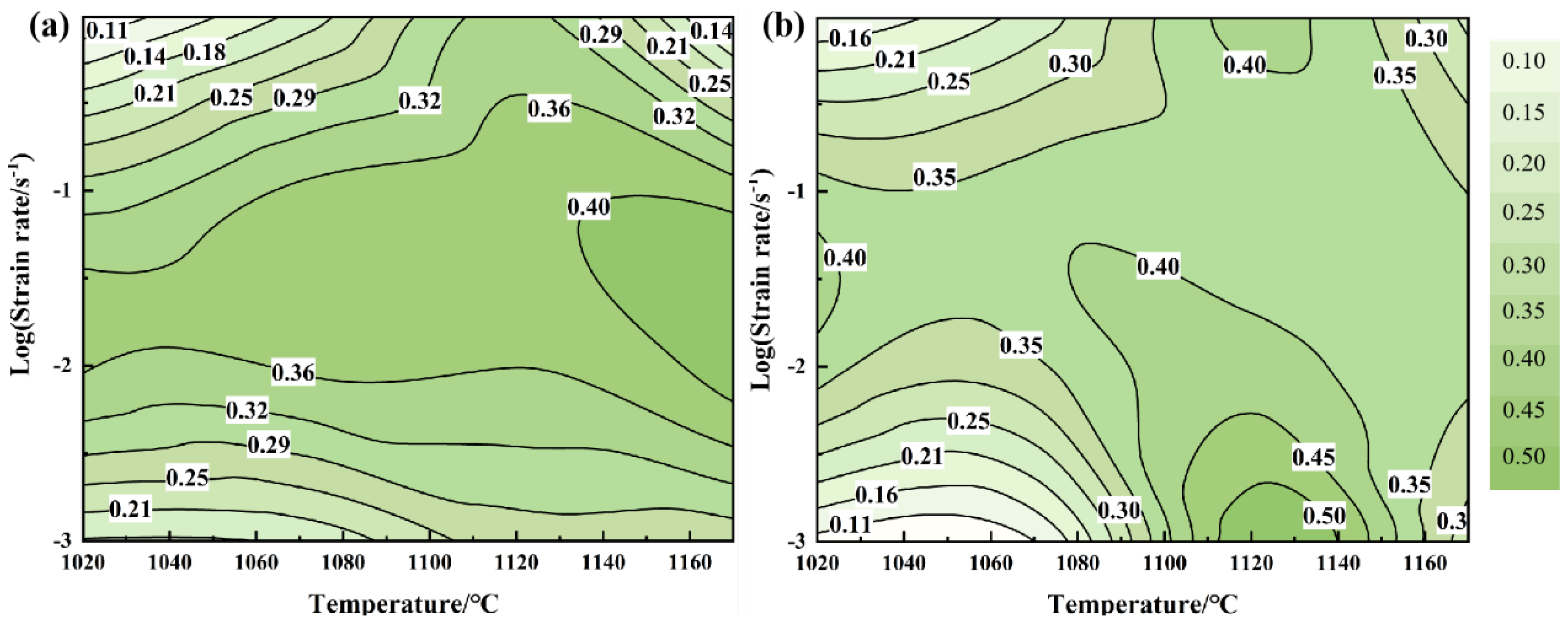
3.2. Establishment of Power Dissipation Diagram
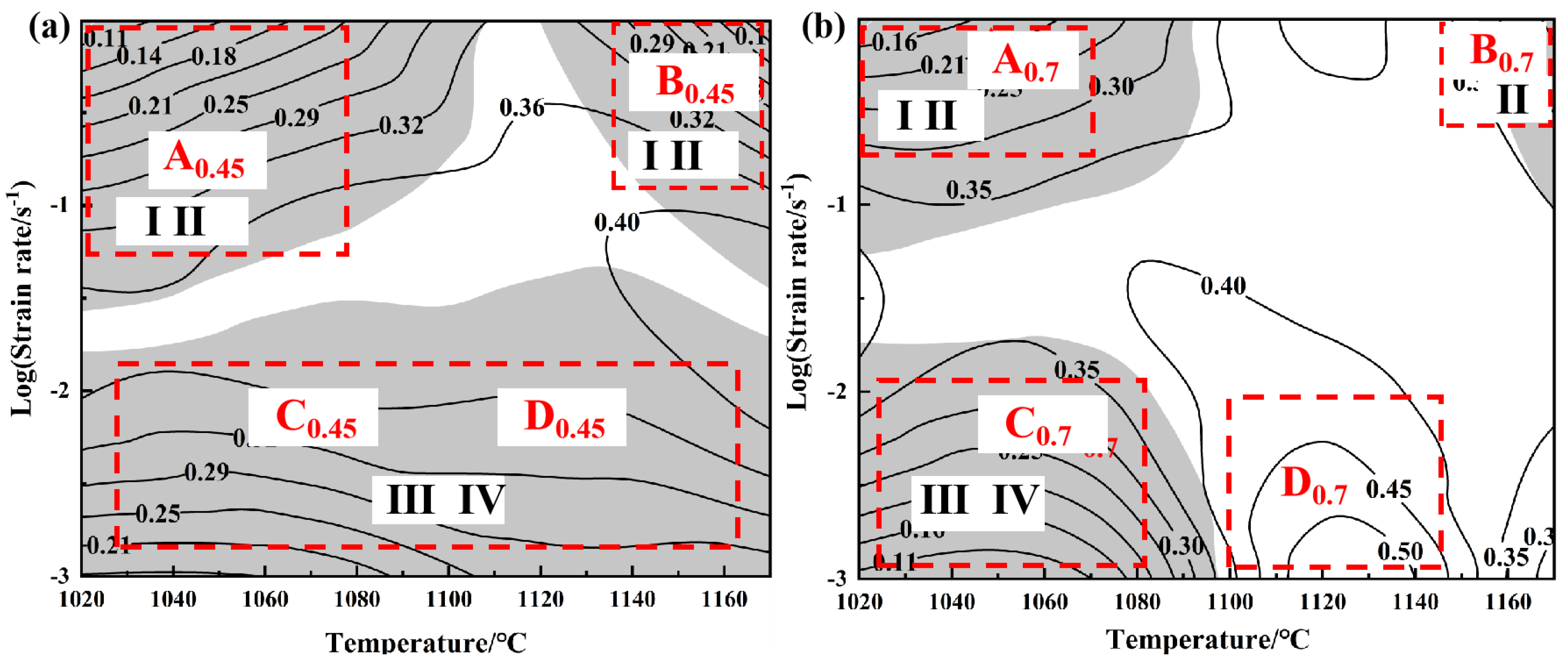
3.3. Thermal Processing Maps Based on Different Instability Criteria
4. Discussion
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Li, H.X.; Wei, H.M.; He, P.; Lin, T.S.; Feng, J.C.; Huang, Y.D. Effects of alloying elements in GH99 superalloy on microstructure evolution of reactive brazing TiAl/GH99 joints. Intermetallics 2013, 34, 69–74. [Google Scholar] [CrossRef]
- Li, W.Q.; Hu, S.P.; Lei, Y.Z.; Lei, Y.; Song, X.G.; Feng, J.C. Interfacial microstructure and mechanical properties of GH99 superalloy and Nb brazed joint using Cu75Pt25 filler. Trans. Nonferrous Met. Soc. China 2020, 30, 2724–2736. [Google Scholar] [CrossRef]
- Hu, Y.L.; Lin, X.; Li, Y.L.; Wang, J.; Zhang, S.Y.; Lu, X.F.; Huang, W.D. Effect of heat treatment on the microstructural evolution and mechanical properties of GH4099 additive-manufactured by directed energy deposition. J. Alloys Compd. 2019, 800, 163–173. [Google Scholar] [CrossRef]
- Zhang, D.; Dong, X.J.; Xu, Y.; Lu, S.Q.; Wei, K.; Huang, L. Dynamic recrystallization mechanism of Ti-6554 alloy during high-temperature deformation. J. Alloys Compd. 2023, 959, 170534. [Google Scholar] [CrossRef]
- Qin, F.C.; Li, Y.T.; Qi, H.P.; Wei, X.J. Microstructure and mechanical properties of as-cast 42CrMo ring blank during hot rolling and subsequent quenching and tempering. J. Mater. Eng. Perform. 2017, 26, 1300–1310. [Google Scholar] [CrossRef]
- Ji, H.C.; Duan, H.L.; Li, Y.G.; Li, W.D.; Huang, X.M.; Pei, W.C.; Lu, Y.H. Optimization the working parameters of as-forged 42CrMo steel by constitutive equation-dynamic recrystallization equation and processing maps. J. Mater. Res. Technol. 2020, 9, 7210–7224. [Google Scholar] [CrossRef]
- Jiao, Y.X.; Qi, Q.Q.; Gong, Y.M.; Gao, Y.F.; Chen, H.Q.; Chen, F.; Zhou, F.W.; Li, X.X. Research on hot deformation behavior and microstructure evolution mechanism of GH4169 superalloy. Mater. Today Commun. 2024, 40, 109958. [Google Scholar] [CrossRef]
- Chen, L.; Zhang, B.; Yang, Y.; Zhao, T.L.; Xu, Y.; Wang, Q.; Zan, B.; Cai, J.; Wang, K.S.; Chen, X. Evolution of hot processing map and microstructure of as-forged nickel-based superalloy during hot deformation. J. Mater. Res. Technol. 2023, 24, 7638–7653. [Google Scholar] [CrossRef]
- Cai, D.Y.; Xiong, L.Y.; Liu, W.C.; Sun, G.D.; Yao, M. Characterization of hot deformation behavior of a Ni-base superalloy using processing map. Mater. Des. 2009, 30, 921–925. [Google Scholar] [CrossRef]
- Murty, S.V.S.N.; Rao, B.N. On the development of instability criteria during hotworking with reference to IN 718. Mater. Sci. Eng. A 1998, 254, 76–82. [Google Scholar] [CrossRef]
- Murty, S.V.S.N.; Rao, B.N.; Kashyap, B.P. Improved ductile fracture criterion for cold forming of spheroidised steel. J. Mater. Process. Technol. 2004, 147, 94–101. [Google Scholar] [CrossRef]
- Somani, M.C.; Muraleedharan, K.; Prasad, Y.V.R.K.; Singh, V. Mechanical processing and microstructural control in hot working of hot isostatically pressed P/M IN-100 superalloy. Mater. Sci. Eng. A 1998, 245, 88–99. [Google Scholar] [CrossRef]
- Prasad, Y.V.R.K.; Gegel, H.L.; Doraivelu, S.M.; Malas, J.C.; Morgan, J.T.; Lark, K.A.; Barker, D.R. Modeling of dynamic material behavior in hot deformation: Forging of Ti-6242. Metall. Trans. A 1984, 15, 1883–1892. [Google Scholar] [CrossRef]
- Malas, J.C.; Seetharaman, V. Using material behavior models to develop process control strategies. JOM 1992, 44, 8–13. [Google Scholar] [CrossRef]
- Wu, Y.S.; Wang, C.S.; Qin, X.Z.; Zhou, L.Z. The Role of Strain and Dynamic Recrystallization During Hot Deformation of a Fe-Ni-Cr-Based Alloy. Adv. Eng. Mater. 2022, 24, 2200250. [Google Scholar] [CrossRef]
- Tan, G.; Li, H.Z.; Wang, Y.; Yang, L.; Qiao, S.C.; Huang, Z.Q.; Liu, M.X. Hot working characteristics of HEXed PM nickel-based superalloy during hot compression. Trans. Nonferrous Met. Soc. China 2020, 30, 2709–2723. [Google Scholar] [CrossRef]
- Wang, Y.L.; Li, Y.; Zhang, H.; Yang, J.L.; Ma, X.D.; Chen, Q.; Guo, J.Z. Quasi-static hot deformation behavior of a novel third-generation Ni-based powder metallurgy superalloy. Proc. Inst. Mech. Eng. Part L J. Mater. Des. Appl. 2020, 235, 743–751. [Google Scholar] [CrossRef]
- Babu, K.A.; Mozumder, Y.H.; Saha, R.; Mandal, S.A. Systematic Assessment of Various Stability/Instability Criteria in Predicting the Hot Deformation-Related Instabilities in Super-304H Stainless Steels. J. Mater. Eng. Perform. 2019, 28, 4718–4730. [Google Scholar] [CrossRef]
- Ma, X.; Zeng, W.D.; Wang, K.X.; Lai, Y.L.; Zhou, Y.G. The investigation on the unstable flow behavior of Ti17 alloy in α+β phase field using processing map. Mater. Sci. Eng. A 2012, 550, 131–137. [Google Scholar] [CrossRef]
- Li, J.Q.; Liu, J.; Cui, Z.S. Hot Deformation Stability of Extruded AZ61 Magnesium Alloy Using Different Instability Criteria. Acta Metall. Sin. 2015, 28, 1364–1372. [Google Scholar] [CrossRef][Green Version]
- Yang, P.R.; Liu, C.X.; Guo, Q.Y.; Liu, Y.C. Variation of activation energy determined by a modified Arrhenius approach: Roles of dynamic recrystallization on the hot deformation of Ni-based superalloy. J. Mater. Sci. Technol. 2021, 72, 162–171. [Google Scholar] [CrossRef]
- Tan, L.M.; Li, Y.P.; He, G.A.; Liu, F.; Nie, Y.; Jiang, L. Optimized hot workability of a powder metallurgy nickel-base superalloy. Mater. Charact. 2019, 147, 340–352. [Google Scholar] [CrossRef]
- Jia, L.; Cui, H.; Yang, S.F.; Lv, S.M.; Xie, X.F.; Qu, J.L. Hot deformation behavior and flow stress modeling of coarse-grain nickel-base GH4151 superalloy ingot materials in cogging. J. Mater. Res. Technol. 2023, 26, 6652–6671. [Google Scholar] [CrossRef]
- Prasad, Y.; Seshacharyulu, T. Processing maps for hot working of titanium alloys. Mater. Sci. Eng. A 1998, 243, 82–88. [Google Scholar] [CrossRef]
- Yang, X.Z.; Zhang, L.C.; Shi, Y.S.; Yu, S.F.; Hua, W.L. Effect of niobium addition on hot deformation behaviors of medium carbon ultra-high strength steels. J. Wuhan Univ. Technol. 2017, 32, 162–172. [Google Scholar] [CrossRef]
- Prasad, Y. Processing maps: A status report. J. Mater. Eng. Perform. 2003, 12, 638–645. [Google Scholar] [CrossRef]
- Li, C.M.; Huang, L.; Zhao, M.J.; Guo, S.Q.; Su, Y.; Li, J.J. Characterization of hot workability of Ti-6Cr-5Mo-5V-4Al alloy based on hot processing map and microstructure evolution. J. Alloys Compd. 2022, 905, 164161. [Google Scholar] [CrossRef]
- Guo, S.L.; Wu, S.S.; Guo, J.T.; Shen, Y.Z.; Zhang, W. An investigation on the hot deformation behavior and processing maps of Co-Ni-Cr-W-based superalloy. J. Manuf. Process. 2022, 74, 100–111. [Google Scholar] [CrossRef]
- Murty, S.V.S.; Rao, B.N. On the flow localization concepts in the processing maps of titanium alloy Ti-24Al-20Nb. J. Mater. Process. Technol. 2000, 104, 103–109. [Google Scholar] [CrossRef]
- Murty, S.V.S.; Rao, B.N. On the hot working characteristics of INCONEL alloy MA 754 using processing maps. Scand. J. Metall. 2003, 29, 146–150. [Google Scholar] [CrossRef]
- Murty, S.V.S.; Rao, B.N.; Kashyap, B.P. On the hot working characteristics of 6061Al-SiC and 6061-Al2O3 particulate reinforced metal matrix composites. Compos. Sci. Technol. 2003, 63, 119–135. [Google Scholar] [CrossRef]
- Murty, S.V.S.; Rao, B.N.; Kashyap, B.P. Identification of flow instabilities in the processing maps of AISI 304 stainless steel. J. Mater. Process. Technol. 2005, 166, 268–278. [Google Scholar] [CrossRef]
- Zhao, X.; Lv, J.J.; Liu, H.L.; Zheng, L. Hot deformation behavior of a novel Ni-W-Co high-density Ni-based alloy with ultra-high W content. J. Alloys Compd. 2023, 950, 169937. [Google Scholar] [CrossRef]
- Kareem, S.A.; Anaele, J.U.; Aikulola, E.O.; Olanrewaju, O.F.; Omiyale, B.O.; Bodunrin, M.O.; Alaneme, K.K. Hot deformation behaviour, constitutive model description, and processing map analysis of superalloys: An overview of nascent developments. J. Mater. Res. Technol. 2023, 26, 8624–8669. [Google Scholar] [CrossRef]
- Zhang, Z.W.; Liu, R.X.; Li, D.Y.; Peng, Y.H.; Zhou, G.W.; Jia, Z.H.; Ma, W.T. Investigation on deformation behaviors and dynamic recrystallization mechanism of spray formed Al-Zn-Mg-Cu alloy under hot compression. J. Mater. Res. Technol. 2024, 28, 4401–4416. [Google Scholar] [CrossRef]
- Tian, Y.H.; Zhang, P.; Zhao, G.H.; Li, H.Y.; Ma, L.F.; Li, J. A systematic study on thermo-mechanical behavior, processing maps and recrystallization mechanism of Incoloy825 superalloy during hot compression. J. Mater. Res. Technol. 2024, 28, 4551–4566. [Google Scholar] [CrossRef]




| Cr (17.0–20.0) | Co (5.0–8.0) | W (5.0–7.0) | Mo (3.5–4.5) | Al (1.7–2.4) | Ti (1.0–1.5) | Fe (≤2.0) | C (≤0.08) | Ni |
|---|---|---|---|---|---|---|---|---|
| 18.30 | 6.40 | 5.90 | 4.02 | 2.19 | 1.16 | 0.24 | 0.045 | Bal. |
| Instability Criteria | Rheological Instability Range (0.45 Strain) | Rheological Instability Range (0.7 Strain) |
|---|---|---|
| Prasad | 1020 °C–1085 °C, 0.05 s−1–1 s−1 1140 °C–1170 °C, 0.06 s−1–1 s−1 | 1020 °C–1080 °C, 0.01 s−1–1 s−1 |
| Murty | 1020 °C–1150 °C, 0.028 s−1–1 s−1 1120 °C–1170 °C, 0.028 s−1–1 s−1 | 1020 °C–1090 °C, 0.056 s−1–1 s−1 1155 °C–1170 °C, 0.1 s−1–1 s−1 |
| Gegel | 1020 °C–1140 °C, 0.001 s−1–0.008 s−1 | 1020 °C–1063 °C, 0.001 s−1–0.007 s−1 |
| Malas | 1020 °C–1170 °C, 0.001 s−1–0.021 s−1 | 1020 °C–1097 °C, 0.001 s−1–0.018 s−1 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Peng, Y.; Ma, X.; Jiang, X.; Zhou, G.; Zhang, H.; Zhang, S.; Chen, L. Thermal Processing Map Study of the GH99 Nickel-Based Superalloy Based on Different Instability Criteria. Crystals 2024, 14, 869. https://doi.org/10.3390/cryst14100869
Peng Y, Ma X, Jiang X, Zhou G, Zhang H, Zhang S, Chen L. Thermal Processing Map Study of the GH99 Nickel-Based Superalloy Based on Different Instability Criteria. Crystals. 2024; 14(10):869. https://doi.org/10.3390/cryst14100869
Chicago/Turabian StylePeng, Yuhan, Xin Ma, Xueyu Jiang, Ge Zhou, Haoyu Zhang, Siqian Zhang, and Lijia Chen. 2024. "Thermal Processing Map Study of the GH99 Nickel-Based Superalloy Based on Different Instability Criteria" Crystals 14, no. 10: 869. https://doi.org/10.3390/cryst14100869
APA StylePeng, Y., Ma, X., Jiang, X., Zhou, G., Zhang, H., Zhang, S., & Chen, L. (2024). Thermal Processing Map Study of the GH99 Nickel-Based Superalloy Based on Different Instability Criteria. Crystals, 14(10), 869. https://doi.org/10.3390/cryst14100869







