Crystallization Kinetics of Lithium Carbonate in a Continuous Stirred-Tank Crystallizer
Abstract
:1. Introduction
2. Determination of Kinetic Data
3. Relative Supersaturation
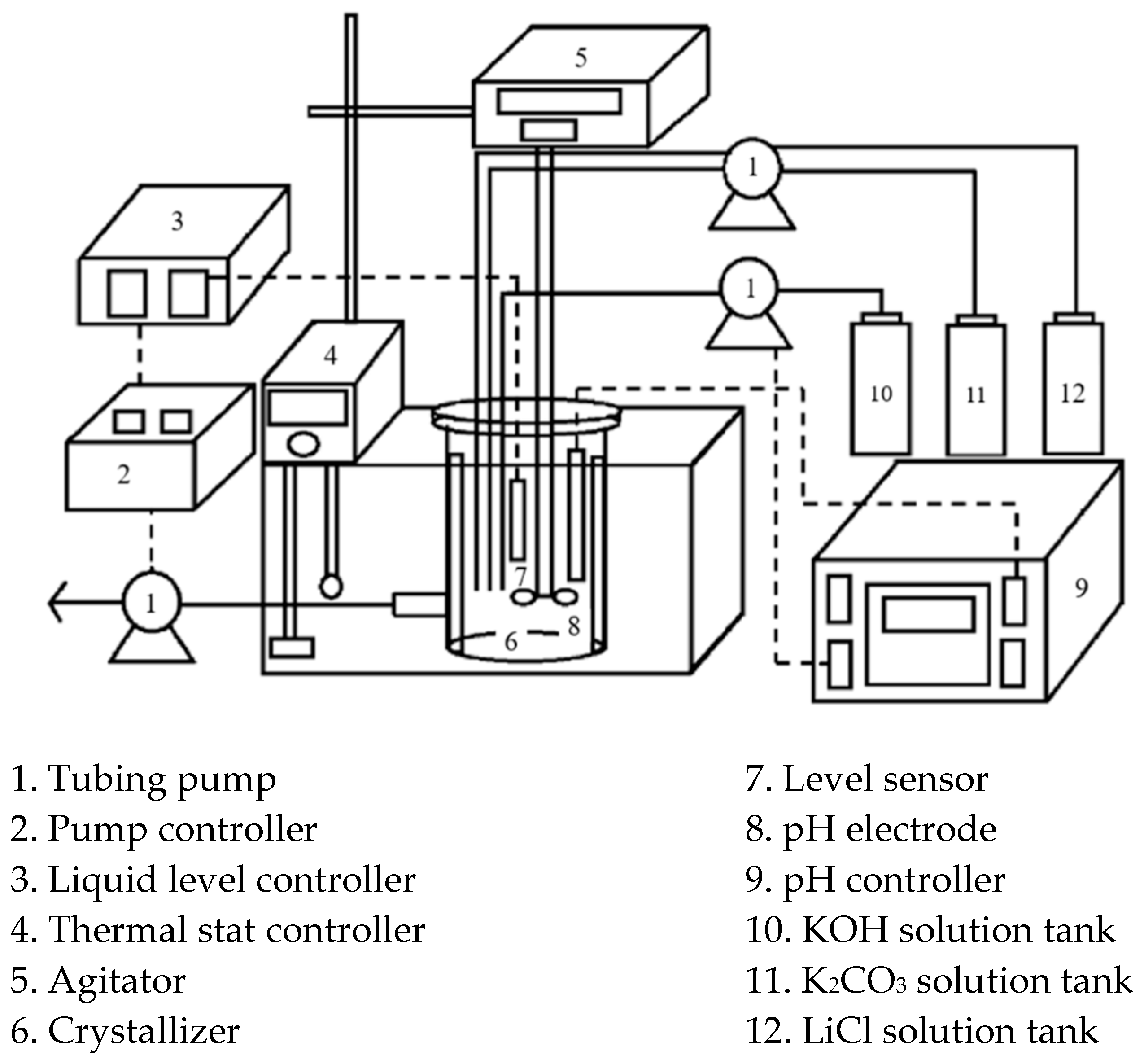
4. Experimental Features
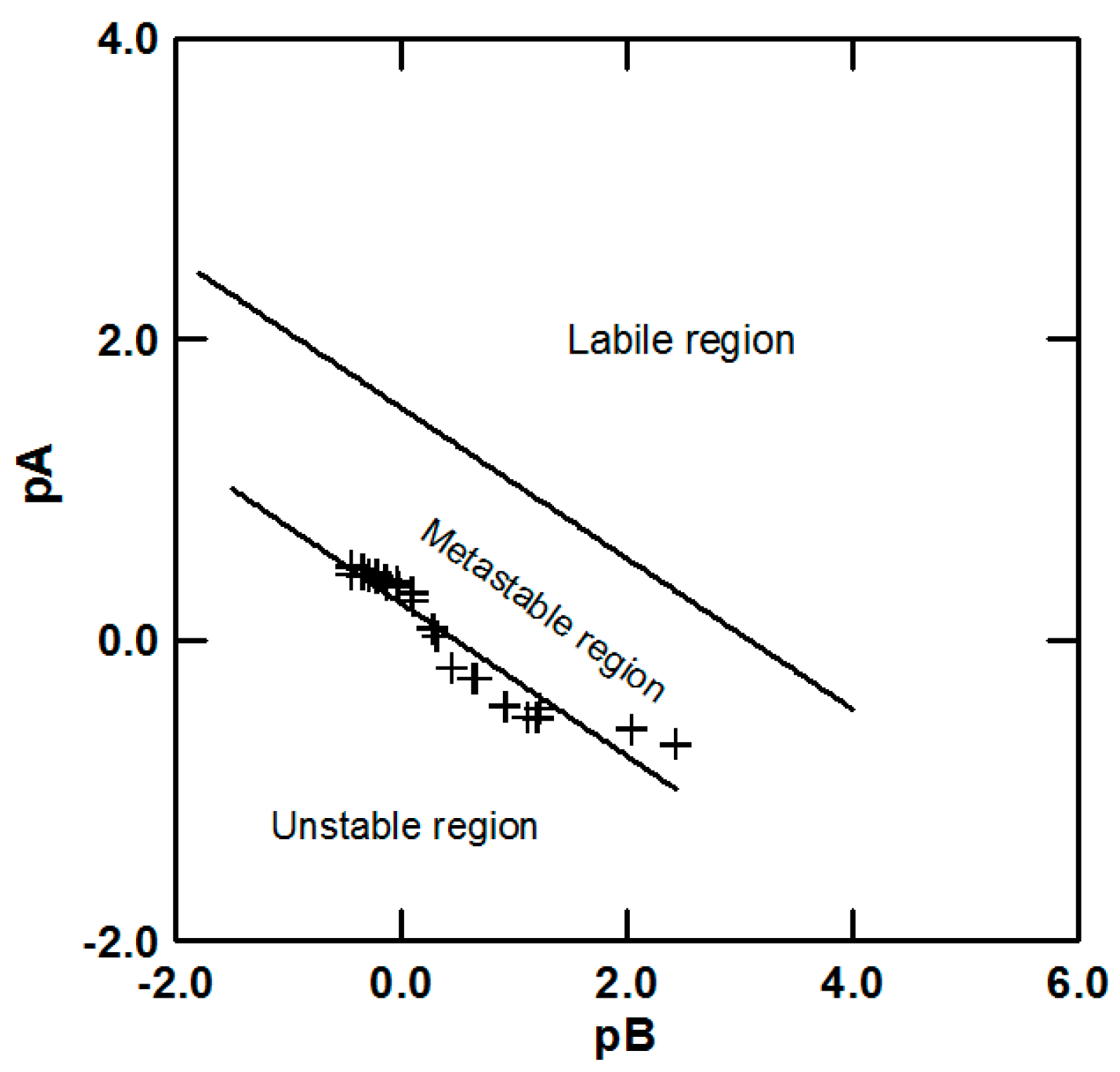
4.1. Determination of Metastable Region
4.2. Crystallization Experiments
5. Result and Discussion
5.1. Metastable Region of Lithium Carbonate
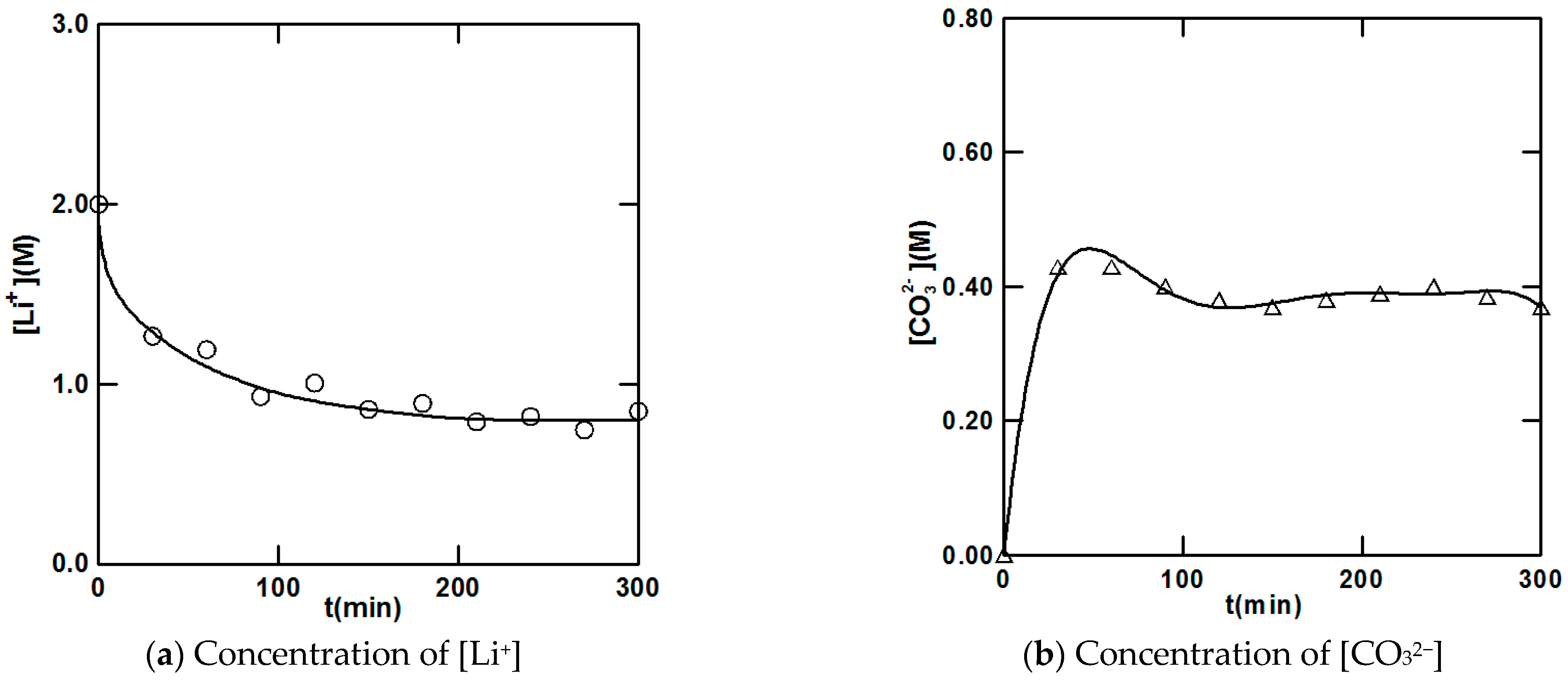
5.2. Crystallization Kinetic Data
5.3. Relative Supersaturation Data
5.4. Growth Kinetics
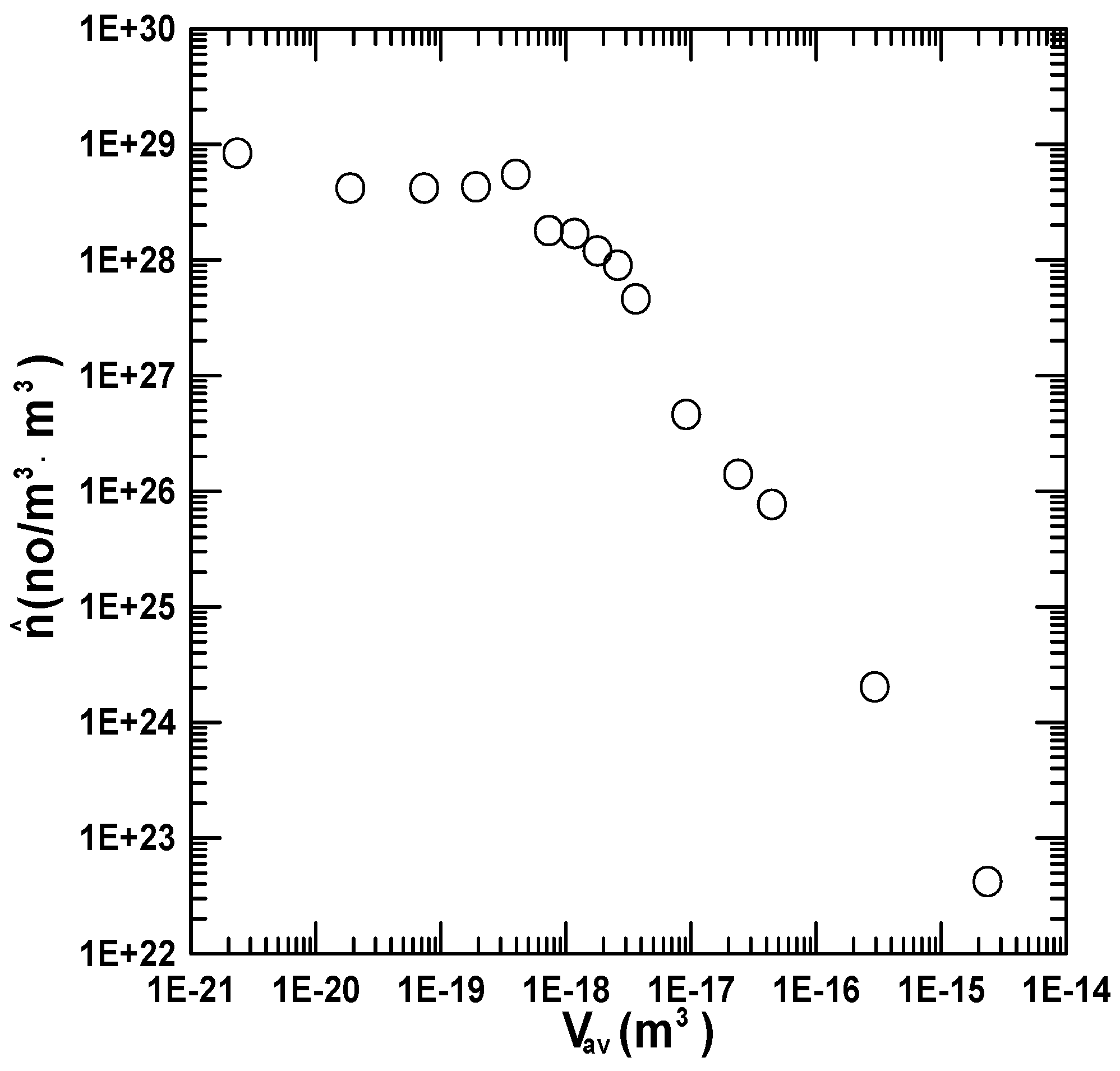
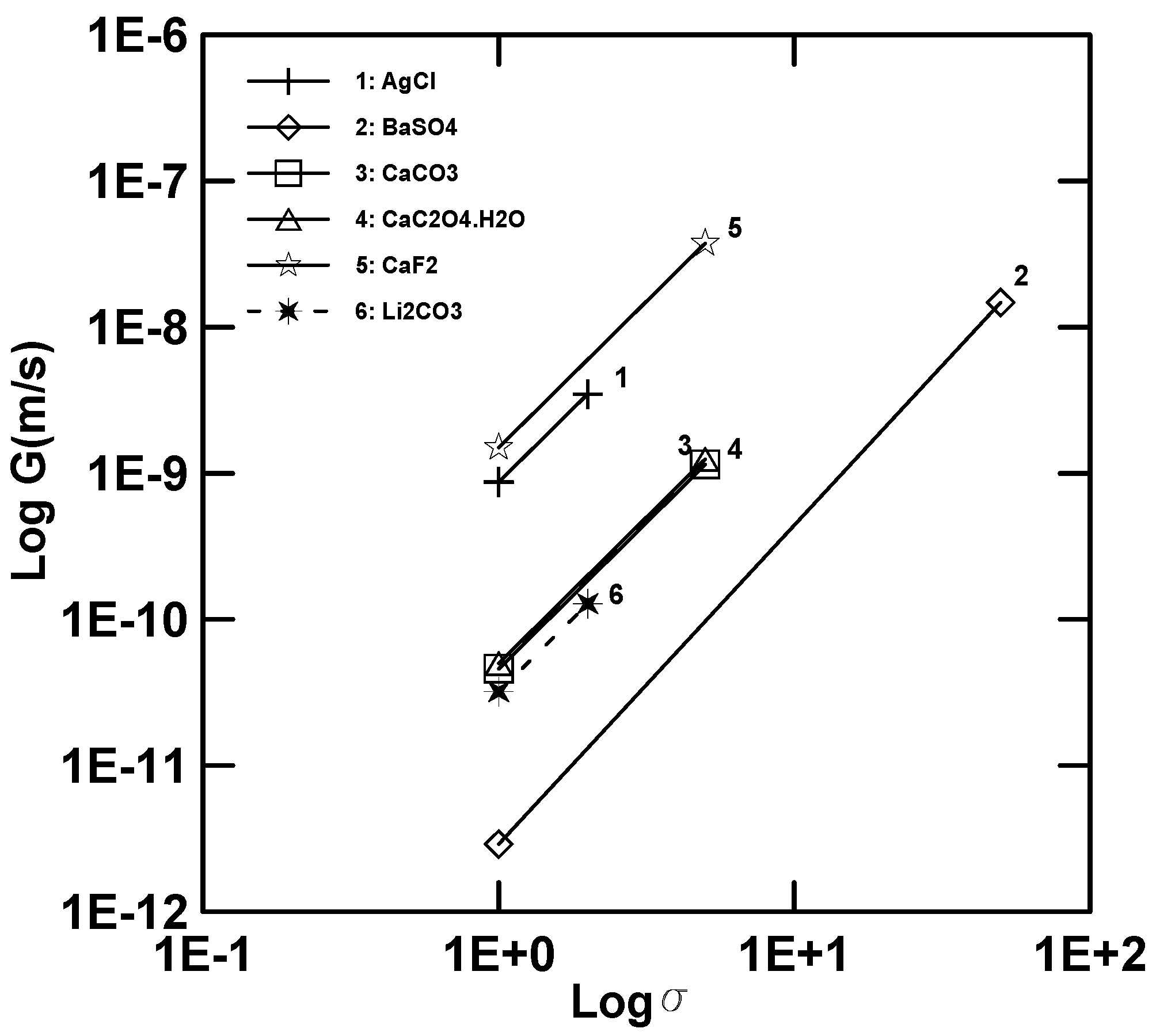
5.5. Nucleation Kinetics
5.6. Agglomeration
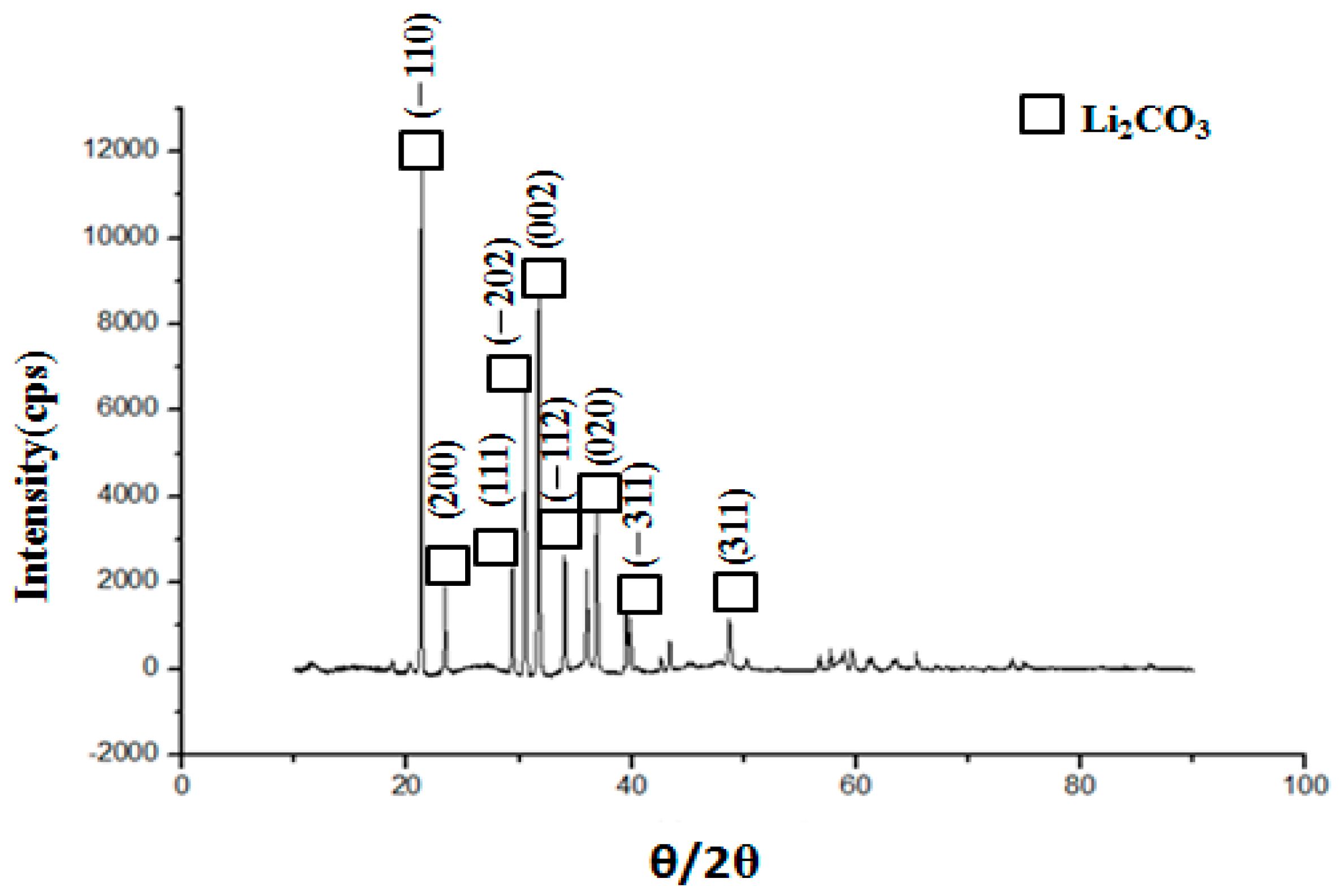
5.7. Morphology of Lithium Carbonate
6. Conclusions
Supplementary Materials
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Battaglia, G.; Berkemeyer, L.; Cipollina, A.; Cortina, J.L.; de Labastida, M.F.; Rodriguez, J.L.; Winter, D. Recovery of lithium carbonate from dilute Li-rich brine via homogenous and heterogeneous precipitation. Ind. Eng. Chem. Res. 2022, 61, 13589–13602. [Google Scholar] [CrossRef] [PubMed]
- Di Maria, A.; Elghoul, Z.; Van Acker, K. Environmental assessment of an innovative lithium production process. Procedia CIRP 2022, 105, 672–677. [Google Scholar] [CrossRef]
- Gao, W.; Zhang, X.; Zheng, X.; Lin, X.; Cao, H.; Zhang, Y.; Sun, Z. Lithium carbonate recovery from cathode scrap of spent lithium-ion battery: A closed-loop process. Environ. Sci. Technol. 2017, 51, 1662–1669. [Google Scholar] [CrossRef] [PubMed]
- Rouquette, L.M.J.; Lemaître, T.; Vieceli, N.; Petranikova, M. Intensification of lithium carbonation in the thermal treatment of spent EV Li-ion batteries via waste utilization and selective recovery by water leaching. Resour. Conserv. Recycl. Adv. 2023, 17, 200125. [Google Scholar] [CrossRef]
- Zhao, C.; Zhang, Y.; Cao, H.; Zheng, X.; Van Gerven, T.; Hu, Y.; Sun, Z. Lithium carbonate recovery from lithium-containing solution by ultrasound assisted precipitation. Ultrason. Sonochem. 2019, 52, 484–492. [Google Scholar] [CrossRef]
- Chen, X.; Luo, C.; Zhang, J.; Kong, J.; Zhou, T. Sustainable recovery of metals from spent lithium-ion batteries: A green process. ACS Sustain. Chem. Eng. 2015, 3, 3104–3113. [Google Scholar] [CrossRef]
- Xu, Z.; Zhang, H.; Wang, R.; Gui, W.; Liu, G.; Yang, Y. System and direct production of battery-grade lithium carbonate from a saline lake. Ind. Eng. Chem. Res. 2014, 20, 3121–3133. [Google Scholar]
- Swain, B. Recovery and recycling of lithium: A review. Sep. Purif. Technol. 2017, 172, 388–403. [Google Scholar] [CrossRef]
- Zhang, P.W.; Yokoyama, T.; Itabashi, O.; Suzuki, T.M.; Inoue, K. Hydrometallurgical process for recovery of metal values from spent lithium-ion secondary batteries. Hydrometallurgy 1998, 47, 259–271. [Google Scholar] [CrossRef]
- Nayl, A.A.; Elkhashab Badawy, S.M.; El-Khateeb, M.A. Acid leaching of mixed spent Li-ion batteries. Arab. J. Chem. 2017, 10, s3632–s3639. [Google Scholar] [CrossRef]
- Han, B.; Porvali, A.; Lundstrom, M.; Louhi-Kultanen, M. Lithium recovery by precipitation from impure solution—Lithium ion battery waste. Chem. Eng. Technol. 2018, 41, 1205–1210. [Google Scholar] [CrossRef]
- Meng, F.; McNeice, J.; Zadeh, S.S.; Ghahreman, A. Review of lithium production and recovery from minerals, brines, and lithium-ion batteries. Miner. Process. Extr. Metall. Rev. 2021, 42, 123–141. [Google Scholar] [CrossRef]
- Zheng, H.; Dong, T.; Sha, Y.; Jiang, D.; Zhang, H.; Zhang, S. Selective extraction of lithium from spent lithium batteries by functional ionic liquid. ACS Sustain. Chem. Eng. 2012, 9, 7022–7029. [Google Scholar] [CrossRef]
- Xu, Z.-G.; Sun, S.-Y. Preparation of battery-grade lithium carbonate with lithium-containing desorption solution. Metals 2021, 11, 1490. [Google Scholar] [CrossRef]
- Cai, W.; Chen, R.; Yang, Y.; Yi, M.; Xiang, L. Removal of SO42− from Li2CO3 by recrystallization in Na2CO3 solution. Crystals 2018, 8, 19. [Google Scholar] [CrossRef]
- Mendieta-George, D.; Pérez-Garibay, R.; Solís-Rodríguez, R.; Rendón Angeles, J.C. Advantages of pH and Temperature Control in the Carbonation Stage for Li2CO3 Production with Sulphated Liquors. ChemistrySelect 2021, 6, 9517–9526. [Google Scholar] [CrossRef]
- Han, B.; Louhi-Kultanen, M. Lithium carbonate precipitation by homogeneous and heterogeneous reactive crystallization. Hydrometall 2020, 195, 105386. [Google Scholar] [CrossRef]
- King, H.E.; Salisbury, A.; Huijsmans, J.; Dzade, N.Y.; Plümper, O. Influence of inorganic solution components on lithium carbonate crystal growth. Cryst. Growth Des. 2019, 19, 6994–7006. [Google Scholar] [CrossRef]
- Yang, W.; Zhou, J.L.; Dai, I.; Zhou, L.; Zhang, M.; Xie, C.; Hao, H.; Hou, B.; Bao, Y.; Yin, Q. Crystallization of lithium carbonate from aqueous solution: New insights into crystal agglomeration. Ind. Eng. Chem. Res. 2019, 58, 18448–18455. [Google Scholar] [CrossRef]
- Wang, J.; Hu, H. Microbubble-assisted pressure carbonation for preparation of high purity lithium carbonate. J. Mater. Res. Technol. 2020, 9, 9498–9505. [Google Scholar] [CrossRef]
- Klapal, F.R. Precipitation of Lithium Carbonate in a Gas Bubble Column with Carbon Dioxide. Diplom-Ingenieur in the. Master’s Program, Chemistry and Chemical Technology; Master’s Thesis, Johannes Kepler University Linz, Linz, Austria, August 2022. [Google Scholar]
- Rigopoulos, S.; Jones, A. Modeling of semibatch agglomerative gas-liquid precipitation of CaCO3 in a bubble column reactor. Ind. Eng. Chem. Res. 2003, 42, 6567–6575. [Google Scholar] [CrossRef]
- Matsumoto, M.; Morita, Y.; Yoshinaga, M.; Hirose, S.; Onoe, K. Reactive crystallization of lithium carbonate nanoparticles by microwave irritation of aqueous solution containing CO2 microbubbles. J. Chem. Eng. Jpn. 2009, 42, s242–s248. [Google Scholar] [CrossRef]
- Sun, Y.; Song, X.; Wang, J.; Yu, J. Preparation of Li2CO3 by gas-liquid reactive crystallization of LiOH and CO2. Cryst. Res. Technol. 2012, 47, 437–442. [Google Scholar] [CrossRef]
- Sun, Y.Z.; Song, X.F.; Jin, M.M.; Jin, W.; Yu, J.G. Gas–liquid reactive crystallization of lithium carbonate by a falling film column. Ind. Eng. Chem. Res. 2013, 52, 17598–17606. [Google Scholar] [CrossRef]
- Tian, M.; Wang, Z.; Cao, J.; Guo, J.; Gong, X. Insight into lithium carbonate crystallization in the mild reaction system LiCl-NH3· H2O-CO2 by stabilizing the solution with NH3 H2O. J. Cryst. Growth 2019, 520, 46–55. [Google Scholar] [CrossRef]
- Zhou, Z.; Liang, F.; Qin, W.; Fei, W. Coupled reaction and solvent extraction process to form Li2CO3: Mechanism and product characterization. AIChE J. 2014, 60, 282–288. [Google Scholar] [CrossRef]
- Chen, P.C.; Liu, S.M.; Jang, C.J.; Hwang, R.C.; Yang, Y.L.; Lee, J.S.; Jang, J.S. Interpretation of gas-liquid reactive crystallization data using a size-independent agglomeration model. J. Crystal Growth 2003, 257, 333–343. [Google Scholar] [CrossRef]
- Schnebelen, M.; Mozet, K.; Jakob, A.; Sy, D.; Plasari, E.; Muhr, H. Agglomeration Mechanisms and Kinetics during the Carbonation of a Suspension of Lime in a Pilot Batch Reactor. Cryst. Struct. Theory Appl. 2015, 4, 35–46. [Google Scholar] [CrossRef]
- Pascual, G.K.; Donnellan, P.; Glennon, B.; Wood, B.; Jones, R.C. Design and optimization of the single-stage continuous mixed suspension−mixed product removal crystallization of 2-Chloro-N-(4-methylphenyl) propenamide. ACS Omega 2022, 7, 13676–13686. [Google Scholar] [CrossRef]
- Jiang, M.; Braatz, R.D. Designs of continuous-flow pharmaceutical crystallizers: Developments and practice. CrystEngComm 2019, 21, 3534. [Google Scholar] [CrossRef]
- Tavare, N.S.; Patwardhan, A.V. Agglomeration in a continuous MSMPR crystallizer. AIChE J. 1992, 38, 377–384. [Google Scholar] [CrossRef]
- Randolph, A.O.; Larson, M.A. Theory of Particulate Processes, 2nd ed.; Academic Press, Inc.: New York, NY, USA, 1988. [Google Scholar]
- Sohnel, O.; Garside, J. Precipitation: Basic Principles and Industrial Applications; Butterworth-Heinemann Ltd.: Oxford, UK, 1992. [Google Scholar]
- Butler, J.N. Carbon Dioxide Equilibria and Their Applications; Addison-Wesley Publishing Company: Boston, MA, USA, 1982. [Google Scholar]
- Chen, P.C.; Shi, W.; Du, R.; Chen, V. Crystallization kinetics of barium carbonate crystals in a lab-scale bubble-column scrubber. J. Taiwan Inst. Chem. Eng. 2014, 45, 2418–2426. [Google Scholar] [CrossRef]
- NancolLas, G.H. The crystal growth of sparingly soluble salts. Croat. Chem. Acta 1973, 45, 225–231. [Google Scholar]
- Nielsen, A.E.; Toft, J.M. Electrolyte crystal growth kinetics. J. Crystal Growth 1984, 67, 278–288. [Google Scholar] [CrossRef]
- Chen, P.C.; Chen, C.C.; Fun, M.H.; Liao, O.Y.; Jiang, J.J.; Wang, Y.S.; Chen, C.S. Mixing and crystallization kinetics in gas-liquid reactive crystallization. Chem. Eng. Technol. 2004, 27, 519–528. [Google Scholar] [CrossRef]
- Ibis, F.; Yu, T.W.; Penha, F.M.; Ganguly, D.; Nuhu, M.A.; van der Heijden, A.E.D.M.; Kramer, H.J.M.; Era, H.B. Nucleation kinetics of calcium oxalate monohydrate as a function of pH, magnesium, and osteopontin concentration quantified with droplet microfluidics. Biomicrofluidics 2021, 15, 064103. [Google Scholar] [CrossRef]
- Małysiak, A.; Walica, T.; Fronczyk, T.; Lemanowicz, M. Influence of hydrodynamic conditions on precipitation kinetics of barium sulfate in a multifunctional reactor. Processes 2022, 10, 146. [Google Scholar] [CrossRef]
- Synowiec, P.M.; Stec, M. Analysis of CaF2 Precipitation Process in the Selected Static Mixers. J. Chem. 2019, 2019, 6728492. [Google Scholar] [CrossRef]
- Tsuge, H.; Kotaki, Y.; Hilbino, S.I. Reactive crystallization of calcium carbonate by liquid-liquid reaction. J. Chem. Eng. Jpn. 1987, 20, 374–379. [Google Scholar] [CrossRef]
- Saffman, P.G.; Turner, J.S. Turner, 1956: On the collision of drops in turbulent clouds. J. Fluid Mech. 1956, 1, 16–30. [Google Scholar] [CrossRef]
- Collier, A.P.; Hounslow, N.J. Growth and aggregation rates for calcite and calcium oxalate monohydrate. AIChE J. 1999, 45, 2298–2305. [Google Scholar] [CrossRef]
- Livk, I.; Ilievki, D. A macroscopic agglomeration kernel model for gibbsite precipitation in turbulent and laminar flows. Chem. Eng. Sci. 2007, 62, 3787–3797. [Google Scholar] [CrossRef]
- Ilievski, D.; White, E.T. Agglomeration during precipitation: Agglomeration mechanism indentification for Al(OH)3 crystals in stirred caustic aluminate solutions. Chem. Eng. Sci. 1994, 49, 3227–3239. [Google Scholar] [CrossRef]
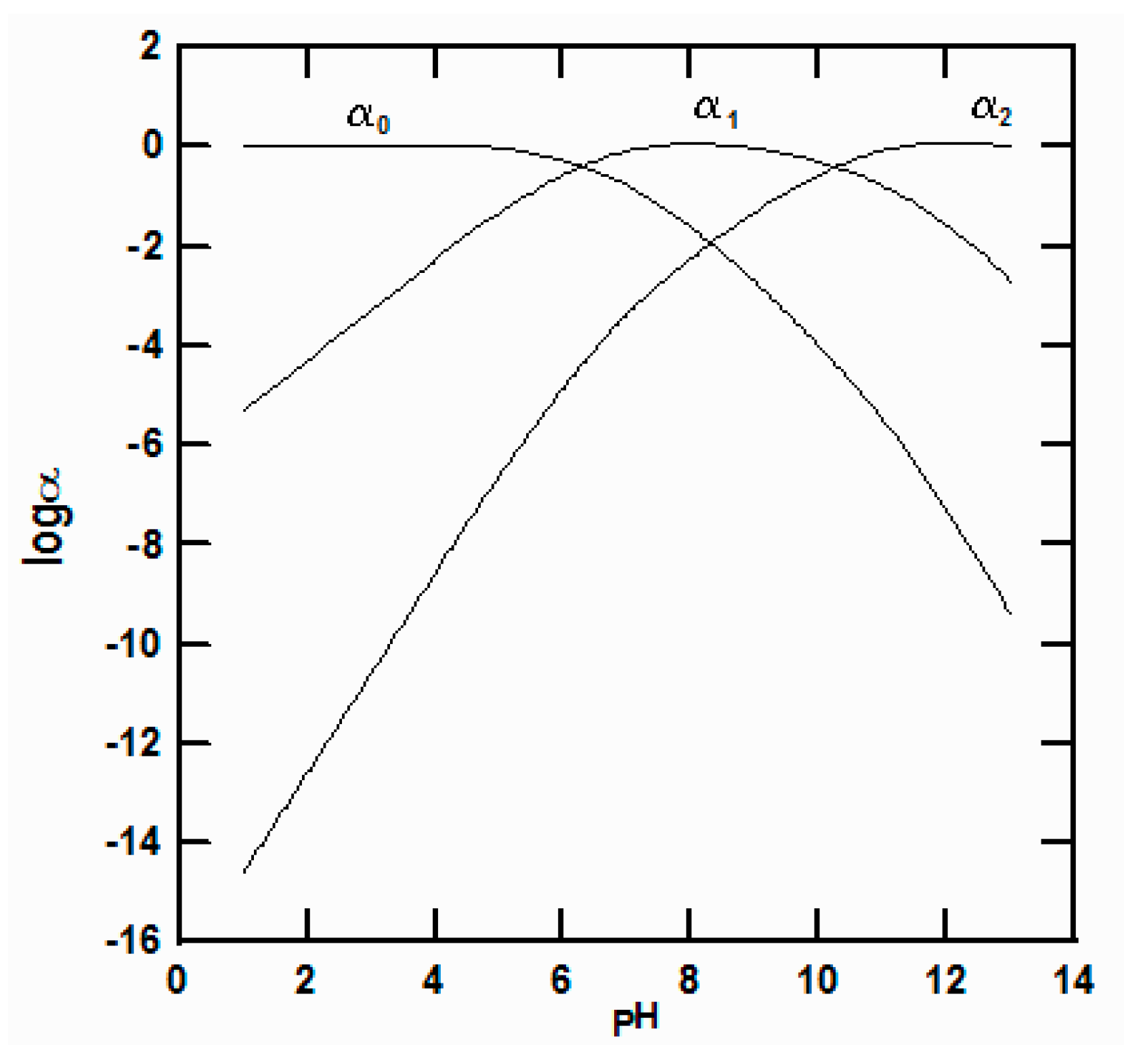


| Mass Action Equations | Stability Constants |
|---|---|
| Kw = 1.47 × 10−14 | |
| K1 = 4.71 × 10−7 | |
| K2 = 5.13 × 10−11 | |
| Ksp = 8.15 × 10−4 |
| No. | G (m/s) | B0 (no/m3·s) | β (m3 /no·s) | N (rpm) | d (μm) | Gv (m3/s) | t (min) | MT (kg/m3) |
|---|---|---|---|---|---|---|---|---|
| 1 | 3.00 × 10−11 | 3.47 × 109 | 1.20 × 10−12 | 800 | 12.5 | 1.48 × 10−20 | 14.21 | 0.02 |
| 2 | 1.26 × 10−10 | 5.23 × 1012 | 2.39 × 10−15 | 1000 | 4.5 | 8.17 × 10−21 | 17.97 | 1.22 |
| 3 | 7.38 × 10−11 | 4.87 × 109 | 9.10 × 10−14 | 1200 | 10.6 | 2.61 × 10−20 | 14.42 | 0.015 |
| 4 | 7.51 × 10−11 | 4.35 × 1011 | 3.53 × 10−14 | 800 | 20.8 | 1.02 × 10−19 | 8.38 | 0.53 |
| 5 | 1.50 × 10−10 | 5.46 × 1012 | 1.78 × 10−19 | 1000 | 1.28 | 8.12 × 10−22 | 9.55 | 2.69 |
| 6 | 4.60 × 10−11 | 5.98 × 1012 | 1.13 × 10−14 | 1200 | 32.7 | 1.55 × 10−19 | 9.29 | 5.88 |
| 7 | 1.23 × 10−10 | 5.20 × 1011 | 8.05 × 10−14 | 800 | 31.9 | 3.91 × 10−19 | 6.32 | 1.11 |
| 8 | 1.21 × 10−10 | 1.69 × 1011 | 1.47 × 10−13 | 1000 | 20.7 | 1.62 × 10−19 | 5.84 | 0.18 |
| 9 | 1.49 × 10−10 | 4.59 × 1011 | 7.00 × 10−14 | 1200 | 29.7 | 4.13 × 10−19 | 5.90 | 1.10 |
| 10 | 1.93 × 10−10 | 5.00 × 1011 | 4.69 × 10−14 | 800 | 19.9 | 2.39 × 10−19 | 4.58 | 0.63 |
| 11 | 1.29 × 10−10 | 3.40 × 1012 | 1.73 × 10−14 | 1000 | 20.5 | 1.71 × 10−19 | 4.53 | 1.93 |
| 12 | 2.11 × 10−10 | 1.07 × 1012 | 1.84 × 10−14 | 1200 | 19.4 | 2.50 × 10−19 | 4.52 | 1.52 |
| No. | I | γ1 | γ2 | C1 | C2 | σ |
|---|---|---|---|---|---|---|
| 1 | 2.14 | 0.5176 | 0.07450 | 0.802 | 0.362 | 1.22 |
| 2 | 2.50 | 0.5076 | 0.06846 | 1.164 | 0.448 | 1.93 |
| 3 | 2.04 | 0.5208 | 0.07713 | 0.898 | 0.291 | 1.27 |
| 4 | 2.51 | 0.8074 | 0.06803 | 1.204 | 0.446 | 1.99 |
| 5 | 2.40 | 0.5101 | 0.07012 | 1.066 | 0.428 | 1.76 |
| 6 | 2.36 | 0.5112 | 0.07081 | 1.061 | 0.404 | 1.71 |
| 7 | 2.32 | 0.5123 | 0.07153 | 1.205 | 0.353 | 1.84 |
| 8 | 2.48 | 0.5081 | 0.06878 | 1.275 | 0.410 | 2.04 |
| 9 | 2.46 | 0.5086 | 0.06911 | 1.152 | 0.433 | 1.90 |
| 10 | 2.50 | 0.5076 | 0.06846 | 1.030 | 0.483 | 1.78 |
| 11 | 2.40 | 0.5117 | 0.07117 | 1.056 | 0.427 | 1.57 |
| 12 | 2.46 | 0.5086 | 0.06911 | 0.965 | 0.481 | 1.65 |
| Sparingly Soluble Substances | B0 (no/m3·s) | References |
|---|---|---|
| BaCO3 | 5.65 × 109–8.88 × 1011 | [39] |
| CaC2O4·H2O | 6.61 × 109–1.17 × 1012 | [40] |
| BaSO4 | 2.00 × 1010–1.20 × 1011 | [41] |
| CaF2 | 1.12 × 1019–8.4 × 1019 | [42] |
| CaCO3 | 1.64 × 108–9.00 × 1010 | [43] |
| Li2CO3 | 3.47 × 109–5.98 × 1012 | This work |
| Sparingly Soluble Substances | Β (m3/no·s) | References |
|---|---|---|
| BaCO3 | 2.66 × 10−16−1.49 × 10−13 | [39] |
| CaC2O4·H2O | 2.00 × 10−15–2.10 × 10−14 | [45] |
| Al(OH)3 | 1.00 × 10−17–2.20 × 10−15 | [46,47] |
| CaCO3 | 5.29 × 10−16–6.23 × 10−14 | [29] |
| Li2CO3 | 1.78 × 10−19–1.20 × 10−12 | This work |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Chen, P.-C.; Jhuang, J.-H.; Tseng, C.-E.; Lin, Z.-Y. Crystallization Kinetics of Lithium Carbonate in a Continuous Stirred-Tank Crystallizer. Crystals 2024, 14, 1021. https://doi.org/10.3390/cryst14121021
Chen P-C, Jhuang J-H, Tseng C-E, Lin Z-Y. Crystallization Kinetics of Lithium Carbonate in a Continuous Stirred-Tank Crystallizer. Crystals. 2024; 14(12):1021. https://doi.org/10.3390/cryst14121021
Chicago/Turabian StyleChen, Pao-Chi, Jyun-Hong Jhuang, Chung-En Tseng, and Zhong-Yi Lin. 2024. "Crystallization Kinetics of Lithium Carbonate in a Continuous Stirred-Tank Crystallizer" Crystals 14, no. 12: 1021. https://doi.org/10.3390/cryst14121021
APA StyleChen, P.-C., Jhuang, J.-H., Tseng, C.-E., & Lin, Z.-Y. (2024). Crystallization Kinetics of Lithium Carbonate in a Continuous Stirred-Tank Crystallizer. Crystals, 14(12), 1021. https://doi.org/10.3390/cryst14121021






