Next Article in Journal
Impact of Synthesis Parameters on the Crystallinity of Macroscopic Zeolite Y Spheres Shaped Using Resin Hard Templates
Previous Article in Journal
Surface Cladding of Mild Steel Coated with Ni Containing TiO2 Nanoparticles Using a High-Temperature Arc from TIG Welding
 
 
Search for Articles:
Title / Keyword
Author / Affiliation / Email
Journal
Article Type
 
 
Advanced Search
 
Section
Special Issue
Volume
Issue
Number
Page
 
Journals
Crystals
Volume 14
Issue 12
10.3390/cryst14121050
crystals-logo
Submit to this Journal Review for this Journal Propose a Special Issue
► Article Menu

Article Menu

share Share announcement Help format_quote Cite question_answer Discuss in SciProfiles
first_page
settings
Order Article Reprints
Font Type:
Arial Georgia Verdana
Font Size:
Aa Aa Aa
Line Spacing:
Column Width:
Background:
Article

An Overlooked Supramolecular Synthon in Multicomponent Trimethylglycine Crystals: Moderate Hydrogen Bonding Between Carboxylate and H-N Groups of Guanidine Species

by
Andrei V. Churakov
1,
Alexander G. Medvedev
1,
Nikita E. Frolov
2 and
Mikhail V. Vener
1,*
1
N.S. Kurnakov Institute of General and Inorganic Chemistry, Russian Academy of Sciences, Leninskii Prosp. 31, Moscow 119991, Russia
2
V. M. Gorbatov Federal Research Center for Food Systems, Talalikhina St. 26, Moscow 109316, Russia
*
Author to whom correspondence should be addressed.
Crystals 2024, 14(12), 1050; https://doi.org/10.3390/cryst14121050
Submission received: 14 October 2024 / Revised: 24 November 2024 / Accepted: 28 November 2024 / Published: 30 November 2024
(This article belongs to the Section Crystal Engineering)
Browse Figures
Versions Notes

Abstract

:
Three novel multicomponent crystals of trimethylglycine with 2-cyanoguanidine, guanidinium and aminoguanidinium chlorides are synthesized and structurally characterized. All three crystal packings are based on the supramolecular synthon formed by two N–H groups of the guanidine species and carboxylate group of trimethylglycine (graph set notation R22(8)). Its enthalpy is about 50 kJ/mol. The three-dimensional structure of crystals is stabilized by intermolecular interactions of various types. The energy of C–H∙∙∙X− interactions, where X = O, Cl, reaches 16 kJ/mol due to the acidic nature of methyl hydrogens. The possible structure of the trimethylglycine–urea–2H2O complex is discussed. Its theoretical metric and spectroscopic parameters are in reasonable agreement with the available literature data on the deep eutectic solvent trimethylglycine–urea.

1. Introduction

Much attention is paid to the creation of single- and multi-component crystals with functional properties [1,2], in particular, pharmaceutical two-component crystals [3,4,5]. In such studies, the concept of supramolecular synthon is widely used [6,7,8,9]. Different types of these synthons exist in multicomponent crystals and are caused by intermolecular hydrogen bonds (H-bonds), see Figure 4 in [10]. The energy of these H-bonds has been estimated [11,12]. Of particular note are the supramolecular synthons formed between acids and aminopyrimidines, 2-aminopyridines, etc. [13,14,15]. Such synthons are very suitable for the creation of multicomponent crystals of active pharmaceutical ingredients (APIs) [13] and can play a role in fine-tuning their solubility [16]. Depending on the strength of the base, ionic or neutral synthons can be formed (Scheme 2 in [13]). This makes it difficult to predict which of the two supramolecular synthons is formed in any given case.
Trimethylglycine (betaine, TMG) plays an important role in the metabolism of plants, animals and humans [17,18]. It is now widely used as a component of pharmaceuticals and dietary supplements [19,20]. TMG is a zwitterion in gas and condensed phases. In the absence of strong monobasic acids [21], it forms H-bonds via the carboxylate group. This simplifies the process of creation of multi-component API crystals. Different types of synthons formed by the carboxylate group of TMG with hydroxyl groups were studied in [22]. The resulting strong intermolecular bonds O–H∙∙∙O− form a variety of supramolecular heterosynthons, in particular, a nine-membered cycle with two O–H∙∙∙O− bonds between L-ascorbic acid and TMG zwitterion, which can be described by graph set notation R22(9) [23]. The Cambridge Structural Database [24] contains the structures of various multi-component crystals of TMG with polybasic inorganic acids. For example, in crystalline TMG–arsenate (Table S1), there is a heterosynthon with two short O–H∙∙∙O− bonds (graph set notation R22(8)). Much less attention has been paid to the creation of multi-component crystals in which the carboxylate group of TMG interacts with the coformer molecule via N–H∙∙∙O bonds. Such bonds are realized in the urea–TMG inclusion compound [25]. The distance between the “heavy” atoms of the N–H∙∙∙O fragment is around 3.0 Å, and comparable to those in crystalline urea [26].
TMG is a co-crystal former used to improve the tabletability of paracetamol [27], the solubility of flavonoids [28], etc. [29,30]. Due to its biological and pharmaceutical applications [31,32,33], TMG is a promising compound for obtaining highly soluble co-crystals of the “drug-drug” or “API-API” type [34,35]. In this paper, we considered guanidine species as APIs, since they are a group of arginine metabolites [36]. A number of in vitro and animal studies have shown that guanidines exert pro-inflammatory effects on monocyte and macrophage function [37]. Potential areas of application of TMG crystals with guanidine compounds are both the creation of highly soluble API–API crystals and their use in natural deep eutectic solvents (NADESs) based on TMG [38].
In the present study, three multicomponent crystals of TMG with guanidine species were synthesized and structurally characterized (Scheme 1). Periodic (solid-state) DFT calculations allow us to identify and quantify intermolecular interactions in these crystals. The results of this study, in conjunction with our previous paper devoted to aqueous complexes of TMG [39], allowed us to create a NADES structure consisting of TMG, urea and water with a molar ratio of components (1:1:2) under non-anhydrous conditions.

2. Materials and Methods

2.1. Synthesis

Betaine anhydrous (97%) was obtained from TCI Chemicals (Tokyo, Japan), 2-cyanoguanidine (98.5%) and guanidinium chloride (99.5%) were purchased from Chemcraft (Kaliningrad, Russia), and aminoguanidinium chloride (98%) and methanol (99%) were purchased from Thermo Fisher Scientific (Waltham, MA, USA). [TMG•Gu+Cl−] (2:1) was prepared by dissolving TMG (0.2342 g, 2 mmol) and guanidinium chloride (0.0955 g, 1 mmol) in 10 mL of methanol. The solution was slowly evaporated until colorless crystals precipitated at room temperature. The crystalline powder was filtered and dried in a vacuum desiccator for 30 min. [TMG•Cy] (1:1) was prepared by dissolving TMG (0.1171 g, 1 mmol) and 2-cyanoguanidine (0.0841 g, 1 mmol) in 5 mL of methanol. The colorless crystals were obtained by slow evaporation of the solvent at room temperature. The crystalline powder was filtered and dried in a vacuum desiccator for 30 min. [TMG•Agu+Cl−] (2:1) was prepared by dissolving TMG (0.2342 g, 2 mmol) and aminoguanidinium chloride (0.1105 g, 1 mmol) in 5 mL of methanol. The colorless crystals were obtained by slow evaporation of the solvent at room temperature. The crystalline powder was filtered and dried in a vacuum desiccator for 30 min.

2.2. Single-Crystal XRD

Single crystals of [TMG•Gu+Cl−], [TMG•Cy] and [TMG•Agu+Cl−] suitable for X-ray diffraction analysis were collected from the corresponding mother liquor without additional recrystallization. Single-crystal diffraction data were collected using a Bruker D8 Venture diffractometer (Bruker AXS, Bremen, Germany) with graphite-monochromated Cu-Kα radiation (λ = 1.54178 Å) for 2-cyanoguanidine [TMG•Cy] and [TMG•Gu+Cl−] and a Bruker SMART Photon II machine (Mo-Kα radiation, λ = 0.71073 Å) for [TMG•Agu+Cl−]. Absorption corrections based on measurements of equivalent reflections were applied [40]. The structures were solved by direct methods and refined using full matrix least-squares on F2 with anisotropic thermal parameters for all non-hydrogen atoms [41]. All hydrogen atoms were found with difference Fourier synthesis and refined isotropically. Experimental details are listed in Table S2. The crystallographic data were deposited with the Cambridge Crystallographic Data Centre as supplementary publications under the CCDC numbers 2381711-2381713. This information can be obtained free of charge from the Cambridge Crystallographic Data Centre via www.ccdc.cam.ac.uk/data_request/cif, accessed on 18 July 2024.

2.3. Computational Details

2.3.1. Periodic DFT Computations

PBE [42] and B3LYP functionals [43,44] were used in the present study. The consistent introduction of dispersion corrections into the B3LYP method is not straightforward [45,46]. Therefore, the D3 correction [47] was only taken into account in the PBE calculations. PBE-D3 and B3LYP are successfully used in calculating various properties of multi-component crystals [48,49,50,51,52,53,54]. The atoms were described with a 6-31G** basis set. Computations were conducted using CRYSTAL17 [55]. When optimizing the crystal structure, experimental values of the space group and unit cell parameters were used [56], known as the “AtomOnly” option [55]. Computation details are given in the Supplementary Materials.

2.3.2. The Enthalpy of H-Bonds and the Energy of Intermolecular Interactions

Unlike molecular complexes in vacuum, the quantitative characterization of non-covalent interactions and intermolecular H-bonds in crystals is not unambiguous. The exceptions are a few crystals in which the enthalpy of sublimation is determined by some type of non-covalent interaction or H-bond, with typical examples being CF4 [57,58] and water ices [59,60]. For a number of intermolecular interactions of a certain type and strength, empirical approaches have been proposed that allow one to estimate the enthalpy or energy of the interaction from metric [61] or electro-topological parameters [62]. The values of these parameters can be found with experiments or calculated using periodic (solid-state) DFT methods. It should be noted that the works [61,62] consider precisely intermolecular H-bonds in molecular complexes and crystals.
In this study, it was assumed that a non-covalent (intermolecular) interaction and H-bond is realized when there is a point (3,-1) on the bond path [63] between the atoms of neighboring molecules in a crystal. Bader’s analysis of the crystal electron density was conducted using Topond 14 [64].
The enthalpy of H-bond ΔHHB in kJ/mol was estimated using [61]
−ΔHHB = 0.134·R(H∙∙∙O) −3.05,
R(H∙∙∙O) denotes the distance H∙∙∙O in nm. Its values were computed using PBE-D3 and B3LYP.
The energy of non-covalent interaction Eint in kJ/mol was estimated using [62]
Eint = 0.429·Gb,
Gb denotes the local electronic kinetic energy density at the bond critical point [63].

3. Results

In the present work, three crystals of TMG with guanidinium chloride [TMG•Gu+Cl−] (2:1), 2-Cyanoguanidine [TMG•Cy] (1:1), and aminoguanidinium chloride [TMG•Agu+Cl−] (2:1) were obtained and structurally characterized (see Table S1, Figures S1–S5). The details, results and discussion of phase characterization using powder XRD and thermal analysis are given in the Supporting Information file (Materials and Methods section, Figures S6–S12).
The asymmetric unit in the structure [TMG•Gu+Cl−] (2:1) consists of two crystallographically independent TMG molecules, one guanidine cation and one chloride anion (Figure S1). In crystal, these components are combined in almost planar centrosymmetric insular motif (Figure S2) via N–H∙∙∙−O2C– and N–H∙∙∙Cl− moderate H-bonds. It should be noted that the guanidine cation is linked to both TMG zwitterions via two almost linear H-bonds due to the successful geometric complementarity of the carboxyl and guanidine fragments. The structure [TMG•Agu+Cl−] (2:1), as previously mentioned [TMG•Gu+Cl−] (2:1), comprises two independent TMG molecules, one aminoguanidine cation and one chloride anion (Figure S5). In crystal, all building units are combined in chains passing along the a-axis via N–H∙∙∙−O2C– and N–H∙∙∙Cl− interactions. The structure [TMG•Cy] (1:1) consists of one independent TMG zwitterion and one cyanoguanidine molecule (Figure S3). In crystal, adjacent molecules are linked in the chains parallel to the c-axis via N–H∙∙∙O and N–H∙∙∙N bonds. In contrast to the [TMG•Gu+Cl−] (2:1) structure, guanidine moieties serve as both the donor and acceptor of H-bonds (Figure S4). In all three structures, bond lengths and angles adopt ordinary values for TMG and guanidine derivatives. All active NH hydrogen atoms are involved in hydrogen bonding.
The three crystals contain a supramolecular heterosynthon built by two N–H groups of the guanidine derivative and TMG carboxylate group of R22(8) topology. The heterodimeric R22(8) synthon between guanidinium and carboxylate ions is the building block in organic crystals [65,66,67]. The orientation of molecules in the synthon is determined by lateral H-bonds and is coplanar in [TMG•Gu+Cl−] (2:1) and [GB•Agu+Cl−] (2:1) and twisted in [TMG•Cy] (1:1). In ternary crystals, guanidine derivatives do not form H-bonds with each other. The guanidine derivatives form five “unique” intermolecular H-bonds with three adjacent TMG molecules and an H-bond with the chlorine ion (Figure 1 and Figure 2).
The N–H∙∙∙O− bonds forming two R22(8) synthons are almost linear, with the N∙∙∙O distance varying from 2.794 to 2.983 Å (Table 1), in agreement with the literature data [3,66,68,69]. The fifth N–H∙∙∙O− bond is formed with the third TMG molecule, which lies in the plane formed by two R22(8) synthons. This H-bond is highly nonlinear (Table 1). The sixth N–H group interacts with the chlorine ion. This anion locates well below the plane and interacts with four C–H groups of the three TMG molecules that locate in the different planes.
2-cyanoguanidine forms four “unique” intermolecular hydrogen bonds with three neighboring molecules: two TMG and one 2-cyanoguanidine (Figure 3). As a result of the interaction of guanidine derivatives in this two-component crystal, a R22(8) synthon with two N–H...N bonds arises.
The hydrogen bond enthalpy ΔHHB of the three crystals, calculated using Equation (1), is given in Table 2. The total enthalpy of the R22(8) synthon formed by two N–H groups of the guanidine derivative and the TMG carboxylate group (46–53 kJ/mol) is practically independent of the nature of the guanidine derivative. The obtained ΔHHB values are consistent with the literature data [70]. The total enthalpy of the R22(8) synthon with two N–H...N bonds equals to 35 kJ/mol. This value is consistent with the literature data [71,72,73].
The B3LYP and PBE-D3 levels give similar metric parameters of H-bonded fragments in the three crystals and, therefore, close values of enthalpies of H-bonds (Table 2). Comparison of Table 2 and Table S3 shows that Equations (1) and (2) lead to similar values of ΔHHB and Eint. This is due to the fact that relatively weak hydrogen bonds [74] exist in the crystals under consideration [75].
In all crystals, TMG zwitterions interact with each other via C–H∙∙∙ O− bonds. Their energy, estimated using Equation (2), is about 13 kJ/mol, which is consistent with the literature data [39,76]. The energy of some C–H∙∙∙O− bonds can reach 16 kJ/mol. This is due to the acidic nature of the hydrogens of the methylene and methyl groups.
In the crystals under consideration, a large number of different non-covalent interactions are also realized. The most common are the C∙∙∙N, C–H∙∙∙N, H∙∙∙H, and C–H∙∙∙Cl− interactions. Their energy, estimated by Equation (2), usually does not exceed ~6 kJ/mol. However, the energy of some interactions turns out to be higher than this value. In particular, C–H∙∙∙Cl− interactions occur with an energy of about 10 kJ/mol. The obtained energies are consistent with literature data [77].
In recent years, Raman spectroscopy has been widely used in the study of polymorphism of molecular crystals [51], including APIs [78], H-bonds and non-covalent interactions in single- [79] and multi-component [56,80,81] molecular crystals, etc. [52]. A discussion of the theoretical Raman spectra of the three crystals is given in the Supplementary Materials.

4. Discussion

Recently, much attention has been paid to the development of NADES [82,83], which is composed, in particular, of urea, TMG and guanidine species [38,84,85]. The nature of the intermolecular interactions between NADES components has been investigated, e.g., see [86,87]; however, most studies have focused on the macroscopic properties of NADES. The results of the present study, in conjunction with our previous paper devoted to aqueous complexes of TMG [39], have allowed us to create a NADES structure consisting of TMG, urea and water with a molar ratio of components (1:1:2) [38]. This complex will be further designated as TMG–urea–2H2O.
The structure of TMG with two water molecules is shown in Figure 1 [39]. It corresponds to the global minimum, and the total enthalpy of intermolecular hydrogen bonds in it is about 100 kJ/mol (Scheme 1 in [39]). From the results of the present study, it follows that the N–H groups of urea will form a heterosynthon with two N–H∙∙∙O− bonds with the carboxylate group of TMG (graph set notation R22(8)). Geometry optimization of the TMG–urea–2H2O complex was performed using the B3LYP/6-31G** approximation. The structure of this complex is shown in Figure 5 [39]. The total enthalpy of intermolecular H-bonds in the TMG–urea–2H2O complex is about 138 kJ/mol. Obviously, it will be quite stable in non-aqueous conditions. In contrast, the solvate-separated TMG–urea complexes discussed in [87] should be treated as short-lived species [88].
To verify the created structure of the TMG–urea–2H2O complex, its metric and spectral parameters were compared with available literary data (details of non-periodic computations and Cartesian coordinates of the complex are given in the Supplementary Materials). The distance between the TMG oxygen and the water oxygen of the O2–H∙∙∙O1 fragment (Figure 4) is 2.75 Å, which is consistent with the value of 2.67 Å obtained in the molecular dynamics simulations of TMG–urea mixtures [86]. The calculated IR spectrum of the complex contains three bands lying in the range of 1700–1450 cm−1, which is consistent with the data presented in Figure 5 of Ref. [87]. According to our computations, the band at about 1600 cm−1 is associated with bending vibrations of two water molecules. The calculated values of chemical shifts of hydrogen atoms δ(1H) of the complex are compared with the available literature data in Table 3. The agreement is satisfactory.

5. Conclusions

Three novel multicomponent crystals of N,N,N-trimethyl-glycine (TMG) with guanidinium chloride [TMG•Gu+Cl−] (2:1), 2-cyanoguanidine [TMG•Cy] (1:1), and aminoguanidinium chloride [TMG•Agu+Cl−] (2:1) were synthesized and structurally characterized. All three crystal packings are based on a synthon formed by two N–H groups of the guanidine derivative and the carboxylate group of TMG (graph set notation R22(8)). The N–H∙∙∙O− bonds forming R22(8) synthons are almost linear, with the N∙∙∙O distance varying from 2.794 to 2.983 Å. Crystalline [TMG•Cy] (1:1) is an example of the R22(8) synthon with N–H∙∙∙O− bonds between the neutral molecule and TMG.
Intermolecular interactions in three crystals are identified and quantified using periodic DFT calculations. The total enthalpy of the R22(8) synthon formed by two N–H groups of the guanidine derivative and the TMG carboxylate group (46–53 kJ/mol) is practically independent of the nature of the guanidine derivative. As a result of the interaction of guanidine derivatives in the [TMG•Cy] (1:1) crystal, the R22(8) synthon with two N–H...N bonds arises. Its enthalpy equals 35 kJ/mol. The three-dimensional structure of crystals is stabilized by C–H∙∙∙X− interactions, where X = O, Cl. Their energy reaches 10 and 16 kJ/mol, respectively, due to the acidic nature of methyl hydrogens.

Supplementary Materials

The following supporting information can be downloaded at: https://www.mdpi.com/article/10.3390/cryst14121050/s1, Table S1: Multicomponent TMG crystals grouped by heterosynthon type, Table S2: Crystallographic data, details of the SC-XRD experiment and structure refinement for multicomponent crystals of N,N,N-trimethyl-glycine with guanidine derivatives obtained in this study, Table S3: The difference between the computed and experimental value of the distance between heavy atoms ΔR of unique H-bonds in the three crystals. The H-bond energy Eint (kJ/mol) was evaluated using Equation (2). The values calculated at the PBE-D3 level are given in italics, Table S4: Wavenumbers (cm−1) of the Raman-active vibrations of the three crystals in the low-frequency region calculated using solid-state DFT in the B3LYP/6-31G** and PBE-D3/6-31G** approximations., Table S5: Wavenumbers (cm−1) of the Raman-active modes of three crystals in the high-frequency region calculated using solid-state DFT in the B3LYP/6-31G** and PBE-D3/6-31G** approximations, Figure S1: Asymmetric unit in the structure [TMG•Gu+Cl−] (2:1). Thermal ellipsoids are shown at 50% probability level. Hydrogen bonds are drawn as dashed lines, Figure S2: Hydrogen bonded insular motif in the structure [TMG•Gu+Cl−] (2:1), Figure S3: Asymmetric unit in the structure [TMG•Cy] (1:1). Thermal ellipsoids are shown at 50% probability level. Hydrogen bonds are drawn as dashed lines, Figure S4: Hydrogen bonded chains along c-axis in the structure [TMG•Cy] (1:1), Figure S5: Asymmetric unit in the structure [TMG•Agu+Cl−] (2:1). Thermal ellipsoids are shown at 50% probability level. Hydrogen bonds are drawn as dashed lines, Figure S6: Comparison of theoretical (a) and experimental (b) X-ray powder diffractograms of [TMG•Gu+Cl−] (2:1), Figure S7: Comparison of theoretical (a) and experimental (b) X-ray powder diffractograms of [TMG•Cy] (1:1), Figure S8: Comparison of theoretical (a) and experimental (b) X-ray powder diffractograms of [TMG•Agu+Cl−] (2:1), Figure S9: The thermal analysis of [TMG•Gu+Cl−] (2:1): weight loss (blue) and DTA signal (red), Figure S10: The thermal analysis of [TMG•Cy] (1:1): weight loss (blue) and DTA signal (red), Figure S11: The DSC cycling curves of [TMG•Cy] (1:1), Figure S12: The thermal analysis of [TMG•Agu+Cl−] (2:1): weight loss (blue) and DTA signal (red), Figure S13: Displacements of atoms of the most intense mode in three crystals (solid-state DFT calculations using the B3LYP/6-31G** approximation), Cartesian coordinates (Å) of the TMG–urea–2H2O complex, Video file TMG_Cy.avi confirming the assumption about the phase transition and subsequent melting [TMG•Cy] (1:1).

Author Contributions

Conceptualization, A.V.C. and M.V.V.; experimental methodology, A.V.C. and A.G.M.; theoretical methodology, M.V.V.; investigation, A.G.M., A.V.C. and N.E.F.; single-crystal XRD experiment, A.V.C.; writing—original draft preparation, N.E.F. and M.V.V.; writing—review and editing, A.G.M. and M.V.V.; visualization, N.E.F.; supervision, M.V.V. and A.V.C. All authors have read and agreed to the published version of the manuscript.

Funding

This work was supported by the Ministry of Science and Higher Education of the Russian Federation, as part of the State Assignment of the Kurnakov Institute of General and Inorganic Chemistry RAS.

Data Availability Statement

Crystal structures of [TMG•Gu+Cl−] (2:1), [TMG•Cy] (1:1) and [TMG•Agu+Cl−] (2:1) have been deposited with the Cambridge Crystallographic Data Centre, under the CCDC numbers 2381711-2381713.

Acknowledgments

M.V.V. thanks Oleg G. Kharlanov (Lomonosov Moscow State University) for the useful discussions of low-frequency Raman spectra and German L. Perlovich (Institute of Solution Chemistry RAS, Ivanovo) for the possibility of conducting computations using Crystal17. X-ray diffraction studies were performed using the equipment of the JRC PMR IGIC RAS.

Conflicts of Interest

The authors declare no conflicts of interest.

References

  1. Bellas, M.K.; Matzger, A.J. Peroxosolvate Discovery Method Leads to First Cocrystal with Three Energetic Components. Chem. Commun. 2022, 58, 8806–8809. [Google Scholar] [CrossRef] [PubMed]
  2. Jaime-Adán, E.; Hernández-Ortega, S.; Toscano, R.A.; Germán-Acacio, J.M.; Sánchez-Pacheco, A.D.; Hernández-Vergara, M.; Barquera, J.E.; Valdés-Martínez, J. Competition of Hydrogen Bonds, Halogen Bonds, and π–π Interactions in Crystal Structures. Exploring the Effect of One Atom Substitution. Cryst. Growth Des. 2024, 24, 1888–1897. [Google Scholar] [CrossRef]
  3. Babu, N.J.; Reddy, L.S.; Nangia, A. Amide−N-Oxide Heterosynthon and Amide Dimer Homosynthon in Cocrystals of Carboxamide Drugs and Pyridine N-Oxides. Mol. Pharm. 2007, 4, 417–434. [Google Scholar] [CrossRef] [PubMed]
  4. Li, N.; Chen, Y.; Chen, R.; Zhang, M.; Wu, T.; Liu, K. Synthesis and Structure Characterization of Three Pharmaceutical Compounds Based on Tinidazole. Crystals 2023, 13, 947. [Google Scholar] [CrossRef]
  5. Voronin, A.P.; Ramazanova, A.G.; Churakov, A.V.; Vologzhanina, A.V.; Kulikova, E.S.; Perlovich, G.L. Virtual Screening, Polymorphism, and Formation Thermodynamics Study of Riluzole Multicomponent Crystals with Dihydroxybenzoic Acids. Cryst. Growth Des 2024. [Google Scholar] [CrossRef]
  6. Desiraju, G.R. Crystal Engineering: From Molecule to Crystal. J. Am. Chem. Soc. 2013, 135, 9952–9967. [Google Scholar] [CrossRef]
  7. Shishkin, O.V.; Zubatyuk, R.I.; Shishkina, S.V.; Dyakonenko, V.V.; Medviediev, V.V. Role of Supramolecular Synthons in the Formation of the Supramolecular Architecture of Molecular Crystals Revisited from an Energetic Viewpoint. Phys. Chem. Chem. Phys. 2014, 16, 6773. [Google Scholar] [CrossRef]
  8. Mukherjee, A.; Desiraju, G.R. Combinatorial Exploration of the Structural Landscape of Acid–Pyridine Cocrystals. Cryst. Growth Des. 2014, 14, 1375–1385. [Google Scholar] [CrossRef]
  9. Mukherjee, A. Building upon Supramolecular Synthons: Some Aspects of Crystal Engineering. Cryst. Growth Des. 2015, 15, 3076–3085. [Google Scholar] [CrossRef]
  10. Deng, Y.; Liu, S.; Jiang, Y.; Martins, I.C.B.; Rades, T. Recent Advances in Co-Former Screening and Formation Prediction of Multicomponent Solid Forms of Low Molecular Weight Drugs. Pharmaceutics 2023, 15, 2174. [Google Scholar] [CrossRef]
  11. Dunitz, J.D.; Gavezzotti, A. Supramolecular Synthons: Validation and Ranking of Intermolecular Interaction Energies. Cryst. Growth Des. 2012, 12, 5873–5877. [Google Scholar] [CrossRef]
  12. Vener, M.V.; Levina, E.O.; Koloskov, O.A.; Rykounov, A.A.; Voronin, A.P.; Tsirelson, V.G. Evaluation of the Lattice Energy of the Two-Component Molecular Crystals Using Solid-State Density Functional Theory. Cryst. Growth Des. 2014, 14, 4997–5003. [Google Scholar] [CrossRef]
  13. Bis, J.A.; Zaworotko, M.J. The 2-Aminopyridinium-Carboxylate Supramolecular Heterosynthon: A Robust Motif for Generation of Multiple-Component Crystals. Cryst. Growth Des. 2005, 5, 1169–1179. [Google Scholar] [CrossRef]
  14. Ebenezer, S.; Muthiah, P.T. Design of Co-Crystals/Salts of Aminopyrimidines and Carboxylic Acids through Recurrently Occurring Synthons. Cryst. Growth Des. 2012, 12, 3766–3785. [Google Scholar] [CrossRef]
  15. Garg, U.; Azim, Y.; Kar, A.; Pradeep, C.P. Cocrystals/Salt of 1-Naphthaleneacetic Acid and Utilizing Hirshfeld Surface Calculations for Acid–Aminopyrimidine Synthons. CrystEngComm 2020, 22, 2978–2989. [Google Scholar] [CrossRef]
  16. da Silva, C.C.; Cirqueira, M.d.L.; Martins, F.T. Lamivudine Salts with 1,2-Dicarboxylic Acids: A New and a Rare Synthon with Double Pairing Motif Fine-Tuning Their Solubility. CrystEngComm 2013, 15, 6311. [Google Scholar] [CrossRef]
  17. Holm, P.I.; Bleie, Ø.; Ueland, P.M.; Lien, E.A.; Refsum, H.; Nordrehaug, J.E.; Nygaård, O. Betaine as a Determinant of Postmethionine Load Total Plasma Homocysteine Before and After B-Vitamin Supplementation. Arterioscler. Thromb. Vasc. Biol. 2004, 24, 301–307. [Google Scholar] [CrossRef]
  18. Schwab, U.; Törrönen, A.; Toppinen, L.; Alfthan, G.; Saarinen, M.; Aro, A.; Uusitupa, M. Betaine Supplementation Decreases Plasma Homocysteine Concentrations but Does Not Affect Body Weight, Body Composition, or Resting Energy Expenditure in Human Subjects. Am. J. Clin. Nutr. 2002, 76, 961–967. [Google Scholar] [CrossRef]
  19. Mäkelä, P. Agro-Industrial Uses of Glycinebetaine. Sugar Tech. 2004, 6, 207–212. [Google Scholar] [CrossRef]
  20. Turck, D.; Castenmiller, J.; De Henauw, S.; Hirsch-Ernst, K.I.; Kearney, J.; Maciuk, A.; Mangelsdorf, I.; McArdle, H.J.; Naska, A.; Pelaez, C.; et al. Safety of Betaine as a Novel Food Pursuant to Regulation (EU) 2015/2283. EFSA J. 2019, 17, e05658. [Google Scholar] [CrossRef]
  21. Godzisz, D.; Ilczyszyn, M.M.; Ilczyszyn, M. Classification and Nature of Hydrogen Bonds to Betaine. X-Ray, 13 C CP MAS and IR Description of Low Barrier Hydrogen Bonds. J. Mol. Struct. 2002, 606, 123–137. [Google Scholar] [CrossRef]
  22. Kavuru, P.; Aboarayes, D.; Arora, K.K.; Clarke, H.D.; Kennedy, A.; Marshall, L.; Ong, T.T.; Perman, J.; Pujari, T.; Wojtas, Ł.; et al. Hierarchy of Supramolecular Synthons: Persistent Hydrogen Bonds between Carboxylates and Weakly Acidic Hydroxyl Moieties in Cocrystals of Zwitterions. Cryst. Growth Des. 2010, 10, 3568. [Google Scholar] [CrossRef]
  23. Etter, M.C. Encoding and Decoding Hydrogen-Bond Patterns of Organic Compounds. Acc. Chem. Res. 1990, 23, 120–126. [Google Scholar] [CrossRef]
  24. Groom, C.R.; Bruno, I.J.; Lightfoot, M.P.; Ward, S.C. The Cambridge Structural Database. Acta Crystallogr. B Struct. Sci. Cryst. Eng. Mater 2016, 72, 171–179. [Google Scholar] [CrossRef]
  25. Yang, Y.; Lu, Z. Novel Urea/Thiourea-Betaine Inclusion Compounds Consolidated by Host-Guest Hydrogen Bonds. Mol. Cryst. Liq. Cryst. 2021, 722, 47–57. [Google Scholar] [CrossRef]
  26. Swaminathan, S.; Craven, B.M.; McMullan, R.K. The Crystal Structure and Molecular Thermal Motion of Urea at 12, 60 and 123 K from Neutron Diffraction. Acta Crystallogr. Sect. B 1984, 40, 300–306. [Google Scholar] [CrossRef]
  27. Maeno, Y.; Fukami, T.; Kawahata, M.; Yamaguchi, K.; Tagami, T.; Ozeki, T.; Suzuki, T.; Tomono, K. Novel Pharmaceutical Cocrystal Consisting of Paracetamol and Trimethylglycine, a New Promising Cocrystal Former. Int. J. Pharm. 2014, 473, 179–186. [Google Scholar] [CrossRef]
  28. Zhang, Z.; Li, D.; Luo, C.; Huang, C.; Qiu, R.; Deng, Z.; Zhang, H. Cocrystals of Natural Products: Improving the Dissolution Performance of Flavonoids Using Betaine. Cryst. Growth Des. 2019, 19, 3851–3859. [Google Scholar] [CrossRef]
  29. Kamal, G.; Abdullah, S.; Basingab, F.; Bani-Jaber, A.; Hamdan, I.I. Curcumin-Betaine Solid Dispersion for Enhancing Curcumin Dissolution and Potentiating Pharmacological Synergism in Gastric Cancer Cells. J. Drug Deliv. Sci. Technol. 2023, 79, 103951. [Google Scholar] [CrossRef]
  30. Oliveira, P.V.; Aguiar, G.P.S.; Siebel, A.M.; Müller, L.G.; Lerin, L.A.; Botti, G.; Bianchi, A.; Bernardi, T.; Gentili, V.; Rizzo, R.; et al. Synthesis of Naringenin-Betaine Cocrystal by Gas Antisolvent Technique and Cell Models for in Vitro Permeation Studies. J. Drug Deliv. Sci. Technol. 2024, 96, 105671. [Google Scholar] [CrossRef]
  31. Ashraf, M.; Foolad, M.R. Roles of Glycine Betaine and Proline in Improving Plant Abiotic Stress Resistance. Environ. Exp. Bot. 2007, 59, 206–216. [Google Scholar] [CrossRef]
  32. Figueroa-Soto, C.G.; Valenzuela-Soto, E.M. Glycine Betaine Rather than Acting Only as an Osmolyte Also Plays a Role as Regulator in Cellular Metabolism. Biochimie 2018, 147, 89–97. [Google Scholar] [CrossRef]
  33. Dobrijević, D.; Pastor, K.; Nastić, N.; Özogul, F.; Krulj, J.; Kokić, B.; Bartkiene, E.; Rocha, J.M.; Kojić, J. Betaine as a Functional Ingredient: Metabolism, Health-Promoting Attributes, Food Sources, Applications and Analysis Methods. Molecules 2023, 28, 4824. [Google Scholar] [CrossRef] [PubMed]
  34. Port, A.; Almansa, C.; Enrech, R.; Bordas, M.; Plata-Salamán, C.R. Differential Solution Behavior of the New API-API Co-Crystal of Tramadol-Celecoxib (CTC) versus Its Constituents and Their Combination. Cryst. Growth Des. 2019, 19, 3172–3182. [Google Scholar] [CrossRef]
  35. Perlovich, G.L. Two-Component Molecular Crystals: What Is the Difference between Drug-Drug, Drug-GRAS, and CF-CF Databases? Evaluation of Melting Points and Ideal Solubility of Unknown Co-Crystals. Cryst. Growth Des. 2021, 21, 5058–5071. [Google Scholar] [CrossRef]
  36. Rosner, M.H.; Husain-Syed, F.; Reis, T.; Ronco, C.; Vanholder, R. Uremic Encephalopathy. Kidney Int. 2022, 101, 227–241. [Google Scholar] [CrossRef]
  37. Devetzis, V.; Zarogoulidis, P.; Kakolyris, S.; Vargemezis, V.; Chatzaki, E. The Corticotropin Releasing Factor System in the Kidney: Perspectives for Novel Therapeutic Intervention in Nephrology. Med. Res. Rev. 2013, 33, 847–872. [Google Scholar] [CrossRef]
  38. Cvjetko Bubalo, M.; Andreou, T.; Panić, M.; Radović, M.; Radošević, K.; Radojčić Redovniković, I. Natural Multi-Osmolyte Cocktails Form Deep Eutectic Systems of Unprecedented Complexity: Discovery, Affordances and Perspectives. Green Chem. 2023, 25, 3398–3417. [Google Scholar] [CrossRef]
  39. Frolov, N.E.; Shishkina, A.V.; Vener, M.V. Specific Proton-Donor Properties of Glycine Betaine. Metric Parameters and Enthalpy of Noncovalent Interactions in Its Dimer, Water Complexes and Crystalline Hydrate. Int. J. Mol. Sci. 2023, 24, 12971. [Google Scholar] [CrossRef]
  40. Sheldrick, G. SADABS, Program for Scaling and Correction of Area Detector Data. University of Gottingen: Göttingen, Germany, 1996. [Google Scholar]
  41. Sheldrick, G.M. A Short History of SHELX. Acta Crystallogr. A 2008, 64, 112–122. [Google Scholar] [CrossRef]
  42. Perdew, J.P.; Burke, K.; Ernzerhof, M. Generalized Gradient Approximation Made Simple. Phys. Rev. Lett. 1996, 77, 3865. [Google Scholar] [CrossRef] [PubMed]
  43. Becke, A.D. Density-Functional Thermochemistry. III. The Role of Exact Exchange. J. Chem. Phys. 1993, 98, 2155–2160. [Google Scholar] [CrossRef]
  44. Lee, C.; Yang, W.; Parr, R.G. Development of the Colle-Salvetti Correlation-Energy Formula into a Functional of the Electron Density. Phys. Rev. B 1988, 37, 785. [Google Scholar] [CrossRef] [PubMed]
  45. Goerigk, L.; Grimme, S. A Thorough Benchmark of Density Functional Methods for General Main Group Thermochemistry, Kinetics, and Noncovalent Interactions. Phys. Chem. Chem. Phys. 2011, 13, 6670. [Google Scholar] [CrossRef]
  46. Merten, C. Modelling Solute–Solvent Interactions in VCD Spectra Analysis with the Micro-Solvation Approach. Phys. Chem. Chem. Phys. 2023, 25, 29404–29414. [Google Scholar] [CrossRef]
  47. Grimme, S.; Ehrlich, S.; Goerigk, L. Effect of the Damping Function in Dispersion Corrected Density Functional Theory. J. Comput. Chem. 2011, 32, 1456–1465. [Google Scholar] [CrossRef]
  48. Mohaček-Grošev, V.; Grdadolnik, J.; Stare, J.; Hadži, D. Identification of Hydrogen Bond Modes in Polarized Raman Spectra of Single Crystals of α-Oxalic Acid Dihydrate. J. Raman Spectrosc. 2009, 40, 1605–1614. [Google Scholar] [CrossRef]
  49. Yushina, I.D.; Kolesov, B.A.; Bartashevich, E.V. Raman Spectroscopy Study of New Thia- and Oxazinoquinolinium Triodides. New J. Chem. 2015, 39, 6163–6170. [Google Scholar] [CrossRef]
  50. Cutini, M.; Civalleri, B.; Corno, M.; Orlando, R.; Brandenburg, J.G.; Maschio, L.; Ugliengo, P. Assessment of Different Quantum Mechanical Methods for the Prediction of Structure and Cohesive Energy of Molecular Crystals. J. Chem. Theory Comput. 2016, 12, 3340–3352. [Google Scholar] [CrossRef]
  51. Bedoya-Martínez, N.; Schrode, B.; Jones, A.O.F.; Salzillo, T.; Ruzié, C.; Demitri, N.; Geerts, Y.H.; Venuti, E.; Della Valle, R.G.; Zojer, E.; et al. DFT-Assisted Polymorph Identification from Lattice Raman Fingerprinting. J. Phys. Chem. Lett. 2017, 8, 3690–3695. [Google Scholar] [CrossRef]
  52. Vener, M.V.; Kharlanov, O.G.; Sosorev, A.Y. High-Mobility Naphthalene Diimide Derivatives Revealed by Raman-Based In Silico Screening. Int. J. Mol. Sci. 2022, 23, 13305. [Google Scholar] [CrossRef]
  53. Rogers, F.J.M.; Radhanpura, K.; Horvat, J.; Farrant, D. On the Use of a Volume Constraint to Account for Thermal Expansion Effects on the Low-Frequency Vibrations of Molecular Crystals. Phys. Chem. Chem. Phys. 2022, 24, 10405–10419. [Google Scholar] [CrossRef]
  54. Beērziņš, K.; Sutton, J.J.; Fraser-Miller, S.J.; Rades, T.; Korter, T.M.; Gordon, K.C. Solving the Computational Puzzle: Toward a Pragmatic Pathway for Modeling Low-Energy Vibrational Modes of Pharmaceutical Crystals. Cryst. Growth Des. 2020, 20, 6947–6955. [Google Scholar] [CrossRef]
  55. Dovesi, R.; Erba, A.; Orlando, R.; Zicovich-Wilson, C.M.; Civalleri, B.; Maschio, L.; Rérat, M.; Casassa, S.; Baima, J.; Salustro, S.; et al. Quantum-Mechanical Condensed Matter Simulations with CRYSTAL. Wiley Interdiscip. Rev. Comput. Mol. Sci. 2018, 8, e1360. [Google Scholar] [CrossRef]
  56. Voronin, A.P.; Surov, A.O.; Churakov, A.V.; Parashchuk, O.D.; Rykounov, A.A.; Vener, M.V. Combined X-Ray Crystallographic, IR/Raman Spectroscopic, and Periodic DFT Investigations of New Multicomponent Crystalline Forms of Anthelmintic Drugs: A Case Study of Carbendazim Maleate. Molecules 2020, 25, 2386. [Google Scholar] [CrossRef]
  57. Chickos, J.S.; Gavezzotti, A. Sublimation Enthalpies of Organic Compounds: A Very Large Database with a Match to Crystal Structure Determinations and a Comparison with Lattice Energies. Cryst. Growth Des. 2019, 19, 6566–6576. [Google Scholar] [CrossRef]
  58. Levina, E.O.; Chernyshov, I.Y.; Voronin, A.P.; Alekseiko, L.N.; Stash, A.I.; Vener, M.V. Solving the Enigma of Weak Fluorine Contacts in the Solid State: A Periodic DFT Study of Fluorinated Organic Crystals. RSC Adv. 2019, 9, 12520–12537. [Google Scholar] [CrossRef]
  59. Ruckenstein, E.; Shulgin, I.L.; Shulgin, L.I. Cooperativity in Ordinary Ice and Breaking of Hydrogen Bonds. J. Phys. Chem. B 2007, 111, 7114–7121. [Google Scholar] [CrossRef]
  60. Vener, M.V.; Egorova, A.N.; Tsirelson, V.G. Hydrogen Bonds and O⋯O Interactions in Proton-Ordered Ices. DFT Computations with Periodic Boundary Conditions. Chem. Phys. Lett. 2010, 500, 272–276. [Google Scholar] [CrossRef]
  61. Rozenberg, M.; Loewenschuss, A.; Marcus, Y. An Empirical Correlation between Stretching Vibration Redshift and Hydrogen Bond Length. Phys. Chem. Chem. Phys. 2000, 2, 2699–2702. [Google Scholar] [CrossRef]
  62. Mata, I.; Alkorta, I.; Espinosa, E.; Molins, E. Relationships between Interaction Energy, Intermolecular Distance and Electron Density Properties in Hydrogen Bonded Complexes under External Electric Fields. Chem. Phys. Lett. 2011, 507, 185–189. [Google Scholar] [CrossRef]
  63. Bader, R.F.W. A Quantum Theory of Molecular Structure and Its Applications. Chem. Rev. 1991, 91, 893–928. [Google Scholar] [CrossRef]
  64. Gatti, C.; Cassasa, S. TOPOND14 User’s Manual; CNR-ISTM of Milano: Milano, Italy, 2013. [Google Scholar]
  65. Yadav, V.N.; Görbitz, C.H. A Supramolecular 2:1 Guanidinium-Carboxylate Based Building Block for Generation of Water Channels and Clusters in Organic Materials. CrystEngComm 2013, 15, 439–442. [Google Scholar] [CrossRef]
  66. Adachi, T.; Ward, M.D. Versatile and Resilient Hydrogen-Bonded Host Frameworks. Acc. Chem. Res. 2016, 49, 2669–2679. [Google Scholar] [CrossRef]
  67. Dillon, A.M.; Yusov, A.; Chaudhry, M.T.; Newman, J.A.; Demkiw, K.M.; Woerpel, K.A.; Lee, A.Y.; Ward, M.D. Supramolecular Mille-Feuille: Adaptive Guest Inclusion in a New Aliphatic Guanidinium Monosulfonate Hydrogen-Bonded Framework. Cryst. Growth Des. 2024, 24, 3483–3490. [Google Scholar] [CrossRef]
  68. Oruganti, M.; Khade, P.; Das, U.K.; Trivedi, D.R. The Hierarchies of Hydrogen Bonds in Salts/Cocrystals of Isoniazid and Its Schiff Base—A Case Study. RSC Adv. 2016, 6, 15868–15876. [Google Scholar] [CrossRef]
  69. Yadav, B.; Balasubramanian, S.; Chavan, R.B.; Thipparaboina, R.; Naidu, V.G.M.; Shastri, N.R. Hepatoprotective Cocrystals and Salts of Riluzole: Prediction, Synthesis, Solid State Characterization, and Evaluation. Cryst. Growth Des. 2018, 18, 1047–1061. [Google Scholar] [CrossRef]
  70. Surov, A.O.; Vasilev, N.A.; Churakov, A.V.; Parashchuk, O.D.; Artobolevskii, S.V.; Alatortsev, O.A.; Makhrov, D.E.; Vener, M.V. Two Faces of Water in the Formation and Stabilization of Multicomponent Crystals of Zwitterionic Drug-like Compounds. Symmetry 2021, 13, 425. [Google Scholar] [CrossRef]
  71. Tupikina, E.Y.; Sigalov, M.; Shenderovich, I.G.; Mulloyarova, V.V.; Denisov, G.S.; Tolstoy, P.M. Correlations of NHN Hydrogen Bond Energy with Geometry and 1 H NMR Chemical Shift Difference of NH Protons for Aniline Complexes. J. Chem. Phys. 2019, 150, 114305. [Google Scholar] [CrossRef]
  72. Voronin, A.P.; Perlovich, G.L.; Vener, M.V. Effects of the Crystal Structure and Thermodynamic Stability on Solubility of Bioactive Compounds: DFT Study of Isoniazid Cocrystals. Comput. Theor. Chem. 2016, 1092, 1–11. [Google Scholar] [CrossRef]
  73. Mirzaei, M.; Sadeghi, F.; Molčanov, K.; Zarȩba, J.K.; Gomila, R.M.; Frontera, A. Recurrent Supramolecular Motifs in a Series of Acid–Base Adducts Based on Pyridine-2,5-Dicarboxylic Acid N -Oxide and Organic Bases: Inter- and Intramolecular Hydrogen Bonding. Cryst. Growth Des. 2020, 20, 1738–1751. [Google Scholar] [CrossRef]
  74. Steiner, T. The Hydrogen Bond in the Solid State. Angew. Chem. Int. Ed. 2002, 41, 48–76. [Google Scholar] [CrossRef]
  75. Medvedev, A.G.; Churakov, A.V.; Navasardyan, M.A.; Prikhodchenko, P.V.; Lev, O.; Vener, M.V. Fast Quantum Approach for Evaluating the Energy of Non-Covalent Interactions in Molecular Crystals: The Case Study of Intermolecular H-Bonds in Crystalline Peroxosolvates. Molecules 2022, 27, 4082. [Google Scholar] [CrossRef]
  76. Voronin, A.P.; Volkova, T.V.; Ilyukhin, A.B.; Trofimova, T.P.; Perlovich, G.L. Structural and Energetic Aspects of Adamantane and Memantine Derivatives of Sulfonamide Molecular Crystals: Experimental and Theoretical Characterisation. CrystEngComm 2018, 20, 6680. [Google Scholar] [CrossRef]
  77. Serebryanskaya, T.V.; Novikov, A.S.; Gushchin, P.V.; Haukka, M.; Asfin, R.E.; Tolstoy, P.M.; Kukushkin, V.Y. Identification and H(D)-bond energies of C–H(D)...Cl interactions in chloride–haloalkane clusters: A combined X-ray crystallographic, spectroscopic, and theoretical study. Phys. Chem. Chem. Phys. 2016, 18, 14104–14112. [Google Scholar] [CrossRef]
  78. Kendrick, J.; Burnett, A.D. Exploring the Stability and Disorder in the Polymorphs of L-Cysteine through Density Functional Theory and Vibrational Spectroscopy. Cryst. Growth Des. 2023, 23, 5734–5747. [Google Scholar] [CrossRef]
  79. Takahashi, M. Terahertz Vibrations and Hydrogen-Bonded Networks in Crystals. Crystals 2014, 4, 74–103. [Google Scholar] [CrossRef]
  80. Surov, A.O.; Vasilev, N.A.; Vener, M.V.; Parashchuk, O.D.; Churakov, A.V.; Magdysyuk, O.V.; Perlovich, G.L. Pharmaceutical Salts of Fenbendazole with Organic Counterions: Structural Analysis and Solubility Performance. Cryst. Growth Des. 2021, 21, 4516–4530. [Google Scholar] [CrossRef]
  81. Song, M.; Yang, F.; Su, C.; Deng, B. Characterizing Hydrogen Bonds in Crystalline Form of Guanidinium Salicylate in the Terahertz Range. RSC Adv. 2020, 11, 307–319. [Google Scholar] [CrossRef]
  82. Tian, Y.; Sun, D.-W.; Zhu, Z. Development of Natural Deep Eutectic Solvents (NADESs) as Anti-Freezing Agents for the Frozen Food Industry: Water-Tailoring Effects, Anti-Freezing Mechanisms and Applications. Food Chem. 2022, 371, 131150. [Google Scholar] [CrossRef]
  83. Wawoczny, A.; Gillner, D. The Most Potent Natural Pharmaceuticals, Cosmetics, and Food Ingredients Isolated from Plants with Deep Eutectic Solvents. J. Agric. Food Chem. 2023, 71, 10877–10900. [Google Scholar] [CrossRef] [PubMed]
  84. Dai, Y.; van Spronsen, J.; Witkamp, G.-J.; Verpoorte, R.; Choi, Y.H. Natural Deep Eutectic Solvents as New Potential Media for Green Technology. Anal. Chim. Acta 2013, 766, 61–68. [Google Scholar] [CrossRef] [PubMed]
  85. Olivares, B.; Martínez, F.; Rivas, L.; Calderón, C.; Munita, J.M.; Campodonico, P.R. A Natural Deep Eutectic Solvent Formulated to Stabilize β-Lactam Antibiotics. Sci. Rep. 2018, 8, 14900. [Google Scholar] [CrossRef] [PubMed]
  86. Kumar, N.; Kishore, N. Synergistic Behavior of Glycine Betaine-Urea Mixture: A Molecular Dynamics Study. J. Chem. Phys. 2013, 139, 115104. [Google Scholar] [CrossRef]
  87. Nava-Ocampo, M.F.; Al Fuhaid, L.; Santana, A.; Bucs, S.S.; Verpoorte, R.; Hae Choi, Y.; Witkamp, G.J.; Vrouwenvelder, J.S.; Farinha, A.S.F. Structural Properties and Stability of the Betaine-Urea Natural Deep Eutectic Solvent. J. Mol. Liq. 2021, 343, 117655. [Google Scholar] [CrossRef]
  88. Vener, M.V.; Odinokov, A.V.; Wehmeyer, C.; Sebastiani, D. The Structure and IR Signatures of the Arginine-Glutamate Salt Bridge. Insights from the Classical MD Simulations. J. Chem. Phys. 2015, 142, 215166. [Google Scholar] [CrossRef]
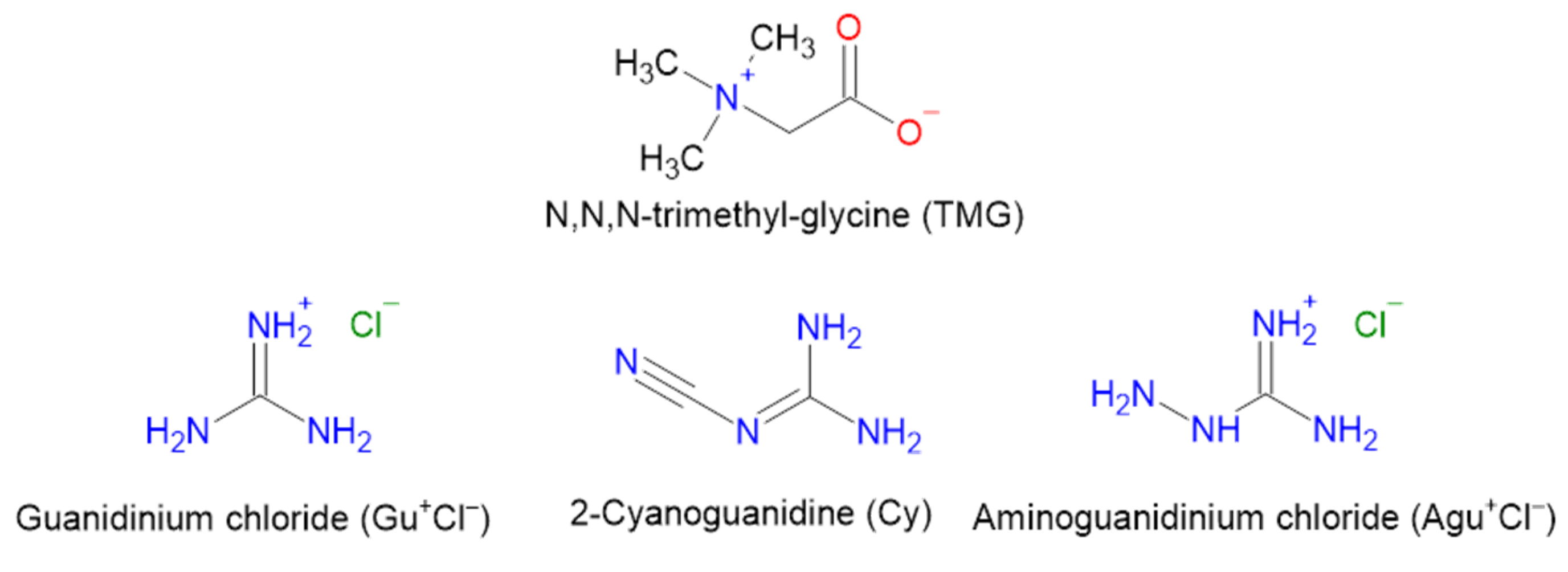
Crystals 14 01050 sch001
Scheme 1. Molecular structures of TMG and the studied guanidine species.
Scheme 1. Molecular structures of TMG and the studied guanidine species.
Crystals 14 01050 sch001
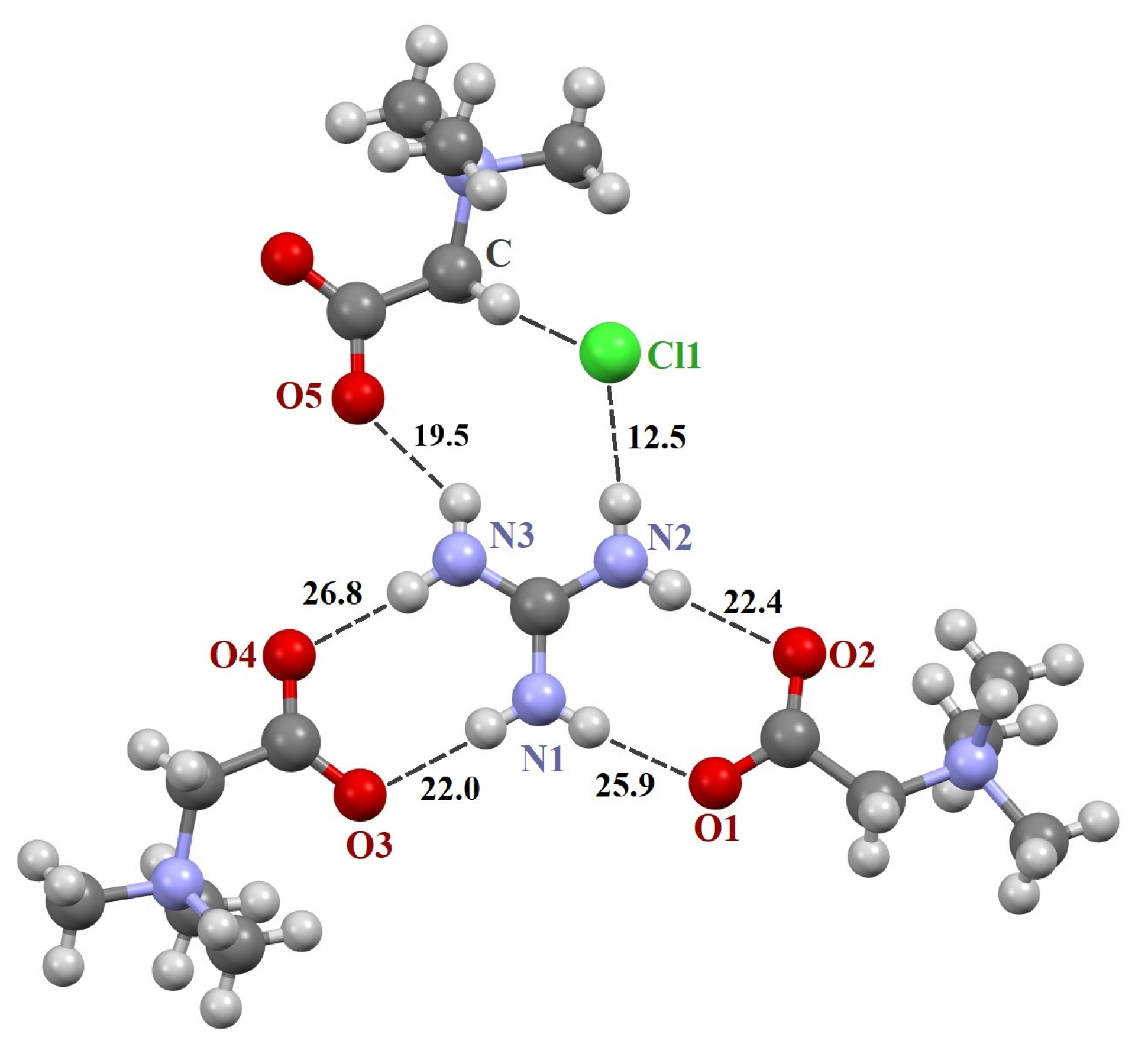
Crystals 14 01050 g001
Figure 1. Fragments of crystal structures [TMG•Gu+Cl−] (2:1). Unique H-bonds are drawn as dashed lines. Numbers indicate the H-bond enthalpies (kJ/mol) evaluated using Equation (1) at the B3LYP level.
Figure 1. Fragments of crystal structures [TMG•Gu+Cl−] (2:1). Unique H-bonds are drawn as dashed lines. Numbers indicate the H-bond enthalpies (kJ/mol) evaluated using Equation (1) at the B3LYP level.
Crystals 14 01050 g001
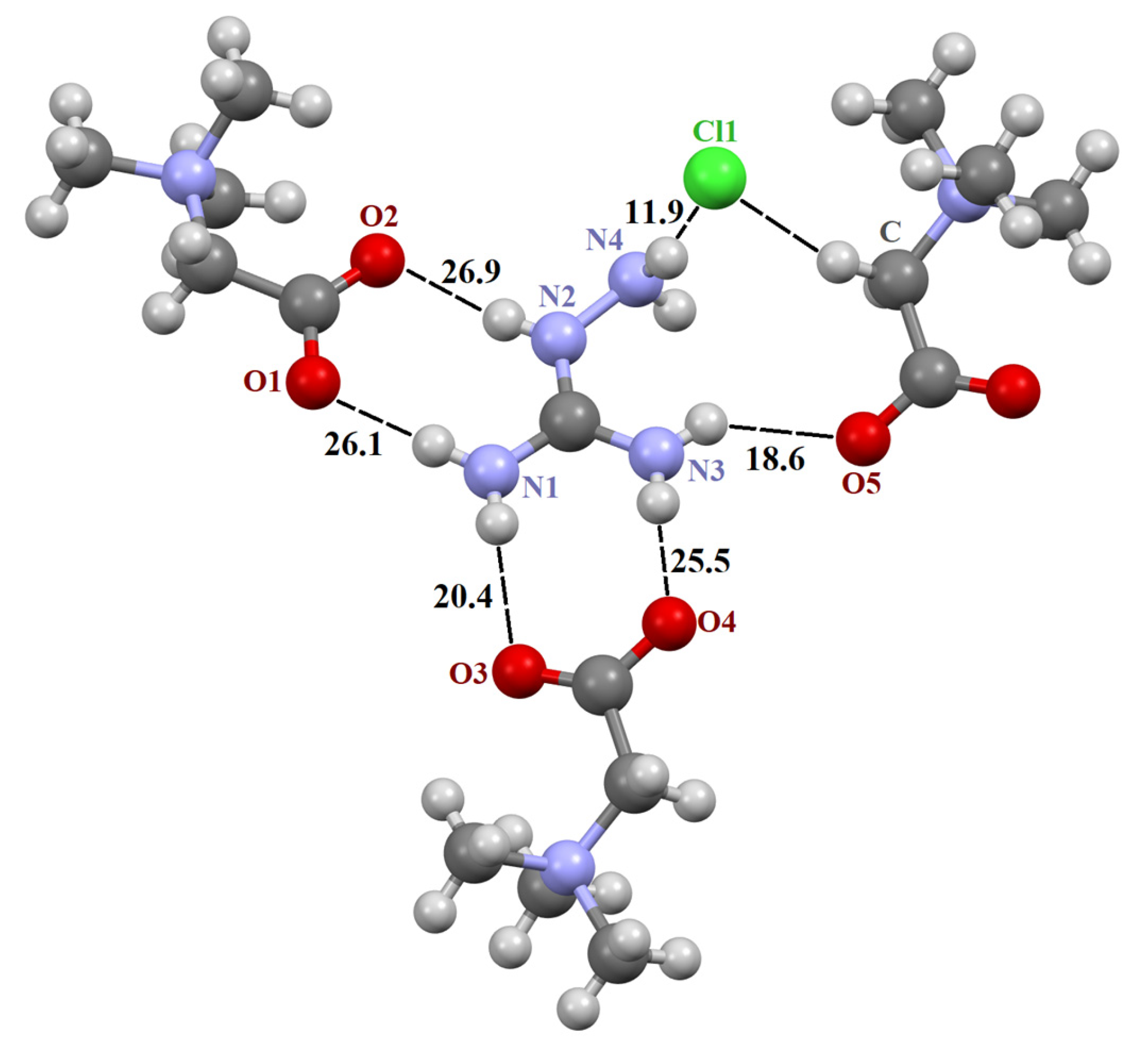
Crystals 14 01050 g002
Figure 2. Fragment of crystal structure [TMG•Agu+Cl−] (2:1). Unique H-bonds are drawn as dashed lines. Numbers indicate the H-bond enthalpies (kJ/mol) evaluated using Equation (1) at the B3LYP level.
Figure 2. Fragment of crystal structure [TMG•Agu+Cl−] (2:1). Unique H-bonds are drawn as dashed lines. Numbers indicate the H-bond enthalpies (kJ/mol) evaluated using Equation (1) at the B3LYP level.
Crystals 14 01050 g002
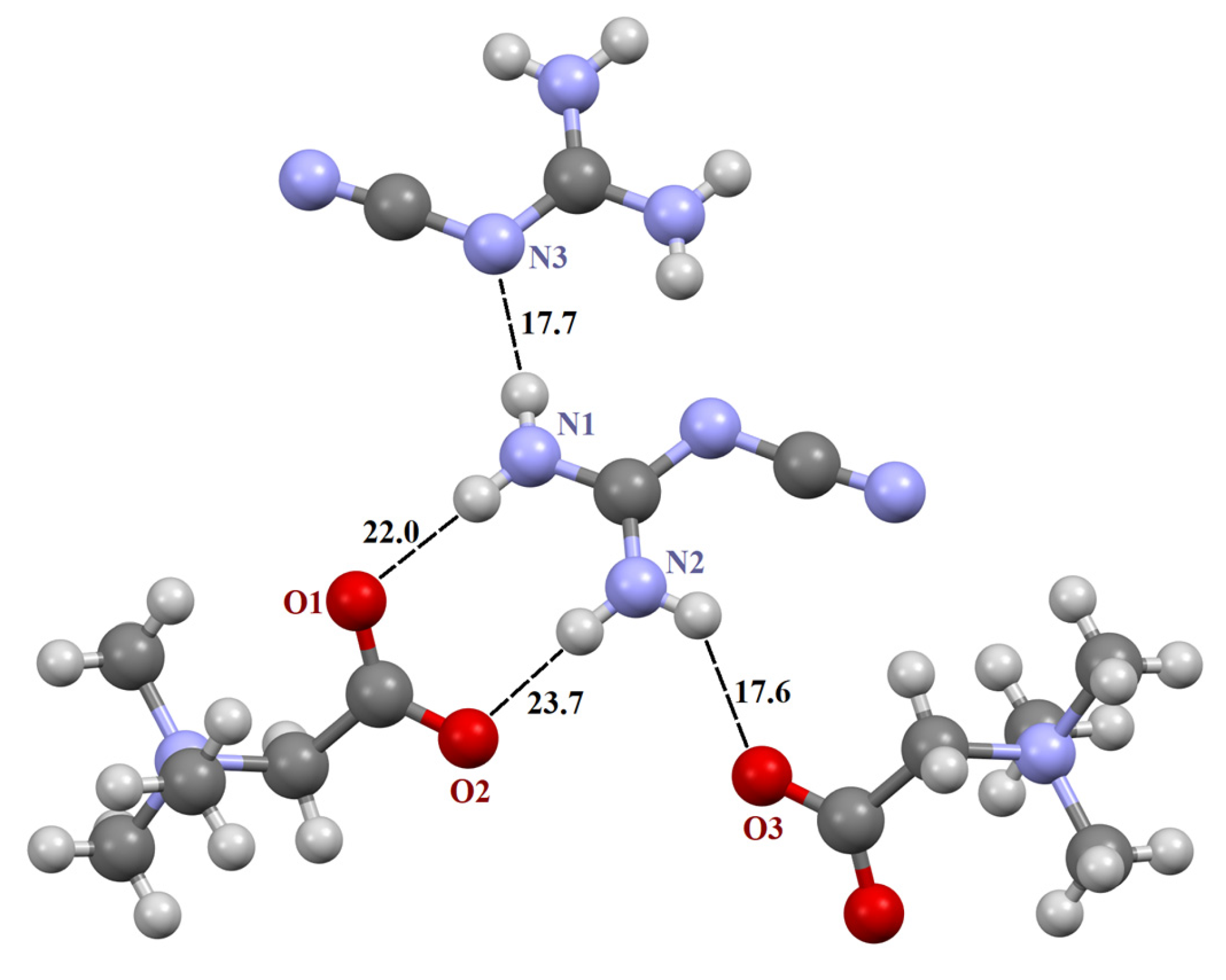
Crystals 14 01050 g003
Figure 3. Fragment of crystal structure [TMG•Cy] (1:1). Unique H-bonds are drawn as dashed lines. Numbers indicate the H-bond enthalpies (kJ/mol) evaluated using Equation (1) at the B3LYP level.
Figure 3. Fragment of crystal structure [TMG•Cy] (1:1). Unique H-bonds are drawn as dashed lines. Numbers indicate the H-bond enthalpies (kJ/mol) evaluated using Equation (1) at the B3LYP level.
Crystals 14 01050 g003
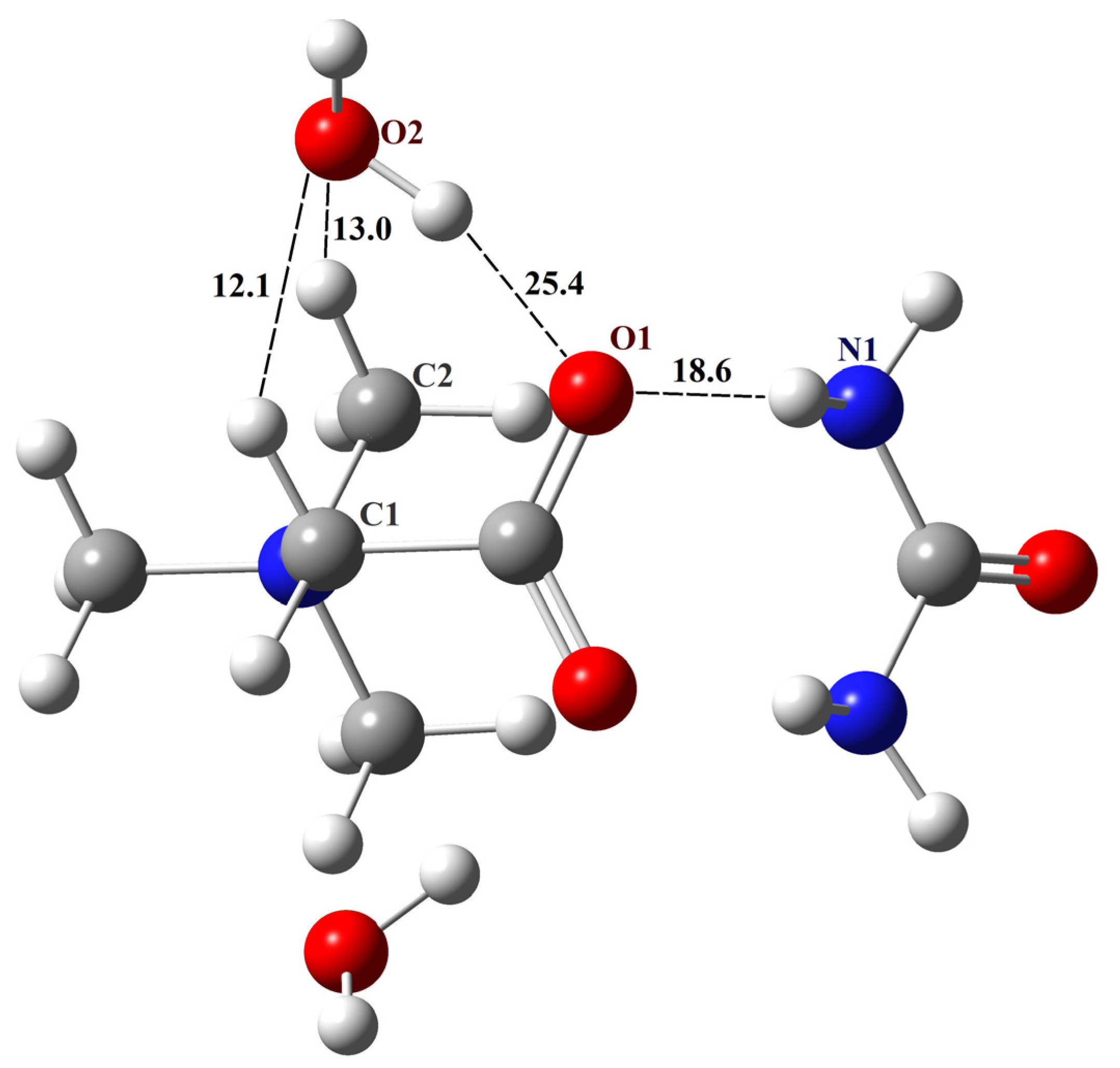
Crystals 14 01050 g004
Figure 4. The structure of the TMG–urea–2H2O complex. Unique H-bonds are drawn as dashed lines. Numbers indicate the H-bond enthalpies (kJ/mol) evaluated using Equation (1) at the B3LYP level.
Figure 4. The structure of the TMG–urea–2H2O complex. Unique H-bonds are drawn as dashed lines. Numbers indicate the H-bond enthalpies (kJ/mol) evaluated using Equation (1) at the B3LYP level.
Crystals 14 01050 g004
Table 1. Experimental values of metric parameters of H-bonded fragments in the three crystals: distance between heavy atoms R(X∙∙∙Y), Rexp, and fragment angle X–H∙∙∙Y (Angle), where X = N, C and Y = O, Cl, N.
Table 1. Experimental values of metric parameters of H-bonded fragments in the three crystals: distance between heavy atoms R(X∙∙∙Y), Rexp, and fragment angle X–H∙∙∙Y (Angle), where X = N, C and Y = O, Cl, N.
Fragment (a)[TMG•Gu+Cl−] (2:1)[TMG•Agu+Cl−] (2:1) [TMG•Cy] (1:1)
Rexp, ÅAngle, deg. Rexp, ÅAngle, deg.Rexp, ÅAngle, deg.
N1–H∙∙∙O12.818173.42.798176.62.912177.7
N2–H∙∙∙O22.887172.12.801173.92.863169.4
N1–H∙∙∙O32.900175.82.983165.1--
N3–H∙∙∙O42.794175.22.807174.7--
N3–H∙∙∙O52.862136.62.893141.9--
N2–H∙∙∙Cl13.218163.3----
N4–H∙∙∙Cl1--3.290166.6--
N1–H∙∙∙N3----3.010172.7
N2–H∙∙∙O3----2.853135.0
C–H∙∙∙Cl13.621159.33.598162.4--
(a) atomic numeration is given in Figure 1, Figure 2 and Figure 3.
Table 2. The difference between the computed and experimental value of the distance between heavy atoms ΔR (a) of unique H-bonds in the three crystals. The H-bond enthalpy ΔHHB (kJ/mol) was estimated using Equation (1). The values calculated at the PBE-D3 level are given in italics.
Table 2. The difference between the computed and experimental value of the distance between heavy atoms ΔR (a) of unique H-bonds in the three crystals. The H-bond enthalpy ΔHHB (kJ/mol) was estimated using Equation (1). The values calculated at the PBE-D3 level are given in italics.
Fragment (b)[TMG•Gu+Cl−] (2:1)[TMG•Agu+Cl−] (2:1) [TMG•Cy] (1:1)
ΔR, Å−ΔHHBΔR, Å−ΔHHBΔR, Å−ΔHHB
N1–H∙∙∙O1
 		0.01
0.017		25.9
26.8		−0.011
- (c)		26.1
-		0.014
0.016		22.0
22.4
N2–H∙∙∙O2
 		−0.003
0.017		22.4
23.7		0.012
-		26.9
-		0.011
0.027		23.7
24.8
N1–H∙∙∙O3
 		−0.002
−0.003		22.0
22.4		0.053
-		20.4
-		--
N3–H∙∙∙O4
 		0.004
−0.011		26.8
28.0		−0.009
-		25.5
-		--
N3–H∙∙∙O5 (d)
 		0.046
0.056		19.5
20.0		0.030
-		18.6
-		--
N2–H∙∙∙Cl1
 		−0.039
−0.026		12.5
13.1		----
N4–H∙∙∙Cl1
 		--−0.023
-		11.9
-		--
N1–H∙∙∙N3
 		----−0.020
−0.001		17.7
18.5
N2–H∙∙∙O3 (c)
 		----0.001
0.011		17.6
18.2
(a) ΔR = Rexp − Rcalc, Rexp values are given in Table 1; (b) atomic numeration is given in Figure 1, Figure 2 and Figure 3; (c) PBE-D3 calculations yielded one imaginary frequency (10 cm−1) for this crystal; therefore, the enthalpy values computed in this approximation are not given in the table; (d) this H-bond is highly nonlinear (see Table 1).
Table 3. Comparison of the calculated values of δ(1H) of the TMG–urea–2H2O complex compared with the available literature data (Figure 4A1 of Ref. [87]).
Table 3. Comparison of the calculated values of δ(1H) of the TMG–urea–2H2O complex compared with the available literature data (Figure 4A1 of Ref. [87]).
This Study[87]
δ(1H), ppmAssignmentδ(1H), ppmAssignment
6.58H-bonded OH--
6.36H-bonded NH5.94NH2
4.56, 4.24, 4.14H-bonded CH of CH3 and CH2 groups4.54H2O
3.01, 2.86“free” NH and CH of CH3 groups3.00CH3
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.

Share and Cite

MDPI and ACS Style

Churakov, A.V.; Medvedev, A.G.; Frolov, N.E.; Vener, M.V. An Overlooked Supramolecular Synthon in Multicomponent Trimethylglycine Crystals: Moderate Hydrogen Bonding Between Carboxylate and H-N Groups of Guanidine Species. Crystals 2024, 14, 1050. https://doi.org/10.3390/cryst14121050

AMA Style

Churakov AV, Medvedev AG, Frolov NE, Vener MV. An Overlooked Supramolecular Synthon in Multicomponent Trimethylglycine Crystals: Moderate Hydrogen Bonding Between Carboxylate and H-N Groups of Guanidine Species. Crystals. 2024; 14(12):1050. https://doi.org/10.3390/cryst14121050

Chicago/Turabian Style

Churakov, Andrei V., Alexander G. Medvedev, Nikita E. Frolov, and Mikhail V. Vener. 2024. "An Overlooked Supramolecular Synthon in Multicomponent Trimethylglycine Crystals: Moderate Hydrogen Bonding Between Carboxylate and H-N Groups of Guanidine Species" Crystals 14, no. 12: 1050. https://doi.org/10.3390/cryst14121050

APA Style

Churakov, A. V., Medvedev, A. G., Frolov, N. E., & Vener, M. V. (2024). An Overlooked Supramolecular Synthon in Multicomponent Trimethylglycine Crystals: Moderate Hydrogen Bonding Between Carboxylate and H-N Groups of Guanidine Species. Crystals, 14(12), 1050. https://doi.org/10.3390/cryst14121050

Note that from the first issue of 2016, this journal uses article numbers instead of page numbers. See further details here.

Article Metrics

Back to TopTop