Numerical Simulation of Fracture Failure in Three-Point Bending Specimens of Yellow River Granular Ice
Abstract
1. Introduction
2. Numerical Modeling of River Ice
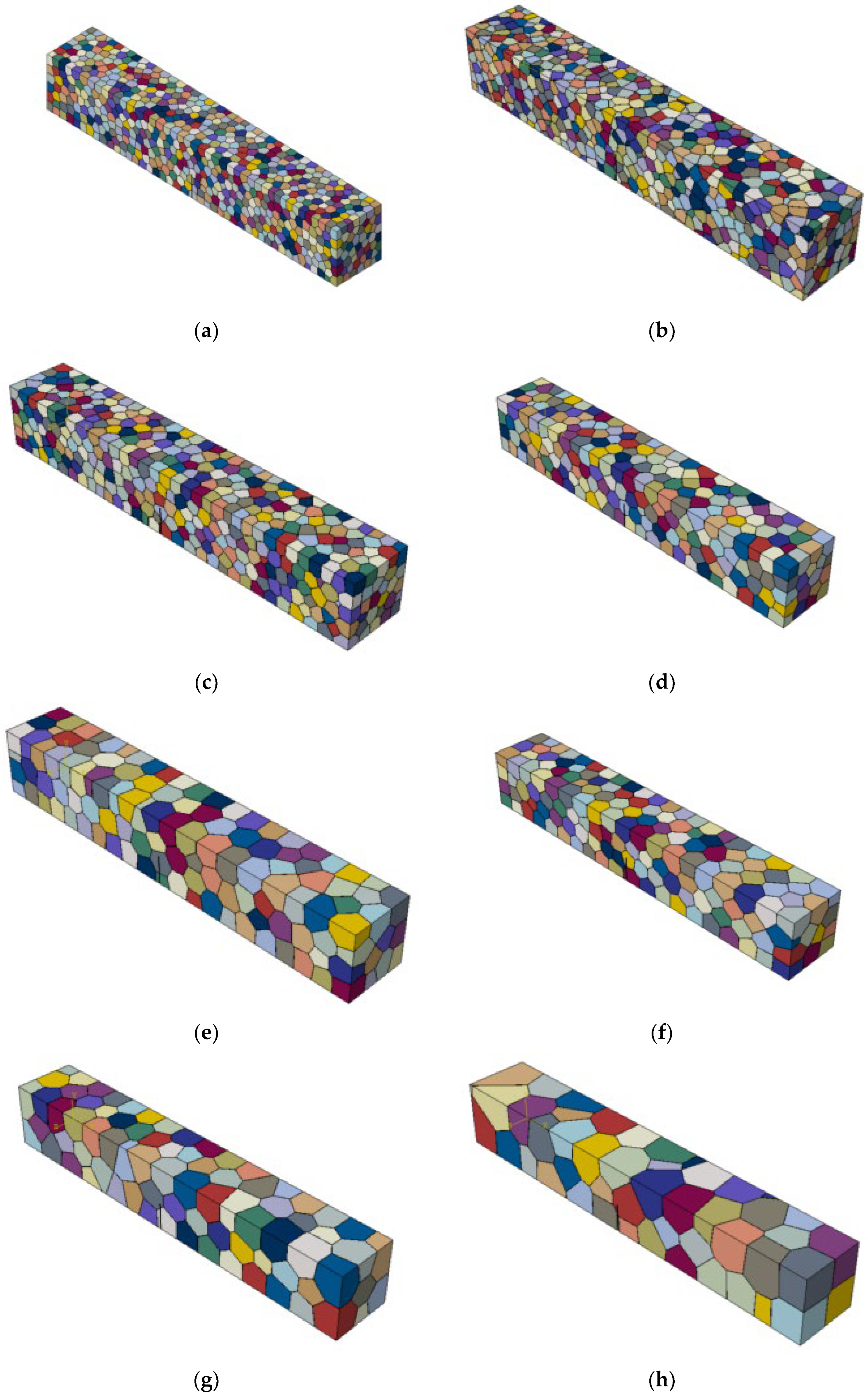
2.1. Generation of Ice Grains
2.2. Generation of Grain Boundaries and Initial Defects
2.3. Determination of Constitutive Relationships and Damage Criteria
2.4. Selection of Mesoscopic Parameters
2.4.1. Selection of the Elastic Modulus of Ice Grains
2.4.2. Selection of Tensile Strength of Ice Crystals
2.4.3. Strength of Grain Boundaries
3. Analysis of Numerical Simulation Results
3.1. Analysis of the Fracture Failure Process
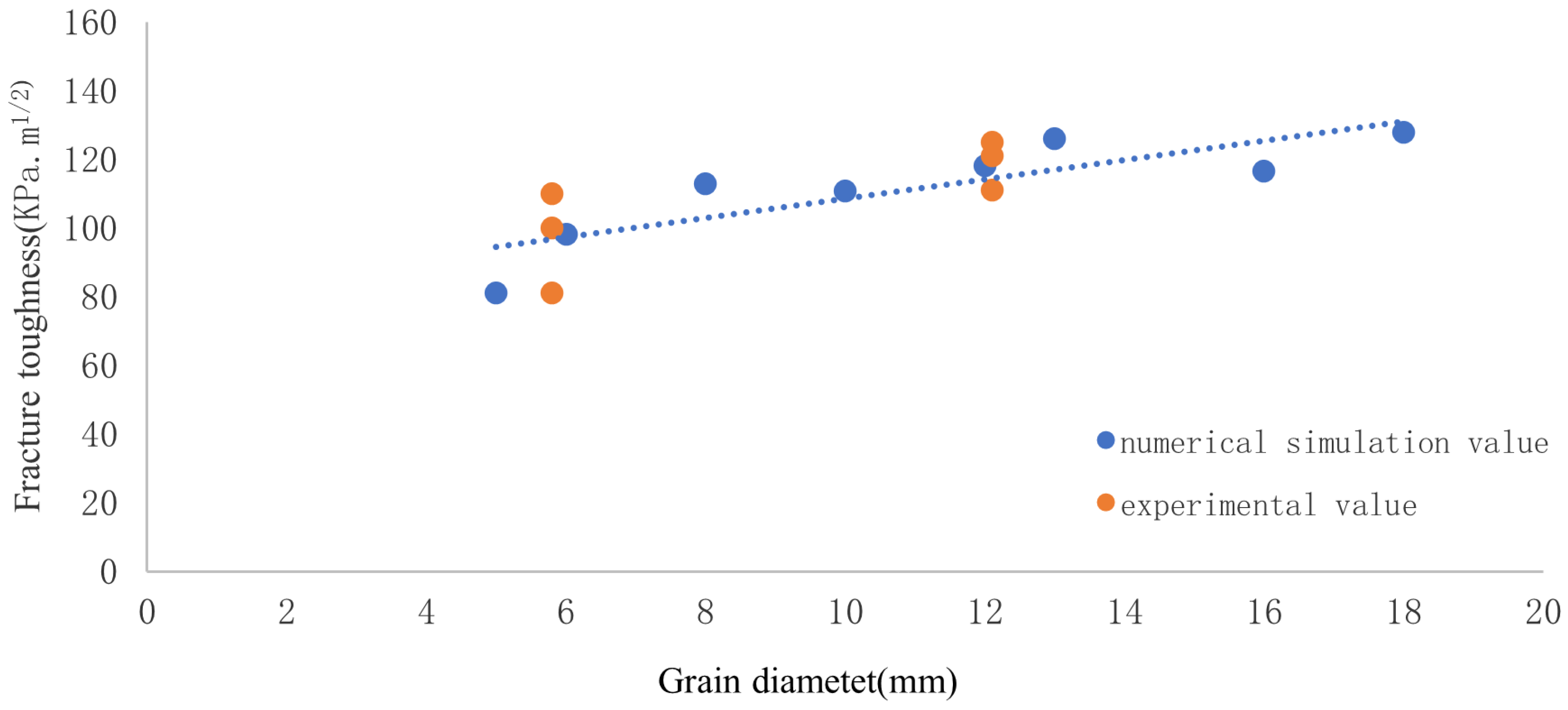
3.2. Comparative Analysis of Test Results
4. Discussion
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Wang, D.W.; Zhang, F.H. Characteristics and causes of ice flood in Ningxia-inner Mongolia section of the yellow river valley. Meteorol. Mon. 2006, 32, 32–38. [Google Scholar]
- Li, Z.; Yang, L.; Wang, G. The management of soil and water conservation in the loess plateau of China: Present situations, problems, and counter-solutions. Acta Ecol. Sin. 2019, 39, 7398–7409. [Google Scholar]
- Zhang, Y.L. Microstructure characteristics of river ice in Inner Mongolia section of the yellow river and its influencing factors. J. Hydraul. Eng. 2021, 52, 1418–1429. [Google Scholar]
- Deng, Y.; Wang, J.; Li, Z. Numerical simulation of uniaxial compression failure process of river ice. J. Hydraul. Eng. 2018, 49, 1339–1345. [Google Scholar]
- Juan, W.; Zhou, J.; Yu, D.; Vadim, G.; Peng, Z. Numerical simulation of ice fractures process of the yellow river based on disk specimen. Crystals 2020, 10, 598. [Google Scholar] [CrossRef]
- Han, D. Numerical simulation of ice bending strength test based on improved SPH method. Huazhong Univ. Sci. Technol. (Nat. Sci. Ed.) 2018, 46, 54–58. [Google Scholar]
- Xue, Y.L. Simulation of three-point bending test of ice based on peridynamic. Harbin Eng. Univ. 2018, 39, 607–613. [Google Scholar]
- Zhai, B.Y.; Liu, L.; Zhang, B.S. A river ice dynamic model based on coupling of discrete element method and hydrodynamics. J. Hydraul. Eng. ASCE 2020, 51, 617–630. [Google Scholar]
- Jun, W.; Sang, L.S.; Song, F.H.; Cheng, T.J. Research progress on the ice blocks stability in front of ice cover. J. Hydraul. Eng. ASCE 2023, 24, 1277–1286. [Google Scholar]
- Wang, E.L.; Xu, C.G. Research progress on mechanical properties of freshwater ice in China. Hydro Sci. Cold Zone Eng. 2019, 2, 37–43. [Google Scholar]
- Qi, C.; Goldsby, D.L. An experimental investigation of the effect of grain size on “dislocation creep” of ice. J. Geophys. Res. Solid Earth 2021, 126, e2021JB021824. [Google Scholar] [CrossRef]
- Gribanov, I.; Taylor, R.; Sarracino, R. Parallel implementation of implicit finite element model with cohesive zones and collision response using cuda. Numer. Methods Eng. 2018, 115, 771–790. [Google Scholar] [CrossRef]
- Gribanov, I.; Taylor, R.; Sarracino, R. Cohesive zone micromechanical model for compressive and tensile failure of polycrystalline ice. Eng. Fract. Mech. 2018, 196, 142–156. [Google Scholar] [CrossRef]
- Lu, W.; Lubbad, R.; Lset, S.; Hyland, K. Cohesive zone method based simulations of ice wedge bending: A comparative study of element erosion, cem, dem and xfem. In Proceedings of the 21st IAHR International Symposium on Ice, Dalian, China, 11 June 2012. [Google Scholar]
- Wang, J.H. Analysis of ice crystal structure characteristics of the yellow river in Inner Mongolia during freezing period. Yellow River 2021, 43, 41–45. [Google Scholar]
- Chen, W.T.; Zhang, P.; Chen, X.P. Study on influence of unfrozen water on mechanical properties of ice crystals by molecular dynamics simulations. J. Glaciol. Geocryol. 2023, 45, 624–640. [Google Scholar]
- Duval, P. Creep and fabrics of polycrystalline ice under shear and compression. J. Glaciol. 1981, 27, 129–140. [Google Scholar] [CrossRef]
- Xu, P.; Li, L.H. Experimental study on uniaxial compressive strength characteristics of conventional model ice in tank. Chin. J. Ship Res. 2024, 19, 1–17. [Google Scholar]
- Jones, S.J. High strain-rate compression tests on ice. J. Phys. Chem. B 1997, 101, 6099–6101. [Google Scholar] [CrossRef]
- Schulson, E.M. Brittle failure of ice. Eng. Fract. Mech. 2001, 68, 1839–1887. [Google Scholar] [CrossRef]
- Yu, C.G.; Tian, Y.K. Experimental investigation on elastic modulus of model ice with cantilever beam method. J. Ship Mech. 2021, 25, 1066–1072. [Google Scholar]
- Gammon, P.H.; Kiefte, H.; Clouter, M.J. Elastic constants of ice samples by brillouin spectroscopy. J. Phys. Chem. 1983, 87, 4025–4029. [Google Scholar] [CrossRef]
- Derradji, A.; Sinha, N.K.; Evgin, E. Mathematical modelling of monotonic and cyclic behaviour of fresh water columnar grained s-2 ice. Cold Reg. Sci. Technol. 2000, 31, 59–81. [Google Scholar] [CrossRef]
- Sinha, N.K. Elasticity of natural types of polycrystalline ice. Cold Reg. Sci. Technol. 1989, 17, 127–135. [Google Scholar] [CrossRef]
- Schulson, E.M.; Lim, P.N.; Lee, R. A brittle to ductile transition in ice under tension. Philos. Mag. 1984, 49, 353–363. [Google Scholar] [CrossRef]
- Kolari, K. Simulation of the temperature and grain size dependent uniaxial compressive strength using 3d wing crack model. In Proceedings of the 23rd International Conference on Port and Ocean Engineering under Arctic Conditions, POAC ’15, Trondheim, Norway, 14–18 June 2015. [Google Scholar]
- Schulson, E.M.; Duval, P. Creep and Fracture of Ice; Cambridge University Press: Cambridge, UK, 2019. [Google Scholar]
- Petrovic, J.J. Review mechanical properties of ice and snow. J. Mater. Sci. 2003, 38, 1–6. [Google Scholar] [CrossRef]
- Weiss, J.; Schulson, E.M. The failure of fresh-water granular ice under multiaxial compressive loading. Acta Metall. Mater. 1995, 43, 2303–2315. [Google Scholar] [CrossRef]
- Currier, J.H.; Schulson, E.M.; Lawrence, W.F. A study on the tensile strength of ice as a function of grain size. Acta Metall. 1982, 30, 1511–1514. [Google Scholar] [CrossRef]
- Chen, Y.Y.; Xiao, K.L. Atomistic study on the anomalous temperature-dependent dynamic tensile strength of ice under shock loading. Philos. Mag. 2021, 101, 1289–1304. [Google Scholar] [CrossRef]
- Yu, C.G.; Tian, Y.K.; Gang, X.H. Investigation on the tensile strength of model ice based on brazilian disc splitting test. J. Ship Mech. 2020, 24, 1158–1166. [Google Scholar]
- Yang, F.C.; Tang, M.G.; Zhao, H.L. Research on tensile strength and influencing factors of debris ice based on Brazil split test. J. Eng. Geol. 2024, 32, 1546–1554. [Google Scholar]
- Elvin, A.A.; Sunder, S.S. Microcracking due to grain boundary sliding in polycrystalline ice under uniaxial compression. Acta Mater. 1996, 44, 43–56. [Google Scholar] [CrossRef]
- Cole, D.M. The microstructure of ice and its influence on mechanical properties. Eng. Fract. Mech. 2001, 68, 1797–1822. [Google Scholar] [CrossRef]
- Caswell, T.E.; Cooper, R.F.; Goldsby, D.L. The constant-hardness creep compliance of polycrystalline ice. Geophys. Res. Lett. 2015, 42, 6261–6268. [Google Scholar] [CrossRef]
- ASTM E1820-24; Standard Test Method for Measurement of Fracture Toughness. ASTM International: West Conshohocken, PA, USA, 2024.
- Dempsey, J.P.; Wei, Y.; Defranco, S.J. Notch sensitivity and brittleness in fracture testing of s2 columnar freshwater ice. Int. J. Fract. 1992, 53, 101–120. [Google Scholar] [CrossRef]
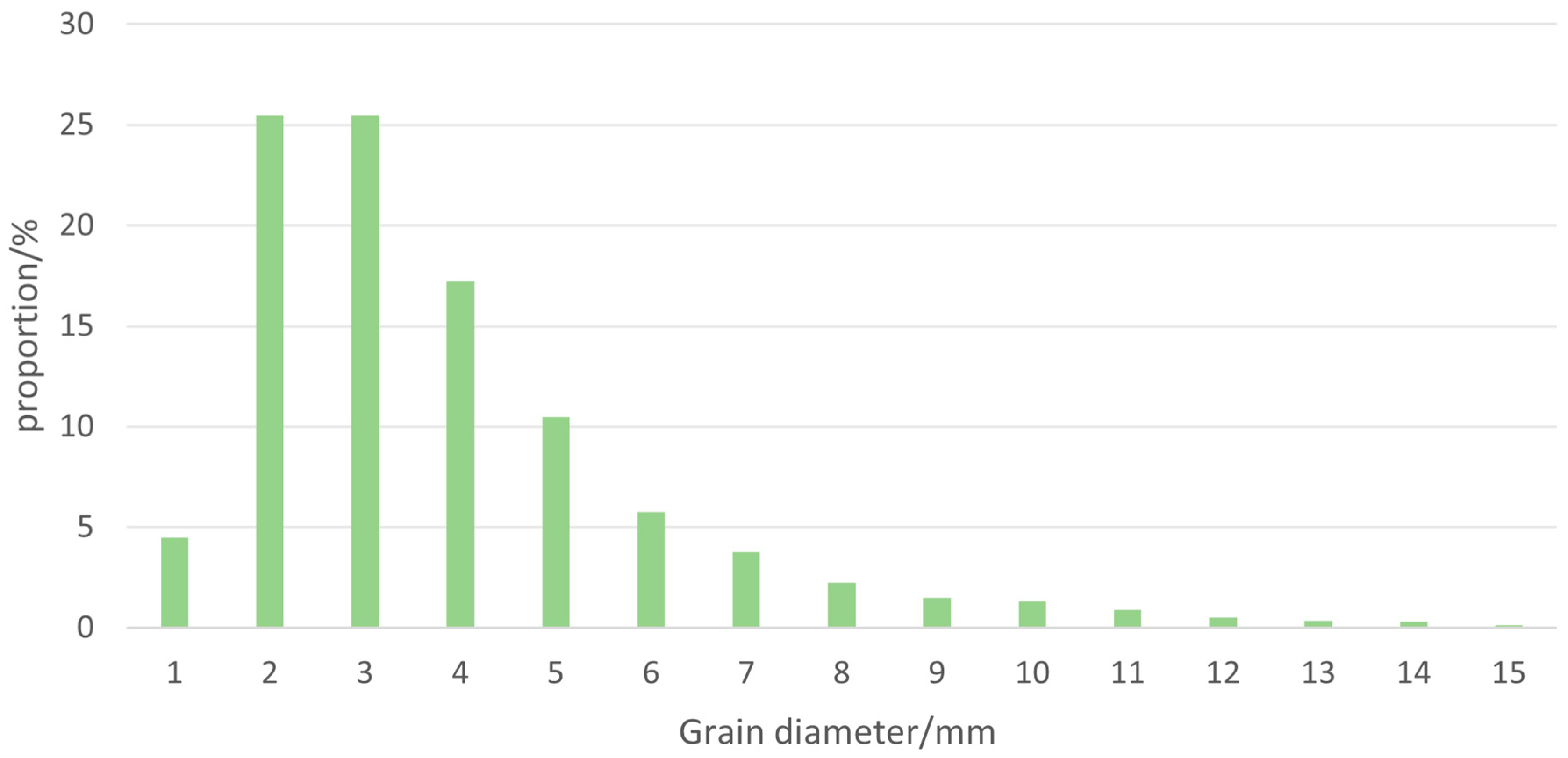





| Temperature (°C) | Strain Rate (s−1) | Elastic Modulus of Grain (MPa) | Strength of Grain (MPa) | Poisson’s Ratio of Grain | Elastic Modulus of Crystal Boundary (MPa) | Strength Crystal Boundary (MPa) | Initial Defect Content (%) | Grain Size (mm) |
|---|---|---|---|---|---|---|---|---|
| −5 | 10−4~10−5 | 9000 | 2 | 0.3 | 4000 | 1 | 6% | 1–15 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Deng, Y.; Liang, J.; Wang, J. Numerical Simulation of Fracture Failure in Three-Point Bending Specimens of Yellow River Granular Ice. Crystals 2024, 14, 1071. https://doi.org/10.3390/cryst14121071
Deng Y, Liang J, Wang J. Numerical Simulation of Fracture Failure in Three-Point Bending Specimens of Yellow River Granular Ice. Crystals. 2024; 14(12):1071. https://doi.org/10.3390/cryst14121071
Chicago/Turabian StyleDeng, Yu, Ju Liang, and Juan Wang. 2024. "Numerical Simulation of Fracture Failure in Three-Point Bending Specimens of Yellow River Granular Ice" Crystals 14, no. 12: 1071. https://doi.org/10.3390/cryst14121071
APA StyleDeng, Y., Liang, J., & Wang, J. (2024). Numerical Simulation of Fracture Failure in Three-Point Bending Specimens of Yellow River Granular Ice. Crystals, 14(12), 1071. https://doi.org/10.3390/cryst14121071






