Strain-Modulated Electronic Transport Properties in Two-Dimensional Green Phosphorene with Different Edge Morphologies
Abstract
:1. Introduction
2. Materials and Methods
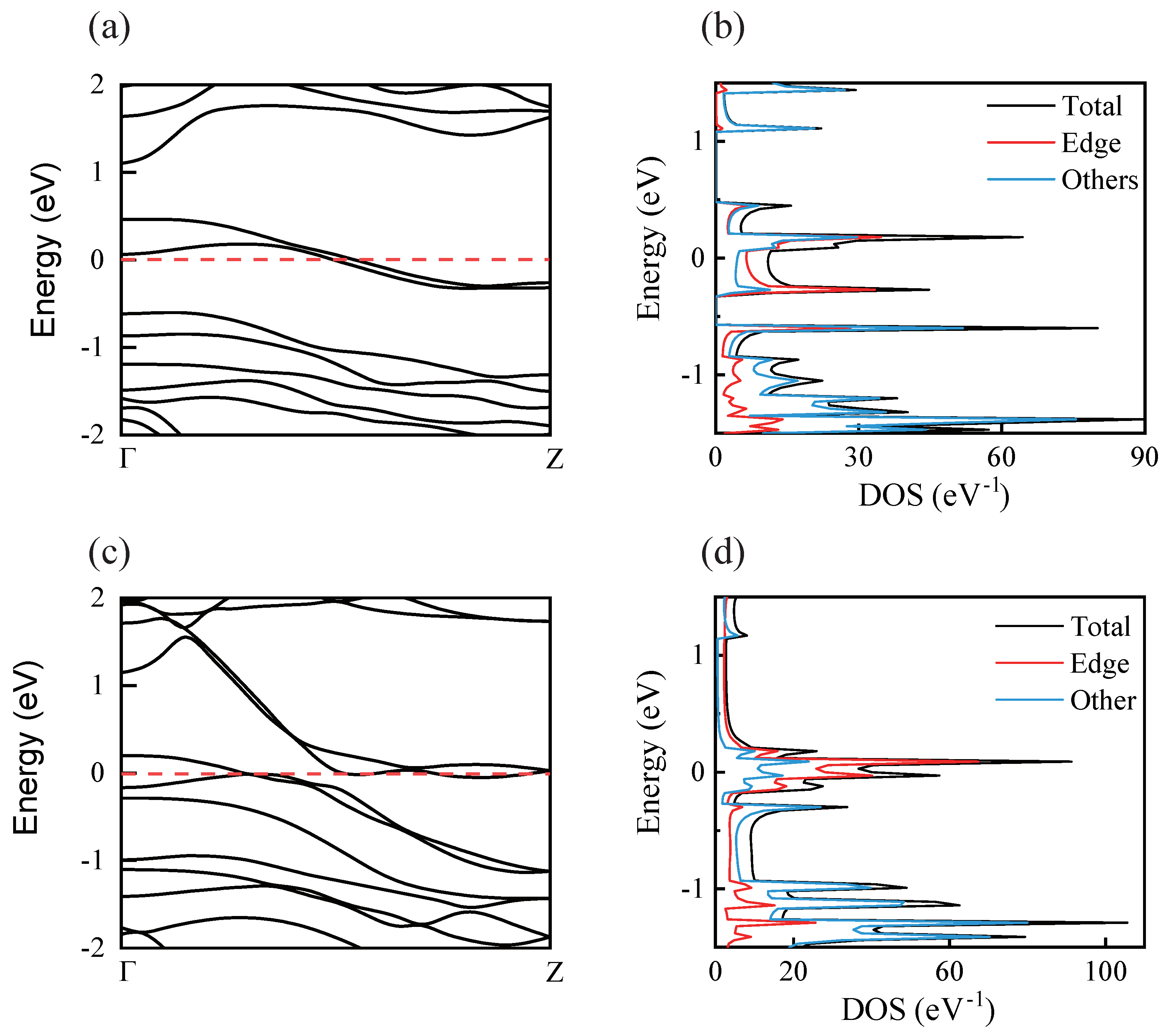
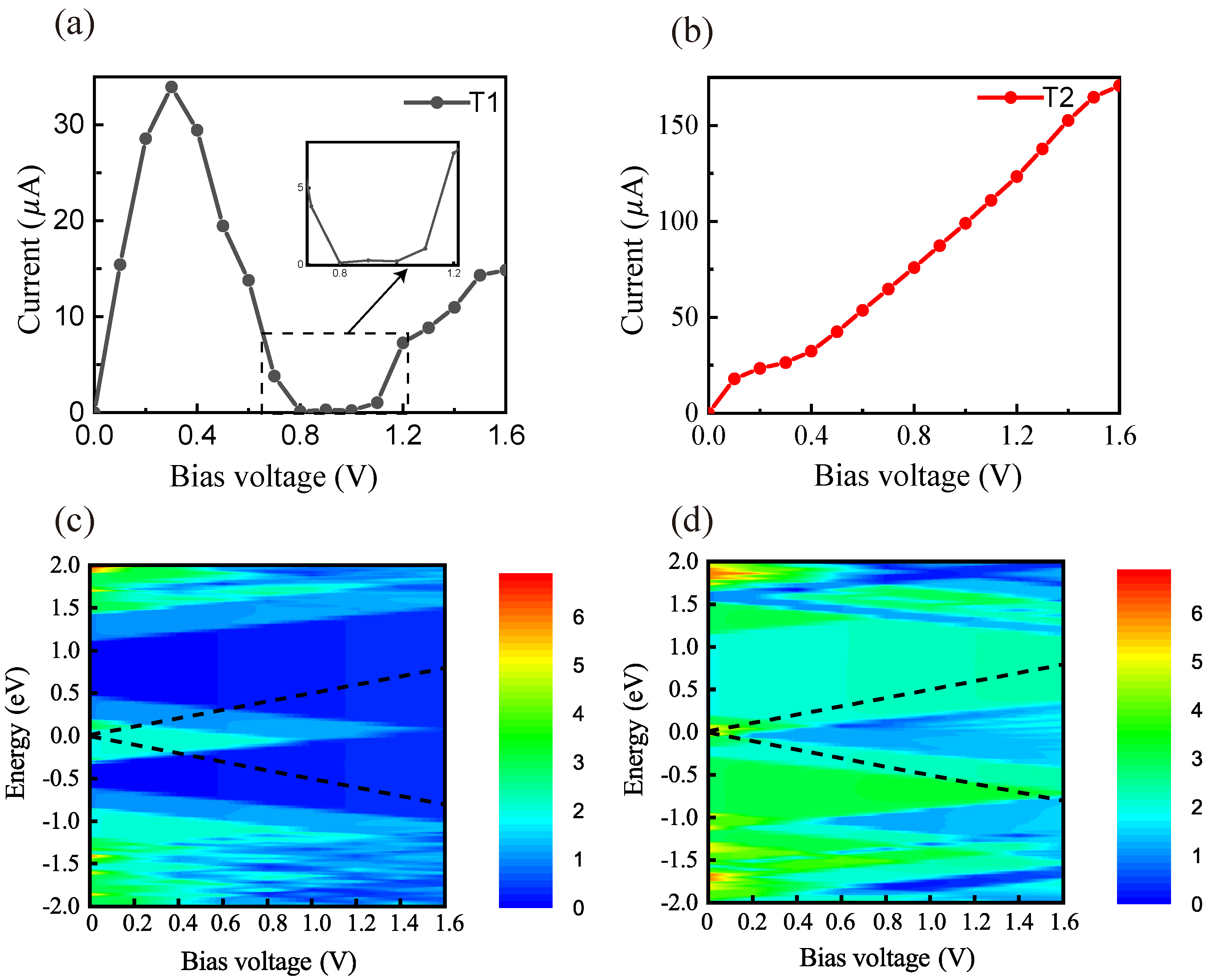
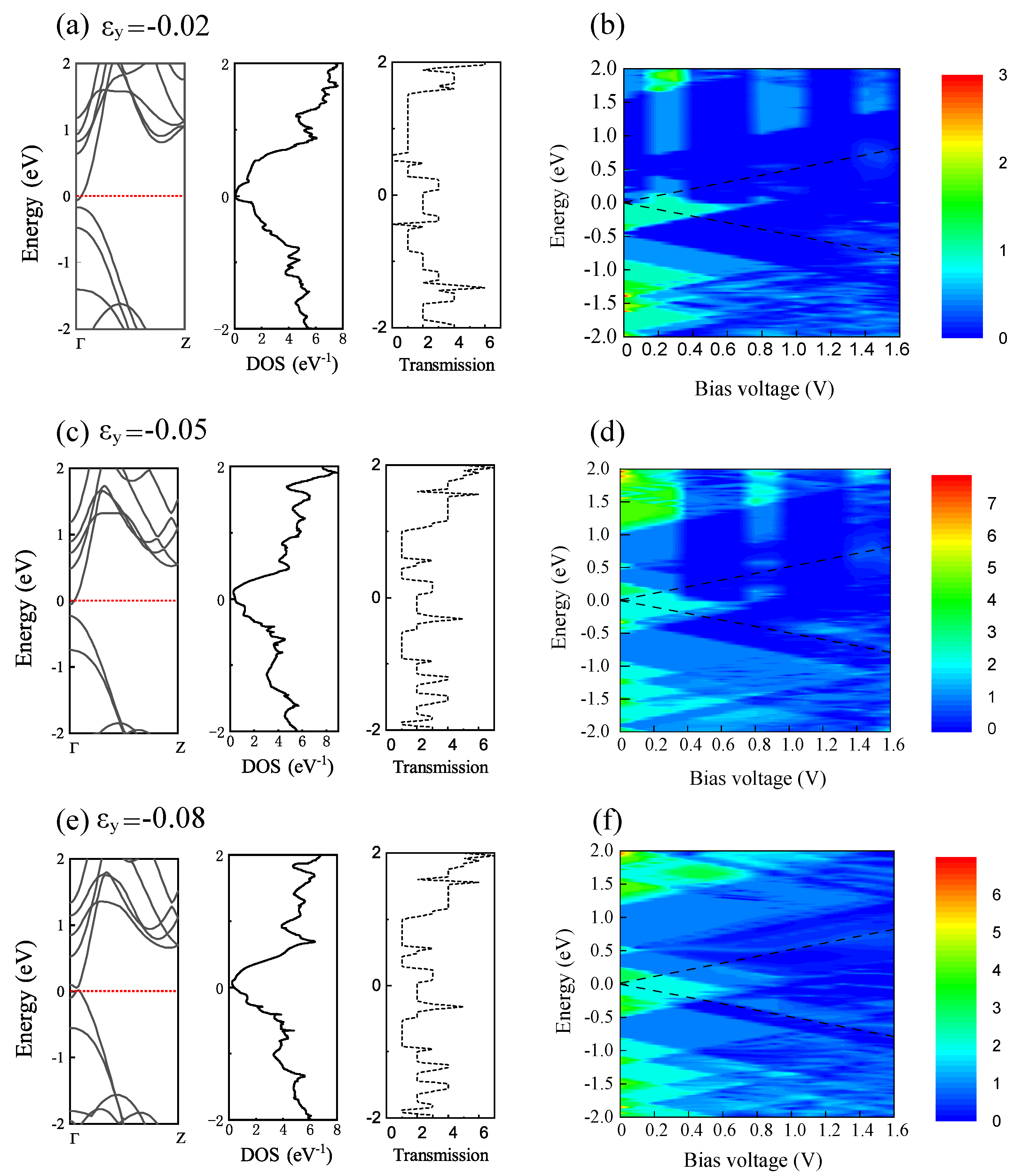
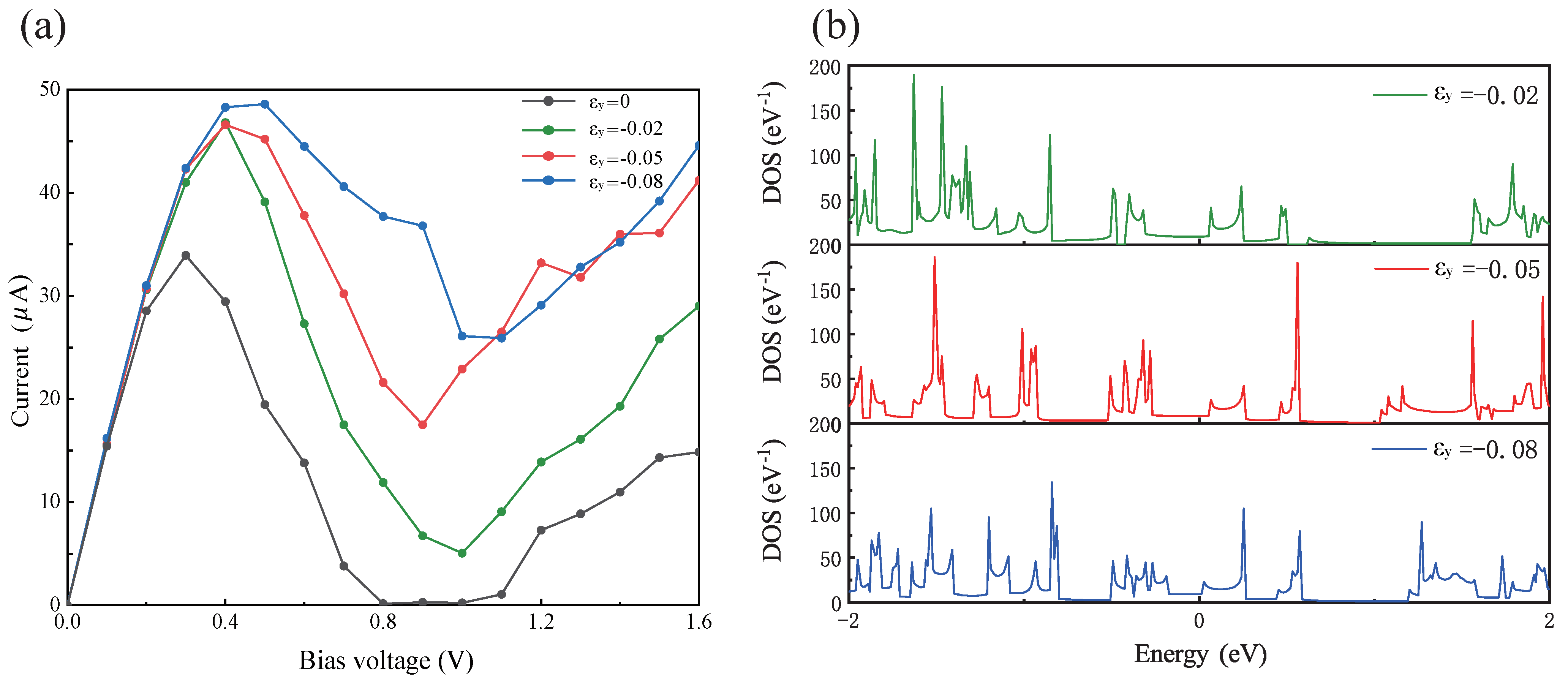
3. Results
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Zhou, Y.; Zhang, D.; Zhang, J.; Ye, C.; Miao, X. Negative differential resistance behavior in phosphorus-doped armchair graphene nanoribbon junctions. J. Appl. Phys. 2014, 115, 073703. [Google Scholar] [CrossRef]
- Hong, X.K.; Kuang, Y.W.; Qian, C.; Tao, Y.M.; Yu, H.L.; Zhang, D.B.; Liu, Y.S.; Feng, J.F.; Yang, X.F.; Wang, X.F. Axisymmetric All-Carbon Devices with High-Spin Filter Efficiency, Large-Spin Rectifying, and Strong-Spin Negative Differential Resistance Properties. J. Phys. Chem. C 2015, 120, 668–676. [Google Scholar] [CrossRef]
- Wu, Q.; Liu, R.; Qiu, Z.; Li, D.; Li, J.; Wang, X.; Ding, G. Cr3X4 (X = Se, Te) monolayers as a new platform to realize robust spin filters, spin diodes and spin valves. Phys. Chem. Chem. Phys. 2022, 24, 24873–24880. [Google Scholar] [CrossRef]
- Dong, X.; Peng, Z.; Chen, T.; Xu, L.; Ma, Z.; Liu, G.; Cen, K.; Xu, Z.; Zhou, G. Electronic structures and transport properties of low-dimensional GaN nanoderivatives: A first-principles study. Appl. Surf. Sci. 2021, 561, 150038. [Google Scholar] [CrossRef]
- Huang, L.; Chen, S.Z.; Zeng, Y.J.; Wu, D.; Li, B.L.; Feng, Y.X.; Fan, Z.Q.; Tang, L.M.; Chen, K.Q. Switchable Spin Filters in Magnetic Molecular Junctions Based on Quantum Interference. Adv. Electron. Mater. 2020, 6, 2000689. [Google Scholar] [CrossRef]
- Luisier, M. Atomistic simulation of transport phenomena in nanoelectronic devices. Chem. Soc. Rev. 2014, 43, 4357–4367. [Google Scholar] [CrossRef]
- Zhou, Y.; Zheng, X.; Cheng, Z.-Q.; Chen, K.-Q. Current Superposition Law Realized in Molecular Devices Connected in Parallel. J. Phys. Chem. C 2019, 123, 10462–10468. [Google Scholar] [CrossRef]
- Chen, Q.; Zheng, X.; Jiang, P.; Zhou, Y.-H.; Zhang, L.; Zeng, Z. Electric field induced tunable half-metallicity in an A-type antiferromagnetic bilayer LaBr2. Phys. Rev. B 2022, 106, 245423. [Google Scholar] [CrossRef]
- He, X.; Chen, J.; Li, S.; Lin, M.; Wang, Y.; Zheng, Y.; Lu, H. The tunability of electronic and transport properties of InSe/MoSe2 van der Waals heterostructure: A first-principles study. Surf. Interfaces 2023, 36, 102634. [Google Scholar] [CrossRef]
- Wang, X.; Feng, Z.; Rong, J.; Zhang, Y.; Zhong, Y.; Feng, J.; Yu, X.; Zhan, Z. Planar net-τ: A new high-performance metallic carbon anode material for lithium-ion batteries. Carbon 2019, 142, 438–444. [Google Scholar] [CrossRef]
- Wang, Z.F.; Jin, K.-H.; Liu, F. Quantum spin Hall phase in 2D trigonal lattice. Nat. Commun. 2016, 7, 12746. [Google Scholar] [CrossRef] [PubMed]
- Li, X.; Wang, X.; Zhang, L.; Lee, S.; Dai, H. Chemically Derived, Ultrasmooth Graphene Nanoribbon Semiconductors. Science 2008, 319, 1229–1232. [Google Scholar] [CrossRef]
- Su, H.-P.; Shao, Z.-G. Lithium enhancing electronic transport properties of monolayer 6,6,12-graphyne from first principles. Surf. Interfaces 2021, 22, 100903. [Google Scholar] [CrossRef]
- Wu, Q.-H.; Zhao, P.; Liu, H.-Y.; Liu, D.-S.; Chen, G. Odd–even dependence of rectifying behavior in carbon chains modified diphenyl–dimethyl molecule. Chem. Phys. Lett. 2014, 62, 605–606. [Google Scholar] [CrossRef]
- Wu, X.; Xiao, S.; Quan, J.; Tian, C.; Gao, G. Perylene-based molecular device: Multifunctional spintronic and spin caloritronic applications. Phys. Chem. Chem. Phys. 2023, 25, 7354–7365. [Google Scholar] [CrossRef]
- Kinikar, A.; Phanindra Sai, T.; Bhattacharyya, S.; Agarwala, A.; Biswas, T.; Sarker, S.K.; Krishnamurthy, H.R.; Jain, M.; Shenoy, V.B.; Ghosh, A. Quantized edge modes in atomic-scale point contacts in graphene. Nat. Nanotechnol. 2017, 12, 564–568. [Google Scholar] [CrossRef]
- Wu, Q.; Shen, L.; Yang, M.; Cai, Y.; Huang, Z.; Feng, Y.P. Electronic and transport properties of phosphorene nanoribbons. Phys. Rev. B 2015, 92, 035436. [Google Scholar] [CrossRef]
- Stegner, A.R.; Pereira, R.N.; Klein, K.; Lechner, R.; Dietmueller, R.; Brandt, M.S.; Stutzmann, M.; Wiggers, H. Electronic Transport in Phosphorus-Doped Silicon Nanocrystal Networks. Phys. Rev. Lett. 2008, 100, 026803. [Google Scholar] [CrossRef]
- Jia, C.; Cao, L.; Zhou, X.; Zhou, B.; Zhou, G. Low-bias negative differential resistance in junction of a benzene between zigzag-edged phosphorene nanoribbons. J. Phys. Condens. Matter 2018, 30, 265301. [Google Scholar] [CrossRef] [PubMed]
- Zheng, C.; Wu, K.; Jiang, K.; Yao, K.; Zhu, S.; Lu, Y. Perfect spin filtering effect, tunnel magnetoresistance and thermoelectric effect in metals-adsorbed blue phosphorene nanoribbons. Physica B 2022, 626, 413580. [Google Scholar] [CrossRef]
- Han, W.H.; Kim, S.; Lee, I.-H.; Chang, K.J. Prediction of Green Phosphorus with Tunable Direct Band Gap and High Mobility. J. Phys. Chem. Lett. 2017, 8, 4627–4632. [Google Scholar] [CrossRef]
- Qu, H.; Guo, S.; Zhou, W.; Wu, Z.; Cao, J.; Li, Z.; Zeng, H.; Zhang, S. Enhanced interband tunneling in two-dimensional tunneling transistors through anisotropic energy dispersion. Phys. Rev. B 2022, 105, 075413. [Google Scholar] [CrossRef]
- Liu, C.; Fu, B.; Yin, H.; Zhang, G.; Dong, C. Strain-tunable magnetism and nodal loops in monolayer MnB. Appl. Phys. Lett. 2020, 117, 103101. [Google Scholar] [CrossRef]
- Rezania, H.; Nourian, E.; Abdi, M.; Astinchap, B. Strain and magnetic field effects on the electronic and transport properties of γ-graphyne. RSC Adv. 2023, 13, 7988–7999. [Google Scholar] [CrossRef]
- Roldán, R.; Castellanos-Gomez, A.; Cappelluti, E.; Guinea, F. Strain engineering in semiconducting two-dimensional crystals. J. Phys. Condens. Matter 2015, 27, 313201. [Google Scholar] [CrossRef]
- Chen, Q.-Y. First-principles study on superconductive properties of compressive strain-engineered cryogenic superconducting heavy metal lead (Pb). Commun. Theor. Phys. 2021, 73, 035703. [Google Scholar] [CrossRef]
- Yang, N.; Chen, Q.; Xu, Y.; Luo, J.; Yang, H.; Jin, G. Strain-modulated electronic transport in two-dimensional carbon allotropes. AIP Adv. 2022, 12, 045102. [Google Scholar] [CrossRef]
- Ren, Y.; Cheng, F.; Zhou, X.-Y.; Chang, K.; Zhou, G.-H. Tunable mechanical, electronic and magnetic properties of monolayer C3N nanoribbons by external fields. Carbon 2019, 143, 14–20. [Google Scholar] [CrossRef]
- Ren, Y.; Liu, P.; Zhou, B.; Zhou, X.; Zhou, G. Crystallographic Characterization of Black Phosphorene and its Application in Nanostructures. Phys. Rev. Appl. 2019, 12, 064025. [Google Scholar] [CrossRef]
- Chen, J.; Zhang, Z.; Lu, H. Structure design and properties investigation of Bi2O2Se/graphene van der Waals heterojunction from first-principles study. Surf. Interfaces 2022, 33, 102289. [Google Scholar] [CrossRef]
- Brandbyge, M.; Mozos, J.L.; Ordejón, P.; Taylor, J.; Stokbro, K. Density-functional method for nonequilibrium electron transport. Phys. Rev. B 2022, 65, 165401. [Google Scholar] [CrossRef]
- Zhu, Y.; Li, H.; Chen, T.; Liu, D.; Zhou, Q. Investigation of the electronic and magnetic properties of low-dimensional FeCl2 derivatives by first-principles calculations. Vacuum 2020, 182, 109694. [Google Scholar] [CrossRef]
- Li, Y.-F.; Zhao, P.; Xu, Z.; Chen, G. Effect of linkage mode on the spin-polarized transport of a TPV radical-based molecular device. Chem. Phys. Lett. 2022, 794, 139515. [Google Scholar] [CrossRef]
- Poljak, M.; Suligoj, T. Immunity of electronic and transport properties of phosphorene nanoribbons to edge defects. Nano Res. 2016, 9, 1723–1734. [Google Scholar] [CrossRef]
- Zhang, W.; Basaran, C.; Ragab, T. Impact of geometry on transport properties of armchair graphene nanoribbon heterojunction. Carbon 2017, 124, 422–428. [Google Scholar] [CrossRef]
- Wu, Q.; Ang, L.K. Giant tunneling magnetoresistance in atomically thin VSi2N4/MoSi2N4/VSi2N4 magnetic tunnel junction. Appl. Phys. Lett. 2022, 120, 022401. [Google Scholar] [CrossRef]
- Chen, Q.-Y.; Liu, M.-Y.; Cao, C.; He, Y. Strain-tunable electronic and optical properties of novel anisotropic green phosphorene: A first-principles study. Nanotechnology 2019, 30, 335710. [Google Scholar] [CrossRef]
- Han, X.; Stewart, H.M.; Shevlin, S.A.; Catlow, C.R.A.; Guo, Z.X. Strain and Orientation Modulated Bandgaps and Effective Masses of Phosphorene Nanoribbons. Nano Lett. 2014, 14, 4607–4614. [Google Scholar] [CrossRef]
- Singsen, S.; Watwiangkham, A.; Ngamwongwan, L.; Fongkaew, I.; Jungthawan, S.; Suthirakun, S. Defect Engineering of Green Phosphorene Nanosheets for Detecting Volatile Organic Compounds: A Computational Approach. ACS Appl. Nano Mater. 2023, 6, 1496–1506. [Google Scholar] [CrossRef]
- QuantumATK Version T-2022.03, Synopsys QuantumATK. Available online: http://www.quantumwise.com (accessed on 1 December 2023).

Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Li, S.; Yang, H. Strain-Modulated Electronic Transport Properties in Two-Dimensional Green Phosphorene with Different Edge Morphologies. Crystals 2024, 14, 239. https://doi.org/10.3390/cryst14030239
Li S, Yang H. Strain-Modulated Electronic Transport Properties in Two-Dimensional Green Phosphorene with Different Edge Morphologies. Crystals. 2024; 14(3):239. https://doi.org/10.3390/cryst14030239
Chicago/Turabian StyleLi, Shuo, and Hai Yang. 2024. "Strain-Modulated Electronic Transport Properties in Two-Dimensional Green Phosphorene with Different Edge Morphologies" Crystals 14, no. 3: 239. https://doi.org/10.3390/cryst14030239
APA StyleLi, S., & Yang, H. (2024). Strain-Modulated Electronic Transport Properties in Two-Dimensional Green Phosphorene with Different Edge Morphologies. Crystals, 14(3), 239. https://doi.org/10.3390/cryst14030239




