Crystalline Microstructure, Microsegregations, and Mechanical Properties of Inconel 718 Alloy Samples Processed in Electromagnetic Levitation Facility
Abstract
:1. Introduction
2. Materials and Methods
2.1. Electromagnetic Levitation (EML)
2.2. Microstructure Investigation
2.3. Mechanical Characterization
3. Results and Discussion
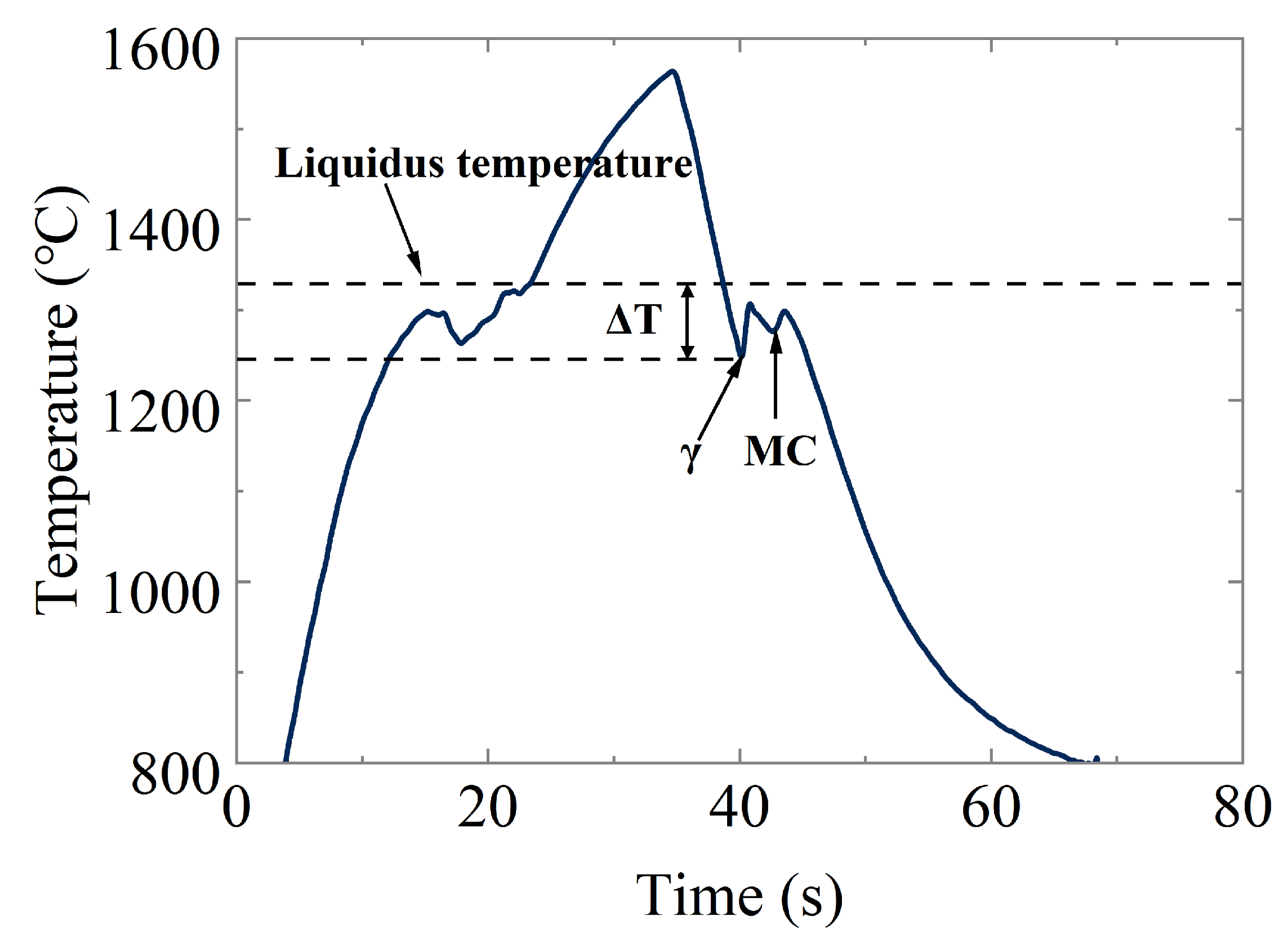
3.1. Thermal Behavior of the Samples
3.2. Microstructure Analysis
3.3. Dendrite Arm Spacing Analysis (Linear Intercept Method)
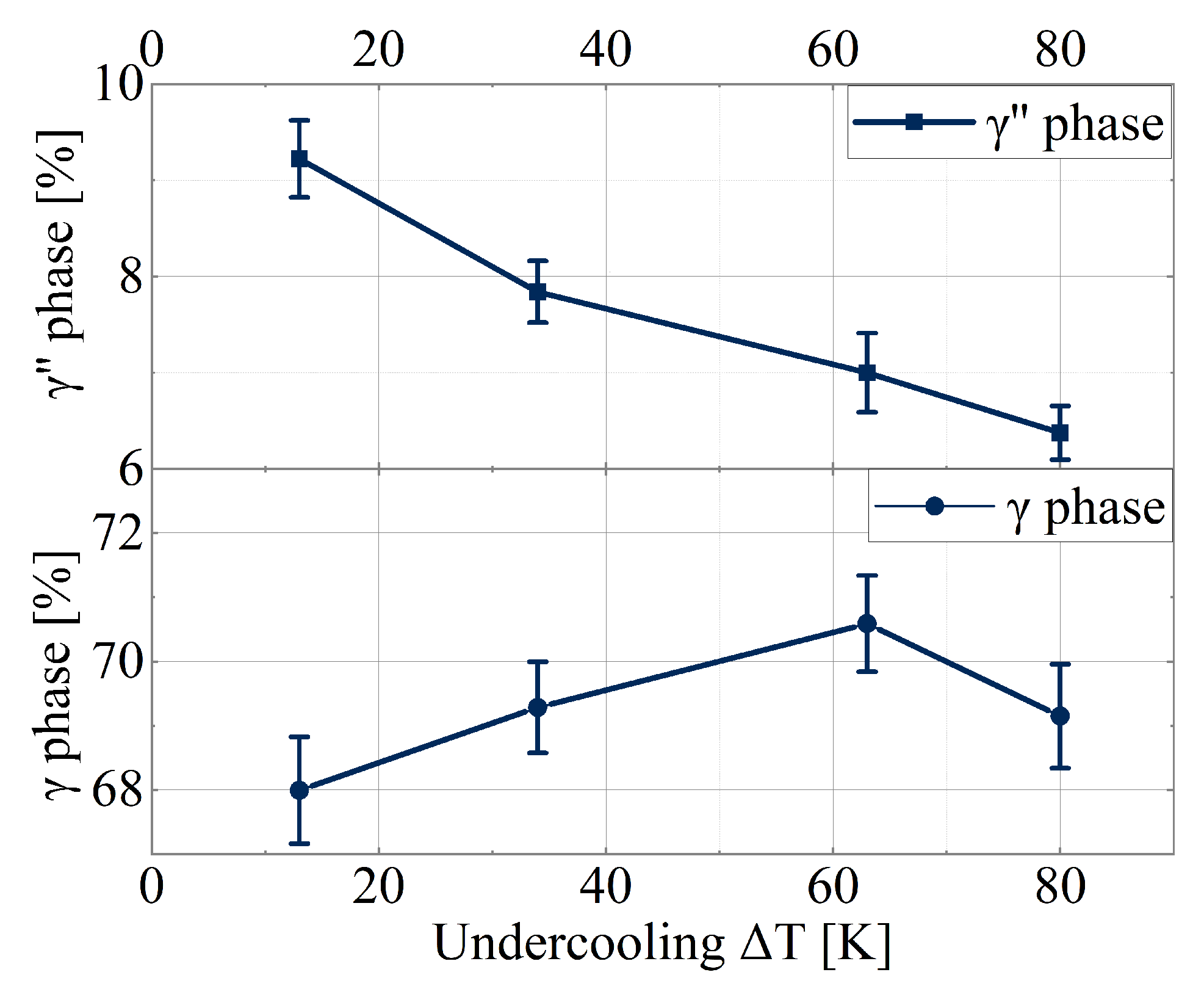
3.4. Phase Fraction Using Scanning Electron Microscopy Image Analysis
3.5. Mechanical Properties
4. Conclusions
- -
- The sharp change in the shape of the recalescence front exists at K;
- -
- The crystalline microstructure changes at K;
- -
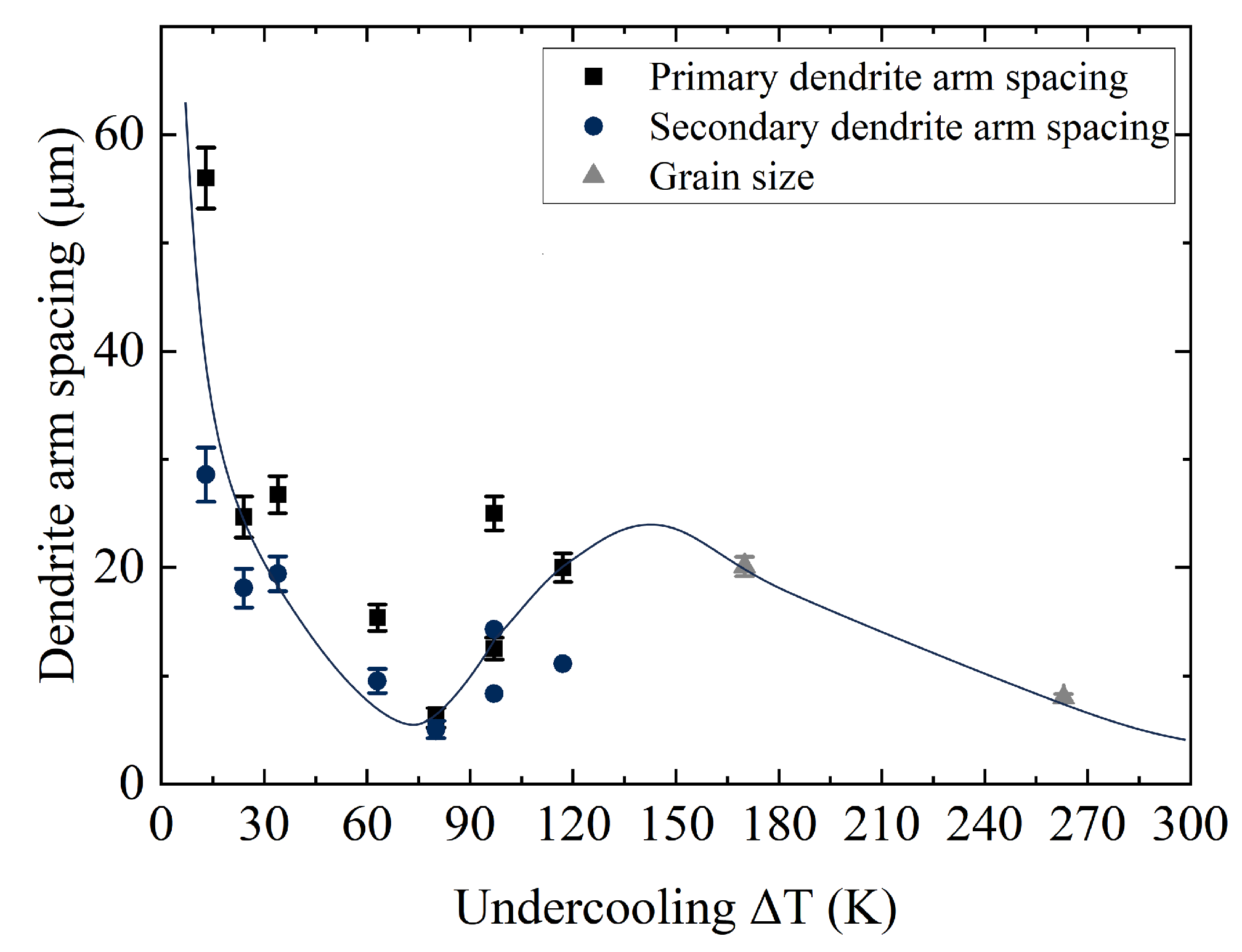
- The characteristic dendritic arm spacings change by the novel exponential law at K.
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| IN718 | Inconel 718 |
| EML | Electromagnetic levitation |
| S/L | Solid–liquid |
| TLA | Three letter acronym |
| SEM | Scanning electron microscopy |
| BSE | Backscattered electron |
| PDAS | Primary dendrite arm spacing |
| SDAS | Secondary dendrite arm spacing |
| EBSD | Electron backscattering diffraction |
| EDS | Energy-dispersive X-ray spectrometer |
Appendix A. Sharp Interface Model and Predictions of Crystal Growth Kinetics
- -
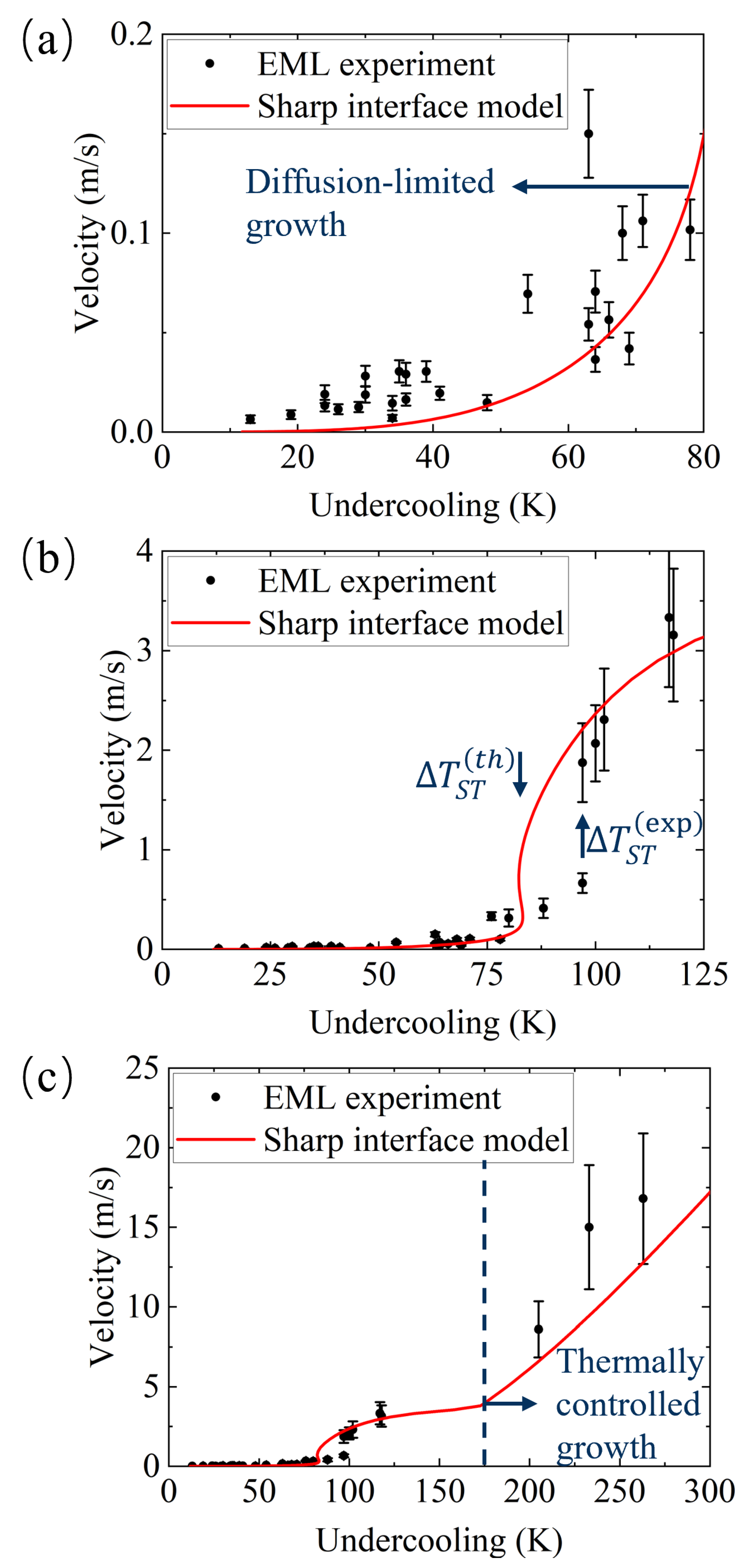
- Theoretically well-described region of small values of undercooling in which the dendrite growth proceeds in the solute diffusion-limited mode (Figure A1a); some discrepancy between theoretical curve and experimental data might be attributed to the ternary approximation in solidification analysis of the multicomponent IN718 alloy.
- -
- Theoretical description of the transition from solute diffusion-limited to thermally controlled growth with a small shift of the model prediction, with relatively experimental data for its beginning; see the difference in undercooling between and in Figure A1b.
- -
- The whole range of undercooling, including the sharp change to the purely thermally controlled growth at (m/s) (Figure A1c).
| Parameter | Sharp Interface Model | Refs. |
|---|---|---|
| Niobium concentration, | 5 wt% | pw |
| Chromium concentration, | 18 wt% | pw |
| Niobium partition coefficient *, | pw | |
| Chromium partition coefficient *, | pw | |
| Equilibrium liquidus slope of Ni-Nb, | K/wt% | [37] |
| Equilibrium liquidus slope of Ni-Cr, | K/wt% | [37] |
| Melting point, | 1726 K | pw |
| Gibbs–Thomson coefficient, | K·m | [38] |
| Adiabatic temperature of solidification, | K | pw |
| Nb diffusion coefficient, | m2/s | [39] |
| Cr diffusion coefficient, | m2/s | [39] |
| Thermal diffusivity, | m2/s | [39] |
| Kinetic growth coefficient, | m/s/K | pw |
| Capillary anisotropy strength, | pw | |
| Bulk diffusion speed, | m/s | pw |
| Diffusion speed of Nb at the interface, | m/s | pw |
| Diffusion speed of Cr at the interface, | m/s | pw |
| Stability constant, | pw |
- -
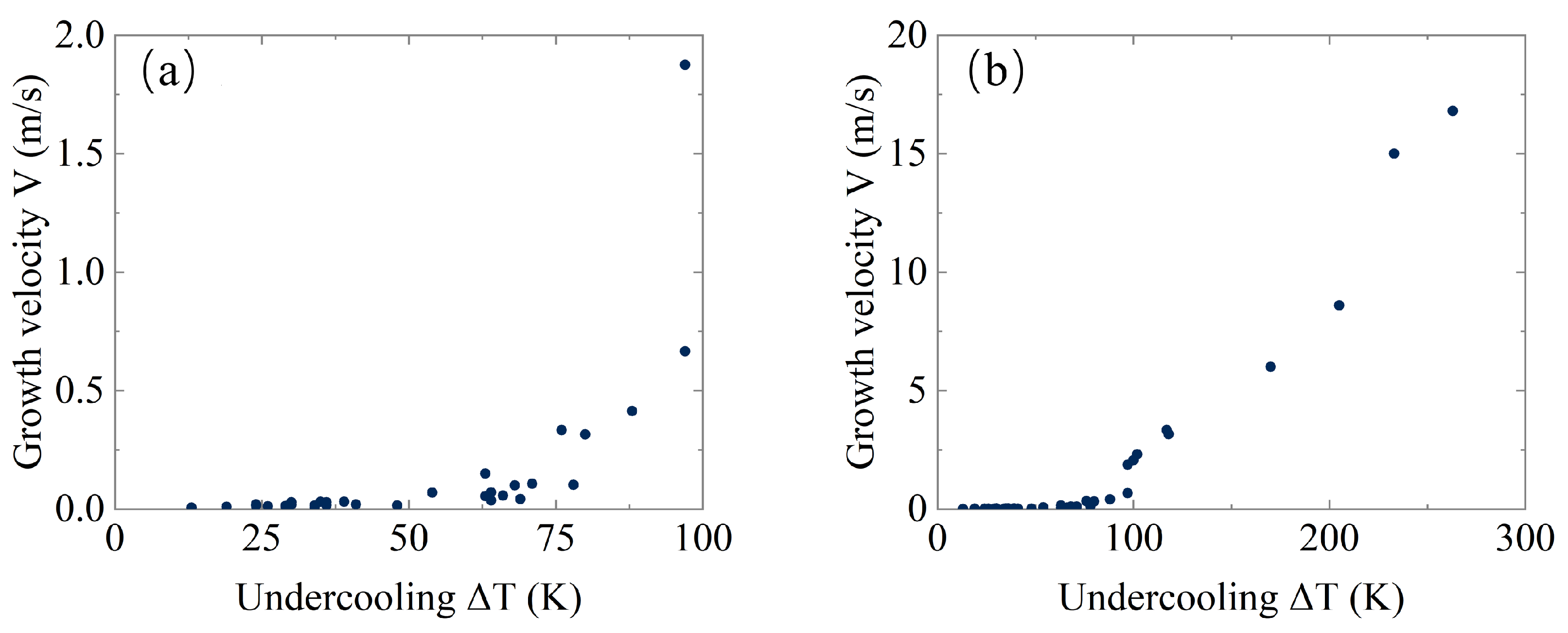
- The sharp change in the shape of recalescence front that is fixed at K (see Figure 3b–c);
- -
- Drastic change in the crystalline microstructure fixed at K (see Figure 4b–c);
- -
- Novel exponential behavior of the dendrite arm spacing fixed at K (see Figure 5).
References
- Reed, R.C. The Superalloys: Fundamentals and Applications; Cambridge University Press: Cambridge, MA, USA, 2006. [Google Scholar] [CrossRef]
- Rezayat, M.; Aboutorabi Sani, A.; Talafi Noghani, M.; Saghafi Yazdi, M.; Taheri, M.; Moghanian, A.; Mohammadi, M.A.; Moradi, M.; Mateo García, A.M.; Besharatloo, H. Effect of Lateral Laser-Cladding Process on the Corrosion Performance of Inconel 625. Metals 2023, 13, 367. [Google Scholar] [CrossRef]
- Medeiros, S.; Prasad, Y.; Frazier, W.G.; Srinivasan, R. Modeling grain size during hot deformation of IN 718. Scr. Mater. 1999, 42, 17–23. [Google Scholar] [CrossRef]
- Li, R.; Yao, M.; Liu, W.; He, X. Isolation and determination for delta, γ′ and γ′′ phases in Inconel 718 alloy. Scr. Mater. 2002, 46, 635–638. [Google Scholar] [CrossRef]
- Miller, M.; Babu, S.; Burke, M. Intragranular precipitation in alloy 718. Mater. Sci. Eng. A 1999, 270, 14–18. [Google Scholar] [CrossRef]
- Hong, S.; Chen, W.; Wang, T. A diffraction study of the γ′′ phase in INCONEL 718 superalloy. Metall. Mater. Trans. A 2001, 32, 1887–1901. [Google Scholar] [CrossRef]
- Sencer, B.; Bond, G.; Garner, F.; Hamilton, M.; Maloy, S.A.; Sommer, W. Correlation of radiation-induced changes in mechanical properties and microstructural development of Alloy 718 irradiated with mixed spectra of high-energy protons and spallation neutrons. J. Nucl. Mater. 2001, 296, 145–154. [Google Scholar] [CrossRef]
- Zhang, W.; Liu, F.; Liu, F.; Huang, C.; Liu, L.; Zheng, Y.; Lin, X. Effect of Al content on microstructure and microhardness of Inconel 718 superalloy fabricated by laser additive manufacturing. J. Mater. Res. Technol. 2022, 16, 1832–1845. [Google Scholar] [CrossRef]
- Fleck, M.; Querfurth, F.; Glatzel, U. Phase field modeling of solidification in multi-component alloys with a case study on the Inconel 718 alloy. J. Mater. Res. 2017, 32, 4605–4615. [Google Scholar] [CrossRef]
- Rahul, M.; Agilan, M.; Mohan, D.; Phanikumar, G. Integrated experimental and simulation approach to establish the effect of elemental segregation in Inconel 718 welds. Materialia 2022, 26, 101593. [Google Scholar] [CrossRef]
- Antonsson, T.; Fredriksson, H. The effect of cooling rate on the solidification of INCONEL 718. Metall. Mater. Trans. B 2005, 36, 85–96. [Google Scholar] [CrossRef]
- Knorovsky, G.A.; Cieslak, M.J.; Headley, T.J.; Romig, A.D.; Hammetter, W.F. INCONEL 718: A solidification diagram. Metall. Trans. A 1989, 20, 2149–2158. [Google Scholar] [CrossRef]
- Herlach, D.M.; Galenko, P.K.; Holland-Moritz, D. Metastable Solids from Undercooled Melts; Elsevier: Amsterdam, The Netherlands, 2007. [Google Scholar]
- Kropotin, N.; Fang, Y.; Yu, C.; Seyring, M.; Freiberg, K.; Lippmann, S.; Pinomaa, T.; Laukkanen, A.; Provatas, N.; Galenko, P.K. Modelling of the Solidifying Microstructure of Inconel 718: Quasi-Binary Approximation. Modelling 2023, 4, 323–335. [Google Scholar] [CrossRef]
- Elahi, S.; Tavakoli, R.; Boukellal, A.; Isensee, T.; Romero, I.; Tourret, D. Multiscale simulation of powder-bed fusion processing of metallic alloys. Comput. Mater. Sci. 2022, 209, 111383. [Google Scholar] [CrossRef]
- Herlach, D.; Eckler, K.; Karma, A.; Schwarz, M. Grain refinement through fragmentation of dendrites in undercooled melts. Mater. Sci. Eng. A 2001, 304, 20–25. [Google Scholar] [CrossRef]
- Toropova, L.V.; Alexandrov, D.V.; Kao, A.; Rettenmayr, M.; Galenko, P.K. Electromagnetic levitation method as a containerless experimental technique. Phys. Uspekhi 2023, 66, 722–733. [Google Scholar] [CrossRef]
- Publication Number SMC-045. Copyright© Special Metals Corporation. 2007. Available online: http://www.specialmetals.com (accessed on 1 December 2023).
- Kurz, W.; Fisher, D.; Rappaz, M. Fundamentals of Solidification, 5th ed.; Trans Tech Publications Ltd.: Zurich, Switzerland, 2023. [Google Scholar]
- Boettinger, W.J.; Coriell, S.R.; Greer, A.; Karma, A.; Kurz, W.; Rappaz, M.; Trivedi, R. Solidification microstructures: Recent developments, future directions. Acta Mater. 2000, 48, 43–70. [Google Scholar] [CrossRef]
- Schwarz, M.; Karma, A.; Eckler, K.; Herlach, D.M. Physical Mechanism of Grain Refinement in Solidification of Undercooled Melts. Phys. Rev. Lett. 1994, 73, 1380–1383. [Google Scholar] [CrossRef]
- Karma, A. Model of grain refinement in solidification of undercooled melts. Int. J. Non-Equilib. Process. 1998, 11, 201–233. [Google Scholar]
- Vandersluis, E.; Ravindran, C.R. Comparison of Measurement Methods for Secondary Dendrite Arm Spacing. Metallogr. Microstruct. Anal. 2017, 6, 89–94. [Google Scholar] [CrossRef]
- Kirkwood, D.H. A simple model for dendrite arm coarsening during solidification. Mater. Sci. Eng. 1985, 73, L1–L4. [Google Scholar] [CrossRef]
- Galenko, P.K.; Jou, D. Rapid solidification as non-ergodic phenomenon. Phys. Rep. 2019, 818, 1–70. [Google Scholar] [CrossRef]
- Galenko, P.K.; Reutzel, S.; Herlach, D.M.; Fries, S.G.; Steinbach, I.; Apel, M. Dendritic solidification in undercooled Ni–Zr–Al melts: Experiments and modeling. Acta Mater. 2009, 57, 6166–6175. [Google Scholar] [CrossRef]
- Barbieri, A.; Langer, J.S. Predictions of dendritic growth rates in the linearized solvability theory. Phys. Rev. A 1989, 39, 5314–5325. [Google Scholar] [CrossRef]
- Ben Amar, M.; Pelcé, P. Impurity effect on dendritic growth. Phys. Rev. A 1989, 39, 4263–4269. [Google Scholar] [CrossRef]
- Brener, E.A.; Mel’nikov, V.I. Two-dimensional dendritic growth at arbitrary Peclet number. J. Phys. 1990, 51, 157–166. [Google Scholar] [CrossRef]
- Müller-Krumbhaar, H.; Abel, T.; Brener, E.; Hartmann, M.; Eissfeldt, N.; Temkin, D. Growth-Morphologies in Solidification and Hydrodynamics. JSME Int. J. Ser. B Fluids Therm. Eng. 2002, 45, 129–132. [Google Scholar] [CrossRef]
- Trivedi, R.; Kurz, W. Morphological stability of a planar interface under rapid solidification conditions. Acta Metall. 1986, 34, 1663–1670. [Google Scholar] [CrossRef]
- Trivedi, R.; Kurz, W. Dendritic growth. Int. Mater. Rev. 1994, 39, 49–74. [Google Scholar] [CrossRef]
- Alexandrov, D.V.; Galenko, P.K. Selected mode of dendritic growth with n-fold symmetry in the presence of a forced flow. EPL Europhys. Lett. 2017, 119, 16001. [Google Scholar] [CrossRef]
- Alexandrov, D.V.; Galenko, P.K.; Toropova, L.V. Thermo-solutal and kinetic modes of stable dendritic growth with different symmetries of crystalline anisotropy in the presence of convection. Philos. Trans. R. Soc. A Math. Phys. Eng. Sci. 2018, 376, 20170215. [Google Scholar] [CrossRef] [PubMed]
- Yuan, K.; Guo, W.; Li, P.; Wang, J.; Su, Y.; Lin, X.; Li, Y. Influence of process parameters and heat treatments on the microstructures and dynamic mechanical behaviors of Inconel 718 superalloy manufactured by laser metal deposition. Mater. Sci. Eng. A 2018, 721, 215–225. [Google Scholar] [CrossRef]
- Chen, M.; Du, Q.; Shi, R.; Fu, H.; Liu, Z.; Xie, J. Phase field simulation of microstructure evolution and process optimization during homogenization of additively manufactured Inconel 718 alloy. Front. Mater. 2022, 9, 1043249. [Google Scholar] [CrossRef]
- Nie, P.; Ojo, O.; Li, Z. Numerical modeling of microstructure evolution during laser additive manufacturing of a nickel-based superalloy. Acta Mater. 2014, 77, 85–95. [Google Scholar] [CrossRef]
- Ferreira, D.; Bezerra, B.; Collyer, M.; Garcia, A.; Ferreira, I.L. The use of computational thermodynamics for the determination of surface tension and Gibbs–Thomson coefficient of multicomponent alloys. Contin. Mech. Thermodyn. 2018, 30, 1145–1154. [Google Scholar] [CrossRef]
- Connétable, D.; Ter-Ovanessian, B.; Andrieu, É. Diffusion and segregation of niobium in fcc-nickel. J. Phys. Condens. Matter 2012, 24, 095010. [Google Scholar] [CrossRef]
- Galenko, P.; Hanke, R.; Paul, P.; Koch, S.; Rettenmayr, M.; Gegner, J.; Herlach, D.; Dreier, W.; Kharanzhevski, E. Solidification kinetics of CuZr alloy: Ground-based and microgravity experiments. IOP Conf. Ser. Mater. Sci. Eng. 2017, 192, 012028. [Google Scholar] [CrossRef]
- Jou, D.; Casas-Vazquez, J.; Lebon, G. Extended Irreversible Thermodynamics, 4th ed.; Springer: Dordrecht, The Netherlands, 2010. [Google Scholar]
- Lebon, G.; Jou, D.; Casas-Vazquez, J. Understanding Non-Equilibrium Thermodynamics; Springer: Berlin/Heidelberg, Germany, 2008. [Google Scholar]



| Element | Ni | Cr | Nb | Mo | Ti | Al | C | Fe |
|---|---|---|---|---|---|---|---|---|
| Measured concentration | 52.78 | 18.7 | 4.95 | 3.04 | 1.01 | 0.55 | 0.046 | Balance |
| Powder concentration | 54 | 18 | 8 | 2 | 0 | 0 | 0 | Balance |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Fang, Y.; Yu, C.; Kropotin, N.; Seyring, M.; Freiberg, K.; Kolbe, M.; Lippmann, S.; Galenko, P.K. Crystalline Microstructure, Microsegregations, and Mechanical Properties of Inconel 718 Alloy Samples Processed in Electromagnetic Levitation Facility. Crystals 2024, 14, 244. https://doi.org/10.3390/cryst14030244
Fang Y, Yu C, Kropotin N, Seyring M, Freiberg K, Kolbe M, Lippmann S, Galenko PK. Crystalline Microstructure, Microsegregations, and Mechanical Properties of Inconel 718 Alloy Samples Processed in Electromagnetic Levitation Facility. Crystals. 2024; 14(3):244. https://doi.org/10.3390/cryst14030244
Chicago/Turabian StyleFang, Yindong, Chu Yu, Nikolai Kropotin, Martin Seyring, Katharina Freiberg, Matthias Kolbe, Stephanie Lippmann, and Peter K. Galenko. 2024. "Crystalline Microstructure, Microsegregations, and Mechanical Properties of Inconel 718 Alloy Samples Processed in Electromagnetic Levitation Facility" Crystals 14, no. 3: 244. https://doi.org/10.3390/cryst14030244
APA StyleFang, Y., Yu, C., Kropotin, N., Seyring, M., Freiberg, K., Kolbe, M., Lippmann, S., & Galenko, P. K. (2024). Crystalline Microstructure, Microsegregations, and Mechanical Properties of Inconel 718 Alloy Samples Processed in Electromagnetic Levitation Facility. Crystals, 14(3), 244. https://doi.org/10.3390/cryst14030244






