High-Entropy Engineering in Thermoelectric Materials: A Review
Abstract
1. Introduction
2. Understanding Entropy Engineering in TE Materials
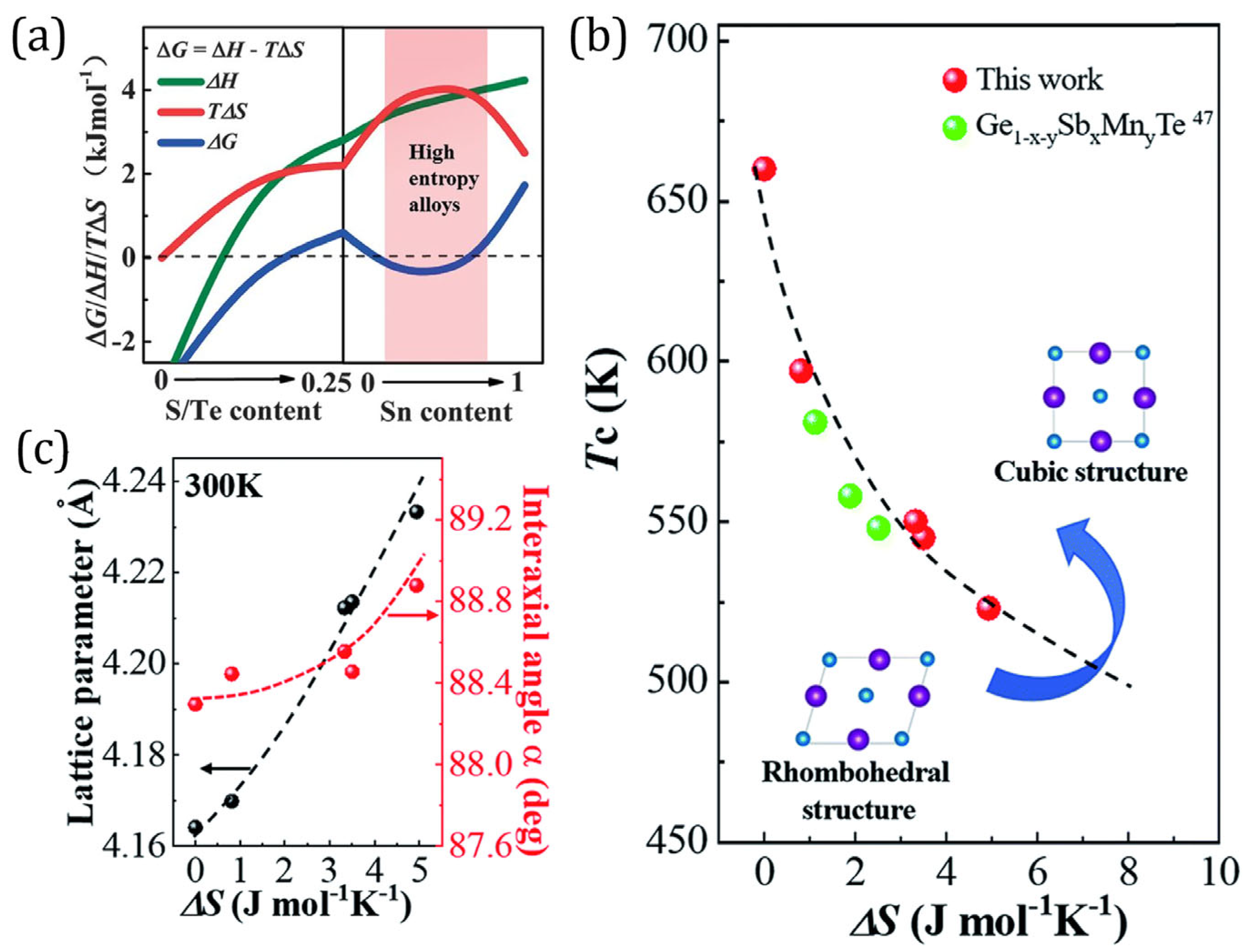
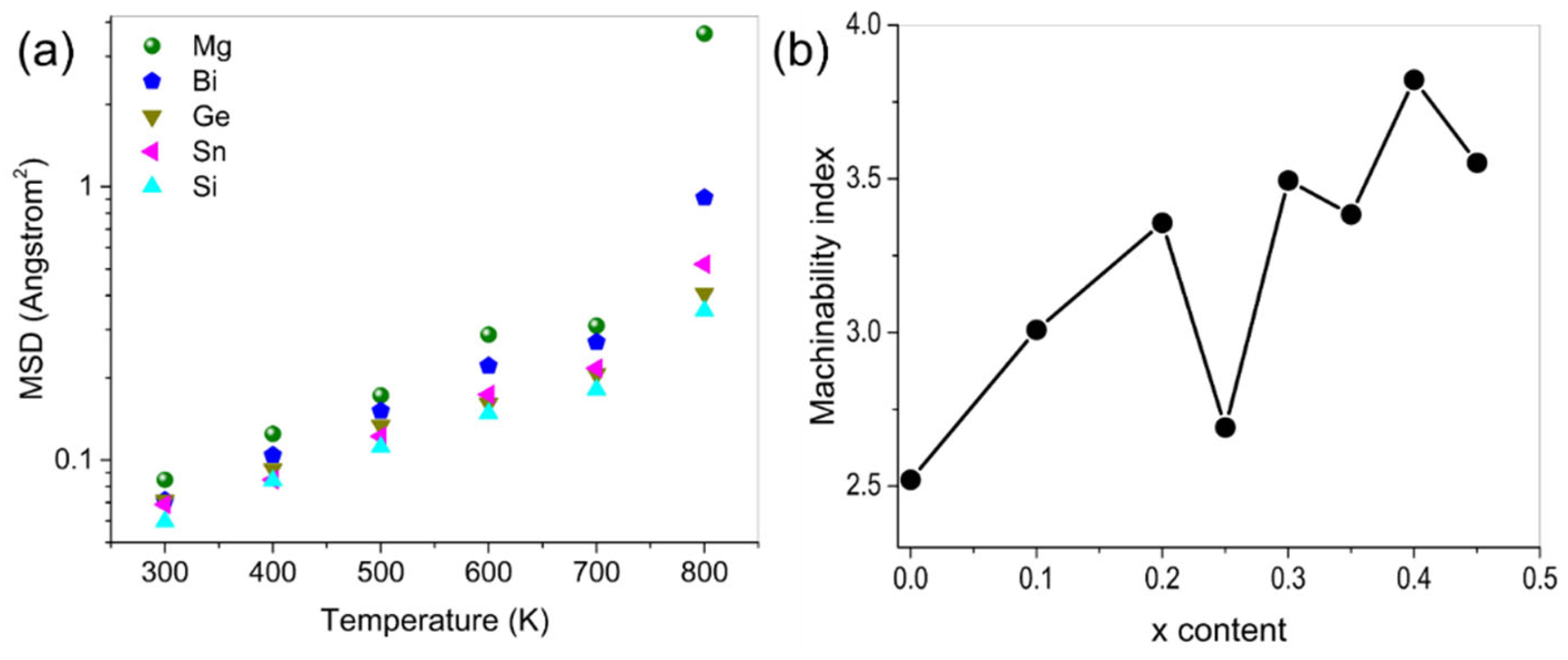
2.1. Lattice Distortion
2.2. Structural Stabilization
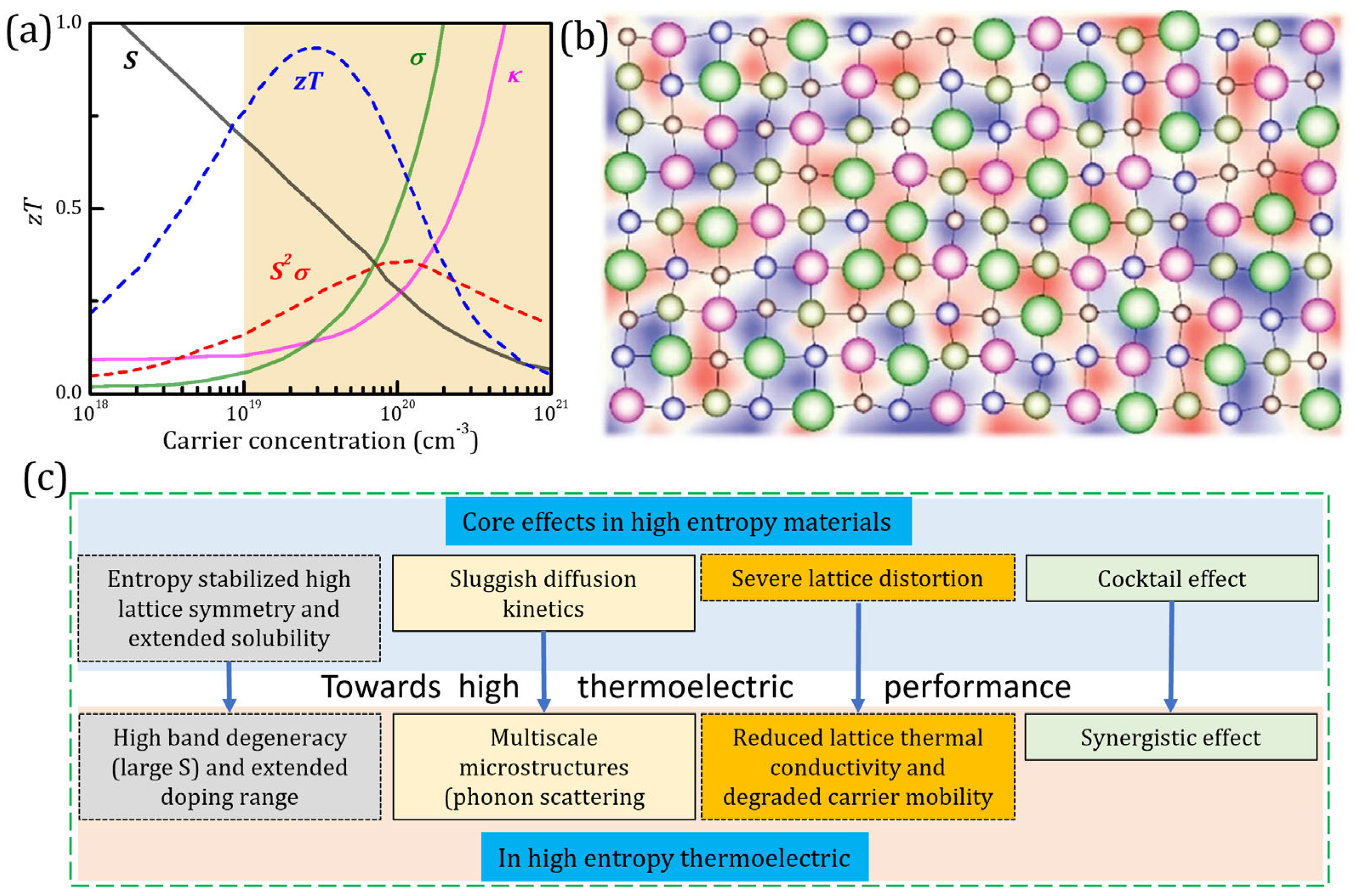
2.3. Cocktail Effect
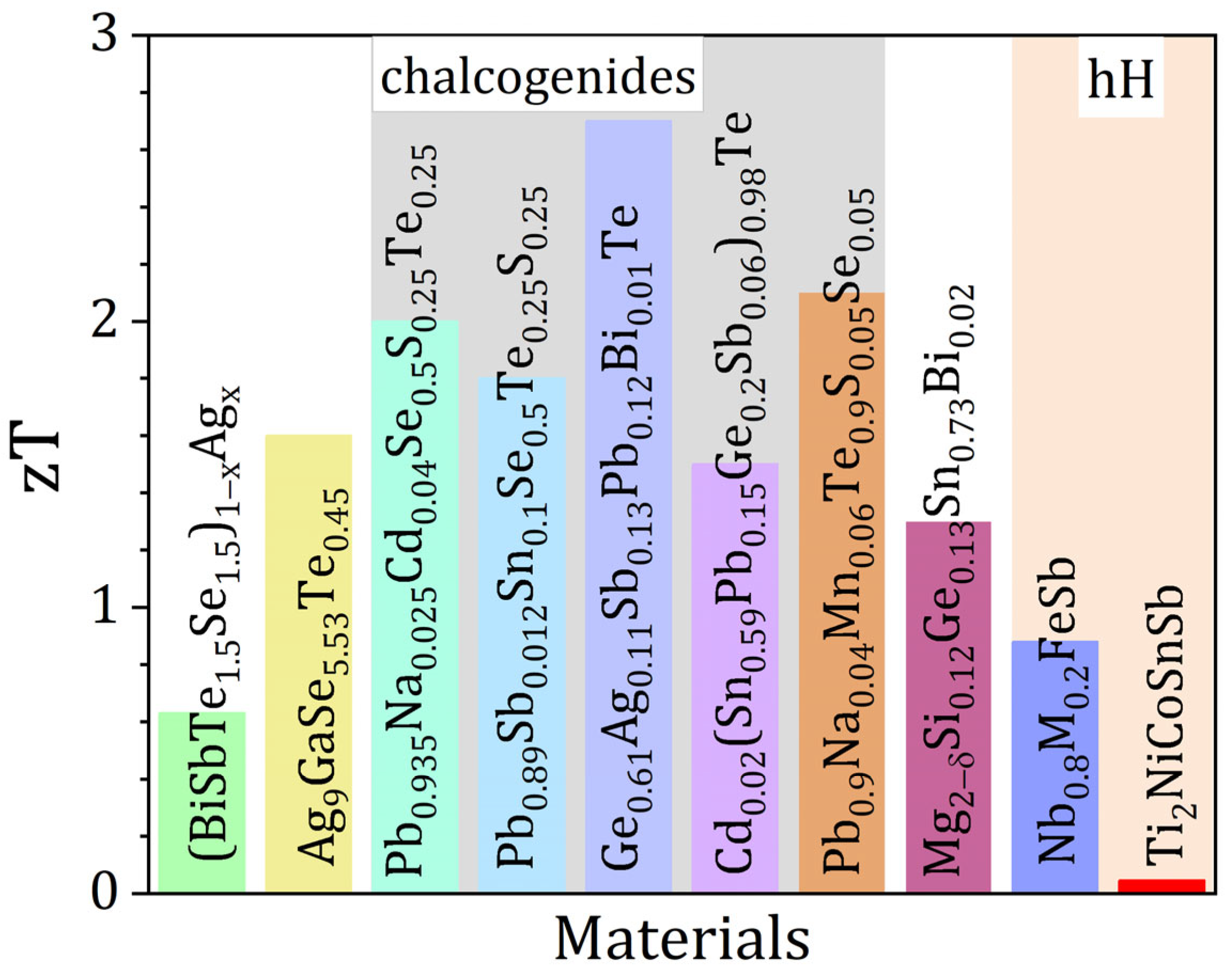
3. Entropy Engineering to Enhance Materials’ zT
| Year | High-Entropy TE Materials | PF (μWcm−1K−1) | κ (Wm−1K−1) | zTmax | zTpeak (K) | Ref. |
|---|---|---|---|---|---|---|
| 2016 | (BiSbTe1.5Se1.5)1−xAgx [x = 0.9%] | 6.5 | 0.43 | 0.63 | 450 | [39] |
| 2017 | Pb0.94SnTeSeLa0.06 | 12.6 | 1.37 | 0.8 | 873 | [40] |
| 2018 | (Sn0.74Ge0.2Pb0.1)0.75Mn0.275Te | 17.9 | 1.13 | 1.42 | 900 | [41] |
| 2018 | Nb0.8M0.2FeSb (M = Hf, Zr, Mo, V, Ti; equimolar) | 42.2 | 4.19 | 0.88 | 873 | [12] |
| 2018 | Ag9GaSe5.53Te0.45 | 6.7 | 0.35 | 1.6 | 850 | [42] |
| 2019 | Ti2NiCoSnSb | 5.7 | 10.5 | 0.047 | 860 | [43] |
| 2019 | Ge0.84In0.01Pb0.1Sb0.05Te0.997I0.003 | 30.6 | 1.19 | 2.1 | 800 | [36] |
| 2020 | AgSnSbSe1.5Te1.5 | 9.8 | 0.62 | 1.14 | 723 | [44] |
| 2020 | Ag0.25Pb0.5Bi0.25S0.4Se0.5Te0.1 | 4.6 | 0.61 | 0.54 | 723 | [45] |
| 2021 | Ga0.025(Sn0.25Pb0.25Mn0.25Ge0.25)0.975Te | 18.5 | 1 | 1.52 | 823 | [46] |
| 2021 | AgMnGeSbTe4-1 mol% Ag8GeTe6 | 13.9 | 0.85 | 1.27 | 773 | [47] |
| 2021 | Cu0.8Ag0.2(ZnGe)0.1(GaIn)0.4Te2 | 6 | 0.48 | 1.02 | 820 | [48] |
| 2021 | Pb0.935Na0.025Cd0.04Se0.5S0.25Te0.25 | 16.2 | 0.73 | 2 | 900 | [9] |
| 2021 | Pb0.89Sb0.012Sn0.1Se0.5Te0.25S0.25 | 12.5 | 0.63 | 1.8 | 900 | [8] |
| 2022 | Ge0.61Ag0.11Sb0.13Pb0.12Bi0.01Te | 28.6 | 0.834 | 2.7 | 750 | [10] |
| 2022 | MFe0.7Co0.3Sb (M = equimolar Ti, Zr, Hf, V, Nb, Ta) | 7.8 | 2.88 | 0.25 | 923 | [11] |
| 2022 | AgMnSn0.25Pb0.75SbTe4 | 11.3 | 0.67 | 1.3 | 773 | [37] |
| 2022 | Cd0.02(Sn0.59Pb0.15Ge0.2Sb0.06)0.98Te | 19.1 | 1.02 | 1.5 | 800 | [18] |
| 2022 | Cu1.87Ag0.13(In0.06Sn0.94)Se2S | 4.35 | 0.25 | 1.52 | 873 | [49] |
| 2022 | Ge0.82Sb0.08Te0.9(MnZnCdTe3)0.1 | 17.2 | 1 | 1.24 | 723 | [50] |
| 2023 | Mg2−δSi0.12Ge0.13Sn0.73Bi0.02 | 40 | 2.15 | 1.3 | 700 | [18] |
| 2023 | Pb0.9Na0.04Mn0.06Te0.9S0.05Se0.05 | 22.1 | 0.87 | 2.1 | 825 | [51] |
3.1. Phase Stabilization
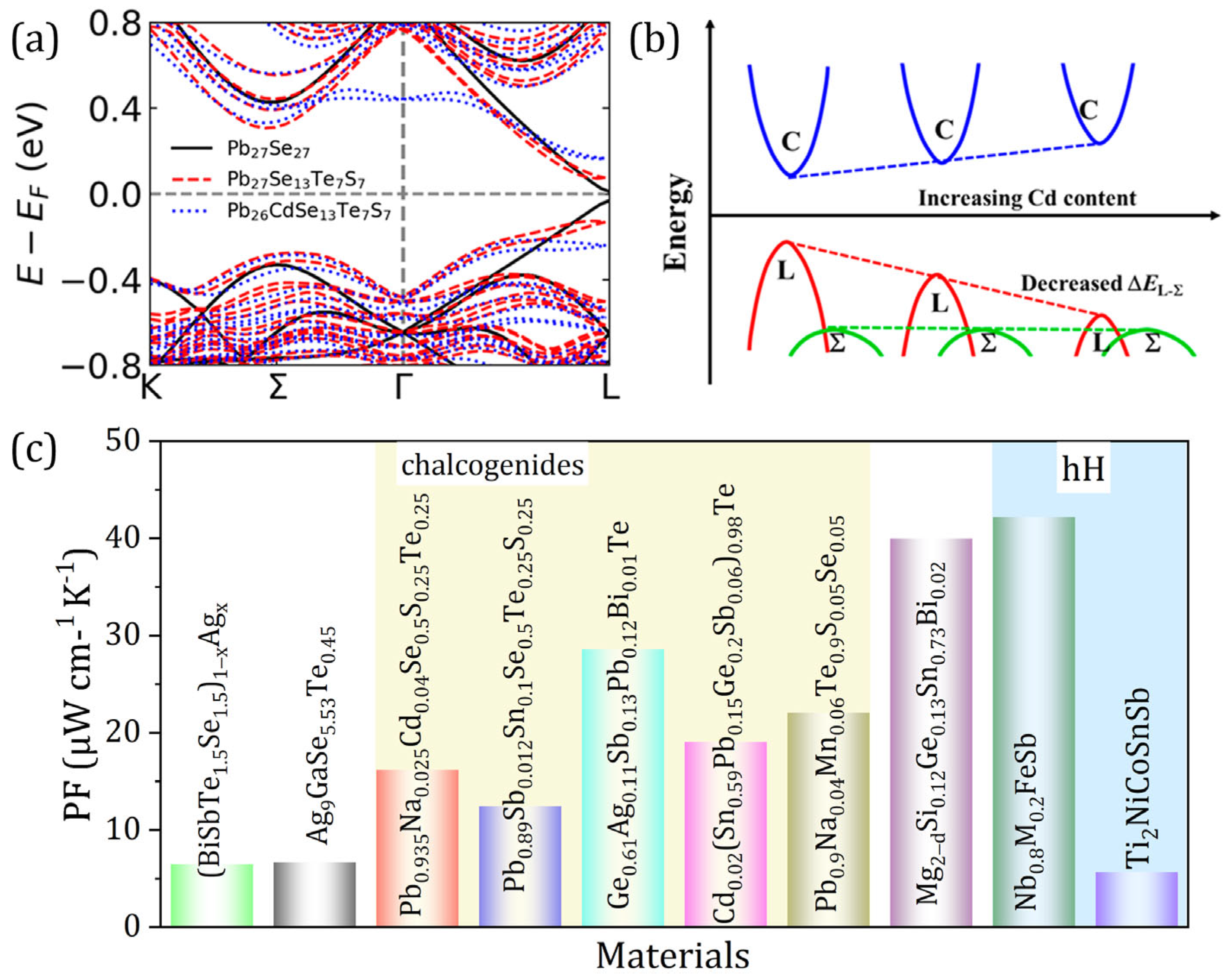
3.2. Optimization of Power Factor
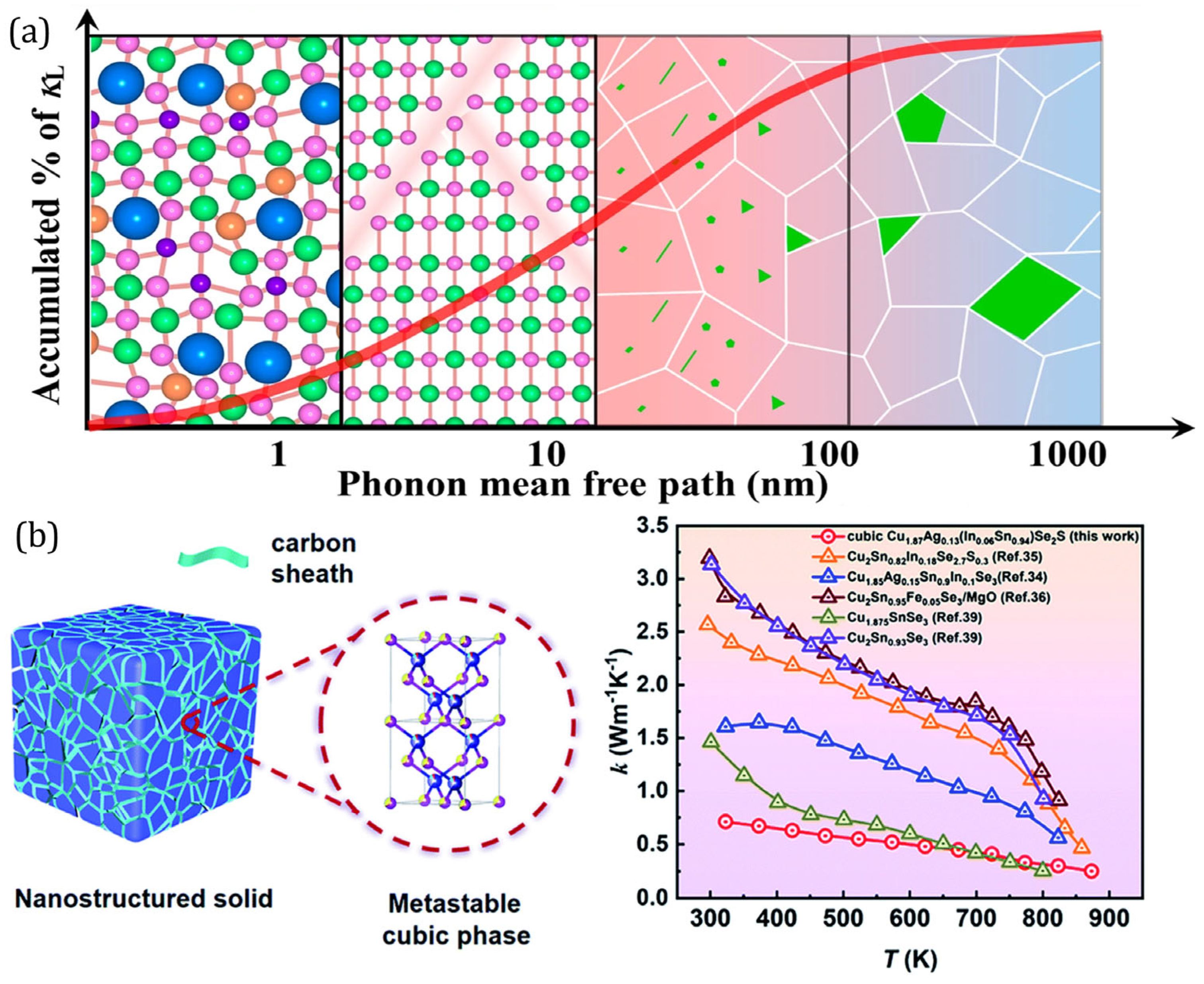
3.3. Low Thermal Conductivity
4. Robust Mechanical Properties
4.1. Materials’ Mechanical Properties
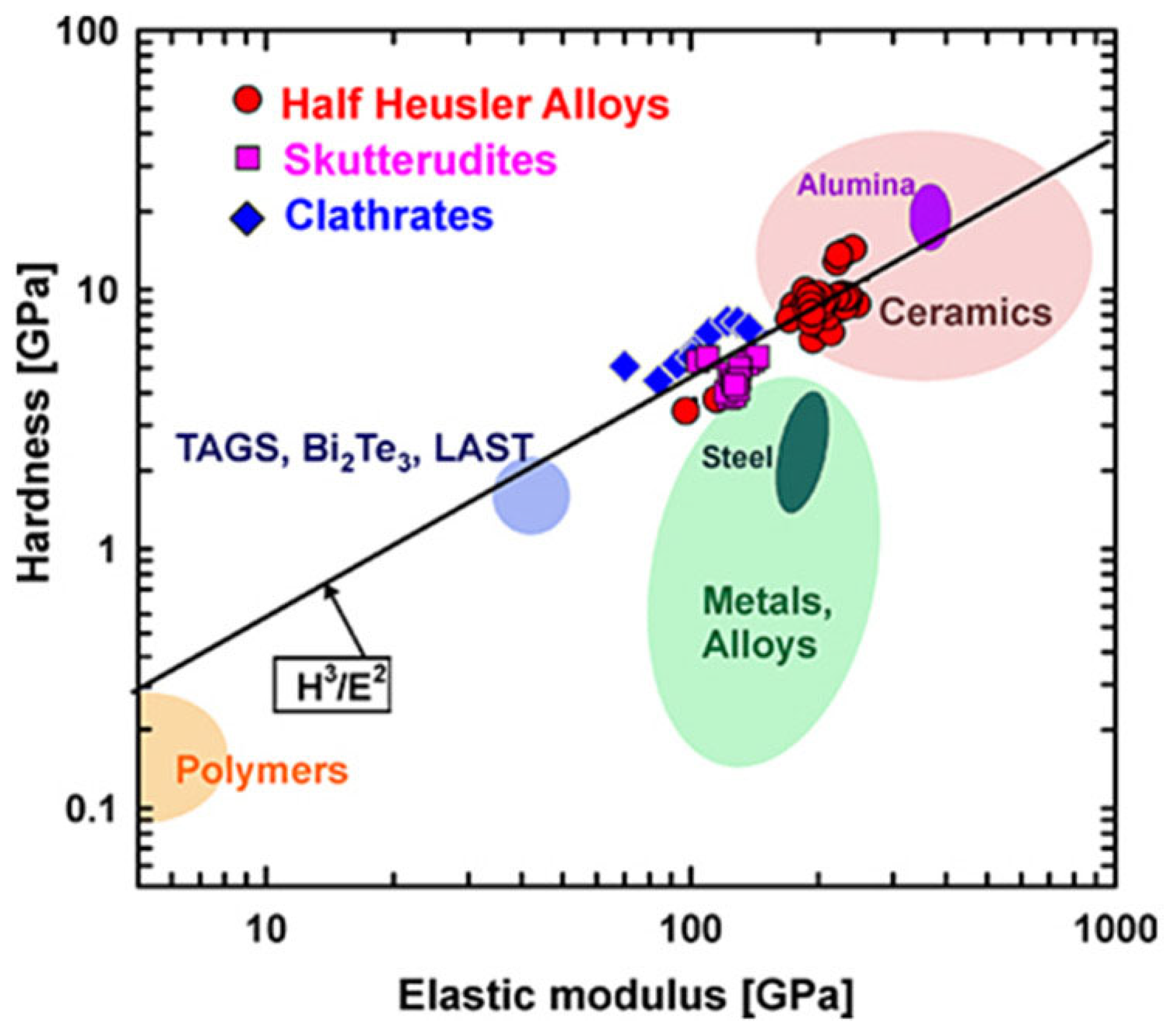
4.1.1. Hardness (H)
4.1.2. Elastic Modulus
4.1.3. Indentation Fracture Toughness
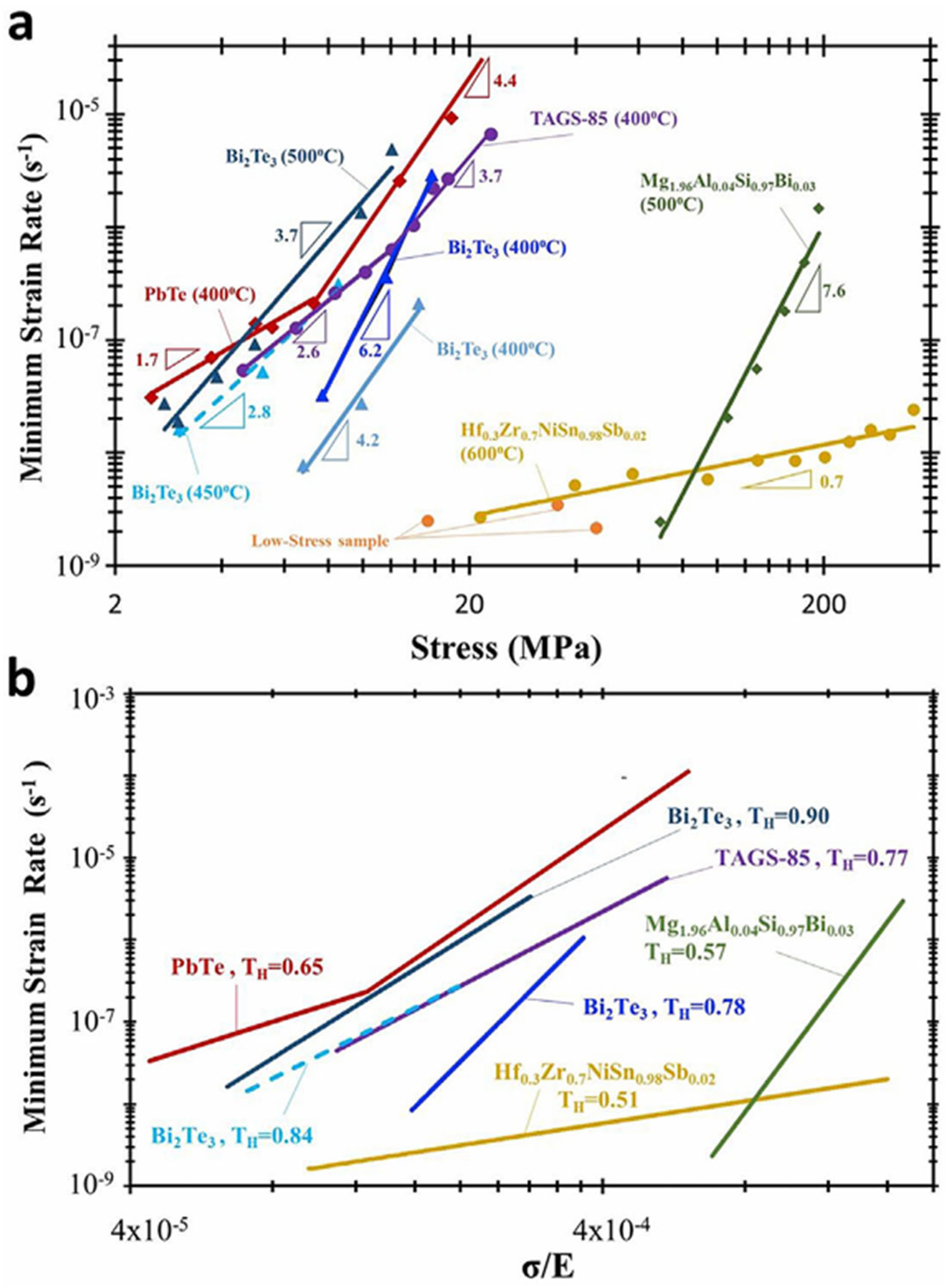
4.1.4. Mechanical Response at High Temperatures—Compressive Strength, Creep
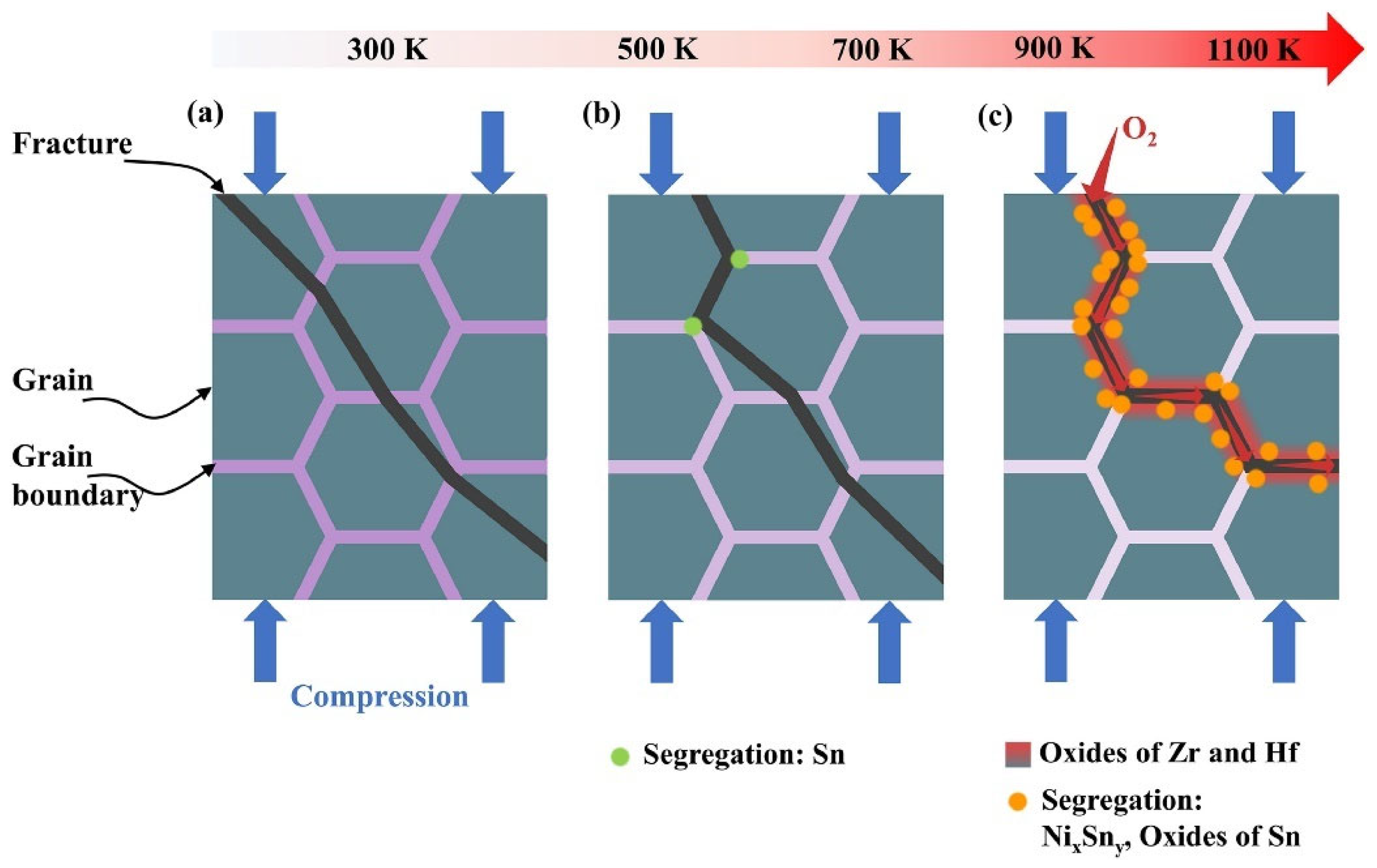
4.2. Mechanical Failure Modes of TE Devices
5. Computational Design of Entropy-Engineered TE Materials
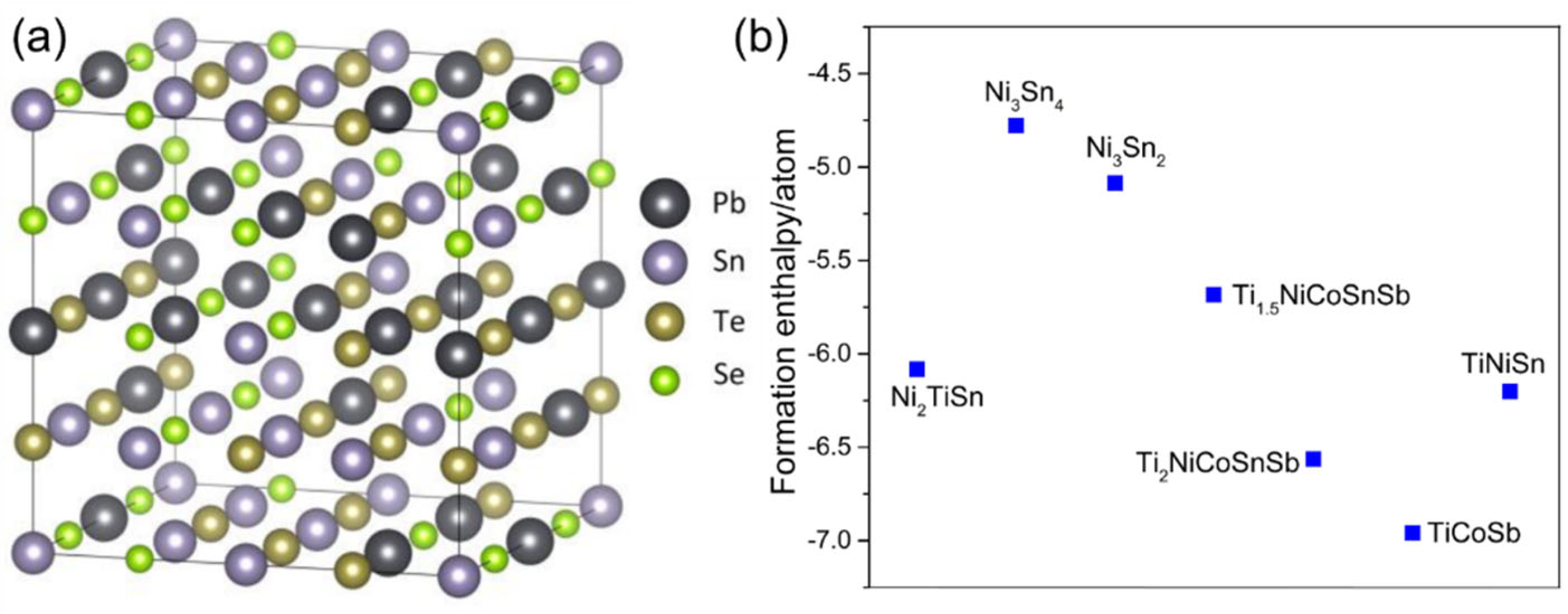
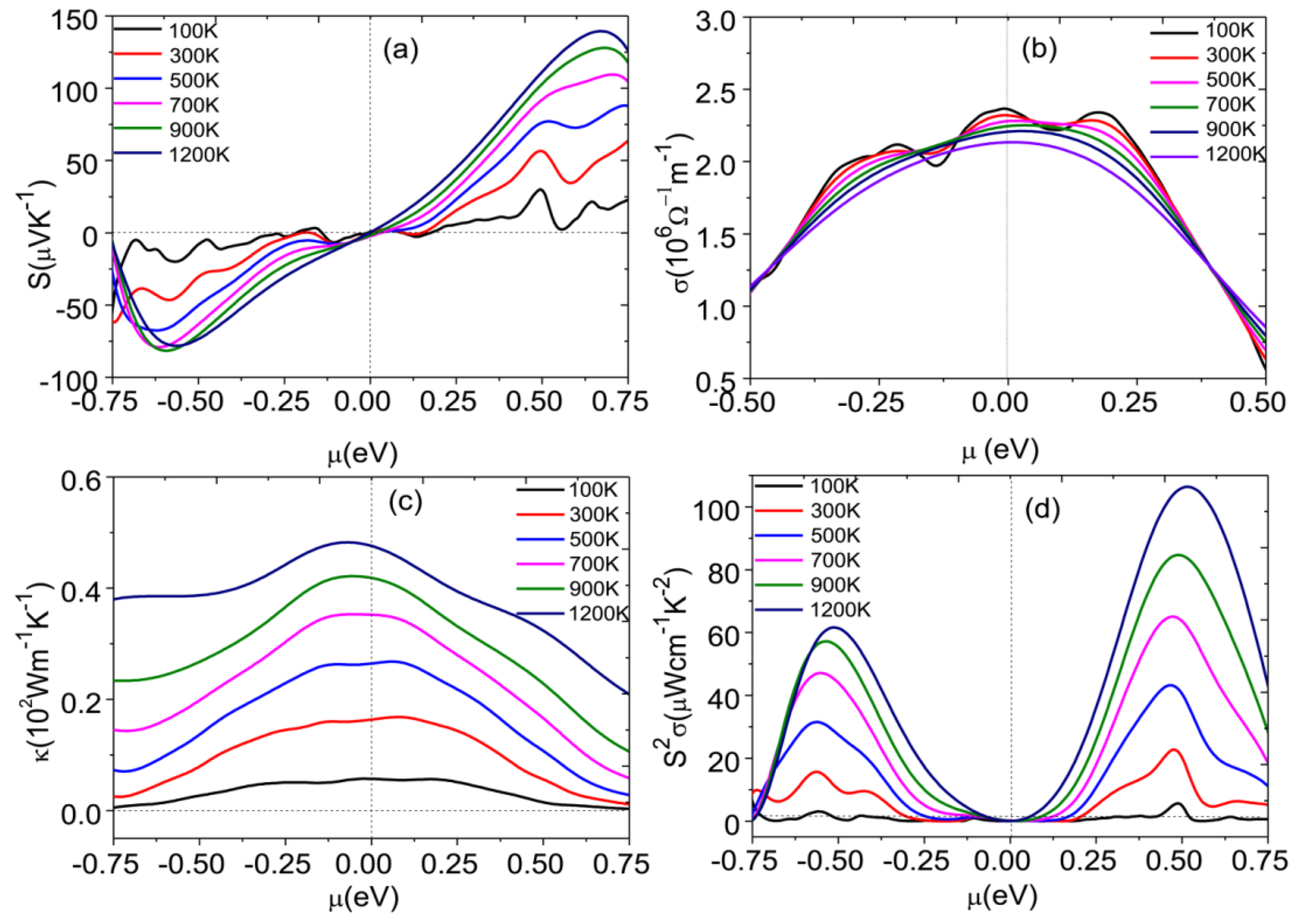
5.1. Ab Initio-Based Methods
5.2. CALPHAD Method
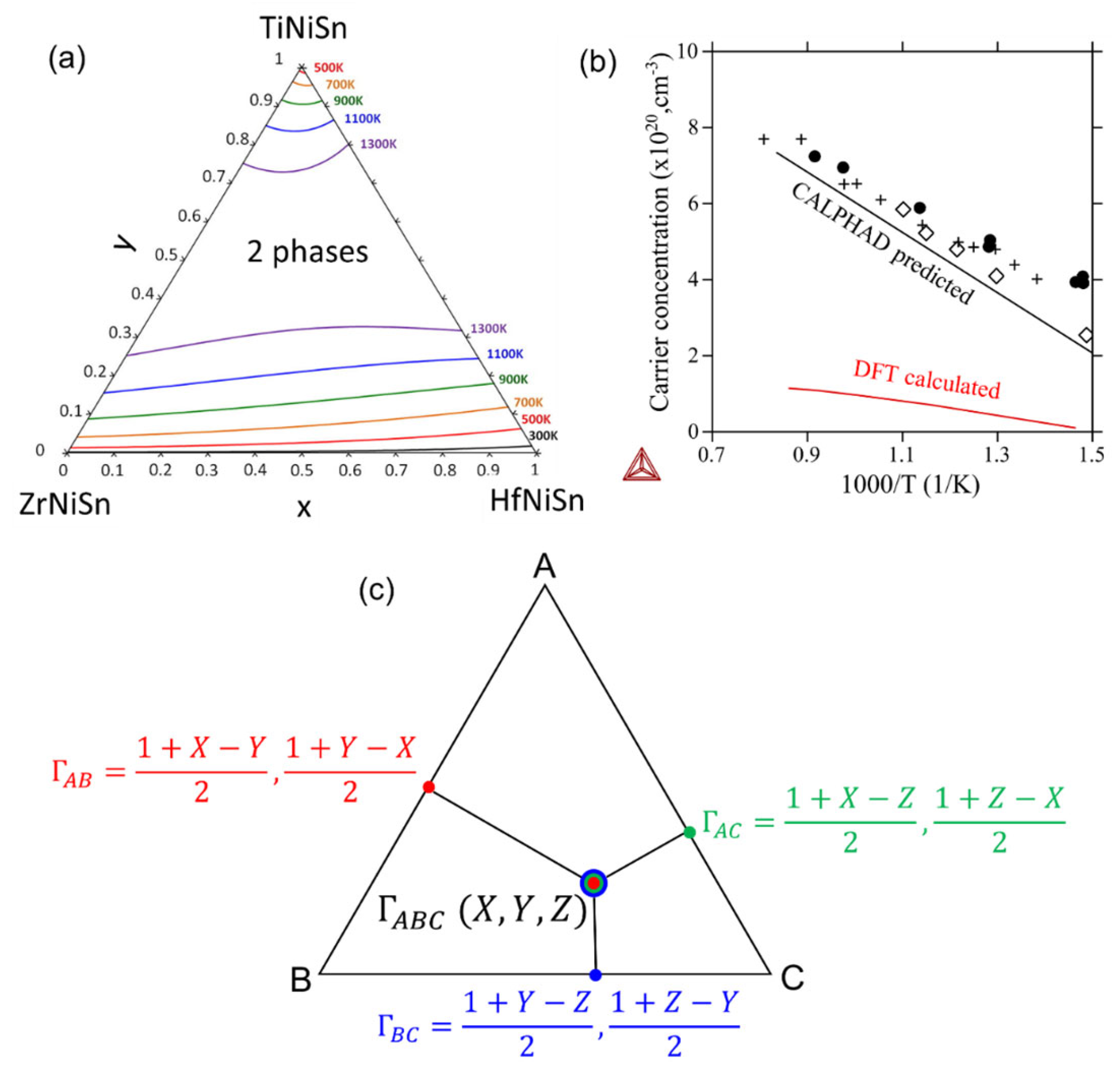
5.3. Data-Driven Methods
6. Concluding Remarks
- (1)
- (2)
- reduces the phase transition temperature, thereby extending the stability region of high-symmetry crystal structures over a wide range of temperatures [50]. The high-symmetry crystal structures lead to large band degeneracy and form overlapping or multiple bands near the Fermi level. This results in more equivalent positions in real and reciprocal space, thereby increasing the density of states and , which in turn improves [30,50,113].
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Kanatzidis, M.G.; Chang, C. High-Entropy Thermoelectric Materials Emerging. Mater. Lab 2023, 2, 220048. [Google Scholar] [CrossRef]
- Dong, J.; Yan, Q.; Gao, J. High Entropy Strategy on Thermoelectric Materials. Mater. Lab 2023, 2, 230001. [Google Scholar] [CrossRef]
- Yeh, J.W.; Chen, S.K.; Lin, S.J.; Gan, J.Y.; Chin, T.S.; Shun, T.T.; Tsau, C.H.; Chang, S.Y. Nanostructured High-Entropy Alloys with Multiple Principal Elements: Novel Alloy Design Concepts and Outcomes. Adv. Eng. Mater. 2004, 6, 299. [Google Scholar] [CrossRef]
- Cantor, B.; Chang, I.T.H.; Knight, P.; Vincent, A.J.B. Microstructural Development in Equiatomic Multicomponent Alloys. Mater. Sci. Eng. A 2004, 213, 375–377. [Google Scholar] [CrossRef]
- Murty, B.S.; Yeh, J.-W.; Ranganathan, S.; Bhattacharjee, P.P. High-Entropy Alloys, 2nd ed.; Elsevier: Amsterdam, The Netherlands, 2019. [Google Scholar]
- Xin, Y.; Li, S.; Qian, Y.; Zhu, W.; Yuan, H.; Jiang, P.; Guo, R.; Wang, L. High-Entropy Alloys as a Platform for Catalysis: Progress, Challenges, and Opportunities. ACS Catal. 2020, 10, 11280. [Google Scholar] [CrossRef]
- Fan, L.; Li, Y.; Li, J.; Xiang, Q.; Wang, X.; Wen, T.; Zhong, Z.; Liao, Y. High entropy dielectrics. J. Adv. Dielectr. 2023, 13, 2350014. [Google Scholar] [CrossRef]
- Jiang, B.; Yu, Y.; Cui, J.; Liu, X.; Xie, L.; Liao, J.; Zhang, Q.; Huang, Y.; Ning, S.; Jia, B.; et al. High-Entropy-Stabilized Chalcogenides with High Thermoelectric Performance. Science 2021, 371, 830. [Google Scholar] [CrossRef] [PubMed]
- Jiang, B.; Yu, Y.; Chen, H.; Cui, J.; Liu, X.; Xie, L.; He, J. Entropy Engineering Promotes Thermoelectric Performance in P-Type Chalcogenides. Nat. Commun. 2021, 12, 3234. [Google Scholar] [CrossRef]
- Jiang, B.; Wang, W.; Liu, S.; Wang, Y.; Wang, C.; Chen, Y.; Xie, L.; Huang, M.; He, J. High Figure-of-Merit and Power Generation in High-Entropy GeTe-Based Thermoelectrics. Science 2022, 377, 208. [Google Scholar] [CrossRef]
- Chen, K.; Zhang, R.; Bos, J.W.G.; Reece, M.J. Synthesis and Thermoelectric Properties of High-Entropy Half-Heusler MFe1−xCoxSb (M = Equimolar Ti, Zr, Hf, V, Nb, Ta). J. Alloys Compd. 2022, 892, 162045. [Google Scholar] [CrossRef]
- Yan, J.; Liu, F.; Ma, G.; Gong, B.; Zhu, J.; Wang, X.; Ao, W.; Zhang, C.; Li, Y.; Li, J. Suppression of the Lattice Thermal Conductivity in NbFeSb-Based Half-Heusler Thermoelectric Materials through High Entropy Effects. Scr. Mater. 2018, 157, 129. [Google Scholar] [CrossRef]
- Li, W.; Goyal, G.K.; Stokes, D.; Raman, L.; Ghosh, S.; Sharma, S.; Nozariasbmarz, A.; Liu, N.; Singh, S.; Zhang, Y.; et al. High-Performance Skutterudite/Half-Heusler Cascaded Thermoelectric Module Using the Transient Liquid Phase Sintering Joining Technique. ACS Appl. Mater. Interfaces 2023, 15, 2961. [Google Scholar] [CrossRef] [PubMed]
- Li, W.; Wang, J.; Poudel, B.; Kang, H.B.; Huxtable, S.; Nozariasbmarz, A.; Saparamadu, U.; Priya, S. Filiform Metal Silver Nanoinclusions To Enhance Thermoelectric Performance of P-Type Ca 3 Co 4 O 9+δ Oxide. ACS Appl. Mater. Interfaces 2019, 11, 42131. [Google Scholar] [CrossRef] [PubMed]
- Li, W.; Stokes, D.; Poudel, B.; Saparamadu, U.; Nozariasbmarz, A.; Kang, H.B.; Priya, S. High-Efficiency Skutterudite Modules at a Low Temperature Gradient. Energies 2019, 12, 4292. [Google Scholar] [CrossRef]
- Nie, G.; Li, W.; Guo, J.; Yamamoto, A.; Kimura, K.; Zhang, X.; Isaacs, E.B.; Dravid, V.; Wolverton, C.; Kanatzidis, M.G.; et al. High Performance Thermoelectric Module through Isotype Bulk Heterojunction Engineering of Skutterudite Materials. Nano Energy 2019, 66, 104193. [Google Scholar] [CrossRef]
- Li, W.; Ghosh, S.; Liu, N.; Poudel, B. Half-Heusler Thermoelectrics: Advances from Materials Fundamental to Device Engineering. Joule 2024, in press. [Google Scholar] [CrossRef]
- Zhang, Q.; Guo, Z.; Wang, R.; Tan, X.; Song, K.; Sun, P.; Hu, H.; Cui, C.; Liu, G.Q.; Jiang, J. High-Performance Thermoelectric Material and Module Driven by Medium-Entropy Engineering in SnTe. Adv. Funct. Mater. 2022, 32, 2205458. [Google Scholar] [CrossRef]
- Zhu, H.; Li, W.; Nozariasbmarz, A.; Liu, N.; Zhang, Y.; Priya, S.; Poudel, B. Half-Heusler Alloys as Emerging High Power Density Thermoelectric Cooling Materials. Nat. Commun. 2023, 14, 3300. [Google Scholar] [CrossRef] [PubMed]
- Li, W.; Poudel, B.; Nozariasbmarz, A.; Sriramdas, R.; Zhu, H.; Kang, H.B.; Priya, S. Bismuth Telluride/Half-Heusler Segmented Thermoelectric Unicouple Modules Provide 12% Conversion Efficiency. Adv. Energy Mater. 2020, 10, 2001924. [Google Scholar] [CrossRef]
- Nozariasbmarz, A.; Saparamadu, U.; Li, W.; Kang, H.B.; Dettor, C.; Zhu, H.; Poudel, B.; Priya, S. High-Performance Half-Heusler Thermoelectric Devices through Direct Bonding Technique. J. Power Sources 2021, 493, 229695. [Google Scholar] [CrossRef]
- Snyder, G.J.; Toberer, E.S. Complex Thermoelectric Materials. Nat. Mater. 2008, 7, 105. [Google Scholar] [CrossRef] [PubMed]
- Zhang, Y.; Li, Z.; Singh, S.; Nozariasbmarz, A.; Li, W.; Genç, A.; Xia, Y.; Zheng, L.; Lee, S.H.; Karan, S.K.; et al. Defect-Engineering-Stabilized AgSbTe 2 with High Thermoelectric Performance. Adv. Mater. 2023, 35, 2208994. [Google Scholar] [CrossRef] [PubMed]
- Zhu, H.; He, R.; Mao, J.; Zhu, Q.; Li, C.; Sun, J.; Ren, W.; Wang, Y.; Liu, Z.; Tang, Z.; et al. Discovery of ZrCoBi Based Half Heuslers with High Thermoelectric Conversion Efficiency. Nat. Commun. 2018, 9, 2497. [Google Scholar] [CrossRef] [PubMed]
- Li, W.; Wang, J.; Xie, Y.; Gray, J.L.; Heremans, J.J.; Kang, H.B.; Poudel, B.; Huxtable, S.T.; Priya, S. Enhanced Thermoelectric Performance of Yb-Single-Filled Skutterudite by Ultralow Thermal Conductivity. Chem. Mater. 2019, 31, 862. [Google Scholar] [CrossRef]
- Li, W.; Poudel, B.; Kishore, R.A.; Nozariasbmarz, A.; Liu, N.; Zhang, Y.; Priya, S. Toward High Conversion Efficiency of Thermoelectric Modules through Synergistical Optimization of Layered Materials. Adv. Mater. 2023, 35, 2210407. [Google Scholar] [CrossRef] [PubMed]
- Kang, H.B.; Poudel, B.; Li, W.; Lee, H.; Saparamadu, U.; Nozariasbmarz, A.; Kang, M.G.; Gupta, A.; Heremans, J.J.; Priya, S. Decoupled Phononic-Electronic Transport in Multi-Phase n-Type Half-Heusler Nanocomposites Enabling Efficient High Temperature Power Generation. Mater. Today 2020, 36, 63. [Google Scholar] [CrossRef]
- Wang, H.; He, Q.; Gao, X.; Shang, Y.; Zhu, W.; Zhao, W.; Chen, Z.; Gong, H.; Yang, Y. Multifunctional High Entropy Alloys Enabled by Severe Lattice Distortion. Adv. Mater. 2023, 36, e2305453. [Google Scholar] [CrossRef] [PubMed]
- Schweidler, S.; Botros, M.; Strauss, F.; Wang, Q.; Ma, Y.; Velasco, L.; Marques, G.C.; Sarkar, A.; Kübel, C.; Hahn, H.; et al. High-Entropy Materials for Energy and Electronic Applications. Nat. Rev. Mater. 2024, 9, 266–281. [Google Scholar] [CrossRef]
- Toda-Caraballo, I.; Rivera-Díaz-del-Castillo, P.E.J. A Criterion for the Formation of High Entropy Alloys Based on Lattice Distortion. Intermetallics 2016, 71, 76. [Google Scholar] [CrossRef]
- Usharani, N.J.; Shringi, R.; Sanghavi, H.; Subramanian, S.; Bhattacharya, S.S.; Size, R.O. Alio-/Multi-Valency and Non-Stoichiometry in the Synthesis of Phase-Pure High Entropy Oxide (Co,Cu,Mg,Na,Ni,Zn)O. Dalton Trans. 2020, 49, 7123. [Google Scholar] [CrossRef]
- Fultz, B. Vibrational Thermodynamics of Materials. Prog. Mater. Sci. 2010, 55, 247. [Google Scholar] [CrossRef]
- Xia, J.; Yang, J.; Wang, Y.; Jia, B.; Li, S.; Sun, K.; Zhao, Q.; Mao, D.; Li, H.F.; He, J. Synergistic Entropy Engineering with Vacancies: Unraveling the Cocktail Effect for Extraordinary Thermoelectric Performance in SnTe-Based Materials. Adv. Funct. Mater. 2024, 2024, 2401635. [Google Scholar] [CrossRef]
- Liu, R.; Chen, H.; Zhao, K.; Qin, Y.; Jiang, B.; Zhang, T.; Sha, G.; Shi, X.; Uher, C.; Zhang, W.; et al. Entropy as a Gene-Like Performance Indicator Promoting Thermoelectric Materials. Adv. Mater. 2017, 29, 1702712. [Google Scholar] [CrossRef] [PubMed]
- Ren, W.; Song, Q.; Zhu, H.; Mao, J.; You, L.; Gamage, G.; Zhou, J.; Zhou, T.; Jiang, J.; Wang, C.; et al. Intermediate-Level Doping Strategy to Simultaneously Optimize Power Factor and Phonon Thermal Conductivity for Improving Thermoelectric Figure of Merit. Mater. Today Phys. 2020, 15, 100250. [Google Scholar] [CrossRef]
- Qiu, Y.; Jin, Y.; Wang, D.; He, W.; Zhao, L.D.; Guan, M.; Peng, S.; Liu, R.; Gao, X. Realizing High Thermoelectric Performance in GeTe through Decreasing the Phase Transition Temperature via Entropy Engineering. J. Mater. Chem. A Mater. 2019, 7, 26393. [Google Scholar] [CrossRef]
- Ma, Z.; Luo, Y.; Li, W.; Xu, T.; Wei, Y.; Li, C.; Haruna, A.Y.; Jiang, Q.; Zhang, D.; Yang, J. High Thermoelectric Performance and Low Lattice Thermal Conductivity in Lattice-Distorted High-Entropy Semiconductors AgMnSn1-XPbxSbTe4. Chem. Mater. 2022, 34, 8959. [Google Scholar] [CrossRef]
- Gao, H.; Zhao, K.; Wuliji, H.; Zhu, M.; Xu, B.; Lin, H.; Fei, L.; Zhang, H.; Zhou, Z.; Lei, J.; et al. Adaptable Sublattice Stabilized High-Entropy Materials with Superior Thermoelectric Performance. Energy Environ. Sci. 2023, 16, 6046. [Google Scholar] [CrossRef]
- Fan, Z.; Wang, H.; Wu, Y.; Liu, X.J.; Lu, Z.P. Thermoelectric High-Entropy Alloys with Low Lattice Thermal Conductivity. RSC Adv. 2016, 6, 52164. [Google Scholar] [CrossRef]
- Fan, Z.; Wang, H.; Wu, Y.; Liu, X.; Lu, Z. Thermoelectric Performance of PbSnTeSe High-Entropy Alloys. Mater. Res. Lett. 2017, 5, 187. [Google Scholar] [CrossRef]
- Hu, L.; Zhang, Y.; Wu, H.; Li, J.; Li, Y.; Mckenna, M.; He, J.; Liu, F.; Pennycook, S.J.; Zeng, X. Entropy Engineering of SnTe: Multi-Principal-Element Alloying Leading to Ultralow Lattice Thermal Conductivity and State-of-the-Art Thermoelectric Performance. Adv. Energy Mater. 2018, 8, 1802116. [Google Scholar] [CrossRef]
- Jiang, B.; Qiu, P.; Chen, H.; Huang, J.; Mao, T.; Wang, Y.; Song, Q.; Ren, D.; Shi, X.; Chen, L. Entropy Optimized Phase Transitions and Improved Thermoelectric Performance in N-Type Liquid-like Ag9GaSe6 Materials. Mater. Today Phys. 2018, 5, 20. [Google Scholar] [CrossRef]
- Karati, A.; Nagini, M.; Ghosh, S.; Shabadi, R.; Pradeep, K.G.; Mallik, R.C.; Murty, B.S.; Varadaraju, U.V. Ti 2NiCoSnSb—A New Half-Heusler Type High-Entropy Alloy Showing Simultaneous Increase in Seebeck Coefficient and Electrical Conductivity for Thermoelectric Applications. Sci. Rep. 2019, 9, 5331. [Google Scholar] [CrossRef] [PubMed]
- Luo, Y.; Hao, S.; Cai, S.; Slade, T.J.; Luo, Z.Z.; Dravid, V.P.; Wolverton, C.; Yan, Q.; Kanatzidis, M.G. High Thermoelectric Performance in the New Cubic Semiconductor AgSnSbSe3by High-Entropy Engineering. J. Am. Chem. Soc. 2020, 142, 15187. [Google Scholar] [CrossRef]
- Yamashita, A.; Goto, Y.; Miura, A.; Moriyoshi, C.; Kuroiwa, Y.; Mizuguchi, Y. N-Type Thermoelectric Metal Chalcogenide (Ag,Pb,Bi)(S,Se,Te) Designed by Multi-Site-Type High-Entropy Alloying. Mater. Res. Lett. 2021, 9, 366. [Google Scholar] [CrossRef]
- Wang, X.; Yao, H.; Zhang, Z.; Li, X.; Chen, C.; Yin, L.; Hu, K.; Yan, Y.; Li, Z.; Yu, B.; et al. Enhanced Thermoelectric Performance in High Entropy Alloys Sn 0.25 Pb 0.25 Mn 0.25 Ge 0.25 Te. ACS Appl. Mater. Interfaces 2021, 13, 18638. [Google Scholar] [CrossRef] [PubMed]
- Ma, Z.; Xu, T.; Li, W.; Cheng, Y.; Li, J.; Zhang, D.; Jiang, Q.; Luo, Y.; Yang, J. High Entropy Semiconductor AgMnGeSbTe4 with Desirable Thermoelectric Performance. Adv. Funct. Mater. 2021, 31, 2103197. [Google Scholar] [CrossRef]
- Cai, J.; Yang, J.; Liu, G.; Wang, H.; Shi, F.; Tan, X.; Ge, Z.; Jiang, J. Ultralow Thermal Conductivity and Improved ZT of CuInTe2 by High-Entropy Structure Design. Mater. Today Phys. 2021, 18, 100394. [Google Scholar] [CrossRef]
- Zhang, W.; Lou, Y.; Dong, H.; Wu, F.; Tiwari, J.; Shi, Z.; Feng, T.; Pantelides, S.T.; Xu, B. Phase-Engineered High-Entropy Metastable FCC Cu2−yAgy(InxSn1−x)Se2S Nanomaterials with High Thermoelectric Performance. Chem. Sci. 2022, 13, 10461. [Google Scholar] [CrossRef] [PubMed]
- Huang, Y.; Zhi, S.; Zhang, S.; Yao, W.; Ao, W.; Zhang, C.; Liu, F.; Li, J.; Hu, L. Regulating the Configurational Entropy to Improve the Thermoelectric Properties of (GeTe)1−x(MnZnCdTe3)x Alloys. Materials 2022, 15, 6798. [Google Scholar] [CrossRef]
- Zhang, M.; Cai, J.; Gao, F.; Zhang, Z.; Li, M.; Chen, Z.; Wang, Y.; Hu, D.; Tan, X.; Liu, G.; et al. Improved Thermoelectric Performance of P-Type PbTe by Entropy Engineering and Temperature-Dependent Precipitates. ACS Appl. Mater. Interfaces 2024, 16, 907. [Google Scholar] [CrossRef]
- Yang, J.; Meisner, G.P.; Chen, L. Strain Field Fluctuation Effects on Lattice Thermal Conductivity of ZrNiSn-Based Thermoelectric Compounds. Appl. Phys. Lett. 2004, 85, 1140. [Google Scholar] [CrossRef]
- Chen, R.; Yan, Y.; Zhang, W.; Liu, F.; Kang, H.; Guo, E.; Chen, Z.; Wang, T. Enhanced Thermoelectric Properties of Zr0.85–x Hf x Nb0.15–y Ta y CoSb Medium-Entropy Alloys: Tradeoff between “What to Alloy” and “How Much to Alloy. Chem. Mater. 2023, 35, 2202–2212. [Google Scholar] [CrossRef]
- Zhang, X.; Huang, M.; Li, H.; Chen, J.; Xu, P.; Xu, B.; Wang, Y.; Tang, G.; Yang, S. Ultralow Lattice Thermal Conductivity and Improved Thermoelectric Performance in a Hf-Free Half-Heusler Compound Modulated by Entropy Engineering. J. Mater. Chem. A Mater. 2023, 11, 8150–8161. [Google Scholar] [CrossRef]
- Banerjee, R.; Chatterjee, S.; Ranjan, M.; Bhattacharya, T.; Mukherjee, S.; Jana, S.S.; Dwivedi, A.; Maiti, T. High-Entropy Perovskites: An Emergent Class of Oxide Thermoelectrics with Ultralow Thermal Conductivity. ACS Sustain. Chem. Eng. 2020, 8, 17022. [Google Scholar] [CrossRef]
- Zheng, Y.; Zou, M.; Zhang, W.; Yi, D.; Lan, J.; Nan, C.-W.; Lin, Y.-H. Electrical and Thermal Transport Behaviours of High-Entropy Perovskite Thermoelectric Oxides. J. Adv. Ceram. 2021, 10, 377. [Google Scholar] [CrossRef]
- Bao, X.; Hou, S.; Wu, Z.; Wang, X.; Yin, L.; Liu, Y.; He, H.; Duan, S.; Wang, B.; Mao, J.; et al. Mechanical Properties of Thermoelectric Generators. J. Mater. Sci. Technol. 2023, 148, 64. [Google Scholar] [CrossRef]
- Wu, L.; Feng, X.; Cao, K.; Li, G. Toughening Thermoelectric Materials: From Mechanisms to Applications. Int. J. Mol. Sci. 2023, 24, 6325. [Google Scholar] [CrossRef]
- He, R.; Gahlawat, S.; Guo, C.; Chen, S.; Dahal, T.; Zhang, H.; Liu, W.; Zhang, Q.; Chere, E.; White, K.; et al. Studies on Mechanical Properties of Thermoelectric Materials by Nanoindentation. Phys. Status Solidi A Appl. Mater. Sci. 2015, 212, 2191. [Google Scholar] [CrossRef]
- Tavares, S.; Yang, K.; Meyers, M.A. Heusler Alloys: Past, Properties, New Alloys, and Prospects. Prog. Mater. Sci. 2023, 132, 101017. [Google Scholar] [CrossRef]
- Rogl, G.; Rogl, P. Mechanical Properties of Skutterudites. Sci. Adv. Mater. 2011, 3, 517. [Google Scholar] [CrossRef]
- Lu, T.; Wang, B.; Li, G.; Yang, J.; Zhang, X.; Chen, N.; Liu, T.-H.; Yang, R.; Niu, P.; Kan, Z.; et al. Synergistically Enhanced Thermoelectric and Mechanical Performance of Bi2Te3 via Industrial Scalable Hot Extrusion Method for Cooling and Power Generation Applications. Mater. Today Phys. 2023, 32, 101035. [Google Scholar] [CrossRef]
- Guttmann, G.M.; Gelbstein, Y. Mechanical Properties of Thermoelectric Materials for Practical Applications, in Bringing Thermoelectricity into Reality; InTech: Rijeka, Croatia, 2018. [Google Scholar]
- Verges, M.A.; Schilling, P.J.; Germond, J.D.; Upadhyay, P.; Miller, W.K.; Takas, N.J.; Poudeu, P.F.P. Indentation Testing of Bulk Zr0.5Hf0.5Co1–xIrxSb0.99Sn0.01 Half-Heusler Alloys. MRS Proc. 2010, 1267, 1267. [Google Scholar] [CrossRef]
- O’Connor, C.J. Nanostructured Composite Materials for High Temperature Thermoelectric Energy Conversion; New Orleans University: New Orleans, LA, USA, 2012; p. 0026. [Google Scholar]
- Fan, X. Mechanical Characterization of Hydroxyapatite, Thermoelectric Materials and Doped Ceria; Michigan State University: East Lansing, MI, USA, 2013. [Google Scholar]
- Rogl, G.; Grytsiv, A.; Gürth, M.; Tavassoli, A.; Ebner, C.; Wünschek, A.; Puchegger, S.; Soprunyuk, V.; Schranz, W.; Bauer, E.; et al. Mechanical Properties of Half-Heusler Alloys. Acta Mater. 2016, 107, 178. [Google Scholar] [CrossRef]
- Jung, D.Y.; Kurosaki, K.; Kim, C.E.; Muta, H.; Yamanaka, S. Thermal Expansion and Melting Temperature of the Half-Heusler Compounds: MNiSn (M = Ti, Zr, Hf). J. Alloys Compd. 2010, 489, 328. [Google Scholar] [CrossRef]
- Lu, Y.; Zhang, P.; Wang, J.; Song, Q.; Chen, Z.; Wang, Y.; Chen, L.; Bai, S.; Wang, W. Temperature-Dependent Compression Properties and Failure Mechanisms of ZrNiSn-Based Half-Heusler Thermoelectric Compounds. J. Mater. Sci. Technol. 2024, 193, 29–36. [Google Scholar] [CrossRef]
- Al Malki, M.M.; Qiu, Q.; Zhu, T.; Snyder, G.J.; Dunand, D.C. Creep Behavior and Postcreep Thermoelectric Performance of the N-Type Half-Heusler Alloy Hf0.3Zr0.7NiSn0.98Sb0.02. Mater. Today Phys. 2019, 9, 100134. [Google Scholar] [CrossRef]
- Zhang, L.; Shi, X.L.; Yang, Y.L.; Chen, Z.G. Flexible Thermoelectric Materials and Devices: From Materials to Applications. Mater. Today 2021, 46, 62–108. [Google Scholar] [CrossRef]
- Aljaghtham, M. A Comparative Performance Analysis of Thermoelectric Generators with a Novel Leg Geometries. Energy Rep. 2024, 11, 859. [Google Scholar] [CrossRef]
- Li, M.; Dizaji, H.S.; Asaadi, S.; Jarad, F.; Anqi, A.E.; Wae-hayee, M. Thermo-Economic, Exergetic and Mechanical Analysis of Thermoelectric Generator with Hollow Leg Structure; Impact of Leg Cross-Section Shape and Hollow-to-Filled Area Ratio. Case Stud. Therm. Eng. 2021, 27, 101314. [Google Scholar] [CrossRef]
- Kreese, G.; Furthmuller, J. Efficiency of Ab-Initio Total Energy Calculations for Metals and Semiconductors Using a Plane-Wave Basis Set. Comput. Mater. Sci. 1996, 6, 15. [Google Scholar] [CrossRef]
- Kreese, G.; Furthmuller, J. Efficient Iterative Schemes for Ab Initio Total-Energy Calculations Using a Plane-Wave Basis Set. Phys. Rev. B 1996, 54, 11169. [Google Scholar] [CrossRef] [PubMed]
- Blaha, P.; Schwarz, K.; Tran, F.; Laskowski, R.; Madsen, G.K.H.; Marks, L.D. WIEN2k: An APW+lo Program for Calculating the Properties of Solids. J. Chem. Phys. 2020, 152, 074101. [Google Scholar] [CrossRef] [PubMed]
- Van De Walle, A.; Tiwary, P.; De Jong, M.; Olmsted, D.L.; Asta, M.; Dick, A.; Shin, D.; Wang, Y.; Chen, L.Q.; Liu, Z.K. Efficient Stochastic Generation of Special Quasirandom Structures. Calphad 2013, 42, 13. [Google Scholar] [CrossRef]
- Van De Walle, A.; Asta, M.; Cederb, G. The Alloy Theoretic Automated Toolkit: A User Guide. Calphad 2002, 26, 539–553. [Google Scholar] [CrossRef]
- Akai, H. Fast Korringa-Kohn-Rostoker Coherent Potential Approximation and Its Application to FCC Ni-Fe Systems. J. Phys. Condens. Matter 1989, 1, 8045. [Google Scholar] [CrossRef]
- Bellaiche, L.; Vanderbilt, D. Virtual Crystal Approximation Revisited: Application to Dielectric and Piezoelectric Properties of Perovskites. Phys. Rev. B 2000, 61, 7877. [Google Scholar] [CrossRef]
- Xia, M.; Record, M.; Boulet, P. Investigation of PbSnTeSe High-Entropy Thermoelectric Alloy. Materials 2023, 16, 235. [Google Scholar] [CrossRef] [PubMed]
- Mishra, S.R.; Karati, A.; Ghosh, S.; Mallik, R.C.; Shabadi, R.; Krishnan, P.S.S.R.; Yadav, S.K.; Ramanujan, R.V.; Murty, B.S. Lowering Thermal Conductivity in Thermoelectric Ti2−xNiCoSnSb Half Heusler High Entropy Alloys. J. Mater. Sci. 2023, 58, 10736. [Google Scholar] [CrossRef]
- Huang, L.F.; Lu, X.Z.; Tennessen, E.; Rondinelli, J.M. An Efficient Ab-Initio Quasiharmonic Approach for the Thermodynamics of Solids. Comput. Mater. Sci. 2016, 120, 84. [Google Scholar] [CrossRef]
- Togo, A.; Tanaka, I. First Principles Phonon Calculations in Materials Science. Scr. Mater. 2015, 108, 1. [Google Scholar] [CrossRef]
- Born, M. On the Stability of Crystal Lattices. I. In Mathematical Proceedings of the Cambridge Philosophical Society; Cambridge University Press: Cambridge, UK, 1940; Volume 36, p. 160. [Google Scholar]
- Mizokami, K.; Togo, A.; Tanaka, I. Lattice Thermal Conductivities of Two SiO2 Polymorphs by First-Principles Calculations and the Phonon Boltzmann Transport Equation. Phys. Rev. B 2018, 97, 224306. [Google Scholar] [CrossRef]
- Madsen, G.K.H.; Singh, D.J. BoltzTraP. A Code for Calculating Band-Structure Dependent Quantities. Comput. Phys. Commun. 2006, 175, 67. [Google Scholar] [CrossRef]
- Ma, H.; Li, J.; Yang, G.; Yang, Y.; Mao, X.; Li, C.; Yin, F. Improved Thermoelectric Property of Ti0.75HfMo0.25CrGe by Doping Ti2CrGe Heusler Alloy with Hf and Mo: Confirmation of Entropy “Gene” in Thermoelectric Materials Design. J. Appl. Phys. 2018, 124, 235104. [Google Scholar] [CrossRef]
- Botu, V.; Ramprasad, R. Adaptive Machine Learning Framework to Accelerate Ab Initio Molecular Dynamics. Int. J. Quantum Chem. 2015, 115, 1074. [Google Scholar] [CrossRef]
- Hasan, S.; Adhikari, P.; San, S.; Ching, W.Y. Ab Initio Study of Mechanical and Thermal Properties of GeTe-Based and PbSe-Based High-Entropy Chalcogenides. Sci. Rep. 2023, 13, 16218. [Google Scholar] [CrossRef] [PubMed]
- Reuss, A. Berechnung Der Fließgrenze von Mischkristallen Auf Grund Der Plastizitätsbedingung Für Einkristalle. ZAMM—J. Appl. Math. Mech./Z. Für Angew. Math. Und Mech. 1929, 9, 49. [Google Scholar] [CrossRef]
- Hill, R. The Elastic Behaviour of a Crystalline Aggregate. Proc. Phys. Soc. Sect. A 1952, 65, 349. [Google Scholar] [CrossRef]
- Sun, Z.; Music, D.; Ahuja, R.; Schneider, J.M. Theoretical Investigation of the Bonding and Elastic Properties of Nanolayered Ternary Nitrides. Phys. Rev. B Condens. Matter Mater. Phys. 2005, 71, 193402. [Google Scholar] [CrossRef]
- Saunders, N.; Miodownik, A.P. CALPHAD (Calculation of Phase Diagrams): A Comprehensive Guide; Elsevier: Amsterdam, The Netherlands, 1998. [Google Scholar]
- Lukas, H.; Fries, S.G.; Sundman, B. Computational Thermodynamics: The Calphad Method; Cambridge University Press: Cambridge, UK, 2007. [Google Scholar]
- Li, X.; Li, Z.; Chen, C.; Ren, Z.; Wang, C.; Liu, X.; Zhang, Q.; Chen, S. CALPHAD as a Powerful Technique for Design and Fabrication of Thermoelectric Materials. J. Mater. Chem. A Mater. 2021, 9, 6634. [Google Scholar] [CrossRef]
- Berche, A.; Tédenac, J.C.; Jund, P. Phase Separation in the Half-Heusler Thermoelectric Materials (Hf, Ti, Zr) NiSn. Scr. Mater. 2017, 139, 122. [Google Scholar] [CrossRef]
- Borgsmiller, L.; Zavanelli, D.; Snyder, G.J. Phase-Boundary Mapping to Engineer Defects in Thermoelectric Materials. PRX Energy 2022, 1, 022001. [Google Scholar] [CrossRef]
- Ohno, S.; Aydemir, U.; Amsler, M.; Pöhls, J.H.; Chanakian, S.; Zevalkink, A.; White, M.A.; Bux, S.K.; Wolverton, C.; Snyder, G.J. Achieving ZT > 1 in Inexpensive Zintl Phase Ca9Zn4+xSb9 by Phase Boundary Mapping. Adv. Funct. Mater. 2017, 27, 1606361. [Google Scholar] [CrossRef]
- Tang, Y.; Chen, S.; Snyder, G.J. Temperature Dependent Solubility of Yb in Yb–CoSb3 Skutterudite and Its Effect on Preparation, Optimization and Lifetime of Thermoelectrics. J. Mater. 2015, 1, 75. [Google Scholar] [CrossRef]
- Peters, M.C.; Doak, J.W.; Saal, J.E.; Olson, G.B.; Voorhees, P.W. Using First-Principles Calculations in CALPHAD Models to Determine Carrier Concentration of the Binary PbSe Semiconductor. J. Electron. Mater. 2019, 48, 1031. [Google Scholar] [CrossRef]
- Gurunathan, R.; Sarker, S.; Borg, C.K.H.; Saal, J.; Ward, L.; Mehta, A.; Snyder, G.J. Mapping Thermoelectric Transport in a Multicomponent Alloy Space. Adv. Electron. Mater. 2022, 8, 2200327. [Google Scholar] [CrossRef]
- Rickman, J.M.; Chan, H.M.; Harmer, M.P.; Smeltzer, J.A.; Marvel, C.J.; Roy, A.; Balasubramanian, G. Materials Informatics for the Screening of Multi-Principal Elements and High-Entropy Alloys. Nat. Commun. 2019, 10, 2618. [Google Scholar] [CrossRef] [PubMed]
- Xi, J.; Zhu, W.; Li, X.; Jiang, D.; Dronskowski, R.; Shi, X. Discovery of High-Performance Thermoelectric Chalcogenides through Reliable High-Throughput Material Screening. J. Am. Chem. Soc. 2018, 140, 10785–10793. [Google Scholar] [CrossRef] [PubMed]
- Li, R.; Li, X.; Xi, L.; Yang, J.; Singh, D.J.; Zhang, W. High-Throughput Screening for Advanced Thermoelectric Materials: Diamond-Like ABX 2 Compounds. ACS Appl. Mater. Interfaces 2019, 11, 24859–24866. [Google Scholar] [CrossRef] [PubMed]
- Wang, X.; Sheng, Y.; Ning, J.; Xi, J.; Xi, L.; Qiu, D.; Yang, J.; Ke, X. A Critical Review of Machine Learning Techniques on Thermoelectric Materials. J. Phys. Chem. Lett. 2023, 14, 1808–1822. [Google Scholar] [CrossRef]
- Zhang, R.Z.; Gucci, F.; Zhu, H.; Chen, K.; Reece, M.J. Data-Driven Design of Ecofriendly Thermoelectric High-Entropy Sulfides. Inorg. Chem. 2018, 57, 13027. [Google Scholar] [CrossRef]
- Zhang, Z.; Chen, H.; Wei, T.R.; Zhao, K.; Shi, X. Data-Driven Discovery of High-Performance Multicomponent Solid Solution Thermoelectric Materials. Mater. Today Energy 2022, 28, 101070. [Google Scholar] [CrossRef]
- Murdoch, W.J.; Singh, C.; Kumbier, K.; Abbasi-Asl, R.; Yu, B. Definitions, Methods, and Applications in Interpretable Machine Learning. Proc. Natl. Acad. Sci. USA 2019, 116, 22071. [Google Scholar] [CrossRef] [PubMed]
- Li, W.; Liu, M. Interpretable Machine Learning Workflow for Evaluating and Analyzing the Performance of High-Entropy GeTe-Based Thermoelectric Materials. ACS Appl. Electron. Mater. 2023, 5, 4523. [Google Scholar] [CrossRef]
- Lundberg, S.M.; Allen, P.G.; Lee, S.-I. A Unified Approach to Interpreting Model Predictions. Adv. Neural Inf. Process Syst. 2017, 30, 4768–4777. [Google Scholar]
- Zhang, Z.; Zhao, K.; Chen, H.; Ren, Q.; Yue, Z.; Wei, T.R.; Qiu, P.; Chen, L.; Shi, X. Entropy Engineering Induced Exceptional Thermoelectric and Mechanical Performances in Cu2-YAgyTe1-2xSxSex. Acta Mater. 2022, 224, 117512. [Google Scholar] [CrossRef]
- Cai, J.; Wang, H.; Liu, G.; Jiang, J. Designing High Entropy Structure in Thermoelectrics. Wuji Cailiao Xuebao/J. Inorg. Mater. 2021, 36, 399. [Google Scholar] [CrossRef]
- Karthikeyan, V.; Surjadi, J.U.; Li, X.; Fan, R.; Theja, V.C.S.; Li, W.J.; Lu, Y.; Roy, V.A.L. Three Dimensional Architected Thermoelectric Devices with High Toughness and Power Conversion Efficiency. Nat. Commun. 2023, 14, 2069. [Google Scholar] [CrossRef]
- Biswas, K.; He, J.; Blum, I.D.; Wu, C.I.; Hogan, T.P.; Seidman, D.N.; Dravid, V.P.; Kanatzidis, M.G. High-Performance Bulk Thermoelectrics with All-Scale Hierarchical Architectures. Nature 2012, 489, 414. [Google Scholar] [CrossRef]


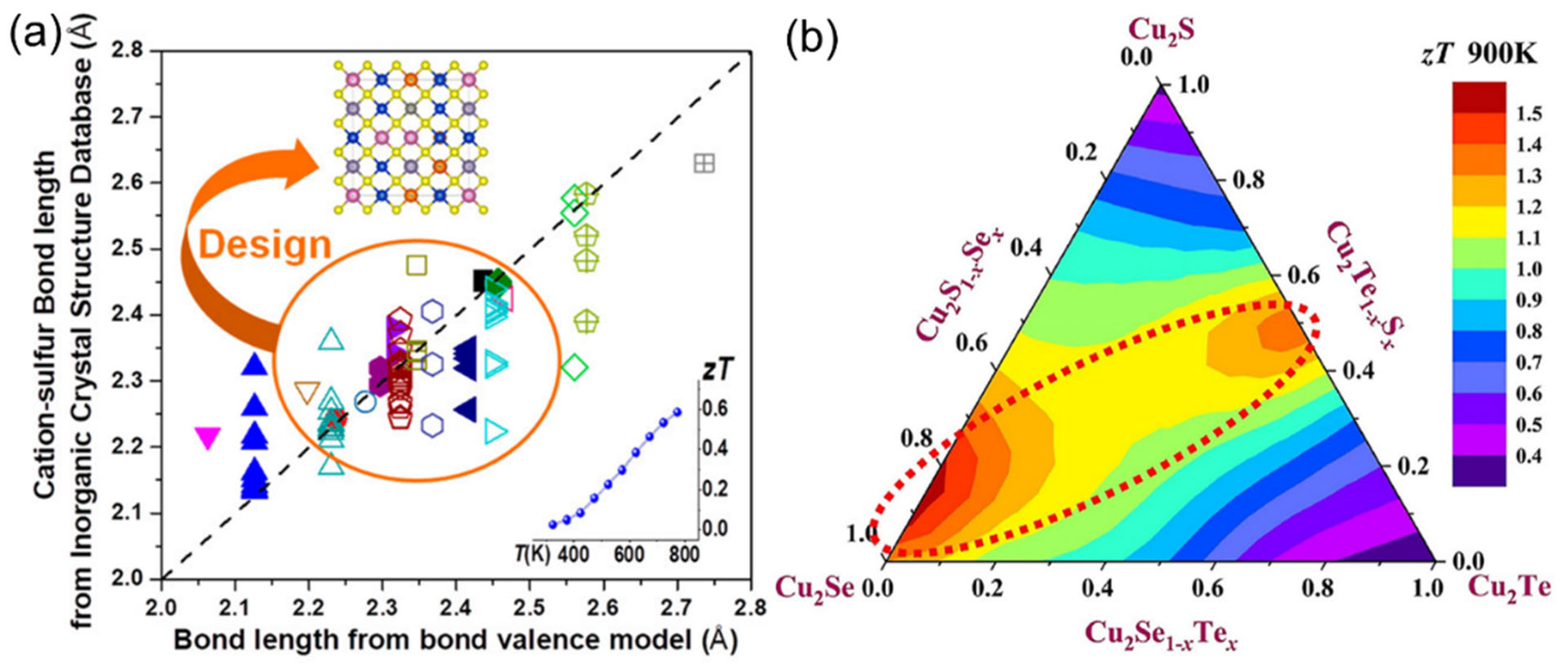
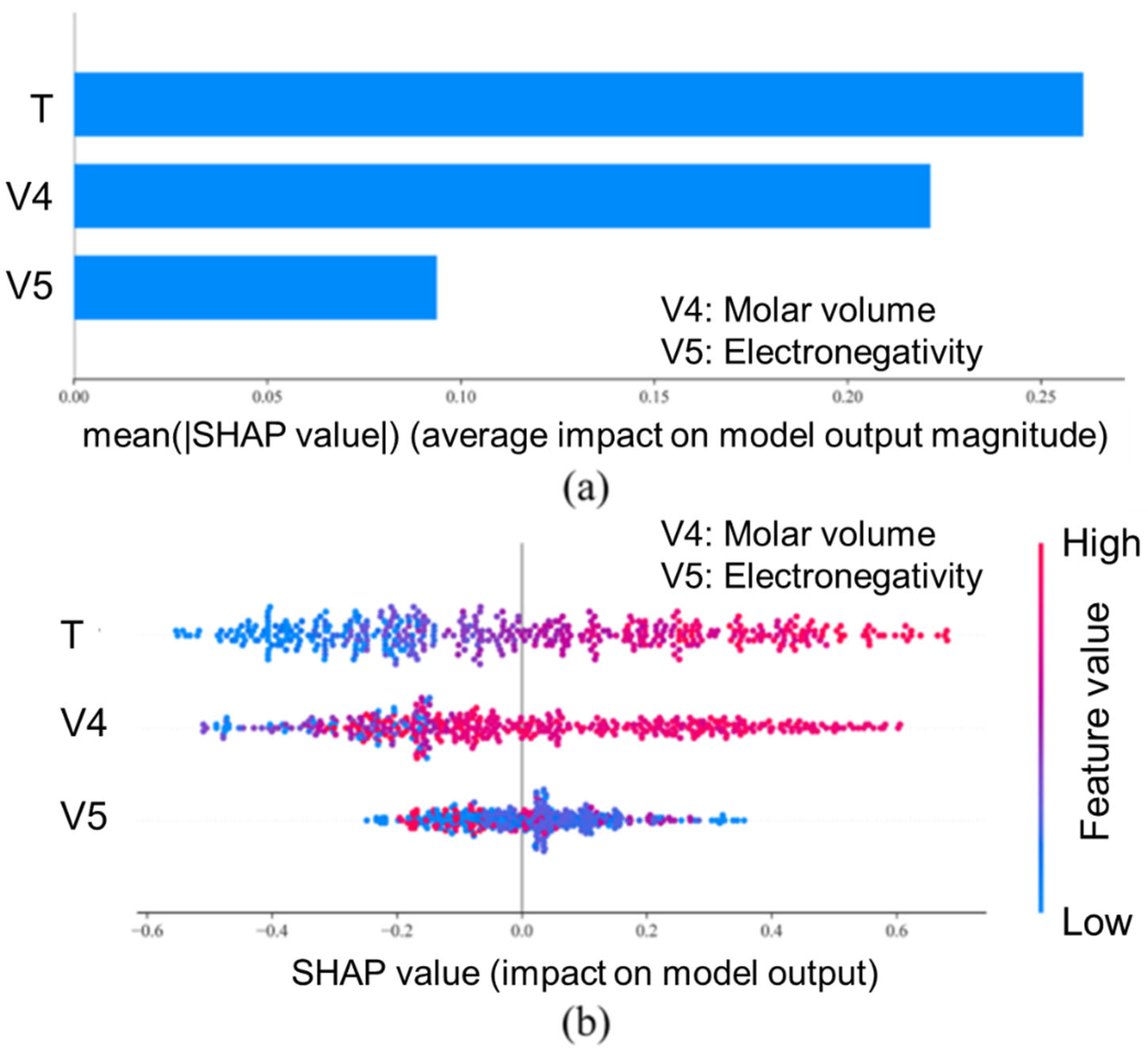
| Factors | Advantages of Materials | Entropy Engineering Effects |
|---|---|---|
| Composition | The compositional variation affects and extends solid solubility | Structural stabilization and cocktail effect |
| Access to increased composition space in a multicomponent domain | Structural stabilization due to | |
| Electrical | Changes in band structure and defect density, high electrical conductivity | , lattice distorsion, cocktail effect |
| Thermal | Lower thermal conductivity | Lattice distortion induced phonon scattering |
| Mechanical | Distortion modified defect interaction | Lattice distortion, cocktail effect |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ghosh, S.; Raman, L.; Sridar, S.; Li, W. High-Entropy Engineering in Thermoelectric Materials: A Review. Crystals 2024, 14, 432. https://doi.org/10.3390/cryst14050432
Ghosh S, Raman L, Sridar S, Li W. High-Entropy Engineering in Thermoelectric Materials: A Review. Crystals. 2024; 14(5):432. https://doi.org/10.3390/cryst14050432
Chicago/Turabian StyleGhosh, Subrata, Lavanya Raman, Soumya Sridar, and Wenjie Li. 2024. "High-Entropy Engineering in Thermoelectric Materials: A Review" Crystals 14, no. 5: 432. https://doi.org/10.3390/cryst14050432
APA StyleGhosh, S., Raman, L., Sridar, S., & Li, W. (2024). High-Entropy Engineering in Thermoelectric Materials: A Review. Crystals, 14(5), 432. https://doi.org/10.3390/cryst14050432








