Investigations on the Carrier Mobility of Cs2NaFeCl6 Double Perovskites
Abstract
1. Introduction
2. Methods
2.1. First Principle Calculations
2.2. Mobility Calculations
3. Results and Discussions
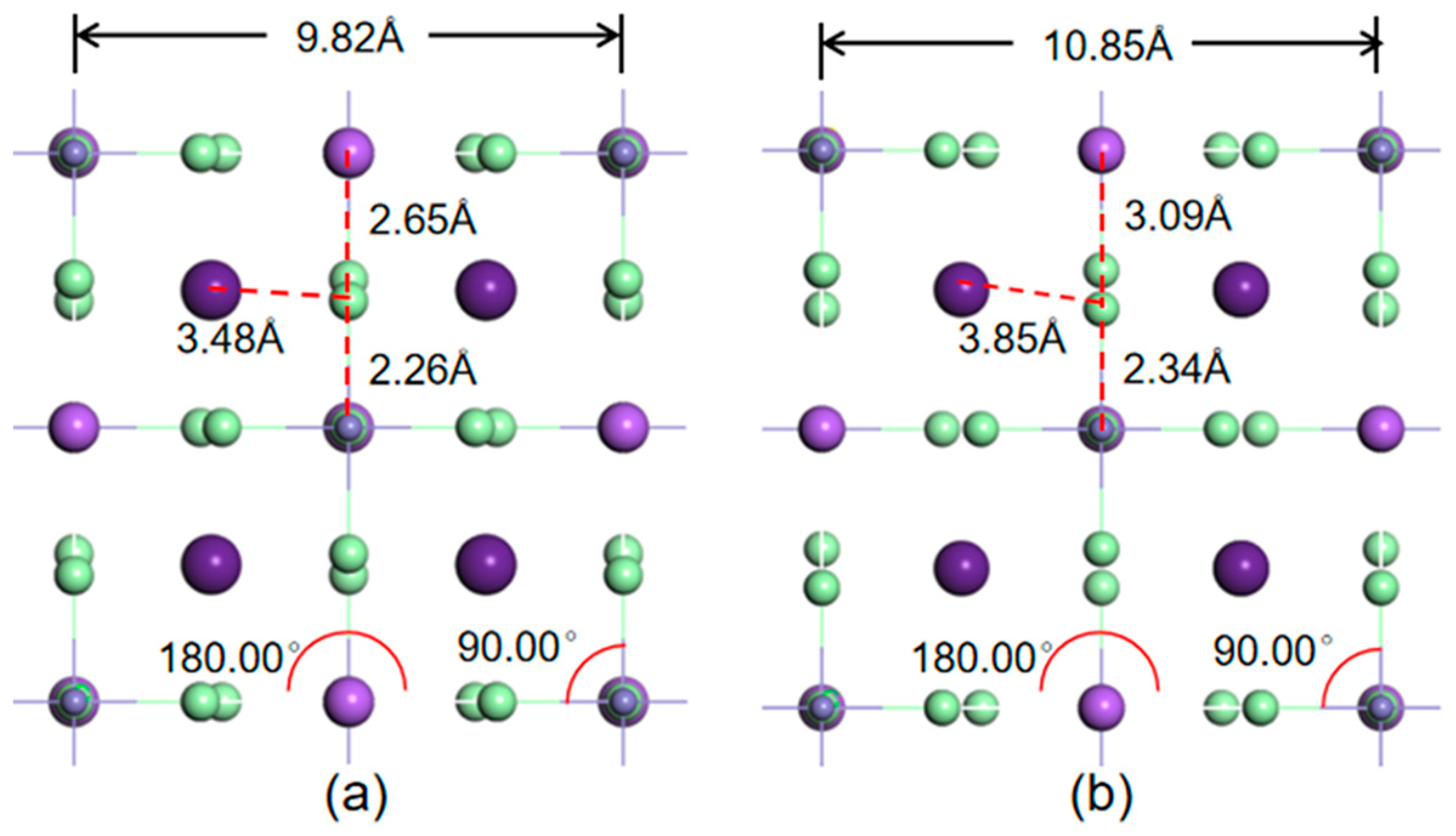
3.1. Geometric Structures
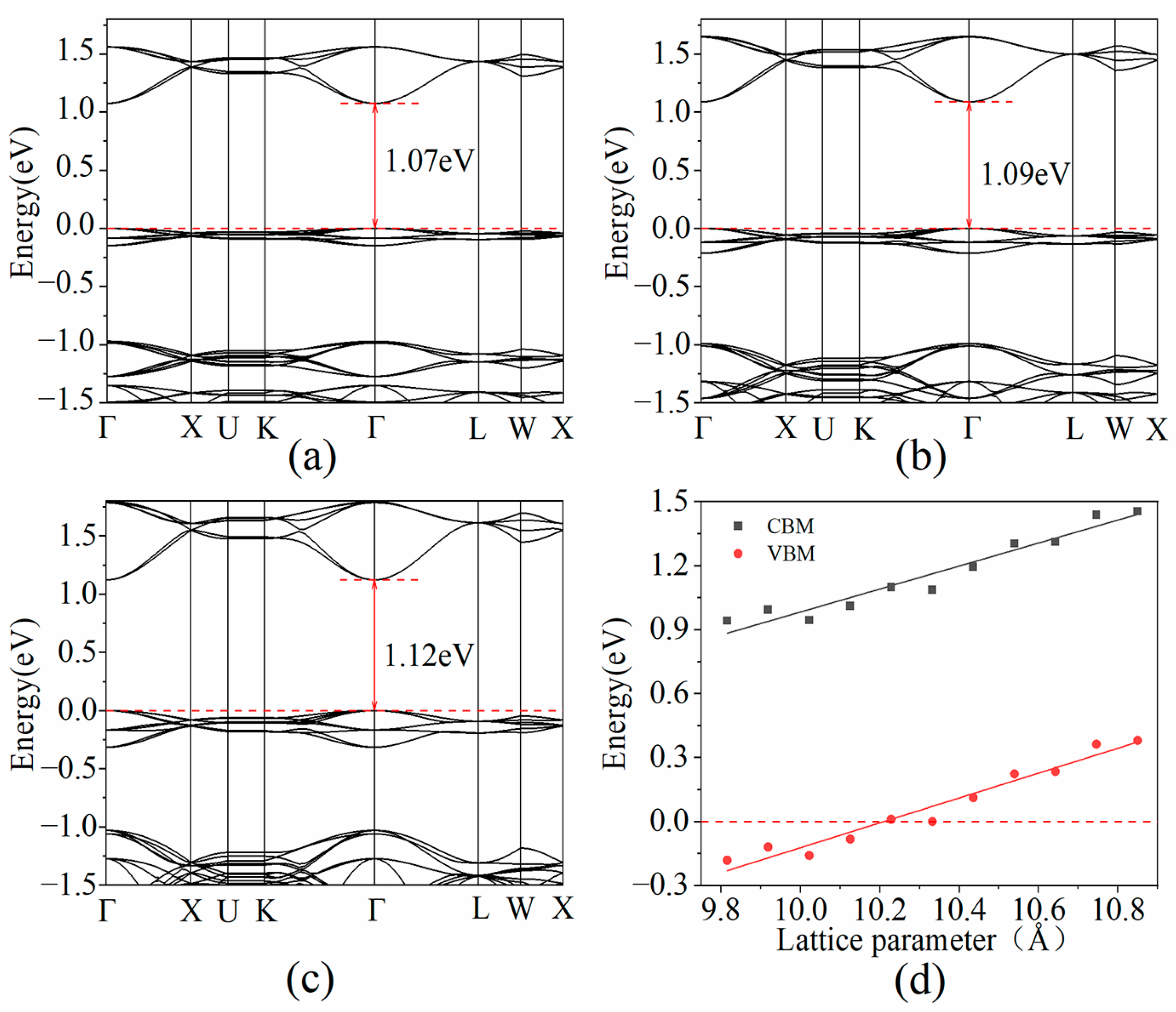
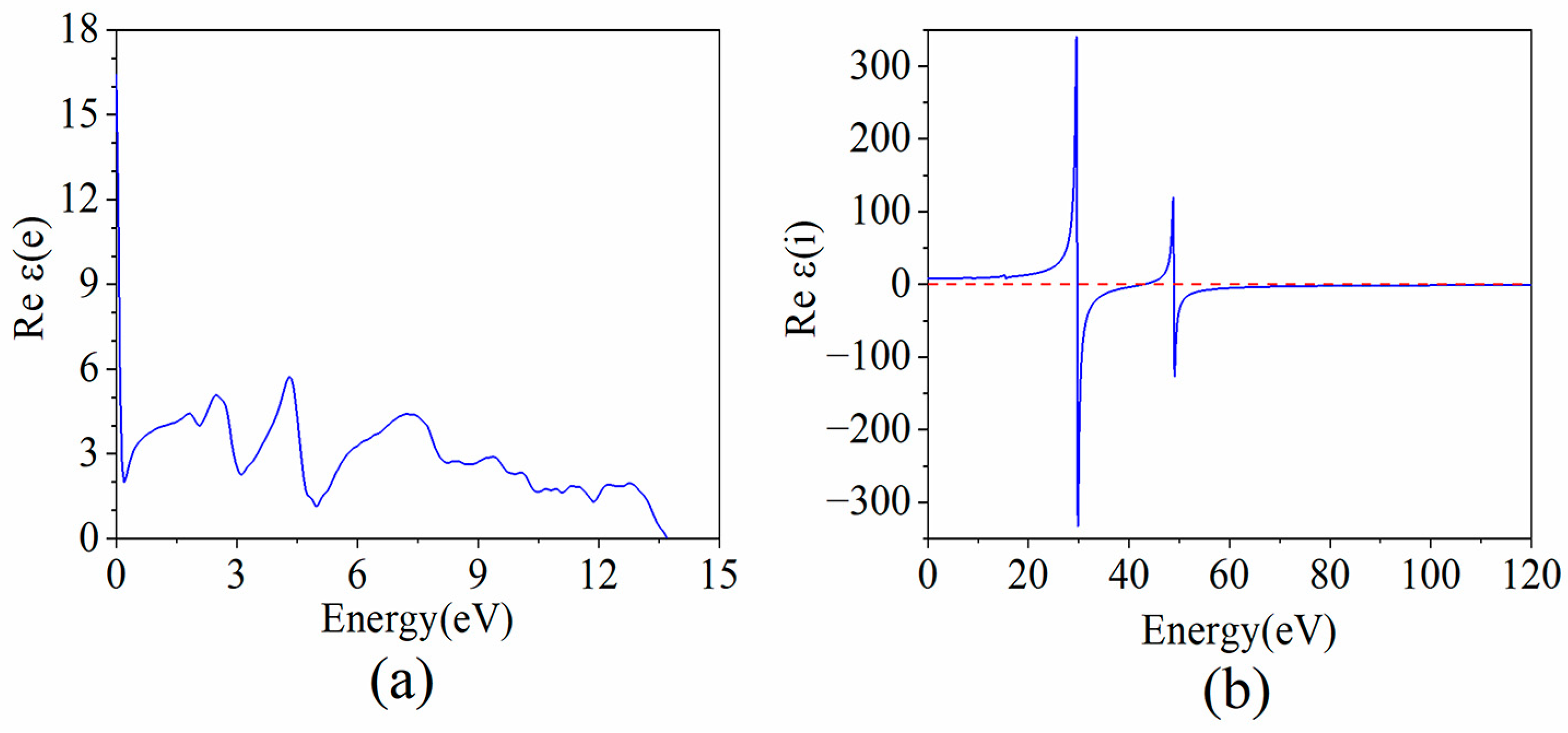
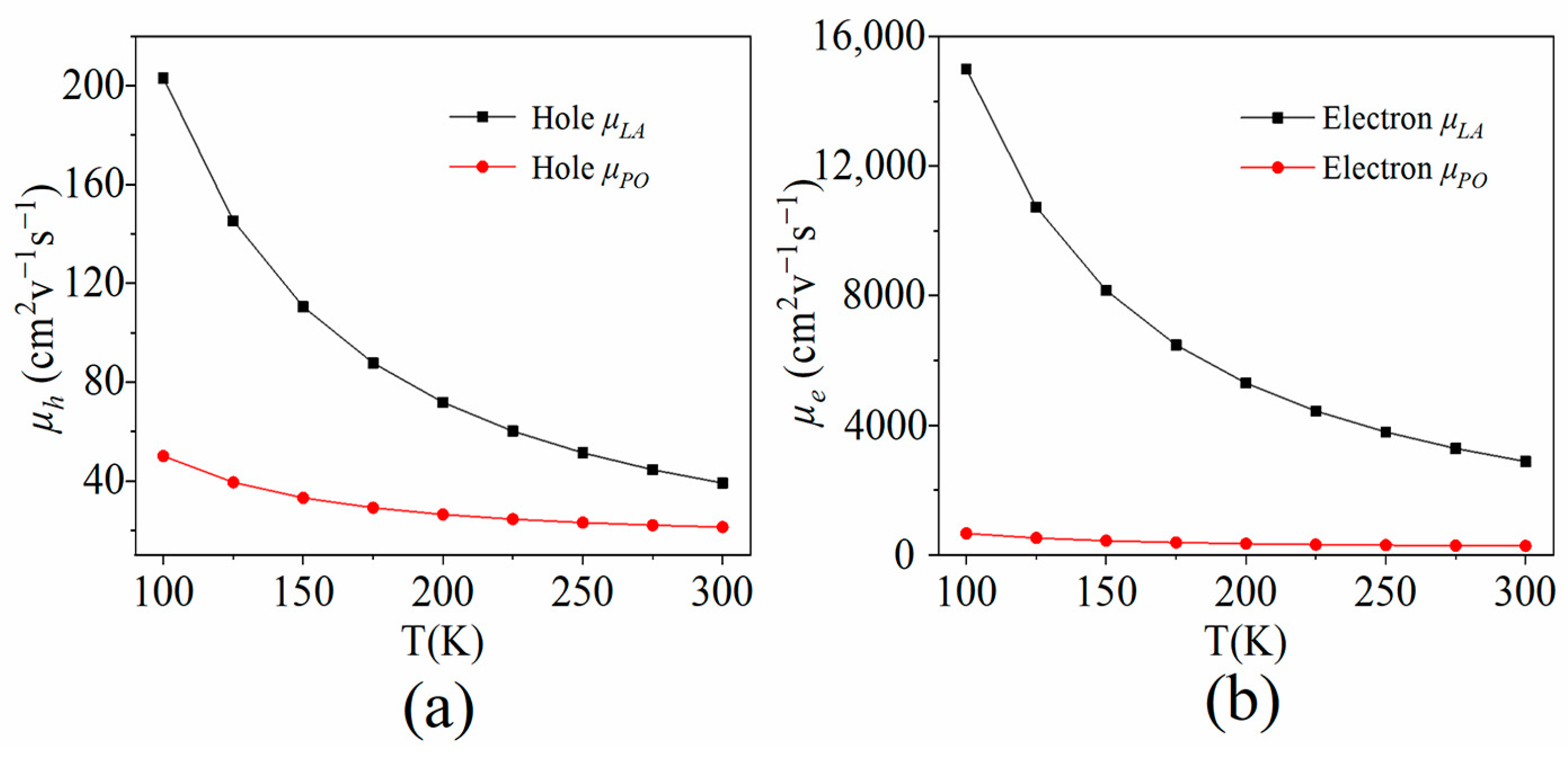
3.2. LA Phonon-Determined Carrier Mobility
3.3. PO Phonon-Determined Carrier Mobility
3.4. The Dominant Factor for Mobility
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Li, Q.; Liu, Y.; Guo, S.; Zhou, H. Solar energy storage in the rechargeable batteries. Nano Today 2017, 16, 46–60. [Google Scholar] [CrossRef]
- Liu, X.; Yuan, Y.; Liu, J.; Liu, B.; Chen, X.; Ding, J.; Han, X.; Deng, Y.; Zhong, C.; Hu, W. Utilizing solar energy to improve the oxygen evolution reaction kinetics in zinc–air battery. Nat. Commun. 2019, 10, 4767. [Google Scholar] [CrossRef] [PubMed]
- Zhao, J.; Xu, Z.; Zhou, Z.; Xi, S.; Xia, Y.; Zhang, Q.; Huang, L.; Mei, L.; Jiang, Y.; Gao, J.; et al. A Safe Flexible Self-Powered Wristband System by Integrating Defective MnO2–x Nanosheet-Based Zinc-Ion Batteries with Perovskite Solar Cells. ACS Nano 2021, 15, 10597–10608. [Google Scholar] [CrossRef] [PubMed]
- Yang, Y.; Hoang, M.T.; Bhardwaj, A.; Wilhelm, M.; Mathur, S.; Wang, H. Perovskite solar cells based self-charging power packs: Fundamentals, applications and challenges. Nano Energy 2022, 94, 106910. [Google Scholar] [CrossRef]
- Melskens, J.; van de Loo, B.W.H.; Macco, B.; Black, L.E.; Smit, S.; Kessels, W.M.M. Passivating Contacts for Crystalline Silicon Solar Cells: From Concepts and Materials to Prospects. IEEE J. Photovolt. 2018, 8, 373–388. [Google Scholar] [CrossRef]
- Zhou, J.; Tan, L.; Liu, Y.; Li, H.; Liu, X.; Li, M.; Wang, S.; Zhang, Y.; Jiang, C.; Hua, R.; et al. Highly efficient and stable perovskite solar cells via a multifunctional hole transporting material. Joule 2024, 8, 1–16. [Google Scholar] [CrossRef]
- Kojima, A.; Teshima, K.; Shirai, Y.; Miyasaka, T. Organometal Halide Perovskites as Visible-Light Sensitizers for Photovoltaic Cells. J. Am. Chem. Soc. 2009, 131, 6050–6051. [Google Scholar] [CrossRef] [PubMed]
- Liu, M.; Johnston, M.B.; Snaith, H.J. Efficient planar heterojunction perovskite solar cells by vapour deposition. Nature 2013, 501, 395–398. [Google Scholar] [CrossRef] [PubMed]
- Wu, L.; Lu, P.; Li, Y.; Sun, Y.; Wong, J.; Yang, K. First-principles characterization of two-dimensional (CH3(CH2)3NH3)2(CH3NH3)n−1GenI3n+1 perovskite. J. Mater. Chem. A 2018, 6, 24389–24396. [Google Scholar] [CrossRef]
- Najim, A.; Hartiti, B.; Absike, H.; Tchognia Nkuissi, H.J.; Labrim, H.; Fadili, S.; Thevenin, P.; Ertugrul, M. Theoretical investigation of structural, electronic, and optical properties of halide cubic perovskite CsPbBr3−xIx. Mater. Sci. Semicond. Process. 2022, 141, 106442. [Google Scholar] [CrossRef]
- Kanoun, M.B.; Goumri-Said, S. Insights into the impact of Mn-doped inorganic CsPbBr3 perovskite on electronic structures and magnetism for photovoltaic application. Mater. Today Energy 2021, 21, 100796. [Google Scholar] [CrossRef]
- Yang, B.; Chen, J.; Yang, S.; Hong, F.; Sun, L.; Han, P.; Pullerits, T.; Deng, W.; Han, K. Lead-Free Silver-Bismuth Halide Double Perovskite Nanocrystals. Angew. Chem. Int. Ed. 2018, 57, 5359–5363. [Google Scholar] [CrossRef] [PubMed]
- Pan, W.; Wu, H.; Luo, J.; Deng, Z.; Ge, C.; Chen, C.; Jiang, X.; Yin, W.-J.; Niu, G.; Zhu, L.; et al. Cs2AgBiBr6 single-crystal X-ray detectors with a low detection limit. Nat. Photonics 2017, 11, 726–732. [Google Scholar] [CrossRef]
- Steele, J.A.; Pan, W.; Martin, C.; Keshavarz, M.; Debroye, E.; Yuan, H.; Banerjee, S.; Fron, E.; Jonckheere, D.; Kim, C.W.; et al. Photophysical Pathways in Highly Sensitive Cs2AgBiBr6 Double-Perovskite Single-Crystal X-ray Detectors. Adv. Mater. 2018, 30, 1804450. [Google Scholar] [CrossRef]
- Luo, J.; Wang, X.; Li, S.; Liu, J.; Guo, Y.; Niu, G.; Yao, L.; Fu, Y.; Gao, L.; Dong, Q.; et al. Efficient and stable emission of warm-white light from lead-free halide double perovskites. Nature 2018, 563, 541–545. [Google Scholar] [CrossRef]
- Yu, G.; Xue, S.; Yin, R.; Wu, Q.; Gao, T.; Song, Y.; Wang, R.; Cong, W.Y.; Guan, C.; Lu, Y.B. How the Copper Dopant Alters the Geometric and Photoelectronic Properties of the Lead-Free Cs2AgSbCl6 Double Perovskite. Adv. Theory Simul. 2021, 4, 2100142. [Google Scholar] [CrossRef]
- Yin, R.; Yu, G.; Cong, W.-Y.; Guan, C.; Li, J.; Lu, Y.-B. Modulation Effect Generated by A Cations in Hybrid A2BB’X6 Double Halogen Perovskite Materials. ACS Appl. Mater. Interfaces 2020, 12, 44798–44804. [Google Scholar] [CrossRef]
- Cheng, P.; Wu, T.; Li, Y.; Jiang, L.; Deng, W.; Han, K. Combining theory and experiment in the design of a lead-free ((CH3NH3)2AgBiI6) double perovskite. New J. Chem. 2017, 41, 9598–9601. [Google Scholar] [CrossRef]
- Gao, W.; Ran, C.; Xi, J.; Jiao, B.; Zhang, W.; Wu, M.; Hou, X.; Wu, Z. High-Quality Cs2AgBiBr6 Double Perovskite Film for Lead-Free Inverted Planar Heterojunction Solar Cells with 2.2 % Efficiency. ChemPhysChem 2018, 19, 1696–1700. [Google Scholar] [CrossRef]
- Igbari, F.; Wang, R.; Wang, Z.-K.; Ma, X.-J.; Wang, Q.; Wang, K.-L.; Zhang, Y.; Liao, L.-S.; Yang, Y. Composition Stoichiometry of Cs2AgBiBr6 Films for Highly Efficient Lead-Free Perovskite Solar Cells. Nano Lett. 2019, 19, 2066–2073. [Google Scholar] [CrossRef]
- Jacoboni, C.; Canali, C.; Ottaviani, G.; Quaranta, A.A. A review of some charge transport properties of silicon. Solid-State Electron. 1977, 20, 77–89. [Google Scholar]
- Stoumpos, C.C.; Malliakas, C.D.; Peters, J.A.; Liu, Z.; Sebastian, M.; Im, J.; Chasapis, T.C.; Wibowo, A.C.; Chung, D.Y.; Freeman, A.J.; et al. Crystal Growth of the Perovskite Semiconductor CsPbBr3: A New Material for High-Energy Radiation Detection. Cryst. Growth Des. 2013, 13, 2722–2727. [Google Scholar] [CrossRef]
- Valverde-Chávez, D.A.; Ponseca, C.S.; Stoumpos, C.C.; Yartsev, A.; Kanatzidis, M.G.; Sundström, V.; Cooke, D.G. Intrinsic femtosecond charge generation dynamics in single crystal CH3NH3PbI3. Energy Environ. Sci. 2015, 8, 3700–3707. [Google Scholar] [CrossRef]
- Stoumpos, C.C.; Malliakas, C.D.; Kanatzidis, M.G. Semiconducting Tin and Lead Iodide Perovskites with Organic Cations: Phase Transitions, High Mobilities, and Near-Infrared Photoluminescent Properties. Inorg. Chem. 2013, 52, 9019–9038. [Google Scholar] [CrossRef] [PubMed]
- Leveillee, J.; Volonakis, G.; Giustino, F. Phonon-Limited Mobility and Electron–Phonon Coupling in Lead-Free Halide Double Perovskites. J. Phys. Chem. Lett. 2021, 12, 4474–4482. [Google Scholar] [CrossRef] [PubMed]
- Longo, G.; Mahesh, S.; Buizza, L.R.V.; Wright, A.D.; Ramadan, A.J.; Abdi-Jalebi, M.; Nayak, P.K.; Herz, L.M.; Snaith, H.J. Understanding the Performance-Limiting Factors of Cs2AgBiBr6 Double-Perovskite Solar Cells. ACS Energy Lett. 2020, 5, 2200–2207. [Google Scholar] [CrossRef]
- Sirtl, M.T.; Ebadi, F.; van Gorkom, B.T.; Ganswindt, P.; Janssen, R.A.J.; Bein, T.; Tress, W. The Bottlenecks of Cs2AgBiBr6 Solar Cells: How Contacts and Slow Transients Limit the Performance. Adv. Opt. Mater. 2021, 9, 2100202. [Google Scholar] [CrossRef]
- Jain, M.; Bhumla, P.; Kumar, M.; Bhattacharya, S. Lead-Free Alloyed Double Perovskites: An Emerging Class of Materials for Optoelectronic Applications. J. Phys. Chem. C 2022, 126, 6753–6760. [Google Scholar] [CrossRef]
- Ji, F.; Klarbring, J.; Zhang, B.; Wang, F.; Wang, L.; Miao, X.; Ning, W.; Zhang, M.; Cai, X.; Bakhit, B.; et al. Remarkable Thermochromism in the Double Perovskite Cs2NaFeCl6. Adv. Opt. Mater. 2023, 12, 2301102. [Google Scholar] [CrossRef]
- Li, W.; Rahman, N.U.; Xian, Y.; Yin, H.; Bao, Y.; Long, Y.; Yuan, S.; Zhang, Y.; Yuan, Y.; Fan, J. Regulation of the order–disorder phase transition in a Cs2NaFeCl6 double perovskite towards reversible thermochromic application. J. Semicond. 2021, 42, 072202. [Google Scholar] [CrossRef]
- Armer, M.; Dörflinger, P.; Weis, A.; Büchner, C.; Gottscholl, A.; Höcker, J.; Frank, K.; Nusser, L.; Sirtl, M.T.; Nickel, B.; et al. Low Temperature Optical Properties of Novel Lead-Free Cs2NaFeCl6 Perovskite Single Crystals. Adv. Photon Res. 2023, 4, 2300017. [Google Scholar] [CrossRef]
- Xian, Y.; Yin, H.; Bao, Y.; Xiao, Y.; Yuan, S.; Rahman, N.U.; Yuan, Y.; Zhang, Y.; Meng, X.; Jin, S.; et al. Engineered Electronic Structure and Carrier Dynamics in Emerging Cs2AgxNa1–xFeCl6 Perovskite Single Crystals. J. Phys. Chem. Lett. 2020, 11, 9535–9542. [Google Scholar] [PubMed]
- Kresse, G.; Furthmüller, J. Efficient iterative schemes for ab initio total-energy calculations using a plane-wave basis set. Phys. Rev. B 1996, 54, 11169–11186. [Google Scholar] [CrossRef] [PubMed]
- Kresse, G.; Joubert, D. From ultrasoft pseudopotentials to the projector augmented-wave method. Phys. Rev. B 1999, 59, 1758–1775. [Google Scholar] [CrossRef]
- Su, Y.; Wang, H.; Shi, L.-B.; Wang, Y.-Z.; Liu, Q.; Qian, P. An investigation on carrier transport behavior of tetragonal halide perovskite: First-principles calculation. Mater. Sci. Semicond. Process. 2022, 150, 106836. [Google Scholar] [CrossRef]
- Hendry, E.; Wang, F.; Shan, J.; Heinz, T.F.; Bonn, M. Electron transport inTiO2 probed by THz time-domain spectroscopy. Phys. Rev. B 2004, 69, 081101. [Google Scholar] [CrossRef]
- Steele, J.A.; Puech, P.; Keshavarz, M.; Yang, R.; Banerjee, S.; Debroye, E.; Kim, C.W.; Yuan, H.; Heo, N.H.; Vanacken, J.; et al. Giant Electron–Phonon Coupling and Deep Conduction Band Resonance in Metal Halide Double Perovskite. ACS Nano 2018, 12, 8081–8090. [Google Scholar] [PubMed]
- La-o-vorakiat, C.; Xia, H.; Kadro, J.; Salim, T.; Zhao, D.; Ahmed, T.; Lam, Y.M.; Zhu, J.-X.; Marcus, R.A.; Michel-Beyerle, M.-E.; et al. Phonon Mode Transformation Across the Orthohombic–Tetragonal Phase Transition in a Lead Iodide Perovskite CH3NH3PbI3: A Terahertz Time-Domain Spectroscopy Approach. J. Phys. Chem. Lett. 2015, 7, 1–6. [Google Scholar] [CrossRef]
- Zhang, B.; Klarbring, J.; Ji, F.; Simak, S.I.; Abrikosov, I.A.; Gao, F.; Rudko, G.Y.; Chen, W.M.; Buyanova, I.A. Lattice Dynamics and Electron–Phonon Coupling in Double Perovskite Cs2NaFeCl6. J. Phys. Chem. C 2023, 127, 1908–1916. [Google Scholar] [CrossRef]
- Verma, A.S.; Kumar, A. Bulk modulus of cubic perovskites. J. Alloys Compd. 2012, 541, 210–214. [Google Scholar] [CrossRef]
- Chu, W.; Zheng, Q.; Prezhdo, O.; Zhao, J.; Saidi, W.A. Low-frequency lattice phonons in halide perovskites explain high defect tolerance toward electron-hole recombination. Sci. Adv. 2020, 6, eaaw7453. [Google Scholar] [CrossRef] [PubMed]
- Yu, Z.-G. Rashba Effect and Carrier Mobility in Hybrid Organic–Inorganic Perovskites. J. Phys. Chem. Lett. 2016, 7, 3078–3083. [Google Scholar] [CrossRef] [PubMed]
- Xie, J.; Zhang, Z.Y.; Yang, D.Z.; Xue, D.S.; Si, M.S. Theoretical Prediction of Carrier Mobility in Few-Layer BC2N. J. Phys. Chem. Lett. 2014, 5, 4073–4077. [Google Scholar] [CrossRef] [PubMed]
- Verdi, C.; Giustino, F. Fröhlich Electron-Phonon Vertex from First Principles. Phys. Rev. Lett. 2015, 115, 176401. [Google Scholar] [CrossRef]
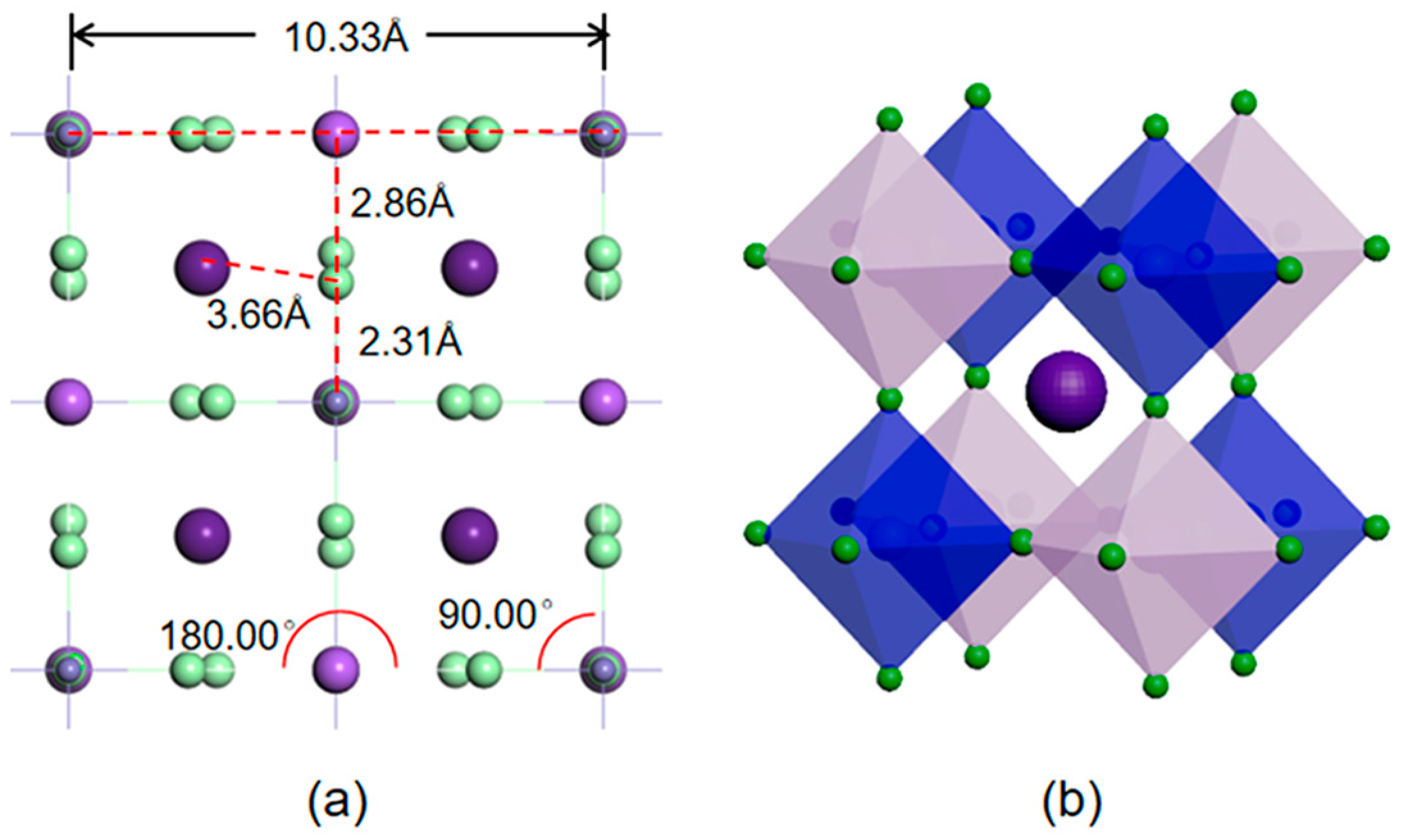
| a (Å) | Cs-Cl (Å) | Na-Cl (Å) | Fe-Cl (Å) | t |
|---|---|---|---|---|
| 10.33 | 3.66 | 2.86 | 2.31 | 1.00 |
| Carrier | m* (m0) | Cα (GPa) | E (eV) | μ (cm2 v−1 s−1) |
|---|---|---|---|---|
| Electron | 0.42 | 20.32 | 1.94 | 2886.08 |
| Hole | 2.22 | 20.32 | 2.08 | 39.09 |
| Carrier | ω (THz) | α | mp (m0) | μ (cm2 v−1 s−1) |
|---|---|---|---|---|
| Electron | 1.67 | 0.58 | 0.46 | 1194.25 |
| 4.91 | 0.34 | 0.44 | 709.42 | |
| 8.75 | 0.25 | 0.44 | 749.62 | |
| Total | 279.25 | |||
| Hole | 1.67 | 1.33 | 2.72 | 88.08 |
| 4.91 | 0.78 | 2.51 | 54.21 | |
| 8.75 | 0.58 | 2.44 | 58.27 | |
| Total | 21.29 |
| Carrier | μLA (cm2 v−1 s−1) | μPO (cm2 v−1 s−1) | μTotle (cm2 v−1 s−1) |
|---|---|---|---|
| Electron | 2886.08 | 279.25 | 254.61 |
| Hole | 39.09 | 21.29 | 13.78 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Xing, J.; Zhao, Y.; Cong, W.-Y.; Guan, C.; Wu, Z.; Liu, D.; Lu, Y.-B. Investigations on the Carrier Mobility of Cs2NaFeCl6 Double Perovskites. Crystals 2024, 14, 547. https://doi.org/10.3390/cryst14060547
Xing J, Zhao Y, Cong W-Y, Guan C, Wu Z, Liu D, Lu Y-B. Investigations on the Carrier Mobility of Cs2NaFeCl6 Double Perovskites. Crystals. 2024; 14(6):547. https://doi.org/10.3390/cryst14060547
Chicago/Turabian StyleXing, Jiyuan, Yiting Zhao, Wei-Yan Cong, Chengbo Guan, Zhongchen Wu, Dong Liu, and Ying-Bo Lu. 2024. "Investigations on the Carrier Mobility of Cs2NaFeCl6 Double Perovskites" Crystals 14, no. 6: 547. https://doi.org/10.3390/cryst14060547
APA StyleXing, J., Zhao, Y., Cong, W.-Y., Guan, C., Wu, Z., Liu, D., & Lu, Y.-B. (2024). Investigations on the Carrier Mobility of Cs2NaFeCl6 Double Perovskites. Crystals, 14(6), 547. https://doi.org/10.3390/cryst14060547






