The Temperature-Dependent Thermal Conductivity of C- and O-Doped Si3N4: First-Principles Calculations
Abstract
:1. Introduction
2. Calculation Method
2.1. Theoretical Model
2.2. Calculations
3. Results and Discussion
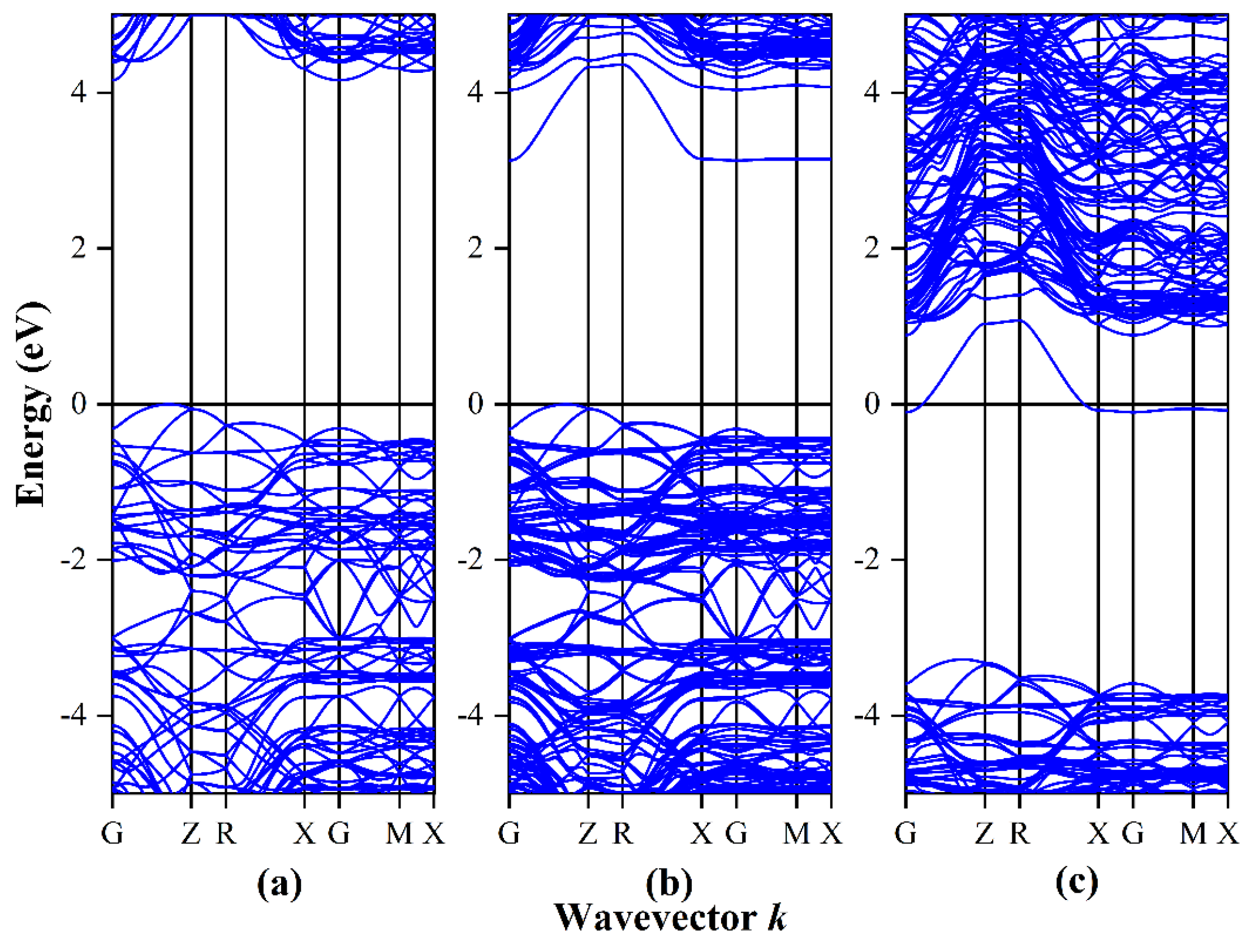
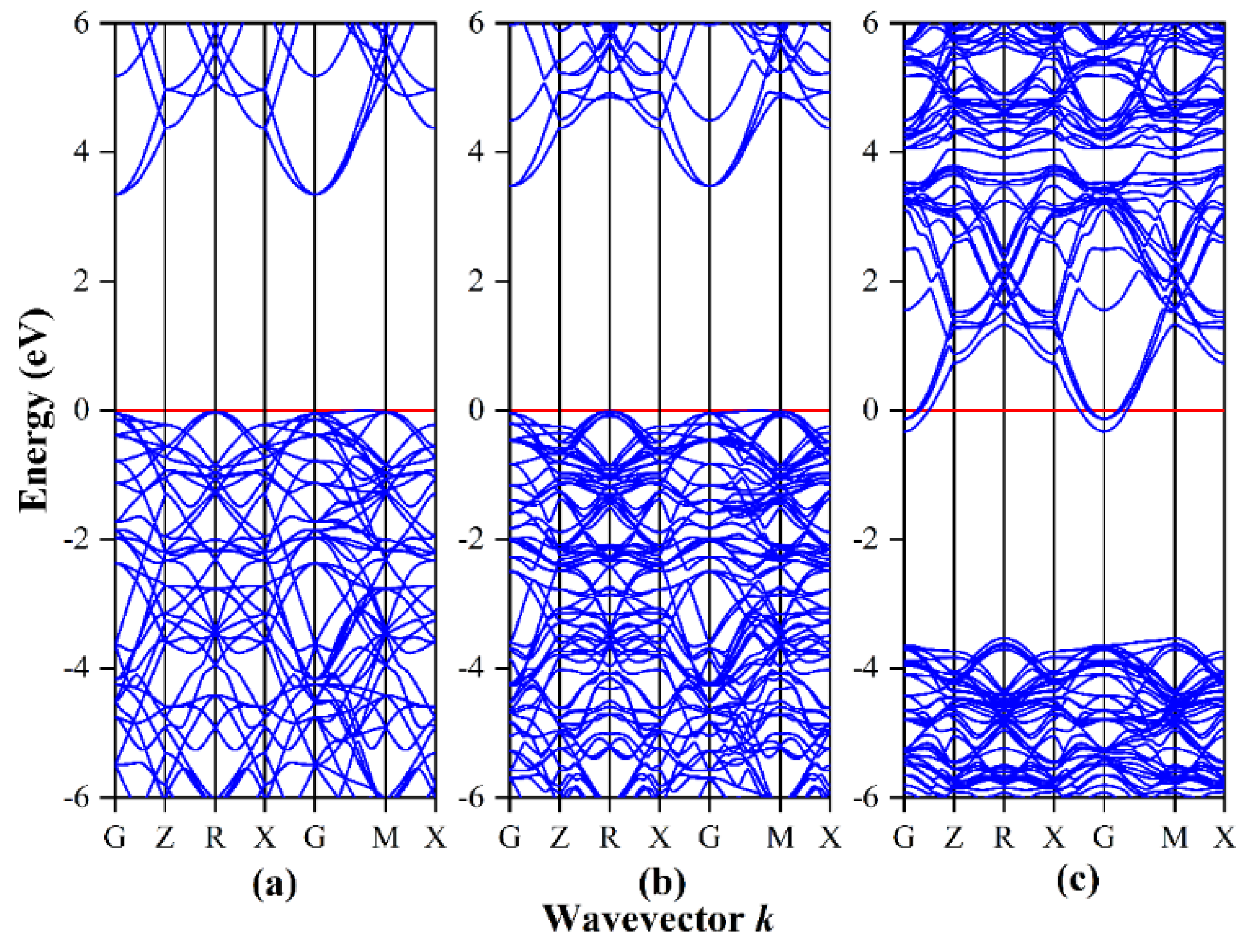
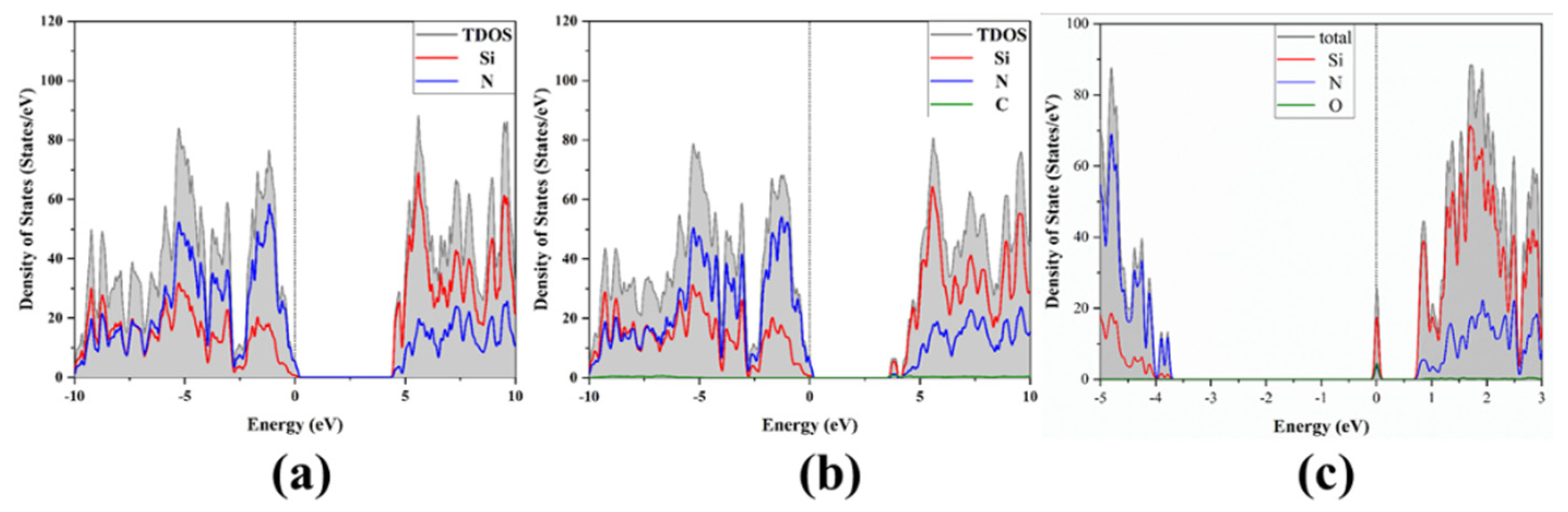
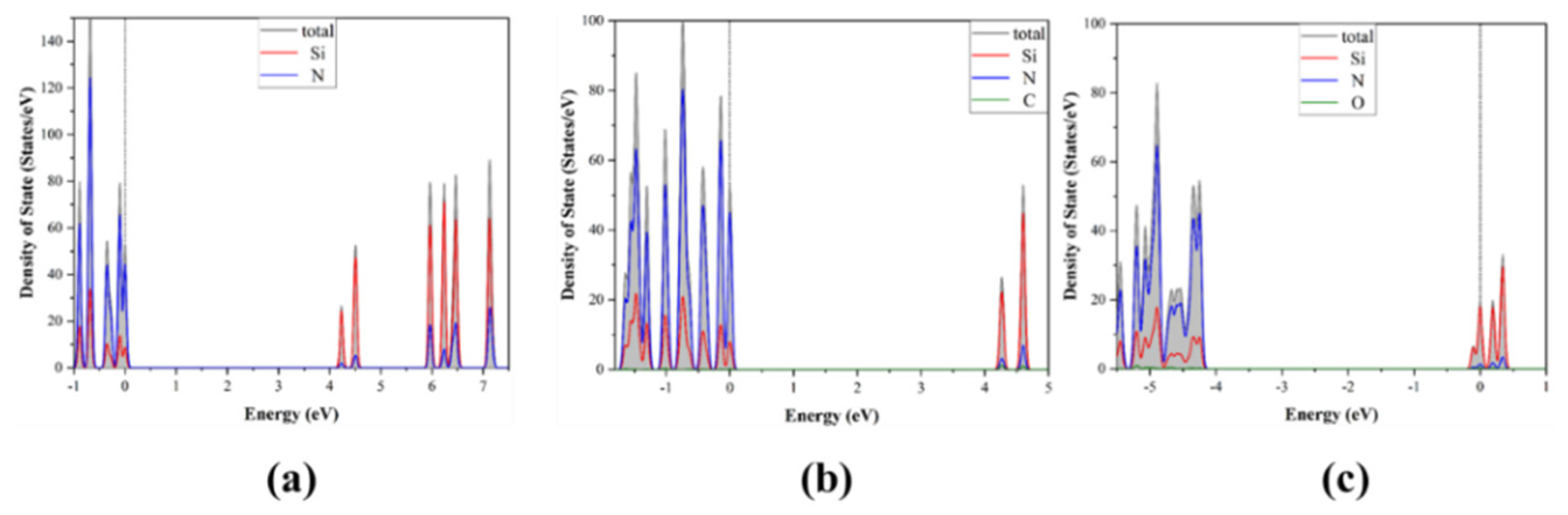
3.1. Band Structure and Density of States
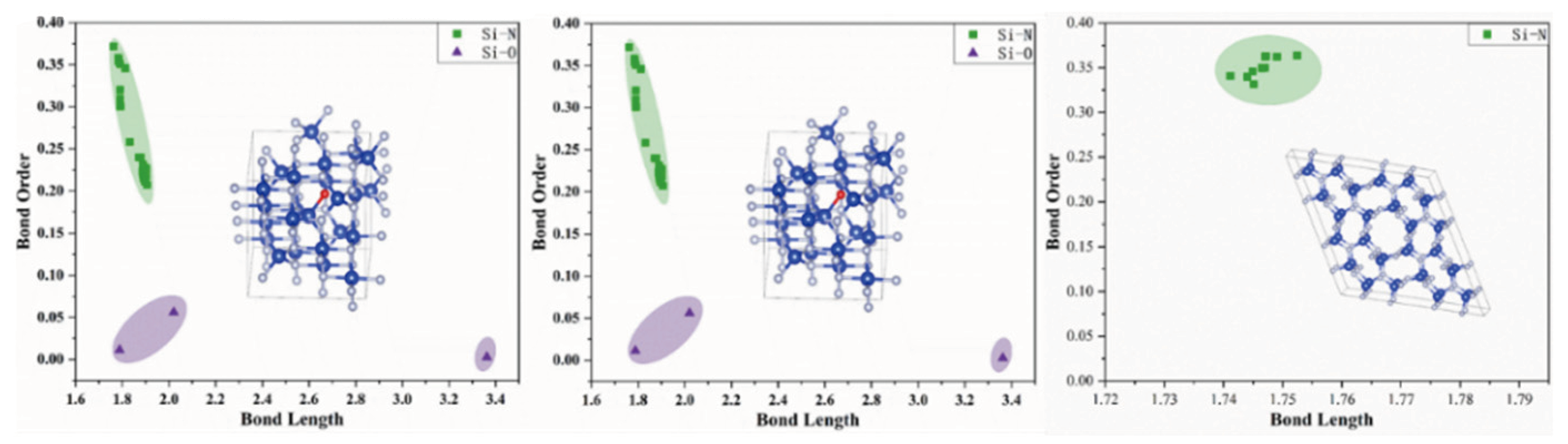
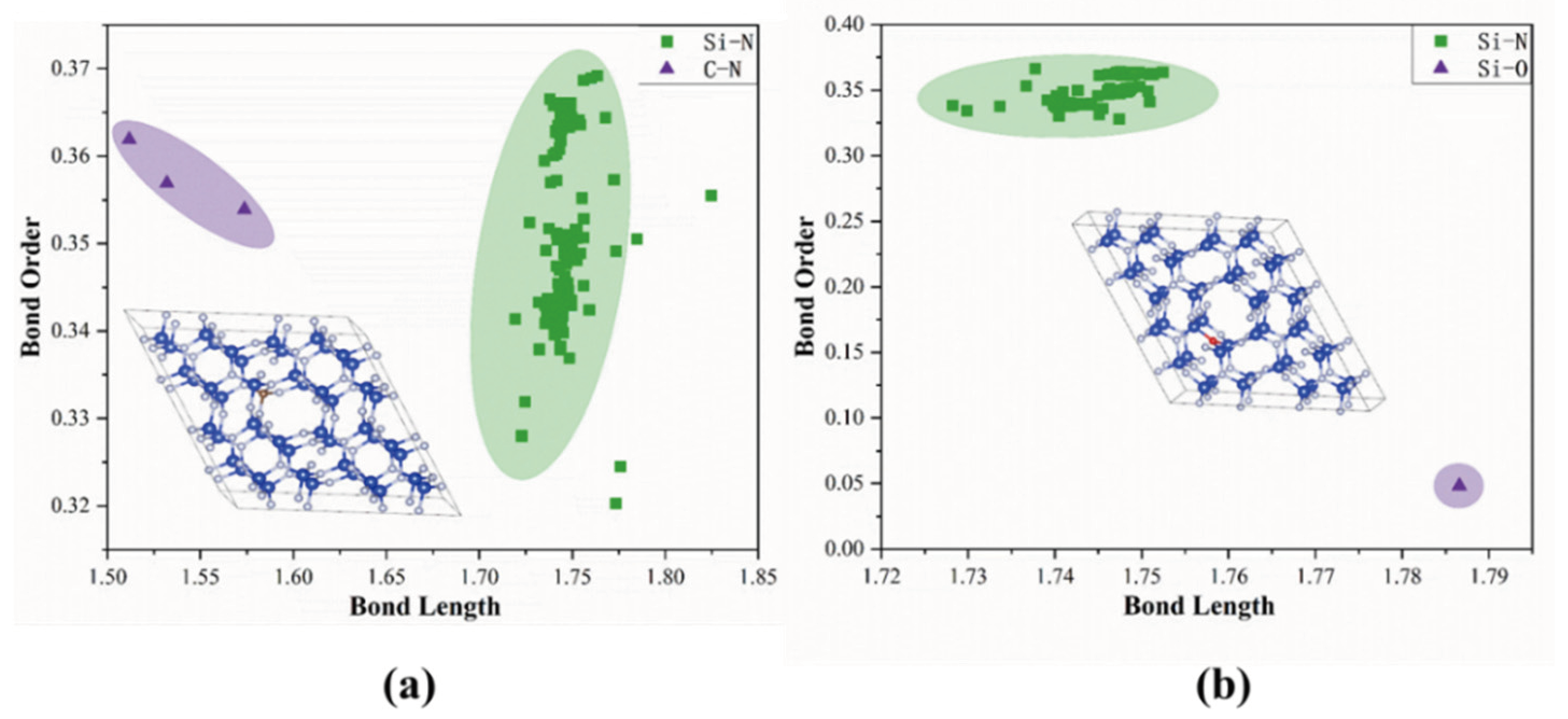
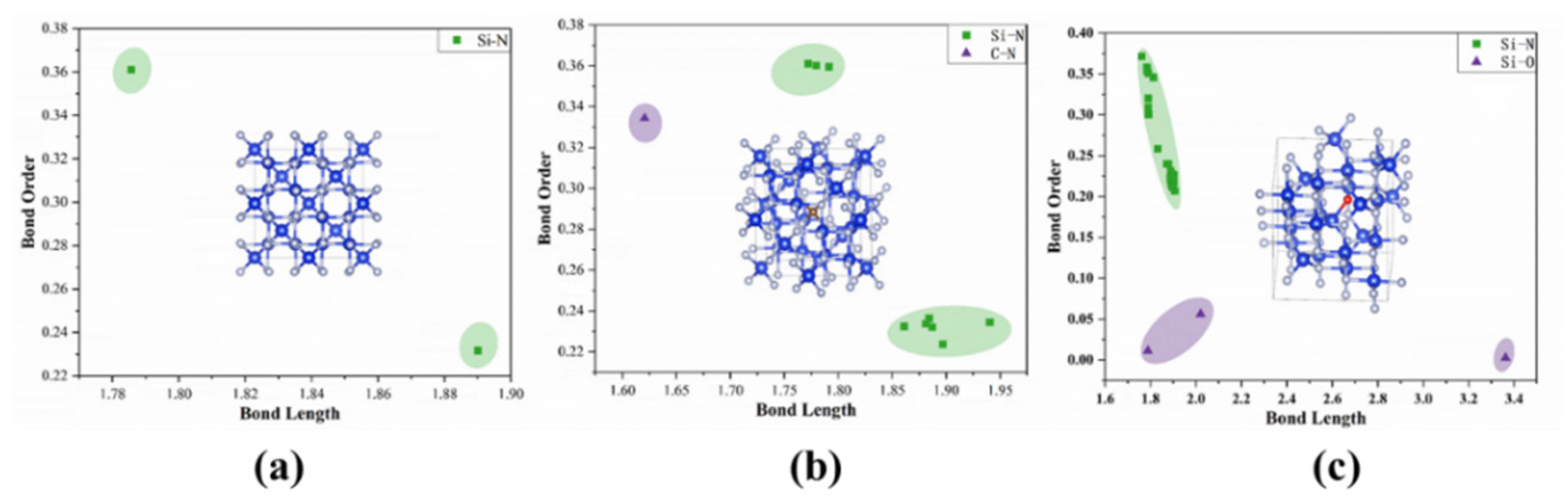
3.2. Bond Order
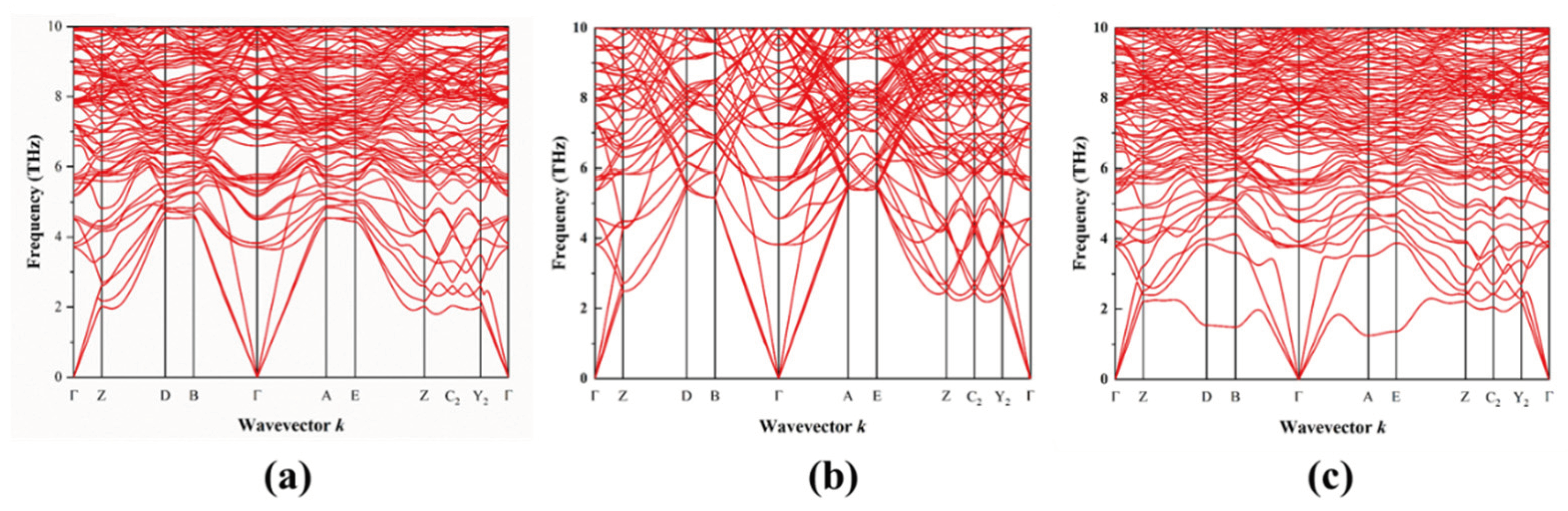
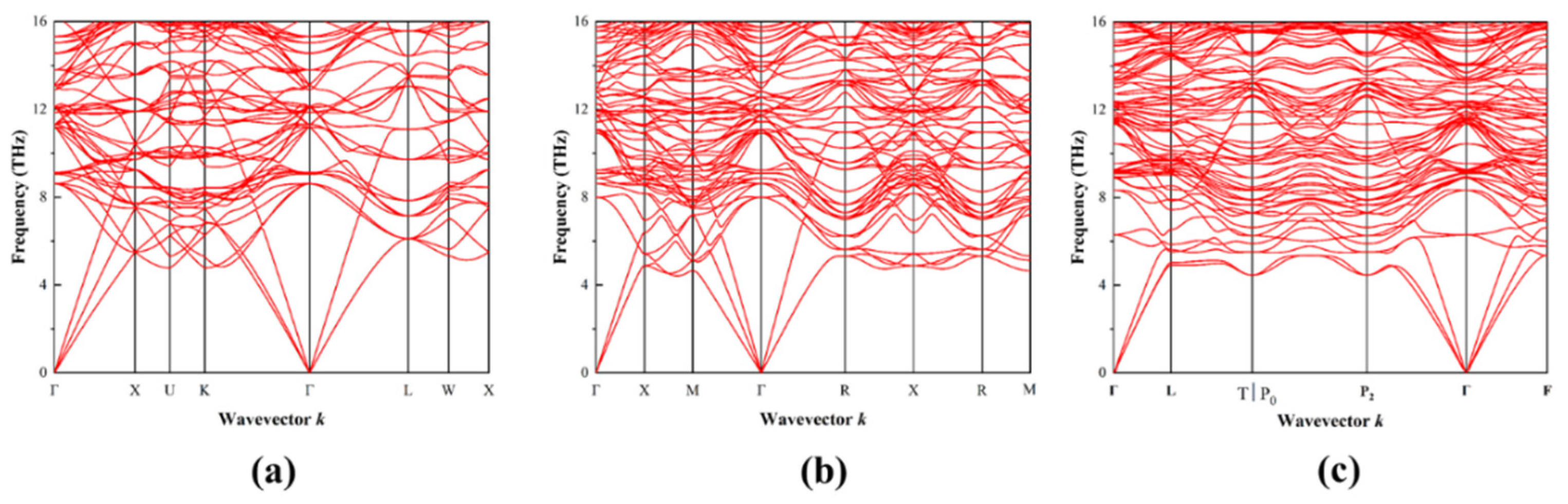
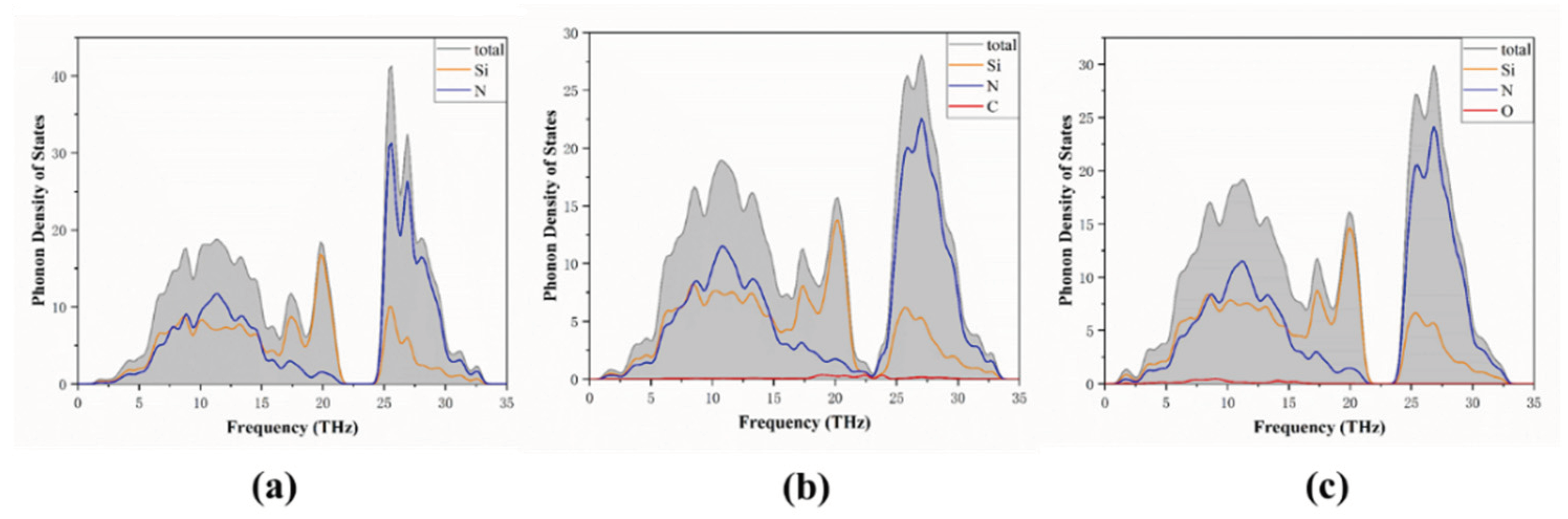
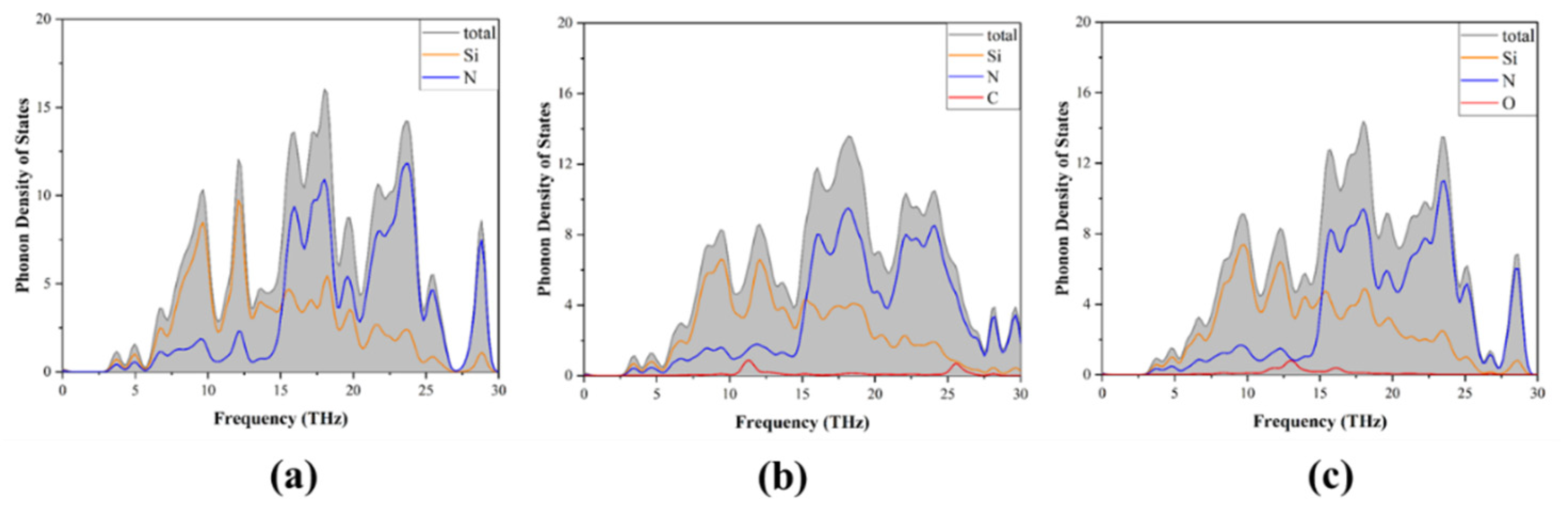
3.3. Phonon Properties
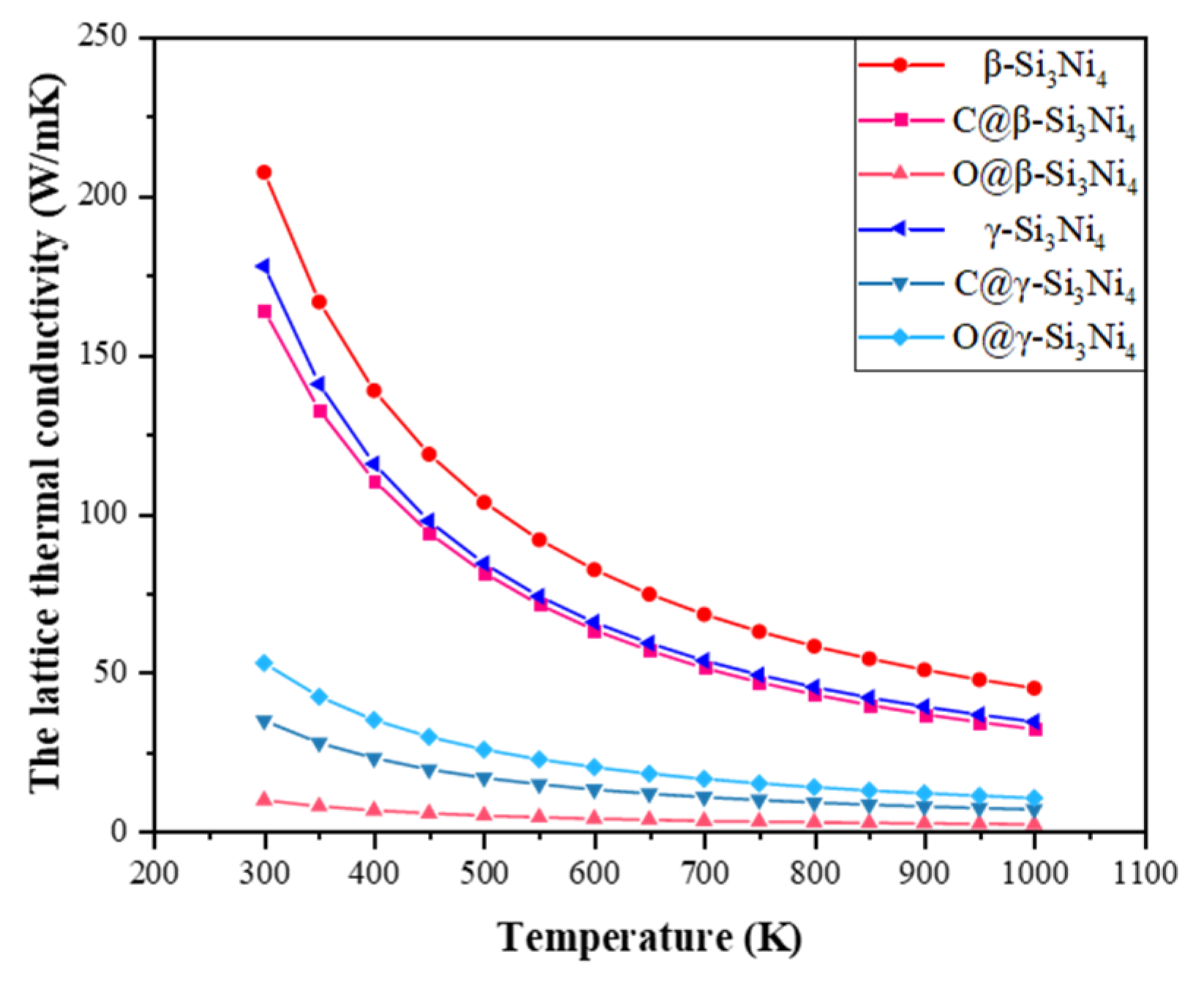
3.4. Thermal Properties
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Riley, F.L. Silicon nitride and related materials. J. Am. Ceram. Soc. 2010, 83, 245–265. [Google Scholar] [CrossRef]
- Lin, H.; Ferber, M. Mechanical reliability evaluation of silicon nitride ceramic components after exposure in industrial gas turbines. J. Eur. Ceram. Soc. 2002, 22, 2789–2797. [Google Scholar] [CrossRef]
- Haggerty, J.S.; Lightfoot, A. Opportunities for enhancing the thermal conductivities of SiC and Si3N4 ceramics through improved processing. In Proceedings of the 19th Annual Conference on Composites, Advanced Ceramics, Materials, and Structures—A: Ceramic Engineering and Science Proceedings, Cocoa Beach, FL, USA, 8–12 January 1995; Volume 16, pp. 475–487. [Google Scholar]
- Zhu, X.W.; Sakka, Y.; Zhou, Y.; Hirao, K.; Itatani, K. A Strategy for Fabrication Textured Silicon Nitride with Enhanced Thermal Conductivity. J. Eur. Ceram. Soc. 2014, 34, 2585–2589. [Google Scholar] [CrossRef]
- Watari, K. High thermal conductivity non-oxide ceramics. J. Ceram. Soc. Jpn. 2001, 109, S7–S16. [Google Scholar] [CrossRef]
- Kitayama, M.; Hirao, K.; Toriyama, M.; Kanzaki, S. Thermal conductivity of β-Si3N4: I, effects of various microstructural factors. J. Am. Ceram. Soc. 1999, 82, 3105–3112. [Google Scholar] [CrossRef]
- Yokota, H.; Ibukiyama, M. Effect of lattice impurities on the thermalconductivity of β-Si3N4. J. Eur. Ceram. Soc. 2003, 23, 55–60. [Google Scholar] [CrossRef]
- Lu, H.H.; Huang, J.L. Microstructure in Silicon Nitride Containing b-Phase Seeding: III, Grain Growth and Coalescence. J. Am. Ceram. Soc. 2001, 84, 1891–1895. [Google Scholar] [CrossRef]
- Yokota, H.; Ibukiyama, M. Microstructure Tailoring for High Thermal Conductivity of β-Si3N4 Ceramics. J. Am. Ceram. Soc. 2003, 86, 197–199. [Google Scholar] [CrossRef]
- Zhu, X.; Zhou, Y.; Hirao, K. Effects of processing method and additivecomposition on microstructure and thermal conductivity of Si3N4 ceramics. J. Eur. Ceram. Soc. 2006, 26, 711–718. [Google Scholar] [CrossRef]
- Hirao, K.; Watari, K.; Hayashi, H.; Kitayama, M. High thermal conductivity silicon nitride ceramic. MRS Bull. 2001, 26, 451–455. [Google Scholar] [CrossRef]
- Zhu, X.; Zhou, Y.; Hirao, K.; Ishigaki, T.; Sakka, Y. Potential use of only Yb2O3 in producing dense Si3N4 ceramics with high thermal conductivity by gas pressure sintering. Sci. Technol. Adv. Mater. 2010, 11, 065001. [Google Scholar] [CrossRef] [PubMed]
- Ishibe, T.; Kaneko, T.; Uematsu, Y.; Sato-Akaba, H.; Komura, M.; Iyoda, T.; Nakamura, Y. Tunable Thermal Switch via Order–Order Transition in Liquid Crystalline Block Copolymer. Nano Lett. 2022, 22, 6105–6111. [Google Scholar] [CrossRef] [PubMed]
- Zeidell, A.M.; Filston, D.S.; Waldrip, M.; Iqbal, H.F.; Chen, H.; McCulloch, I.; Jurchescu, O.D. Large-area uniform polymer transistor arrays on flexible substrates: Towards high-throughput sensor fabrication. Adv. Mater. Technol. 2020, 5, 2000390. [Google Scholar] [CrossRef]
- Becher, P.F.; Painter, G.S.; Shibata, N.; Waters, S.B.; Lin, H.T. Effects of Rare-earth(RE) intergranular adsorption on the phase transformation, microstructureevolution, and mechanical properties in silicon nitride with RE2O3 + MgO additives: RE = La, Gd, and Lu. J. Am. Ceram. Soc. 2008, 91, 2328–2336. [Google Scholar] [CrossRef]
- Xiang, H.; Feng, Z.; Li, Z.; Zhou, Y. Theoretical predicted high-thermal-conductivity cubic Si3N4 and Ge3N4: Promising substrate materials for high-power electronic devices. Sci. Rep. 2018, 8, 14374. [Google Scholar] [CrossRef] [PubMed]
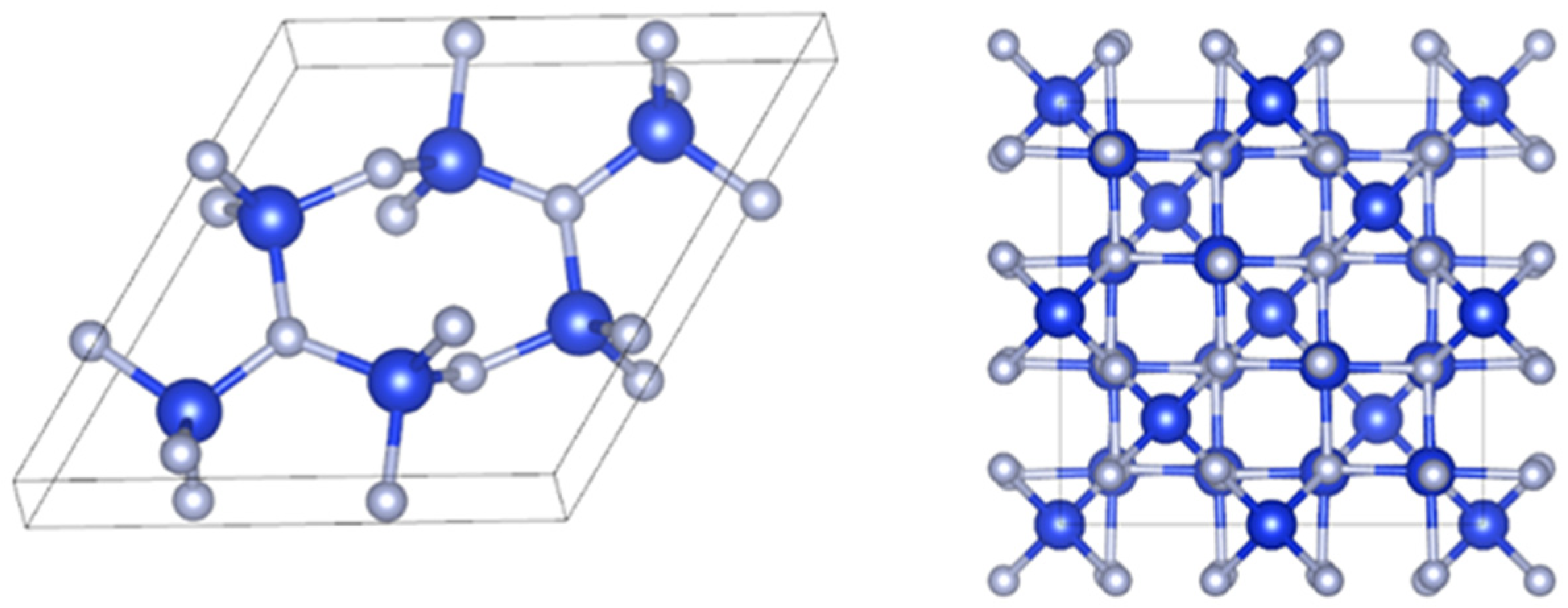
| Crystal Form | a/Å | b/Å | c/Å | V/Å3 |
|---|---|---|---|---|
| β-Si3N4 | 15.319 | 15.319 | 5.850 | 1188.834 |
| C@β-Si3N4 | 15.259 | 15.274 | 5.834 | 1177.650 |
| O@β-Si3N4 | 15.334 | 15.333 | 5.850 | 1192.140 |
| γ-Si3N4 | 7.787 | 7.787 | 7.787 | 472.263 |
| C@γ-Si3N4 | 7.742 | 7.742 | 7.742 | 463.991 |
| O@γ-Si3N4 | 7.799 | 7.799 | 7.799 | 474.300 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Shao, H.; Qiu, J.; Liu, X.; Hou, X.; Zhang, J. The Temperature-Dependent Thermal Conductivity of C- and O-Doped Si3N4: First-Principles Calculations. Crystals 2024, 14, 549. https://doi.org/10.3390/cryst14060549
Shao H, Qiu J, Liu X, Hou X, Zhang J. The Temperature-Dependent Thermal Conductivity of C- and O-Doped Si3N4: First-Principles Calculations. Crystals. 2024; 14(6):549. https://doi.org/10.3390/cryst14060549
Chicago/Turabian StyleShao, Hongfei, Jiahao Qiu, Xia Liu, Xuejun Hou, and Jinyong Zhang. 2024. "The Temperature-Dependent Thermal Conductivity of C- and O-Doped Si3N4: First-Principles Calculations" Crystals 14, no. 6: 549. https://doi.org/10.3390/cryst14060549
APA StyleShao, H., Qiu, J., Liu, X., Hou, X., & Zhang, J. (2024). The Temperature-Dependent Thermal Conductivity of C- and O-Doped Si3N4: First-Principles Calculations. Crystals, 14(6), 549. https://doi.org/10.3390/cryst14060549





