Phase-Field Simulation of Grain Growth in Uranium Silicide Nuclear Fuel
Abstract
:1. Introduction
2. Phase-Field Model of U3Si2 Grain Growth
2.1. Establishment of Phase-Field Model
2.2. Dimensionalization of Parameters
3. Results
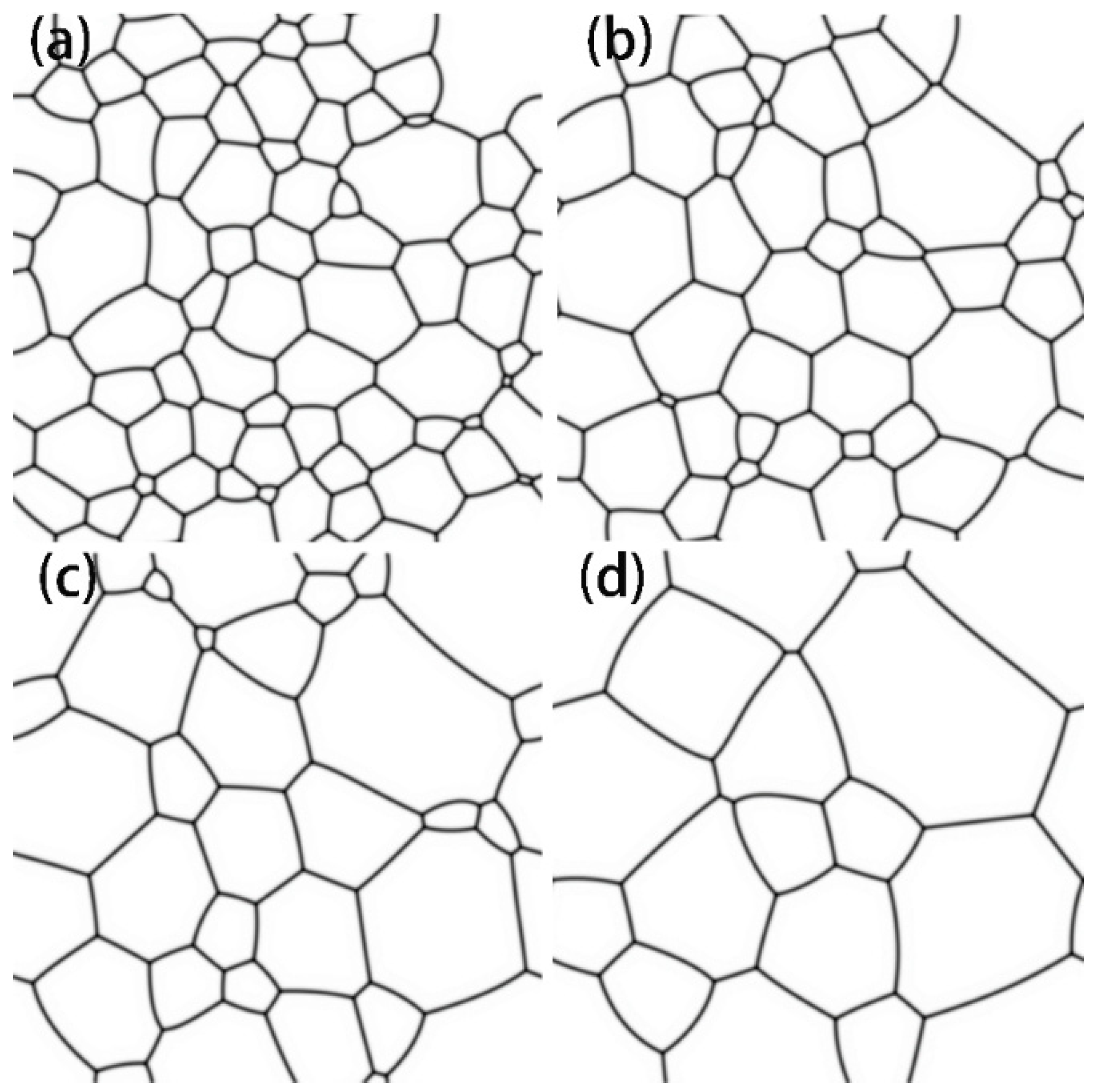
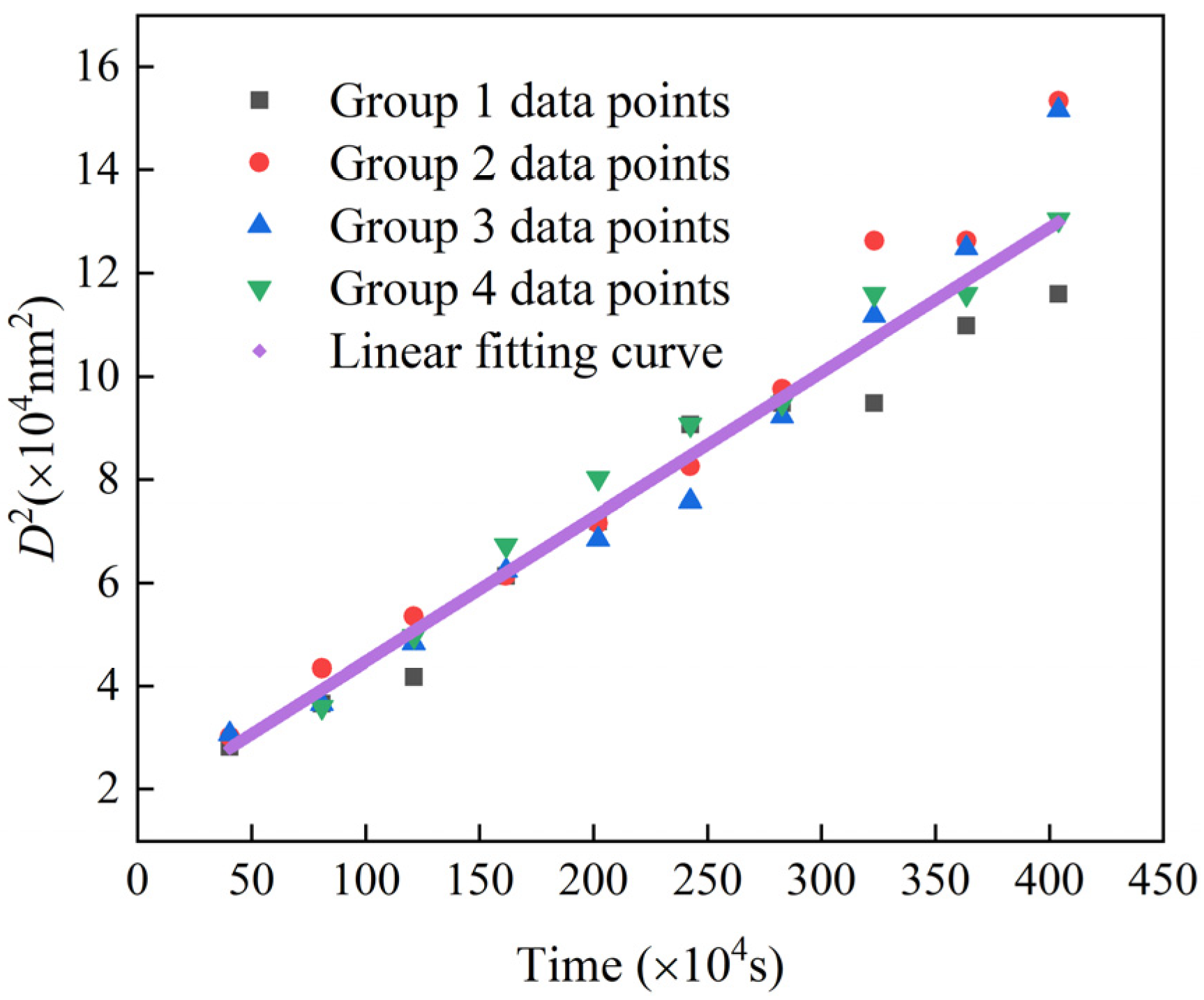
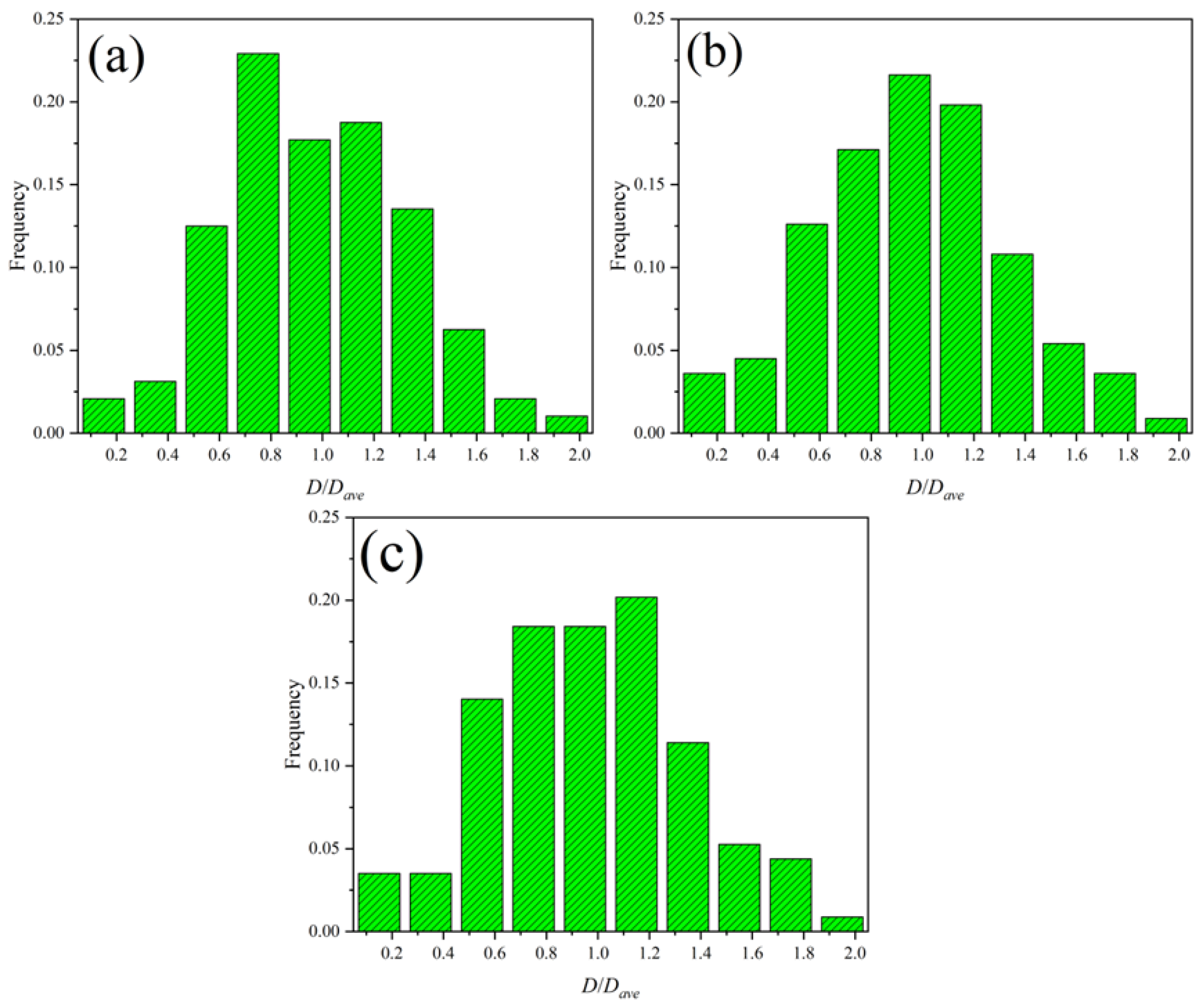
3.1. Isotropic Grain Growth of U3Si2
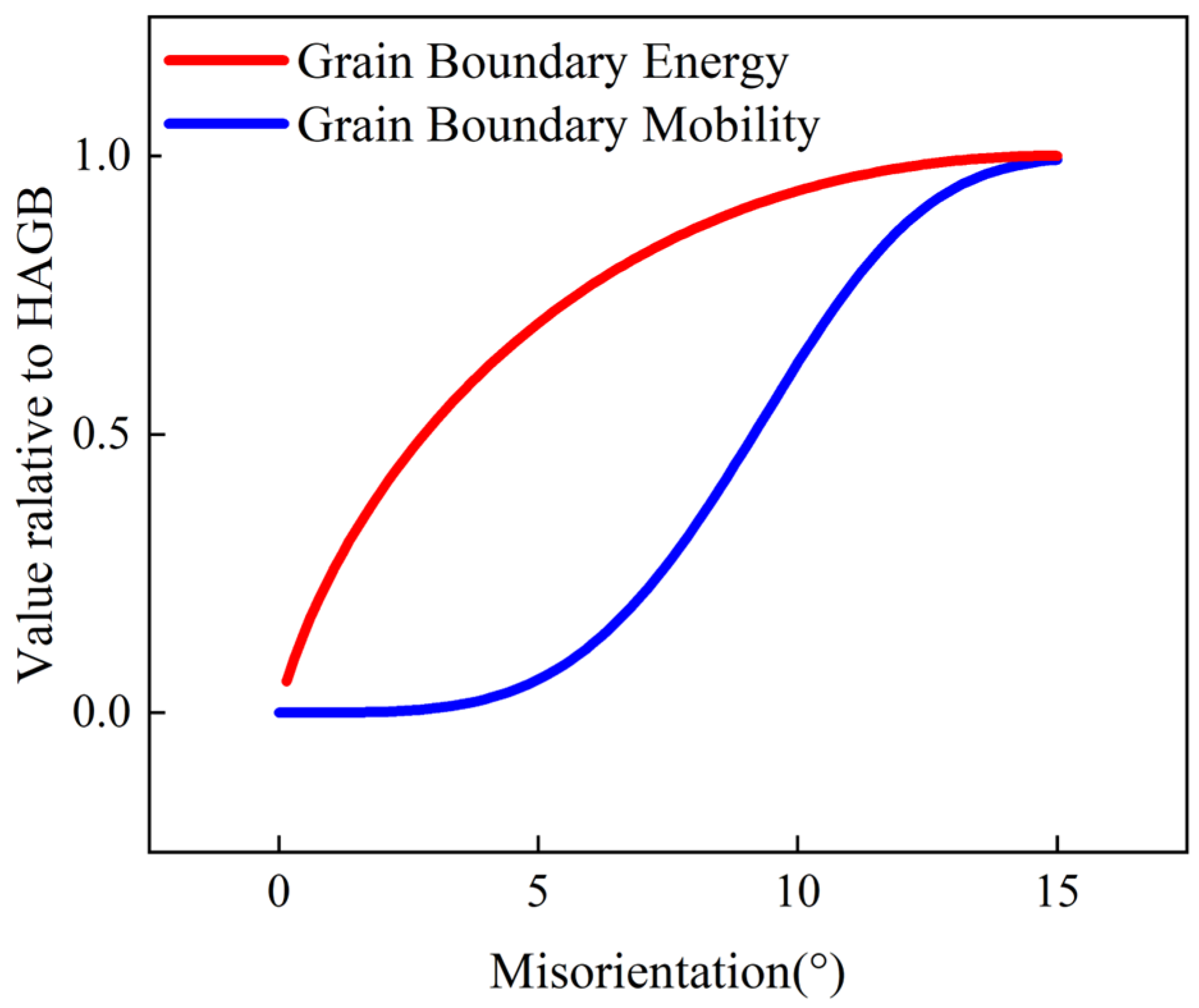
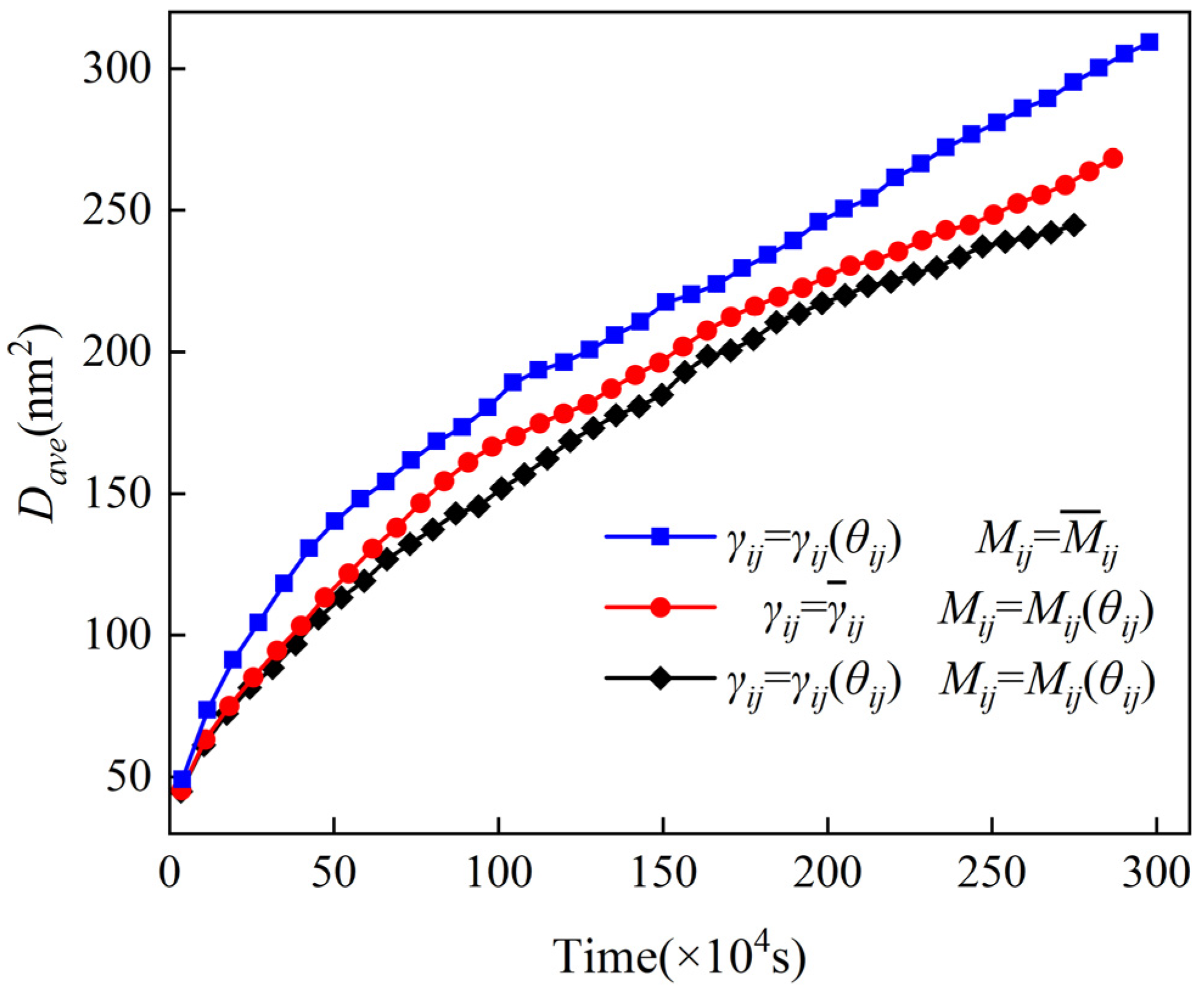
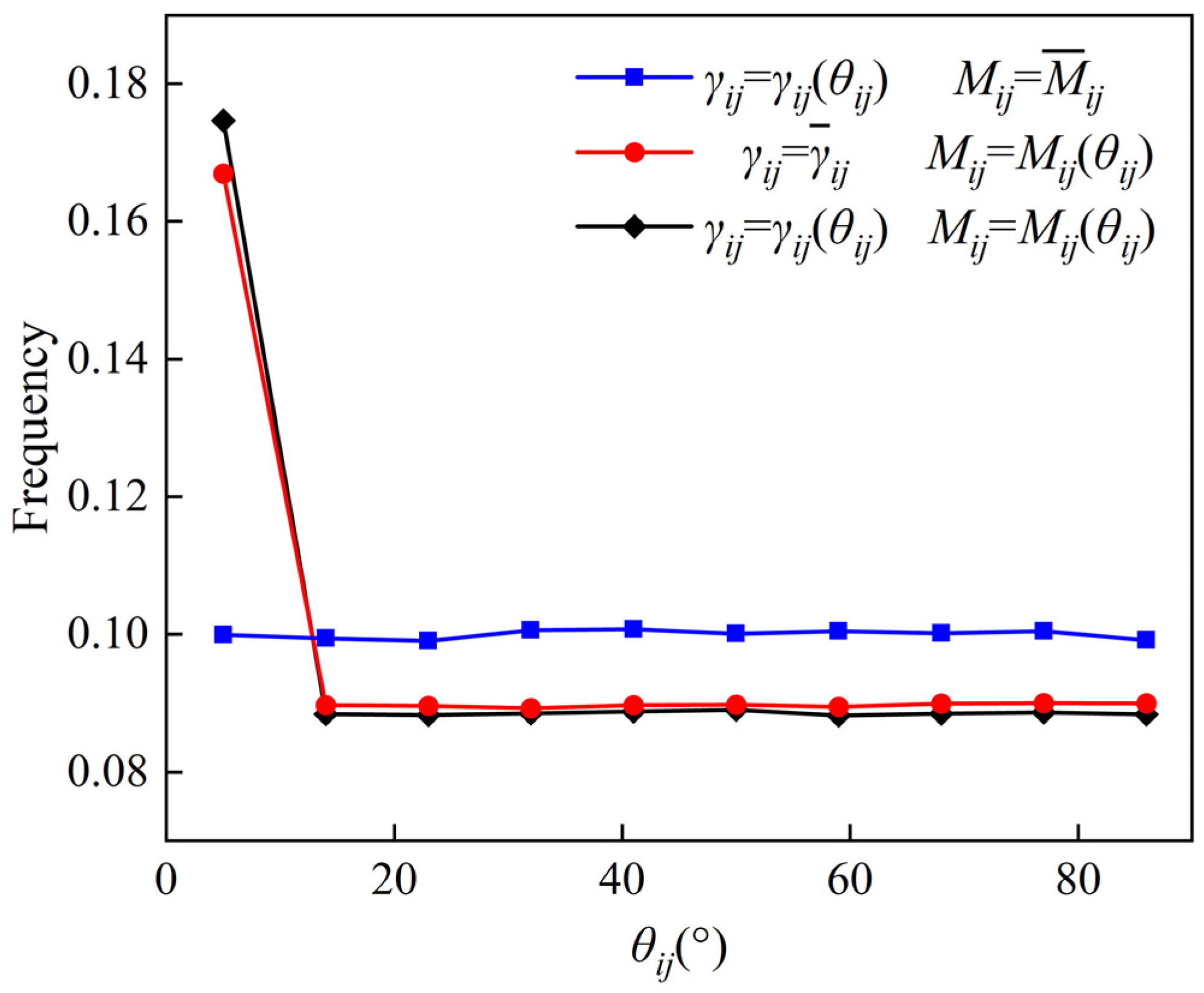
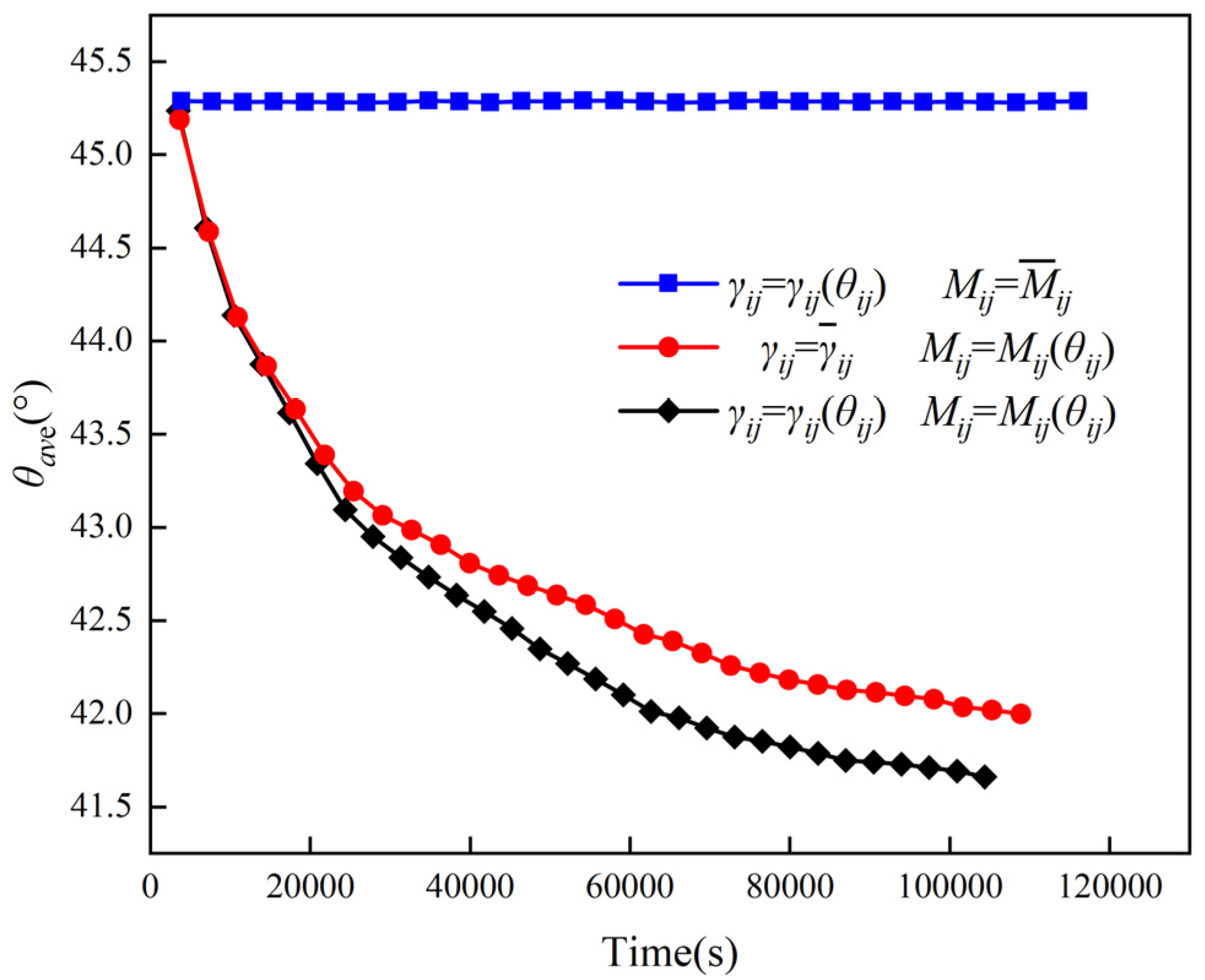
3.2. Anisotropic Grain Growth of U3Si2
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Ronchi, C.; Sheindlin, M.; Musella, M. Thermal conductivity of uranium dioxide up to 2900 K from simultaneous measurement of the heat capacity and thermal diffusivity. J. Appl. Phys. 1999, 85, 776–789. [Google Scholar] [CrossRef]
- Ronchi, C.; Hiernaut, J.; Selfslag, R. Laboratory measurement of the heat capacity of urania up to 8000 K: I. Experiment. Nucl. Sci. Eng. 1993, 113, 1–19. [Google Scholar] [CrossRef]
- Zinkle, S.J.; Terrani, K.A.; Gehin, J.C. Accident tolerant fuels for LWRs: A perspective. J. Nucl. Mater. 2014, 448, 374–379. [Google Scholar] [CrossRef]
- Wachs, D.; Woolstenhulme, N. Advanced fuel cycle technology: Special session in honor of Dr. Michael Lineberry. Trans. Am. Nucl. Soc. 2014, 110, 33095. [Google Scholar]
- Watkins, J.K.; Wagner, A.R.; Gonzales, A. Challenges and opportunities to alloyed and composite fuel architectures to mitigate high uranium density fuel oxidation: Uranium diboride and uranium carbide. J. Nucl. Mater. 2022, 560, 153502. [Google Scholar] [CrossRef]
- White, J.T.; Nelson, A.T.; Dunwoody, J.T. Thermophysical properties of U3Si2 to 1773 K. J. Nucl. Mater. 2015, 464, 275–280. [Google Scholar] [CrossRef]
- Fink, J. Thermophysical properties of uranium dioxide. J. Nucl. Mater. 2000, 279, 1–18. [Google Scholar] [CrossRef]
- Youinou, G.J.; Sen, R.S. Impact of accident-tolerant fuels and claddings on the overall fuel cycle: A preliminary systems analysis. Nucl. Technol. 2014, 188, 123–138. [Google Scholar] [CrossRef]
- Lopes, D.A.; Benarosch, A.; Middleburgh, S. Spark plasma sintering and microstructural analysis of pure and Mo doped U3Si2 pellets. J. Nucl. Mater. 2017, 496, 234–241. [Google Scholar] [CrossRef]
- Mohamad, A.; Ohishi, Y.; Muta, H. Thermal and mechanical properties of polycrystalline U3Si2 synthesized by spark plasma sintering. J. Nucl. Sci. Technol. 2018, 55, 1141–1150. [Google Scholar] [CrossRef]
- Gong, B.; Yao, T.; Lei, P. Spark plasma sintering (SPS) densified U3Si2 pellets: Microstructure control and enhanced mechanical and oxidation properties. J. Alloys Compd. 2020, 825, 154022. [Google Scholar] [CrossRef]
- Buckley, J.; Goddard, D.; Abram, T. Studies on the spark plasma sintering of U3Si2: Processing parameters and interactions. J. Nucl. Mater. 2021, 544, 152655. [Google Scholar] [CrossRef]
- Zou, J.; Xu, S.; Chen, J. Effects of spark plasma sintering parameters on the microstructure of U3Si2 pellets. J. Nucl. Mater. 2023, 585, 154649. [Google Scholar] [CrossRef]
- Hoggan, R.E.; Tolman, K.R.; Cappia, F. Grain size and phase purity characterization of U3Si2 fuel pellets. J. Nucl. Mater. 2018, 512, 199–213. [Google Scholar] [CrossRef]
- Moelans, N.; Wendler, F.; Nestler, B. Comparative study of two phase-field models for grain growth. Comput. Mater. Sci. 2009, 46, 479–490. [Google Scholar] [CrossRef]
- Krill, I.C.; Longqin, C. Computer simulation of 3-D grain growth using a phase-field model. Acta Mater. 2002, 50, 3059–3075. [Google Scholar] [CrossRef]
- Longqin, C.; Yang, W. Computer simulation of the domain dynamics of a quenched system with a large number of nonconserved order parameters: The grain-growth kinetics. Phys. Rev. B 1994, 50, 15752. [Google Scholar]
- Steinbach, I.; Pezzolla, F.; Nestler, B. A phase field concept for multiphase systems. Phys. D Nonlinear Phenom. 1996, 94, 135–147. [Google Scholar] [CrossRef]
- Kobayashi, R.; Warren, J.A.; Carter, W.C. A continuum model of grain boundaries. Phys. D Nonlinear Phenom. 2000, 140, 141–150. [Google Scholar] [CrossRef]
- Adabavazeh, Z.; Hwang, W.S.; Dezfoli, A.R. Pinning effect of cerium inclusions during austenite grains growth in SS400 steel at 1300 C: A combined phase field and experimental study. Crystals 2017, 7, 308. [Google Scholar] [CrossRef]
- Gao, N.; Zhao, Y.; Xia, W. Phase-Field Crystal Studies on Grain Boundary Migration, Dislocation Behaviors, and Topological Transition under Tension of Square Polycrystals. Crystals 2023, 13, 777. [Google Scholar] [CrossRef]
- Cheniour, A.; Tonks, M.R.; Gong, B. Development of a grain growth model for U3Si2 using experimental data, phase field simulation and molecular dynamics. J. Nucl. Mater. 2020, 532, 152069. [Google Scholar] [CrossRef]
- Cheniour, A. Study of U3Si2 Fuel Microstructure Behavior Under LWR Conditions Using the Phase Field Method. Doctoral Dissertation, University of Florida, Gainesville, FL, USA, 2020. [Google Scholar]
- Ma, C.; Zhao, M.; Xin, T. Phase-field simulation of grain nucleation, growth, and Rayleigh distribution of U3Si2 nuclear fuel. Front. Energy Res. 2023, 10, 1080819. [Google Scholar] [CrossRef]
- Van der Waals, J.D. The thermodynamic theory of capillarity under the hypothesis of a continuous variation of density. J. Stat. Phys. 1979, 20, 200–244. [Google Scholar] [CrossRef]
- Van der Waals, J.D.; Kohnstamm, P. Lehrbuch der Thermodynamik; Johann-Ambrosius-Barth Verlag: Leipzig, Germany; Amsterdam, The Netherlands, 1908. [Google Scholar]
- Moelans, N.; Blanpain, B.; Wollants, P. A phase field model for the simulation of grain growth in materials containing finely dispersed incoherent second-phase particles. Acta Mater. 2005, 53, 1771–1781. [Google Scholar] [CrossRef]
- Cahn, J.W.; Hilliard, J.E. Free Energy of a Nonuniform System. I. Interfacial Free Energy. J. Chem. Phys. 1958, 28, 258–267. [Google Scholar] [CrossRef]
- Yang, Z.; Liu, W.; Liu, X. Effects of grain boundaries and temperature on spinodal decomposition in a binary Fe-Cr alloy: A phase-field simulation. Ann. Nucl. Energy 2023, 193, 110030. [Google Scholar] [CrossRef]
- Moelans, N.; Blanpain, B.; Wollants, P. Quantitative analysis of grain boundary properties in a generalized phase field model for grain growth in anisotropic systems. Phys. Rev. B 2008, 78, 024113. [Google Scholar] [CrossRef]
- Ahmed, K.; Yablinsky, C.A.; Schulte, A. Phase field modeling of the effect of porosity on grain growth kinetics in polycrystalline ceramics. Model. Simul. Mater. Sci. Eng. 2013, 21, 065005. [Google Scholar] [CrossRef]
- Beeler, B.; Baskes, M.; Andersson, D. Molecular dynamics investigation of grain boundaries and surfaces in U3Si2. J. Nucl. Mater. 2019, 514, 290–298. [Google Scholar] [CrossRef]
- Lücke, K.; Rixen, R.; Rosenbaum, F.W. On the Theory of Grain Boundary Motion. In The Nature and Behavior of Grain Boundaries: A Symposium Held at the TMS-AIME Fall Meeting in Detroit, MI, USA, 18–19 October 1971; Hu, H., Ed.; Springer: New York, NY, USA, 1972; pp. 245–283. [Google Scholar]
- Allen, S.M.; Cahn, J.W. A microscopic theory for antiphase boundary motion and its application to antiphase domain coarsening. Acta Metall. 1979, 27, 1085–1095. [Google Scholar] [CrossRef]
- Kazaryan, A.; Wang, Y.; Dregia, S. Generalized phase-field model for computer simulation of grain growth in anisotropic systems. Phys. Rev. B 2000, 61, 14275. [Google Scholar] [CrossRef]
- Kazaryan, A.; Wang, Y.; Dregia, S. Grain growth in systems with anisotropic boundary mobility: Analytical model and computer simulation. Phys. Rev. B 2001, 63, 184102. [Google Scholar] [CrossRef]
- Kazaryan, A.; Patton, B.; Dregia, S. On the theory of grain growth in systems with anisotropic boundary mobility. Acta Mater. 2002, 50, 499–510. [Google Scholar] [CrossRef]
- Kazaryan, A.; Wang, Y.; Dregia, S. Grain growth in anisotropic systems: Comparison of effects of energy and mobility. Acta Mater. 2002, 50, 2491–2502. [Google Scholar] [CrossRef]
- Niño, J.D.; Johnson, O.K. Influence of grain boundary energy anisotropy on the evolution of grain boundary network structure during 3D anisotropic grain growth. Comput. Mater. Sci. 2023, 217, 111879. [Google Scholar] [CrossRef]
- Holm, E.A.; Hassold, G.N.; Miodownik, M.A. On misorientation distribution evolution during anisotropic grain growth. Acta Mater. 2001, 49, 2981–2991. [Google Scholar] [CrossRef]
- Humphreys, F.J. A unified theory of recovery, recrystallization and grain growth, based on the stability and growth of cellular microstructures—I. The basic model. Acta Mater. 1997, 45, 4231–4240. [Google Scholar] [CrossRef]
- Miyoshi, E.; Takaki, T. Multi-phase-field study of the effects of anisotropic grain-boundary properties on polycrystalline grain growth. J. Cryst. Growth 2017, 474, 160–165. [Google Scholar] [CrossRef]
- Wang, T.; Qiu, N.; Wen, X. First-principles investigations on the electronic structures of U3Si2. J. Nucl. Mater. 2016, 469, 194–199. [Google Scholar] [CrossRef]
- Read, W.T.; Shockley, W. Dislocation Models of Crystal Grain Boundaries. Phys. Rev. 1950, 78, 275–289. [Google Scholar] [CrossRef]

| Temperature (K) | (J/m2) |
|---|---|
| 0 | 0.84 |
| 400 | 0.89 |
| 800 | 0.96 |
| 1200 | 1.04 |
| 1600 | 1.22 |
| Value of Phase-Field Parameters | K (nm2/s) | Error (nm2/s) | ||
|---|---|---|---|---|
| 1.0 | 1.0 | 0.5 | 0.0253 | 0.00157 |
| 1.0 | 1.0 | 1.0 | 0.0312 | 0.00159 |
| 1.0 | 1.0 | 2.0 | 0.027 | 0.0021 |
| 0.5 | 1.0 | 0.5 | 0.0261 | 0.00141 |
| 2.0 | 1.0 | 0.5 | 0.032 | 0.00124 |
| 1.0 | 0.5 | 0.5 | 0.0332 | 0.00288 |
| 1.0 | 2.0 | 0.5 | 0.02445 | 0.00175 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Pan, X.; La, Y.; Liao, Y.; Wang, Y.; Lu, Y.; Liu, W. Phase-Field Simulation of Grain Growth in Uranium Silicide Nuclear Fuel. Crystals 2024, 14, 691. https://doi.org/10.3390/cryst14080691
Pan X, La Y, Liao Y, Wang Y, Lu Y, Liu W. Phase-Field Simulation of Grain Growth in Uranium Silicide Nuclear Fuel. Crystals. 2024; 14(8):691. https://doi.org/10.3390/cryst14080691
Chicago/Turabian StylePan, Xiaoqiang, Yongxiao La, Yuxuan Liao, Yifan Wang, Yonghong Lu, and Wenbo Liu. 2024. "Phase-Field Simulation of Grain Growth in Uranium Silicide Nuclear Fuel" Crystals 14, no. 8: 691. https://doi.org/10.3390/cryst14080691





