Extended Caking Method for Strain Analysis of Polycrystalline Diffraction Debye–Scherrer Rings
Abstract
:1. Introduction
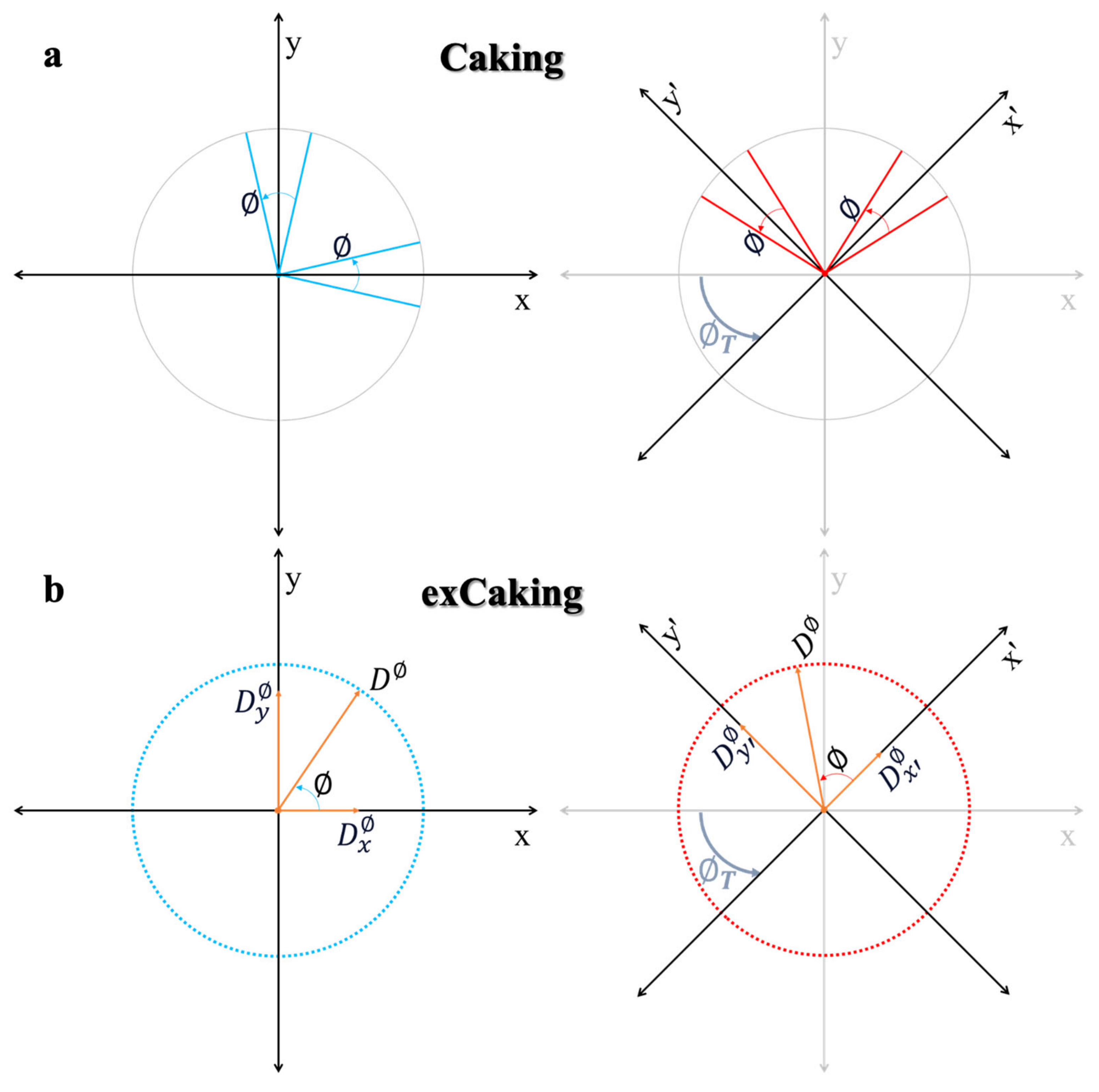
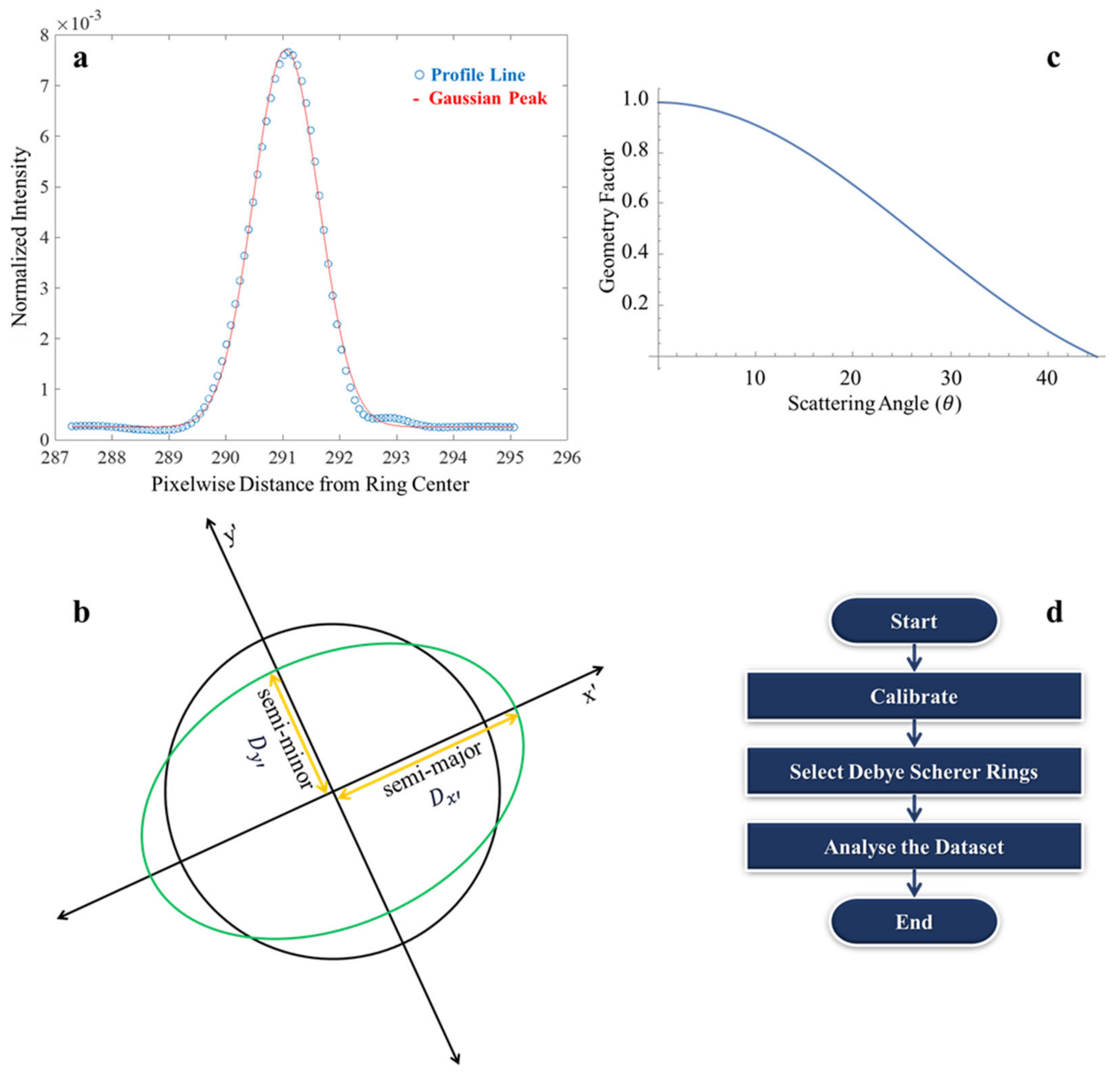
2. Methodology
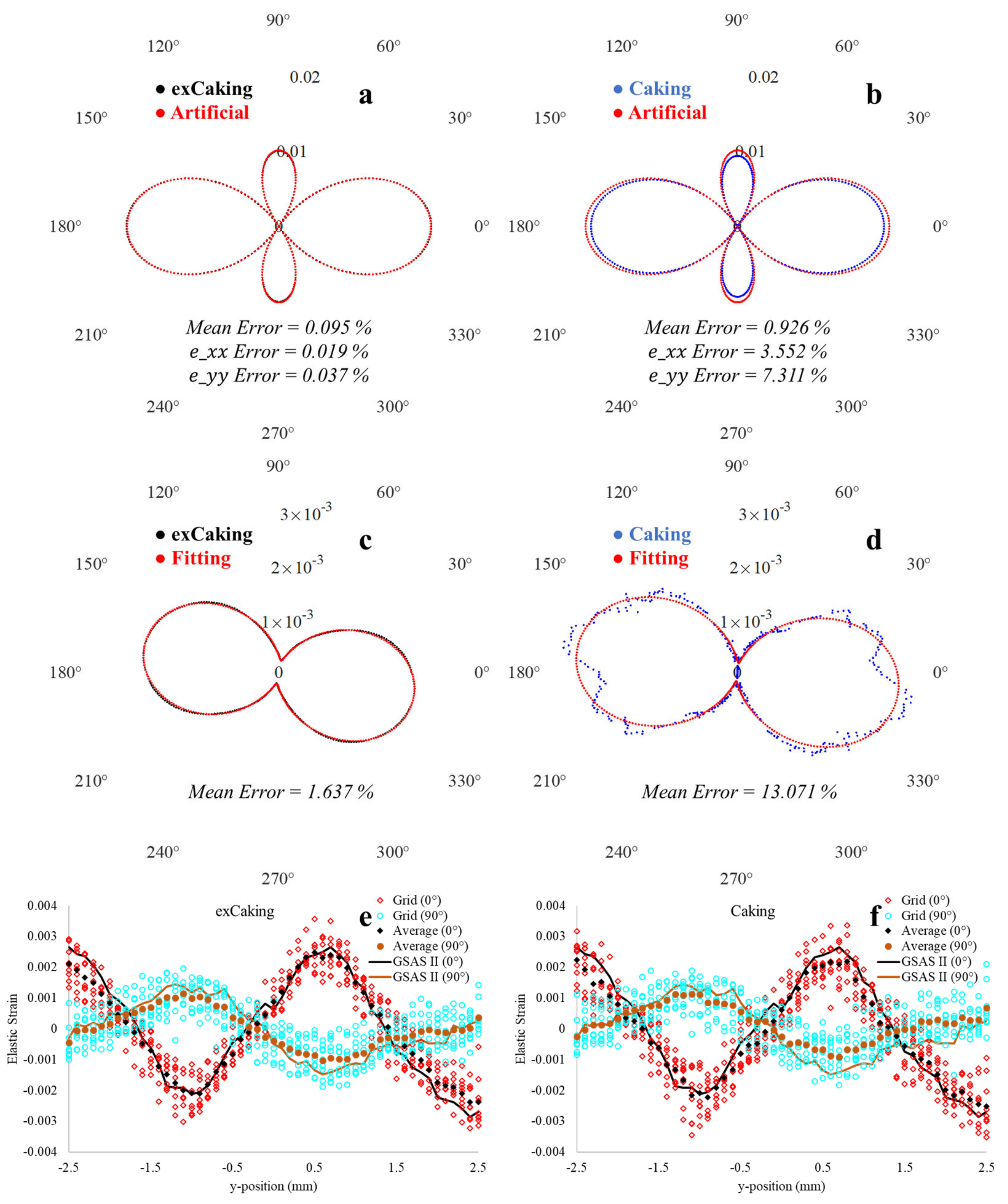
3. Results
4. Conclusions
Supplementary Materials
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Authier, A. Early Days of X-ray Crystallography; OUP Oxford: Oxford, UK, 2013. [Google Scholar] [CrossRef]
- Friedrich, W.; Knipping, P.; Laue, M. Interferenzerscheinungen Bei Röntgenstrahlen. Ann. Phys. 1913, 346, 971–988. [Google Scholar] [CrossRef]
- Laue, M. Eine Quantitative Prüfung Der Theorie Für Die Interferenzerscheinungen Bei Röntgenstrahlen. Ann. Phys. 1913, 346, 989–1002. [Google Scholar] [CrossRef]
- Bragg, W.L. The Specular Reflection of X-rays. Nature 1912, 90, 410. [Google Scholar] [CrossRef]
- Debye, P.; Scherrer, P. Interferenz an Regellos Orientierten Teilchen Im Röntgenlicht I. Phys. Z. 1916, 17, 277. [Google Scholar]
- Kohara, S.; Ohara, K.; Tajiri, H.; Song, C.; Sakata, O.; Usuki, T.; Benino, Y.; Mizuno, A.; Masuno, A.; Okada, J.T.; et al. Synchrotron X-ray Scattering Measurements of Disordered Materials. Z. Phys. Chem. 2016, 230, 339–368. [Google Scholar] [CrossRef]
- Li, Z.; Wu, Z.; Mo, G.; Xing, X.; Liu, P. A Small-Angle x-Ray Scattering Station at Beijing Synchrotron Radiation Facility. Instrum. Sci. Technol. 2014, 42, 128–141. [Google Scholar] [CrossRef]
- Reinartz, I.; Sarter, M.; Otten, J.; Höfig, H.; Pohl, M.; Schug, A.; Stadler, A.M.; Fitter, J. Structural Analysis of a Genetically Encoded Fret Biosensor by Saxs and Md Simulations. Sensors 2021, 21, 4144. [Google Scholar] [CrossRef] [PubMed]
- Bernier, J.V.; Park, J.S.; Pilchak, A.L.; Glavicic, M.G.; Miller, M.P. Measuring Stress Distributions in Ti-6Al-4V Using Synchrotron X-ray Diffraction. Metall. Mater. Trans. A Phys. Metall. Mater. Sci. 2008, 39, 3120–3133. [Google Scholar] [CrossRef]
- Miller, W.H. A Treatise on Crystallography; Online access with subscription: JISC Historical Texts; For J. & J.J. Deighton: Cambridge, UK, 1839. [Google Scholar]
- Muslih, M.R.; Nishida, M.; Sugeng, B.; Sadeli, Y. Improvements of the X-ray Diffractometer (XRD) to Become Small Angle X-ray Scattering (SAXS) and Residual Stress Diffractometer. AIP Conf. Proc. 2021, 2381, 020047. [Google Scholar] [CrossRef]
- Fauth, F.; Peral, I.; Popescu, C.; Knapp, M. The New Material Science Powder Diffraction Beamline at ALBA Synchrotron. Powder Diffr. 2013, 28, 360–370. [Google Scholar] [CrossRef]
- Straas, T.; Becker, J.; Iversen, B.B.; Als-Nielsen, J. The Debye–Scherrer Camera at Synchrotron Sources: A Revisit. J. Synchrotron Radiat. 2012, 20, 98–104. [Google Scholar] [CrossRef]
- MacDonald, M.J.; Vorberger, J.; Gamboa, E.J.; Drake, R.P.; Glenzer, S.H.; Fletcher, L.B. Calculation of Debye-Scherrer Diffraction Patterns from Highly Stressed Polycrystalline Materials. J. Appl. Phys. 2016, 119, 215902. [Google Scholar] [CrossRef]
- Miyazaki, T.; Fujimoto, Y.; Sasaki, T. Improvement in X-ray Stress Measurement Using Debye-Scherrer Rings by in-Plane Averaging. J. Appl. Crystallogr. 2016, 49, 241–249. [Google Scholar] [CrossRef]
- Karamched, P.S.; Xiong, Y.; Nguyen, C.-T.; Collins, D.M.; Magazzeni, C.M.; Wilkinson, A.J. Weighted Ellipse Fitting Routine for Spotty or Incomplete Debye-Scherrer Rings on a 2D Detector. arXiv 2021, arXiv:2110.05467. [Google Scholar]
- Sirhindi, R.; Khan, N. Clustering-Based Detection of Debye-Scherrer Rings. J. Comput. Inf. Sci. Eng. 2023, 23, 041013. [Google Scholar] [CrossRef]
- Shahzad, S.; Khan, N.; Nawaz, Z.; Ferrero, C. Automatic Debye-Scherrer Elliptical Ring Extraction via a Computer Vision Approach. J. Synchrotron. Radiat. 2018, 25, 439–450. [Google Scholar] [CrossRef] [PubMed]
- Li, C.; Xiao, P.; Cernik, R. The Nondestructive Measurement of Strain Distributions in Air Plasma Sprayed Thermal Barrier Coatings as a Function of Depth from Entire Debye-Scherrer Rings Strain Mapping in APS TBCs from Debye-Scherrer Rings. J. Appl. Crystallogr. 2020, 53, 69–75. [Google Scholar] [CrossRef] [PubMed]
- Keckes, J.; Bartosik, M.; Daniel, R.; Mitterer, C.; Maier, G.; Ecker, W.; Vila-Comamala, J.; David, C.; Schoeder, S.; Burghammer, M. X-ray Nanodiffraction Reveals Strain and Microstructure Evolution in Nanocrystalline Thin Films. Scr. Mater. 2012, 67, 748–751. [Google Scholar] [CrossRef]
- Uzun, F.; Basoalto, H.; Liogas, K.; Fares Slim, M.; Lik Lee, T.; Besnard, C.; Ivan Wang, Z.; Chen, J.; Dolbnya, I.P.; Korsunsky, A.M. Tomographic Eigenstrain Reconstruction for Full-Field Residual Stress Analysis in Large Scale Additive Manufacturing Parts. Addit. Manuf. 2024, 81, 104027. [Google Scholar] [CrossRef]
- Akrivos, V.; Smith, M.C.; Muransky, O.; Ohms, C.; Youtsos., A. A residual stress measurement and numerical analysis round robin on a three-pass slot nickel-base repair weld. Procedia Manuf. 2020, 51, 779–786. [Google Scholar] [CrossRef]
- Smith, M.C.; Smith, A.C.; Wimpory, R.; Ohms, C. A Review of the NeT Task Group 1 Residual Stress Measurement and Analysis Round Robin on a Single Weld Bead-on-Plate Specimen. Int. J. Press. Vessel. Pip. 2014, 120–121, 93–140. [Google Scholar] [CrossRef]
- Statnik, E.S.; Salimon, A.I.; Uzun, F.; Korsunsky, A.M. Polar Transformation of 2D X-ray Diffraction Patterns for 2D Strain Evaluation. Proc. World Congr. Eng. 2019, 2019, 2–6. [Google Scholar]
- Uzun, F.; Salimon, A.I.; Statnik, E.S.; Besnard, C.; Chen, J.; Moxham, T.; Salvati, E.; Wang, Z.; Korsunsky, A.M. Polar Transformation of 2D X-ray Diffraction Patterns and the Experimental Validation of the HDIC Technique. Measurement 2019, 151, 107193. [Google Scholar] [CrossRef]
- Mukhopadhyay, D. Identifying the Causes of Residual Stress in Polycrystalline Diamond Compact (PDC) Cutters by X-ray Diffraction Technique. Results Mater. 2021, 11, 100216. [Google Scholar] [CrossRef]
- Ortiz, A.L.; Tian, J.W.; Villegas, J.C.; Shaw, L.L.; Liaw, P.K. Interrogation of the Microstructure and Residual Stress of a Nickel-Base Alloy Subjected to Surface Severe Plastic Deformation. Acta Mater. 2008, 56, 413–426. [Google Scholar] [CrossRef]
- Vorster, W.J.J.; Zhang, S.Y.; Golshan, M.; Laundy, D.; Dini, D.; Korsunsky, A.M. Comparison of X-ray Diffraction Measurement of Residual Elastic Strains: Monochromatic Beam and Image Plate versus White Beam Energy-Dispersive Analysis. J. Strain Anal. Eng. Des. 2007, 42, 23–37. [Google Scholar] [CrossRef]
- Higginbotham, A.; McGonegle, D. Prediction of Debye-Scherrer Diffraction Patterns in Arbitrarily Strained Samples. J. Appl. Phys. 2014, 115, 174906. [Google Scholar] [CrossRef]
- Smith, N.L.; Coukouma, A.; Dubnik, S.; Asher, S.A. Debye Ring Diffraction Elucidation of 2D Photonic Crystal Self-Assembly and Ordering at the Air-Water Interface†. Phys. Chem. Chem. Phys. 2017, 19, 31813. [Google Scholar] [CrossRef]
- Gelfi, M.; Bontempi, E.; Roberti, R.; Depero, L.E. X-ray Diffraction Debye Ring Analysis for Stress Measurement (DRAST): A New Method to Evaluate Residual Stresses. Acta Mater. 2004, 52, 583–589. [Google Scholar] [CrossRef]
- Mildner, D.F.R.; Cubitt, R. The Effect of Gravity on the Debye-Scherrer Ring in Small-Angle Neutron Scattering. J. Appl. Crystallogr. 2012, 45, 124–126. [Google Scholar] [CrossRef]
- Thompson, P.; Wood, I.G. X-ray Rietveld Refinement Using Debye-Scherrer Geometry. J. Appl. Cryst. 1983, 16, 458–472. [Google Scholar] [CrossRef]
- Guinebretière, R. X-ray Diffraction by Polycrystalline Materials; ISTE Ltd: London, UK, 2007; ISBN 9781905209217. [Google Scholar]
- Salvalaglio, M.; Voigt, A.; Elder, K.R. ARTICLE Closing the Gap between Atomic-Scale Lattice Deformations and Continuum Elasticity. Npj Comput. Mater. 2019, 5, 48. [Google Scholar] [CrossRef]
- Zhang, H.; Sui, T.; Salvati, E.; Daisenberger, D.; Lunt, A.; Fong, K.; Song, X.; Korsunsky, A. Digital Image Correlation of 2D X-ray Powder Diffraction Data for Lattice Strain Evaluation. Materials 2018, 11, 427. [Google Scholar] [CrossRef]
- Korsunsky, A.M. A Critical Discussion of the Sin2 ψ Stress Measurement Technique. Mater. Sci. Forum 2008, 571–572, 219–224. [Google Scholar] [CrossRef]
- Withers, P.J. Synchrotron X-ray Diffraction. In Practical Residual Stress Measurement Methods; Schajer, G.S., Ed.; John Wiley & Sons, Ltd.: Hoboken, NJ, USA, 2013; pp. 163–194. ISBN 9781118402832. [Google Scholar]
- Hammond, C. X-ray Diffraction of Polycrystalline Materials. In The Basics of Crystallography and Diffraction; Oxford Academic: Oxford, UK, 2015. [Google Scholar]
- Dolabella, S.; Borzì, A.; Dommann, A.; Neels, A.; Dolabella, S.; Borzì, A.; Dommann, A.; Neels, A. Lattice Strain and Defects Analysis in Nanostructured Semiconductor Materials and Devices by High-Resolution X-ray Diffraction: Theoretical and Practical Aspects. Small Methods 2022, 6, 2100932. [Google Scholar] [CrossRef] [PubMed]
- Farajian, M.; Nitschke-Pagel, T.; Wimpory, R.C.; Hofmann, M.; Klaus, M. Residual Stress Field Determination in Welds by Means of X-ray, Synchrotron and Neutron Diffraction (Ermittlung Des Schweißeigenspannungsfeldes Mittels Röntgen-, Synchrotron-Und Neutronenbeugungsverfahren). Materialwiss. Werkstofftech. 2011, 42, 996–1002. [Google Scholar] [CrossRef]
- Maurya, P.; Kota, N.; Gibmeier, J.; Wanner, A.; Roy, S. Review on Study of Internal Load Transfer in Metal Matrix Composites Using Diffraction Techniques. Mater. Sci. Eng. A 2022, 840, 142973. [Google Scholar] [CrossRef]
- Huang, Q.; Shi, R.; Muránsky, O.; Beladi, H.; Kabra, S.; Schimpf, C.; Volkova, O.; Biermann, H.; Mola, J. Neutron Diffraction Analysis of Stress and Strain Partitioning in a Two-Phase Microstructure with Parallel-Aligned Phases. Sci. Rep. 2020, 10, 13536. [Google Scholar] [CrossRef]
- Uzun, F.; Papadaki, C.; Wang, Z.; Korsunsky, A.M. Neutron Strain Scanning for Experimental Validation of the Artificial Intelligence Based Eigenstrain Contour Method. Mech. Mater. 2020, 143, 103316. [Google Scholar] [CrossRef]
- Wimpory, R.C.; Ohms, C.; Hofmann, M.; Schneider, R.; Youtsos, A.G. Statistical Analysis of Residual Stress Determinations Using Neutron Diffraction. International J. Press. Vessel. Pip. 2009, 86, 48–62. [Google Scholar] [CrossRef]
- Woo, W.; An, G.B.; Kingston, E.J.; Dewald, A.T.; Smith, D.J.; Hill, M.R. Through-Thickness Distributions of Residual Stresses in Two Extreme Heat-Input Thick Welds: A Neutron Diffraction, Contour Method and Deep Hole Drilling Study. Acta Mater. 2013, 61, 3564–3574. [Google Scholar] [CrossRef]
- Brown, D.W.; Bernardin, J.D.; Carpenter, J.S.; Clausen, B.; Spernjak, D.; Thompson, J.M. Neutron Diffraction Measurements of Residual Stress in Additively Manufactured Stainless Steel. Mater. Sci. Eng. A 2016, 678, 291–298. [Google Scholar] [CrossRef]
- Pratihar, S.; Turski, M.; Edwards, L.; Bouchard, P.J. Neutron Diffraction Residual Stress Measurements in a 316L Stainless Steel Bead-on-Plate Weld Specimen. Int. J. Press. Vessel. Pip. 2009, 86, 13–19. [Google Scholar] [CrossRef]
- Jiang, W.; Woo, W.; An, G.-B.; Park, J.-U. Neutron Diffraction and Finite Element Modeling to Study the Weld Residual Stress Relaxation Induced by Cutting. Mater. Des. 2013, 51, 415–420. [Google Scholar] [CrossRef]
- Wang, Z.; Denlinger, E.; Michaleris, P.; Stoica, A.D.; Ma, D.; Beese, A.M. Residual Stress Mapping in Inconel 625 Fabricated through Additive Manufacturing: Method for Neutron Diffraction Measurements to Validate Thermomechanical Model Predictions. Mater. Des. 2017, 113, 169–177. [Google Scholar] [CrossRef]
- Akrivos, V.; Wimpory, R.C.; Hofmann, M.; Stewart, B.; Muransky, O.; Smith, M.C.; Bouchard, J. Neutron Diffraction Measurements of Weld Residual Stresses in Three-Pass Slot Weld (Alloy 600/82) and Assessment of the Measurement Uncertainty. J. Appl. Crystallogr. 2020, 53, 1181–1194. [Google Scholar] [CrossRef]
- Kelleher, J.; Prime, M.B.; Buttle, D.; Mummery, P.M.; Webster, P.J.; Shackleton, J.; Withers, P.J. The Measurement of Residual Stress in Railway Rails by Diffraction and Other Methods. J. Neutron Res. 2003, 11, 187–193. [Google Scholar] [CrossRef]
- Azanza Ricardo, C.L.; D’Incau, M.; Scardi, P. Revision and Extension of the Standard Laboratory Technique for X-ray Diffraction Measurement of Residual Stress Gradients. J. Appl. Crystallogr. 2007, 40, 675–683. [Google Scholar] [CrossRef]
- Pineault, J.A.; Belassel, M.; Brauss, M.E. X-ray Diffraction Residual Stress Measurement in Failure Analysis. In Failure Analysis and Prevention; ASM International: Detroit, MN, USA, 2002; pp. 484–497. [Google Scholar] [CrossRef]
- Korsunsky, A.M.; Brandt, L.R. The Effect of Deposition Parameters on the Mechanical and Transport Properties in Nanostructured Cu/W Multilayer Coatings. In Functional Thin Films Technology; CRC Press: Boca Raton, FL, USA, 2021; pp. 287–318. ISBN 9780367541774. [Google Scholar]
- Macdonald, C.A. Structured X-ray Optics for Laboratory-Based Materials Analysis. Annu. Rev. Mater. Res. 2017, 47, 115–134. [Google Scholar] [CrossRef]
- Fultz, B.; Howe, J.M. Diffraction and the X-ray Powder Diffractometer. In Transmission Electron Microscopy and Diffractometry of Materials; Springer: Berlin/Heidelberg, Germany, 2001; pp. 1–61. [Google Scholar] [CrossRef]
- Xu, L.; Zhang, S.Y.; Sun, W.; McCartney, D.G.; Hyde, T.H.; James, J.; Drakopoulos, M. Residual Stress Distribution in a Ti-6Al-4V T-Joint Weld Measured Using Synchrotron X-ray Diffraction. J. Strain Anal. Eng. Des. 2015, 50, 445–454. [Google Scholar] [CrossRef]
- Korsunsky, A.M.; Regino, G.M.; Latham, D.P.; Li, H.Y.; Walsh, M.J. Residual Stresses in Rolled and Machined Nickel Alloy Plates: Synchrotron X-ray Diffraction Measurement and Three-Dimensional Eigenstrain Analysis. J. Strain Anal. Eng. Des. 2007, 42, 1–12. [Google Scholar] [CrossRef]
- Korsunsky, A.M.; James, K.E. Residual Stresses in an Induction Hardened Gear Tooth Mapped by Synchrotron X-ray Diffraction. J. Neutron Res. 2003, 11, 241–245. [Google Scholar] [CrossRef]
- Uzun, F.; Basoalto, H.; Liogas, K.; Chen, J.; Dolbnya, I.P.; Ivan, Z.; Korsunsky, A.M. Voxel-Based Full-Field Eigenstrain Reconstruction of Residual Stresses in Additive Manufacturing Parts Using Height Digital Image Correlation. Addit. Manuf. 2023, 77, 103822. [Google Scholar] [CrossRef]
- Korsunsky, A.M. Variational Eigenstrain Analysis of Synchrotron Diffraction Measurements of Residual Elastic Strain in a Bent Titanium Alloy Bar. J. Mech. Mater. Struct. 2006, 1, 259–277. [Google Scholar] [CrossRef]
- Capria, E.; Ciuffini, A.; Drnec, J.; De Nolf, W.; Fares-Slim, M.; Frey, J.; Hinrichsen, B.; Honkimäki, V.; Levantino, M.; Mathon, O.; et al. Adapting the European Synchrotron to Industry. Synchrotron Radiat. News. 2024, 37, 10–15. [Google Scholar] [CrossRef]
- Fauth, F.; Boer, R.; Gil-Ortiz, F.; Popescu, C.; Vallcorba, O.; Peral, I.; Fullà, D.; Benach, J.; Juanhuix, J. The Crystallography Stations at the Alba Synchrotron. Eur. Phys. J. Plus. 2015, 130, 160. [Google Scholar] [CrossRef]
- Korsunsky, A.M.; Collins, S.P.; Owen, R.A.; Daymond, M.R.; Achtioui, S.S.S.; James, K.E.; Alexander Owen, R.; Daymond, M.R.; Achtioui, S.S.S.; James, K.E.; et al. Fast Residual Stress Mapping Using Energy-Dispersive Synchrotron X-ray Diffraction on Station 16.3 at the SRS. J. Synchrotron. Radiat. 2002, 9, 77–81. [Google Scholar] [CrossRef] [PubMed]
- Malmelöv, A.; Hassila, C.J.; Fisk, M.; Wiklund, U.; Lundbäck, A. Numerical Modeling and Synchrotron Diffraction Measurements of Residual Stresses in Laser Powder Bed Fusion Manufactured Alloy 625. Mater. Des. 2022, 216, 110548. [Google Scholar] [CrossRef]
- Valentine, M.D.A.; Dhokia, V.; Flynn, J.; McNair, S.A.M.; Lunt, A.J.G. Characterisation of Residual Stresses and Oxides in Titanium, Nickel, and Aluminium Alloy Additive Manufacturing Powders via Synchrotron X-ray Diffraction. Mater. Today Commun. 2023, 35, 105900. [Google Scholar] [CrossRef]
- Daniels, J.E.; Drakopoulos, M. High-Energy X-ray Diffraction Using the Pixium 4700 Flat-Panel Detector. J. Synchrotron Radiat. 2009, 16, 463–468. [Google Scholar] [CrossRef]
- Hart, M.L.; Drakopoulos, M. Weighted Least Squares Fit of an Ellipse to Describe Complete or Spotty Diffraction Rings on a Planar 2D Detector. arXiv 2013, arXiv:1311.5430. [Google Scholar] [CrossRef]
- Kanatani, K.; Rangarajan, P. Hyper Least Squares Fitting of Circles and Ellipses. Comput. Stat. Data Anal. 2011, 55, 2197–2208. [Google Scholar] [CrossRef]
- Withers, P.J.; Preuss, M.; Webster, P.J.; Hughes, D.J.; Korsunsky, A.M. Residual Strain Measurement by Synchrotron Diffraction. Mater. Sci. Forum 2002, 404-407, 1–12. [Google Scholar] [CrossRef]
- Korsunsky, A.M. A Teaching Essay on Residual Stresses and Eigenstrains; Butterworth-Heinemann: Oxford, UK, 2017; ISBN 978-0-12-810990-8. [Google Scholar]
- Nelson, D.V.; Ricklefs, R.E.; Evans, W.P. Residual Stresses in Quenched and Tempered Plain Carbon Steels. SAE Tech. Pap. 1971, 12, 5–9. [Google Scholar] [CrossRef]
- Uzun, F.; Korsunsky, A.M. The Use of Eigenstrain Theory and Fuzzy Techniques for Intelligent Modeling of Residual Stress and Creep Relaxation in Welded Superalloys. Mater. Today Proc. 2020, 33, 1880–1883. [Google Scholar] [CrossRef]
- Uzun, F.; Korsunsky, A.M. The OxCM Contour Method Solver for Residual Stress Evaluation. Eng. Comput. 2024. [Google Scholar] [CrossRef]
- Uzun, F.; Korsunsky, A.M. Voxel-Based Full-Field Eigenstrain Reconstruction of Residual Stresses. Adv. Eng. Mater. 2023, 25, 2201502. [Google Scholar] [CrossRef]
- Uzun, F.; Korsunsky, A.M. On the Analysis of Post Weld Heat Treatment Residual Stress Relaxation in Inconel Alloy 740H by Combining the Principles of Artificial Intelligence with the Eigenstrain Theory. Mater. Sci. Eng. A 2019, 752, 180–191. [Google Scholar] [CrossRef]
- Soyama, H.; Korsunsky, A.M. A Critical Comparative Review of Cavitation Peening and Other Surface Peening Methods. J. Mater. Process. Tech. 2022, 305, 117586. [Google Scholar] [CrossRef]
- Everton, S.K.; Hirsch, M.; Stavroulakis, P.I.; Leach, R.K.; Clare, A.T. Review of In-Situ Process Monitoring and in-Situ Metrology for Metal Additive Manufacturing. Mater. Des. 2016, 95, 431–445. [Google Scholar] [CrossRef]
- Wang, Z.; Chen, J.; Magdysyuk, O.V.; Uzun, F.; Korsunsky, A.M. Ultra-Fast Quantification of Polycrystalline Texture via Single Shot Synchrotron X-ray or Neutron Diffraction. Mater. Charact. 2022, 186, 111827. [Google Scholar] [CrossRef]
- Salvati, E.; Lunt, A.J.G.; Ying, S.; Sui, T.; Zhang, H.J.; Heason, C.; Baxter, G.; Korsunsky, A.M. Eigenstrain Reconstruction of Residual Strains in an Additively Manufactured and Shot Peened Nickel Superalloy Compressor Blade. Comput. Methods Appl. Mech. Eng. 2017, 320, 335–351. [Google Scholar] [CrossRef]
- Chen, J.; Salvati, E.; Uzun, F.; Papadaki, C.; Wang, Z.; Everaerts, J.; Korsunsky, A.M. An Experimental and Numerical Analysis of Residual Stresses in a TIG Weldment of a Single Crystal Nickel-Base Superalloy. J. Manuf. Process. 2020, 53, 190–200. [Google Scholar] [CrossRef]
- Uzun, F.; Korsunsky, A.M. On the Identification of Eigenstrain Sources of Welding Residual Stress in Bead-on-Plate Inconel 740H Specimens. Int. J. Mech. Sci. 2018, 145, 231–245. [Google Scholar] [CrossRef]
- Uzun, F.; Korsunsky, A.M. On the Application of Principles of Artificial Intelligence for Eigenstrain Reconstruction of Volumetric Residual Stresses in Non Uniform Inconel Alloy 740H Weldments. Finite Elem. Anal. Des. 2019, 155, 43–51. [Google Scholar] [CrossRef]
- Uzun, F.; Everaerts, J.; Brandt, L.R.; Kartal, M.; Salvati, E.; Korsunsky, A.M. The Inclusion of Short-Transverse Displacements in the Eigenstrain Reconstruction of Residual Stress and Distortion in In740h Weldments. J. Manuf. Process. 2018, 36, 601–612. [Google Scholar] [CrossRef]
- Uzun, F.; Lee, T.L.; Wang, Z.I.; Korsunsky, A.M. Full-Field Eigenstrain Reconstruction for the Investigation of Residual Stresses in Finite Length Weldments. J. Mater. Process. Tech. 2024, 325, 118295. [Google Scholar] [CrossRef]
- Uzun, F.; Bilge, A.N. Non-Destructive Investigation of Bulk Residual Stress in Automobile Brake Pads with Its Service Life. J. Found. Appl. Phys. 2016, 3, 94–102. [Google Scholar]
- Jászfi, V.; Prevedel, P.; Raninger, P.; Todt, J.; Mevec, D.; Godai, Y.; Maawad, E.; Ebner, R. Residual Stress Distribution of a Locally and Inductively Quenched and Tempered 50CrMo4 Steel Analysed by Synchrotron Transmission Techniques. Mater. Des. 2022, 221, 110936. [Google Scholar] [CrossRef]
- Guo, D.; Yan, K.; Callaghan, M.D.; Daisenberger, D.; Chatterton, M.; Chen, J.; Wisbey, A.; Mirihanage, W. Solidification Microstructure and Residual Stress Correlations in Direct Energy Deposited Type 316L Stainless Steel. Mater. Des. 2021, 207, 109782. [Google Scholar] [CrossRef]
- Statnik, E.S.; Uzun, F.; Lipovskikh, S.A.; Kan, Y.V.; Eleonsky, S.I.; Pisarev, V.S.; Somov, P.A.; Salimon, A.I.; Malakhova, Y.V.; Seferyan, A.G.; et al. Comparative Multi-Modal, Multi-Scale Residual Stress Evaluation in SLM 3D-Printed Al-Si-Mg Alloy (RS-300) Parts. Metals 2021, 11, 2064. [Google Scholar] [CrossRef]
- Nierlich, W.; Gegner, J. X-ray Diffraction Residual Stress Analysis: One of the Few Advanced Physical Measuring Techniques That Have Established Themselves for Routine Application in Industry. Adv. Solid State Phys. 2008, 47, 301–314. [Google Scholar] [CrossRef]
- Chason, E.; Guduru, P.R. Tutorial: Understanding Residual Stress in Polycrystalline Thin Films through Real-Time Measurements and Physical Models. J. Appl. Phys. 2016, 119, 191101. [Google Scholar] [CrossRef]
- Uzun, F.; Bilge, A.N. Ultrasonic Investigation of the Effect of Carbon Content in Carbon Steels on Bulk Residual Stress. J. Nondestr. Eval. 2015, 34, 11. [Google Scholar] [CrossRef]
- Su, Y.; Oikawa, K.; Shinohara, T.; Kai, T.; Horino, T.; Idohara, O.; Misaka, Y.; Tomota, Y. Residual Stress Relaxation by Bending Fatigue in Induction-Hardened Gear Studied by Neutron Bragg Edge Transmission Imaging and X-ray Diffraction. Int. J. Fatigue 2023, 174, 107729. [Google Scholar] [CrossRef]
- Korsunsky, A.M.; Wells, K.E.; Withers, P.J. Mapping Two-Dimensional State of Strain Using Synchroton X-ray Diffraction. Scr. Mater. 1998, 39, 1705–1712. [Google Scholar] [CrossRef]
- Hasan, M.; Schmahl, W.W.; Hackl, K.; Heinen, R.; Frenzel, J.; Gollerthan, S.; Eggeler, G.; Wagner, M.; Khalil-Allafi, J.; Baruj, A. Hard X-ray Studies of Stress-Induced Phase Transformations of Superelastic NiTi Shape Memory Alloys under Uniaxial Load. Mater. Sci. Eng. A 2008, 481–482, 414–419. [Google Scholar] [CrossRef]
- Statnik, E.S.; Uzun, F.; Salimon, A.I.; Korsunsky, A.M. New Approach for Fast Residual Strain Estimation through Rational 2D Diffraction Pattern Processing. In Proceedings of the Communications in Computer and Information Science (CCIS); Springer: Berlin/Heidelberg, Germany, 2020; Volume 1086, pp. 282–288. [Google Scholar]
- Korsunsky, A.M.; Baimpas, N.; Song, X.; Belnoue, J.; Hofmann, F.; Abbey, B.; Xie, M.; Andrieux, J.; Buslaps, T.; Neo, T.K. Strain Tomography of Polycrystalline Zirconia Dental Prostheses by Synchrotron X-ray Diffraction. Acta Mater. 2011, 59, 2501–2513. [Google Scholar] [CrossRef]
- Brokmeier, H.G.; Maawad, E.; Bolmaro, R.E.; Zhong, Z.Y.; Schell, N. Combined Materials Characterization by Area Detector Investigations Using Hard X-rays. IOP Conf. Ser. Mater. Sci. Eng. 2015, 82, 012104. [Google Scholar] [CrossRef]
- Savage, D.J.; Lutterotti, L.; Biwer, C.M.; Mckerns, M.; Bolme, C.; Knezevic, M.; Vogel, S.C.; Borbély, A. MILK: A Python Scripting Interface to MAUD for Automation of Rietveld Analysis. J. Appl. Crystallogr. 2023, 56, 1277–1286. [Google Scholar] [CrossRef]
- Kieffer, J.; Karkoulis, D. PyFAI, a Versatile Library for Azimuthal Regrouping. J. Phys. Conf. Ser. 2013, 425, 202012. [Google Scholar] [CrossRef]
- Li, C.; Zhang, X.; Chen, Y.; Carr, J.; Jacques, S.; Behnsen, J.; di Michiel, M.; Xiao, P.; Cernik, R. Understanding the Residual Stress Distribution through the Thickness of Atmosphere Plasma Sprayed (APS) Thermal Barrier Coatings (TBCs) by High Energy Synchrotron XRD; Digital Image Correlation (DIC) and Image Based Modelling. Acta Mater. 2017, 132, 1–12. [Google Scholar] [CrossRef]
- Kieffer, J.; Valls, V.; Blanc, N.; Hennig, C. New Tools for Calibrating Diffraction Setups. J. Synchrotron Radiat. 2020, 27, 558–566. [Google Scholar] [CrossRef]
- Riedl, A.; Daniel, R.; Todt, J.; Stefenelli, M.; Holec, D.; Sartory, B.; Krywka, C.; Müller, M.; Mitterer, C.; Keckes, J. A Combinatorial X-ray Sub-Micron Diffraction Study of Microstructure, Residual Stress and Phase Stability in TiAlN Coatings. Surf. Coat. Technol. 2014, 257, 108–113. [Google Scholar] [CrossRef]
- Du, H.; Gong, Y.; Xu, Y.; Zeng, Q.; Xiong, L.; Li, Y.; Nie, Y.; Wang, J.; Jin, X. Obtaining Ultrastrong and Ductile Steel with Hierarchical Lamellar Duplex Phase Microstructure by Two-Stage Martensitic Transformation Mechanism. Metall. Mater. Trans. A Phys. Metall. Mater. Sci. 2022, 53, 1613–1629. [Google Scholar] [CrossRef]
- Li, C.; Jacques, S.D.M.; Chen, Y.; Daisenberger, D.; Xiao, P.; Markocsan, N.; Nylen, P.; Cernik, R.J. A Synchrotron X-ray Diffraction Deconvolution Method for the Measurement of Residual Stress in Thermal Barrier Coatings as a Function of Depth. J. Appl. Crystallogr. 2016, 49, 1904–1911. [Google Scholar] [CrossRef]
- Öztürk, H.; Yan, H.; Hill, J.P.; Noyan, I.C. Correlating Sampling and Intensity Statistics in Nanoparticle Diffraction Experiments. J. Appl. Crystallogr. 2015, 48, 1212–1227. [Google Scholar] [CrossRef]
- Sulyanov, S.N.; Popov, A.N.; Kheiker, D.M. Using a Two-Dimensional Detector for X-ray Powder Diffractometry. J. Appl. Crystallogr. 1994, 27, 934–942. [Google Scholar] [CrossRef]
- Xie, M.Y.; Baimpas, N.; Reinhard, C.; Korsunsky, A.M. Texture Analysis in Cubic Phase Polycrystals by Single Exposure Synchrotron X-ray Diffraction. J. Appl. Phys. 2013, 114, 163502. [Google Scholar] [CrossRef]
- Tumer, D.; Gungorurler, M.; Havitcioglu, H.; Arman, Y. Investigation of Effective Coating of the Tie6Ale4V Alloy and 316L Stainless Steel with Graphene or Carbon Nanotubes with Finite Element Methods. J. Mater. Res. Technol. 2020, 9, 15880–15893. [Google Scholar] [CrossRef]
- Toby, B.H.; Von Dreele, R.B. GSAS-II: The Genesis of a Modern Open-Source All Purpose Crystallography Software Package. J. Appl. Crystallogr. 2013, 46, 544–549. [Google Scholar] [CrossRef]
- Everaerts, J.; Salvati, E.; Uzun, F.; Romano Brandt, L.; Zhang, H.; Korsunsky, A.M. Separating Macro- (Type I) and Micro- (Type II+III) Residual Stresses by Ring-Core FIB-DIC Milling and Eigenstrain Modelling of a Plastically Bent Titanium Alloy Bar. Acta Mater. 2018, 156, 43–51. [Google Scholar] [CrossRef]

Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Uzun, F.; Daisenberger, D.; Liogas, K.; Wang, Z.I.; Chen, J.; Besnard, C.; Korsunsky, A.M. Extended Caking Method for Strain Analysis of Polycrystalline Diffraction Debye–Scherrer Rings. Crystals 2024, 14, 716. https://doi.org/10.3390/cryst14080716
Uzun F, Daisenberger D, Liogas K, Wang ZI, Chen J, Besnard C, Korsunsky AM. Extended Caking Method for Strain Analysis of Polycrystalline Diffraction Debye–Scherrer Rings. Crystals. 2024; 14(8):716. https://doi.org/10.3390/cryst14080716
Chicago/Turabian StyleUzun, Fatih, Dominik Daisenberger, Konstantinos Liogas, Zifan Ivan Wang, Jingwei Chen, Cyril Besnard, and Alexander M. Korsunsky. 2024. "Extended Caking Method for Strain Analysis of Polycrystalline Diffraction Debye–Scherrer Rings" Crystals 14, no. 8: 716. https://doi.org/10.3390/cryst14080716
APA StyleUzun, F., Daisenberger, D., Liogas, K., Wang, Z. I., Chen, J., Besnard, C., & Korsunsky, A. M. (2024). Extended Caking Method for Strain Analysis of Polycrystalline Diffraction Debye–Scherrer Rings. Crystals, 14(8), 716. https://doi.org/10.3390/cryst14080716







