A Relationship between Fracture Toughness Kc and Energy Release Rate Gc According to Fracture Morphology Analysis
Abstract
1. Introduction
2. Methods
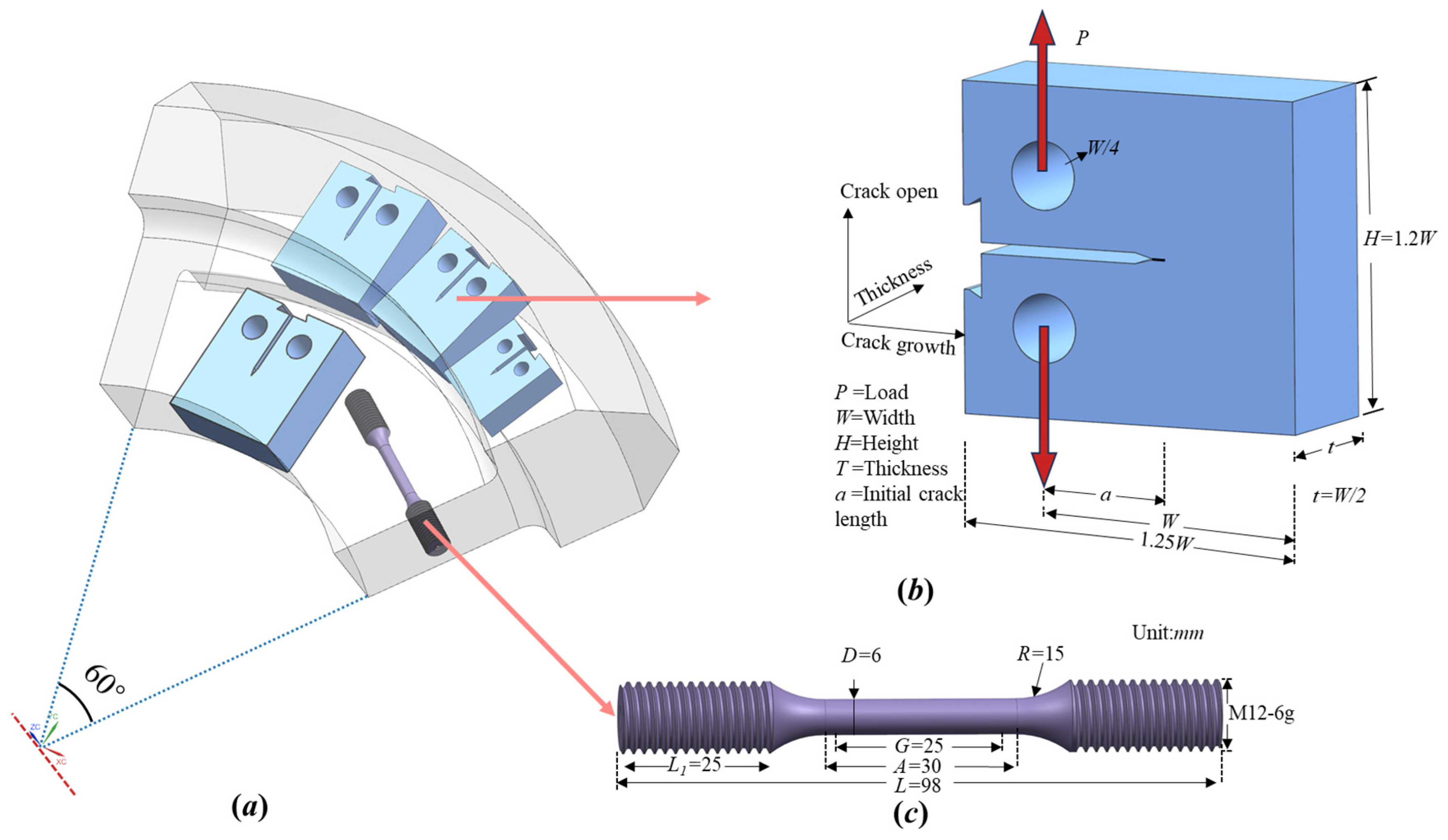
2.1. The Test Methods for Fracture Toughness and Related Constraints
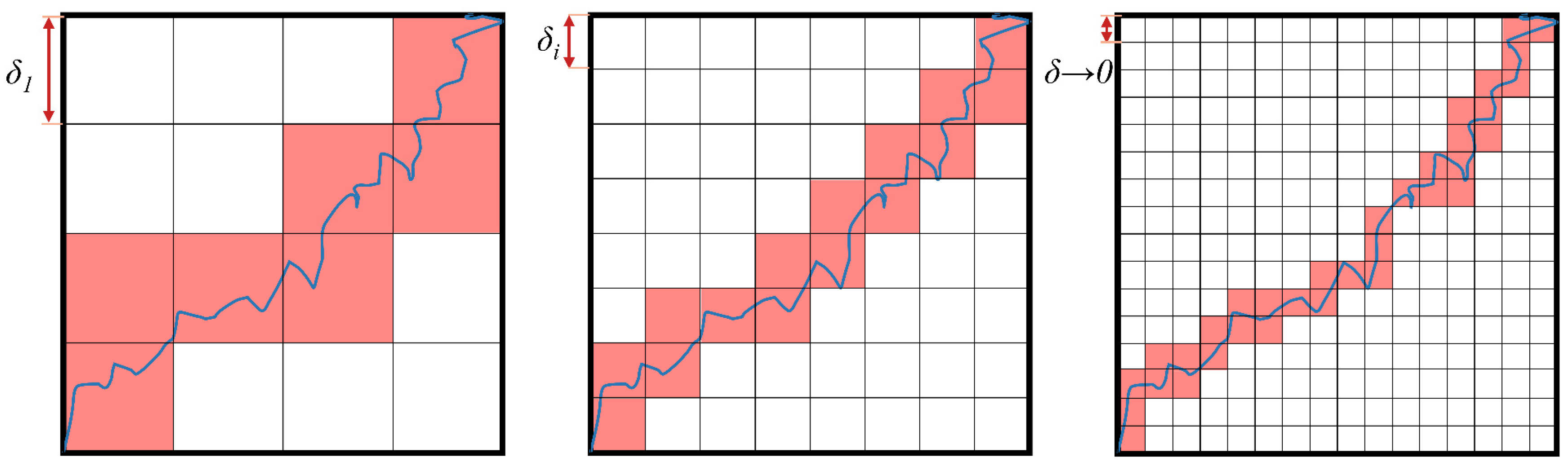
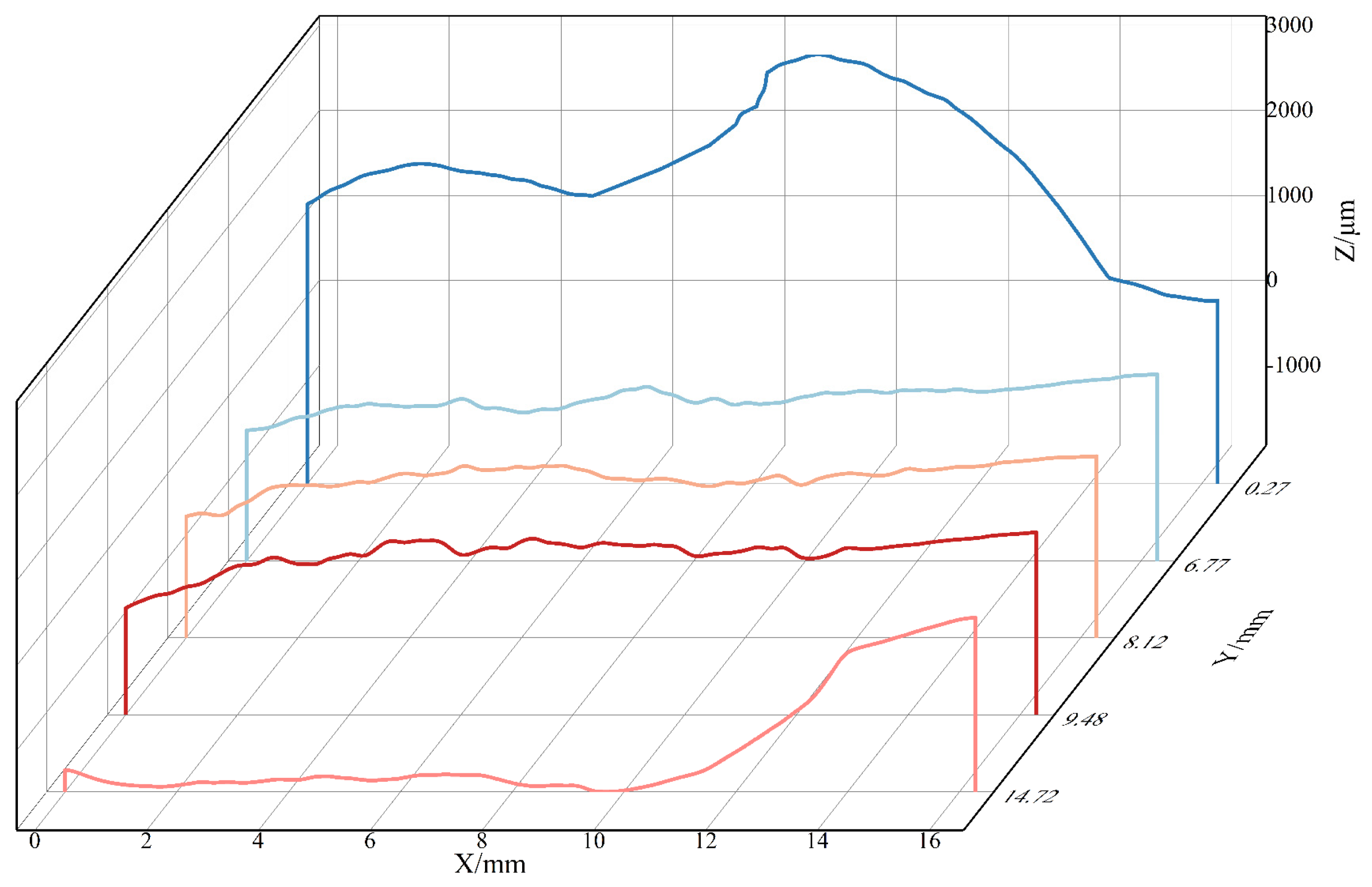
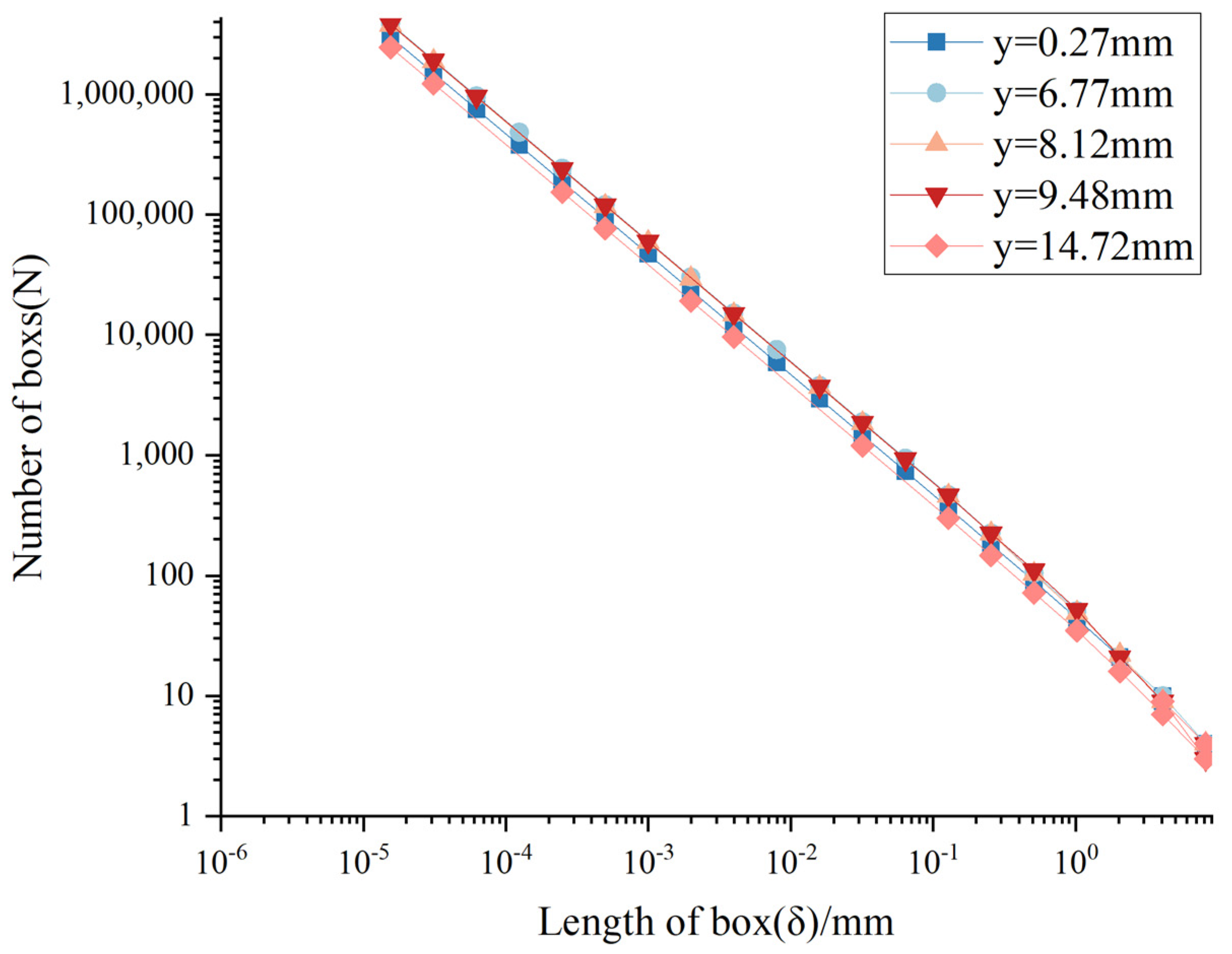
2.2. Fractal Dimension Calculation Method
3. Experimental Section
3.1. Materials and Specimen
3.2. Experiment Procedure
4. Results and Discussion
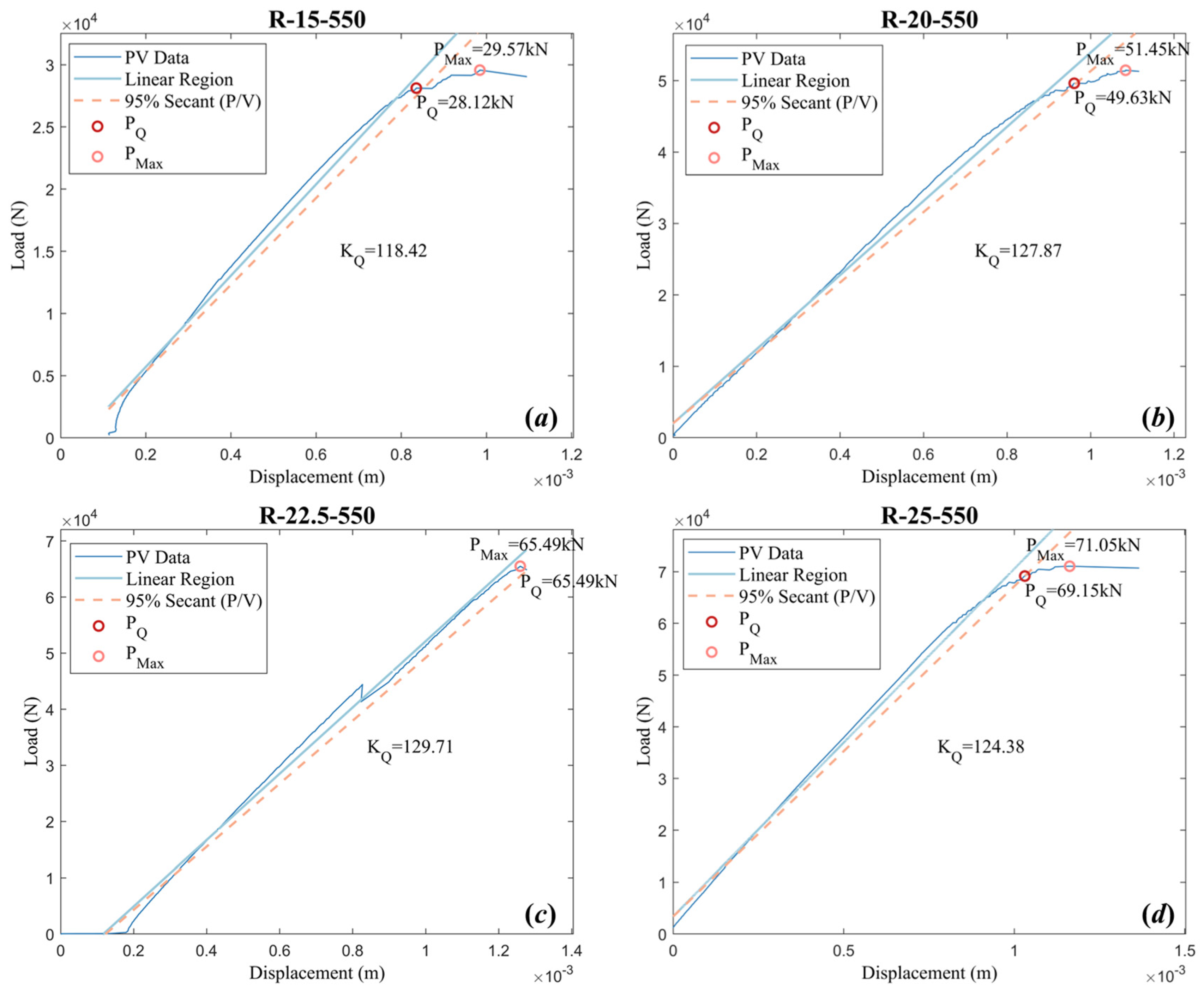
4.1. Experiment Results
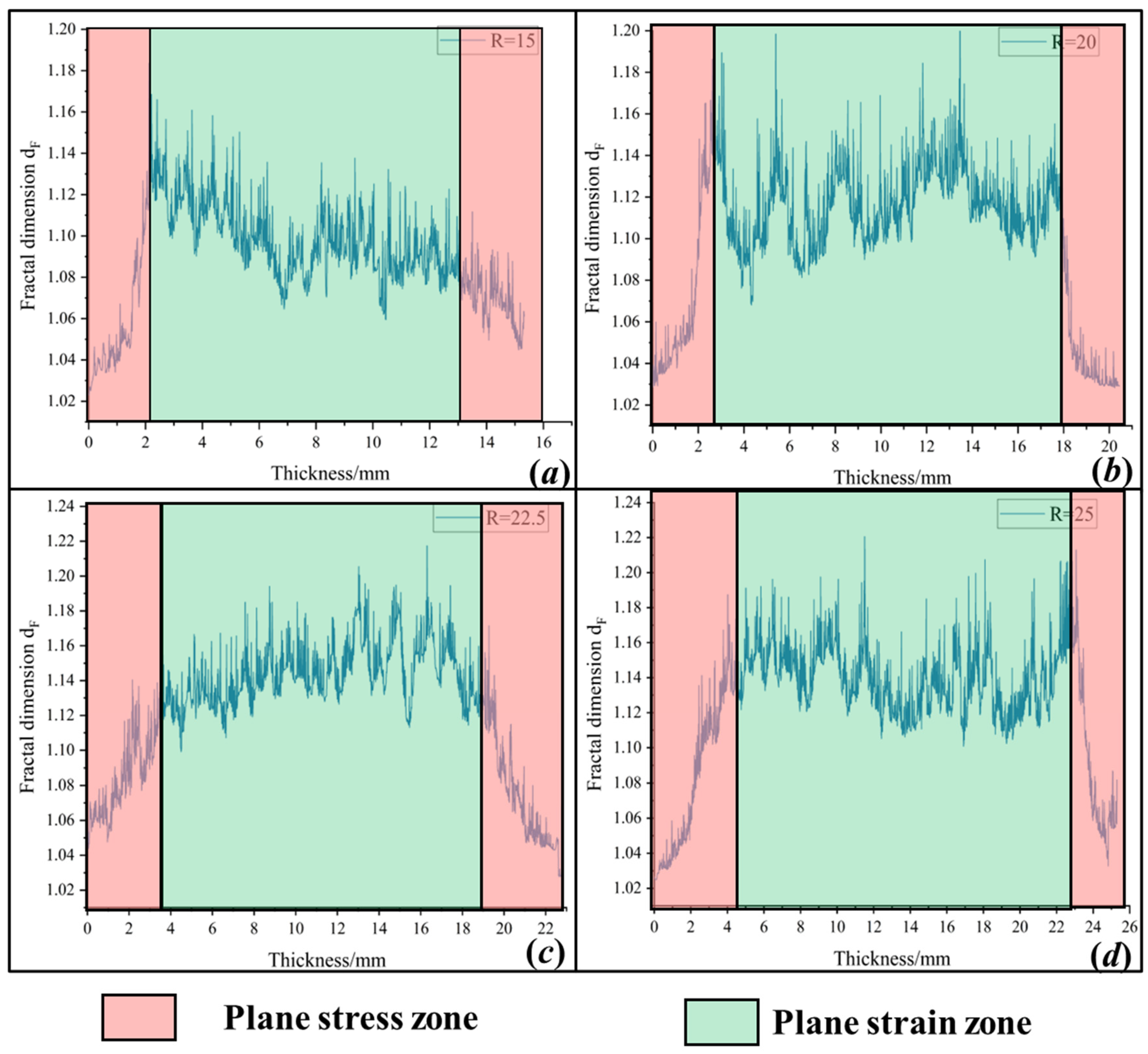
4.2. Fractal Dimension Analysis of Fractures
5. Conclusions
- By incorporating the fractal dimension into the calculation of the true fracture surface area, termed the ubiquitiform surface area, the energy release rate GC could be derived from the external work and ubiquitiform surface area. The proposed method, accounting for distinct fractal dimensions in different fracture regions, yielded KC values closer to the experimental data compared to utilizing the nominal fracture area.
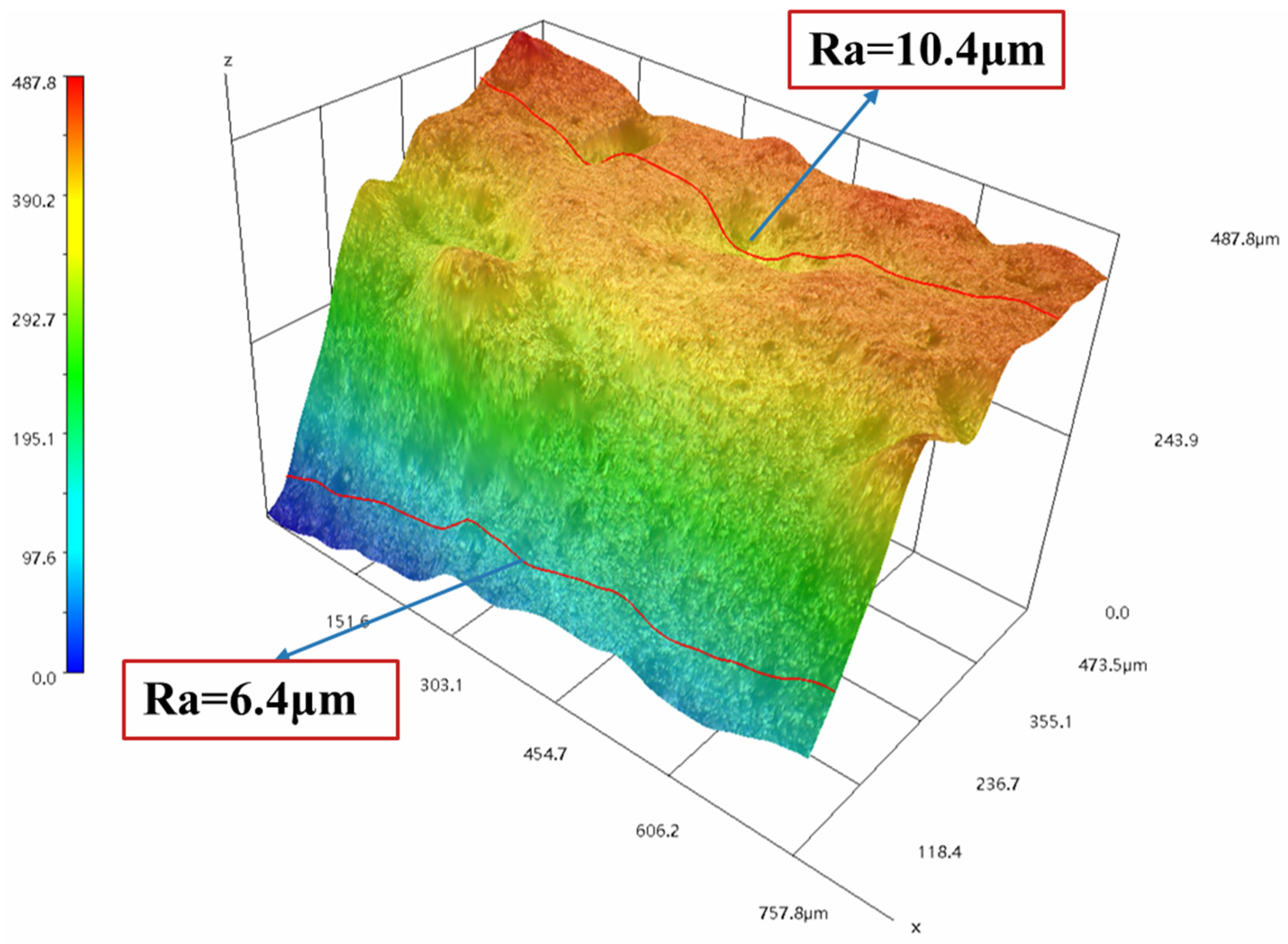
- The fractal dimensions of the plane stress and plane strain fracture regions were determined separately using the box-counting method. The plane strain region exhibited a higher fractal dimension, indicating greater roughness and tortuosity compared to the plane stress region.
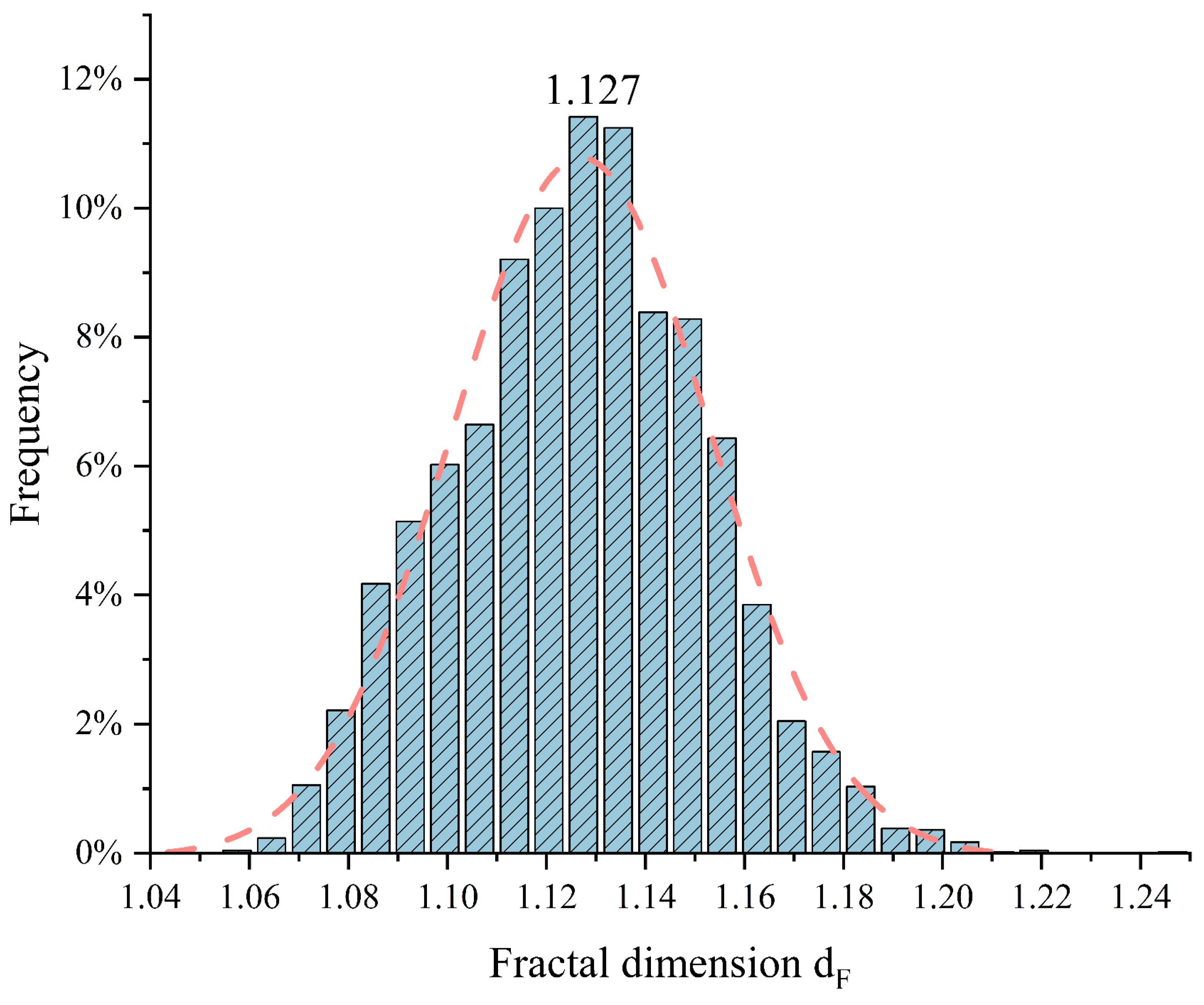
- The fractal dimension in the plane strain fracture region followed a normal distribution. Consequently, the relationship between fracture toughness KC and its dispersion could be quantified through the distribution of fractal dimensions in this region.
- Further research could focus on refining these methods and exploring their applicability to a broader range of materials and loading conditions to generalize the findings.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Nomenclature
| a0 | Initial crack length |
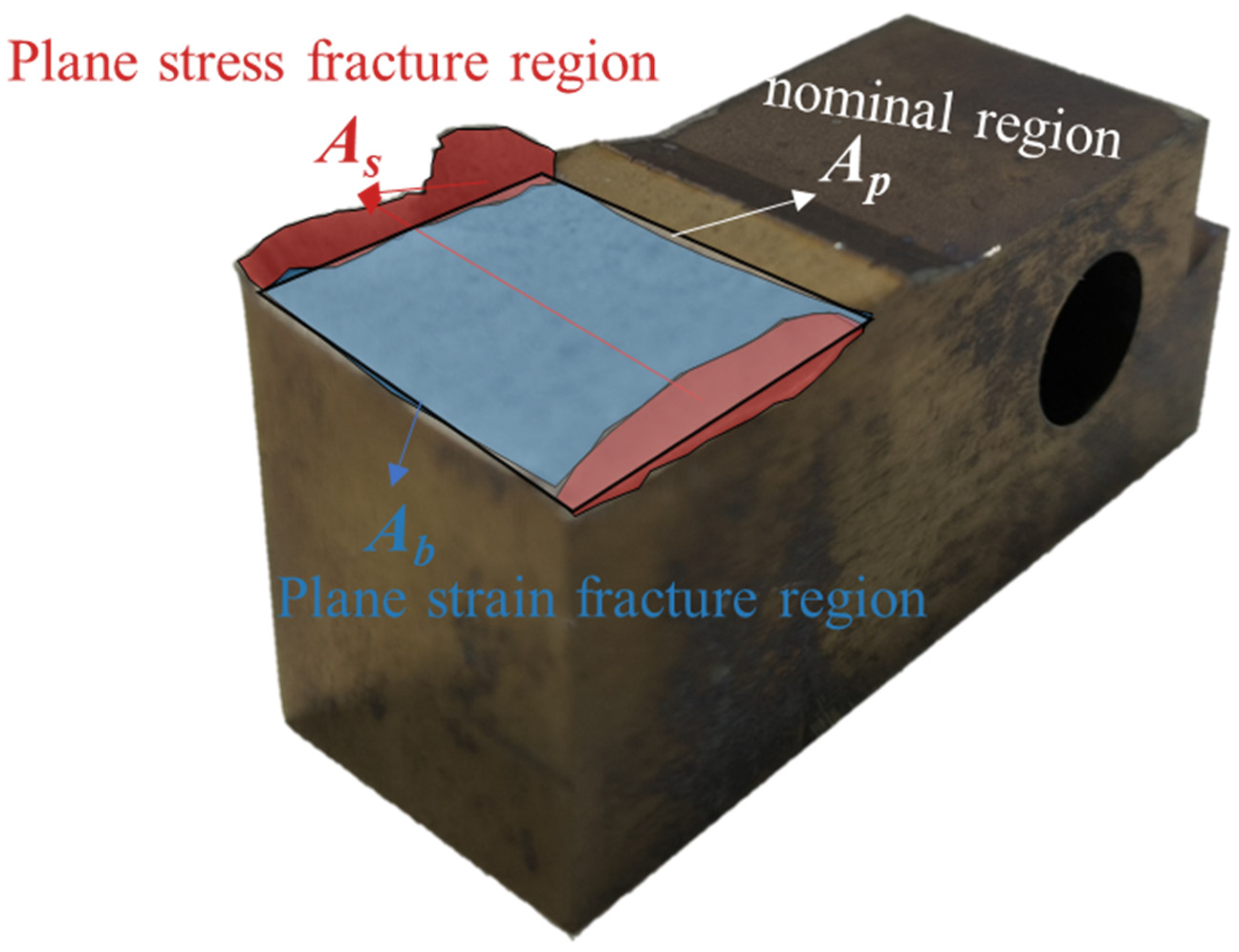
| Ab | Plane strain fracture region |
| Ap | Area of the nominal region |
| At | Total area of As and Ab |
| As | Plane stress fracture region |
| Aauf | Ubiquitiform surface area |
| Atuf | Ubiquitiform surface area of the fracture |
| B | Specimen thickness |
| ΔB | Interval between each curve |
| D | Ubiquitiform complexity |
| dF | Fractal dimension |
| dFi | Fractal dimension of the ith curve |
| E | Young’s modulus |
| GC | Energy release rate |
| i | ith curve |
| KC | Fracture toughness |
| KCu | Fracture toughness by integrating the fractal dimension and fracture energy |
| KIC | Plane strain fracture toughness |
| KQ | Conditional fracture toughness |
| l | Nominal straight-line length of the two-dimensional crack growth curve |
| lF | Corresponding fractal curve length |
| luf | Ubiquitiform length |
| n | Number of divided crack propagation regions curves |
| N(δ) | Number of squares (in box-counting dimension method) |
| Pmax | Maximum load |
| Pq | Critical load |
| W | Width of the specimen |
| Wt | Work performed by an external force |
| δ | The side length δ of the squares (in box-counting dimension method) |
| δe | Elongation |
| Tensile strength | |
| σy | Yield strength |
| v | Poisson’s ratio |
References
- Suresh, S. Fatigue of Materials, 2nd ed.; Cambridge University Press: Cambridge, UK, 1998. [Google Scholar]
- Rouxel, T.; Yoshida, S. The fracture toughness of inorganic glasses. J. Am. Ceram. Soc. 2017, 100, 4374–4396. [Google Scholar] [CrossRef]
- Erarslan, N.; Williams, D.J. The damage mechanism of rock fatigue and its relationship to the fracture toughness of rocks. Int. J. Rock Mech. Min. Sci. 2012, 56, 15–26. [Google Scholar] [CrossRef]
- Li, P.; Cheng, L.; Yan, X.; Huang, D.; Qin, X.; Zhang, X. A temperature-dependent model for predicting the fracture toughness of superalloys at elevated temperature. Theor. Appl. Fract. Mech. 2018, 93, 311–318. [Google Scholar] [CrossRef]
- Ren, X.; Wu, S.; Xing, H.; Fang, X.; Ao, N.; Zhu, T.; Li, Q.; Kang, G. Fracture mechanics based residual life prediction of railway heavy coupler with measured load spectrum. Int. J. Fract. 2022, 234, 313–327. [Google Scholar] [CrossRef]
- Yu, M.; Luo, Z.; Chao, Y.J. Correlations between Charpy V-notch impact energy and fracture toughness of nuclear reactor pressure vessel (RPV) steels. Eng. Fract. Mech. 2015, 147, 187–202. [Google Scholar] [CrossRef]
- ASTM E399-22; Standard Test Method for Linear-Elastic Plane-Strain Fracture Toughness of Metallic Materials. ASTM International: West Conshohocken, PA, USA, 2022.
- ASTM D5045-99; Standard Test Methods for Plane-Strain Fracture Toughness and Strain Energy Release Rate of Plastic Materials. ASTM International: West Conshohocken, PA, USA, 2017.
- Anderson, T.L. Fracture mechanics: Fundamentals and Applications, 3rd ed.; CRC Press: Boca Raton, FL, USA, 2017. [Google Scholar]
- Qiao, Y.; Zhang, Z.; Zhang, S. An Experimental Study of the Relation between Mode I Fracture Toughness, K(Ic), and Critical Energy Release Rate, G(Ic). Materials 2023, 16, 1056. [Google Scholar] [CrossRef] [PubMed]
- Bazant, Z.P.; Planas, J. Fracture and Size Effect in Concrete and Other Quasibrittle Materials; CRC Press: Boca Raton, FL, USA, 1997. [Google Scholar]
- Dutler, N.; Nejati, M.; Valley, B.; Amann, F.; Molinari, G. On the link between fracture toughness, tensile strength, and fracture process zone in anisotropic rocks. Eng. Fract. Mech. 2018, 201, 56–79. [Google Scholar] [CrossRef]
- Zhang, Z.X.; Ouchterlony, F. Energy requirement for rock breakage in laboratory experiments and engineering operations: A review. Rock Mech. Rock Eng. 2022, 55, 629–667. [Google Scholar] [CrossRef]
- Mandelbrot, B.B.; Passoja, D.E.; Paullay, A.J. Fractal character of fracture surfaces of metals. Nature 1984, 308, 721–722. [Google Scholar] [CrossRef]
- Ding, C.; Xu, T.; Chen, Q.; Su, C.; Zhao, P. Study on the relationship between fractal characteristics and mechanical properties of tensile fracture of reinforced concrete structures. KSCE J. Civ. Eng. 2022, 26, 2225–2233. [Google Scholar] [CrossRef]
- Khezrzadeh, H.; Mofid, M. Tensile fracture behavior of heterogeneous materials based on fractal geometry. Theor. Appl. Fract. Mech. 2006, 46, 46–56. [Google Scholar] [CrossRef]
- Ji, G.; Li, K.; Zhang, G.; Li, S.; Zhang, L. An assessment method for shale fracability based on fractal theory and fracture toughness. Eng. Fract. Mech. 2019, 211, 282–290. [Google Scholar] [CrossRef]
- Heping, X. The fractal effect of irregularity of crack branching on the fracture toughness of brittle materials. Int. J. Frac. 1989, 41, 267–274. [Google Scholar] [CrossRef]
- Pimenta, S.; Pinho, S.T. An analytical model for the translaminar fracture toughness of fibre composites with stochastic quasi-fractal fracture surfaces. J. Mech. Phys. Solids 2014, 66, 78–102. [Google Scholar] [CrossRef]
- Thompson, J.Y.; Anusavice, K.J.; Balasubramaniam, B.; Mecholsky, J.J., Jr. Effect of micmcracking on the fracture toughness and fracture surface fractal dimension of lithia-based glass-ceramics. J. Am. Ceram. Soc. 1995, 78, 3045–3049. [Google Scholar] [CrossRef]
- Pande, C.S.; Richards, L.E.; Louat, N.; Dempsey, B.; Schwoeble, A. Fractal characterization of fractured surfaces. Acta Metall. 1987, 35, 1633–1637. [Google Scholar] [CrossRef]
- Richards, L.E.; Dempsey, B.D. Fractal characterization of fractured surfaces in Ti-4.5 Al-5.0 Mo-1.5 Cr (CORONA 5). Scr. Metall. 1988, 22, 687–689. [Google Scholar] [CrossRef]
- Strnadel, B.; Ferfecki, P.; Židlík, P. Statistical characteristics of fracture surfaces in high-strength steel drop weight tear test specimens. Eng. Fract. Mech. 2013, 112, 1–13. [Google Scholar] [CrossRef]
- Carpinteri, A.; Spagnoli, A.; Vantadori, S. Size effect in S–N curves: A fractal approach to finite-life fatigue strength. Int. J. Fatigue 2009, 31, 927–933. [Google Scholar] [CrossRef]
- Chuan, Z.; Yanhui, C.; Weixing, Y. The use of fractal dimensions in the prediction of residual fatigue life of pre-corroded aluminum alloy specimens. Int. J. Fatigue 2014, 59, 282–291. [Google Scholar] [CrossRef]
- Ou, Z.C.; Li, G.Y.; Duan, Z.P.; Huang, F.-L. Ubiquitiform in applied mechanics. J. Theor. Appl. Mech. 2014, 52, 37–46. [Google Scholar]
- Ou, Z.C.; Yang, M.; Li, G.Y.; Duan, Z.-P.; Huang, F.-L. Ubiquitiformal fracture energy. J. Theor. Appl. Mech. 2017, 55, 1101–1108. [Google Scholar] [CrossRef][Green Version]
- Yang, B.; Cao, X.; Han, T.; Li, P.; Shi, J. Effect of heterogeneity on the extension of ubiquitiformal cracks in rock materials. Fractal Fract. 2022, 6, 317. [Google Scholar] [CrossRef]
- Shi, J.; Jiang, H.; Hu, Y.; Cao, X. Test method for fracture toughness GIC based on ubiquitiform theory. Eng. Fract. Mech. 2022, 271, 108640. [Google Scholar] [CrossRef]
- Mu, Z.; Lung, C. Studies on the fractal dimension and fracture toughness of steel. J. Phys. D Appl. Phys. 1988, 21, 848. [Google Scholar] [CrossRef]
- Osovski, S.; Srivastava, A.; Ponson, L.; Bouchaud, E.; Tvergaard, V.; Ravi-Chandar, K.; Needleman, A. The effect of loading rate on ductile fracture toughness and fracture surface roughness. J. Mech. Phys. Solids 2015, 76, 20–46. [Google Scholar] [CrossRef]
- Shi, J.; Zhang, N.; Cao, X.; Hu, Y. Characterization of ubiquitiform crack fracture parameters based on ubiquitiform theory. Acta Mech. 2020, 231, 2589–2601. [Google Scholar] [CrossRef]
- Carpinteri, A. Fractal nature of material microstructure and size effects on apparent mechanical properties. Mech. Mater. 1994, 18, 89–101. [Google Scholar] [CrossRef]
- Issa, M.A.; Issa, M.A.; Islam, M.S.; Chudnovsky, A. Fractal dimension—A measure of fracture roughness and toughness of concrete. Eng. Fract. Mech. 2003, 70, 125–137. [Google Scholar] [CrossRef]
- Brown, W.F.; Srawley, J.E. Plane Strain Crack Toughness Testing of High Strength Metallic Materials; ASTM International: West Conshohocken, PA, USA, 1966. [Google Scholar]
- Srawley, J.E.; Jones, M.H.; Brown, W. Determination of plane strain fracture toughness. Mater. Res. Stand. 1967, 7, 262–266. [Google Scholar]
- Zhuang, D.; Yin, T.; Li, Q.; Wu, Y.; Chen, Y.; Yang, Z. Fractal fracture toughness measurements of heat-treated granite using hydraulic fracturing under different injection flow rates. Theor. Appl. Fract. Mech. 2022, 119, 103340. [Google Scholar] [CrossRef]
- Hu, D.; Mao, J.; Wang, X.; Meng, F.; Song, J.; Wang, R. Probabilistic evaluation on fatigue crack growth behavior in nickel based GH4169 superalloy through experimental data. Eng. Fract. Mech. 2018, 196, 71–82. [Google Scholar] [CrossRef]
- ASTM E8/E8M-22; Standard Test Methods for Tension Testing of Metallic Materials. ASTM International: Conshohocken, PA, USA, 2022.
- Hu, X.; Zhuang, S.; Zheng, H.; Zhao, Z.; Jia, X. Non-Unified Constitutive Models for the Simulation of the Asymmetrical Cyclic Behavior of GH4169 at Elevated Temperatures. Metals 2022, 12, 1868. [Google Scholar] [CrossRef]
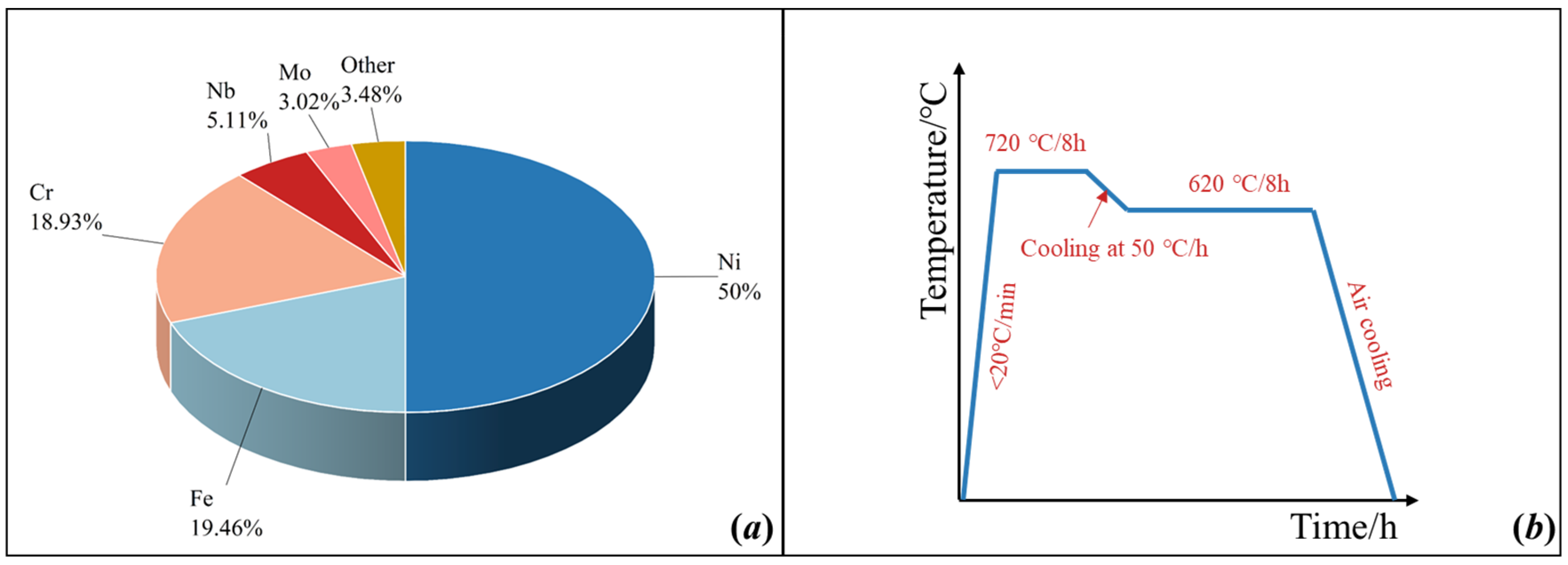



| Mechanical Property | Young’s Modulus E/GPa | Poisson’s Ratio v | Yield Strength σy/MPa | Tensile Strength σb/MPa | Elongation δe |
|---|---|---|---|---|---|
| Value | 180.3 | 0.32 | 1152 | 1344 | 15.4% |
| No. | B (mm) | Ws (mm) | a (mm) | Ws-a (mm) | 2.5(KQ/σy)2 (mm) | Equation (1) Y/N? | KQ |
|---|---|---|---|---|---|---|---|
| R-15 | 15.38 | 29.99 | 16.38 | 13.61 | 26.42 | N | 118.42 |
| R-20 | 20.48 | 39.99 | 21.11 | 18.88 | 30.80 | N | 127.87 |
| R-22.5 | 22.88 | 44.97 | 22.41 | 22.56 | 31.70 | N | 129.71 |
| R-25 | 25.45 | 50.01 | 25.93 | 24.08 | 29.10 | N | 124.38 |
| No. | dFa | Atuf (mm2) | Aauf (mm2) | W (J) | KCu (MPa·m0.5) | KQ (MPa·m0.5) |
|---|---|---|---|---|---|---|
| R-15-550 | 1.0892 | 317.93 | 316.4387 | 48.6504 | 175.68 | 118.42 |
| R-20-550 | 1.1015 | 658.42 | 642.7561 | 72.9385 | 150.94 | 127.87 |
| R-22.5-550 | 1.1235 | 1019.8 | 991.1947 | 84.4629 | 130.79 | 129.71 |
| R-25-550 | 1.1249 | 1216.76 | 1194.168 | 102.9412 | 131.55 | 124.38 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Liu, H.; Yan, J.; Li, A.; He, Z.; Xie, Y.; Yan, H.; Huang, D. A Relationship between Fracture Toughness Kc and Energy Release Rate Gc According to Fracture Morphology Analysis. Crystals 2024, 14, 740. https://doi.org/10.3390/cryst14080740
Liu H, Yan J, Li A, He Z, Xie Y, Yan H, Huang D. A Relationship between Fracture Toughness Kc and Energy Release Rate Gc According to Fracture Morphology Analysis. Crystals. 2024; 14(8):740. https://doi.org/10.3390/cryst14080740
Chicago/Turabian StyleLiu, Haohao, Jinlun Yan, Aofei Li, Zhenyu He, Yuchen Xie, Han Yan, and Dawei Huang. 2024. "A Relationship between Fracture Toughness Kc and Energy Release Rate Gc According to Fracture Morphology Analysis" Crystals 14, no. 8: 740. https://doi.org/10.3390/cryst14080740
APA StyleLiu, H., Yan, J., Li, A., He, Z., Xie, Y., Yan, H., & Huang, D. (2024). A Relationship between Fracture Toughness Kc and Energy Release Rate Gc According to Fracture Morphology Analysis. Crystals, 14(8), 740. https://doi.org/10.3390/cryst14080740







