Localized Structural and Electronic Perturbations Induced by Mono-Vacancy in MgH2: A Comprehensive First-Principles Investigation
Abstract
1. Introduction
2. Computational Methods
2.1. DFT Calculation Details
2.2. Model Configuration
2.3. Verification
3. Results
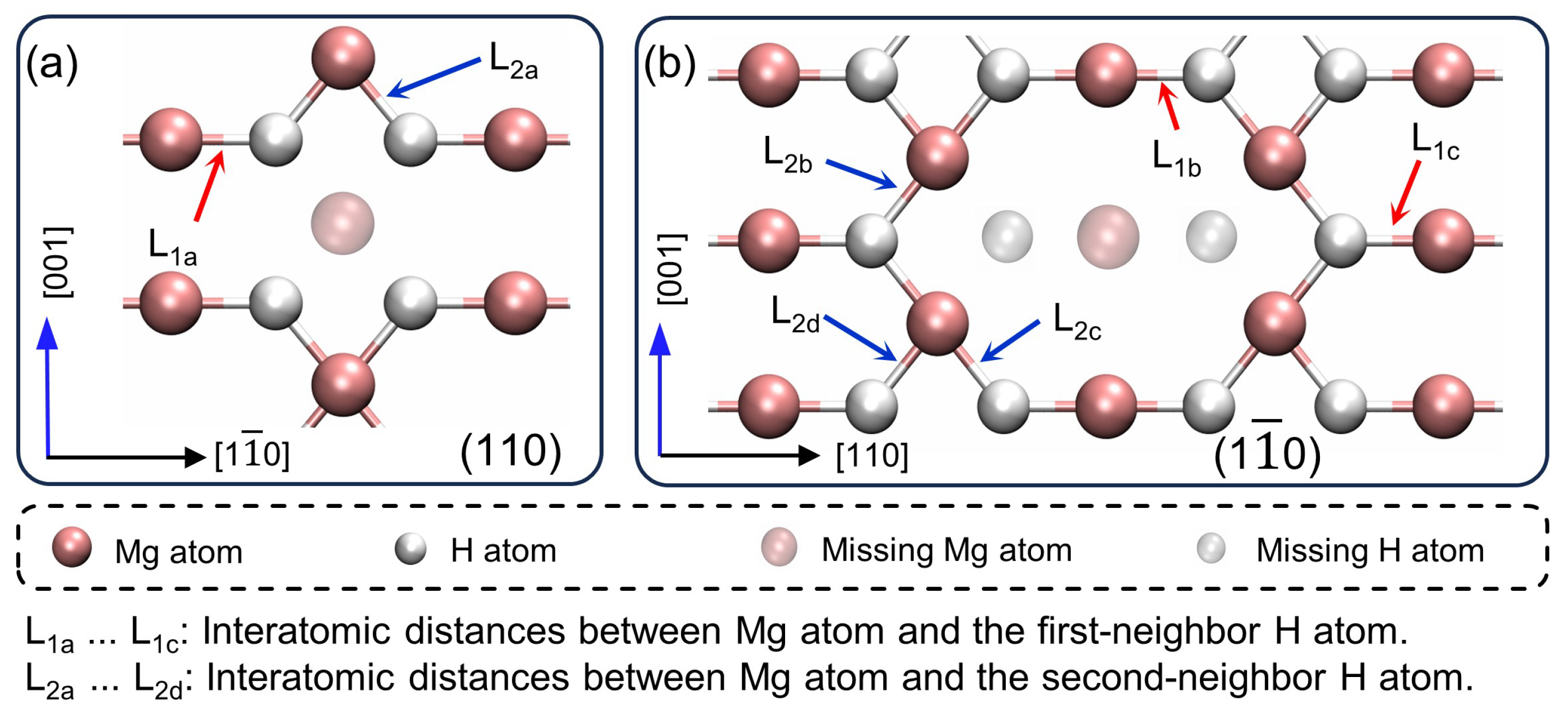
3.1. Crystal Structure
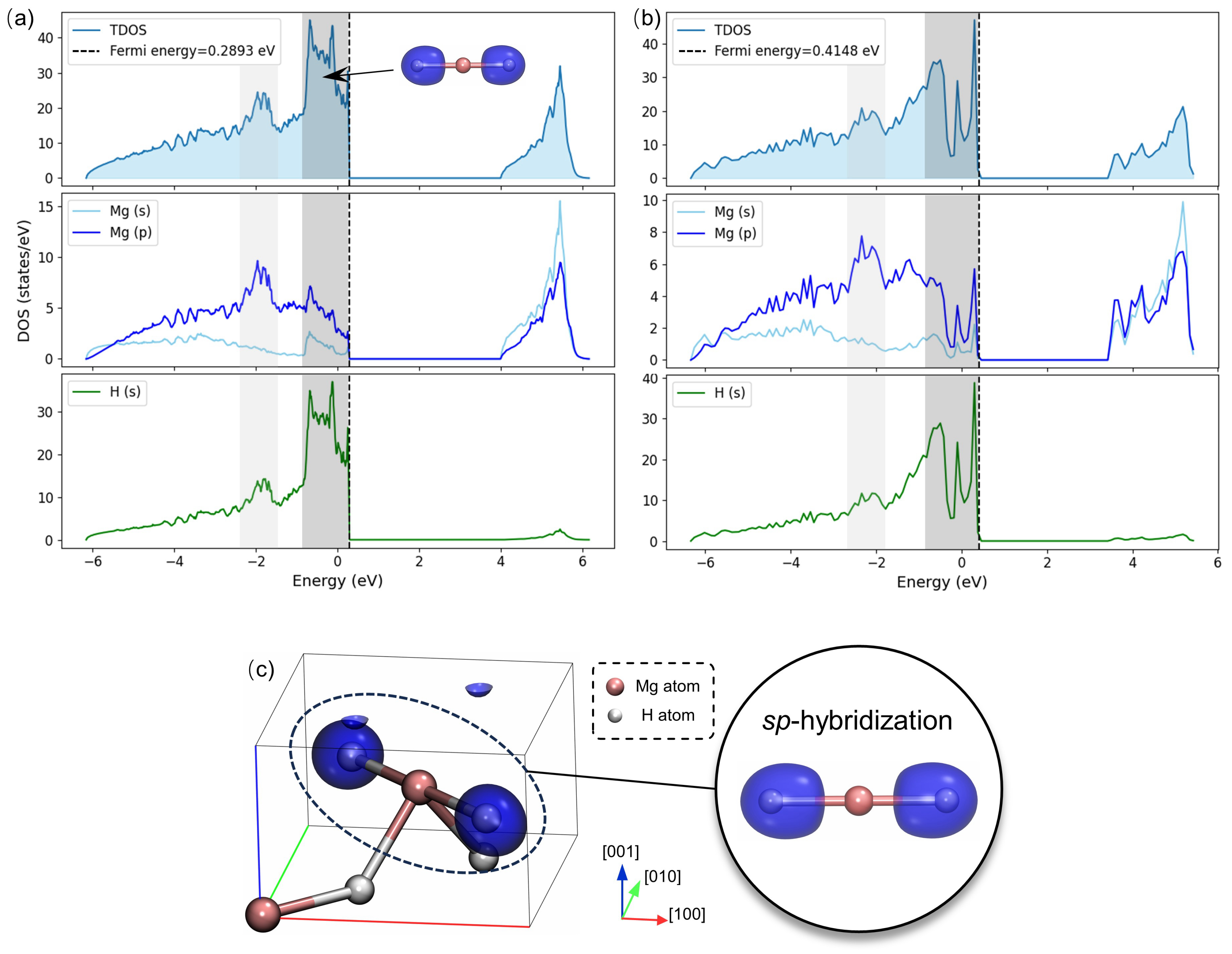
3.2. Electronic Structures and Bonding Nature
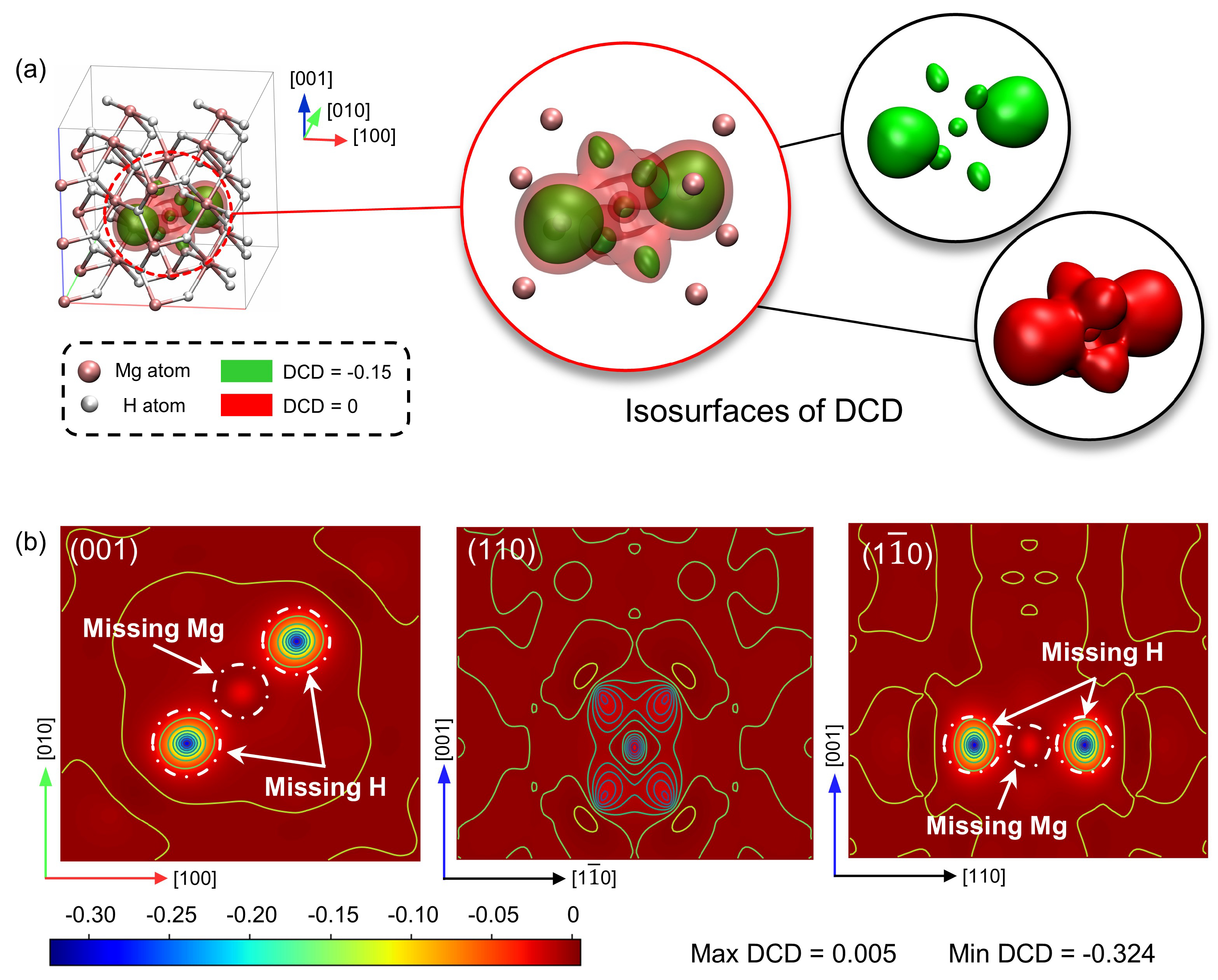
3.3. The Vacancy-Affected Zone (VAZ)
4. Discussion
5. Conclusions
- (1)
- The incorporation of a mono-vacancy in the MgH2 crystal results in a 0.57% reduction of the lattice parameters and a 1.03% expansion of the c parameter. Notwithstanding these alterations, the overall crystalline structure remains largely intact.
- (2)
- Mg-H bonds exhibit strong polar covalent characters with anisotropic effects. The mono-vacancy enhances the polarity of adjacent bonds. These alterations are predominantly localized on the (001) plane, resulting in an increase of up to in bond length and a decrease of 0.065 eV in bond energy.
- (3)
- The VAZ encompasses volumes of 26.505 Å3 for electron density depletion and 19.514 Å3 for potential energy modifications.
- (4)
- The mono-vacancy generates a localized high-potential region, characterized by a peak energy of 0.354 eV. This barrier is encompassed by low-energy regions that offer more energetically favorable pathways for H atom migration.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Gielen, D.; Boshell, F.; Saygin, D. Climate and energy challenges for materials science. Nat. Mater. 2016, 15, 117–120. [Google Scholar] [CrossRef] [PubMed]
- Ali, N.; Ismail, M. Advanced hydrogen storage of the Mg–Na–Al system: A review. J. Magnes. Alloys 2021, 9, 1111–1122. [Google Scholar] [CrossRef]
- Shen, Z.; Wang, Z.; Zhang, M.; Gao, M.; Hu, J.; Du, F.; Liu, Y.; Pan, H. A novel solid-solution MXene (Ti0.5V0.5)3C2 with high catalytic activity for hydrogen storage in MgH2. Materialia 2018, 1, 114–120. [Google Scholar] [CrossRef]
- Yang, X.; Lu, X.; Zhang, J.; Hou, Q.; Zou, J. Progress in improving hydrogen storage properties of Mg-based materials. Mater. Today Adv. 2023, 19, 100387. [Google Scholar] [CrossRef]
- Li, X.; Yuan, Z.; Liu, C.; Sui, Y.; Zhai, T.; Hou, Z.; Han, Z.; Zhang, Y. Research progress in improved hydrogen storage properties of Mg-based alloys with metal-based materials and light metals. Int. J. Hydrogen Energy 2024, 50, 1401–1417. [Google Scholar] [CrossRef]
- Lutz, M.; Linder, M.; Bürger, I. High capacity, low pressure hydrogen storage based on magnesium hydride and thermochemical heat storage: Experimental proof of concept. Appl. Energy 2020, 271, 115226. [Google Scholar] [CrossRef]
- Kušnírová, K.; Varcholová, D.; Molčanová, Z.; Ballóková, B.; Möllmer, J.; Jasminská, N.; Lazár, M.; Brestovič, T.; Podobová, M.; Dzunda, R.; et al. Multicomponent metal alloys tested for hydrogen storage. In Proceedings of the METAL 2022 Conference Proeedings, Brno, Czech Republic, 18–19 May 2022; TANGER Ltd.: Bushey, UK, 2022. [Google Scholar] [CrossRef]
- Nyallang Nyamsi, S.; Lototskyy, M.V.; Yartys, V.A.; Capurso, G.; Davids, M.W.; Pasupathi, S. 200 NL H2 hydrogen storage tank using MgH2–TiH2–C nanocomposite as H storage material. Int. J. Hydrogen Energy 2021, 46, 19046–19059. [Google Scholar] [CrossRef]
- Zhang, M.; Xiao, X.; Wang, X.; Chen, M.; Lu, Y.; Liu, M.; Chen, L. Excellent catalysis of TiO2 nanosheets with high-surface-energy 001 facets on the hydrogen storage properties of MgH2. Nanoscale 2019, 11, 7465–7473. [Google Scholar] [CrossRef]
- Zhang, J.; Yu, X.; Mao, C.; Long, C.; Chen, J.; Zhou, D. Influences and mechanisms of graphene-doping on dehydrogenation properties of MgH2: Experimental and first-principles studies. Energy 2015, 89, 957–964. [Google Scholar] [CrossRef]
- He, Y.; Ding, L.; Wu, X.; Li, Q.; Li, Z.; Zhang, W.; Jin, S. Hydrogen release mechanisms of MgH2 over NiN4-embedded graphene nanosheet: First-principles calculations. Int. J. Hydrogen Energy 2022, 47, 39549–39562. [Google Scholar] [CrossRef]
- Wu, X.; Zhang, R.; Yang, J. A first-principles study of the thermodynamic and electronic properties of Mg and MgH2 nanowires. Phys. Chem. Chem. Phys. 2016, 18, 19412–19419. [Google Scholar] [CrossRef] [PubMed]
- Huen, P.; Paskevicius, M.; Richter, B.; Ravnsbæk, D.; Jensen, T. Hydrogen Storage Stability of Nanoconfined MgH2 upon Cycling. Inorganics 2017, 5, 57. [Google Scholar] [CrossRef]
- Crivello, J.; Dam, B.; Denys, R.; Dornheim, M.; Grant, D.; Huot, J.; Jensen, T.; de Jongh, P.; Latroche, M.; Milanese, C.; et al. Review of magnesium hydride-based materials: Development and optimisation. Appl. Phys. A 2016, 122, 97. [Google Scholar] [CrossRef]
- Tan, Z.; Kong, X.; Ng, B.; Soo, H.; Mohamed, A.; Chai, S. Recent Advances in Defect-Engineered Transition Metal Dichalcogenides for Enhanced Electrocatalytic Hydrogen Evolution: Perfecting Imperfections. ACS Omega 2023, 8, 1851–1863. [Google Scholar] [CrossRef]
- Luna, C.; Germán, E.; Macchi, C.; Juan, A.; Somoza, A. On the perfect MgH2(–Nb,–Zr) systems and the influence of vacancy-like defects on their structural properties. A self-consistent first principle calculations study of the electron and positron parameters. J. Alloys Compd. 2013, 556, 188–197. [Google Scholar] [CrossRef]
- Wang, J.; Du, Y.; Sun, L. Understanding of hydrogen desorption mechanism from defect point of view. Natl. Sci. Rev. 2017, 5, 318–320. [Google Scholar] [CrossRef]
- Wang, X.; Zhang, Y.; Si, H.; Zhang, Q.; Wu, J.; Gao, L.; Wei, X.; Sun, Y.; Liao, Q.; Zhang, Z.; et al. Single-Atom Vacancy Defect to Trigger High-Efficiency Hydrogen Evolution of MoS2. J. Am. Chem. Soc. 2020, 142, 4298–4308. [Google Scholar] [CrossRef]
- Shahriar, R.; Hoque, K.S.; Tristant, D.; Zubair, A. Vacancy induced magnetism and electronic structure modification in monolayer hexagonal boron arsenide: A first-principles study. Appl. Surf. Sci. 2022, 600, 154053. [Google Scholar] [CrossRef]
- Zhang, B.; Zhu, Q.; Xu, C.; Li, C.; Ma, Y.; Ma, Z.; Liu, S.; Shao, R.; Xu, Y.; Jiang, B.; et al. Atomic-scale insights on hydrogen trapping and exclusion at incoherent interfaces of nanoprecipitates in martensitic steels. Nat. Commun. 2022, 13, 3858. [Google Scholar] [CrossRef]
- Bao, L.; Shi, J. A Novel Approach to Grain Shape Factor in 3D Hexagonal Cellular Automaton. Crystals 2023, 13, 544. [Google Scholar] [CrossRef]
- Xie, X.; Hou, C.; Chen, C.; Sun, X.; Pang, Y.; Zhang, Y.; Yu, R.; Wang, B.; Du, W. First-principles studies in Mg-based hydrogen storage Materials: A review. Energy 2020, 211, 118959. [Google Scholar] [CrossRef]
- Giusepponi, S.; Celino, M. Hydrogen Desorption from Mg Hydride: An Ab Initio Study. Crystals 2012, 2, 845–860. [Google Scholar] [CrossRef]
- Giannozzi, P.; Baroni, S.; Bonini, N.; Calandra, M.; Car, R.; Cavazzoni, C.; Ceresoli, D.; Chiarotti, G.; Cococcioni, M.; Dabo, I.; et al. QUANTUM ESPRESSO: A modular and open-source software project for quantum simulations of materials. J. Phys. Condens. Matter 2009, 21, 395502. [Google Scholar] [CrossRef] [PubMed]
- Giannozzi, P.; Andreussi, O.; Brumme, T.; Bunau, O.; Buongiorno Nardelli, M.; Calandra, M.; Car, R.; Cavazzoni, C.; Ceresoli, D.; Cococcioni, M.; et al. Advanced capabilities for materials modelling with Quantum ESPRESSO. J. Phys. Condens. Matter 2017, 29, 465901. [Google Scholar] [CrossRef] [PubMed]
- Humphrey, W.; Dalke, A.; Schulten, K. VMD: Visual molecular dynamics. J. Mol. Graph. 1996, 14, 33–38. [Google Scholar] [CrossRef]
- Hunter, J. Matplotlib: A 2D Graphics Environment. Comput. Sci. Eng. 2007, 9, 90–95. [Google Scholar] [CrossRef]
- Blöchl, P.E. Projector augmented-wave method. Phys. Rev. B 1994, 50, 17953–17979. [Google Scholar] [CrossRef]
- Perdew, J.; Burke, K.; Ernzerhof, M. Generalized Gradient Approximation Made Simple. Phys. Rev. Lett. 1996, 77, 3865–3868. [Google Scholar] [CrossRef]
- Zheng, X.H.; Zheng, J.X. On the use of Monkhorst–Pack scheme to evaluate superconductivity and the issue of umklapp electron–phonon interactions. Phys. Chem. Chem. Phys. 2023, 25, 13049–13060. [Google Scholar] [CrossRef]
- Atkins, P.; de Paula, J.; Friedman, R. Self-consistent fields. In Physical Chemistry: Quanta, Matter, and Change; Oxford University Press: Oxford, UK, 2013. [Google Scholar] [CrossRef]
- Noritake, T.; Aoki, M.; Towata, S.; Seno, Y.; Hirose, Y.; Nishibori, E.; Takata, M.; Sakata, M. Chemical bonding of hydrogen in MgH2. Appl. Phys. Lett. 2002, 81, 2008–2010. [Google Scholar] [CrossRef]
- Jain, A.; Ong, S.; Hautier, G.; Chen, W.; Richards, W.; Dacek, S.; Cholia, S.; Gunter, D.; Skinner, D.; Ceder, G.; et al. Commentary: The Materials Project: A materials genome approach to accelerating materials innovation. APL Mater. 2013, 1, 011002. [Google Scholar] [CrossRef]
- Bortz, M.; Bertheville, B.; Böttger, G.; Yvon, K. Structure of the high pressure phase γ-MgH2 by neutron powder diffraction. J. Alloys Compd. 1999, 287, L4–L6. [Google Scholar] [CrossRef]
- Rici, Y.; Pui, K. Electronic and structural properties of MgH2. Phys. Rev. B Condens. Matter 1988, 37, 8730–8737. [Google Scholar]
- Zhao, X.; Wu, S.; Chen, X.; Liu, L.; Deng, Y.; Zhou, L.; Cai, X. Mechanism of hydrogenation and dehydrogenation in Mg/Cu9Al4 @Mg and MgH2/Cu9Al4 @MgH2: A DFT and experimental investigation. J. Alloys Compd. 2024, 978, 173542. [Google Scholar] [CrossRef]
- Pfrommer, B.; Elsässer, C.; Fähnle, M. Possibility of Li-Mg and Al-Mg hydrides being metallic. Phys. Rev. B 1994, 50, 5089–5093. [Google Scholar] [CrossRef]
- Reshak, A. MgH2 and LiH metal hydrides crystals as novel hydrogen storage material: Electronic structure and optical properties. Int. J. Hydrogen Energy 2013, 38, 11946–11954. [Google Scholar] [CrossRef]
- Noritake, T.; Towata, S.; Aoki, M.; Seno, Y.; Hirose, Y.; Nishibori, E.; Takata, M.; Sakata, M. Charge density measurement in MgH2 by synchrotron X-ray diffraction. J. Alloys Compd. 2003, 356–357, 84–86. [Google Scholar] [CrossRef]
- Becke, A.; Edgecombe, K. A simple measure of electron localization in atomic and molecular systems. J. Chem. Phys. 1990, 92, 5397–5403. [Google Scholar] [CrossRef]
- Lewars, E. The Concept of the Potential Energy Surface; Springer: Dordrecht, The Netherlands, 2011; pp. 9–43. [Google Scholar] [CrossRef]
- Böer, K.W.; Pohl, U.W. Quantum Mechanics of Electrons in Crystals. In Semiconductor Physics; Springer International Publishing: Berlin/Heidelberg, Germany, 2018; pp. 207–242. [Google Scholar] [CrossRef]
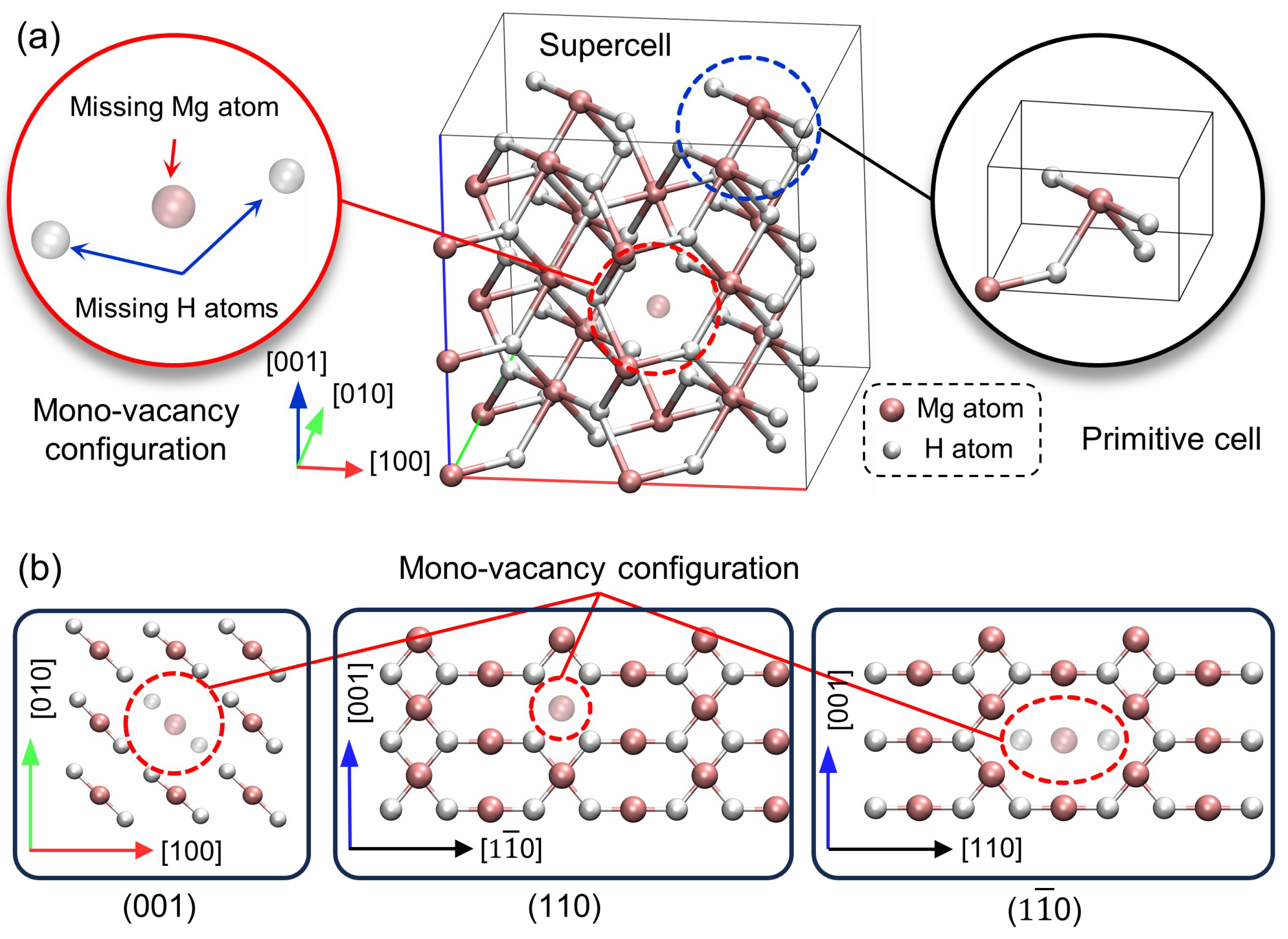


| Parameters | In Present Calculations | In References | Max Deviation |
|---|---|---|---|
| (Å) | 4.511 | 4.518 [32], 4.512 [33], 4.501 [34] | |
| c (Å) | 3.016 | 3.021 [32], 3.016 [33], 3.010 [34] | |
| band gap (eV) | 3.72 | 3.90 [33], 3.60 [35] | |
| formation energy (eV/atom) | −0.276 | −0.278 [33] |
| Interatomic Distances 1 | In Pristine Crystal (Å) | In Defective Crystal (Å) | Deviations |
|---|---|---|---|
| 1.9403 | 1.8238 | −6.39% | |
| 1.9796 | 1.99% | ||
| 2.1126 | 8.16% | ||
| 1.9587 | 1.8589 | −5.37% | |
| 1.9129 | −2.39% | ||
| 1.8994 | −3.12% | ||
| 1.8553 | −5.57% |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Bao, L.; Shi, J.; Le, Q. Localized Structural and Electronic Perturbations Induced by Mono-Vacancy in MgH2: A Comprehensive First-Principles Investigation. Crystals 2024, 14, 750. https://doi.org/10.3390/cryst14090750
Bao L, Shi J, Le Q. Localized Structural and Electronic Perturbations Induced by Mono-Vacancy in MgH2: A Comprehensive First-Principles Investigation. Crystals. 2024; 14(9):750. https://doi.org/10.3390/cryst14090750
Chicago/Turabian StyleBao, Lei, Jun Shi, and Qichi Le. 2024. "Localized Structural and Electronic Perturbations Induced by Mono-Vacancy in MgH2: A Comprehensive First-Principles Investigation" Crystals 14, no. 9: 750. https://doi.org/10.3390/cryst14090750
APA StyleBao, L., Shi, J., & Le, Q. (2024). Localized Structural and Electronic Perturbations Induced by Mono-Vacancy in MgH2: A Comprehensive First-Principles Investigation. Crystals, 14(9), 750. https://doi.org/10.3390/cryst14090750






