Impact of Molecular and Crystal Structure on the Melting Points in Halo-Substituted Phenyl-Quinazolinones
Abstract
1. Introduction
2. Experimental
2.1. Reagents and Techniques
2.2. Synthesis
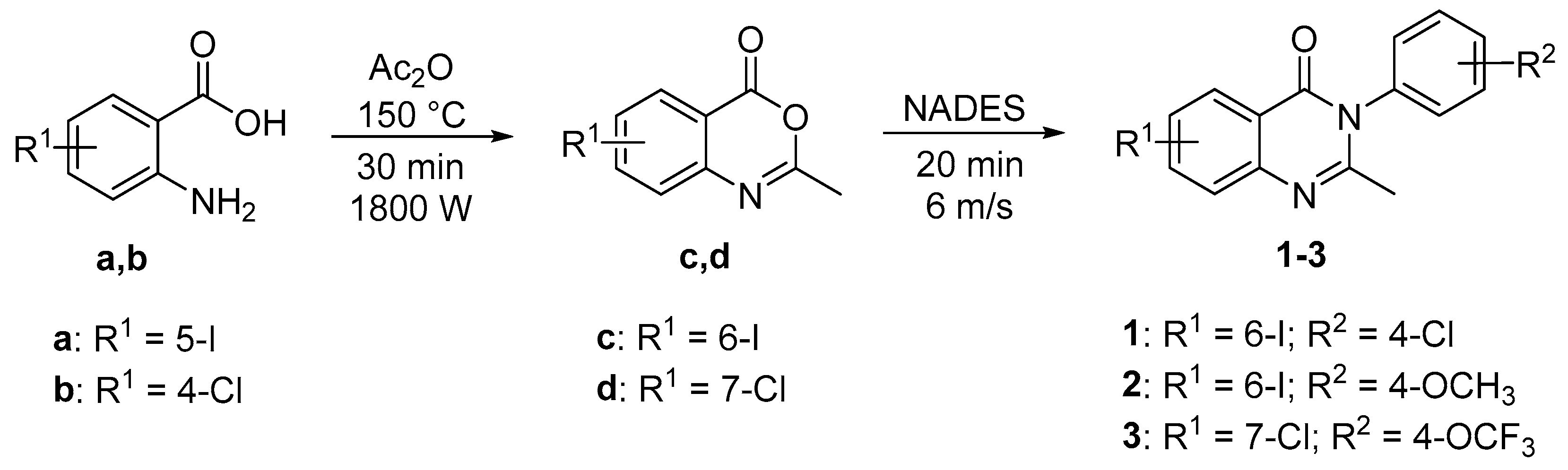
2.2.1. General Procedure for the Synthesis of 2-Methyl-3,1-benzoxazin-4-ones c and d in Solution
2.2.2. General Liquid-Assisted Mechanochemical Procedure for the Synthesis of Quinazolin-4(3H)-ones 1–3
2.3. X-Ray Crystallography
2.4. Hirshfeld Surface Analysis
3. Results and Discussion
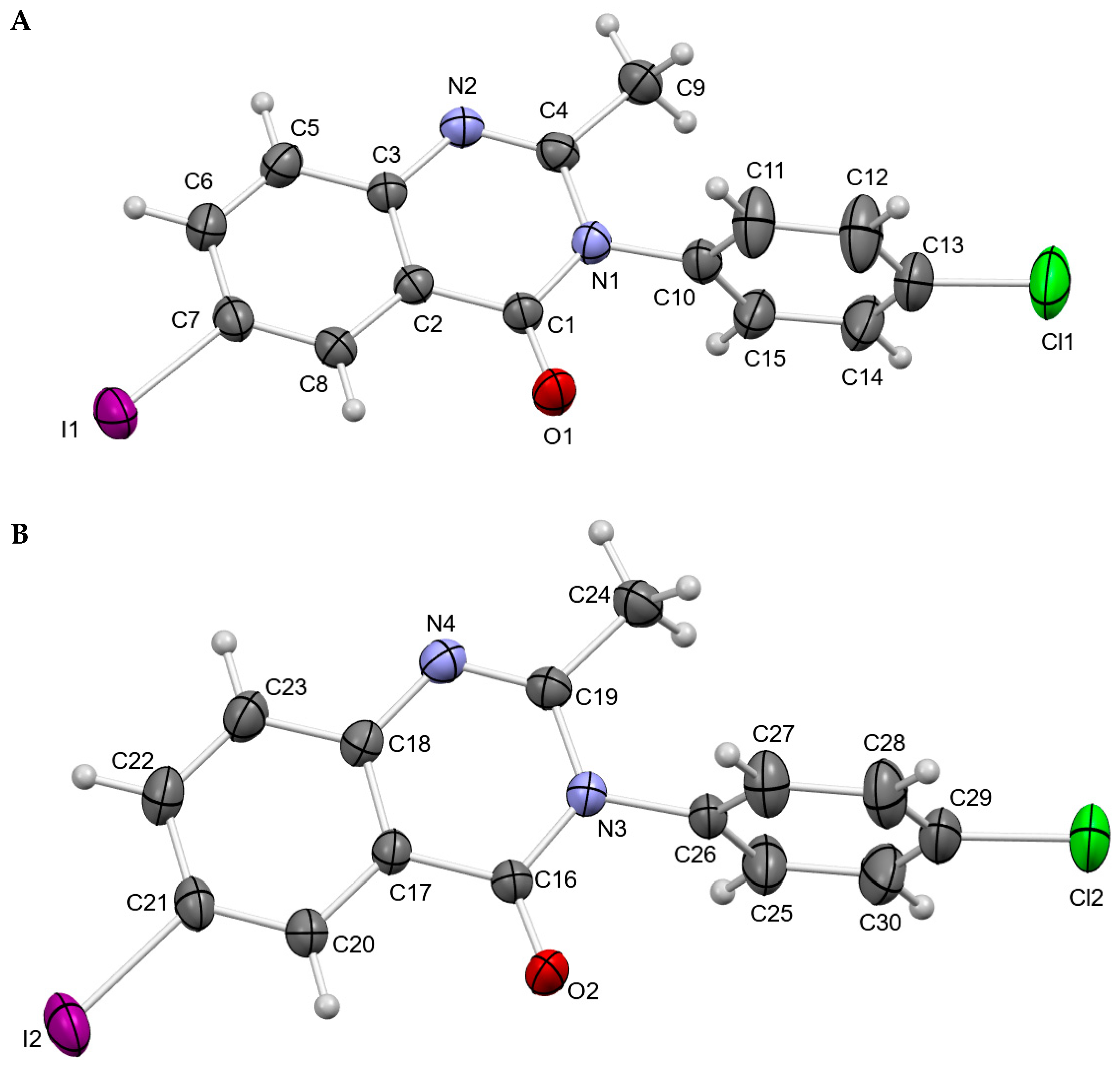
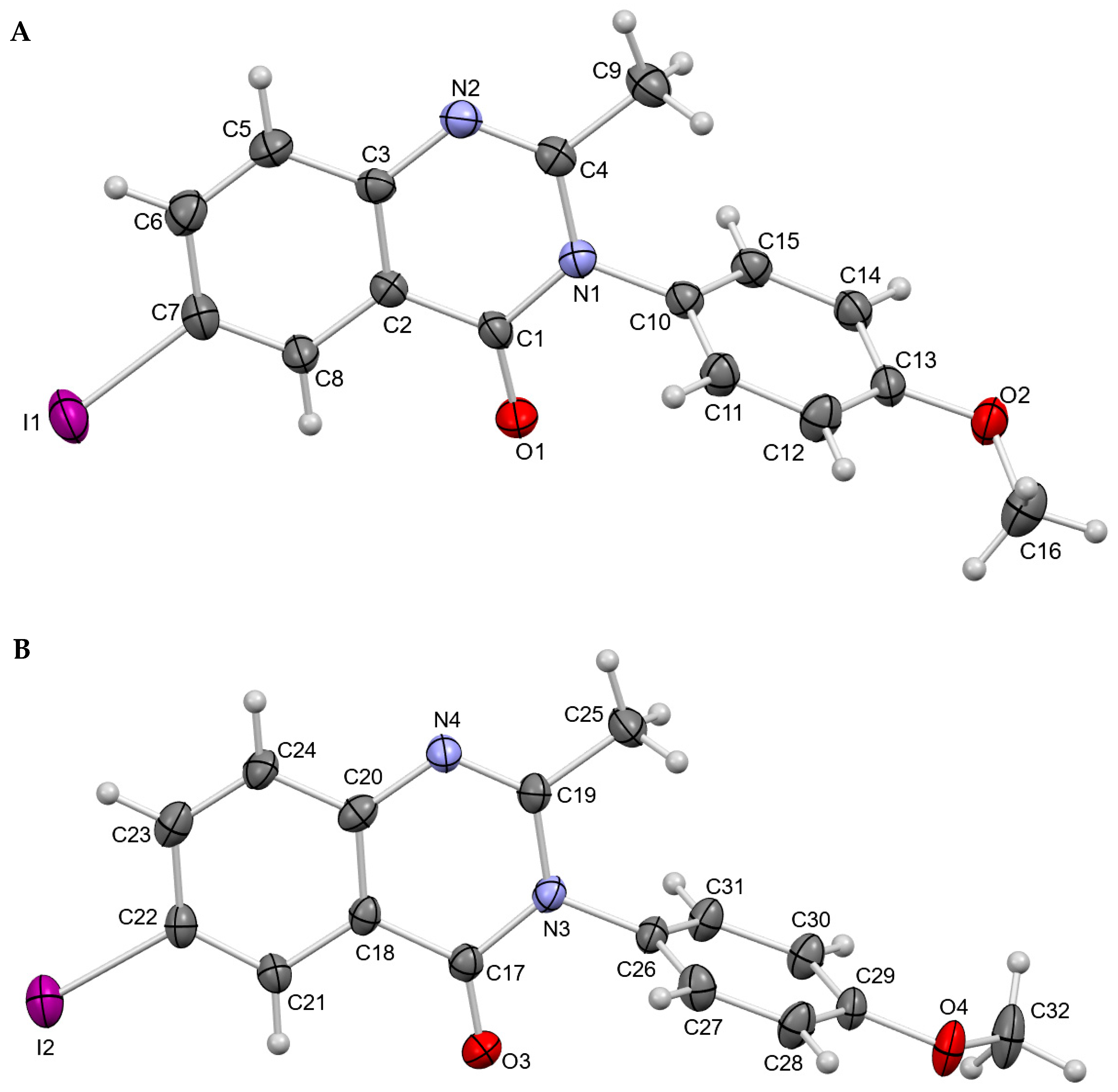
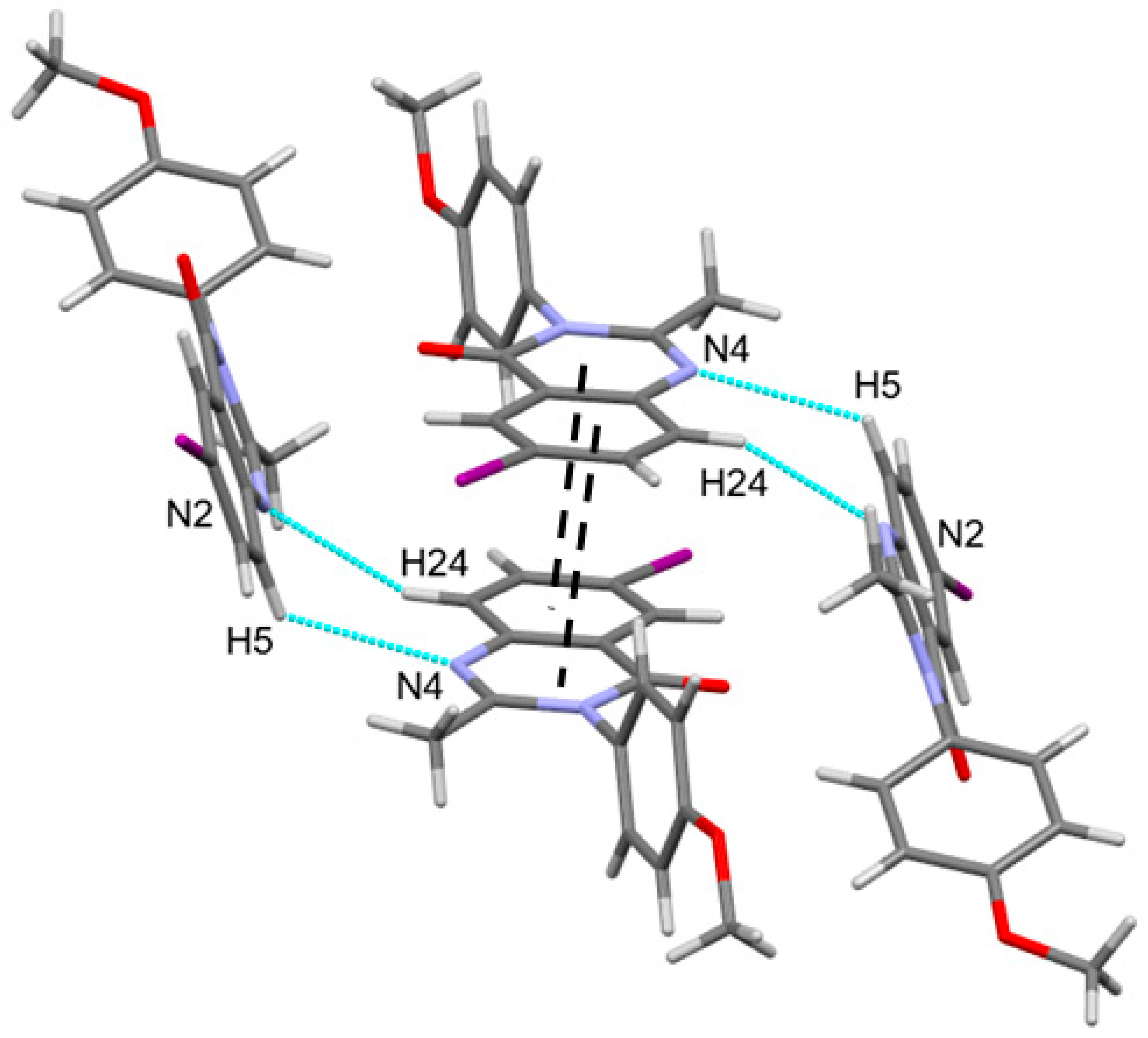
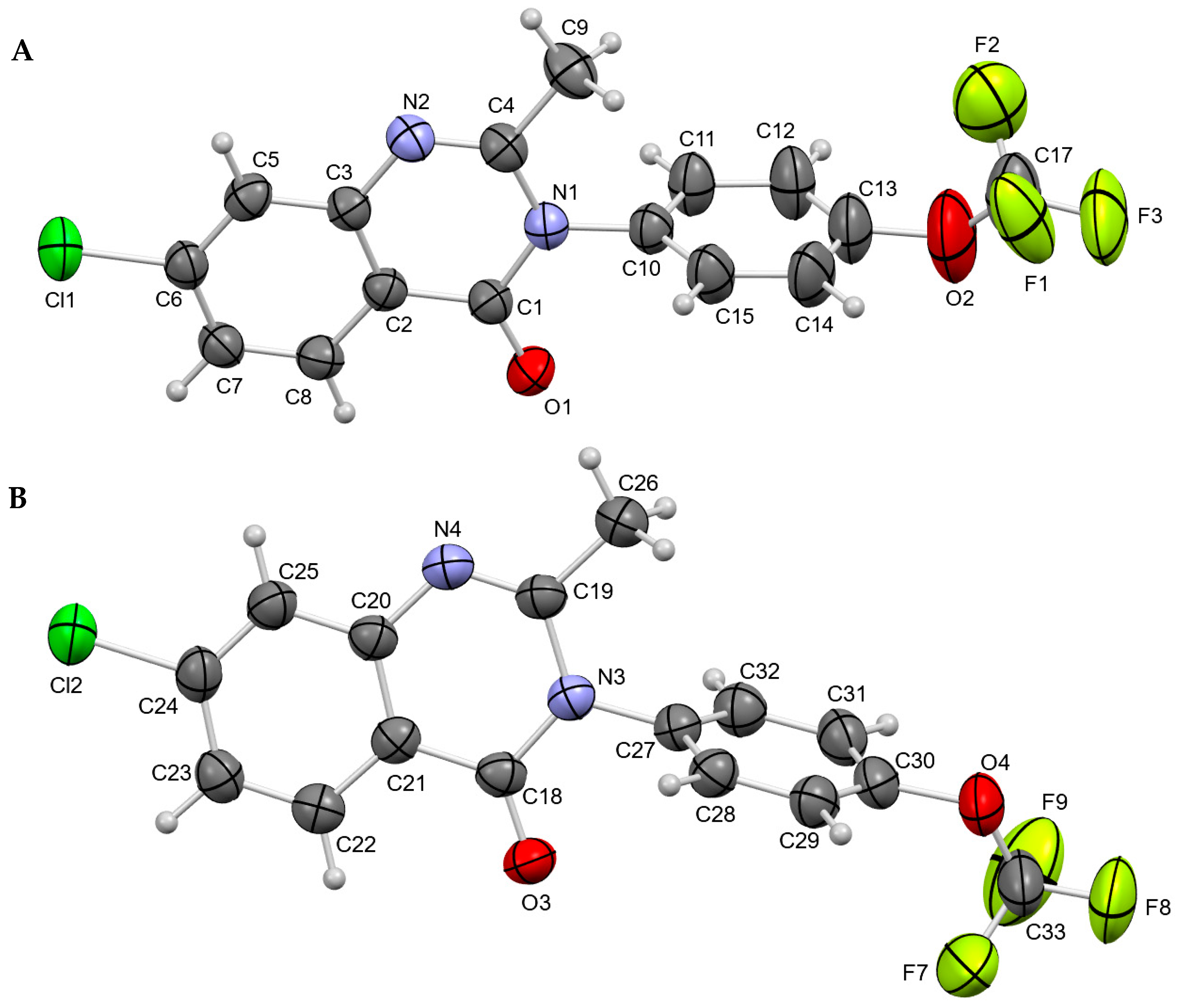
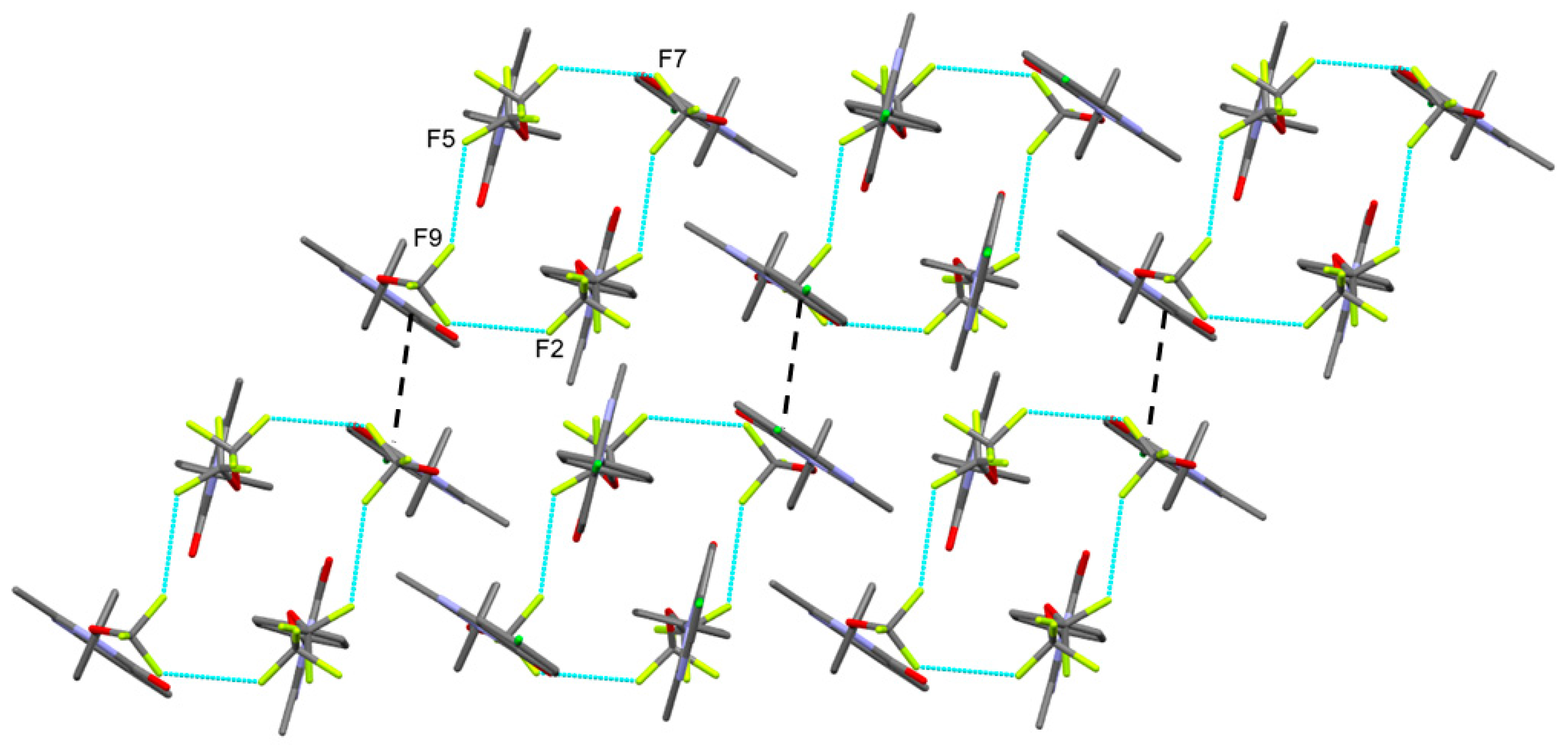
3.1. Crystal Structures
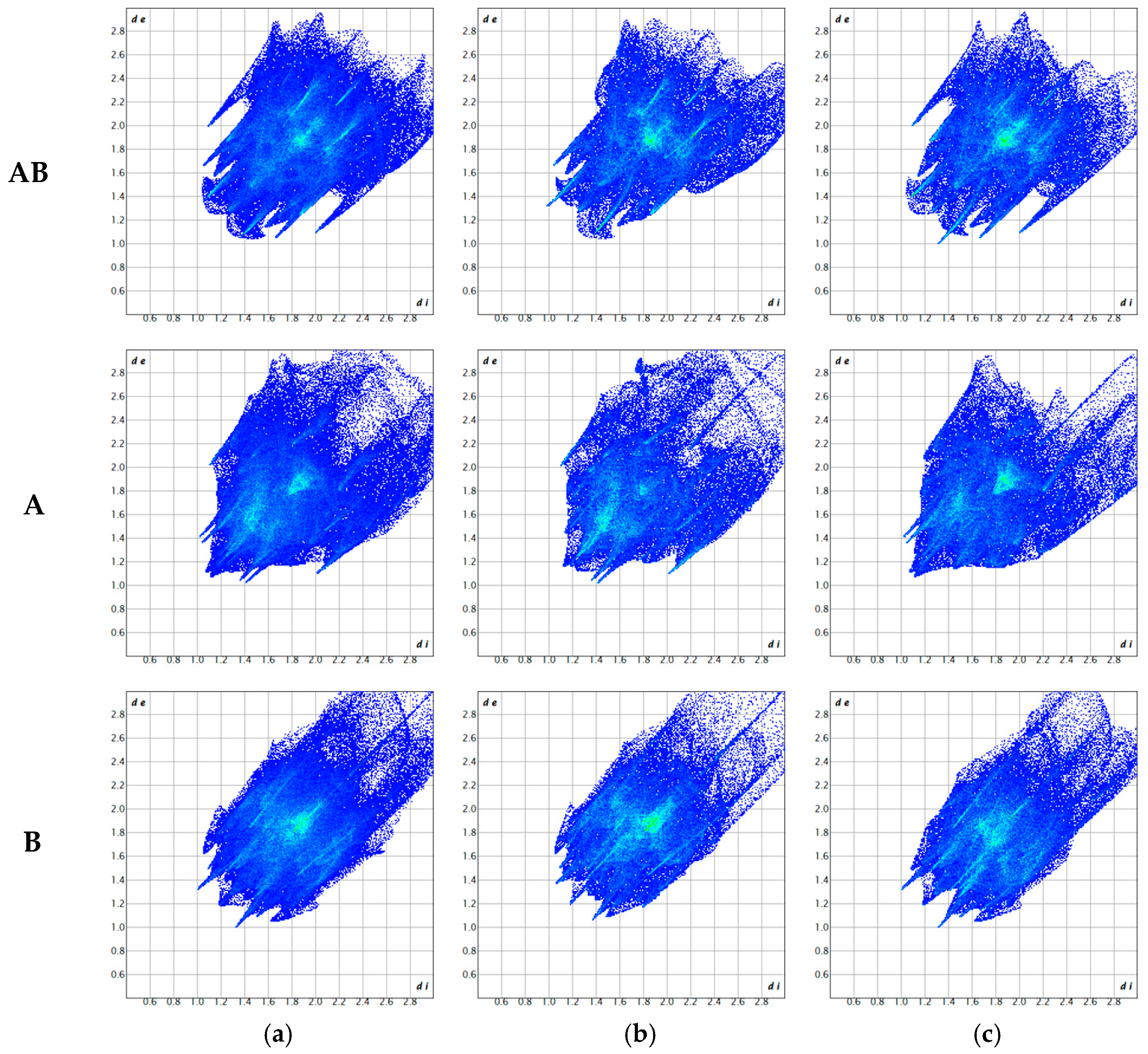
3.2. Hirshfeld Surface Analysis
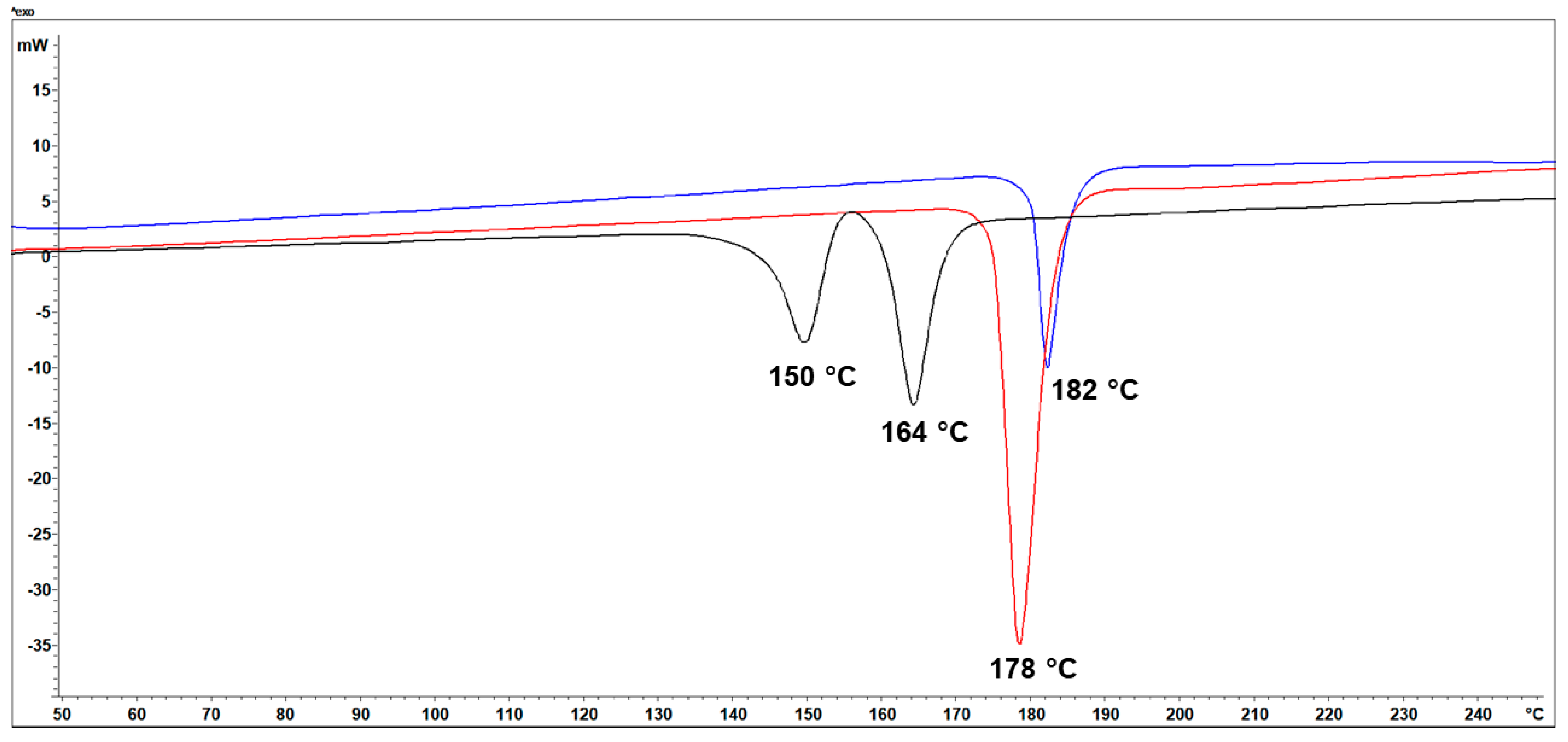
3.3. Thermal Analysis (TG/DSC)
4. Conclusions
Supplementary Materials
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Chu, K.A.; Yalkowsky, S.H. An interesting relationship between drug absorption and melting point. Int. J. Pharm. 2009, 373, 24–40. [Google Scholar] [CrossRef] [PubMed]
- Batisai, E.; Ayamine, A.; Kilinkissa, O.E.Y.; Báthori, N.B. Melting point–solubility–structure correlations in multicomponent crystals containing fumaric or adipic acid. CrystEngComm 2014, 16, 9992–9998. [Google Scholar] [CrossRef]
- Cysewski, P.; Przybyłek, M.; Jeliński, T. Intermolecular interactions as a measure of dapsone solubility in neat solvents and binary solvent mixtures. Materials 2023, 16, 6336. [Google Scholar] [CrossRef] [PubMed]
- Bujak, M.; Podsiadło, M.; Katrusiak, A. Properties and interactions–melting point of tribromobenzene isomers. Acta Crystallogr. Sect. B Struct. Sci. Cryst. Eng. Mater. 2021, B77, 632–637. [Google Scholar] [CrossRef]
- Balić, T.; Paurević, M.; Počkaj, M.; Medvidović-Kosanović, M.; Goman, D.; Széchenyi, A.; Preisz, Z.; Kunsági-Máté, S. Influence of Aliphatic Chain Length on Structural, Thermal and Electrochemical Properties of n-alkylene Benzyl Alcohols: A Study of the Odd–Even Effect. Molecules 2022, 27, 3781. [Google Scholar] [CrossRef]
- Pradeilles, J.A.; Zhong, S.; Baglyas, M.; Tarczay, G.; Butts, C.P.; Myers, E.L.; Aggarwal, V.K. Odd–even alternations in helical propensity of a homologous series of hydrocarbons. Nat. Chem. 2020, 12, 475–480. [Google Scholar] [CrossRef]
- Yalkowsky, S.H.; Alantary, D. Estimation of melting points of organics. J. Pharm. Sci. 2018, 107, 1211–1227. [Google Scholar] [CrossRef] [PubMed]
- Bujak, M. Melting point, molecular symmetry and aggregation of tetrachlorobenzene isomers: The role of halogen bonding. Acta Crystallogr. Sect. B Struct. Sci. Cryst. Eng. Mater. 2018, B74, 458–466. [Google Scholar] [CrossRef]
- Keesom, W.H.; Taconis, K.W. On the crystal structure of chlorine. Physica 1936, 3, 237–242. [Google Scholar] [CrossRef]
- Vonnegut, B.; Warren, B.E. The structure of crystalline bromine. J. Am. Chem. Soc. 1936, 58, 2459–2461. [Google Scholar] [CrossRef]
- Harris, P.M.; Mack, E., Jr.; Blake, F.C. The atomic arrangement in the crystal of orthorhombic iodine. J. Am. Chem. Soc. 1928, 50, 1583–1600. [Google Scholar] [CrossRef]
- Saha, B.K.; Veluthaparambath, R.V.P.; Krishna, G.V. Halogen⋯Halogen Interactions: Nature, Directionality and Applications. Chem. Asian J. 2023, 18, e202300067. [Google Scholar] [CrossRef] [PubMed]
- Ibrahim, M.A.A.; Saeed, R.R.A.; Shehata, M.N.I.; Ahmed, M.N.; Shawky, A.M.; Khowdiary, M.M.; Elkaeed, E.B.; Soliman, M.E.S.; Moussa, N.A.M. Type I–IV halogen⋯halogen interactions: A comparative theoretical study in halobenzene⋯halobenzene homodimers. Int. J. Mol. Sci. 2022, 23, 3114. [Google Scholar] [CrossRef] [PubMed]
- Silva, A.L.; da Silva Filho, D.A.; Moberg, M.E.; Pappenfus, T.M.; Janzen, D.E. Halogen interactions in halogenated oxindoles: Crystallographic and computational investigations of intermolecular interactions. Molecules 2021, 26, 5487. [Google Scholar] [CrossRef]
- Asif, M. The study of pyridazine compounds on prostanoids: Inhibitors of COX, cAMP Phosphodiesterase, and TXA2 Synthase. Int. J. Med. Chem. 2014, 2014, 703238. [Google Scholar]
- Alsibaee, A.M.; Al-Yousef, H.M.; Al-Salem, H.S. Quinazolinones, the winning horse in drug discovery. Molecules 2023, 28, 978. [Google Scholar] [CrossRef] [PubMed]
- Akbari, A.; Zahedifar, M. Synthesis of Quinazolin-4(3H)-ones via a novel approach. J. Saudi Chem. Soc. 2023, 27, 101597. [Google Scholar] [CrossRef]
- Peña-Solórzano, D.; Guilombo, C.E.G.; Ochoa-Puentes, C. Rapid and eco-friendly high yield synthesis of dihydroquinazolinones mediated by urea/zinc chloride eutectic mixture. Sustain. Chem. Pharm. 2019, 14, 100167. [Google Scholar] [CrossRef]
- Terada, S.; Hirai, M.; Honzawa, A.; Kitagawa, O.; Kamizela, A.; Wzorek, A.; Soloshonok, V.A. Possible Case of Halogen Bond-Driven Self-Disproportionation of Enantiomers (SDE) via Achiral Chromatography. Chem.-Eur. J. 2017, 23, 14631–14638. [Google Scholar] [CrossRef] [PubMed]
- Komar, M.; Rastija, V.; Bešlo, D.; Molnar, M. Synthesis of quinazolin-4(3H)-ones in natural deep eutectic solvents: Comparison of various synthetic methods and calculation of ADME properties. J. Mol. Struct. 2024, 1304, 137725. [Google Scholar] [CrossRef]
- STARe Software 10.0; Mettler-Toledo GmbH: Giesen, Germany, 2009.
- Agilent. CrysAlis PRO; Agilent Technologies Ltd.: Yarnton, UK, 2014. [Google Scholar]
- Sheldrick, G.M. SHELXT—Integrated space-group and crystal-structure determination. Acta Crystallogr. Sect. A Found. Adv. 2015, A71, 3–8. [Google Scholar] [CrossRef] [PubMed]
- Sheldrick, G.M. Crystal structure refinement with SHELXL. Acta Crystallogr. Sect. C Struct. Chem. 2015, C71, 3–8. [Google Scholar] [CrossRef] [PubMed]
- Spek, A.L. Structure validation in chemical crystallography. Acta Cryst. 2009, D65, 148–155. [Google Scholar] [CrossRef] [PubMed]
- Macrae, C.F.; Edgington, P.R.; McCabe, P.; Pidcock, E.; Shields, G.P.; Taylor, R.; Towler, M.; van de Streek, J. Mercury: Visualization and analysis of crystal structures. Appl. Cryst. 2006, 39, 453–457. [Google Scholar] [CrossRef]
- Spackman, P.R.; Turner, M.J.; McKinnon, J.J.; Wolff, S.K.; Grimwood, D.J.; Jayatilaka, D.; Spackman, M.A. CrystalExplorer: A program for Hirshfeld surface analysis, visualization and quantitative analysis of molecular crystals. J. Appl. Crystallogr. 2021, 54, 1006–1011. [Google Scholar] [CrossRef]
- Tan, S.L.; Jotani, M.M.; Tiekink, E.R.T. Utilizing Hirshfeld surface calculations, non-covalent interaction (NCI) plots and the calculation of interaction energies in the analysis of molecular packing. Acta Crystallogr. Sect. E Cryst. Commun. 2019, E75, 308–318. [Google Scholar] [CrossRef] [PubMed]
- Balić, T.; Perdih, F.; Počkaj, M.; Molnar, M.; Komar, M.; Balić, I. Polymorphism of coumarin thione-triazole-4-methyl-7-[(4-phenyl-5-thioxo-4,5-dihydro-1H-1,2,4-triazol-3-yl) methoxy]-2H-chromen-2-one. J. Mol. Struct. 2021, 1231, 129957. [Google Scholar] [CrossRef]
- Gilbert, A.S. Molecular symmetry depresses the entropy of fusion of organic molecules with regard to their expected values when comparing structural isomers. Thermochim. Acta 2007, 452, 135–139. [Google Scholar] [CrossRef]
- Groom, C.R.; Bruno, I.J.; Lightfoot, M.P.; Ward, S.C. The Cambridge structural database. Acta Crystallogr. Sect. B Struct. Sci. Cryst. Eng. Mater. 2016, B72, 171–179. [Google Scholar] [CrossRef] [PubMed]
- Snodgrass, H.M.; Mondal, D.; Lewis, J.C. Directed evolution of flavin-dependent halogenases for site-and atroposelective halogenation of 3-aryl-4(3H)-quinazolinones via kinetic or dynamic kinetic resolution. J. Am. Chem. Soc. 2022, 144, 16676–16682. [Google Scholar] [CrossRef] [PubMed]
- Bolte, M. CSD Communications; Cambridge Crystallographic Data Centre: Cambridge, UK, 2019. [Google Scholar]
- Diener, M.E.; Metrano, A.J.; Kusano, S.; Miller, S.J. Enantioselective synthesis of 3-arylquinazolin-4(3H)-ones via peptide-catalyzed atroposelective bromination. J. Am. Chem. Soc. 2015, 137, 12369–12377. [Google Scholar] [CrossRef]
- Xu, L.; Jiang, Y.; Ma, D. Synthesis of 3-substituted and 2,3-disubstituted quinazolinones via Cu-catalyzed aryl amidation. Org. Lett. 2012, 14, 1150–1153. [Google Scholar] [CrossRef]
- Pérez-Ferhmann, M.; Kesternich, V.; Fernández, R.; Verdugo, F.; Brito, I.; Cárdenas, A.; Bolte, M. Crystal structure of 3-(4-methoxy-2-nitrophenyl)-2-methylquinazolin-4(3H)-one, C16H13N3O4. Z. Krist.-New Cryst. Struct. 2014, 229, 415–416. [Google Scholar] [CrossRef]
- El-Azab, A.S.; Abdel-Aziz, A.A.-M.; Ng, S.W.; Tiekink, E.R.T. 2-Methyl-3-(2-methylphenyl)-7-nitroquinazolin-4(3H)-one. Acta Crystallogr. Sect. E Struct. Rep. Online 2012, E68, o863. [Google Scholar] [CrossRef]
- Riwar, L.; Trapp, N.; Kuhn, B.; Diederich, F. Substituent Effects in Parallel-Displaced π–π Stacking Interactions: Distance Matters. Angew. Chem. Int. Ed. 2017, 56, 11252–11257. [Google Scholar] [CrossRef] [PubMed]
- Kudale, V.S.; Wang, J.-J. Metal-free C–H methylation and acetylation of heteroarenes with PEG-400. Green Chem. 2020, 22, 3506–3511. [Google Scholar] [CrossRef]
- Ramanathan, M.; Hsu, M.-T.; Liu, S.-T. Preparation of 4(3H)-quinazolinones from aryldiazonium salt, nitriles and 2-aminobenzoate via a cascade annulation. Tetrahedron 2019, 75, 791–796. [Google Scholar] [CrossRef]
- Hirai, M.; Terada, S.; Yoshida, H.; Ebine, K.; Hirata, T.; Kitagawa, O. Catalytic enantioselective synthesis of N–C axially chiral mebroqualone and its derivatives through reductive asymmetric desymmetrization. Org. Lett. 2016, 18, 5700–5703. [Google Scholar] [CrossRef] [PubMed]
- Imai, T.; Niijima, E.; Terada, S.; Wzorek, A.; Soloshonok, V.A.; Hori, A.; Kitagawa, O. Chirality-dependent halogen bonds in axially chiral quinazolin-4-one derivatives bearing ortho-halophenyl groups. CrystEngComm 2019, 21, 3385–3389. [Google Scholar] [CrossRef]
- Komar, M.; Molnar, M.; Konjarević, A. Screening of Natural Deep Eutectic Solvents for Green Synthesis of 2-methyl-3-substituted Quinazolinones and Microwave-Assisted Synthesis of 3-aryl Quinazolinones in Ethanol. Croat. Chem. Acta 2020, 92, 511–517. [Google Scholar] [CrossRef]
- Bouley, R.; Ding, D.; Peng, Z.; Bastian, M.; Lastochkin, E.; Song, W.; Suckow, M.A.; Schroeder, V.A.; Wolter, W.R.; Mobashery, S.; et al. Structure–activity relationship for the 4(3H)-Quinazolinone antibacterials. J. Med. Chem. 2016, 59, 5011–5021. [Google Scholar] [CrossRef] [PubMed]
- Peyressatre, M.; Arama, D.P.; Laure, A.; González-Vera, J.A.; Pellerano, M.; Masurier, N.; Lisowski, V.; Morris, M.C. Identification of quinazolinone analogs targeting CDK5 kinase activity and glioblastoma cell proliferation. Front. Chem. 2020, 8, 691. [Google Scholar] [CrossRef] [PubMed]
- Kumar, D.; Jadhavar, P.S.; Nautiyal, M.; Sharma, H.; Meena, P.K.; Adane, L.; Pancholia, S.; Chakraborti, A.K. Convenient synthesis of 2,3-disubstituted quinazolin-4(3H)-ones and 2-styryl-3-substituted quinazolin-4(3H)-ones: Applications towards the synthesis of drugs. RSC Adv. 2015, 5, 30819–30825. [Google Scholar] [CrossRef]
- Wolfe, J.F.; Rathman, T.L.; Sleevi, M.C.; Campbell, J.A.; Greenwood, T.D. Synthesis and anticonvulsant activity of some new 2-substituted 3-aryl-4 (3H)-quinazolinones. J. Med. Chem. 1990, 33, 161–166. [Google Scholar] [CrossRef] [PubMed]
- Kumar, P.; Singh, P.; Mishra, A.; Singh, J.; Kumar, A. Synthesis and Biological Activities of Some Indolyl Substituted Pyrazolines. Asian J. Chem. 2010, 20, 6056–6066. [Google Scholar]
- Sharma, P.; Sharma, M.; Rangaswami, S.; Sharma, P.; Sharma, M.; Rangaswami, S.; Sharma, B. Indian Journal of Chemistry, Section B: Organic Chemistry Including Medicinal Chemistry; Council of Scientific & Industrial Research: New Delhi, India, 1979; Volume 17, pp. 443–448. [Google Scholar]
- Rajput, C.S.; Kumar, A.; Bhati, S.K.; Singh, J. Synthesis and Antiinflammatory Activity of 2-[5′-(4-Pyridinyl)-1′,2′,3′-oxadiazol-2-ylthiomethyl]-3-substituted-aryl-6-substituted-quinazolin-4-ones. Asian J. Chem. 2010, 20, 6246–6252. [Google Scholar]
- Ammar, Y.A. Some Reactions with 6-Chloro-2-Methyl 3,1-Benzoxazin-4-One. Orient. J. Chem. 1990, 6, 3. [Google Scholar]






| Compound | 1 | 2 | 3 |
|---|---|---|---|
| CCDC No. | 2410138 | 2410139 | 2410140 |
| Empirical formula | C15H10ClIN2O | C16H13IN2O2 | C16H10ClF3N2O2 |
| Formula weight | 396.60 | 392.198 | 354.71 |
| Temperature/K | 170 | 170 | 170 |
| Crystal system | monoclinic | triclinic | monoclinic |
| Space group | P21/n | P − 1 | C2/c |
| a/Å | 16.08889(17) | 11.3798(4) | 12.0167(4) |
| b/Å | 7.11883(9) | 11.7894(5) | 34.6361(9) |
| c/Å | 26.3180(3) | 12.9902(4) | 15.4003(6) |
| α/° | 90 | 106.081(3) | 90 |
| β/° | 96.4521(10) | 98.102(3) | 93.146(4) |
| γ/° | 90 | 110.848(4) | 90 |
| Volume/Å3 | 2995.21(6) | 1508.25(12) | 6400.1(4) |
| Z | 8 | 4 | 16 |
| ρcalc/g cm−3 | 1.759 | 1.727 | 1.472 |
| μ/mm−1 | 18.415 | 16.738 | 2.533 |
| F(000) | 1536.0 | 771.0 | 2880.0 |
| Crystal size/mm3 | 0.3 × 0.1 × 0.05 | 0.2 × 0.1 × 0.04 | 0.4 × 0.2 × 0.08 |
| Radiation | CuKα (λ = 1.54184) | Cu Kα (λ = 1.54184) | Cu Kα (λ = 1.54184) |
| 2θ range for data collection/° | 6.148 to 159.672 | 8.58 to 161.06 | 7.688 to 131.982 |
| Data ranges | −20 ≤ h ≤ 19, −9 ≤ k ≤ 8, −32 ≤ l ≤ 33 | −13 ≤ h ≤ 14, −15 ≤ k ≤ 14, −16 ≤ l ≤ 12 | −12 ≤ h ≤ 14, −37 ≤ k ≤ 40, −18 ≤ l ≤ 18 |
| Reflections collected | 25894 | 17771 | 22148 |
| Independent reflections | 6385 [Rint = 0.0439, Rsigma = 0.0356] | 6186 [Rint = 0.0701, Rsigma = 0.0575] | 5496 [Rint = 0.0654, Rsigma = 0.0567] |
| Dana/restraints/parameters | 6385/0/364 | 6186/0/384 | 5496/535/472 |
| Goodness-of-fit on F2 | 1.039 | 0.961 | 1.039 |
| Final R indexes [I ≥ 2σ (I)] | R1 = 0.0516, wR2 = 0.1516 | R1 = 0.0517, wR2 = 0.1156 | R1 = 0.0705, wR2 = 0.2012 |
| Final R indexes [all data] | R1 = 0.0566, wR2 = 0.1563 | R1 = 0.0761, wR2 = 0.1490 | R1 = 0.1066, wR2 = 0.2309 |
| Largest diff. peak/hole/e Å−3 | 1.25/−0.85 | 1.28/−1.32 | 0.45/−0.28 |
| 1 | |||||
| D–H∙∙∙A | d(D–H)/Å | d(H···A)/Å | d(D···A)/Å | ∠ (D–H···A)/° | Symmetry code |
| C11–H11···O2 | 0.93 | 2.44 | 3.327(7) | 156 | x, −1 + y, z |
| C15–H15···O2 | 0.93 | 2.53 | 3.371(7) | 148 | x, −1 + y, z |
| C24–H24B···O1 | 0.93 | 2.57 | 3.455(6) | 150 | 1/2 − x, 1/2 + y, 1/2 − z |
| X···X contacts | d(D–X) | d(X–X) | θ1/° | θ2/° | |
| C29–Cl2···Cl2–C29 | 1.746(5) | 3.394(3) | 83.99 | 83.99 | 1 − x, 2 − y, 1 − z |
| C7–I1···Cl2–C29 | 2.098(5) 1.746(5) | 3.720(2) | 164.43 | 79.06 | 3/2 − x, −1/2 + y, 1/2 − z |
| π···π contacts | Cg···Cg/Å | α/° | β/° | Cg···plane/Å | |
| Cg2(C10→C15) ··Cg6(C25→C30) | 3.768(3) | 3.6(2) | 17.4 | 3.5202(18) | x, −1 + y, z |
| 2 | |||||
| D–H∙∙∙A | d(D–H)/Å | d(H···A)/Å | d(D···A)/Å | ∠(D–H···A)/° | Symmetry code |
| C24–H24···N2 | 0.950(11) | 2.552(10) | 3.432(10) | 154.2(9) | 1 − x, −y, 1 − z |
| C25–H25B···O1 | 0.98(4) | 2.51(3) | 3.449(10) | 161(3) | 1 − x, 1 − y, 1 − z |
| π···π contacts | Cg···Cg/Å | α/° | β/° | Cg···plane/Å | |
| Cg5(C18→C21) ··Cg6(C18→C30) | 3.778(4) | 2.8(4) | 20.3 | 3.602(3) | 1 − x, −y, 1 − z |
| Cg6(C26→C31) ··Cg6(C26→C31) | 3.781(5) | 0.0(4) | 20.4 | 3.545(3) | 1 − x, −y, 1 − z |
| 3 | |||||
| D–H∙∙∙A | d(D–H)/Å | d(H···A)/Å | d(D···A)/Å | ∠(D–H···A)/° | Symmetry code |
| C9–H9C···O3 | 0.98 | 2.56 | 3.290(5) | 131 | 1 − x, y, 3/2 − z |
| C11–H11···O1 | 0.95 | 2.55 | 3.361(5) | 144 | 1 − x, y, 3/2 − z |
| C28–H28···O3 | 0.95 | 2.44 | 3.320(4) | 154 | 2 − x, y, 3/2 − z |
| Y–X···π contacts | X···Cg/Å | Y···Cg/Å | γ/° | ∠(Y–X···Cg)/° | |
| C16–F5···Cg6(C27→C32) | 3.424(14) | 4.511(16) | 19.09 | 139.5(10) | −1/2 + x, 1/2 − y, 1/2 + z |
| X···X contacts | d(D–X)/Å | d(X–X)/Å | θ1/° | θ2/° | |
| C17–F2···F7–C33 | 1.305(17) 1.289(8) | 2.732(12) | 128.1(8) | 131.2(6) | x, y, z |
| C16–F5···F9–C33 | 1.32(2) 1.330(11) | 2.818(16) | 134.6(7) | 147.3(7) | 1−x, y, 3/2−z |
| π···π contacts | Cg···Cg/Å | α/° | β/° | Cg···plane/Å | |
| Cg5(C20→C25) ··Cg5(C20→C25) | 3.638(2) | 1.73(17) | 21.0 | 3.3956(15) | 2 − x, y, 3/2 − z |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Đilović, I.; Judaš, N.; Komar, M.; Molnar, M.; Počkaj, M.; Balić, T. Impact of Molecular and Crystal Structure on the Melting Points in Halo-Substituted Phenyl-Quinazolinones. Crystals 2025, 15, 39. https://doi.org/10.3390/cryst15010039
Đilović I, Judaš N, Komar M, Molnar M, Počkaj M, Balić T. Impact of Molecular and Crystal Structure on the Melting Points in Halo-Substituted Phenyl-Quinazolinones. Crystals. 2025; 15(1):39. https://doi.org/10.3390/cryst15010039
Chicago/Turabian StyleĐilović, Ivica, Nenad Judaš, Mario Komar, Maja Molnar, Marta Počkaj, and Tomislav Balić. 2025. "Impact of Molecular and Crystal Structure on the Melting Points in Halo-Substituted Phenyl-Quinazolinones" Crystals 15, no. 1: 39. https://doi.org/10.3390/cryst15010039
APA StyleĐilović, I., Judaš, N., Komar, M., Molnar, M., Počkaj, M., & Balić, T. (2025). Impact of Molecular and Crystal Structure on the Melting Points in Halo-Substituted Phenyl-Quinazolinones. Crystals, 15(1), 39. https://doi.org/10.3390/cryst15010039








