The Effect of Gradient Cooling Behavior on the Microstructure and Mechanical Properties of Al-2at.% Nd Alloy in a Vacuum Environment
Abstract
1. Introduction
2. Experimental Methods
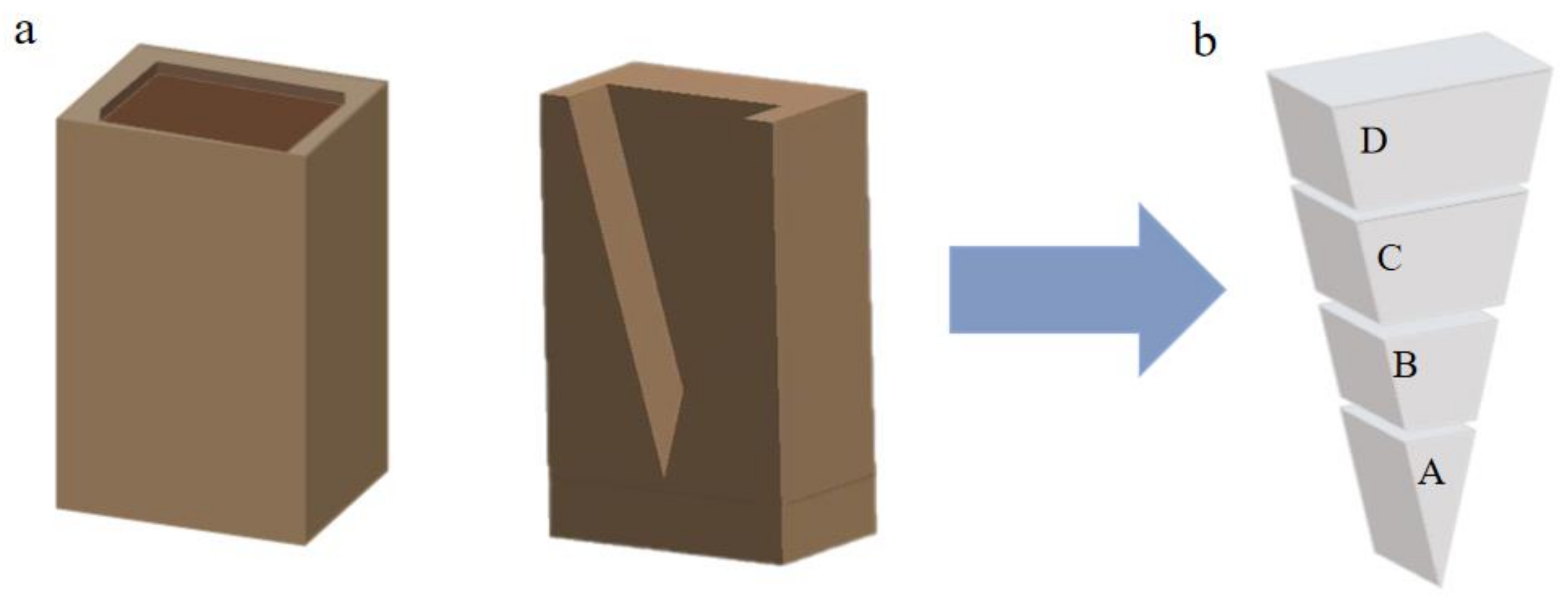
2.1. Sample Preparation
2.2. First-Principles Calculations
3. Results and Discussion
3.1. The Influence of Gradient Cooling Behavior on the Microstructure of Al-2at.% Nd Alloy
3.2. The Effect of Gradient Cooling Behavior on the Properties of Al-2at.% Nd Alloy
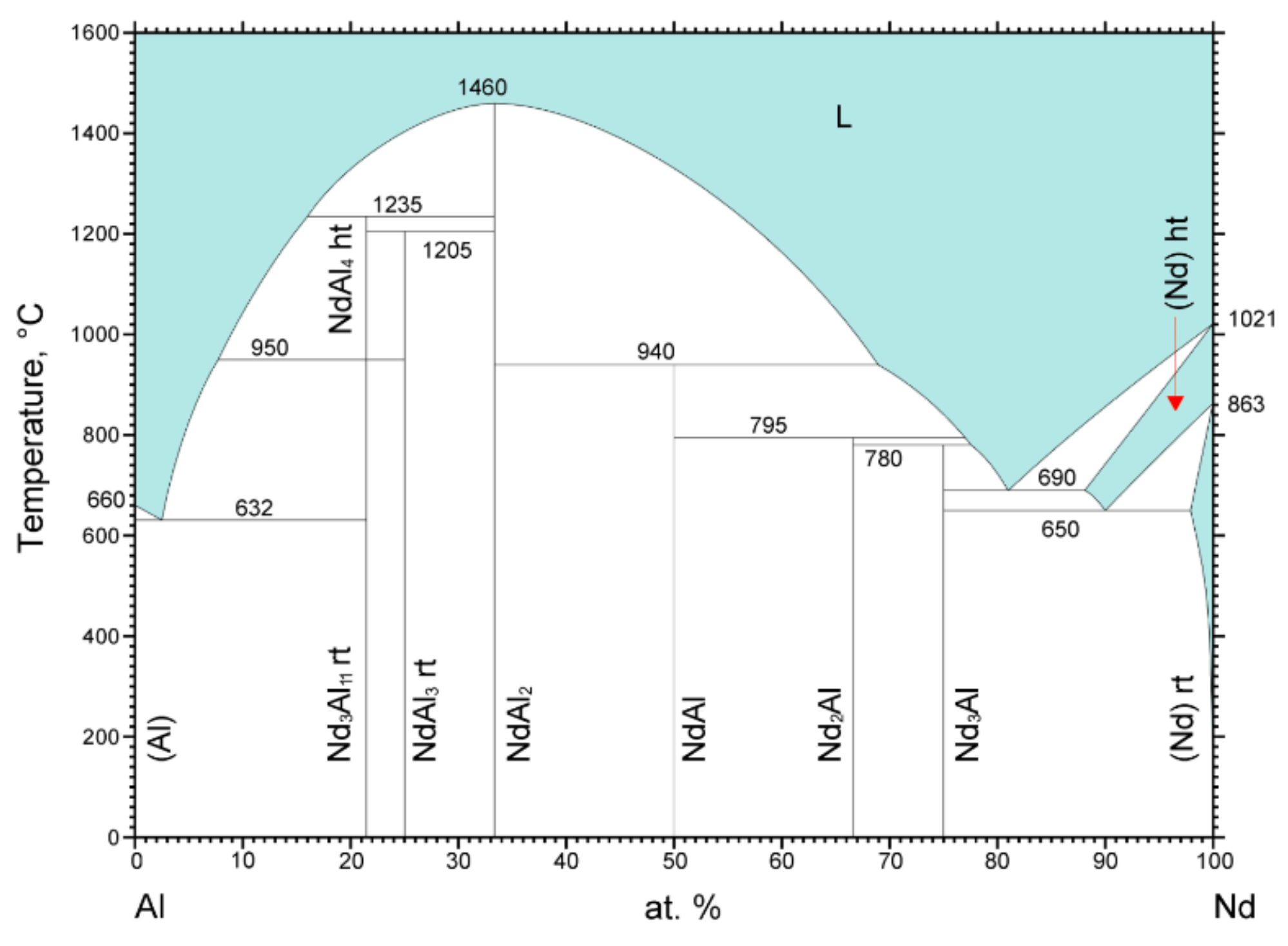
3.3. Crystal Structure and Phase Stability
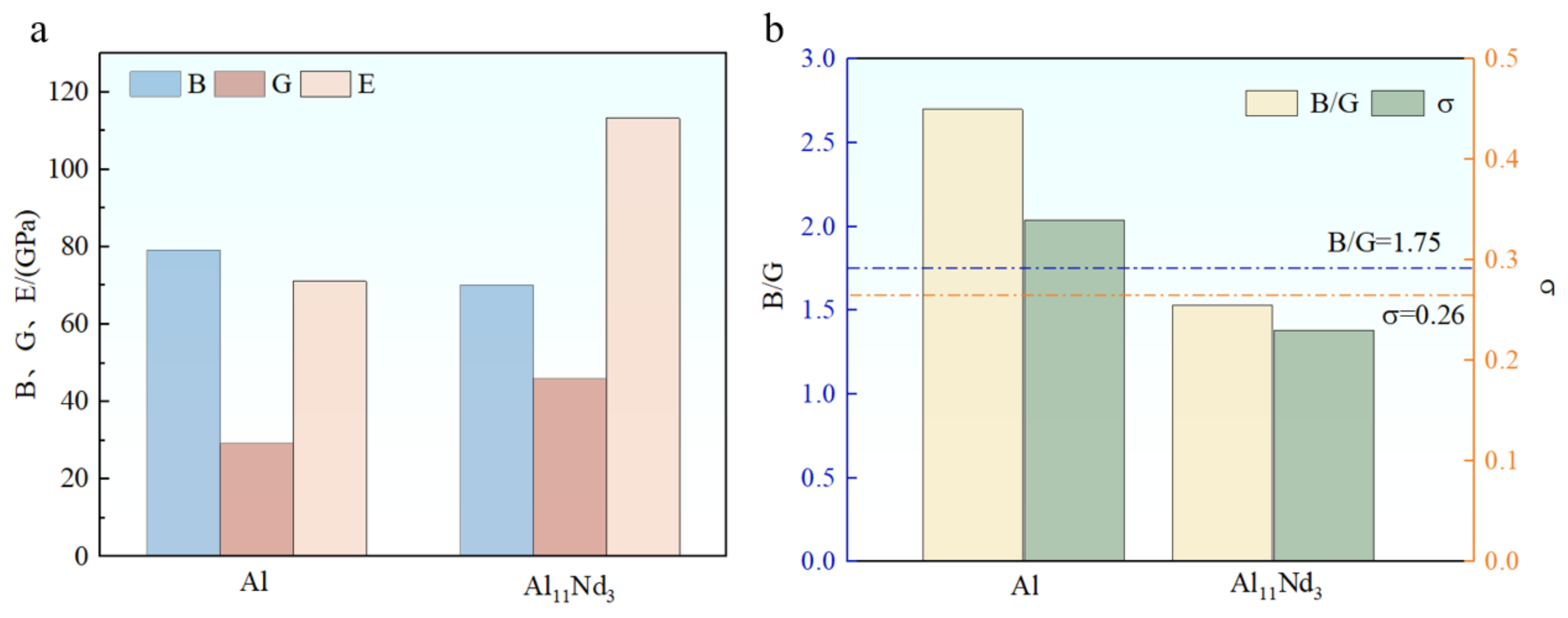
3.4. Mechanical Properties
4. Conclusions
- Under varying cooling rates, the microstructure of the Al-2at.% Nd alloy displays distinct morphologies. The large grain morphology near the mold wall shows columnar crystals. Conversely, at the center of the ingot, a reduction in the cooling rate leads to a transition in grain morphology from a mixed structure of columnar and equiaxed grains to a predominantly equiaxed grain structure.
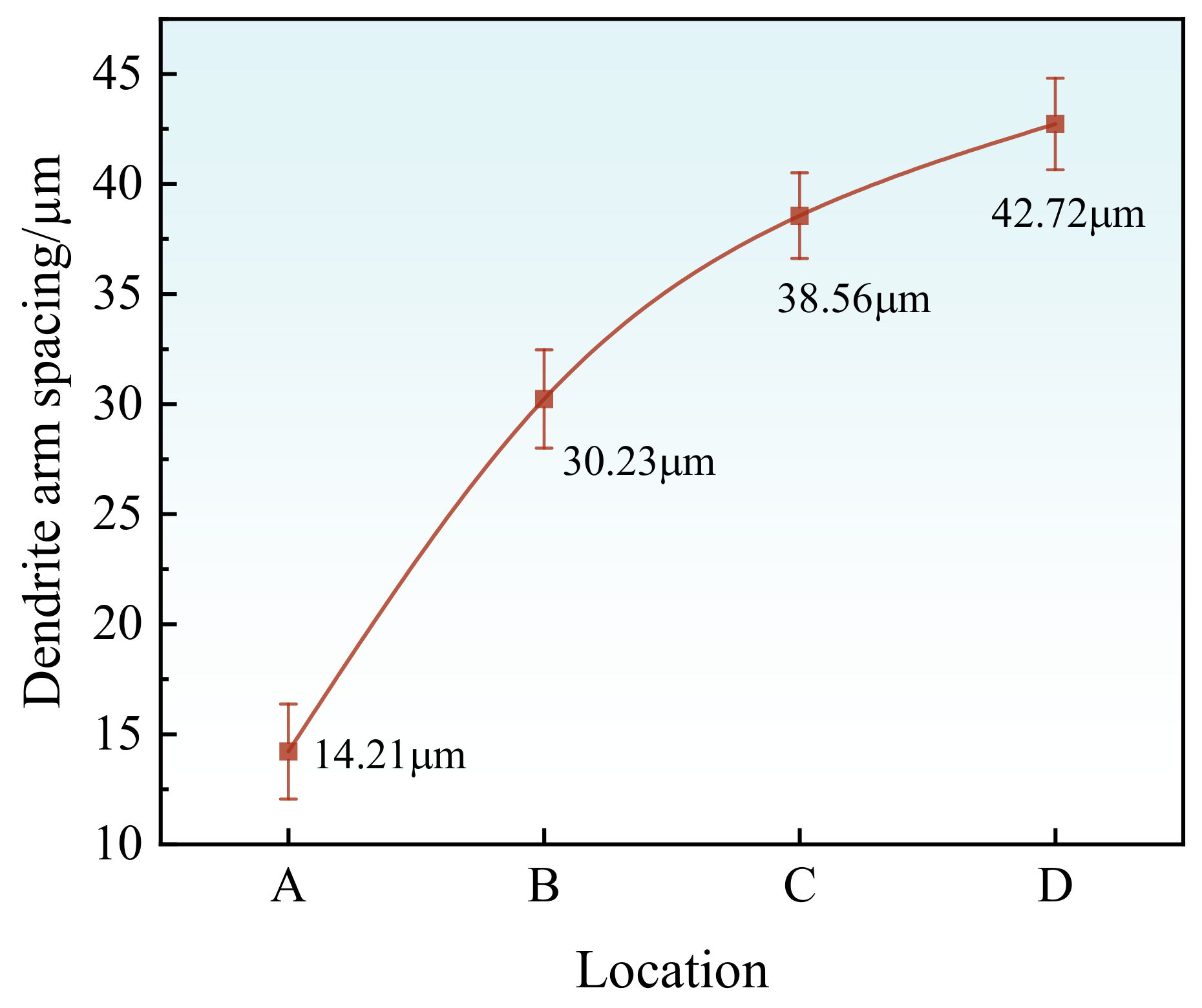
- As the cooling rate diminishes, there is a corresponding increase in grain size, which ranges from 523.28 μm to 743.57 μm. Additionally, the spacing between secondary dendrite arms expands from 14.21 μm to 42.72 μm.
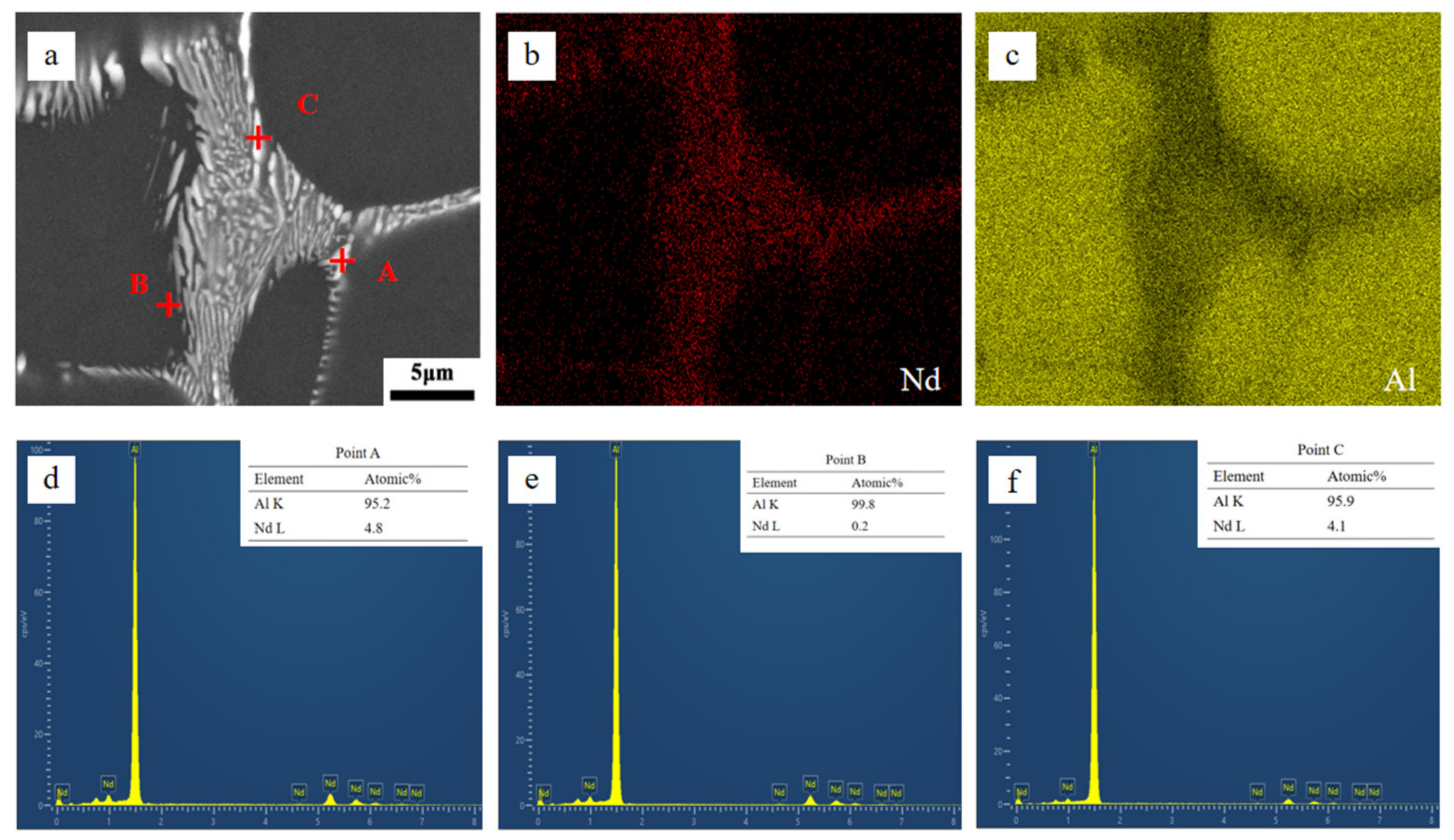
- At higher cooling rates, the morphology of the Al11Nd3 phase is characterized as skeletal and embedded within the aluminum matrix. The eutectic phase of the alloy comprises α-Al and Al11Nd3. The hardness of the Al-2at.% Nd alloy decreases with a decreasing cooling rate and increases by 25.53% with an increasing cooling rate.
- According to first-principles calculations, the Al-Nd binary intermetallic compound’s formation enthalpy is negative, indicating that Al11Nd3 is thermodynamically stable. The Poisson’s ratio of Al11Nd3 is measured at 0.23, and the B/G value is calculated to be 1.53, suggesting that the compound exhibits intrinsic brittleness in its ground state.
Author Contributions
Funding
Institutional Review Board Statement
Data Availability Statement
Conflicts of Interest
References
- Chaudhary, B.; Jain, N.K.; Murugesan, J. Development of friction stir powder deposition process for repairing of aerospace-grade aluminum alloys. CIRP J. Manuf. Sci. Technol. 2022, 38, 252–267. [Google Scholar] [CrossRef]
- Xu, Z.; Liu, C.; Zhang, B.; Huang, H.; Cheng, W. Effects of base metal state on the microstructure and mechanical properties of Al–Mg–Si alloy friction stir-welded joints. J. Manuf. Process. 2020, 56, 248–257. [Google Scholar] [CrossRef]
- Mo, Y.F.; Liu, C.Y.; Teng, G.B.; Jiang, H.J.; Chen, Y.; Yang, Z.X.; Han, S.C. Fabrication of 7075-0.25Sc-0.15Zr Alloy with Excellent Damping and Mechanical Properties by FSP and T6 Treatment. J. Mater. Eng. Perform. 2018, 27, 4162–4167. [Google Scholar] [CrossRef]
- Berry, L.; Wheatley, G.; Ma, W.; Nejad, R.M.; Berto, F. The influence of milling induced residual stress on fatigue life of aluminum alloys. Forces Mech. 2022, 7, 100096. [Google Scholar] [CrossRef]
- Chen, B.; Zhang, C.; Jin, Y. First-principles calculation of interface binding strength and fracture performance of β’/Al interface in Al–Mg–Si–Cu alloy. J. Alloys Compd. 2020, 830, 154515. [Google Scholar] [CrossRef]
- Yin, Q.; Chen, G.; Shu, X.; Zhang, B.; Li, C.; Dong, Z.; Cao, J.; An, R.; Huang, Y. Analysis of interaction between dislocation and interface of aluminum matrix/second phase from electronic behavior. J. Mater. Sci. Technol. 2023, 136, 78–90. [Google Scholar] [CrossRef]
- Huang, J.; Li, M.; Liu, Y.; Chen, J.; Lai, Z.; Hu, J.; Zhou, F.; Zhu, J. A first-principles study on the doping stability and micromechanical properties of alloying atoms in aluminum matrix. Vacuum 2023, 207, 111596. [Google Scholar] [CrossRef]
- Lu, Z.; Li, X.; Zhang, L. Thermodynamic Description of Al-Si-Mg-Ce Quaternary System in Al-Rich Corner and Its Experimental Validation. J. Phase Equilibria Diffus. 2018, 39, 57–67. [Google Scholar] [CrossRef]
- He, Y.; Liu, J.; Qiu, S.; Deng, Z.; Zhang, J.; Shen, Y. Microstructure evolution and mechanical properties of Al-La alloys with varying La contents. Mater. Sci. Eng. A 2017, 701, 134–142. [Google Scholar] [CrossRef]
- Huang, X.; Yan, H. Effect of trace La addition on the microstructure and mechanical property of as-cast ADC12 Al-Alloy. J. Wuhan Univ. Technol. Mater. 2013, 28, 202–205. [Google Scholar] [CrossRef]
- Pan, F.; Yang, M.; Chen, X. A Review on Casting Magnesium Alloys: Modification of Commercial Alloys and Development of New Alloys. J. Mater. Sci. Technol. 2016, 32, 1211–1221. [Google Scholar] [CrossRef]
- Ding, W.; Zhao, X.; Chen, T.; Zhang, H.; Liu, X.; Cheng, Y.; Lei, D. Effect of rare earth Y and Al–Ti–B master alloy on the microstructure and mechanical properties of 6063 aluminum alloy. J. Alloys Compd. 2020, 830, 154685. [Google Scholar] [CrossRef]
- Sarkar, J.; Saimoto, S.; Mathew, B.; Gilman, P. Microstructure, texture and tensile properties of aluminum2at.% neodymium alloy as used in flat panel displays. J. Alloys Compd. 2009, 479, 719–725. [Google Scholar] [CrossRef]
- Zhu, S.; Gibson, M.; Nie, J.; Easton, M.; Abbott, T. Microstructural analysis of the creep resistance of die-cast Mg-4Al-2RE alloy. Scr. Mater. 2008, 58, 477–480. [Google Scholar] [CrossRef]
- Xiao, Y.D.; Li, W.X.; Ma, Z.Q. Crystallization process in rapidly solidified Al-Nd-Ni amorphous alloy prepared by melt spinning. Trans. Nonferrous Met. Soc. China 2004, 14, 665–669. [Google Scholar]
- Liu, T.; Ma, T.; Li, Y.; Ren, Y.; Liu, W. Stabilities, mechanical and thermodynamic properties of Al–RE intermetallics: A first-principles study. J. Rare Earths 2022, 40, 345–352. [Google Scholar] [CrossRef]
- Liu, S.; Esteban-Manzanares, G.; LLorca, J. First Principles Prediction of the Al-Li Phase Diagram. Metall. Mater. Trans. A 2021, 52, 4675–4690. [Google Scholar] [CrossRef]
- Guo, Y.; Wang, W.; Huang, H.; Zhao, H.; Jing, Y.; Yi, G.; Luo, L.; Liu, Y. Effect of doping Zn atom on the structural stability, mechanical and thermodynamic properties of AlLi phase in Mg–Li alloys from first-principles calculations. Philos. Mag. 2020, 100, 1849–1867. [Google Scholar] [CrossRef]
- Gao, M.; Deng, Y.; Wen, D.; Zhao, H. A first-principles study on the site occupancy behavior of transition metals in L12-Al3Li phase. Mater. Res. Express 2020, 7, 046519. [Google Scholar] [CrossRef]
- Gao, M.C.; Rollett, A.D.; Widom, M. Lattice stability of aluminum-rare earth binary systems: A first-principles approach. Phys. Rev. B 2007, 75, 174120. [Google Scholar] [CrossRef]
- Jahnátek, M.; Krajcí, M.; Hafner, J. Response of trialuminides to [110] uniaxial loading: An ab initio study for Al3(Sc, Ti, V). Phys. Rev. B 2007, 76, 014110. [Google Scholar] [CrossRef]
- Joubert, D.; Kresse, G. From ultrasoft pseudopotentials to the projector augmented-wave method. Phys. Rev. B 1999, 59, 1758–1775. [Google Scholar]
- Burke, K.; Ernzerhof, M.; Perdew, J.P. Generalized Gradient Approximation Made Simple. Phys. Rev. Lett. 1997, 78, 1396. [Google Scholar]
- Xue, B.; Xiao, W.; Li, X.; Gao, G.; Li, X.; Zhang, Y.; Wang, L.; Xiong, B. Comprehensive investigation on the structural, electronic and mechanical properties of T-Mg32(Al, Zn)49 phases in Al-Mg-Zn alloys. J. Mater. Sci. Technol. 2024, 173, 237–246. [Google Scholar] [CrossRef]
- Lin, L.; Wang, F.; Yang, L.; Chen, L.; Liu, Z.; Wang, Y. Microstructure investigation and first-principle analysis of die-cast AZ91 alloy with calcium addition. Mater. Sci. Eng. A 2011, 528, 5283–5288. [Google Scholar] [CrossRef]
- Fung, Y.C.; Drucker, D.C. Foundation of Solid Mechanics. J. Appl. Mech. 1966, 33, 238. [Google Scholar] [CrossRef]
- Yao, X.; Wang, H.; He, B.; Zhou, X. Modeling of Columnar-to-Equiaxed Transition in Solidified Al-Si Alloys. Mater. Sci. Forum 2005, 475–479, 3141–3144. [Google Scholar] [CrossRef]
- Okamoto, H. Al-Nd (Aluminum-Neodymium). J. Phase Equilib. 2000, 21, 206. [Google Scholar] [CrossRef]
- Yang, Q.; Shi, W.; Wang, M.; Jia, L.; Wang, W.; Zhang, H. Influence of cooling rate on the microstructure and mechanical properties of Al–Cu–Li–Mg–Zn alloy. J. Mater. Res. Technol. 2023, 25, 3151–3166. [Google Scholar] [CrossRef]
- Ahmad, S.; Ahmad, R.; Jalali-Asadabadi, S.; Ali, Z.; Ahmad, I. First principle studies of structural, magnetic and elastic properties of orthorhombic rare-earth diaurides intermetallics RAu2 (R=La, Ce, Pr and Eu). Mater. Chem. Phys. 2018, 212, 44–50. [Google Scholar] [CrossRef]
- Boucetta, S. Structural and elastic properties of Mg3CuH0.6 ternary hydride by ab initio study. J. Magnes. Alloys 2018, 6, 90–94. [Google Scholar] [CrossRef]
- Liu, Y.; Hu, W.-C.; Li, D.-J.; Li, K.; Jin, H.-L.; Xu, Y.-X.; Xu, C.-S.; Zeng, X.-Q. Mechanical, electronic and thermodynamic properties of C14-type AMg2 (A=Ca, Sr and Ba) compounds from first principles calculations. Comput. Mater. Sci. 2015, 97, 75–85. [Google Scholar] [CrossRef]
- Abraham, J.A.; Pagare, G.; Chouhan, S.S.; Sanyal, S.P. Theoretical calculations of structural, electronic, optical, elastic, and thermal properties of YX3 (X = In, Sn, Tl, and Pb)compounds based on density functional theory. J. Mater. Sci. 2015, 50, 542–554. [Google Scholar] [CrossRef]





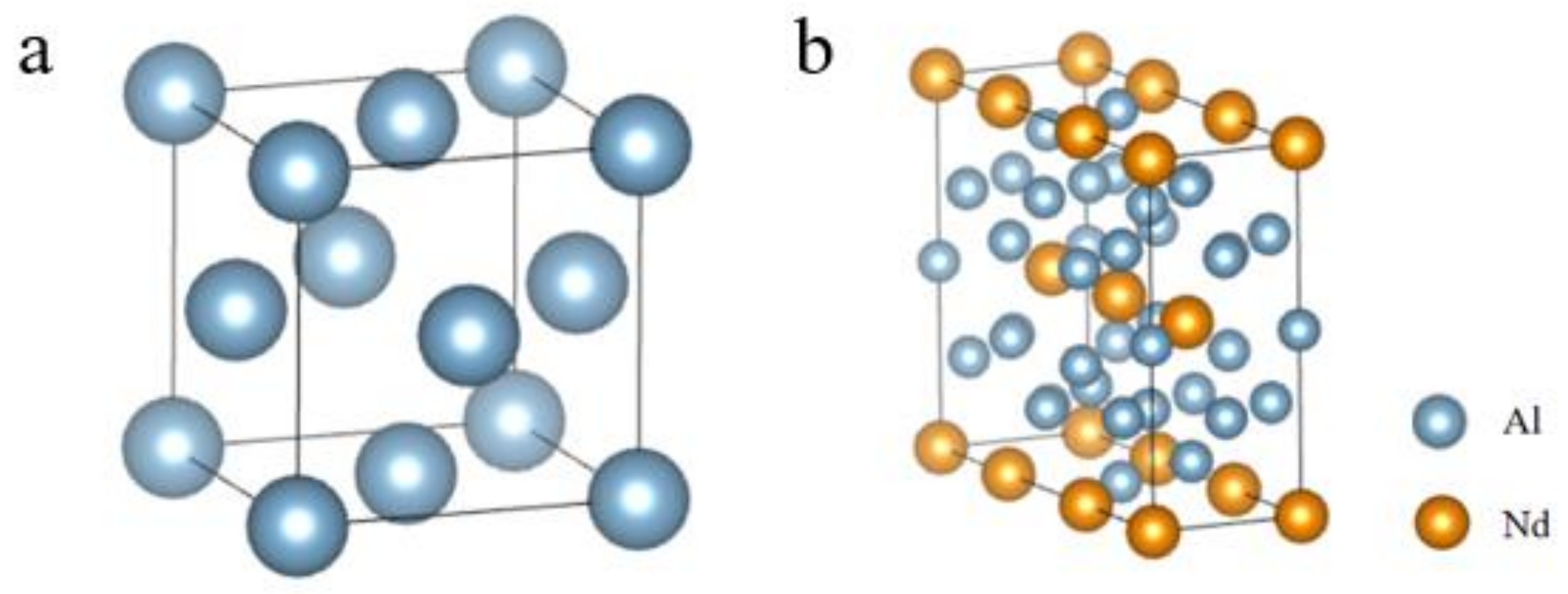
| Compounds | a | b | c | α | β | γ | ΔH |
|---|---|---|---|---|---|---|---|
| Al11Nd3 | 4.43 | 9.99 | 12.94 | 90 | 90 | 90 | −0.42 |
| Al | 4.04 | 4.04 | 4.04 | 90 | 90 | 90 |
| Compounds | C11 | C12 | C13 | C22 | C23 | C33 | C44 | C55 | C66 |
|---|---|---|---|---|---|---|---|---|---|
| Al | 114 | 62 | 32 | ||||||
| Al11Nd3 | 130.8 | 43.2 | 43.3 | 126.7 | 51.8 | 125.9 | 55.4 | 50.3 | 47.9 |
| Compounds | B (Gpa) | G (Gpa) | E (Gpa) | σ | B/G |
|---|---|---|---|---|---|
| Al | 79.2 | 29.3 | 71.1 | 0.34 | 2.70 |
| Al11Nd3 | 70.2 | 46.0 | 113.2 | 0.23 | 1.53 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, X.; Zhang, X.; Wu, W.; Sun, S. The Effect of Gradient Cooling Behavior on the Microstructure and Mechanical Properties of Al-2at.% Nd Alloy in a Vacuum Environment. Crystals 2025, 15, 81. https://doi.org/10.3390/cryst15010081
Wang X, Zhang X, Wu W, Sun S. The Effect of Gradient Cooling Behavior on the Microstructure and Mechanical Properties of Al-2at.% Nd Alloy in a Vacuum Environment. Crystals. 2025; 15(1):81. https://doi.org/10.3390/cryst15010081
Chicago/Turabian StyleWang, Xiangjie, Xinyu Zhang, Wenjie Wu, and Shuchen Sun. 2025. "The Effect of Gradient Cooling Behavior on the Microstructure and Mechanical Properties of Al-2at.% Nd Alloy in a Vacuum Environment" Crystals 15, no. 1: 81. https://doi.org/10.3390/cryst15010081
APA StyleWang, X., Zhang, X., Wu, W., & Sun, S. (2025). The Effect of Gradient Cooling Behavior on the Microstructure and Mechanical Properties of Al-2at.% Nd Alloy in a Vacuum Environment. Crystals, 15(1), 81. https://doi.org/10.3390/cryst15010081








