Ab Initio Thermodynamic Evaluation of Ruthenium Tetroxide (RuO4) Vapor Pressure
Abstract
1. Introduction
2. Calculation Details
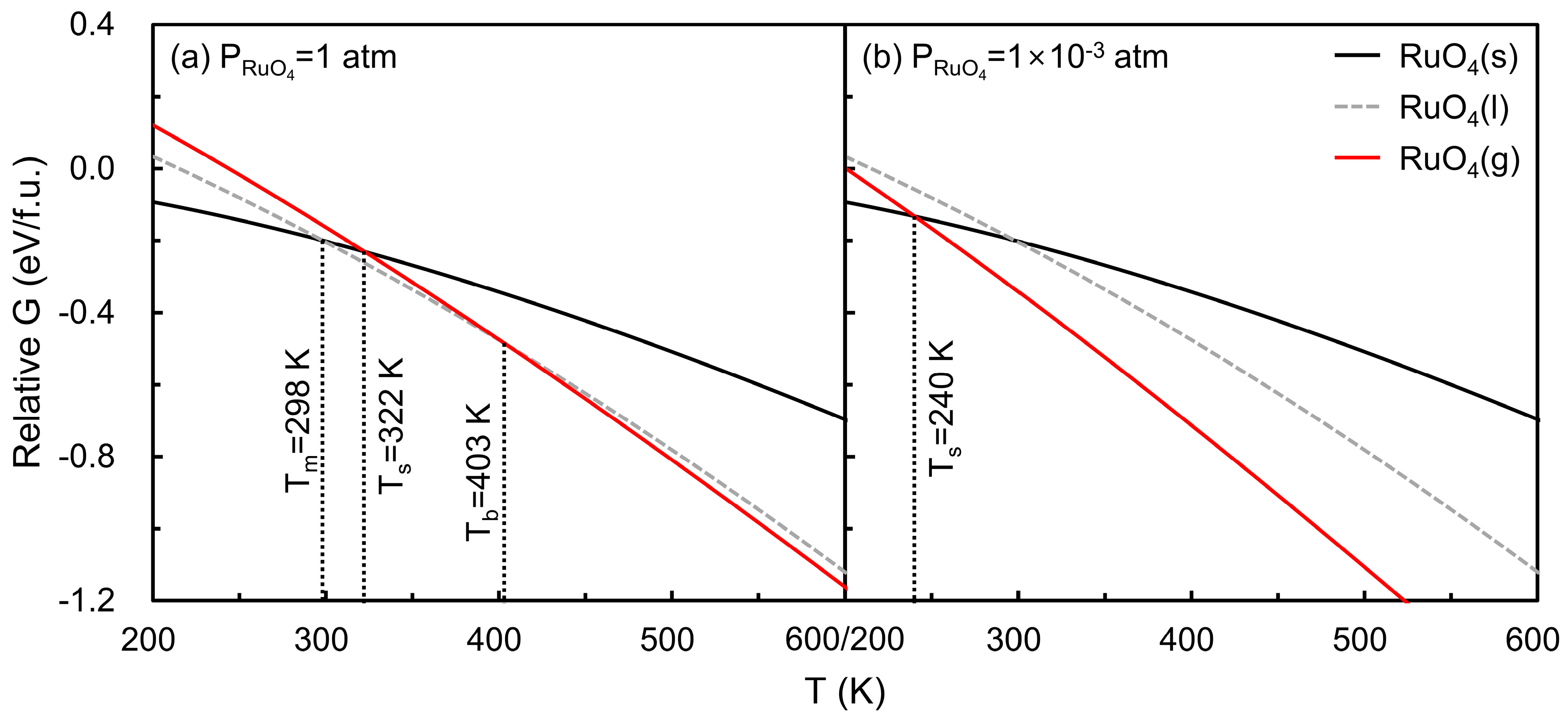
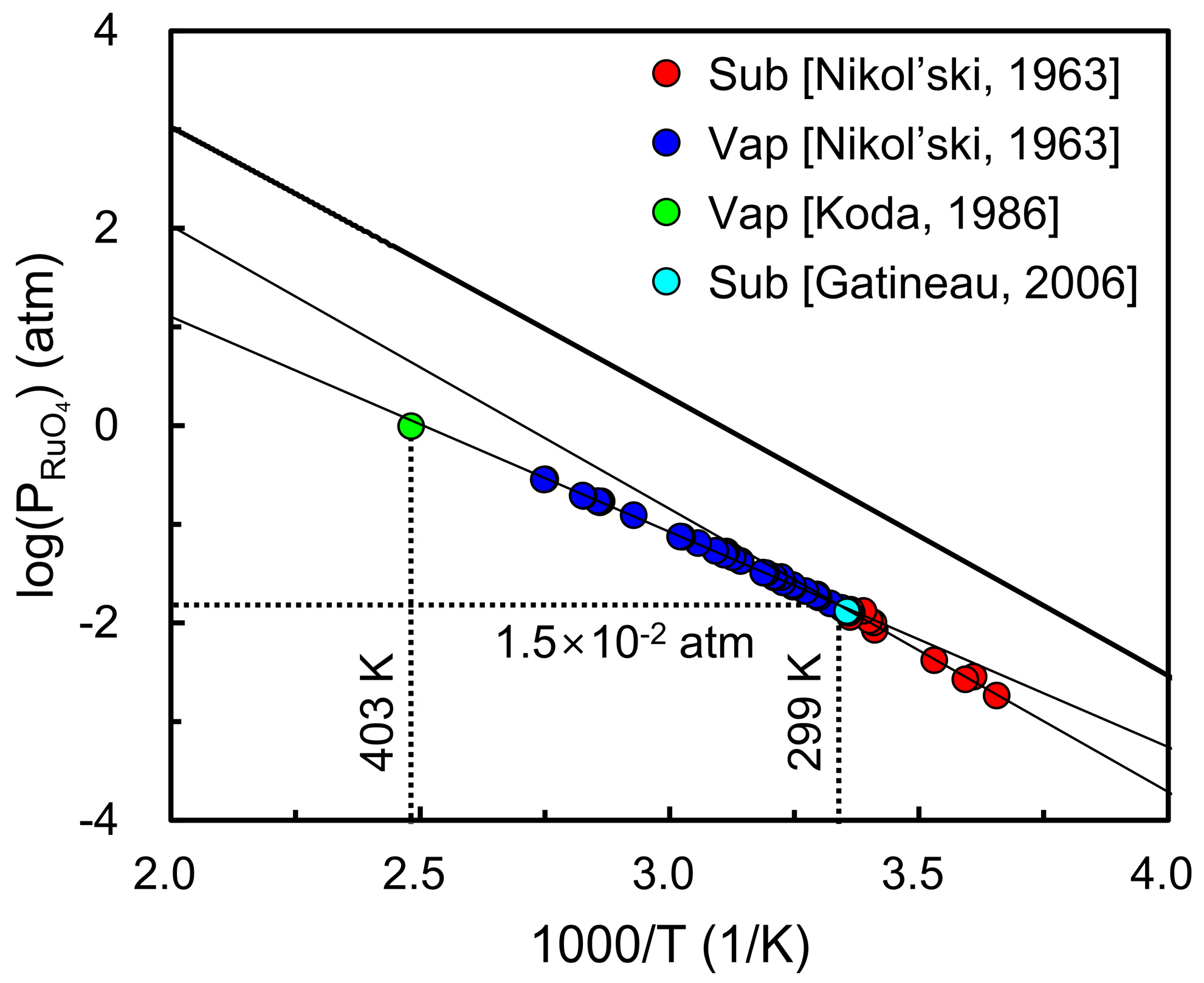
3. Results and Discussion
4. Conclusions
Supplementary Materials
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Han, J.H.; Lee, S.W.; Kim, S.K.; Han, S.; Hwang, C.S.; Dussarrat, C.; Gatineau, J. Growth of RuO2 thin films by pulsed-chemical vapor deposition using RuO4 precursor and 5% H2 reduction gas. Chem. Mater. 2010, 22, 5700–5706. [Google Scholar] [CrossRef]
- Han, J.H.; Han, S.; Lee, W.; Lee, S.W.; Kim, S.K.; Gatineau, J.; Dussarrat, C.; Hwang, C.S. Improvement in the leakage current characteristic of metal-insulator-metal capacitor by adopting RuO2 film as bottom electrode. Appl. Phys. Lett. 2011, 99, 022901. [Google Scholar] [CrossRef]
- Lee, H.-J.; Nabeya, S.; Hong, T.E.; Harada, R.; Kim, S.-H. Low temperature atomic layer deposition of Ru thin films using a new carbonyl-based Ru precursor and non-oxidizing reactants; Applications to the seed layer for Cu metallization. In Proceedings of the IEEE International Interconnect Technology Conference (IITC), Hsinchu, Taiwan, 16–18 May 2017. [Google Scholar]
- Kim, Y.-H.; Kim, M.; Kotsugi, Y.; Cheon, T.; Mohapatra, D.; Jang, Y.; Bae, J.-S.; Hong, T.E.; Ramesh, R.; An, K.-S.; et al. Atomic layer deposited RuO2 diffusion barrier for next generation Ru-interconnects. Adv. Funct. Mater. 2022, 32, 2206667. [Google Scholar] [CrossRef]
- Yoon, S.J.; Lee, S.; Lee, T.I.; Yoon, A.; Cho, B.J. Large grain ruthenium for alternative interconnects. IEEE Electron Device Lett. 2018, 40, 91–94. [Google Scholar] [CrossRef]
- Jeon, W.; Yoo, S.; Kim, H.K.; Lee, W.; An, C.H.; Chung, M.J.; Cho, C.J.; Kim, S.K.; Hwang, C.S. Evaluating the top electrode material for achieving an equivalent oxide thickness smaller than 0.4 nm from an Al-doped TiO2 film. ACS Appl. Mater. Interfaces 2014, 6, 21632–21637. [Google Scholar] [CrossRef] [PubMed]
- Kwon, D.S.; Kim, T.K.; Lim, J.; Seo, H.; Paik, H.; Hwang, C.S. Enhanced electrical properties of an Al-doped TiO2 dielectric film on a TiN electrode by adopting an atomic layer deposited Ru interlayer. ACS Appl. Electron. Mater. 2022, 4, 2005–2014. [Google Scholar] [CrossRef]
- Choi, D.; Kim, C.S.; Naveh, D.; Chung, S.; Warren, A.P.; Nuhfer, N.T.; Toney, M.F.; Coffey, K.R.; Barmak, K. Electron mean free path of tungsten and the electrical resistivity of epitaxial (110) tungsten films. Phys. Rev. B 2012, 86, 045432. [Google Scholar] [CrossRef]
- Dutta, S.; Sankaran, K.; Moors, K.; Pourtois, G.; Van Elshocht, S.; Bömmels, J.; Vandervorst, W.; Tőkei, Z.; Adelmann, C. Thickness dependence of the resistivity of platinum-group metal thin films. J. Appl. Phys. 2017, 122, 025107. [Google Scholar] [CrossRef]
- Milosevic, E.; Kerdsongpanya, S.; Gall, D. The resistivity size effect in epitaxial Ru(0001) and Co(0001) layers. In Proceedings of the IEEE Nanotechnology Symposium (ANTS), New York, NY, USA, 14–15 November 2018. [Google Scholar]
- Founta, V.; Soulié, J.-P.; Sankaran, K.; Vanstreels, K.; Opsomer, K.; Morin, P.; Lagrain, P.; Franquet, A.; Vanhaeren, D.; Conard, T.; et al. Properties of ultrathin molybdenum films for interconnect applications. Materialia 2022, 24, 101511. [Google Scholar] [CrossRef]
- Suntola, T. Atomic layer epitaxy. Mater. Sci. Rep. 1989, 4, 261–312. [Google Scholar] [CrossRef]
- Ritala, M.; Leskelä, M.; Dekker, J.-P.; Mutsaers, C.; Soininen, P.J.; Skarp, J. Perfectly conformal TiN and Al2O3 films deposited by atomic layer deposition. Chem. Vap. Depos. 1999, 5, 7–9. [Google Scholar] [CrossRef]
- George, S.M. Atomic layer deposition: An overview. Chem. Rev. 2010, 110, 111–131. [Google Scholar] [CrossRef] [PubMed]
- Aaltonen, T.; Alén, P.; Ritala, M.; Leskelä, M. Ruthenium thin films grown by atomic layer deposition. Chem. Vap. Depos. 2003, 9, 45–49. [Google Scholar] [CrossRef]
- Aaltonen, T.; Ritala, M.; Arstila, K.; Keinonen, J.; Leskelä, M. Atomic layer deposition of ruthenium thin films from Ru(thd)3 and oxygen. Chem. Vap. Depos. 2004, 10, 215–219. [Google Scholar] [CrossRef]
- Methaapanon, R.; Geyer, S.M.; Brennan, S.; Bent, S.F. Size dependent effects in nucleation of Ru and Ru oxide thin films by atomic layer deposition measured by synchrotron radiation X-ray diffraction. Chem. Mater. 2013, 25, 3458–3463. [Google Scholar] [CrossRef]
- Kozodaev, M.G.; Lebedinskii, Y.Y.; Chernikova, A.G.; Korostylev, E.V.; Chouprik, A.A.; Khakimov, R.R.; Markeev, A.M.; Hwang, C.S. Temperature controlled Ru and RuO2 growth via O* radical-enhanced atomic layer deposition with Ru(EtCp)2. J. Chem. Phys. 2019, 151, 204701. [Google Scholar] [CrossRef]
- Green, M.L.; Gross, M.E.; Papa, L.E.; Schnoes, K.J.; Brasen, D. Chemical vapor deposition of ruthenium dioxide films. J. Electrochem. Soc. 1985, 132, 2677–2685. [Google Scholar] [CrossRef]
- Morozova, N.B.; Zherikova, K.V.; Semyannikov, P.P.; Trubin, S.V.; Igumenov, I.K. Study of temperature dependencies of saturated vapor pressure of ruthenium(III) beta-diketonate derivatives. J. Therm. Anal. Calorim. 2009, 98, 395–399. [Google Scholar] [CrossRef]
- Kawano, K.; Kosuge, H.; Oshima, N.; Funakubo, H. Ruthenium and ruthenium oxide film deposition by MOCVD using Ru(DMPD)2. ECS Trans. 2006, 1, 139–144. [Google Scholar] [CrossRef]
- Shibutami, T.; Kawano, K.; Oshima, N.; Yokoyama, S.; Funakubo, H. Ruthenium film with high nuclear density deposited by MOCVD using a novel liquid precursor. Electrochem. Solid-State Lett. 2003, 1, C117–C119. [Google Scholar] [CrossRef]
- Norman, J.A.T.; Perez, M.; Schulz, S.E.; Waechtler, T. New precursors for CVD copper metallization. Microelectron. Eng. 2008, 85, 2159–2163. [Google Scholar] [CrossRef]
- Van der Straten, O.; Rossnagel, S.M.; Doyle, J.P.; Rodbell, K.P. Metal-organic atomic layer deposition of metals for applications in interconnect technology. ECS Trans. 2006, 1, 51–56. [Google Scholar] [CrossRef]
- Minjauw, M.M.; Dendooven, J.; Capon, B.; Schaekers, M.; Detavernier, C. Atomic layer deposition of ruthenium at 100 °C using the RuO4-precursor and H2. J. Mater. Chem. C 2015, 3, 132–137. [Google Scholar] [CrossRef]
- Minjauw, M.M.; Rijckaert, H.; Van Driessche, I.; Detavernier, C.; Dendooven, J. Nucleation enhancement and area-selective atomic layer deposition of ruthenium using RuO4 and H2 gas. Chem. Mater. 2019, 31, 1491–1499. [Google Scholar] [CrossRef]
- An, C.H.; Jeon, W.; Kim, S.H.; Cho, C.J.; Kwon, D.S.; Kim, D.G.; Lee, W.; Hwang, C.S. Substrate effects on the growth behavior of atomic-layer-deposited Ru thin films using RuO4 precursor and N2/H2 mixed gas. J. Phys. Chem. 2019, 123, 22539–22549. [Google Scholar] [CrossRef]
- Poonkottil, N.; Minjauw, M.M.; Werbrouck, A.; Checchia, S.; Solano, E.; Nisula, M.; Franquet, A.; Detavernier, C.; Dendooven, J. Atomic layer deposition of ruthenium dioxide based on redox reactions between alcohols and ruthenium tetroxide. Chem. Mater. 2022, 34, 8946–8958. [Google Scholar] [CrossRef]
- Poonkottil, N.; Rijckaert, H.; Rajendran, K.; Petit, R.R.; Martin, L.I.D.J.; Thourhout, D.V.; Driessche, I.V.; Detavernier, C.; Dendooven, J. Low temperature area selective atomic layer deposition of ruthenium dioxide thin films using polymers as inhibition layers. Adv. Mater. Interfaces 2023, 10, 2201934. [Google Scholar] [CrossRef]
- Nikol’skii, A. Saturated vapor pressure of ruthenium tetraoxide. Zh. Neorgan. Khim. 1963, 8, 541–543. [Google Scholar]
- Koda, Y. Boiling points and ideal solutions of ruthenium and osmium tetraoxides. J. Chem. Soc. Chem. Commun. 1986, 17, 1347–1348. [Google Scholar] [CrossRef]
- Gatineau, J.; Yanagita, K.; Dussarrat, C. A new RuO4 solvent solution for pure ruthenium film depositions. Microelectron. Eng. 2006, 83, 2248–2252. [Google Scholar] [CrossRef]
- Kim, H.-K.; Lee, N.-Y.; Kim, Y.-C. Evaluation of vapor pressure of MoO2Cl2 and its initial chemical reaction on a SiO2 surface by ab initio thermodynamics. Curr. Appl. Phys. 2024, 61, 115–120. [Google Scholar] [CrossRef]
- Lee, N.-Y.; Kim, S.-H.; Kim, J.-Y.; Kim, Y.-C. Molecular structure and vapor pressure of molybdenum pentachloride using ab-initio thermodynamics. J. Korean Phys. Soc. 2025, 86, 430–434. [Google Scholar] [CrossRef]
- Kresse, G.; Hafner, J. Ab initio molecular dynamics for liquid metals. Phys. Rev. B 1993, 47, 558–561. [Google Scholar] [CrossRef] [PubMed]
- Kresse, G.; Furthmüller, J. Efficiency of ab-initio total energy calculations for metals and semiconductors using a plane-wave basis set. Comput. Mater. Sci. 1996, 6, 15–50. [Google Scholar] [CrossRef]
- Kresse, G.; Joubert, D. From ultrasoft pseudopotentials to the projector augmented-wave method. Phys. Rev. B 1999, 59, 1758–1775. [Google Scholar] [CrossRef]
- Blöchl, P.E. Projector augmented-wave method. Phys. Rev. B 1994, 50, 17953–17979. [Google Scholar] [CrossRef]
- Perdew, J.P.; Burke, K.; Ernzerhof, M. Generalized gradient approximation made simple. Phys. Rev. Lett. 1996, 77, 3865–3868. [Google Scholar] [CrossRef]
- Grimme, S.; Antony, J.; Ehrlich, S.; Krieg, H. A consistent and accurate ab initio parametrization of density functional dispersion correction (DFT-D) for the 94 elements H-Pu. J. Chem. Phys. 2010, 132, 154104. [Google Scholar] [CrossRef]
- Monkhorst, H.J.; Pack, J.D. Special points for Brillouin-zone integrations. Phys. Rev. B 1976, 13, 5188–5192. [Google Scholar] [CrossRef]
- Togo, A.; Chaput, L.; Tadano, T.; Tanaka, I. Implementation strategies in phonopy and phono3py. J. Phys. Condens. Matter 2023, 35, 353001. [Google Scholar] [CrossRef]
- Togo, A. First-principles phonon calculations with phonopy and phono3py. J. Phys. Soc. Jpn. 2023, 92, 012001. [Google Scholar] [CrossRef]
- Cramer, C.J. Essentials of Computational Chemistry: Theories and Models, 2nd ed.; John Wiley & Sons: Chichester, UK, 2013; pp. 1–596. [Google Scholar]
- Wang, V.; Xu, N.; Liu, J.-C.; Tang, G.; Geng, W.-T. VASPKIT: A user-friendly interface facilitating high-throughput computing and analysis using VASP code. Comput. Phys. Commun. 2021, 267, 108033. [Google Scholar] [CrossRef]
- Pley, M.; Wickleder, M.S. Two crystalln modifications of RuO4. J. Solid State Chem. 2005, 178, 3206–3209. [Google Scholar] [CrossRef]
- Jain, A.; Ong, S.P.; Hautier, G.; Chen, W.; Richards, W.D.; Dacek, S.; Cholia, S.; Gunter, D.; Skinner, D.; Ceder, G.; et al. Commentary: The Materials Project: A materials genome approach to accelerating materials innovation. APL Mater. 2013, 1, 011002. [Google Scholar] [CrossRef]
- Saal, J.E.; Kirklin, S.; Aykol, M.; Meredig, B.; Wolverton, C. Materials design and discovery with high-throughput density functional theory: The Open Quantum Materials Database (OQMD). JOM 2013, 65, 1501–1509. [Google Scholar] [CrossRef]
- Kirklin, S.; Saal, J.E.; Meredig, B.; Thompson, A.; Doak, J.W.; Aykol, M.; Rühl, S.; Wolverton, C. The Open Quantum Materials Database (OQMD): Assessing the accuracy of DFT formation energies. npj Comput. Mater. 2015, 1, 132–137. [Google Scholar] [CrossRef]
- Nuta, I.; Virot, F.; Fischer, E.; Chatillon, C. Thermodynamic assessment of RuO4 oxide. Calphad 2023, 80, 102508. [Google Scholar] [CrossRef]
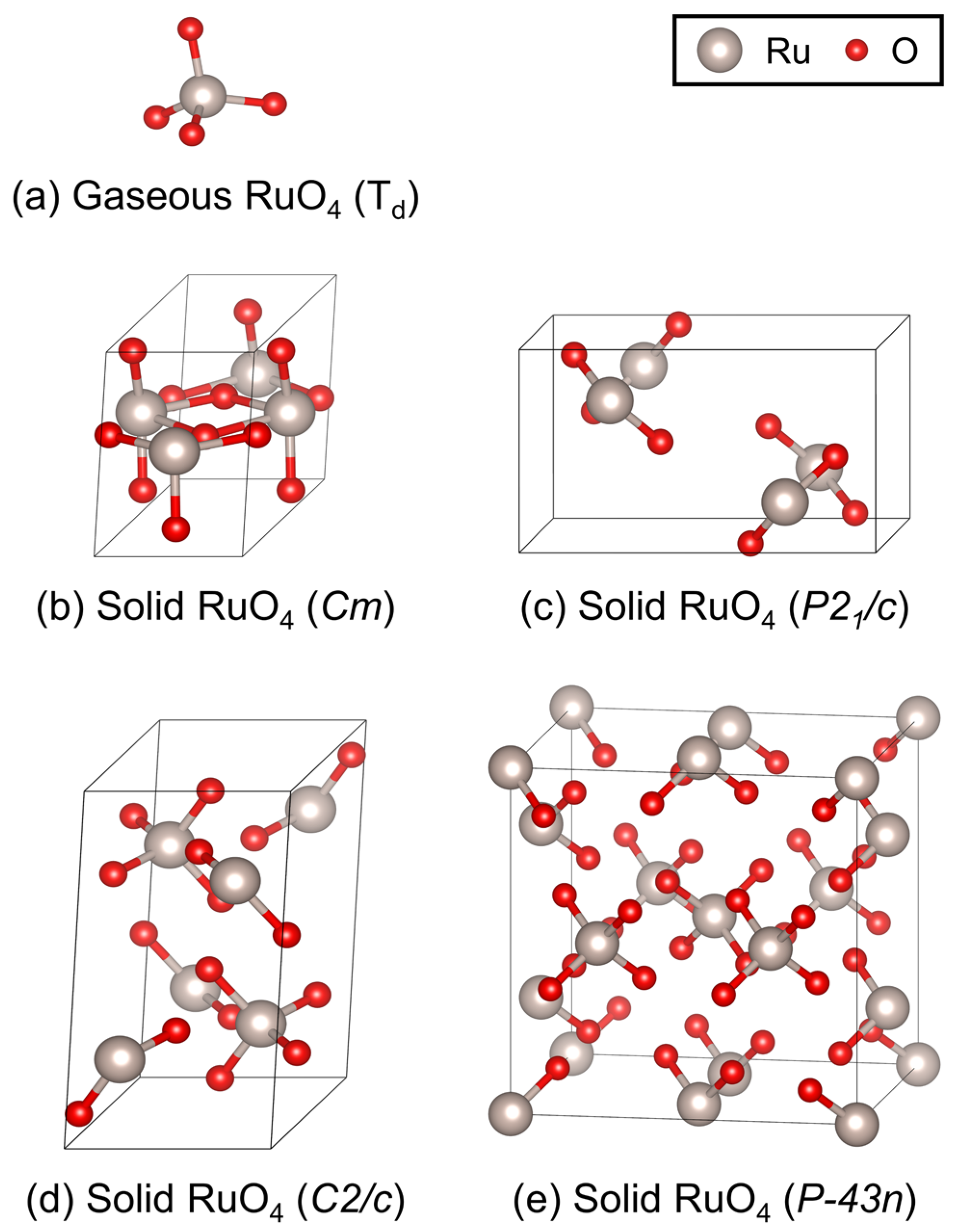

| Lattice Parameters | |||||
|---|---|---|---|---|---|
| a (Å) | b (Å) | c (Å) | β (°) | ||
| Monoclinic Cm | This work | 9.96 | 3.12 | 4.78 | 117.4 |
| Monoclinic P21/c | This work | 4.50 | 8.16 | 4.58 | 100.0 |
| Monoclinic C2/c | [46] | 9.30 | 4.40 | 8.45 | 116.8 |
| This work | 9.25 | 4.39 | 8.38 | 116.5 | |
| Cubic P-43n | [46] | 8.51 | - | - | - |
| This work | 8.49 | - | - | - | |
| (eV/Formula Unit) | |||
|---|---|---|---|
| Materials Project [47] | OQMD [48,49] | This Work | |
| Monoclinic Cm | - | −29.32 | −30.46 |
| Monoclinic P21/c | - | −30.80 | −33.19 |
| Monoclinic C2/c | −32.23 | −31.74 | −33.23 |
| Cubic P−43n | −32.22 | −31.74 | −33.23 |
| Solid RuO4 | 2.92 | 1.97 | - | - | 4.38 |
| Gaseous RuO4 | 0.34 | 0.22 | 0.68 | 0.40 | 0.10 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kim, S.-H.; Kim, J.-Y.; Kim, H.-K.; Lee, N.-Y.; Kim, H.-N.; Thapa, S.; Jo, J.-Y.; Kim, Y.-C. Ab Initio Thermodynamic Evaluation of Ruthenium Tetroxide (RuO4) Vapor Pressure. Crystals 2025, 15, 915. https://doi.org/10.3390/cryst15110915
Kim S-H, Kim J-Y, Kim H-K, Lee N-Y, Kim H-N, Thapa S, Jo J-Y, Kim Y-C. Ab Initio Thermodynamic Evaluation of Ruthenium Tetroxide (RuO4) Vapor Pressure. Crystals. 2025; 15(11):915. https://doi.org/10.3390/cryst15110915
Chicago/Turabian StyleKim, Sun-Hye, Jong-Yoon Kim, Hyun-Kyu Kim, Na-Young Lee, Ha-Neul Kim, Saukinta Thapa, Jun-Yeong Jo, and Yeong-Cheol Kim. 2025. "Ab Initio Thermodynamic Evaluation of Ruthenium Tetroxide (RuO4) Vapor Pressure" Crystals 15, no. 11: 915. https://doi.org/10.3390/cryst15110915
APA StyleKim, S.-H., Kim, J.-Y., Kim, H.-K., Lee, N.-Y., Kim, H.-N., Thapa, S., Jo, J.-Y., & Kim, Y.-C. (2025). Ab Initio Thermodynamic Evaluation of Ruthenium Tetroxide (RuO4) Vapor Pressure. Crystals, 15(11), 915. https://doi.org/10.3390/cryst15110915






