Next Article in Journal
Line Defects in Quasicrystals
Previous Article in Journal
Emission Wavelength Control via Molecular Structure Design of Dinuclear Pt(II) Complexes: Optimizing Optical Properties for Red- and Near-Infrared Emissions
 
 
Search for Articles:
Title / Keyword
Author / Affiliation / Email
Journal
Article Type
 
 
Advanced Search
 
Section
Special Issue
Volume
Issue
Number
Page
 
Journals
Crystals
Volume 15
Issue 3
10.3390/cryst15030274
crystals-logo
Submit to this Journal Review for this Journal Propose a Special Issue
► Article Menu

Article Menu

share Share announcement Help format_quote Cite question_answer Discuss in SciProfiles
first_page
settings
Order Article Reprints
Font Type:
Arial Georgia Verdana
Font Size:
Aa Aa Aa
Line Spacing:
Column Width:
Background:
Article

What Is More Important When Calculating the Thermodynamic Properties of Organic Crystals, Density Functional, Supercell, or Energy Second-Order Derivative Method Choice?

by
Aleksandr S. Dubok
1,2 and
Denis A. Rychkov
1,3,*
1
Institute of Solid State Chemistry and Mechanochemistry SB RAS, 630090 Novosibirsk, Russia
2
Laboratory of Physicochemical Fundamentals of Pharmaceutical Materials, Novosibirsk State University, 2 Pirogova Str., 630090 Novosibirsk, Russia
3
SRF “SKIF”, Boreskov Institute of Catalysis, 630559 Koltsovo, Russia
*
Author to whom correspondence should be addressed.
Crystals 2025, 15(3), 274; https://doi.org/10.3390/cryst15030274
Submission received: 28 January 2025 / Revised: 13 March 2025 / Accepted: 13 March 2025 / Published: 16 March 2025
(This article belongs to the Special Issue Computational Research on Crystals)
Browse Figures
Versions Notes

Abstract

:
Calculation of second-order derivatives of energy using the DFT method is a valuable approach for the estimation of both the thermodynamical and mechanical properties of organic crystals from the first principles. This type of calculation requires specification of several computational parameters, including the functional, supercell, and method of phonon calculations. Nevertheless, the importance of these parameters is presented in the literature very modestly. In this work, we demonstrate the influence of these computational parameters on the accuracy of calculated second-order derivatives using the practical example of pyrazinamide polymorphs, including the plastically bending α form and the β, γ, and brittle δ form. The effects of the settings used on the resulting enthalpies of the polymorphic modifications of pyrazinamide are compared: supercell setting (primitive cell vs. appropriate supercell) has a much stronger impact than functional (PBE-D3BJ vs. Hamada rev-vdW-DF2) which in turn affects results significantly more than the method for second-order derivative computation (FD vs. DFPT approach). Finally, we propose some suggestions for choosing the right settings for calculating second-order derivatives for molecular crystals.

1. Introduction

Polymorphism is a widespread phenomenon that occurs in both organic and inorganic crystals [1,2,3]. The polymorphism of organic crystals has received considerable attention, mainly in the pharmaceutical field, due to its practical role [4,5,6,7,8]. Depending on the structure of the crystal lattice, one and the same substance may have not only different bioavailability [9,10,11] but also different solubility rates [12,13], shelf-life stability [14,15,16,17,18,19], and manufacturing parameters [20,21,22]. In addition, different polymorphic modifications can have different mechanical properties, which may directly affect the production of drug forms, including tableting and phase transitions under pressure [23,24,25,26].
While the prediction of the thermodynamic stability and solubility of organic crystals [27,28,29,30] from first principles [31,32,33,34,35,36,37] is an important unsolved problem in materials science, with it being performed thus far at the first stage using mainly force field methods [38,39,40], additional examination of their computation using non-empirical DFT methods is required. Second-order derivative calculations using the DFT method have proven to be a valuable approach for the estimation of both the thermodynamical stability and the mechanical properties from the first principles [41,42,43]. This can be achieved using phonon modes and elastic tensor analysis performed readily using the second-order derivative calculation results. However, second-order derivative calculations are accompanied by several practical challenges. Firstly, the functional used in the computation process should be optimal in terms of accuracy and computational cost ratio and suitable for the chosen method of phonon calculation [44,45]. Secondly, second-order derivative calculations usually require the construction of a supercell to account for fluctuations disproportionate to the primitive cell [46,47]. The rule of thumb states that supercell vectors should be of the order of 1 to 1.5 nanometers. Nevertheless, the use of large supercells greatly increases the demand for computational resources. Finally, there are two different approaches to calculating second-order derivatives: a finite differences approach and the density functional perturbation theory method [48]. In a finite differences approach (FD), the second-order force constants are computed using finite differences of the forces when each ion is displaced in each independent direction. The number and step size of every displacement should be selected carefully. This may increase the amount of displacement required to calculate the second derivatives and also result in a sufficient increase in the computational cost. Density-functional perturbation theory (DFPT) provides a way to compute the second-order linear response to ionic displacement analytically. This approach requires the usage of non-local dispersion correction functionals but does not require the construction of supercells if not only zone-center (Γ-point) frequencies are calculated. However, not all computational software implements the calculations of phonon dispersion at different q points, including the so-called “gold standard” Vienna ab initio simulation package (VASP 5.4.4). Calculation of vibrations at q ≠ 0 usually requires increased computational cost compared to the q = 0 computations for the primitive cell but should save computational resources compared to supercell usage [49]. A brief overview of DFPT method implementations in various solid-state calculation software is given in Table 1.
Fundamental computational parameters such as energy cutoff, k-points sampling, and pseudopotential quality are explicitly discussed in the classical literature [50,51,52]. Nevertheless, the question of the importance of the functional, supercell, and method of phonon calculations is presented in the literature very modestly and mainly in the manuals of the abovementioned software, several books, and professional community discussions. In this work, we demonstrate the influence of these computational parameters on the accuracy of calculated second-order derivatives using the practical example of pyrazinamide polymorphs (Figure 1) [53,54,55,56].
Recently, the relative stability of pyrazinamide polymorphs over a wide temperature range has been studied using experimental and computational methods [57,58,59,60,61,62,63,64,65]. Differential scanning calorimetry and vapor pressure measurements were used to describe the polymorphs’ stability in the provided experiments [57,58,64]. Electronic structure and phonon calculations using a finite differences approach were performed to determine the temperature dependence of the thermodynamic properties of α, β, γ, and δ pyrazinamide [65]. It was confirmed that the α form was a stable polymorph at room temperature, whereas the β form appeared to be a low-temperature form instead of the previously suggested δ form according to the latest experiments and our previous calculations (Figure 2) [64,65].
Due to the significant amount of obtained data on pyrazinamide polymorph stability in a wide temperature range, it is a convenient example to estimate the influence of various computational parameters on the accuracy/computational cost ratio for practical calculations.

2. Materials and Methods

2.1. Crystallographic Structures

The crystal structures of pyrazinamide polymorphs were chosen from the CCDC database with the lowest R-factors (<4%) solved and refined at 100K temperature: PYRZIN22 (α) [60], PYRZIN18 (β) [57], PYRZIN19 (γ) [57], and PYRZIN16 (δ) [66]. The disordered γ form was treated as two independent structures with “A” and “B” positions only, and energies were calculated further by summing energies in the ratio of 0.866 and 0.134, respectively. These structures were used as starting guesses for all subsequent calculations. All pyrazinamide structures were converted to VASP format using the CIF2Cell code [67] for periodic DFT calculations.

2.2. Periodic DFT Calculations

All periodic DFT calculations were performed using the Vienna ab initio simulation package (VASP 5.4.4) [68,69,70,71] using either the PBE [72] or rev-vdw-DF2 [73] functionals for all cases after functional and dispersion correction benchmarking. A plane-wave basis set with a kinetic energy cutoff of 550 eV and projector augmented wave (PAW) atomic pseudopotentials [74,75] were employed during the DFT calculations. Dense k-point Monkhorst–Pack meshes [76] of 5 × 2 × 1, 1 × 6 × 2, 3 × 7 × 2, and 4 × 4 × 2 were used for the α, β, γ (both “A” and “B”), and δ forms, respectively. A 4 × 2 × 1 mesh was also used for functional and dispersion correction scheme benchmarking to speed up calculations. Typical energy convergence criteria of 1 meV/atom and additional energy criteria of total 0.1 kJ/mol were used to achieve tighter convergence for structural optimization. Gaussian smearing was chosen (ISMEAR = 0) with 0.1 eV width smearing (SIGMA = 0.1). Dispersion correction was used for electronic structure calculations: Grimme D3 with the Becke–Johnson damping function (D3BJ) [77] for the PBE functional and nonlocal correlation energy EcNL for the rev-vdW-DF2 functional of Hamada [73], also known as vdW-DF2-B86R. Armiento–Mattsson (AM05) [78,79,80], Perdew–Burke-Ernzerhof (PBE) [72], revised PBE for solids (PBEsol) [81], Perdew–Wang (PW91) [82], revised PBE from Zhang and Yang (revPBE) [83], and the revised PBE from Hammer et al. (RPBE) [84] density functionals were also employed for studying the unit cell volume deviation of pyrazinamide polymorphic forms. Likewise, additional dispersion correction schemes such as the dDsC dispersion correction method (dDsC) [85,86], the DFT-D2 method of Grimme (DFT-D2) [87], the DFT-D3 method of Grimme with the zero-damping function (DFT-D3) [88], the DFT-D3 method with the Becke–Johnson damping function (DFT-D3(BJ)) [77], the many-body dispersion energy method (MBD@rsSCS) [89,90], no dispersion correction, the Tkatchenko–Scheffler method (TS) [91], and the Tkatchenko–Scheffler method with iterative Hirshfeld partitioning (TS/HI) [92,93] were also employed.
All structures were fully optimized, both the unit cell and ion positions (ISIF = 3). The temperature dependence of Gibbs free energy was treated by computing the second-order derivatives of the total energy with respect to the position of the ions using a finite differences approach (IBRION = 6) for the PBE functional with D3BJ dispersion correction, and both the finite differences approach (IBRION = 6) and the density functional perturbation theory approach (IBRION = 8) for the rev-vdW-DF2 functional. Symmetry was used to reduce the number of displacements for a finite differences approach. A full list of the used symmetry parameters for this and previous [65] work is provided in Table S1.
The second-order derivatives of the total energy with respect to the position of the ions were computed using the default primitive cells as well as supercells of 3 × 2 × 1 (α), 1 × 3 × 1 (β), 2 × 3 × 1 (γ), and 2 × 2 × 2 (δ) constructed to increase the accuracy of the performed calculations (Figure S1). The k-point meshes were reduced for calculations using the supercells in order to preserve the chosen k-point mesh density (2 × 1 × 1, 1 × 2 × 2, 2 × 2 × 2, and 2 × 2 × 1 for the α, β, γ, and δ form supercells, respectively).

2.3. Phonon Calculations

The dynamical matrix (constructed and diagonalized), and the phonon modes and frequencies of each system reported in the OUTCAR file were further extracted to proceed with the Phonopy 2.17.1 package [94,95] to calculate the zero-point energy correction term (ZPE), temperature-dependent vibrational energy, entropy, and free energy. Mesh samplings of the reciprocal space used for the calculation of thermal properties in the Phonopy 2.17.1 package were equal to the meshes used for electronic calculations in VASP.

3. Results

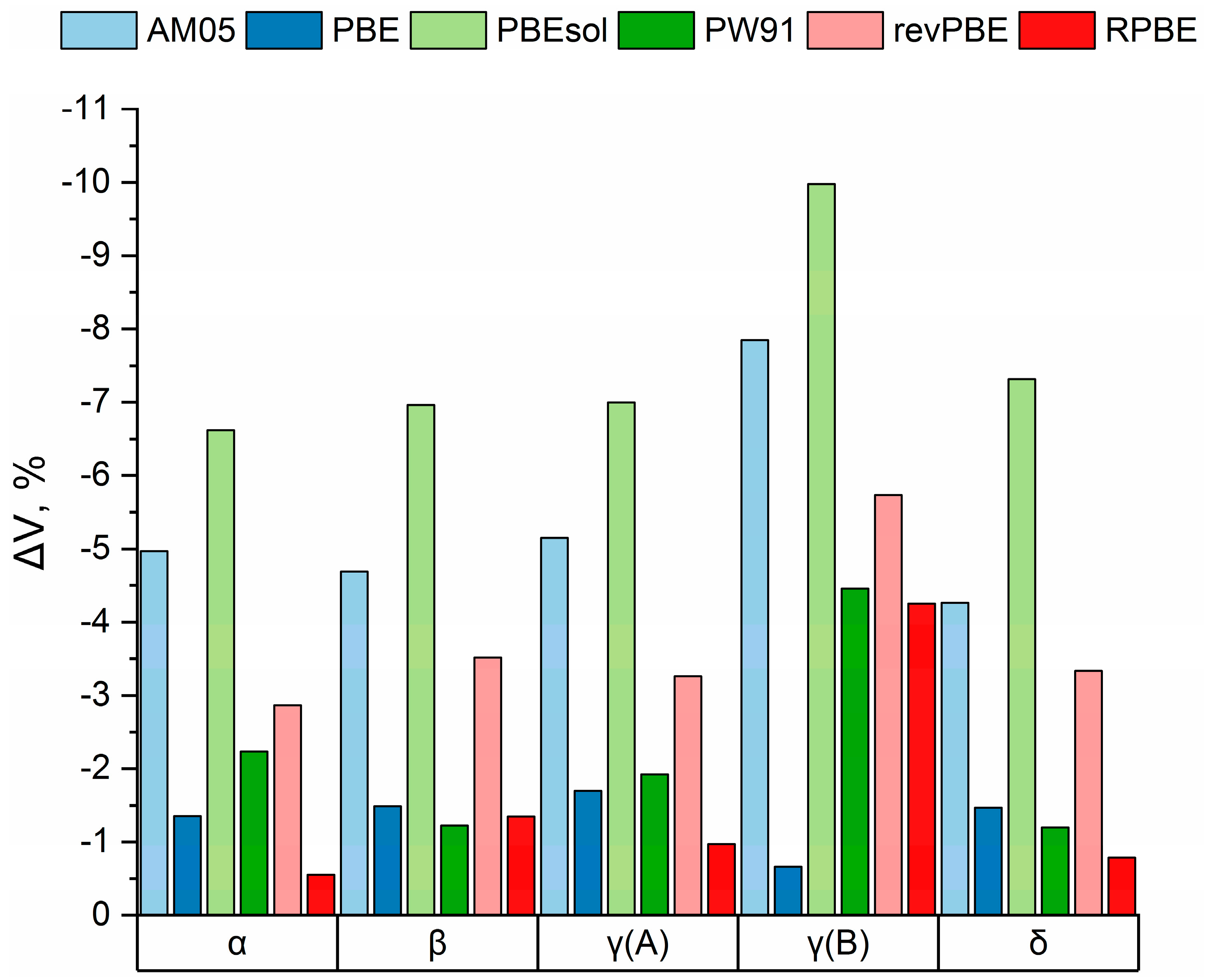
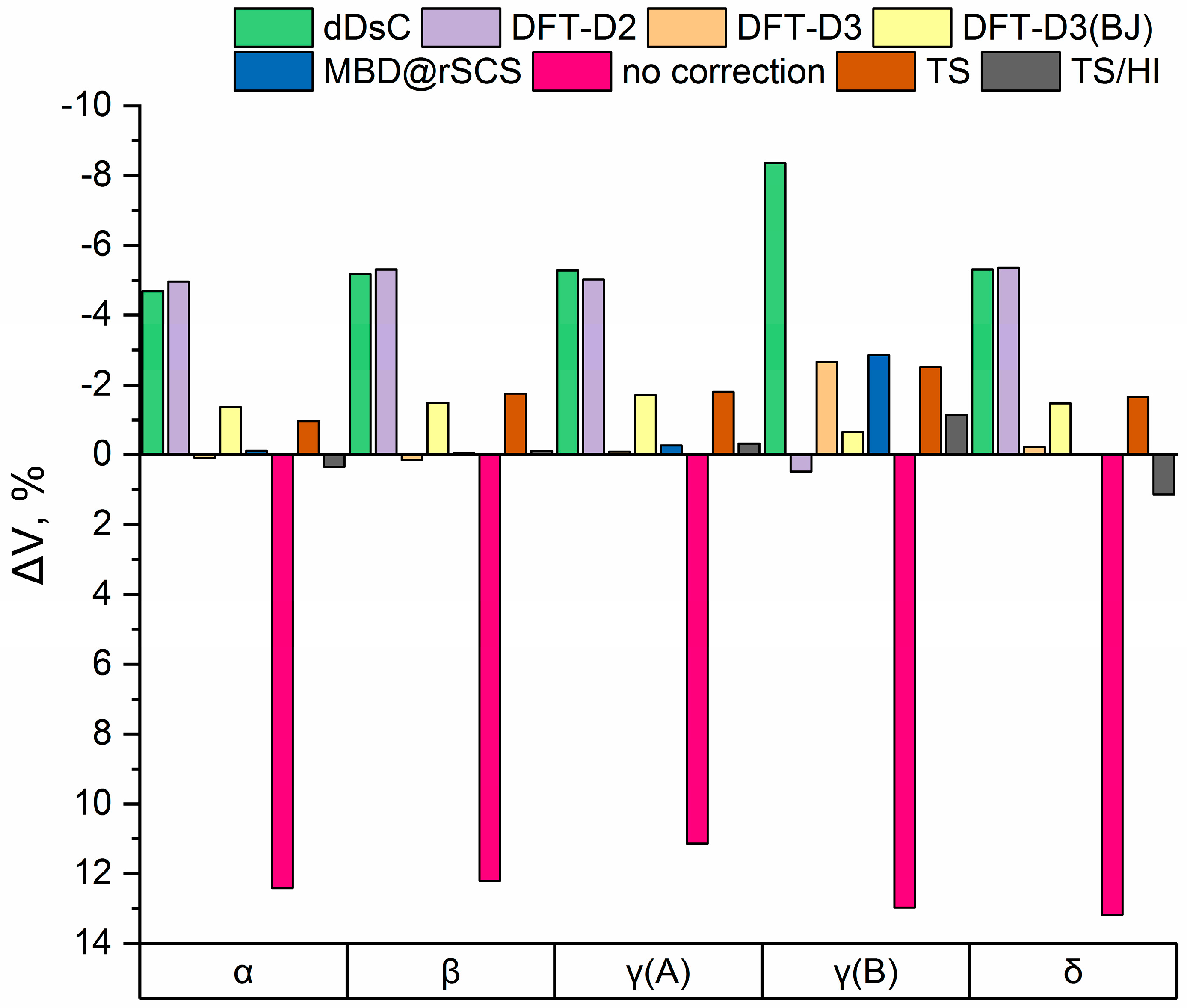
3.1. Electronic Structure Energies and Unit Cell Parameters

Depending on the chosen calculation method, the absolute values of the energies and therefore the relative values of the obtained energies of polymorphic modifications are different [96,97,98]. Therefore, it is important to assess the effect of the different calculation routes and parameters to assess their importance and determine which are the best ones to provide a balanced description of both states so that the relative energies and structural characteristics of the different polymorphs are as close as possible to the experimental results. Figure 3 shows the results of various internal functional benchmarking in terms of the accuracy of unit cell parameter modeling for all four polymorphs (five structures due to γ form crystallographic disorder) of pyrazinamide. The D3BJ dispersion correction scheme was used for all tested functionals, which could affect the poor PBEsol results for these molecular crystals [99,100].
In this particular case, classical PBE outperformed all other tested functionals, showing not only reasonable volumes for all pyrazinamide polymorphs but also the lowest dispersion over various crystalline forms and moderate calculation times (Table S2). Dispersion correction schemes were further tested for the PBE functional to evaluate the best combination (Figure 4, Table S2). Summing up the relative deviation from the experimental unit cell parameters, energy difference (Table S3), and computational time (Table S4), PBE-D3BJ proved to be an optimal choice, which coincides well with the lattice constants and energy benchmarking in work [101]. Thus, all further calculations and comparisons were performed over the PBE-D3BJ level of theory.
The electronic energies for the α, β, and δ forms and γ (A) and γ (B) substructures of the γ form were calculated after optimization. From the obtained electronic energies (the electronic energy of the γ form was obtained by averaging over the γ (A) and γ (B) substructures with their disorder weights), relative energies were calculated, where the β form was chosen as a relative zero energy (Table 2). The series of polymorphs’ relative energies were the same for the PBE-D3BJ and rev-vdW-DF2 methods: β < δ < α < γ. It should also be noted that the values of relative polymorphic energies obtained with the rev-vdW-DF2 method are generally lower than those obtained with PBE-D3BJ. Both functionals were chosen to provide close geometries and energies of solids, whereas the rev-vdw-DF2 functional can be used in conjunction with the DFPT method to obtain energy second-order derivatives.
All polymorphs’ relative energies are less than 4.5 kJ/mol. This coincides well with the upper limit of polymorph energy of 7 kJ/mol obtained by J. Nyman et al. in a study on 1061 experimentally determined ordered crystal structures of 508 polymorphic organic substances [102] and confirmed computationally by Aurora J. Cruz-Cabeza et al. [2]. However, the γ (B) value of the substructure of the disordered γ form was found to be higher than 7 kJ/mol for both methods. This coincides well with the energy difference found for other disordered structures, e.g., tolazamide II disordered structures [103], and confirms possible outliers for the abovementioned empirical rule. Since disordered crystals are often stabilized by a configurational entropy term, their electronic energies are generally found to be higher than the values typical of ordered structures. Thus, it can be claimed that both methods give reasonable values in qualitative agreement with each other.

3.2. Gibbs Energy Calculations at 0 K

The primary way to correct the energies of polymorphic modifications using second-order derivative calculations is to calculate the zero-point vibrational energies (ZPEs) to obtain the thermodynamic potential—the internal energy U, equal to the Helmholtz energy F at 0 K [104,105]. Since the polymorphic modifications of pyrazinamide are modeled at 1 bar pressure, the PV term that distinguishes the Helmholtz energy F from the Gibbs energy G, as well as the internal energy U from enthalpy H, can be neglected.
The ZPE values were obtained from second-order derivative calculations for all polymorphic modifications (Table S5) and added to the electronic energies (Table 3). When ZPE was taken into account, the series of relative energies of the polymorphs did not significantly change but provided varying stabilities of δ and α forms for both the PBE-D3BJ and rev-vdW-DF2 levels of theory (β < δ/α < γ). The lack of supercell usage leads to a slight underestimation of δ form stability.

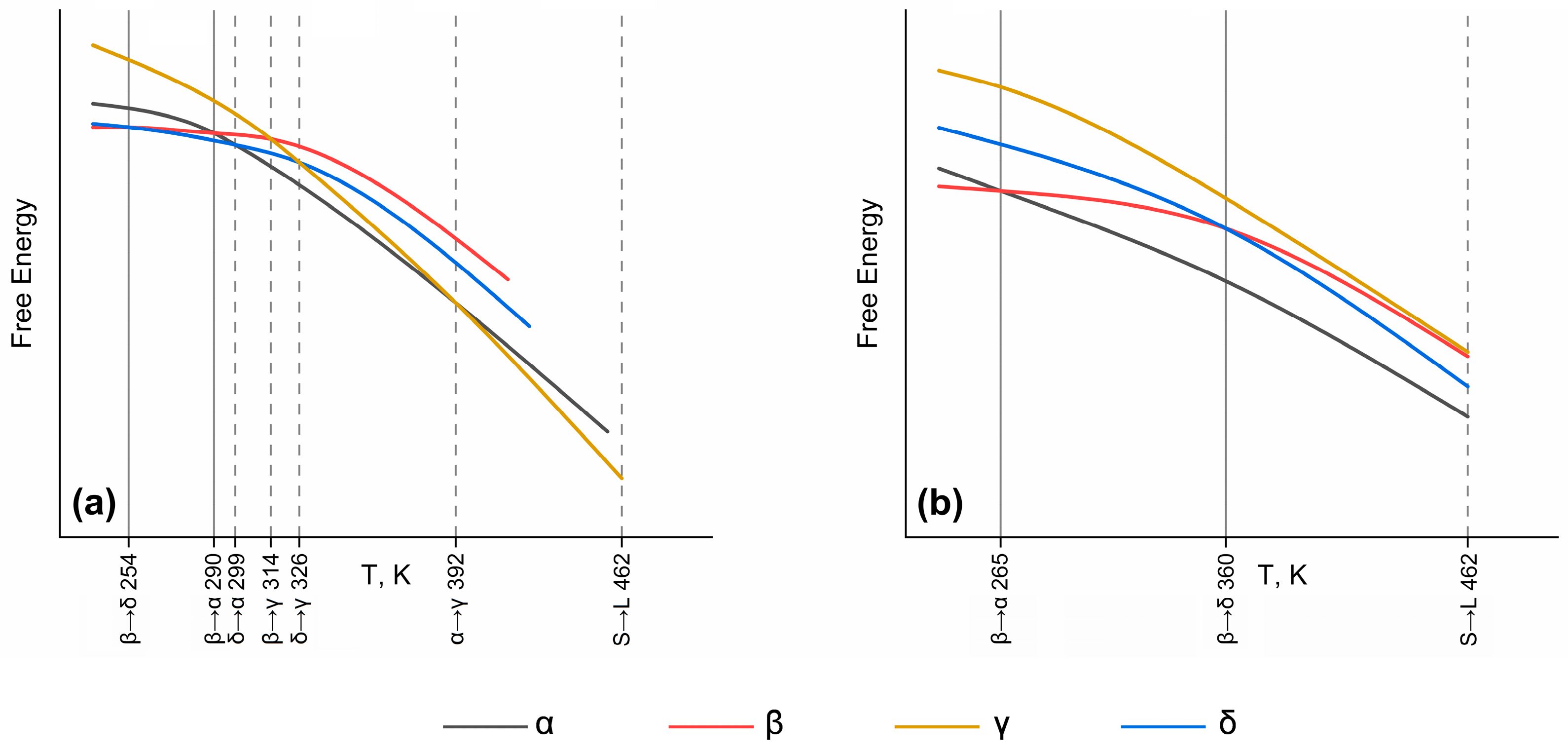
3.3. Thermodynamic Potential Calculations in the 0 K–470 K Temperature Range

The difference between the supercell and primitive cell usage becomes significant when calculating thermodynamic parameters, such as enthalpies and Gibbs energies in a wide range of temperatures (Table 4).
FD calculations using the PBE-D3BJ method with supercells provide enthalpies very close to the experimental values, while DFPT/rev-vdW-DF2 with supercells results in slightly worse agreement with the DSC results [64]. All calculations without supercells mainly show enthalpy overestimation for carefully measured phase transitions (Table 4).
Putting exact values aside, it is valuable to find correlations between methods, which may be a consequence of the usage or absence of supercells, functional choice, or second-order derivative calculation algorithms. A very good correlation between calculations with the use of supercells (as well as the use of primitive cells) was found, which shows the crucial role of supercell construction (Table 5).
Since computational results are mainly affected by supercell use or its absence, we provide a brief comparison of FD and DFPT methods with the same functional and dispersion correction scheme-FD/rev-vdW-DF2 (primitive cell) and DFPT/rev-vdW-DF2 (primitive cell) levels of theory. The calculated enthalpy results have an excellent correlation (r > 0.98), showing almost no difference between the FD and DFPT methods. FD/rev-vdW-DF2 also shows a reasonable correlation of 0.90 with FD/PBE-D3BJ (both without supercells). From this analysis, it is possible to compare the effects of the settings used on the resulting enthalpies of the polymorphic modifications of pyrazinamide: the supercell setting (primitive cell vs. appropriate supercell) has a stronger impact than the functional (PBE-D3BJ vs. rev-vdW-DF2), which in turn affects the results more than the method for second-order derivative computation (FD vs. DFPT).
To better understand how the chosen level of theory (PBE-D3BJ vs. rev-vdW-DF2) as well as the supercell settings (primitive cell vs. supercell with at least 1 nm in each direction) affect the estimation of the relative thermodynamic stability of polymorphs, an attempt was made to analyze the temperature dependences of the Gibbs energy and its enthalpic H and entropic TS terms (Figure 5).
In this figure, the energies are taken with respect to the β form for each temperature point. Therefore, the thermodynamic parameter plots for the β form become horizontal and equal to 0 at this representation. The γ form is treated separately as γ (A), γ (B), and γ and γ (mix), where γ is calculated as a superposition of disordered structures proportional to their ratio in the final structure γ = x1 × γ (A) + x2 × γ (B) and γ (mix) 287 is γ, corrected by T × Smix, where Smix is calculated as the entropy of mixing of ideal solution Smix = R 288 × [x1 × ln(x1) + x2 × ln(x2)], where x1 = 0.866 and x2 = 0.134 for the A disorder and B disorder, correspondingly. The original data (uncorrected to the β form for each temperature) are provided in Figure S2. Calculations performed without supercells predicted that the β form was stable over the entire temperature range, which contradicts the experimental data. The use of supercells reduces the differences in Gibbs energies between polymorphic modifications and leads to the prediction of the thermodynamical possibility of β→ α transition at temperature points between 260 and 270 K and 470 and 480 K (the data have been extrapolated above 470 K for FD/PBE-D3BJ and DFPT/rev-vdW-DF2, respectively. The experimental data suggest that the β form is stable at low temperatures while the α form is stable under ambient conditions. Therefore, the calculated dependences reproduce qualitatively (although not always quantitatively) the α and β forms’ relative stability when supercells are used. Supercell absence drastically affects both enthalpy and entropy terms, while functional choice mainly differs in TS terms, keeping enthalpy trends close; the latter coincides well with previous experimental work (Tables S9–S11) [106].
However, both levels of theory (FD/PBE-D3BJ and DFPT/rev-vdW-DF2) poorly predict the thermodynamics of the disordered high-temperature γ form even with the appropriate supercell setting employed and the mixing entropy correction being introduced to take into account entropic stabilization of disordered structures [61]. The Gibbs energy curve for the γ form calculated using FD/PBE-D3BJ with mixing entropy correction crosses the β form curve and slowly approaches the α form curve and goes almost parallel to the δ form curve. The Gibbs energy curve for the γ form calculated using DFPT/rev-vdW-DF2 moves away from the other polymorph forms (and seems to overestimate the stability of low-temperature phases). Since the FD/PBE-D3BJ level of theory correctly predicted the δ → γ and α → γ transition enthalpy, we can conclude that this deviation from the experiment can be explained by insufficient accuracy in accounting for the entropic stabilization of disordered structures both from theory or XRD experiments, which has already been discussed by N. Wahlberg et. al. [61].

4. Conclusions and Discussion

The effects of the settings used to calculate the thermodynamic parameters of pyrazinamide polymorphs were compared: supercell setting (primitive cell vs. appropriate supercell) has a much stronger impact than the functional choice (PBE-D3BJ vs. rev-vdW-DF2), which in turn affects the results more than the method for second-order derivative computation (finite differences vs. DFPT). This is consistent with the rule of thumb that a suitable supercell has to be used as well as an assumption that finite differences and DFPT should give, in principle, the same results.
A supercell of at least 1 nm in each direction is necessary to obtain reliable thermodynamical potentials of pyrazinamide polymorphs not only for the FD but also for the DFPT approach if the implementation of this method involves the calculation of only gamma point displacements. Thus, given that calculations at q ≠ 0 should also break translational symmetry in the same way as supercell construction, the DFPT method should not be considered as a more accurate alternative to a finite-difference approach (but may be faster).
Functionals and dispersion correction scheme should be tested to verify minor deviation from experimental data prior to thermodynamic calculations of molecular crystals. Both lattice constants and relative energies should be examined, taking into account the accuracy/computational costs ratio. Not only mean but also dispersion values should be taken into account to guarantee an optimal choice for all examined polymorphs.
Although DFPT and FD methods should, in principle, give similar results, it should be borne in mind that the usage of the DFPT method implies the usage of the semi-local functionals, which have not been as widely used as PBE-D3BJ, for example. It follows that the use of DFPT together with the semi-local functional may require additional validation on known experimental data and may not result in the same compromise of accuracy and speed of computation that the widely used PBE-D3BJ provides.
As a result of our comparison of different levels of theory for calculations on pyrazinamide polymorphs systems, we can make some suggestions for choosing the right settings for calculating second derivatives. Firstly, we strongly recommend using a suitable supercell (the length of basis vectors is at least 1 nm) for the calculation of second-order derivatives. Secondly, reasonable functional and dispersion correction choice is substantial for the correct modeling of polymorphic systems. Finally, we recommend choosing the method of calculating second derivatives (DFPT or FD) based on the availability of well-established functionals for the target problem; if there are no semi-local or non-local functionals among these functionals, then it is preferable to use FD, for which a wider range of functionals is available. In the case of polymorphic modifications of molecular organic crystals, we advise to verify all obtained results using available experimental data.

Supplementary Materials

The following supporting information can be downloaded at: https://www.mdpi.com/article/10.3390/cryst15030274/s1. Table S1: VASP symmetry options for various calculations in this and a previous study; Figure S1: Constructed supercells of pyrazinamide polymorphs: (a) α form viewed along the a axis; (b) β form viewed along the b axis; (c) γ form viewed along the b axis, where disordered atom positions are marked as single atoms; and (d) δ form viewed along the a axis; Table S2: Summary of deviation of cell volumes of pyrazinamide polymorph crystalline structures, obtained through optimization using different functionals and dispersion corrections, with respect to the experimental data (PYRZIN22, PYRZIN18, PYRZIN19, and PYRZIN16 for the α, β, γ (both “A” and “B”), and δ forms, respectively; Table S3: Electronic energies of pyrazinamide polymorphs (relative to the β form), obtained using different functionals and dispersion corrections; Table S4: CPU time (in seconds) required for the structural optimization of pyrazinamide polymorph structures using different functionals and dispersion corrections. All of the calculations of CPU time are provided for (2 x) 6-core Intel Xeon X5670, 2.93 GHz (Westmere), with 24 GB RAM; Table S5: Relative ZPE energies for pyrazinamide polymorphs calculated using different methods; Figure S2: Calculated relative thermodynamic parameters for pyrazinamide polymorphs as a function of temperature: (a–c) FD/PBE-D3BJ supercell; (d–f) FD/PBE-D3BJ primitive cell; (g–i) DFPT/rev-vdW-DF2 supercell; (j–l) DFPT/rev-vdW-DF2 primitive cell. From left to right: Gibbs free energy; enthalpy of crystal structures; entropy as the −T × S term. The energies taken with respect to the β form at 0 K. The γ form is treated separately as γ (A), γ (B), and γ and γ (mix) where γ is calculated as a superposition of disordered structures proportional to their ratio in the final structure γ = x1 × γ (A) + x2 × γ (B); γ (mix) is γ, corrected by T × Smix., where Smix is calculated as the standard entropy of mixing Smix = R × [x1 × ln(x1) + x2 × ln(x2)], where x1 = 0.866, and x2 = 0.134 for the A disorder and B disorder, correspondingly; Table S6: Experimental and calculated enthalpies for pyrazinamide polymorph phase transitions at experimental temperatures from the work [64]. This table copies Table 4 from the main text to provide readers with a more convenient comparison of the data obtained from various sources (Tables S7 and S8); Table S7: Experimental and calculated enthalpies for pyrazinamide polymorph phase transitions at experimental temperatures from work [57]; Table S8: Experimental and calculated enthalpies for pyrazinamide polymorph phase transitions at experimental temperatures from work [58]; Table S9: Experimental and calculated entropies for pyrazinamide polymorph phase transitions at experimental temperatures from work; Table S10: Heat capacity temperature dependance (cv(T) in J/mol/K) for pyrazinamide polymorphs calculated using the FD/PBE-D3BJ supercell setting; Table S11: Heat capacity temperature dependance (cv(T) in J/mol/K) for pyrazinamide polymorphs calculated using the DFPT/rev-vdW-DF2 supercell, kJ/mol setting; Table S12: Experimental and optimized unit cell parameters of the α-pyrazinamide polymorph (PYRZIN22) using different functionals and dispersion correction schemes; Table S13: Experimental and optimized unit cell parameters of the β-pyrazinamide polymorph (PYRZIN18) obtained using different functionals and dispersion corrections schemes; Table S14: Experimental and optimized unit cell parameters of the γ(A)-pyrazinamide polymorph (PYRZIN22) obtained using different functionals and dispersion corrections schemes. Table S15: Experimental and optimized unit cell parameters of the γ(B)-pyrazinamide polymorph (PYRZIN22) obtained using different functionals and dispersion corrections schemes. Table S16: Experimental and optimized cell parameters of the δ-pyrazinamide polymorph (PYRZIN22) obtained using different functionals and dispersion corrections schemes.

Author Contributions

Conceptualization, D.A.R.; methodology, D.A.R. and A.S.D.; software, D.A.R. and A.S.D.; validation, D.A.R. and A.S.D.; formal analysis, A.S.D.; investigation, D.A.R. and A.S.D.; resources, D.A.R.; data curation, D.A.R. and A.S.D.; writing—original draft preparation, D.A.R. and A.S.D.; writing—review and editing, D.A.R. and A.S.D.; visualization, A.S.D.; supervision, D.A.R.; project administration, D.A.R.; funding acquisition, D.A.R. All authors have read and agreed to the published version of the manuscript.

Funding

This work was supported by the RSF (Russian Science Foundation) project 23-73-10142 (https://rscf.ru/en/project/23-73-10142/) (accessed on 10 March 2025).

Data Availability Statement

Data are available in the Supplementary Material section and upon reasonable request.

Acknowledgments

The Siberian Branch of the Russian Academy of Sciences (SB RAS) Siberian Supercomputer Center is gratefully acknowledged for providing the supercomputer facilities (http://www.sscc.icmmg.nsc.ru) (accessed on 10 March 2025). The authors also acknowledge the Supercomputing Center of the Novosibirsk State University (http://nusc.nsu.ru) (accessed on 10 March 2025) for providing computational resources.

Conflicts of Interest

The authors declare no conflicts of interest. The funders had no role in the design of the study; in the collection, analysis, or interpretation of the data; in the writing of the manuscript; or in the decision to publish the results.

Abbreviations

The following abbreviations are used in this manuscript:
FDFinite difference
DFPTDensity functional perturbation theory
DFTDensity functional theory
PAWProjector augmented wave (atomic pseudopotentials)
D3BJGrimme D3 with Becke–Johnson damping (function)
PBEPerdew–Burke–Ernzerhof (functional)
rev-vdW-DF2Revised van der Waals density (functional)
AM05Armiento–Mattsson (functional)
PBEsolRevised PBE for solids (functional)
PW91Perdew–Wang (functional)
revPBERevised PBE from Zhang and Yang (functional)
RPBERevised PBE from Hammer et al. (functional)
dDsCdDsC dispersion correction method (dDsC)
DFT-D2DFT-D2 method of Grimme (dispersion correction)
DFT-D3DFT-D3 method of Grimme with zero-damping function (dispersion correction)
DFT-D3BJDFT-D2 method of Grimme with Becke–Johnson damping (dispersion correction)
TSTkatchenko–Scheffler method (dispersion correction)
TS/HITkatchenko–Scheffler method with iterative Hirshfeld partitioning (dispersion correction)
MBD@rsSCSMany-body dispersion energy method (dispersion correction)

References

  1. Brog, J.-P.; Chanez, C.-L.; Crochet, A.; Fromm, K.M. Polymorphism, What It Is and How to Identify It: A Systematic Review. RSC Adv. 2013, 3, 16905. [Google Scholar] [CrossRef]
  2. Cruz-Cabeza, A.J.; Reutzel-Edens, S.M.; Bernstein, J. Facts and Fictions about Polymorphism. Chem. Soc. Rev. 2015, 44, 8619–8635. [Google Scholar] [CrossRef] [PubMed]
  3. Kersten, K.; Kaur, R.; Matzger, A. Survey and Analysis of Crystal Polymorphism in Organic Structures. IUCrJ 2018, 5, 124–129. [Google Scholar] [CrossRef] [PubMed]
  4. Bernstein, J. Polymorphism of Pharmaceuticals. In Polymorphism in Molecular Crystals; Oxford University Press: Oxford, UK, 2020; pp. 342–375. [Google Scholar]
  5. Tandon, R.; Tandon, N.; Gupta, N.; Gupta, R. Art of Synthesis of Desired Polymorphs: A Review. Asian J. Chem. 2018, 30, 5–14. [Google Scholar] [CrossRef]
  6. Ainurofiq, A.; Dinda, K.E.; Pangestika, M.W.; Himawati, U.; Wardhani, W.D.; Sipahutar, Y.T. The Effect of Polymorphism on Active Pharmaceutical Ingredients: A Review. Int. J. Res. Pharm. Sci. 2020, 11, 1621–1630. [Google Scholar] [CrossRef]
  7. Cruz-Cabeza, A.J.; Feeder, N.; Davey, R.J. Open Questions in Organic Crystal Polymorphism. Commun. Chem. 2020, 3, 142. [Google Scholar] [CrossRef]
  8. Braga, D.; Casali, L.; Grepioni, F. The Relevance of Crystal Forms in the Pharmaceutical Field: Sword of Damocles or Innovation Tools? Int. J. Mol. Sci. 2022, 23, 9013. [Google Scholar] [CrossRef]
  9. Kobayashi, Y.; Ito, S.; Itai, S.; Yamamoto, K. Physicochemical Properties and Bioavailability of Carbamazepine Polymorphs and Dihydrate. Int. J. Pharm. 2000, 193, 137–146. [Google Scholar] [CrossRef]
  10. Censi, R.; Di Martino, P. Polymorph Impact on the Bioavailability and Stability of Poorly Soluble Drugs. Molecules 2015, 20, 18759–18776. [Google Scholar] [CrossRef]
  11. Zhou, Y.; Wang, J.; Xiao, Y.; Wang, T.; Huang, X. The Effects of Polymorphism on Physicochemical Properties and Pharmacodynamics of Solid Drugs. Curr. Pharm. Des. 2018, 24, 2375–2382. [Google Scholar] [CrossRef]
  12. Llinàs, A.; Box, K.J.; Burley, J.C.; Glen, R.C.; Goodman, J.M. A New Method for the Reproducible Generation of Polymorphs: Two Forms of Sulindac with Very Different Solubilities. J. Appl. Crystallogr. 2007, 40, 379–381. [Google Scholar] [CrossRef]
  13. Nicoud, L.; Licordari, F.; Myerson, A.S. Estimation of the Solubility of Metastable Polymorphs: A Critical Review. Cryst. Growth Des. 2018, 18, 7228–7237. [Google Scholar] [CrossRef]
  14. McGregor, L.; Rychkov, D.A.D.A.; Coster, P.L.P.L.; Day, S.; Drebushchak, V.A.V.A.; Achkasov, A.F.A.F.; Nichol, G.S.G.S.; Pulham, C.R.C.R.; Boldyreva, E.V.E.V. A New Polymorph of Metacetamol. CrystEngComm 2015, 17, 6183–6192. [Google Scholar] [CrossRef]
  15. Bonilha Dezena, R.M. Ritonavir Polymorphism: Analytical Chemistry Approach to Problem Solving in the Pharmaceutical Industry. Braz. J. Anal. Chem. 2020, 7, 12–17. [Google Scholar] [CrossRef]
  16. Anwar, J.; Zahn, D. Polymorphic Phase Transitions: Macroscopic Theory and Molecular Simulation. Adv. Drug Deliv. Rev. 2017, 117, 47–70. [Google Scholar] [CrossRef] [PubMed]
  17. Belenguer, A.M.; Lampronti, G.I.; Cruz-Cabeza, A.J.; Hunter, C.A.; Sanders, J.K.M. Solvation and Surface Effects on Polymorph Stabilities at the Nanoscale. Chem. Sci. 2016, 7, 6617–6627. [Google Scholar] [CrossRef]
  18. Kras, W.; Carletta, A.; Montis, R.; Sullivan, R.A.; Cruz-Cabeza, A.J. Switching Polymorph Stabilities with Impurities Provides a Thermodynamic Route to Benzamide Form III. Commun. Chem. 2021, 4, 38. [Google Scholar] [CrossRef] [PubMed]
  19. Brits, M.; Liebenberg, W.; de Villiers, M.M. Characterization of Polymorph Transformations That Decrease the Stability of Tablets Containing the WHO Essential Drug Mebendazole. J. Pharm. Sci. 2010, 99, 1138–1151. [Google Scholar] [CrossRef]
  20. Ho, R.; Shin, Y.; Chen, Y.; Poloni, L.; Chen, S.; Sheikh, A.Y. Multiscale Assessment of Api Physical Properties in the Context of Materials Science Tetrahedron Concept. In Chemical Engineering in the Pharmaceutical Industry; John Wiley & Sons, Inc.: Hoboken, NJ, USA, 2019; pp. 689–712. ISBN 9781119600800. [Google Scholar]
  21. Drebushchak, V.A.; McGregor, L.; Rychkov, D.A. Cooling Rate “Window” in the Crystallization of Metacetamol Form II. J. Therm. Anal. Calorim. 2017, 127, 1807–1814. [Google Scholar] [CrossRef]
  22. Mishra, M.K.; Ramamurty, U.; Desiraju, G.R. Solid Solution Hardening of Molecular Crystals: Tautomeric Polymorphs of Omeprazole. J. Am. Chem. Soc. 2015, 137, 1794–1797. [Google Scholar] [CrossRef]
  23. Bag, P.P.; Chen, M.; Sun, C.C.; Reddy, C.M. Direct Correlation among Crystal Structure, Mechanical Behaviour and Tabletability in a Trimorphic Molecular Compound. CrystEngComm 2012, 14, 3865. [Google Scholar] [CrossRef]
  24. Ghosh, S.; Reddy, C.M. Elastic and Bendable Caffeine Cocrystals: Implications for the Design of Flexible Organic Materials. Angew. Chem. Int. Ed. 2012, 51, 10319–10323. [Google Scholar] [CrossRef]
  25. Raju, K.B.; Ranjan, S.; Vishnu, V.S.; Bhattacharya, M.; Bhattacharya, B.; Mukhopadhyay, A.K.; Reddy, C.M. Rationalizing Distinct Mechanical Properties of Three Polymorphs of a Drug Adduct by Nanoindentation and Energy Frameworks Analysis: Role of Slip Layer Topology and Weak Interactions. Cryst. Growth Des. 2018, 18, 3927–3937. [Google Scholar] [CrossRef]
  26. Masunov, A.E.; Wiratmo, M.; Dyakov, A.A.; Matveychuk, Y.V.; Bartashevich, E.V. Virtual Tensile Test for Brittle, Plastic, and Elastic Polymorphs of 4-Bromophenyl 4-Bromobenzoate. Cryst. Growth Des. 2020, 20, 6093–6100. [Google Scholar] [CrossRef]
  27. Domalski, E.S.; Hearing, E.D. Heat Capacities and Entropies of Organic Compounds in the Condensed Phase. Volume III. J. Phys. Chem. Ref. Data 1996, 25, 1. [Google Scholar] [CrossRef]
  28. De Wit, H.G.; Van Miltenburg, J.; De Kruif, C. Thermodynamic Properties of Molecular Organic Crystals Containing Nitrogen, Oxygen, and Sulphur 1. Vapour Pressures and Enthalpies of Sublimation. J. Chem. Thermodyn. 1983, 15, 651–663. [Google Scholar] [CrossRef]
  29. De Wit, H.G.; De Kruif, C.; Van Miltenburg, J. Thermodynamic Properties of Molecular Organic Crystals Containing Nitrogen, Oxygen, and Sulfur II. Molar Heat Capacities of Eight Compounds by Adiabatic Calorimetry. J. Chem. Thermodyn. 1983, 15, 891–902. [Google Scholar] [CrossRef]
  30. De Wit, H.G.M.; Offringa, J.C.A.; De Kruif, C.G.; Van Miltenburg, J.C. Thermodynamic Properties of Molecular Organic Crystals Containing Nitrogen, Oxygen and Sulfur. III. Molar Heat Capacities Measured by Differential Scanning Calorimetry. Thermochim. Acta 1983, 65, 43–51. [Google Scholar] [CrossRef]
  31. Schnieders, M.J.; Baltrusaitis, J.; Shi, Y.; Chattree, G.; Zheng, L.; Yang, W.; Ren, P. The Structure, Thermodynamics, and Solubility of Organic Crystals from Simulation with a Polarizable Force Field. J. Chem. Theory Comput. 2012, 8, 1721–1736. [Google Scholar] [CrossRef]
  32. Palmer, D.S.; McDonagh, J.L.; Mitchell, J.B.O.; van Mourik, T.; Fedorov, M.V. First-Principles Calculation of the Intrinsic Aqueous Solubility of Crystalline Druglike Molecules. J. Chem. Theory Comput. 2012, 8, 3322–3337. [Google Scholar] [CrossRef]
  33. Dybeck, E.C.; Schieber, N.P.; Shirts, M.R. Effects of a More Accurate Polarizable Hamiltonian on Polymorph Free Energies Computed Efficiently by Reweighting Point-Charge Potentials. J. Chem. Theory Comput. 2016, 12, 3491–3505. [Google Scholar] [CrossRef] [PubMed]
  34. Brandenburg, J.G.; Grimme, S. Accurate Modeling of Organic Molecular Crystals by Dispersion-Corrected Density Functional Tight Binding (DFTB). J. Phys. Chem. Lett. 2014, 5, 1785–1789. [Google Scholar] [CrossRef] [PubMed]
  35. Červinka, C.; Fulem, M.; Stoffel, R.P.; Dronskowski, R. Thermodynamic Properties of Molecular Crystals Calculated within the Quasi-Harmonic Approximation. J. Phys. Chem. A 2016, 120, 2022–2034. [Google Scholar] [CrossRef]
  36. Bidault, X.; Chaudhuri, S. Improved Predictions of Thermomechanical Properties of Molecular Crystals from Energy and Dispersion Corrected DFT. J. Chem. Phys. 2021, 154, 164105. [Google Scholar] [CrossRef]
  37. Kapil, V.; Engel, E.A. A Complete Description of Thermodynamic Stabilities of Molecular Crystals. Proc. Natl. Acad. Sci. USA 2022, 119, e2111769119. [Google Scholar] [CrossRef]
  38. Hunnisett, L.M.; Nyman, J.; Francia, N.; Abraham, N.S.; Adjiman, C.S.; Aitipamula, S.; Alkhidir, T.; Almehairbi, M.; Anelli, A.; Anstine, D.M.; et al. The Seventh Blind Test of Crystal Structure Prediction: Structure Generation Methods. Acta Crystallogr. Sect. B Struct. Sci. Cryst. Eng. Mater. 2024, 80, 517–547. [Google Scholar] [CrossRef] [PubMed]
  39. Groom, C.R.; Reilly, A.M. Sixth Blind Test of Organic Crystal-Structure Prediction Methods. Acta Crystallogr. Sect. B Struct. Sci. Cryst. Eng. Mater. 2014, 70, 776–777. [Google Scholar] [CrossRef]
  40. Bardwell, D.A.; Adjiman, C.S.; Arnautova, Y.A.; Bartashevich, E.; Boerrigter, S.X.M.; Braun, D.E.; Cruz-Cabeza, A.J.; Day, G.M.; Della Valle, R.G.; Desiraju, G.R.; et al. Towards Crystal Structure Prediction of Complex Organic—A Report on the Fifth Blind Test. Acta Crystallogr. Sect. B Struct. Sci. 2011, 67, 535–551. [Google Scholar] [CrossRef]
  41. Hoja, J.; Reilly, A.M.; Tkatchenko, A. First-Principles Modeling of Molecular Crystals: Structures and Stabilities, Temperature and Pressure. Wiley Interdiscip. Rev. Comput. Mol. Sci. 2017, 7, e1294. [Google Scholar] [CrossRef]
  42. Hasan, S.; Rulis, P.; Ching, W.Y. First-Principles Calculations of the Structural, Electronic, Optical, and Mechanical Properties of 21 Pyrophosphate Crystals. Crystals 2022, 12, 1139. [Google Scholar] [CrossRef]
  43. Dubok, A.S.; Rychkov, D. Deformcell: A Python Script to Simplify and Fasten Mechanical Properties Calculations of Molecular Crystals in VASP Package for Research and Teaching Purposes. J. Struct. Chem. 2024, 65, 132571. [Google Scholar] [CrossRef]
  44. Mardirossian, N.; Head-Gordon, M. Thirty Years of Density Functional Theory in Computational Chemistry: An Overview and Extensive Assessment of 200 Density Functionals. Mol. Phys. 2017, 115, 2315–2372. [Google Scholar] [CrossRef]
  45. Medvedev, M.G.; Bushmarinov, I.S.; Sun, J.; Perdew, J.P.; Lyssenko, K.A. Density Functional Theory Is Straying from the Path toward the Exact Functional. Science 2017, 355, 49–52. [Google Scholar] [CrossRef] [PubMed]
  46. Kamencek, T.; Wieser, S.; Kojima, H.; Bedoya-Martínez, N.; Dürholt, J.P.; Schmid, R.; Zojer, E. Evaluating Computational Shortcuts in Supercell-Based Phonon Calculations of Molecular Crystals: The Instructive Case of Naphthalene. J. Chem. Theory Comput. 2020, 16, 2716–2735. [Google Scholar] [CrossRef]
  47. Duong, T.C.; Paulson, N.H.; Stan, M.; Chaudhuri, S. An Efficient Approximation of the Supercell Approach to the Calculation of the Full Phonon Spectrum. Calphad 2021, 72, 102215. [Google Scholar] [CrossRef]
  48. Shang, H.; Carbogno, C.; Rinke, P.; Scheffler, M. Lattice Dynamics Calculations Based on Density-Functional Perturbation Theory in Real Space. Comput. Phys. Commun. 2017, 215, 26–46. [Google Scholar] [CrossRef]
  49. Running Phonon Calculations. Available online: https://www.tcm.phy.cam.ac.uk/castep/Phonons_Guide/2-sec:examples.html#sec:dfpt-gamma (accessed on 10 March 2025).
  50. Sholl, D.S.; Steckel, J.A. Density Functional Theory; Wiley: Hoboken, NJ, USA, 2009; ISBN 9780470373170. [Google Scholar]
  51. Lee, J.G. Computational Materials Science, 2nd ed.; CRC Press, Taylor & Francis: Boca Raton, FL, USA, 2016; ISBN 9781315368429. [Google Scholar]
  52. Martin, R.M. Electronic Structure; Cambridge University Press: Cambridge, UK, 2020; ISBN 9781108555586. [Google Scholar]
  53. Takaki, Y.; Sasada, Y.; Watanabé, T. The Crystal Structure of α-Pyrazinamide. Acta Crystallogr. 1960, 13, 693–702. [Google Scholar] [CrossRef]
  54. Rø, G.; Sørum, H. The Crystal and Molecular Structure of β-Pyrazinecarboxamide. Acta Crystallogr. Sect. B Struct. Crystallogr. Cryst. Chem. 1972, 28, 991–998. [Google Scholar] [CrossRef]
  55. Tamura, C.; Kuwano, H. Crystallographic Data of Carboxylic Acids and Carboxyamides of Picoline and Pyrazine Derivatives. Acta Crystallogr. 1961, 14, 693–694. [Google Scholar] [CrossRef]
  56. Rø, G.; Sørum, H. The Crystal and Molecular Structure of δ-Pyrazinecarboxamide. Acta Crystallogr. Sect. B Struct. Crystallogr. Cryst. Chem. 1972, 28, 1677–1684. [Google Scholar] [CrossRef]
  57. Cherukuvada, S.; Thakuria, R.; Nangia, A. Pyrazinamide Polymorphs: Relative Stability and Vibrational Spectroscopy. Cryst. Growth Des. 2010, 10, 3931–3941. [Google Scholar] [CrossRef]
  58. Castro, R.A.E.; Maria, T.M.R.; Évora, A.O.L.; Feiteira, J.C.; Silva, M.R.; Beja, A.M.; Canotilho, J.; Eusébio, M.E.S. A New Insight into Pyrazinamide Polymorphic Forms and Their Thermodynamic Relationships. Cryst. Growth Des. 2010, 10, 274–282. [Google Scholar] [CrossRef]
  59. Borba, A.; Albrecht, M.; Gómez-Zavaglia, A.; Suhm, M.A.; Fausto, R. Low Temperature Infrared Spectroscopy Study of Pyrazinamide: From the Isolated Monomer to the Stable Low Temperature Crystalline Phase. J. Phys. Chem. A 2010, 114, 151–161. [Google Scholar] [CrossRef]
  60. Rajalakshmi, G.; Hathwar, V.R.; Kumaradhas, P. Intermolecular Interactions, Charge-Density Distribution and the Electrostatic Properties of Pyrazinamide Anti-TB Drug Molecule: An Experimental and Theoretical Charge-Density Study. Acta Crystallogr. Sect. B Struct. Sci. Cryst. Eng. Mater. 2014, 70, 568–579. [Google Scholar] [CrossRef] [PubMed]
  61. Wahlberg, N.; Ciochoń, P.; Petriĉek, V.; Madsen, A.Ø. Polymorph Stability Prediction: On the Importance of Accurate Structures: A Case Study of Pyrazinamide. Cryst. Growth Des. 2014, 14, 381–388. [Google Scholar] [CrossRef]
  62. Hoser, A.A.; Rekis, T.; Madsen, A.Ø. Dynamics and Disorder: On the Stability of Pyrazinamide Polymorphs. Acta Crystallogr. Sect. B Struct. Sci. Cryst. Eng. Mater. 2022, 78, 416–424. [Google Scholar] [CrossRef]
  63. David, S.; Nidhin, P.V.; Srinivasan, P. Ab Initio Prediction of the Polymorphic Structures of Pyrazinamide: A Validation Study. J. Serbian Chem. Soc. 2016, 81, 763–776. [Google Scholar] [CrossRef]
  64. Li, K.; Gbabode, G.; Vergé-Depré, M.; Robert, B.; Barrio, M.; Itié, J.-P.; Tamarit, J.-L.; Rietveld, I.B. The Pressure–temperature Phase Diagram of Tetramorphic Pyrazinamide. CrystEngComm 2022, 24, 5041–5051. [Google Scholar] [CrossRef]
  65. Dubok, A.S.; Rychkov, D.A. Relative Stability of Pyrazinamide Polymorphs Revisited: A Computational Study of Bending and Brittle Forms Phase Transitions in a Broad Temperature Range. Crystals 2023, 13, 617. [Google Scholar] [CrossRef]
  66. Nangia, A.; Srinivasulu, A. CSD Communication (Private Communication); CCDC: Boston, MA, USA, 2005. [Google Scholar] [CrossRef]
  67. Björkman, T. CIF2Cell: Generating Geometries for Electronic Structure Programs. Comput. Phys. Commun. 2011, 182, 1183–1186. [Google Scholar] [CrossRef]
  68. Kresse, G.; Hafner, J. Ab Initio Molecular Dynamics for Liquid Metals. Phys. Rev. B 1993, 47, 558–561. [Google Scholar] [CrossRef] [PubMed]
  69. Kresse, G.; Hafner, J. Ab Initio Molecular-Dynamics Simulation of the Liquid-Metal–amorphous-Semiconductor Transition in Germanium. Phys. Rev. B 1994, 49, 14251–14269. [Google Scholar] [CrossRef] [PubMed]
  70. Kresse, G.; Furthmüller, J. Efficient Iterative Schemes for Ab Initio Total-Energy Calculations Using a Plane-Wave Basis Set. Phys. Rev. B 1996, 54, 11169–11186. [Google Scholar] [CrossRef] [PubMed]
  71. Kresse, G.; Furthmüller, J. Efficiency of Ab-Initio Total Energy Calculations for Metals and Semiconductors Using a Plane-Wave Basis Set. Comput. Mater. Sci. 1996, 6, 15–50. [Google Scholar] [CrossRef]
  72. Perdew, J.P.; Burke, K.; Ernzerhof, M. Generalized Gradient Approximation Made Simple. Phys. Rev. Lett. 1996, 77, 3865–3868. [Google Scholar] [CrossRef]
  73. Hamada, I. Van Der Waals Density Functional Made Accurate. Phys. Rev. B 2014, 89, 121103. [Google Scholar] [CrossRef]
  74. Blöchl, P.E. Projector Augmented-Wave Method. Phys. Rev. B 1994, 50, 17953–17979. [Google Scholar] [CrossRef]
  75. Kresse, G.; Joubert, D. From Ultrasoft Pseudopotentials to the Projector Augmented-Wave Method. Phys. Rev. B 1999, 59, 1758–1775. [Google Scholar] [CrossRef]
  76. Monkhorst, H.J.; Pack, J.D. Special Points for Brillouin-Zone Integrations. Phys. Rev. B 1976, 13, 5188–5192. [Google Scholar] [CrossRef]
  77. Grimme, S.; Ehrlich, S.; Goerigk, L. Effect of the Damping Function in Dispersion Corrected Density Functional Theory. J. Comput. Chem. 2011, 32, 1456–1465. [Google Scholar] [CrossRef]
  78. Armiento, R.; Mattsson, A.E. Functional Designed to Include Surface Effects in Self-Consistent Density Functional Theory. Phys. Rev. B 2005, 72, 085108. [Google Scholar] [CrossRef]
  79. Mattsson, A.E.; Armiento, R.; Paier, J.; Kresse, G.; Wills, J.M.; Mattsson, T.R. The AM05 Density Functional Applied to Solids. J. Chem. Phys. 2008, 128, 084714. [Google Scholar] [CrossRef]
  80. Mattsson, A.E.; Armiento, R. Implementing and Testing the AM05 Spin Density Functional. Phys. Rev. B Condens. Matter Mater. Phys. 2009, 79, 155101. [Google Scholar] [CrossRef]
  81. Perdew, J.P.; Ruzsinszky, A.; Csonka, G.I.; Vydrov, O.A.; Scuseria, G.E.; Constantin, L.A.; Zhou, X.; Burke, K. Restoring the Density-Gradient Expansion for Exchange in Solids and Surfaces. Phys. Rev. Lett. 2008, 100, 136406. [Google Scholar] [CrossRef]
  82. Perdew, J.P.; Chevary, J.A.; Vosko, S.H.; Jackson, K.A.; Pederson, M.R.; Singh, D.J.; Fiolhais, C. Atoms, Molecules, Solids, and Surfaces: Applications of the Generalized Gradient Approximation for Exchange and Correlation. Phys. Rev. B 1992, 46, 6671–6687. [Google Scholar] [CrossRef] [PubMed]
  83. Zhang, Y.; Yang, W. Comment on “Generalized Gradient Approximation Made Simple”. Phys. Rev. Lett. 1998, 80, 890. [Google Scholar] [CrossRef]
  84. Hammer, B.; Hansen, L.B.; Nørskov, J.K. Improved Adsorption Energetics within Density-Functional Theory Using Revised Perdew-Burke-Ernzerhof Functionals. Phys. Rev. B Condens. Matter Mater. Phys. 1999, 59, 7413–7421. [Google Scholar] [CrossRef]
  85. Steinmann, S.N.; Corminboeuf, C. A Generalized-Gradient Approximation Exchange Hole Model for Dispersion Coefficients. J. Chem. Phys. 2011, 134, 044117. [Google Scholar] [CrossRef]
  86. Steinmann, S.N.; Corminboeuf, C. Comprehensive Benchmarking of a Density-Dependent Dispersion Correction. J. Chem. Theory Comput. 2011, 7, 3567–3577. [Google Scholar] [CrossRef]
  87. Grimme, S. Semiempirical GGA-type Density Functional Constructed with a Long-range Dispersion Correction. J. Comput. Chem. 2006, 27, 1787–1799. [Google Scholar] [CrossRef]
  88. Grimme, S.; Antony, J.; Ehrlich, S.; Krieg, H. A Consistent and Accurate Ab Initio Parametrization of Density Functional Dispersion Correction (DFT-D) for the 94 Elements H-Pu. J. Chem. Phys. 2010, 132, 154104. [Google Scholar] [CrossRef]
  89. Tkatchenko, A.; DiStasio, R.A.; Car, R.; Scheffler, M. Accurate and Efficient Method for Many-Body van Der Waals Interactions. Phys. Rev. Lett. 2012, 108, 236402. [Google Scholar] [CrossRef]
  90. Ambrosetti, A.; Reilly, A.M.; DiStasio, R.A.; Tkatchenko, A. Long-Range Correlation Energy Calculated from Coupled Atomic Response Functions. J. Chem. Phys. 2014, 140, 18A508. [Google Scholar] [CrossRef] [PubMed]
  91. Tkatchenko, A.; Scheffler, M. Accurate Molecular Van Der Waals Interactions from Ground-State Electron Density and Free-Atom Reference Data. Phys. Rev. Lett. 2009, 102, 073005. [Google Scholar] [CrossRef]
  92. Bučko, T.; Lebègue, S.; Hafner, J.; Ángyán, J.G. Improved Density Dependent Correction for the Description of London Dispersion Forces. J. Chem. Theory Comput. 2013, 9, 4293–4299. [Google Scholar] [CrossRef] [PubMed]
  93. Bučko, T.; Lebègue, S.; Ángyán, J.G.; Hafner, J. Extending the Applicability of the Tkatchenko-Scheffler Dispersion Correction via Iterative Hirshfeld Partitioning. J. Chem. Phys. 2014, 141, 034114. [Google Scholar] [CrossRef]
  94. Togo, A.; Tanaka, I. First Principles Phonon Calculations in Materials Science. Scr. Mater. 2015, 108, 1–5. [Google Scholar] [CrossRef]
  95. Togo, A. First-Principles Phonon Calculations with Phonopy and Phono3py. J. Phys. Soc. Jpn. 2023, 92, 012001. [Google Scholar] [CrossRef]
  96. Borioni, J.L.; Puiatti, M.; Vera, D.M.A.; Pierini, A.B. In Search of the Best DFT Functional for Dealing with Organic Anionic Species. Phys. Chem. Chem. Phys. 2017, 19, 9189–9198. [Google Scholar] [CrossRef] [PubMed]
  97. Venkatraman, V.; Abburu, S.; Alsberg, B.K. Can Chemometrics Be Used to Guide the Selection of Suitable DFT Functionals? Chemom. Intell. Lab. Syst. 2015, 142, 87–94. [Google Scholar] [CrossRef]
  98. Brandenburg, J.G.; Grimme, S. Organic Crystal Polymorphism: A Benchmark for Dispersion-Corrected Mean-Field Electronic Structure Methods. Acta Crystallogr. Sect. B Struct. Sci. Cryst. Eng. Mater. 2016, 72, 502–513. [Google Scholar] [CrossRef]
  99. Terentjev, A.V.; Constantin, L.A.; Pitarke, J.M. Dispersion-Corrected PBEsol Exchange-Correlation Functional. Phys. Rev. B 2018, 98, 214108. [Google Scholar] [CrossRef]
  100. Csonka, G.I.; Perdew, J.P.; Ruzsinszky, A.; Philipsen, P.H.T.; Lebègue, S.; Paier, J.; Vydrov, O.A.; Ángyán, J.G. Assessing the Performance of Recent Density Functionals for Bulk Solids. Phys. Rev. B Condens. Matter Mater. Phys. 2009, 79, 155107. [Google Scholar] [CrossRef]
  101. Beran, G.J.O. Modeling Polymorphic Molecular Crystals with Electronic Structure Theory. Chem. Rev. 2016, 116, 5567–5613. [Google Scholar] [CrossRef] [PubMed]
  102. Nyman, J.; Day, G.M. Static and Lattice Vibrational Energy Differences between Polymorphs. CrystEngComm 2015, 17, 5154–5165. [Google Scholar] [CrossRef]
  103. Fedorov, A.Y.; Rychkov, D.A.; Losev, E.A.; Zakharov, B.A.; Stare, J.; Boldyreva, E.V. Effect of Pressure on Two Polymorphs of Tolazamide: Why No Interconversion? CrystEngComm 2017, 19, 2243–2252. [Google Scholar] [CrossRef]
  104. Dolgonos, G.A.; Hoja, J.; Boese, A.D. Revised Values for the X23 Benchmark Set of Molecular Crystals. Phys. Chem. Chem. Phys. 2019, 21, 24333–24344. [Google Scholar] [CrossRef]
  105. O’Connor, D.; Bier, I.; Hsieh, Y.-T.; Marom, N. Performance of Dispersion-Inclusive Density Functional Theory Methods for Energetic Materials. J. Chem. Theory Comput. 2022, 18, 4456–4471. [Google Scholar] [CrossRef]
  106. Li, K.; Gbabode, G.; Barrio, M.; Tamarit, J.-L.; Vergé-Depré, M.; Robert, B.; Rietveld, I.B. The Phase Relationship between the Pyrazinamide Polymorphs α and γ. Int. J. Pharm. 2020, 580, 119230. [Google Scholar] [CrossRef]
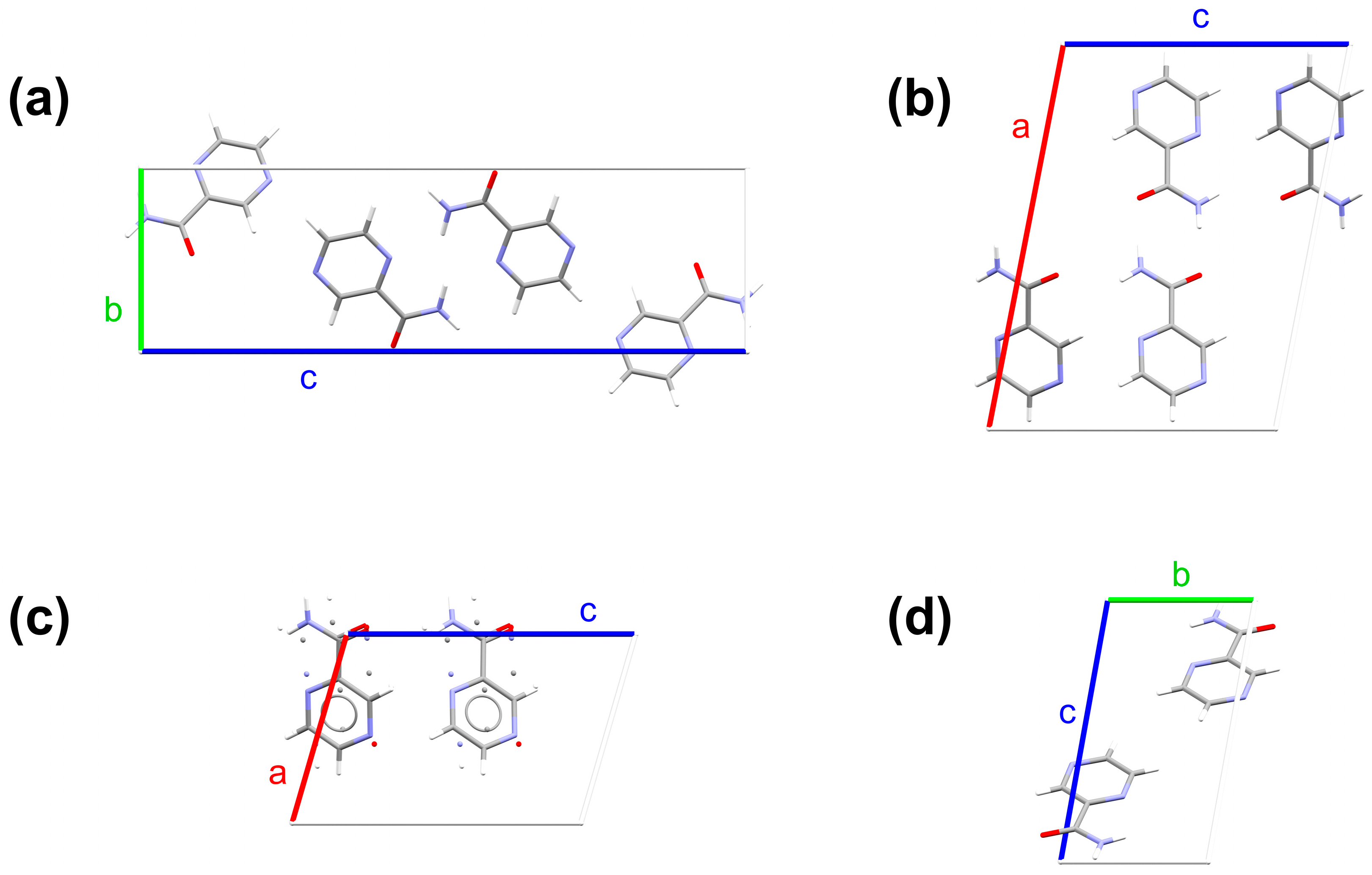
Crystals 15 00274 g001
Figure 1. Primitive cells of pyrazinamide polymorphs: (a) α form viewed along the a axis; (b) β form viewed along the b axis; (c) γ form viewed along the b axis, where disordered atom positions are marked as single atoms; and (d) δ form viewed along the a axis. Colors are: oxygen—red, nitrogen—blue, carbon—grey, hydrogen—white.
Figure 1. Primitive cells of pyrazinamide polymorphs: (a) α form viewed along the a axis; (b) β form viewed along the b axis; (c) γ form viewed along the b axis, where disordered atom positions are marked as single atoms; and (d) δ form viewed along the a axis. Colors are: oxygen—red, nitrogen—blue, carbon—grey, hydrogen—white.
Crystals 15 00274 g001
Crystals 15 00274 g002
Figure 2. An energy–temperature schematic diagram for the four solid phases based on experimental (a) and computational (b) results.
Figure 2. An energy–temperature schematic diagram for the four solid phases based on experimental (a) and computational (b) results.
Crystals 15 00274 g002
Crystals 15 00274 g003
Figure 3. Unit cell volume deviation of pyrazinamide polymorphic structures optimized using different functionals with respect to experimental data (PYRZIN22, PYRZIN18, PYRZIN19, and PYRZIN16) for the α, β, γ (both “A” and “B”), and δ forms, respectively.
Figure 3. Unit cell volume deviation of pyrazinamide polymorphic structures optimized using different functionals with respect to experimental data (PYRZIN22, PYRZIN18, PYRZIN19, and PYRZIN16) for the α, β, γ (both “A” and “B”), and δ forms, respectively.
Crystals 15 00274 g003
Crystals 15 00274 g004
Figure 4. Relative unit cell volume deviation of pyrazinamide polymorphic structures optimized using the PBE functional and different dispersion correction schemes with respect to the experimental data (PYRZIN22, PYRZIN18, PYRZIN19, and PYRZIN16) for the α, β, γ (both “A” and “B”), and δ forms, respectively.
Figure 4. Relative unit cell volume deviation of pyrazinamide polymorphic structures optimized using the PBE functional and different dispersion correction schemes with respect to the experimental data (PYRZIN22, PYRZIN18, PYRZIN19, and PYRZIN16) for the α, β, γ (both “A” and “B”), and δ forms, respectively.
Crystals 15 00274 g004
Crystals 15 00274 g005
Figure 5. Calculated relative thermodynamic parameters for pyrazinamide polymorphs as a function of temperature (a–c) FD/PBE-D3BJ supercell; (d–f) FD/PBE-D3BJ primitive cell; (g–i) DFPT/rev-vdW-DF2 supercell; (j–l) DFPT/rev-vdW-DF2 primitive cell. From left to right: Gibbs free energy; enthalpy of crystal structures; and entropy as the −T × S term.
Figure 5. Calculated relative thermodynamic parameters for pyrazinamide polymorphs as a function of temperature (a–c) FD/PBE-D3BJ supercell; (d–f) FD/PBE-D3BJ primitive cell; (g–i) DFPT/rev-vdW-DF2 supercell; (j–l) DFPT/rev-vdW-DF2 primitive cell. From left to right: Gibbs free energy; enthalpy of crystal structures; and entropy as the −T × S term.
Crystals 15 00274 g005
Table 1. DFPT implementation in the most popular plane-wave DFT software. q = 0 means that only Gamma point calculations (at the center of the Brillouin zone) are supported whereas q ≠ 0 means that generic q-points (also known as q-vectors) are available.
Table 1. DFPT implementation in the most popular plane-wave DFT software. q = 0 means that only Gamma point calculations (at the center of the Brillouin zone) are supported whereas q ≠ 0 means that generic q-points (also known as q-vectors) are available.
SoftwareVASP
(5.4.4/6.4.3)		CASTEP
(23.1.1)		Quantum Espresso
(7.3)		ABINIT
(10.2.3)
DFPT implementationq = 0q = 0 and q ≠ 0q = 0 and q ≠ 0q = 0 and q ≠ 0
Table 2. Relative electronic structure energies (kJ/mol) of pyrazinamide polymorphs obtained from plane-wave periodic DFT calculations using different methods. The energies were accidentally swapped for these two methods in our previous study [65] and are corrected herein by switching off the symmetry option.
Table 2. Relative electronic structure energies (kJ/mol) of pyrazinamide polymorphs obtained from plane-wave periodic DFT calculations using different methods. The energies were accidentally swapped for these two methods in our previous study [65] and are corrected herein by switching off the symmetry option.
Calculation Methodαβγ(A)γ(B)γδ
PBE-D3BJ, kJ/mol *2.7 (III)0 (I)3.110.04.1 (IV)2.1 (II)
rev-vdW-DF2, kJ/mol *2.1 (III)0 (I)2.07.02.6 (IV)1.1 (II)
* The relative stability rank is given in brackets.
Table 3. Relative Gibbs energy * of pyrazinamide polymorphs calculated as a sum of full electronic energies and ZPE vibrations using the finite difference approach (PBE-D3BJ) and DFPT (rev-vdW-DF2) with and without the supercell.
Table 3. Relative Gibbs energy * of pyrazinamide polymorphs calculated as a sum of full electronic energies and ZPE vibrations using the finite difference approach (PBE-D3BJ) and DFPT (rev-vdW-DF2) with and without the supercell.
Calculation MethodAΒγ(A)γ(B)γδ
FD/PBE-D3BJ supercell, kJ/mol2.0 (II–III)0 (I)3.19.64.0 (IV)2.0 (II–III)
FD/PBE-D3BJ primitive cell, kJ/mol1.8 (II)0 (I)2.99.93.8 (IV)2.2 (III)
DFPT/rev-vdW-DF2 supercell, kJ/mol1.5 (III)0 (I)1.96.82.6 (IV)1.0 (II)
DFPT/rev-vdW-DF2 primitive cell, kJ/mol1.3 (II–III)0 (I)1.87.12.5 (IV)1.3 (II–III)
FD/rev-vdW-DF2 primitive cell, kJ/mol1.3(II)0 (I)1.97.22.6 (IV)1.5 (III)
* The relative stability rank is given in brackets.
Table 4. Experimental and calculated enthalpies for pyrazinamide polymorph phase transitions at different experimental temperatures [64].
Table 4. Experimental and calculated enthalpies for pyrazinamide polymorph phase transitions at different experimental temperatures [64].
MethodΔ → αΒ → γΔ → γA → γ
1 Ttrans, K299314326399
1 Exp. ΔH, kJ/mol0.42.22.11.6
FD/PBE-D3BJ supercell, kJ/mol0.2–4.51.71.6
FD/PBE-D3BJ primitive cell, kJ/mol2.03.04.92.9
DFPT/rev-vdW-DF2 supercell, kJ/mol0.72.11.10.3
DFPT/rev-vdW-DF2 primitive cell, kJ/mol2.11.84.72.8
FD/rev-vdW-DF2 primitive cell, kJ/mol1.81.94.63.1
1 Data according to ref. [64]. A full list of experimental data on the temperatures and enthalpies of phase transitions in comparison with the calculated values is provided in the Supplementary Information section (Tables S6–S8).
Table 5. Correlation matrix constructed from the calculated enthalpies at different levels of theory for the phase transitions of pyrazinamide polymorphs at experimental temperatures from ref. [64]. The values in the table correspond to the Pearson correlation coefficients for each pair of different levels of theory. This coefficient has a value from 1 to −1, which corresponds to a perfect direct to inverse linear relationship, respectively; a value of 0 means that the two sets of enthalpies are linearly independent. Colors are provided for clarity.
Table 5. Correlation matrix constructed from the calculated enthalpies at different levels of theory for the phase transitions of pyrazinamide polymorphs at experimental temperatures from ref. [64]. The values in the table correspond to the Pearson correlation coefficients for each pair of different levels of theory. This coefficient has a value from 1 to −1, which corresponds to a perfect direct to inverse linear relationship, respectively; a value of 0 means that the two sets of enthalpies are linearly independent. Colors are provided for clarity.
FD/PBE-D3BJ SupercellFD/PBE-D3BJ Primitive CellDFPT/Rev-Vdw-DF2 SupercellDFPT/Rev-vdW-DF2 Primitive CellFD/Rev-Vdw-DF2 Primitive Cell
FD/PBE-D3BJ supercell10.190.85−0.26−0.16
FD/PBE-D3BJ primitive cell0.1910.180.900.91
DFPT/rev-vdW-DF2 supercell0.850.181−0.24−0.24
DFPT/rev-vdW-DF2 primitive cell−0.260.90−0.2410.98
FD/rev-vdW-DF2 primitive cell−0.160.91−0.240.981
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.

Share and Cite

MDPI and ACS Style

Dubok, A.S.; Rychkov, D.A. What Is More Important When Calculating the Thermodynamic Properties of Organic Crystals, Density Functional, Supercell, or Energy Second-Order Derivative Method Choice? Crystals 2025, 15, 274. https://doi.org/10.3390/cryst15030274

AMA Style

Dubok AS, Rychkov DA. What Is More Important When Calculating the Thermodynamic Properties of Organic Crystals, Density Functional, Supercell, or Energy Second-Order Derivative Method Choice? Crystals. 2025; 15(3):274. https://doi.org/10.3390/cryst15030274

Chicago/Turabian Style

Dubok, Aleksandr S., and Denis A. Rychkov. 2025. "What Is More Important When Calculating the Thermodynamic Properties of Organic Crystals, Density Functional, Supercell, or Energy Second-Order Derivative Method Choice?" Crystals 15, no. 3: 274. https://doi.org/10.3390/cryst15030274

APA Style

Dubok, A. S., & Rychkov, D. A. (2025). What Is More Important When Calculating the Thermodynamic Properties of Organic Crystals, Density Functional, Supercell, or Energy Second-Order Derivative Method Choice? Crystals, 15(3), 274. https://doi.org/10.3390/cryst15030274

Note that from the first issue of 2016, this journal uses article numbers instead of page numbers. See further details here.

Article Metrics

Back to TopTop