Tunable Dual Plasmon-Induced Transparency Based on Homogeneous Graphene-Metal Metasurfaces at Terahertz Frequency
Abstract
1. Introduction
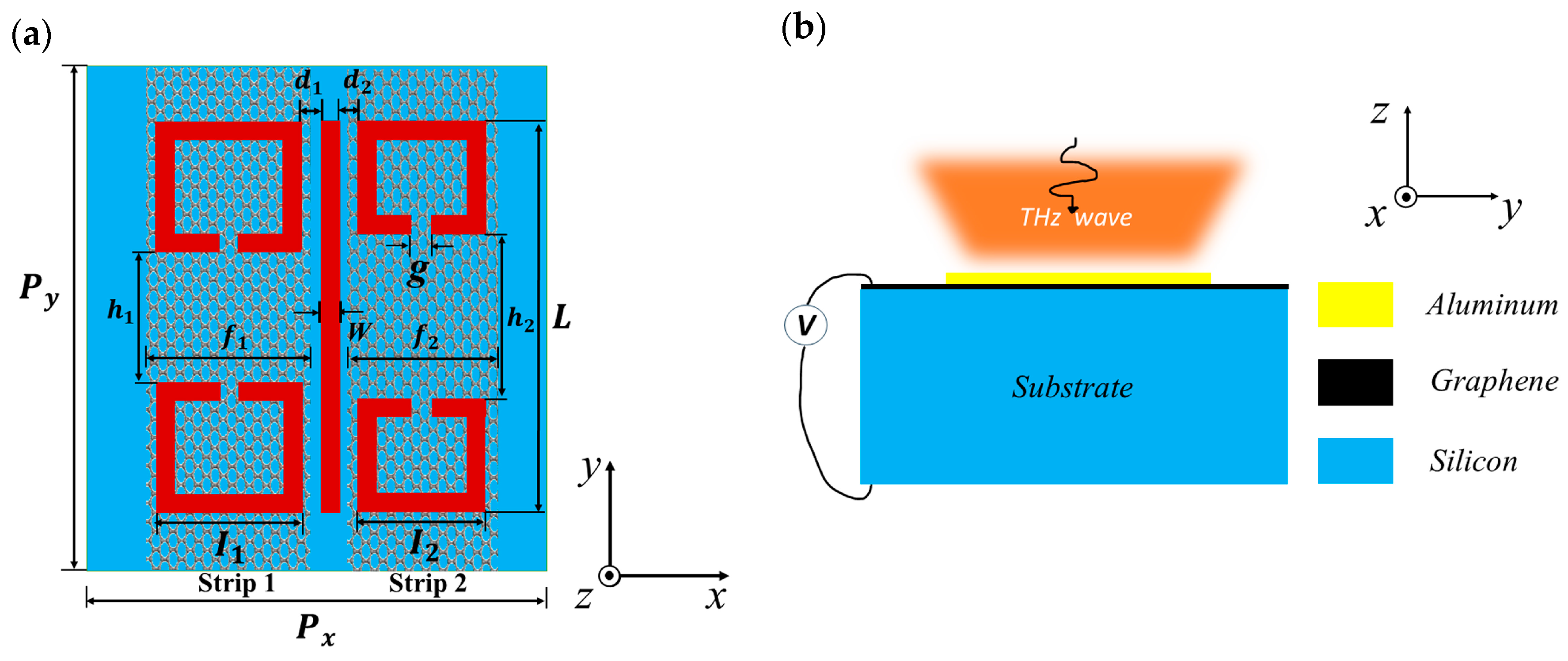
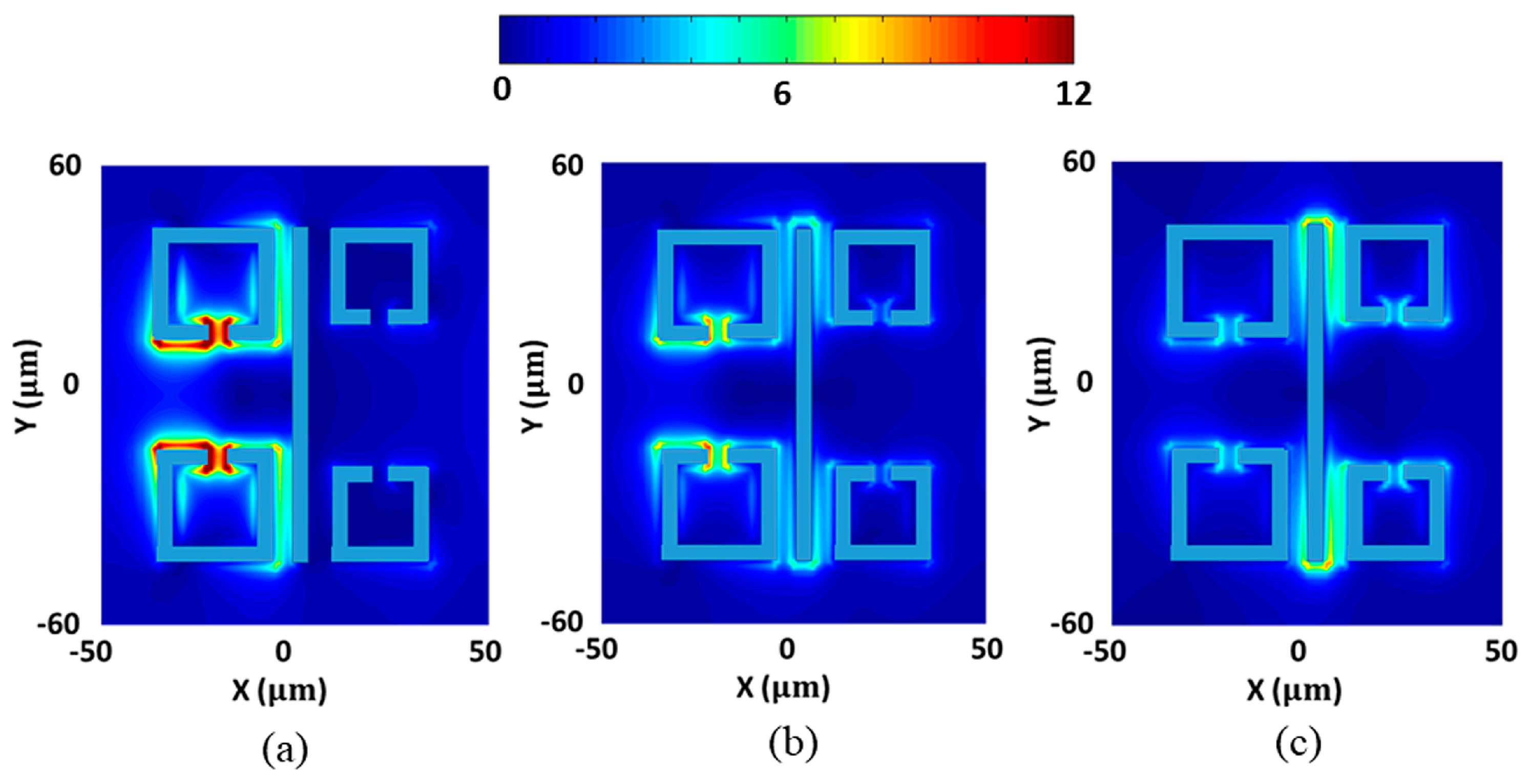
2. Materials and Methods
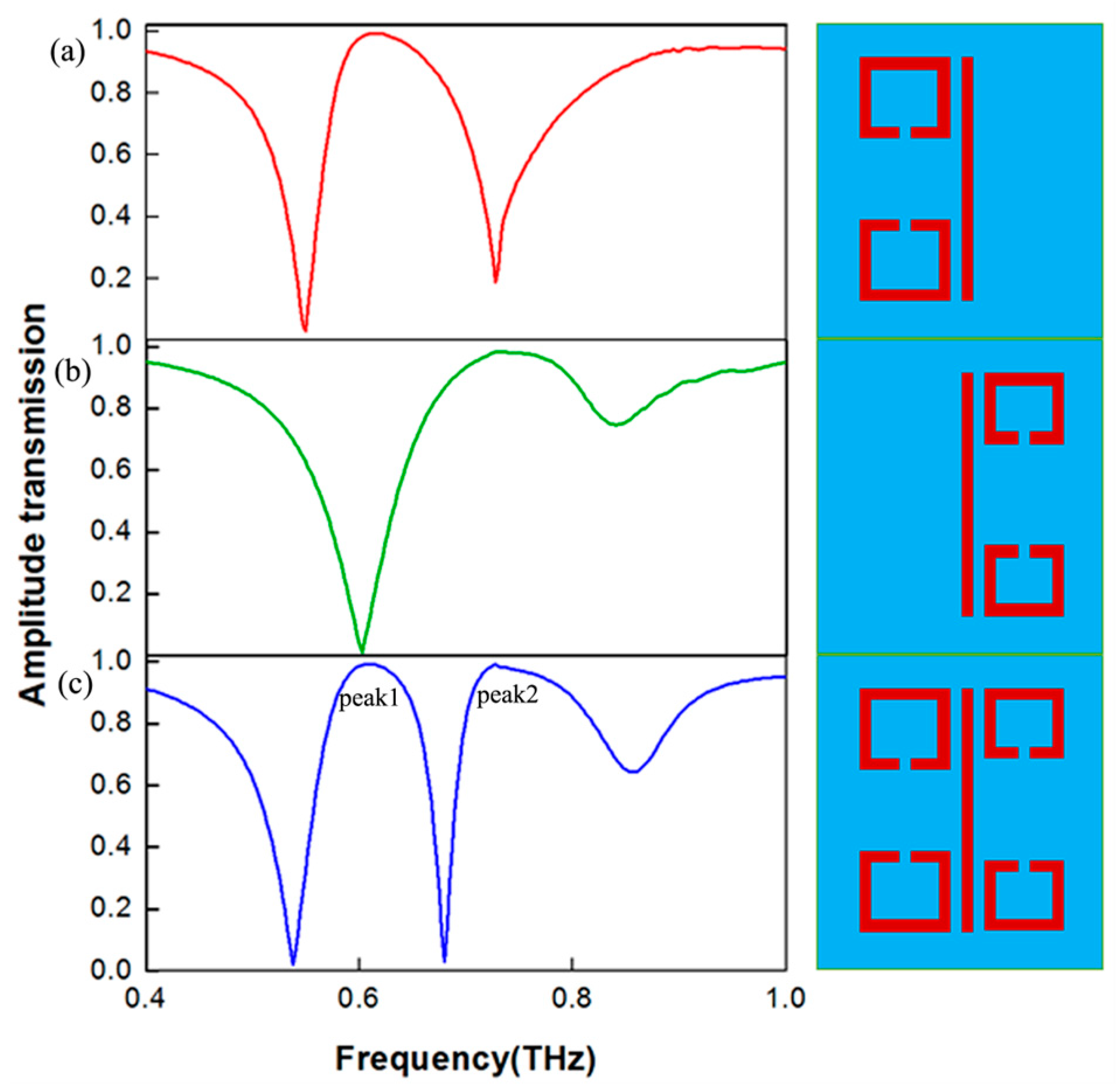
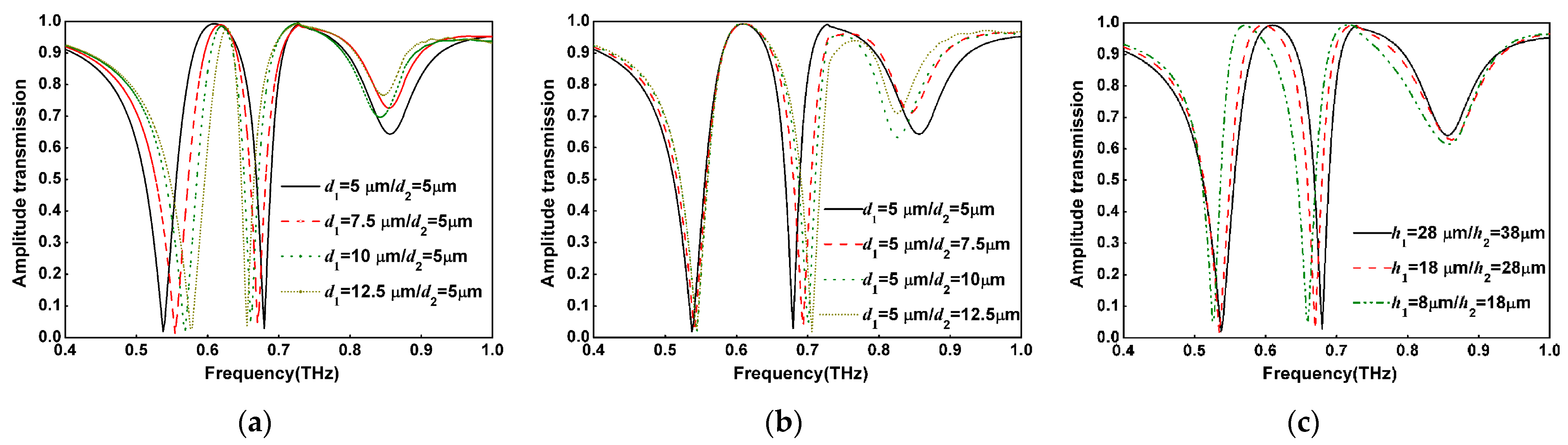
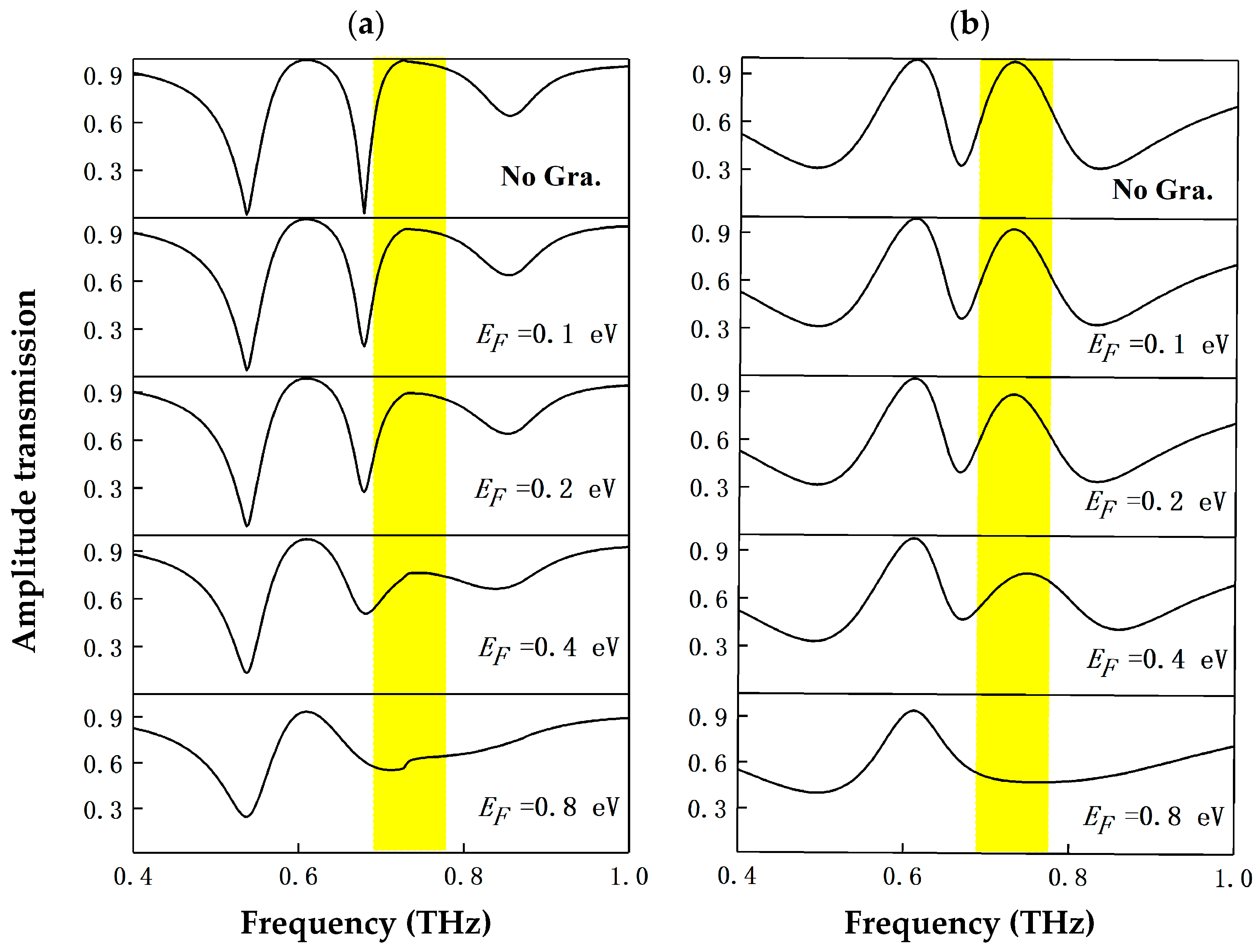
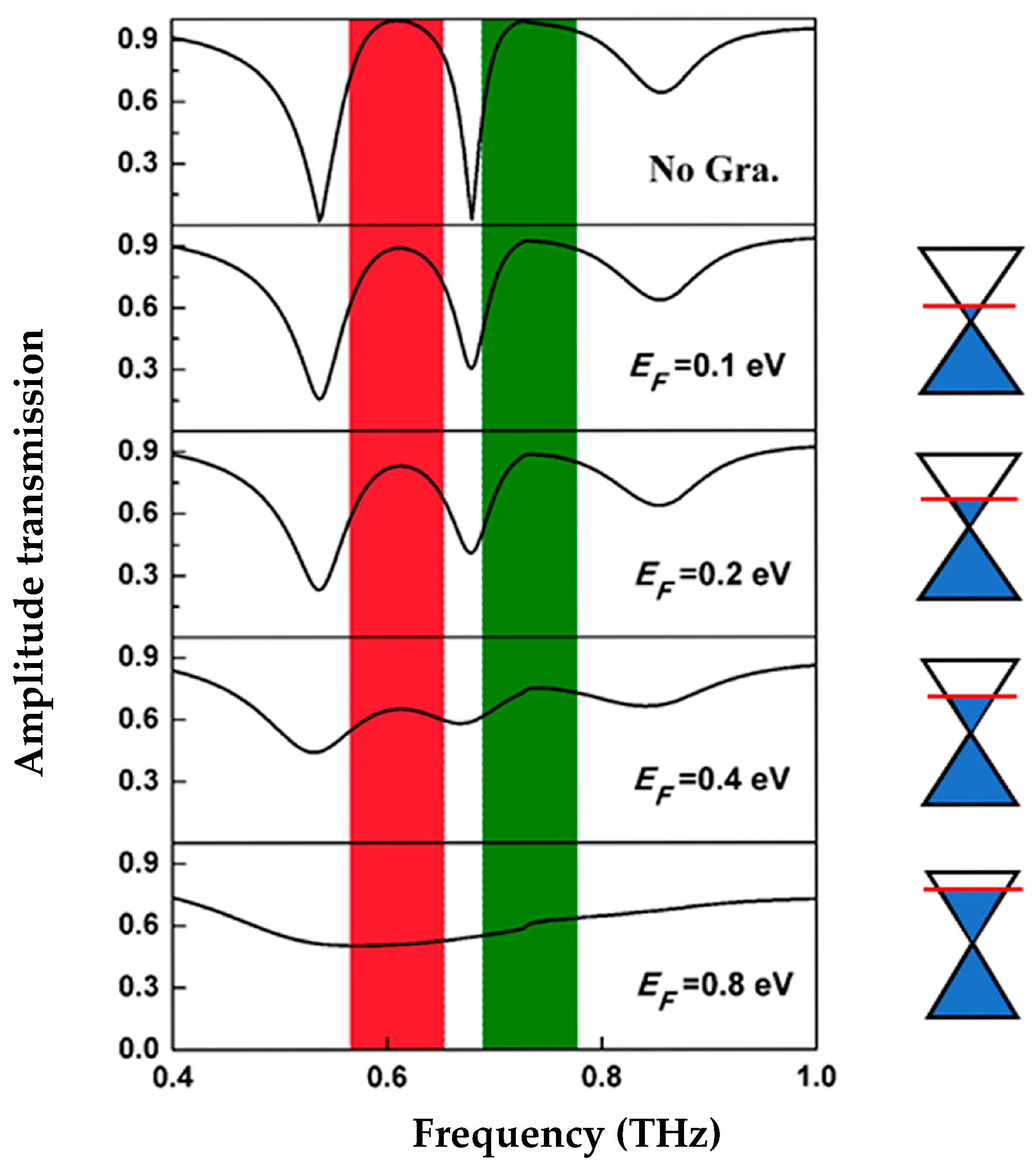
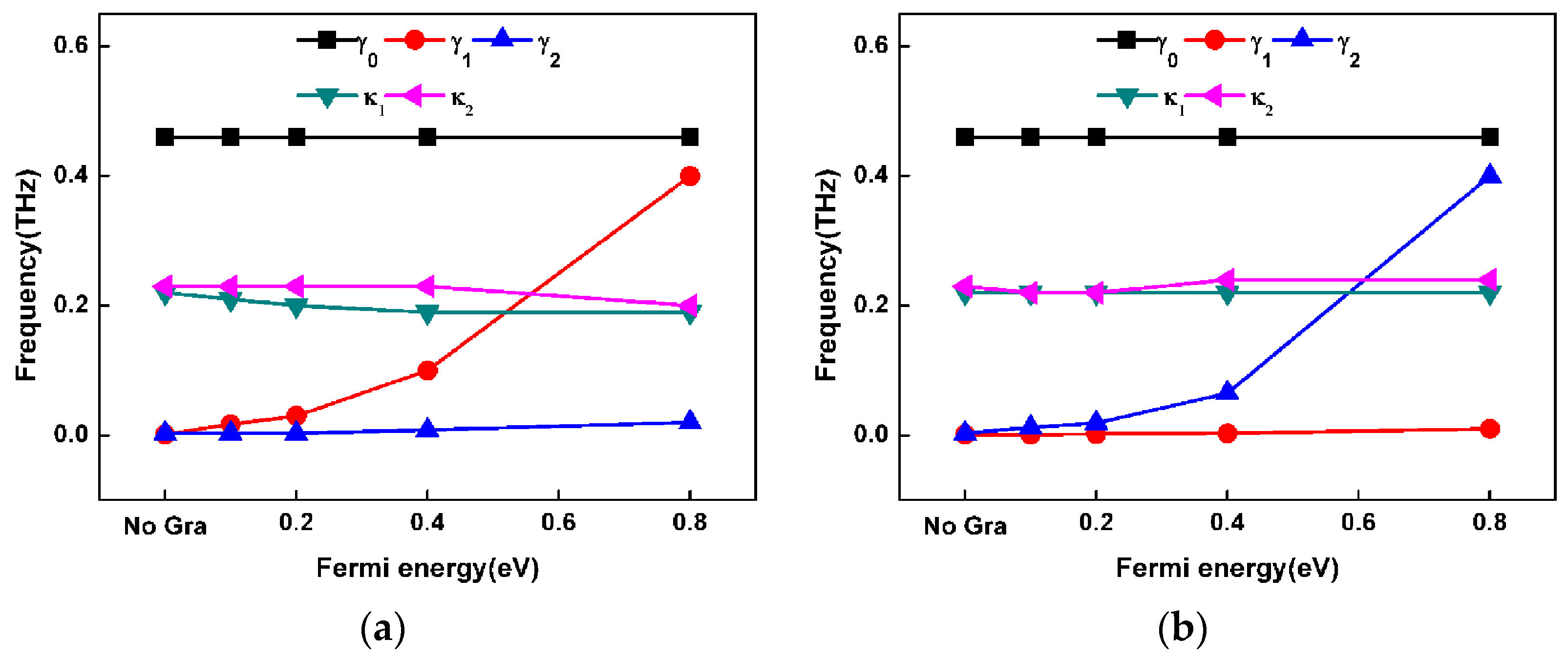
3. Passive Controlled Dual-PIT
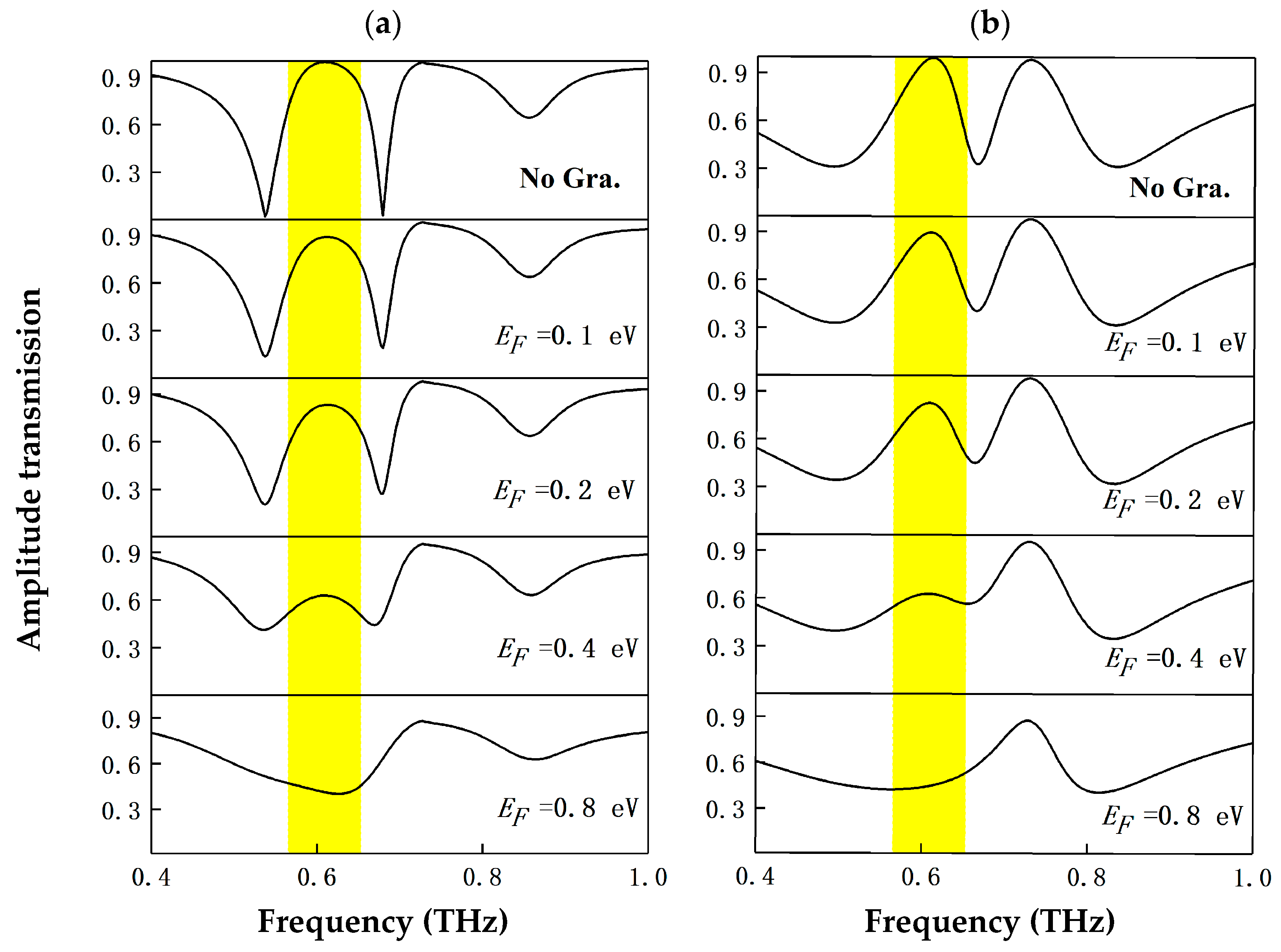
4. Active Controlled Dual-PIT
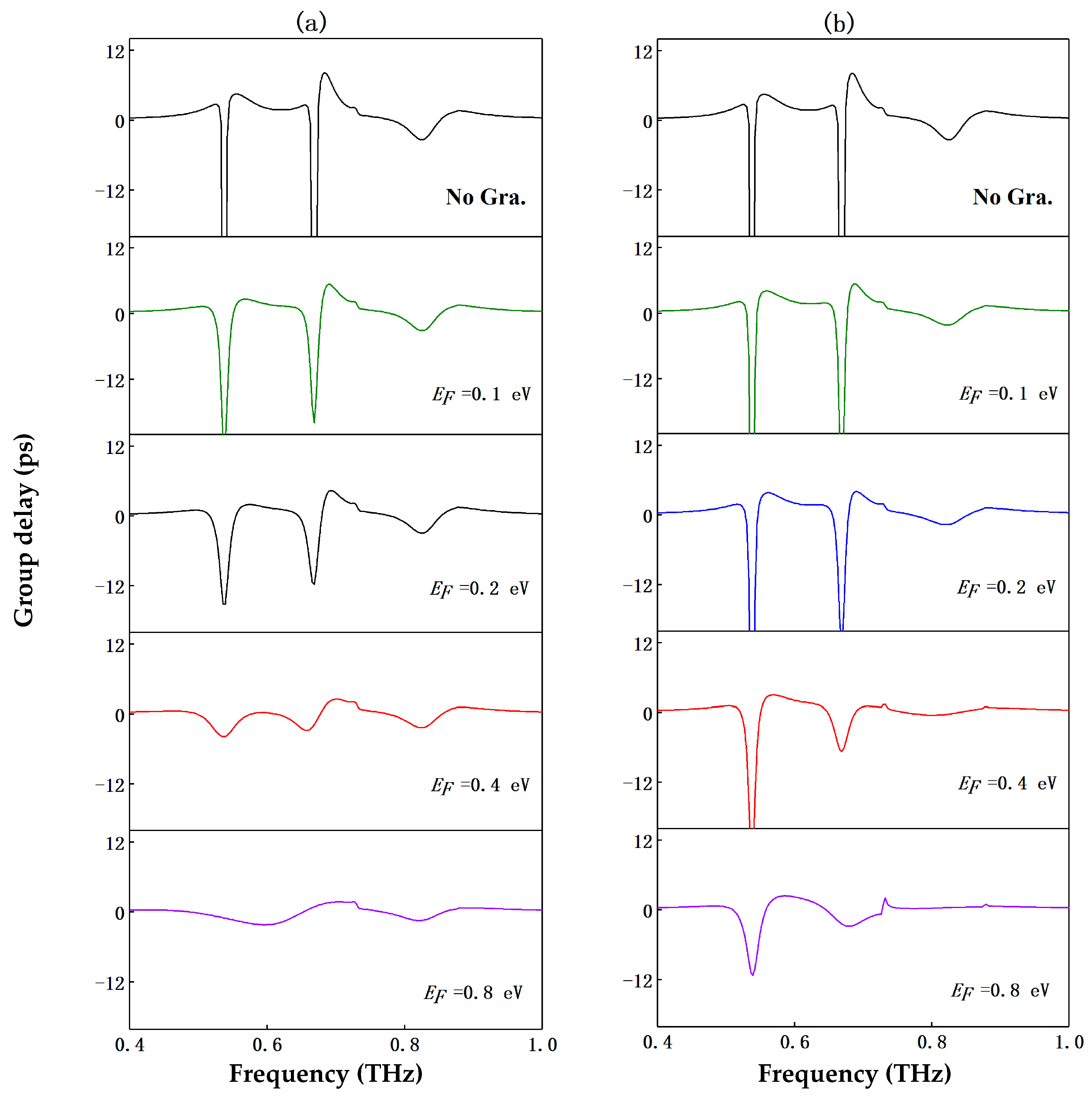
5. Tunable Dual Slow-Light Effect
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Zhao, X.G.; Schalch, J.; Zhang, J.D.; Seren, H.R.; Duan, G.W.; Averitt, R.D.; Zhang, X. Electromechanically tunable metasurface transmission waveplate at terahertz frequencies. Optica 2018, 5, 303–310. [Google Scholar] [CrossRef]
- Glybovski, S.B.; Tretyakov, S.A.; Belov, P.A.; Kivshar, Y.S.; Simovski, C.R. Metasurfaces: From microwaves to visible. Phys. Rep.-Rev. Sec. Phys. Lett. 2016, 634, 1–72. [Google Scholar] [CrossRef]
- Sun, S.L.; He, Q.; Hao, J.M.; Xiao, S.Y.; Zhou, L. Electromagnetic metasurfaces: Physics and applications. Adv. Opt. Photonics 2019, 11, 380–479. [Google Scholar] [CrossRef]
- Li, F.J.; Wang, S.; Zhong, R.; Hu, M.X.; Jiang, Y.; Zheng, M.J.; Wang, M.; Li, X.P.; Peng, R.W.; Deng, Z.L. Metasurface polarization optics: From classical to quantum. Appl. Phys. Rev. 2024, 11, 041332. [Google Scholar] [CrossRef]
- Taghvaee, H.; Liu, F.; Diaz-Rubio, A.; Tretyakov, S. Subwavelength focusing by engineered power-flow conformal metamirrors. Phys. Rev. B 2021, 104, 235409. [Google Scholar] [CrossRef]
- Yao, Z.B.; Ke, Y.C.; Lang, Y.H.; Wu, T.; Zhang, X.Q.; Xu, Q.; Han, J.G. Design and analysis of terahertz filters based on multilayer metamaterials. Appl. Opt. 2022, 61, 5799–5805. [Google Scholar] [CrossRef]
- Koshelev, K.; Tang, Y.T.; Li, K.F.; Choi, D.Y.; Li, G.X.; Kivshart, Y. Nonlinear Metasurfaces Governed by Bound States in the Continuum. ACS Photonics 2019, 6, 1639–1644. [Google Scholar] [CrossRef]
- Degl’Innocenti, R.; Lin, H.Y.; Navarro-Cía, M. Recent progress in terahertz metamaterial modulators. Nanophotonics 2022, 11, 1485–1514. [Google Scholar] [CrossRef]
- Leitenstorfer, A.; Moskalenko, A.S.; Kampfrath, T.; Kono, J.; Castro-Camus, E.; Peng, K.; Qureshi, N.; Turchinovich, D.; Tanaka, K.; Markelz, A.G.; et al. The 2023 terahertz science and technology roadmap. J. Phys. D Appl. Phys. 2023, 56, 223001. [Google Scholar] [CrossRef]
- Gu, J.Q.; Singh, R.; Liu, X.J.; Zhang, X.Q.; Ma, Y.F.; Zhang, S.; Maier, S.A.; Tian, Z.; Azad, A.K.; Chen, H.T.; et al. Active control of electromagnetically induced transparency analogue in terahertz metamaterials. Nat. Commun. 2012, 3, 1151. [Google Scholar] [CrossRef]
- Nurmohammadi, T.; Abbasian, K.; Mashayekhi, M.Z. Graphene-based tunable plasmon-induced transparency utilizing circular and two rectangular gold rings in the near-infrared spectrum. Mater. Sci. Semicond. Process. 2022, 144, 106601. [Google Scholar] [CrossRef]
- Kang, Y.Q.; Xi, H.Y.; Meng, T.H.; Lin, Q.W.; Dong, L.J. Experimental demonstration of polarization and direction insensitive metamaterial analog of electromagnetically induced transparency by bright-bright mode coupling. Results Phys. 2022, 37, 105514. [Google Scholar] [CrossRef]
- Niu, X.X.; Hu, X.Y.; Yan, Q.C.; Zhu, J.K.; Cheng, H.T.; Huang, Y.F.; Lu, C.C.; Fu, Y.L.; Gong, Q.H. Plasmon-induced transparency effect for ultracompact on-chip devices. Nanophotonics 2019, 8, 1125–1149. [Google Scholar] [CrossRef]
- Geim, A.K.; Novoselov, K.S. The rise of graphene. Nat. Mater. 2007, 6, 183–191. [Google Scholar] [CrossRef]
- Grigorenko, A.N.; Polini, M.; Novoselov, K.S. Graphene plasmonics. Nat. Photonics 2012, 6, 749–758. [Google Scholar] [CrossRef]
- Zeng, C.; Lu, H.; Mao, D.; Du, Y.Q.; Hua, H.; Zhao, W.; Zhao, J.L. Graphene-empowered dynamic metasurfaces and metadevices. Opto-Electron. Adv. 2022, 5, 200098. [Google Scholar] [CrossRef]
- Chen, M.M.; Xiao, Z.Y.; Lu, X.J.; Lv, F.; Zhou, Y.J. Simulation of dynamically tunable and switchable electromagnetically induced transparency analogue based on metal-graphene hybrid metamaterial. Carbon 2020, 159, 273–282. [Google Scholar] [CrossRef]
- Shu, C.; Mei, J.S. Analogue of tunable electromagnetically induced transparency based on graphene-nanostrip in two perpendicular polarization directions. Opt. Commun. 2019, 439, 16–20. [Google Scholar] [CrossRef]
- Wang, G.Q.; Zhang, X.B.; Wei, X.Y.; Zhang, G.Q. Tunable and polarization-independent plasmon-induced transparency in a fourfold symmetric metal-graphene terahertz metamaterial. Crystals 2019, 9, 632. [Google Scholar] [CrossRef]
- Kim, T.H.; Kim, S.W.; Lee, B.W. Tunable plasmon-induced transparency based on graphene metasurface structure for mid-infrared sensing applications. Curr. Appl. Phys. 2025, 73, 30–40. [Google Scholar] [CrossRef]
- Guo, G.X.; Zhang, X.Q.; Niu, L.; Wu, T.; Chen, X.Y.; Xu, Q.; Han, J.G.; Zhang, W.L. Programmable graphene metasurface for terahertz propagation control based on electromagnetically induced transparency. Carbon 2023, 208, 345–354. [Google Scholar] [CrossRef]
- Jung, H.; Jo, H.; Lee, W.; Kim, B.; Choi, H.; Kang, M.S.; Lee, H. Electrical control of electromagnetically induced transparency by terahertz metamaterial funneling. Adv. Opt. Mater. 2019, 7, 1801205. [Google Scholar] [CrossRef]
- Mashayekhi, M.Z.; Abbasian, K.; Nurmohammadi, T. Dual-wavelength active and tunable modulation at telecommunication wavelengths using graphene-metal hybrid metamaterial based on plasmon induced transparency. Phys. Scr. 2022, 97, 095503. [Google Scholar] [CrossRef]
- Chen, H.T.; Zhang, Z.J.; Yang, J.B.; Zhou, Z.G. Controlled and tunable plasmon-induced transparency based on graphene metasurfaces in atmospheric windows. Diam. Relat. Mater. 2022, 127, 109210. [Google Scholar] [CrossRef]
- Liu, Z.M.; Zhang, X.; Zhou, F.Q.; Luo, X.; Zhang, Z.B.; Qin, Y.P.; Zhuo, S.S.; Gao, E.D.; Li, H.J.; Yi, Z. Triple plasmon-induced transparency and optical switch desensitized to polarized light based on a mono-layer metamaterial. Opt. Express 2021, 29, 13949–13959. [Google Scholar] [CrossRef]
- Indu, K.K.N.; Devi, K.M.; Chowdhury, D.R. Graphene and metal hybridized terahertz metasurfaces toward tunable plasmon-induced transparency effects. Curr. Appl. Phys. 2022, 39, 158–165. [Google Scholar] [CrossRef]
- Zhao, X.L.; Yuan, C.; Lv, W.H.; Xu, S.L.; Yao, J.Q. Plasmon-induced transparency in metamaterial based on graphene and split-ring resonators. IEEE Photonics Technol. Lett. 2015, 27, 1321–1324. [Google Scholar] [CrossRef]
- Ordal, M.A.; Bell, R.J.; Alexander, R.W.; Long, L.L.; Querry, M.R. Optical properties of fourteen metals in the infrared and far infrared: Al, Co, Cu, Au, Fe, Pb, Mo, Ni, Pd, Pt, Ag, Ti, V, and W. Appl. Opt. 1985, 24, 4493–4499. [Google Scholar]
- Ishikawa, A.; Tanaka, T. Plasmon hybridization in graphene metamaterials. Appl. Phys. Lett. 2013, 102, 253110. [Google Scholar] [CrossRef]
- Xia, S.X.; Zhai, X.; Wang, L.L.; Sun, B.; Liu, J.Q.; Wen, S.C. Dynamically tunable plasmonically induced transparency in sinusoidally curved and planar graphene layers. Opt. Express 2016, 24, 17886–17899. [Google Scholar] [CrossRef]
- Xu, H.; Li, H.J.; He, Z.H.; Chen, Z.Q.; Zheng, M.F.; Zhao, M.Z. Dual tunable plasmon-induced transparency based on silicon-air grating coupled graphene structure in terahertz metamaterial. Opt. Express 2017, 25, 20780–20790. [Google Scholar] [CrossRef] [PubMed]
- Jnawali, G.; Rao, Y.; Yan, H.G.; Heinz, T.F. Observation of a transient decrease in terahertz conductivity of single-layer graphene induced by ultrafast optical excitation. Nano Lett. 2013, 13, 524–530. [Google Scholar] [CrossRef] [PubMed]
- Li, M.; Li, H.J.; Xu, H.; Xiong, C.X.; Zhao, M.Z.; Liu, C.; Ruan, B.X.; Zhang, B.H.; Wu, K. Dual-frequency on-off modulation and slow light analysis based on dual plasmon-induced transparency in terahertz patterned graphene metamaterial. New J. Phys. 2020, 22, 103030. [Google Scholar] [CrossRef]
- Hu, H.; Zhai, F.; Hu, D.B.; Li, Z.J.; Bai, B.; Yang, X.X.; Dai, Q. Broadly tunable graphene plasmons using an ion-gel top gate with low control voltage. Nanoscale 2015, 7, 19493–19500. [Google Scholar] [CrossRef]
- Sun, T.; Li, G.-M.; Li, J.-D.; Wang, Y.-H.; Li, X.-M.; Cao, H.-Z.; Ma, R.-D.; Xu, S.-T.; Zhang, H.-F.; Fan, F.; et al. Terahertz metal-graphene hybrid metamaterial for active manipulation of electromagnetically induced transparency. Opt. Commun. 2024, 565, 130694. [Google Scholar] [CrossRef]
- Wang, G.; Zhang, X.; Zhang, L.; Wei, X. Dynamically tunable plasmon-induced transparency based on radiative–radiative-coupling in a terahertz metal–graphene metamaterial. Crystals 2019, 9, 146. [Google Scholar] [CrossRef]
- Li, Q.; Su, H.; Zhu, J.; Wang, S. Active control of dual electromagnetically induced transparency in terahertz graphene-metal hybrid metasurfaces. Front. Mater. 2022, 9, 966535. [Google Scholar] [CrossRef]
- Wu, T.; Wang, G.; Jia, Y.; Shao, Y.; Chen, C.; Han, J.; Gao, Y.; Gao, Y. Dual-spectral plasmon-induced transparent terahertz metamaterial with independently tunable amplitude and frequency. Nanomaterials 2021, 11, 2876. [Google Scholar] [CrossRef] [PubMed]
- Bai, Z.Y.; Hang, C.; Huang, G.X. Classical analogs of double electromagnetically induced transparency. Opt. Commun. 2013, 291, 253–258. [Google Scholar] [CrossRef]
- Zhao, X.L.; Yuan, C.; Lv, W.H.; Xu, S.L.; Yao, J.Q. A polarization-independent terahertz plasmon-induced transparency metamaterial based on hybrid graphene-gold structure for bio-sensing. J. Mod. Opt. 2016, 63, 200–206. [Google Scholar] [CrossRef]
- Balci, O.; Kakenov, N.; Karademir, E.; Balci, S.; Cakmakyapan, S.; Polat, E.O.; Caglayan, H.; Özbay, E.; Kocabas, C. Electrically switchable metadevices via graphene. Sci. Adv. 2018, 4, 9. [Google Scholar] [CrossRef] [PubMed]
- Bhattacharya, A.; Sarkar, R.; Kumar, G. Toroidal electromagnetically induced transparency based meta-surfaces and its applications. iScience 2022, 25, 20. [Google Scholar] [CrossRef] [PubMed]
- Zhang, S.W.; Wen, F.; Zhai, M.H.; Li, Z.; Ye, H.P.; Zhang, H.X.; Gu, Y.X.; Lei, Y.; Wang, W.; Zhang, Y.P.; et al. Terahertz dynamic multiband perfect absorber with a digital coding graphene-diamond metasurface. Phys. Rev. Appl. 2024, 22, 024004. [Google Scholar] [CrossRef]
- Xiong, Z.Y.; Shen, L.Y.; Long, J.; Li, X.; Zhou, K.; Choi, G.M.; Ou, K.T.; Yang, G.Y.; Ma, W.C.; Lee, H.S.; et al. Ultrahigh concentration exfoliation and aqueous dispersion of few-layer graphene by excluded volume effect. Nat. Commun. 2024, 15, 10807. [Google Scholar] [CrossRef]

| Reference | Modulation Type | Modulation Depth | Insertion Loss | Graphene Shape | Modulation Band | Material |
|---|---|---|---|---|---|---|
| [35] | Single-frequency | 89% | 2.6 dB | Pattern | Terahertz | Au+ Graphene |
| [36] | Single-frequency | 91.6% | 1.2 dB | Pattern | Terahertz | Al+ Graphene |
| [11] | Single-frequency | 11% | 1.1 dB | Whole | Near-infrared | Au+ Graphene |
| [37] | Dual-frequency | 24%; 14% | 0.5 dB; 0.2 dB | Pattern | Terahertz | Al+ Graphene |
| [38] | Dual-frequency | 82.4%; 74.7% | 1 dB; 0.9 dB | Pattern | Terahertz | Au+ Graphene |
| This work | Dual-frequency | 61%; 44% | 0.04 dB; 0.04 dB | Pattern | Terahertz | Al+ Graphene |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, G.; Meng, H. Tunable Dual Plasmon-Induced Transparency Based on Homogeneous Graphene-Metal Metasurfaces at Terahertz Frequency. Crystals 2025, 15, 328. https://doi.org/10.3390/cryst15040328
Wang G, Meng H. Tunable Dual Plasmon-Induced Transparency Based on Homogeneous Graphene-Metal Metasurfaces at Terahertz Frequency. Crystals. 2025; 15(4):328. https://doi.org/10.3390/cryst15040328
Chicago/Turabian StyleWang, Guanqi, and Hao Meng. 2025. "Tunable Dual Plasmon-Induced Transparency Based on Homogeneous Graphene-Metal Metasurfaces at Terahertz Frequency" Crystals 15, no. 4: 328. https://doi.org/10.3390/cryst15040328
APA StyleWang, G., & Meng, H. (2025). Tunable Dual Plasmon-Induced Transparency Based on Homogeneous Graphene-Metal Metasurfaces at Terahertz Frequency. Crystals, 15(4), 328. https://doi.org/10.3390/cryst15040328






