Structural and Optical Properties of Defected and Exotic Calcium Monochalcogenide Nanoparticles: Insights from DFT and TD-DFT Calculations
Abstract
:1. Introduction
2. Computational Methods
3. Results and Discussion
3.1. CaxYx NPs
3.1.1. Elongated CaxYx NPs Along One Direction
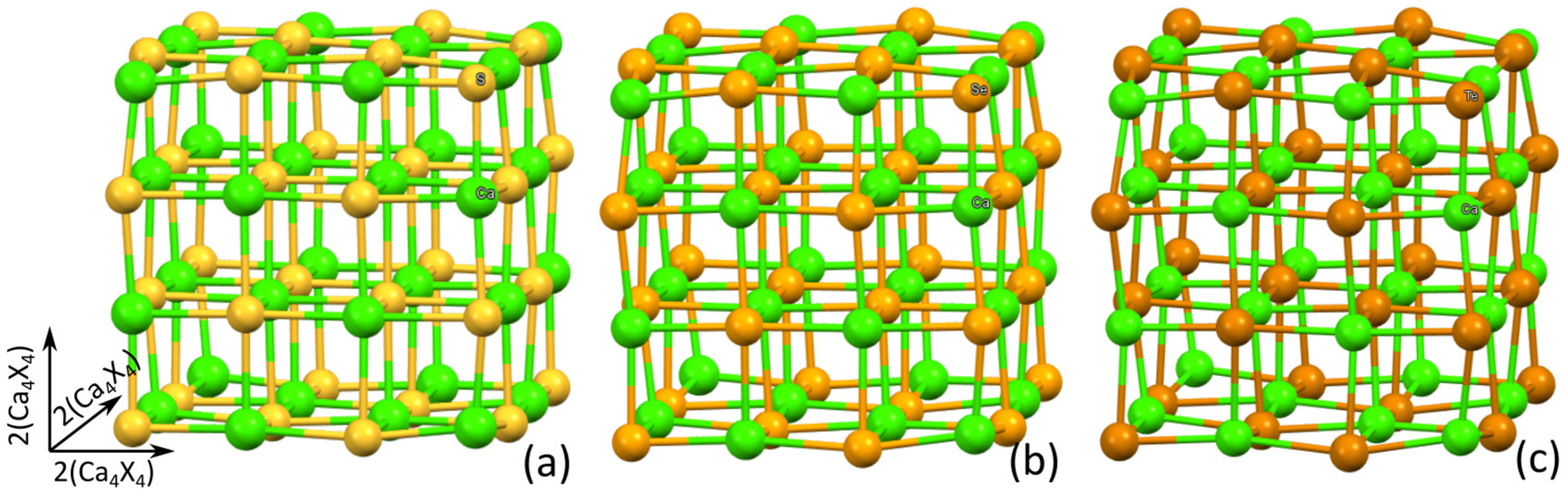
3.1.2. Elongated CaxYx NPs Along Two Perpendicular Directions
3.1.3. Elongated NPs Along Three Perpendicular Directions
3.2. Defected and Exotic Ca-Based Nanostructures
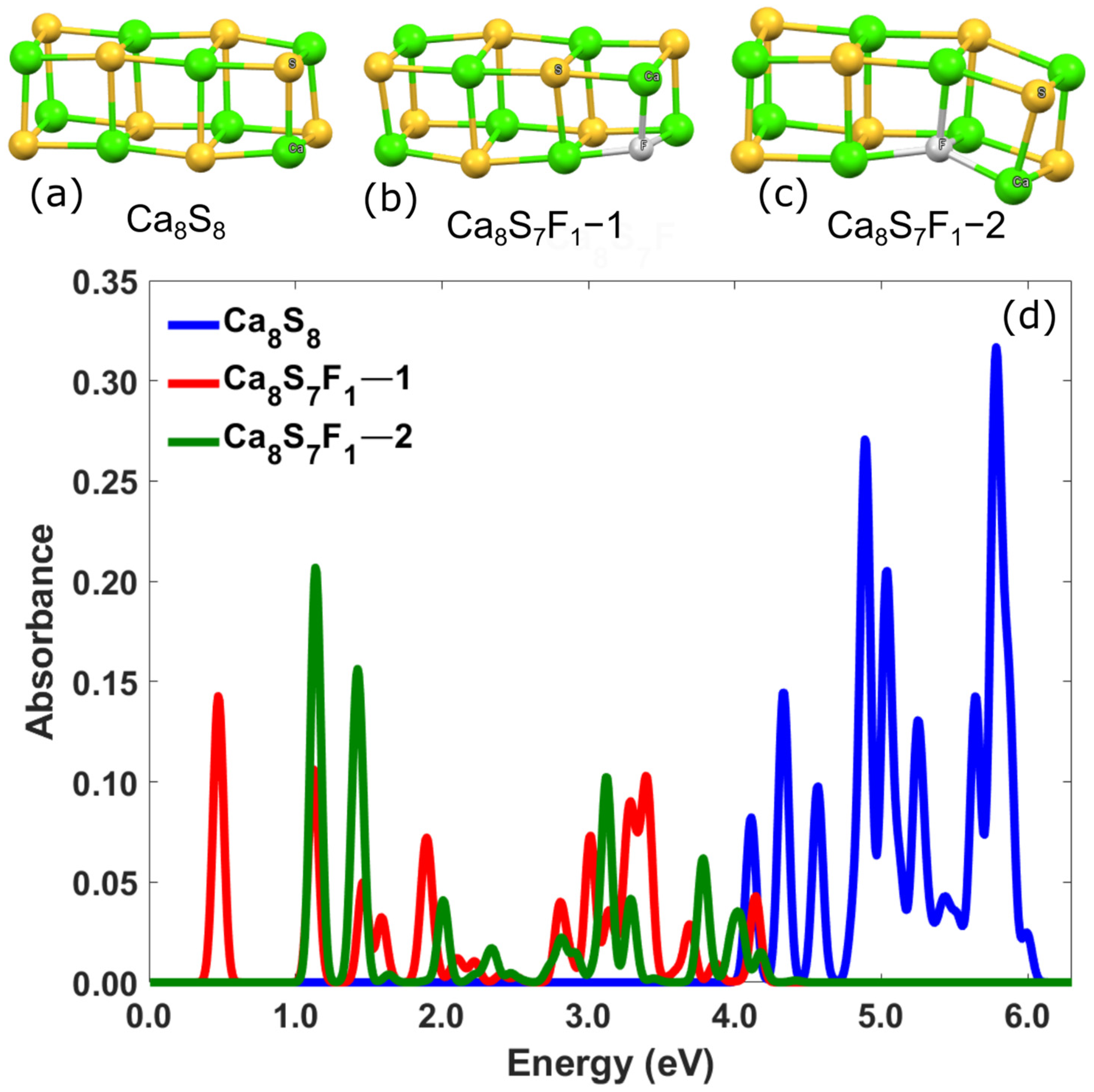
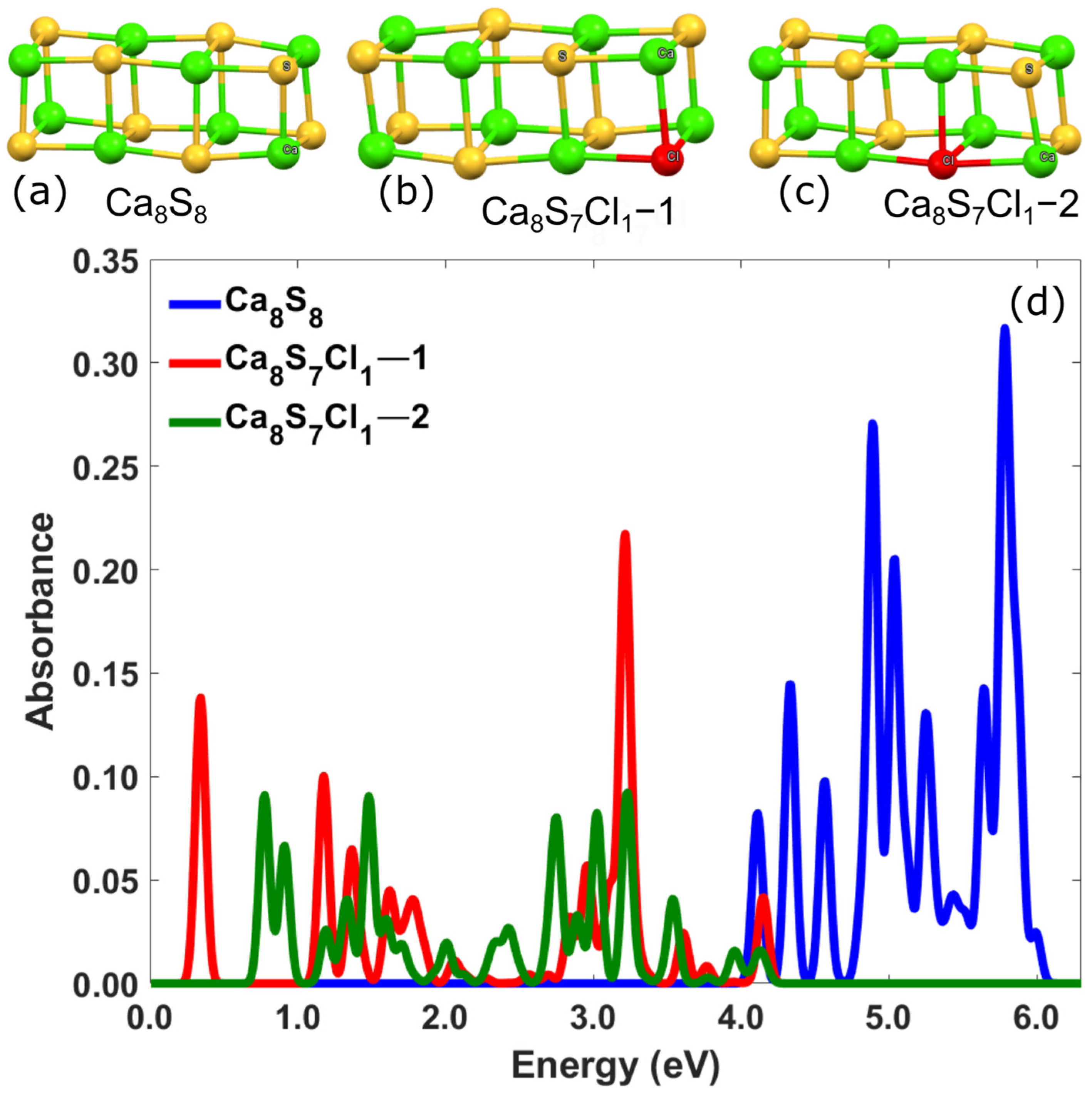
3.2.1. Ca-Based Nanostructures with Defects: Substitution of S by Halogens (F, Cl)
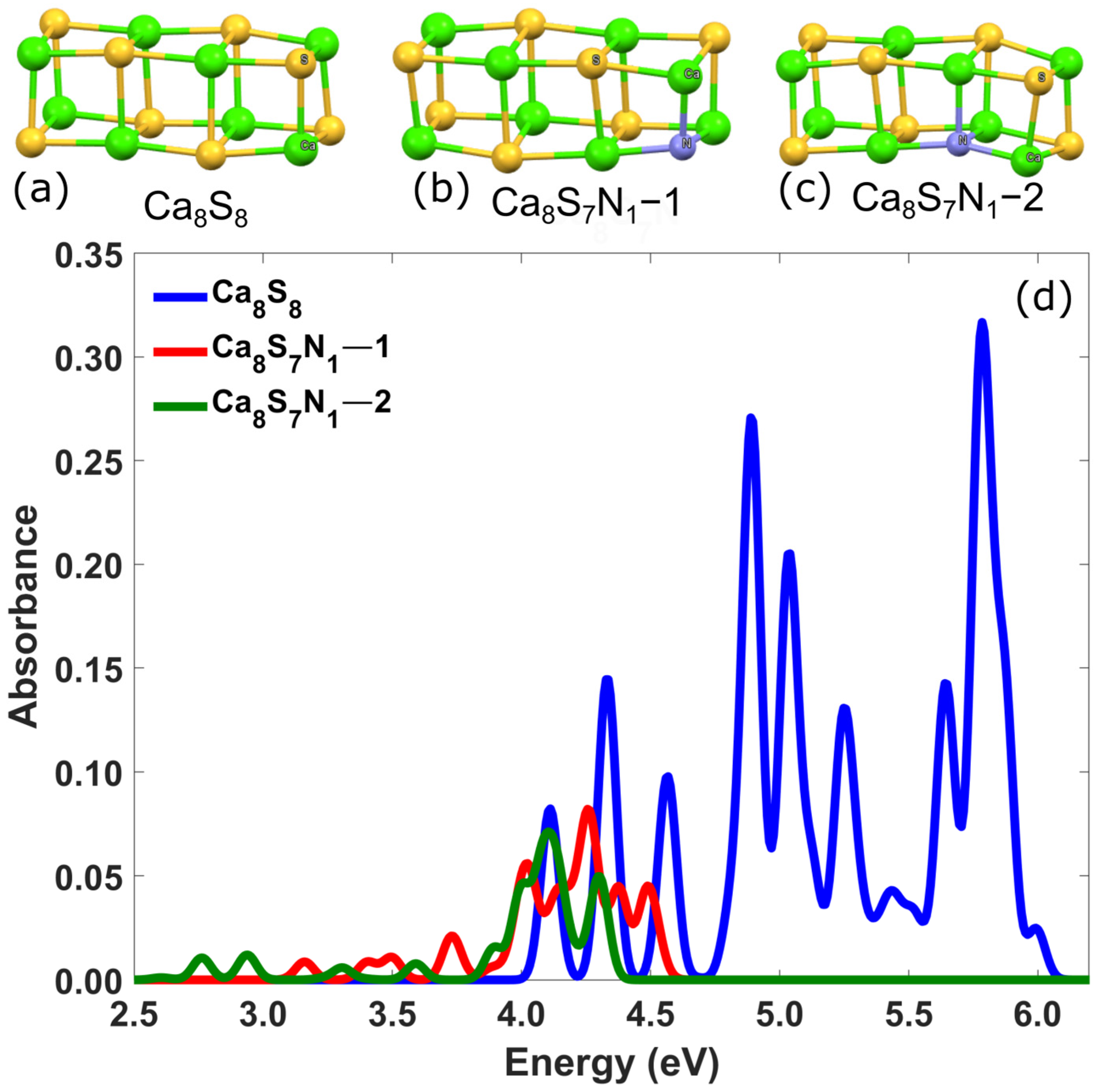
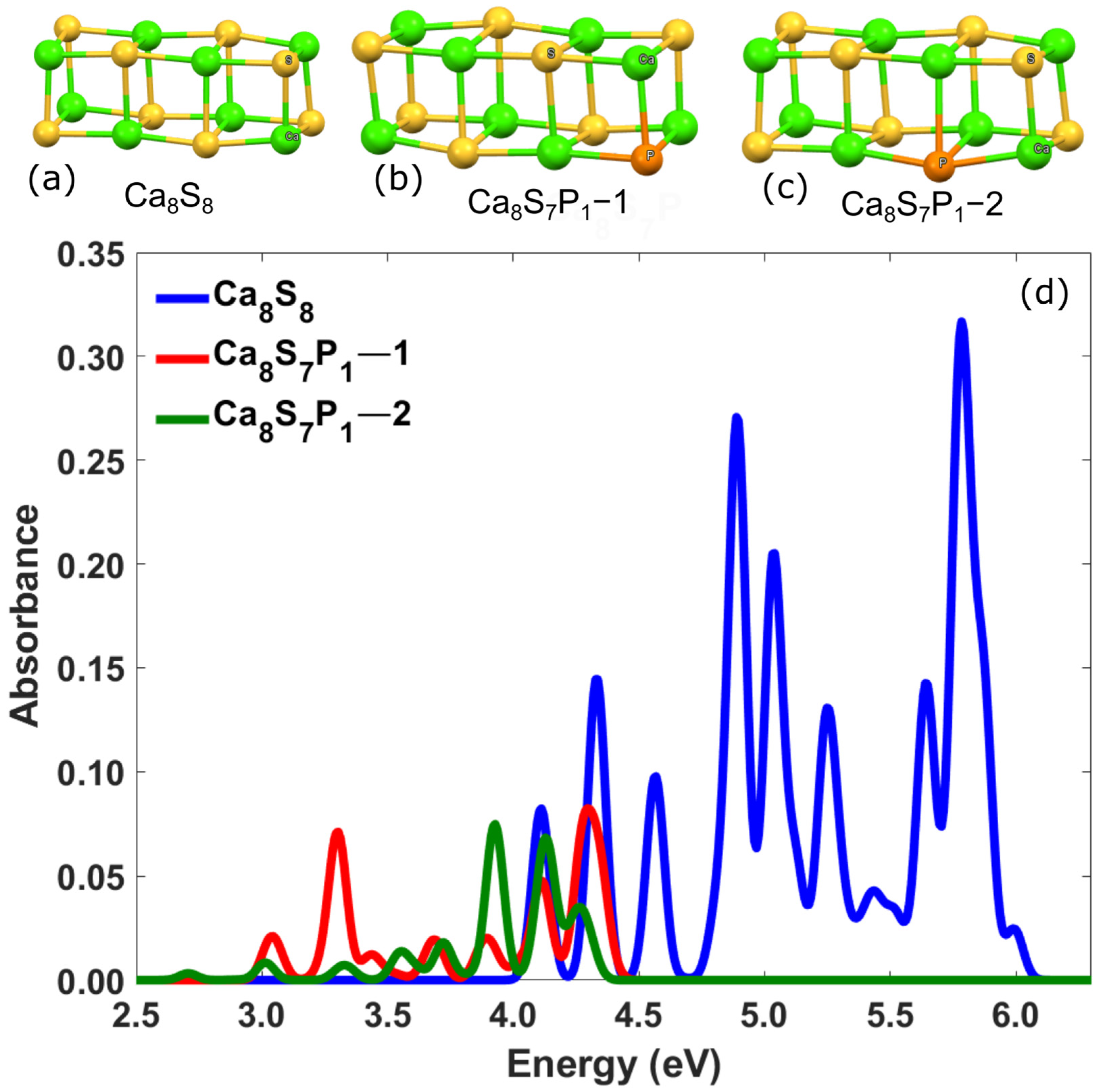
3.2.2. Ca-Based Nanostructures with Defects: Substitution of a Sulfur Atom by Pnictogens (N, P)
3.2.3. Exotic Ca-Based Nanostructures: Creating a Hole in the Structure
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Ong, W.-J.; Zheng, N.; Antonietti, M. Advanced nanomaterials for energy conversion and storage: Current status and future opportunities. Nanoscale 2021, 13, 9904–9907. [Google Scholar] [CrossRef] [PubMed]
- Yang, Y.; Zhang, C.; Lai, C.; Zeng, G.; Huang, D.; Cheng, M.; Wang, J.; Chen, F.; Zhou, C.; Xiong, W. BiOX (X = Cl, Br, I) photocatalytic nanomaterials: Applications for fuels and environmental management. Adv. Colloid Interface Sci. 2018, 254, 76–93. [Google Scholar] [CrossRef] [PubMed]
- Wang, M.; Zhou, H.; Wang, F. Photocatalytic biomass conversion for hydrogen and renewable carbon-based chemicals. Joule 2024, 8, 604–621. [Google Scholar] [CrossRef]
- El-Ghany, W.A.A. Review on the optical and electrical properties of chalcogenide thin films: Challenges and applications. Phys. Chem. Chem. Phys. 2025, 27, 4567–4586. [Google Scholar] [CrossRef]
- Aravantinos-Zafiris, N.; Chronis, A.G.; Sigalas, M.M. Structural and optical properties of exotic magnesium monochalcogenide nanoparticles. Mater. Today Commun. 2021, 28, 102622. [Google Scholar] [CrossRef]
- Zabed, H.M.; Islam, J.; Chowdhury, F.I.; Zhao, M.; Awasthi, M.K.; Nizami, A.-S.; Uddin, J.; Thomas, S.; Qi, X. Recent insights into heterometal-doped copper oxide nanostructure-based catalysts for renewable energy conversion and generation. Renew. Sustain. Energy Rev. 2022, 168, 112887. [Google Scholar] [CrossRef]
- Malehmir, S.; Esmaili, M.A.; Mahabady, M.K.; Sobhani-Nasab, A.; Atapour, A.; Ganjali, M.R.; Ghasemi, A.; Hasan-Abad, A.M. A review: Hemocompatibility of magnetic nanoparticles and their regenerative medicine, cancer therapy, drug delivery, and bioimaging applications. Front. Chem. 2023, 11, 1249134. [Google Scholar] [CrossRef]
- Huang, H.; Feng, W.; Chen, Y. Two-dimensional biomaterials: Material science, biological effect and biomedical engineering applications. Chem. Soc. Rev. 2021, 50, 11381–11485. [Google Scholar] [CrossRef]
- Sharma, G.; Kumar, A.; Lichtfouse, E. Nanophotocatalysis and Environmental Applications: Materials and Technology; Asiri, A.M., Ed.; Springer: Berlin/Heidelberg, Germany, 2019; Volume 29. [Google Scholar] [CrossRef]
- Qi, C.; Lin, J.; Fu, L.-H.; Huang, P. Calcium-based biomaterials for diagnosis, treatment, and theranostics. Chem. Soc. Rev. 2017, 47, 357–403. [Google Scholar] [CrossRef]
- Sun, T.; Zhang, Y.S.; Pang, B.; Hyun, D.C.; Yang, M.; Xia, Y. Engineered nanoparticles for drug delivery in cancer therapy. In Nanomaterials and Neoplasms; Taylor & Francis Group: Abingdon, UK, 2019; pp. 31–142. [Google Scholar] [CrossRef]
- Lin, Y.; Zheng, Y.; Guo, Y.; Yang, Y.; Li, H.; Fang, Y.; Wang, C. Peptide-functionalized carbon dots for sensitive and selective Ca2+ detection. Sens. Actuators B Chem. 2018, 273, 1654–1659. [Google Scholar] [CrossRef]
- Rao, V.N.; Ravi, P.; Sathish, M.; Vijayakumar, M.; Sakar, M.; Karthik, M.; Balakumar, S.; Reddy, K.R.; Shetti, N.P.; Aminabhavi, T.M.; et al. Metal chalcogenide-based core/shell photocatalysts for solar hydrogen production: Recent advances, properties and technology challenges. J. Hazard. Mater. 2021, 415, 125588. [Google Scholar] [CrossRef]
- Karantagli, E.; Sigalas, M.; Garoufalis, C.S. Exotic nanoparticles of group IV monochalcogenides. Solid State Commun. 2019, 295, 38–42. [Google Scholar] [CrossRef]
- Wobbe, M.C.C.; Zwijnenburg, M.A. Chemical trends in the optical properties of rocksalt nanoparticles. Phys. Chem. Chem. Phys. 2015, 17, 28892–28900. [Google Scholar] [CrossRef]
- Chronis, A.G.; Sigalas, M.M.; Koukaras, E.N. Absorption spectrum of magnesium and aluminum hydride nanoparticles. Mater. Chem. Phys. 2019, 228, 244–253. [Google Scholar] [CrossRef]
- Chronis, A.G.; Michos, F.I.; Garoufalis, C.S.; Sigalas, M.M. Structural and optical properties of Be, Mg and Ca nanorods and nanodisks. Phys. Chem. Chem. Phys. 2021, 23, 1849–1858. [Google Scholar] [CrossRef]
- Perdew, J.P.; Burke, K.; Ernzerhof, M. Generalized gradient approximation made simple. Phys. Rev. Lett. 1996, 77, 3865–3868. [Google Scholar] [CrossRef]
- Weigend, F.; Ahlrichs, R. Balanced basis sets of split valence, triple zeta valence and quadruple zeta valence quality for H to Rn: Design and assessment of accuracy. Phys. Chem. Chem. Phys. 2005, 7, 3297–3305. [Google Scholar] [CrossRef]
- Yanai, T.; Tew, D.P.; Handy, N.C. A new hybrid exchange–correlation functional using the Coulomb-attenuating method (CAM-B3LYP). Chem. Phys. Lett. 2004, 393, 51–57. [Google Scholar] [CrossRef]
- TURBOMOLE; TURBOMOLE GmbH: Karlsruhe, Germany, 2019.
- Li, C.; Cui, Y.; Tian, H.; Ren, B.; Li, Q.; Li, Y.; Yang, H. Quantum Chemistry Study on the Structures and Electronic Properties of Bimetallic Ca2-Doped Magnesium Ca2Mgn (n = 1–15) Clusters. Nanomaterials 2022, 12, 1654. [Google Scholar] [CrossRef]
- Schlipf, M.; Betzinger, M.; Ležaić, M.; Friedrich, C.; Blügel, S. Structural, electronic, and magnetic properties of the europium chalcogenides: A hybrid-functional DFT study. Phys. Rev. B 2013, 88, 094433. [Google Scholar] [CrossRef]
- Sahoo, R.K.; Khatua, R.; Sahu, S. Theoretical study of linear and non-linear optical properties of small CaCn (n = 2–7) clusters. Mater. Today Proc. 2022, 66, 3397–3400. [Google Scholar] [CrossRef]
- Aravantinos-Zafiris, N.; Michos, F.I.; Sigalas, M.M. Vibrational Spectrum of Magnesium Monochalcogenide Nanoparticles. Nanomaterials 2024, 14, 1918. [Google Scholar] [CrossRef] [PubMed]
- Goings, J.J.; Caricato, M.; Frisch, M.J.; Li, X. Assessment of low-scaling approximations to the equation of motion coupled-cluster singles and doubles equations. J. Chem. Phys. 2014, 141, 164116. [Google Scholar] [CrossRef]
- Zhao, Y.; Truhlar, D.G. The M06 suite of density functionals for main group thermochemistry, thermochemical kinetics, noncovalent interactions, excited states, and transition elements: Two new functionals and systematic testing of four M06-class functionals and 12 other functionals. Theor. Chem. Acc. 2008, 120, 215–241. [Google Scholar] [CrossRef]
- Adamo, C.; Barone, V. Toward reliable density functional methods without adjustable parameters: The PBE0 model. J. Chem. Phys. 1999, 110, 6158–6170. [Google Scholar] [CrossRef]
- Becke, A.D. Density-functional thermochemistry. III. The role of exact exchange. J. Chem. Phys. 1993, 98, 5648–5652. [Google Scholar] [CrossRef]
- Fadlallah, M. Magnetic, electronic, optical, and photocatalytic properties of nonmetal- and halogen-doped anatase TiO2 nanotubes. Phys. E Low-Dimens. Syst. Nanostruct. 2017, 89, 50–56. [Google Scholar] [CrossRef]
- Carmona, F.J.; Dal Sasso, G.; Bertolotti, F.; Ramírez-Rodríguez, G.B.; Delgado-López, J.M.; Pedersen, J.S.; Masciocchi, N.; Guagliardi, A. The role of nanoparticle structure and morphology in the dissolution kinetics and nutrient release of nitrate-doped calcium phosphate nanofertilizers. Sci. Rep. 2020, 10, 12396. [Google Scholar] [CrossRef]
- Fatemi, A.; Jamshidi-Ghaleh, K.; Tohidi, T.; Bayat, F. CaCl2 doping effect on optical and structural properties of halide perovskites under ligand assisted reprecipitation synthesis. Phys. B Condens. Matter 2024, 691, 416360. [Google Scholar] [CrossRef]
- Zhang, X.; Gao, L.; Yu, H.; Liao, Q.; Kang, Z.; Zhang, Z.; Zhang, Y. Single-atom vacancy doping in two-dimensional transition metal dichalcogenides. Acc. Mater. Res. 2021, 2, 655–668. [Google Scholar] [CrossRef]
- Cavallini, M.; Gentili, D. Atomic Vacancies in Transition Metal Dichalcogenides: Properties, Fabrication, and Limits. Chempluschem 2022, 87, e202100562. [Google Scholar] [CrossRef] [PubMed]
- Aravantinos-Zafiris, N.; Sigalas, M.M. Phononic Band Gaps in Graphene-Like Materials and Nanotubes. J. Surfaces Interfaces Mater. 2013, 1, 184–188. [Google Scholar] [CrossRef]
- Sgouros, A.P.; Neupane, M.R.; Sigalas, M.M.; Aravantinos-Zafiris, N.; Lake, R.K. Nanoscale phononic interconnects in THz frequencies. Phys. Chem. Chem. Phys. 2014, 16, 23355–23364. [Google Scholar] [CrossRef] [PubMed]
- Sun, M.; Schwingenschlögl, U. Unique omnidirectional negative Poisson’s ratio in δ-phase carbon monochalcogenides. J. Phys. Chem. C 2021, 125, 4133–4138. [Google Scholar] [CrossRef]
- Xu, Y.; Liu, Y.; Chen, Y.; Zhang, Y.; Ma, C.; Zhang, H.; Sun, S.; Ji, Y. Two-dimensional direct semiconductor Boron Monochalcogenide γ-BTe: Room-temperature single-bound exciton and novel donor material in excitonic solar cells. ACS Appl. Mater. Interfaces 2020, 12, 58349–58359. [Google Scholar] [CrossRef] [PubMed]
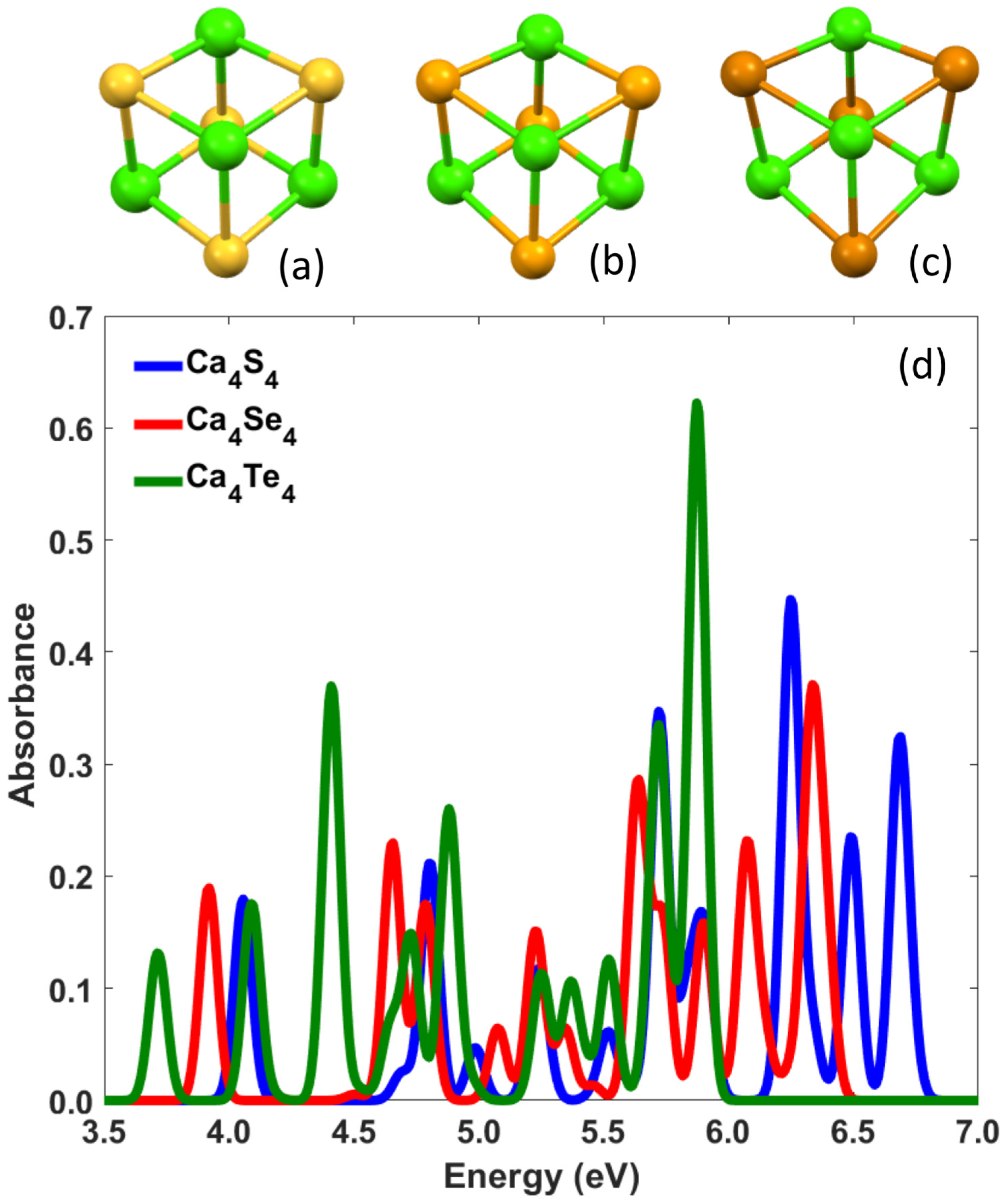
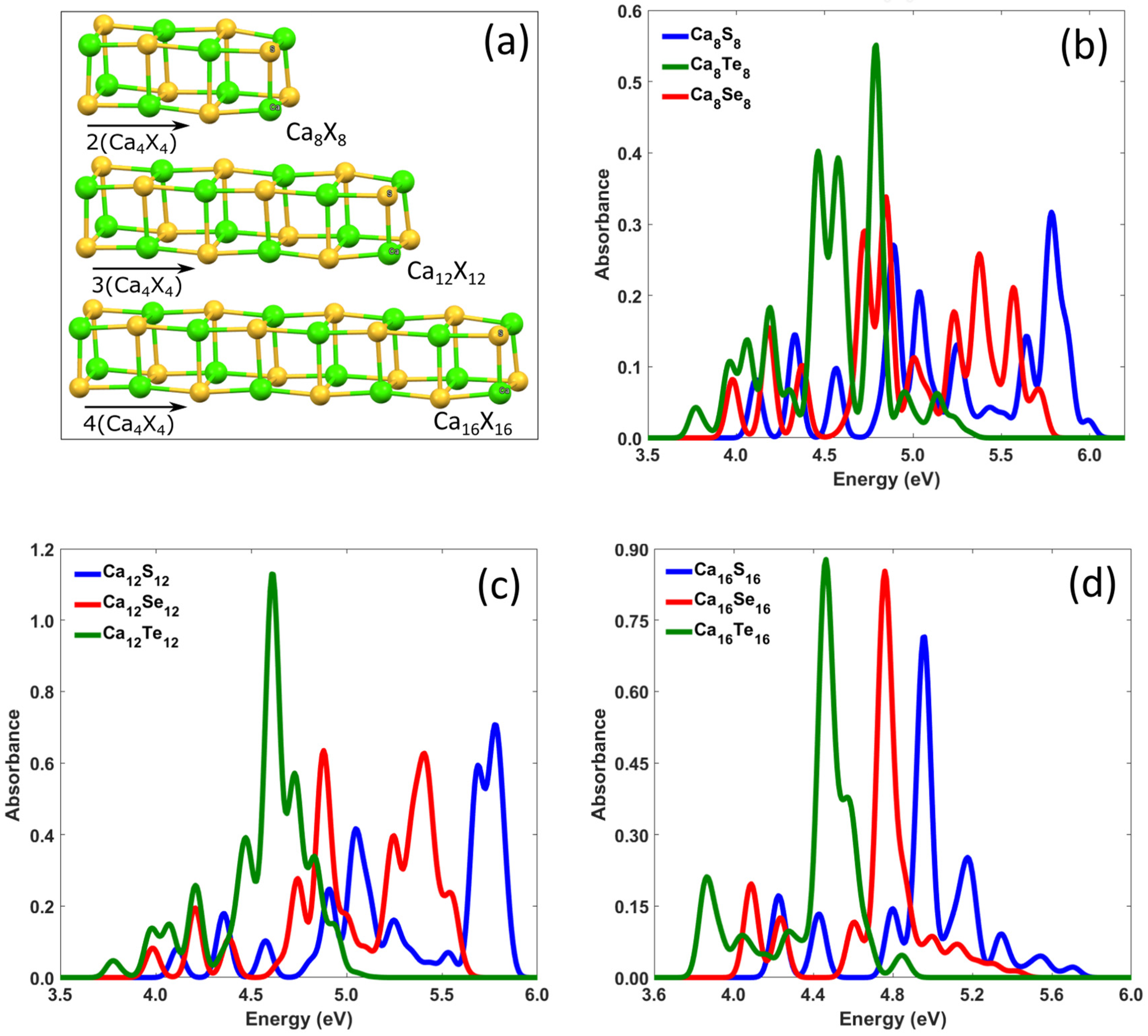


| Ca4S4 | Ca4Se4 | Ca4Te4 | |
|---|---|---|---|
| EOM-CCSD | 4.18 | 4.06 | 3.86 |
| CAM-B3LYP | 4.06 | 3.92 | 3.72 |
| M06-2X | 3.97 | 3.84 | 3.61 |
| PBE0 | 3.80 | 3.67 | 3.47 |
| B3LYP | 3.51 | 3.40 | 3.25 |
| PBE | 3.16 | 3.08 | 2.96 |
| Nanoparticle | HOMO-LUMO Gap (eV) | Optical Gap (eV) | Oscillator Strength | Binding Energy per f.u. (eV) |
|---|---|---|---|---|
| Ca4S4 | 6.35 | 4.05 | 0.18 | 7.00 |
| Ca4Se4 | 6.16 | 3.92 | 0.19 | 6.49 |
| Ca4Te4 | 5.82 | 3.71 | 0.13 | 5.68 |
| Ca8S8 | 6.41 | 4.33 | 0.14 | 7.51 |
| Ca8Se8 | 6.17 | 4.18 | 0.15 | 6.96 |
| Ca8Te8 | 5.75 | 3.96 | 0.10 | 6.07 |
| Ca12S12 | 6.45 | 4.36 | 0.18 | 7.69 |
| Ca12Se12 | 6.20 | 4.20 | 0.19 | 7.11 |
| Ca12Te12 | 5.76 | 3.97 | 0.12 | 6.20 |
| Ca12S12_2D_L1 | 6.36 | 4.11 | 0.06 | 7.63 |
| Ca12Se12_2D_L1 | 5.51 | 3.98 | 0.05 | 5.03 |
| Ca12Te12_2D_L1 | 5.72 | 3.76 | 0.03 | 6.17 |
| Ca16S16 | 6.40 | 4.22 | 0.03 | 7.90 |
| Ca16Se16 | 6.18 | 4.08 | 0.03 | 7.31 |
| Ca16Te16 | 5.81 | 3.92 | 0.06 | 6.36 |
| Ca16S16_1D | 6.47 | 4.36 | 0.2 | 7.77 |
| Ca16Se16_1D | 6.22 | 4.21 | 0.21 | 7.20 |
| Ca16Te16_1D | 5.77 | 3.97 | 0.14 | 6.27 |
| Ca16S16_2D_L2 | 6.41 | 4.11 | 0.03 | 7.73 |
| Ca16Se16_2D_L2 | 6.16 | 3.97 | 0.04 | 7.16 |
| Ca16Te16_2D_L2 | 5.74 | 3.77 | 0.02 | 6.24 |
| Ca32S32 | 6.17 | 4.47 | 0.34 | 8.22 |
| Ca32Se32 | 5.98 | - | - | 7.60 |
| Ca32Te32 | 5.65 | - | - | 6.59 |
| Ca32S32–2DH | 6.50 | 4.30 | 0.05 | 7.95 |
| Ca32Se32–2DH | 6.20 | - | - | 7.36 |
| Ca32Te32–2DH | 5.75 | - | - | 6.41 |
| Ca8S7Cl1–1 | 1.89 | 1.17 | 0.10 | - |
| Ca8S7Cl1–2 | 1.86 | 0.77 | 0.09 | - |
| Ca8S7P1–1 | 4.62 | 3.31 | 0.03 | - |
| Ca8S7P1–2 | 4.08 | 3.72 | 0.02 | - |
| Ca8S7F1–1 | 2.17 | 1.12 | 0.11 | - |
| Ca8S7F1–2 | 2.63 | 1.14 | 0.21 | - |
| Ca8S7N1–1 | 5.47 | 3.73 | 0.02 | - |
| Ca8S7N1–2 | 5.00 | 2.76 | 0.01 | - |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Moustris, P.G.; Chronis, A.G.; Michos, F.I.; Aravantinos-Zafiris, N.; Sigalas, M.M. Structural and Optical Properties of Defected and Exotic Calcium Monochalcogenide Nanoparticles: Insights from DFT and TD-DFT Calculations. Crystals 2025, 15, 392. https://doi.org/10.3390/cryst15050392
Moustris PG, Chronis AG, Michos FI, Aravantinos-Zafiris N, Sigalas MM. Structural and Optical Properties of Defected and Exotic Calcium Monochalcogenide Nanoparticles: Insights from DFT and TD-DFT Calculations. Crystals. 2025; 15(5):392. https://doi.org/10.3390/cryst15050392
Chicago/Turabian StyleMoustris, Panagiotis G., Alexandros G. Chronis, Fotios I. Michos, Nikos Aravantinos-Zafiris, and Mihail M. Sigalas. 2025. "Structural and Optical Properties of Defected and Exotic Calcium Monochalcogenide Nanoparticles: Insights from DFT and TD-DFT Calculations" Crystals 15, no. 5: 392. https://doi.org/10.3390/cryst15050392
APA StyleMoustris, P. G., Chronis, A. G., Michos, F. I., Aravantinos-Zafiris, N., & Sigalas, M. M. (2025). Structural and Optical Properties of Defected and Exotic Calcium Monochalcogenide Nanoparticles: Insights from DFT and TD-DFT Calculations. Crystals, 15(5), 392. https://doi.org/10.3390/cryst15050392







