Phosphorus SAD Phasing for Nucleic Acid Structures: Limitations and Potential
Abstract
:1. Introduction
2. Results
2.1. Z-DNA
2.2. Dickerson-Drew Dodecamer
2.3. 2’-Thiomethyl-Modified DNA Decamer
3. Discussion
3.1. Anomalous Signal
3.2. Identification of Correct Solutions
3.3. Limitation of P-SAD
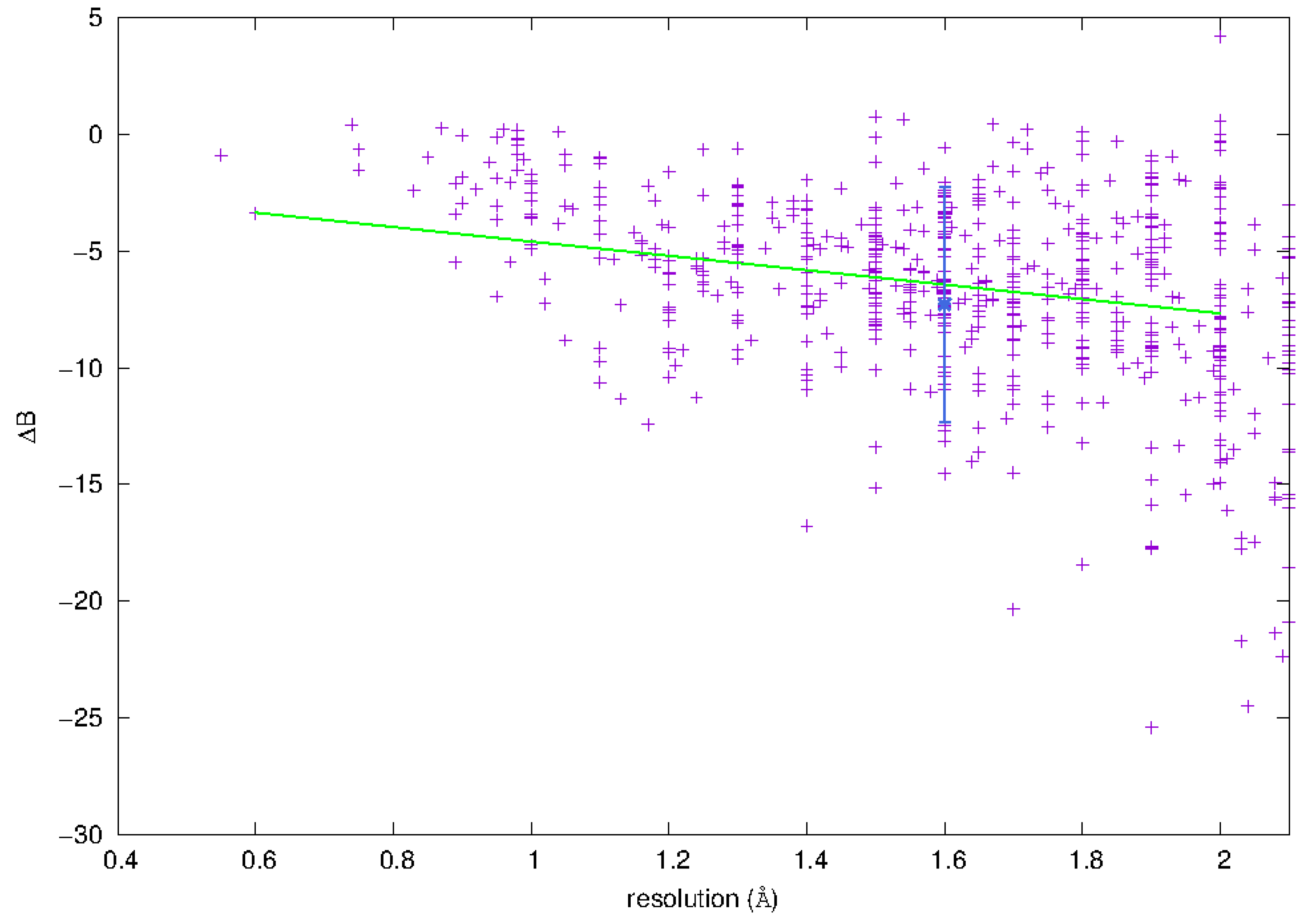
3.3.1. Phosphorus Mobility
3.4. Potential for P-SAD
3.4.1. Phasing and Data Collection
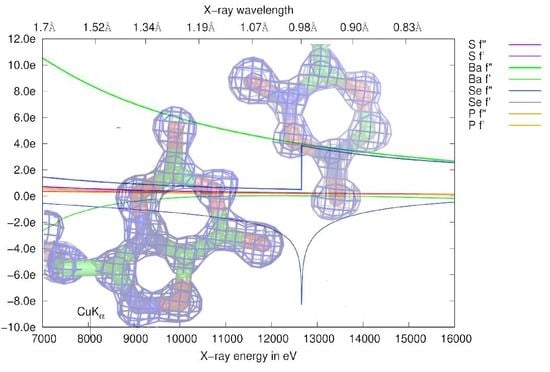
3.4.2. Choice of Wavelength
3.4.3. Radiation Damage
3.4.4. Successful Application of P-SAD
4. Materials and Methods
4.1. Crystallization
4.2. Diffraction Data Collection
4.3. Diffraction Data Phasing and Model Refinement
4.4. Data Quality Indicators
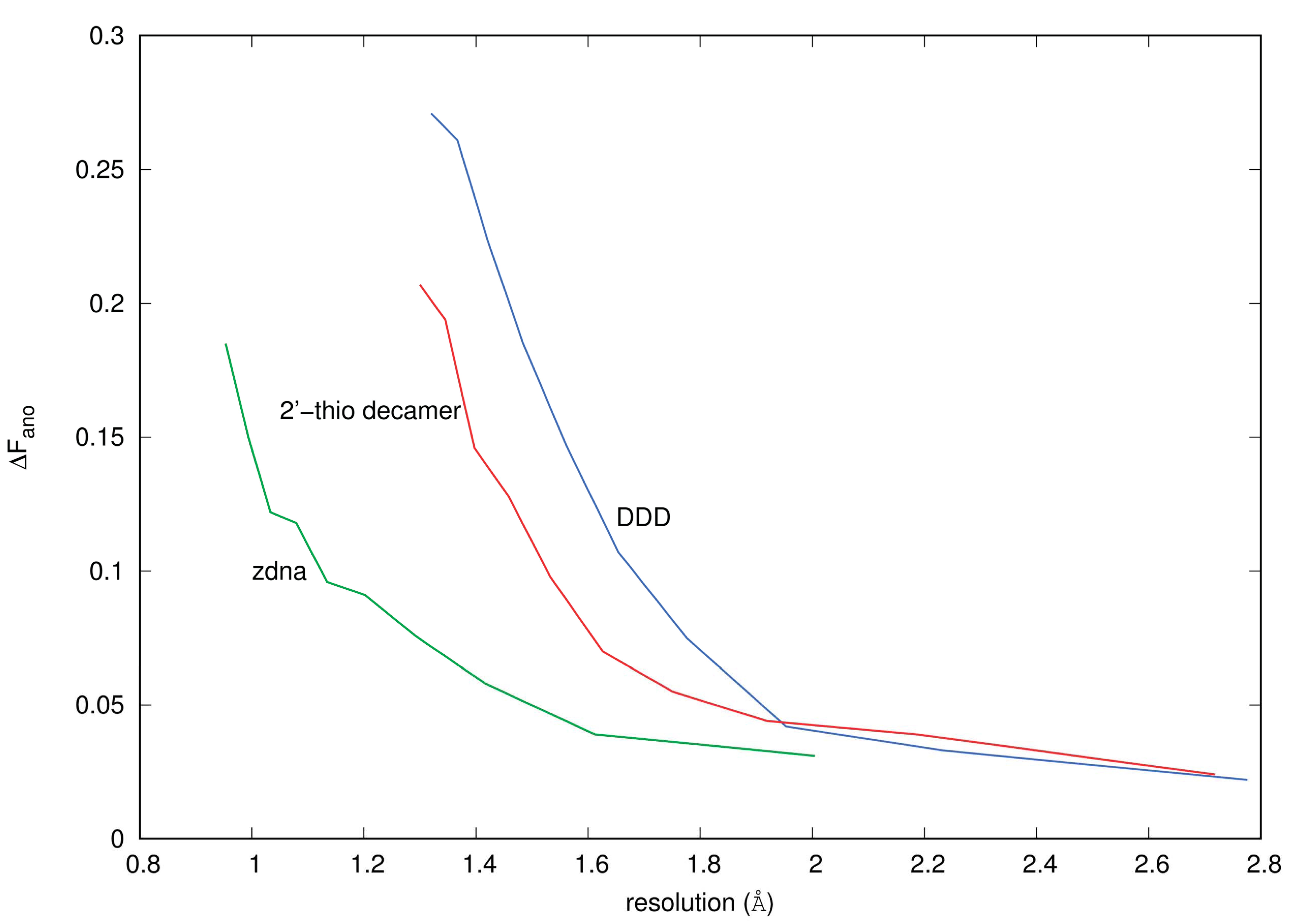
4.4.1. ΔFano/F
4.4.2. Measurability
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Cate, J.H.; Hanna, R.L.; Doudna, J.A. A magnesium core at the heart of a ribozyme domain. Nat. Struc. Bio. 1997, 4, 553–558. [Google Scholar] [CrossRef]
- Tereshko, V.; Minasov, G.; Egli, M. The Dickerson-Drew B-DNA dodecamer revisited - at atomic resolution. J. Am. Chem. Soc. 1999, 121, 470–471. [Google Scholar] [CrossRef]
- Tereshko, V.; Minasov, G.; Egli, M. A “hydrat-ion” spine in a B-DNA minor groove. J. Am. Chem. Soc. 1999, 121, 3590–3595. [Google Scholar] [CrossRef]
- Minasov, G.; Tereshko, V.; Egli, M. Atomic-resolution crystal structures of B-DNA reveal specific influences of divalent metal ions on conformation and packing. J. Mol. Biol. 1999, 291, 83–99. [Google Scholar] [CrossRef] [PubMed]
- Chiu, T.K.; Dickerson, R.E. 1 Å Crystal structures of B-DNA reveal sequence-specific binding and groove-specific bending of DNA by magnesium and calcium. J. Mol. Biol. 2000, 301, 915–945. [Google Scholar] [CrossRef] [PubMed]
- Robinson, H.; Gao, Y.G.; Sanishvili, R.; Joachimiak, A.; Wang, A.H.J. Hexahydrated magnesium ions bind in the deep major groove and at the outer mouth of A-form nucleic acid duplexes. Nucleic Acids Res. 2000, 28, 1760–1766. [Google Scholar] [CrossRef] [PubMed]
- Tereshko, V.; Wilds, C.J.; Minasov, G.; Prakash, T.P.; Maier, M.A.; Howard, A.; Wawrzak, Z.; Manoharan, M.; Egli, M. Detection of alkali metal ions in DNA crystals using state-of-the-art X-ray diffraction experiments. Nucleic Acids Res. 2001, 29, 1208–1215. [Google Scholar] [CrossRef] [PubMed]
- Egli, M. DNA-cation interactions: quo vadis? Chem. Biol. 2002, 9, 277–286. [Google Scholar] [CrossRef]
- Egli, M.; Minasov, G.; Su, L.; Rich, A. Metal ion and flexibility in a viral RNA pseudoknot and atomic resolution. Proc. Natl. Acad. Sci. USA. 2002, 99, 4302–4307. [Google Scholar] [CrossRef] [PubMed]
- Basu, S.; Rambo, R.P.; Strauss-Soukup, J.; Cate, J.; Ferré-D’Amaré, A.R.; Strobel, S.A.; Doudna, J.A. A specific monovalent metal ion integral to the AA platform of the RNA tetraloop receptor. Nat. Struct. Biol. 1998, 5, 986–992. [Google Scholar] [CrossRef] [PubMed]
- Conn, G.L.; Gittis, A.G.; Lattman, E.E.; Misra, V.K.; Draper, D.E. A compact RNA tertiary structure contains a buried backbone-K+ complex. J. Mol. Biol. 2002, 318, 963–973. [Google Scholar] [CrossRef]
- Ennifar, E.; Walter, P.; Dumas, P. An efficient method for solving RNA structures: MAD phasing by replacing magnesium with zinc. Acta Crystallogr. Sect. D Biol. Crystallogr. 2001, D57, 330–332. [Google Scholar] [CrossRef]
- Ennifar, E.; Walter, P.; Dumas, P. A crystallographic study of the binding of 13 metal ions to two related RNA duplexes. Nucleic Acids Res. 2003, 31, 2671–2682. [Google Scholar] [CrossRef] [PubMed]
- Petsko, G.A. Preparation of isomorphous heavy atom derivatives. Methods Enzymol. 1985, 114, 147–156. [Google Scholar] [PubMed]
- Rould, M.A. Screening for heavy-atom derivatives and obtaining accurate isomorphous differences. Methods Enzymol. 1997, 276, 461–472. [Google Scholar]
- Holbrook, S.R.; Kim, S.H. Crystallization and heavy atom derivatives of polynucleotides. Methods Enzymol. 1985, 114, 167–176. [Google Scholar] [PubMed]
- Kim, S.H.; Shin, W.C.; Warrant, R.W. Heavy metal ion-nucleic acid interaction. Methods Enzymol. 1985, 114, 156–167. [Google Scholar] [PubMed]
- Cate, J.H.; Gooding, A.R.; Podell, E.; Zhou, K.; Golden, B.L.; Kundrot, C.E.; Cech, T.R.; Doudna, J.A. Crystal structure of a group I ribozyme domain: principles of RNA packing. Science 1996, 273, 1678–1685. [Google Scholar] [CrossRef] [PubMed]
- Su, L.; Chen, L.; Egli, M.; Berger, J.M.; Rich, A. A minor groove RNA triplex in the crystal structure of a viral pseudoknot involved in ribosomal frameshifting. Nat. Struc. Bio. 1999, 6, 285–292. [Google Scholar]
- Keel, A.Y.; Rambo, R.P.; Batey, R.T.; Kieft, J.S. A general strategy to solve the phase problem in RNA crystallography. Structure 2007, 15, 761–772. [Google Scholar] [CrossRef] [PubMed]
- Hendrickson, W.A. Maturation of MAD phasing for the determination of macromolecular structures. J. Synchrotron Rad. 1999, 6, 845–851. [Google Scholar] [CrossRef]
- Dauter, Z.; Dauter, M.; Dodson, E. Jolly SAD. Acta Crystallogr. Sect. D Biol. Crystallogr. 2002, D58, 494–506. [Google Scholar] [CrossRef]
- Correll, C.C.; Freeborn, B.; Moore, P.B.; Steitz, T.A. Use of chemically modified nucleotides to determine a 62-nucleotide RNA crystal structure: a survey of phosphorothioates, Br, Pt and Hg. J. Biomol. Struct. Dyn. 1997, 15, 16–172. [Google Scholar] [CrossRef] [PubMed]
- Ennifar, E.; Carpentier, P.; Ferrer, J.; Walter, P.; Dumas, P. X-ray induced debromination of nucleic acids at the Br K aborption edge and implications for MAD phasing. Acta Crystallogr. Sect. D Biol. Crystallogr. 2002, D58, 1262–1269. [Google Scholar] [CrossRef]
- Egli, M.; Lubini, P.; Pallan, P.S. The long and winding road to the structure of homo-DNA. Chem. Soc. Rev. 2007, 36, 31–45. [Google Scholar] [CrossRef] [PubMed]
- Sanishvili, R.; Besnard, C.; Camus, F.; Fleurant, M.; Pattison, P.; Bricogne, G.; Schiltz, M. Polarization-dependence of anomalous scattering in brominated DNA and RNA molecules, and importance of crystal orientation in single- and multiple-wavelength anomalous diffraction phasing. J. Appl. Crystallogr. 2007, 40, 552–558. [Google Scholar] [CrossRef]
- Hendrickson, W.A.; Horton, J.R.; LeMaster, D.M. Selenomethionyl proteins produced for analysis by multiwavelength anomalous diffraction (MAD): a vehicle for direct determination of three-dimensional structure. EMBO J. 1990, 9, 1665–1672. [Google Scholar] [PubMed]
- Doublié, S. Selenomethionyl protein expression. In Macromolecular Crystallography Protocols, Volume 1, Preparation and Crystallization of Macromolecules; Humana Press: Totowa, NJ, USA, 2006. [Google Scholar]
- Hendrickson, W.A. Synchrotron crystallography. Trends Biochem. Sci. 2001, 25, 637–643. [Google Scholar] [CrossRef]
- Du, Q.; Carrasco, N.; Teplova, M.; Wilds, C.J.; Kong, X.; Egli, M.; Huang, Z. Internal derivatization of oligonucleotides with selenium for X-ray crystallography using MAD. J. Am. Chem. Soc. 2002, 124, 24–25. [Google Scholar] [CrossRef] [PubMed]
- Teplova, M.; Wilds, C.J.; Wawrzak, Z.; Tereshko, V.; Du, Q.; Carrasco, N.; Huang, Z.; Egli, M. Covalent incorporation of selenium into oligonucleotides for X-ray crystal structure determination via MAD: proof of principle. Biochimie 2002, 84, 849–858. [Google Scholar] [CrossRef]
- Wilds, C.J.; Pattanayek, R.; Pan, C.; Wawrzak, Z.; Egli, M. Selenium-assisted nucleic acid crystallography: use of DNA phosphoroselenoates for MAD phasing. J. Am. Chem. Soc. 2002, 124, 14910–14916. [Google Scholar] [CrossRef] [PubMed]
- Höbartner, C.; Rieder, R.; Kreutz, C.; Puffer, B.; Lang, K.; Polonskaia, A.; Serganov, A.; Micura, R. Syntheses of RNAs with up to 100 nucleotides containing site-specific 2’-methylseleno labels for use in X-ray crystallography. J. Am. Chem. Soc. 2005, 127, 12035–12045. [Google Scholar] [CrossRef] [PubMed]
- Serganov, A.; Keiper, S.; Malinina, L.; Tereshko, V.; Skripkin, E.; Höbartner, C.; Polonskaia, A.; Phan, A.T.; Wombacher, R.; Micura, R.; Dauter, Z.; Jaschke, A.; Patel, D.J. Structural basis for Diels-Alder ribozyme catalyzed carbon-carbon bond formation. Nat. Struct. Bio. 2005, 12, 218–224. [Google Scholar] [CrossRef] [PubMed]
- Egli, M.; Pallan, P.S.; Pattanayek, R.; Wilds, C.J.; Lubini, P.; Minasov, G.; Dobler, M.; Leumann, C.; Eschenmoser, A. Crystal structure of homo-DNA and nature’s choice of pentose of hexose in the genetic system. J. Am. Chem. Soc. 2006, 128, 10847–10856. [Google Scholar] [CrossRef] [PubMed]
- Pallan, P.S.; Egli, M. Selenium modification of nucleic acids: Preparation of oligonucleotides with incorporated 2’-SeMe-uridine for crystallographic phasing of nucleic acid structures. Nat. Protoc. 2007, 2, 647–651. [Google Scholar] [CrossRef] [PubMed]
- Pallan, P.S.; Egli, M. Selenium modification of nucleic acids: Preparation of phosphorothioate derivatives for crystallographic phasing of nucleic acid structures. Nat. Protoc. 2007, 2, 640–646. [Google Scholar] [CrossRef] [PubMed]
- Sheng, J.; Huang, Z. Selenium derivatization of nucleic acids for phase and structure determination in nucleic acid X-ray crystallography. Int. J. Mol. Sci. 2008, 9, 258–271. [Google Scholar] [CrossRef] [PubMed]
- Kwiatkowski, W.; Noel, J.P.; Choe, S. Use of Cr Kα radiation to enhance the signal from anomalous scatterers including sulfur. J. Appl. Crystallogr. 2000, 33, 876–881. [Google Scholar] [CrossRef]
- Yang, C.; Pflugrath, J.W. Applications of anomalous scattering form S atoms for improved phasing of protein diffraction data at Cu Kα wavelength. Acta Crystallogr. Sect. D Biol. Crystallogr. 2001, D57, 1480–1490. [Google Scholar] [CrossRef]
- Debreczeni, J.E.; Bunkóczi, G.; Girmann, B.; Sheldrick, G.M. In-house phase determination of the lima bean trypsin inhibitor: a low resolution sulfur-SAD case. Acta Crystallogr. Sect. D Biol. Crystallogr. 2003, D59, 393–395. [Google Scholar] [CrossRef]
- Debreczeni, J.E.; Bunkóczi, G.; Ma, Q.; Blaser, H.; Sheldrick, G.M. In-house measurement of the sulfur anomalous signal and its use for phasing. Acta Crystallogr. Sect. D Biol. Crystallogr. 2003, D59, 688–696. [Google Scholar] [CrossRef]
- Yang, C.; Pflugrath, J.W.; Courville, D.A.; Stence, C.N.; Ferrara, J.D. Away from the edge: SAD phasing from the sulfur anomalous signal measured in-house with chromium radiation. Acta Crystallogr. Sect. D Biol. Crystallogr. 2003, D59, 1943–1957. [Google Scholar] [CrossRef]
- Cianci, M.; Helliwell, J.R.; Moorcroft, D.; Olczak, A.; Raferty, J.; Rizkallah, P.J. The role of wavelength and source in the search for sulfur-atom positions evaluated in two case studies: lysozyme at room temperature and cryo apocrustacyanin A1. J. Appl. Crystallogr. 2004, 37, 555–564. [Google Scholar] [CrossRef]
- Olsen, J.G.; Flensburg, C.; Olsen, O.; Bricogne, G.; Hendricksen, A. Solving the structure of the bubble protein using the anomalous sulfur signal from single-crystal in-house Cu Kα diffraction data only. Acta Crystallogr. Sect. D Biol. Crystallogr. 2004, D60, 250–255. [Google Scholar] [CrossRef] [PubMed]
- Kitago, Y.; Watanabe, N.; Tanaka, I. Structure determination of a novel protein by sulfur SAD using chromium radiation in combination with a new crystal-mounting method. Acta Crystallogr. Sect. D Biol. Crystallogr. 2005, D61, 1013–1021. [Google Scholar] [CrossRef] [PubMed]
- Nagem, R.A.P.; Ambrosio, A.L.B.; Rojas, A.L.; Navarro, M.V.A.S.; Golubev, A.M.; Garratta, R.C.; Polikarpov, I. Getting the most out of X-ray home souces. J. Mol. Biol. 2005, D61, 1022–1030. [Google Scholar]
- Watanabe, N.; Kitago, Y.; Tanaka, I.; Wang, J.; Gu, Y.; Zheng, C.; Fan, H. Comparison of phasing methods for sulfur-SAD using in-house chromium radiation: Case studies for standard proteins and a 69 kDa protein. Acta Crystallogr. Sect. D Biol. Crystallogr. 2005, D61, 1533–1540. [Google Scholar] [CrossRef] [PubMed]
- Sarma, G.N.; Karplus, P.A. In-house sulfur SAD phasing: A case study of the effects of data quality and resolution cutoffs. Acta Crystallogr. Sect. D Biol. Crystallogr. 2006, D62, 707–716. [Google Scholar] [CrossRef] [PubMed]
- Wang, B.C. Resolution of phase ambiguity in macromolecular crystallography. Methods Enzymol. 1985, 115, 90–112. [Google Scholar] [PubMed]
- Ramagopal, U.A.; Dauter, M.; Dauter, Z. Phasing on anomalous signal of sulfurs: what is the limit? Acta Crystallogr. Sect. D Biol. Crystallogr. 2003, D59, 1020–1027. [Google Scholar] [CrossRef]
- Dauter, Z.; Adamiak, D.A. Anomalous signal of phosphorus used for phasing DNA oligomer: Importance of data redundancy. Acta Crystallogr. Sect. D Biol. Crystallogr. 2001, D57, 990–995. [Google Scholar] [CrossRef]
- Wing, R.; Drew, H.; Takano, T.; Broka, C.; Takano, S.; Itakura, K.; Dickerson, R.E. Crystal structure analysis of a complete turn of B-DNA. Nature 1980, 287, 755–758. [Google Scholar] [CrossRef] [PubMed]
- Sheldrick, G.M. Experimental phasing with SHELXC/D/E: Combining chain tracing with density modification. Acta Crystallogr. Sect. D Biol. Crystallogr. 2010, D66, 479–485. [Google Scholar] [CrossRef] [PubMed]
- Pape, T.; Scheider, T.R. HKL2MAP: A graphical user interface for phasing with SHELX programs. J. Appl. Crystallogr. 2004, 37, 843–844. [Google Scholar] [CrossRef]
- Matthews, B.W. Solvent content of protein crystals. J. Mol. Biol. 1968, 33, 491–497. [Google Scholar] [CrossRef]
- Kantardjieff, K.; Rupp, B. Matthews coefficient probabilities: Improved estimates for unit cell contents of proteins, DNA, and protein-nucleic acid complex crystals. Protein Sci. 2003, 12, 1865–1871. [Google Scholar] [CrossRef] [PubMed]
- Schneider, T.R.; Sheldrick, G.M. Substructure solution with SHELXD. Acta Crystallogr. Sect. D Biol. Crystallogr. 2002, D58, 1772–1779. [Google Scholar] [CrossRef]
- Burla, M.C.; Caliandro, R.; Camalli, M.; Carrozzini, B.; Cascarano, G.; Caro, L.D.; Giacovazzo, C.; Polidori, G.; Spagna, R. SIR2004: an improved tool for crystal structure determination and refinement. J. Appl. Crystallogr. 2005, 38, 381–388. [Google Scholar] [CrossRef]
- Bricogne, G.; Vonrhein, C.; Flensburg, C.; Schlitz, M.; Paciorek, W. Generation, representation and flow of phase information in structure determination: recent developments in and around SHARP 2.0. Acta Crystallogr. Sect. D Biol. Crystallogr. 2003, D59, 2023–2030. [Google Scholar] [CrossRef]
- Terwilliger, T.C.; Berendzen, J. Automated MAD and MIR structure solution. Acta Crystallogr. Sect. D: Biol. Crystallogr. 1999, D55, 849–861. [Google Scholar] [CrossRef]
- Watkins, D.; Moulaei, T.; Komeda, S.; Williams, L.D. Application of anomalous diffraction methods to the study of DNA and DNA-complexes. Methods Mol. Bio. 2010, 613, 133–152. [Google Scholar]
- Caliandro, R.; Carrozzini, B.; Cascarano, G.L.; DeCaro, L.; Giacovazzo, C.; Siliqi, D. Advances in the free lunch method. J. Appl. Crystallogr. 2007, 40, 931–937. [Google Scholar] [CrossRef]
- Luo, Z.; Dauter, M.; Dauter, Z. Phosphates in the Z-DNA dodecamer are flexible, but their P-SAD signal is sufficient for structure solution. Acta Crystallogr. Sect. D Biol. Crystallogr. 2014, D70, 1790–1800. [Google Scholar] [CrossRef] [PubMed]
- Shen, Q.; Wang, J.; Ealick, S.E. Anomalous difference signal in protein crystals. Acta Crystallogr. Sect. D Biol. Crystallogr. 2003, A59, 371–373. [Google Scholar] [CrossRef]
- Hays, F.A.; Teegarden, A.T.; Jones, Z.J.R.; Harms, M.; Raup, D.; Watson, J.; Cavaliere, E.; Ho, P.S. How sequence defines structure: a crystallographic map of DNA structure and conformation. Proc. Natl. Acad. Sci. USA. 2005, 102, 7157. [Google Scholar] [CrossRef] [PubMed]
- Gao, Y.G.; Robinson, H.; Wang, A.H. High-resolution A-DNA structures of d(AGGGGCCCCT), an A-DNA model of poly(dG) x poly(dC). Eur. J. Biochem. 1999, 261, 413. [Google Scholar] [CrossRef] [PubMed]
- Ng, H.L.; Kopka, M.L.; Dickerson, R.E. The structure of a stable intermediate in the A->B DNA helix transition. Proc. Natl. Acad. Sci. USA. 2000, 97, 2035. [Google Scholar] [CrossRef] [PubMed]
- Thota, N.; Li, X.H.; Bingman, M.; Sundaralingam, M. High-resolution refinement of the hexagonal A-DNA octamer d(GTGTACAC) at 1.4 Å. Acta Crystallogr. Sect. D Biol. Crystallogr. 1993, D49, 282. [Google Scholar] [CrossRef] [PubMed]
- Drew, H.R.; Dickerson, R.E. Conformation and dynamics in a Z-DNA tetramer. J. Mol. Biol. 1981, 152, 723. [Google Scholar] [CrossRef]
- Pan, B.; Sundaralingam, M. Crystal structure of rGd(CGCGCG): a Z-DNA hexamer with a 5’-(rG) overhang. Acta Crystallogr. Sect. D Biol. Crystallogr. 2003, D59, 433–437. [Google Scholar] [CrossRef]
- Girard, E.; Prange, T.; Kahn, R.; Fourme, R. Adaptation of the base-paired double-helix molecular architecture to extreme pressure. Nucleic Acids Res. 2007, 35, 4800. [Google Scholar] [CrossRef] [PubMed]
- Bingman, C.; Li, X.; Zon, G.; Sundaralingam, M. Crystal and molecular structure of d(GTGCGCAC): investigation of the effects of base sequence on the conformation of octamer complexes. Biochemistry 1992, 31, 12803. [Google Scholar] [CrossRef] [PubMed]
- Ramakrishnan, B.; Sundaralingam, M. High resolution crystal structure of the A-DNA decamer d(CCCGCCGGG). Novel intermolecular base-paired G*(G.C) triplets. J. Mol. Biol. 1993, 231, 431–444. [Google Scholar] [CrossRef] [PubMed]
- Mueller-Dieckmann, C.; Panjikar, S.; Tucker, P.A.; Weiss, M.S. On the routine use of soft X-rays in macromolecular crystallography. Part III. the optimal data-collection wavelength. Acta Crystallogr. Sect. D Biol. Crystallogr. 2005, D61, 1263–1272. [Google Scholar] [CrossRef] [PubMed]
- Kitayner, M.; Rozenberg, H.; Rabinovich, D.; Shakked, Z. Structures of the DNA-binding site of Runt-domain transcription regulators. Acta Crystallogr. Sect. D Biol. Crystallogr. 2005, D61, 236–246. [Google Scholar] [CrossRef] [PubMed]
- Mandal, P.K.; Venkadesh, S.; Gautham, N. Crystal structures of d(CACGCG).d(CGCGTG) grown with different metal ions. To be published.
- Ramakrishnan, B.; Sundaralingam, M. Evidence for crystal environment dominating base sequence effects on DNA conformation: Crystal structures of the orthorhombic and hexagonal polymorphs of the A-DNA decamer d(GCGGGCCCGC) and comparison with their isomorphous crystal structures. Biochemistry 1993, 32, 11458–11468. [Google Scholar] [CrossRef] [PubMed]
- Johansson, E.; Parkinson, G.; Neidle, S. A new crystal form for the dodecamer C-G-C-G-A-A-T-T-C-G-C-G: symmetry effects on the sequence-dependent DNA structure. J. Mol. Biol. 2000, 300, 551–561. [Google Scholar] [CrossRef] [PubMed]
- Mandal, P.K.; Venkadesh, S.; Nandini, M.; Gautham, N. Crystal studies of d(CACGCG).d(CGCGTG) grown with various metal ions. To be published.
- Heinemann, U.; Lauble, H.; Frank, R.; Blocker, H. Crystal structure analysis of an A-DNA fragment at 1.8 Åresolution: d(GCCCGGGC). Nucleic Acids Res. 1987, 15, 9531–9550. [Google Scholar] [CrossRef] [PubMed]
- Han, G.W.; Kopka, M.L.; Cascio, D.; Grzeskowiak, K.; Dickerson, R.E. Structure of a DNA analog of the primer for HIV-1 RT second strand synthesis. J. Mol. Biol. 1997, 269, 811–826. [Google Scholar] [CrossRef] [PubMed]
- Mandal, P.K.; Venkadesh, S.; Gautham, N. Crystal structure of d(CACGCG).d(CGCGTG) grown in the presence of SnCl2. To be published.
- Drew, H.R.; Wing, R.M.; Takano, T.; Broka, C.; Tanaka, S.; Itakura, K.; Dickerson, R.E. Structure of a B-DNA dodecamer: Conformation and dynamics. Proc. Natl. Acad. Sci. USA. 1981, 78, 2179–2183. [Google Scholar] [CrossRef] [PubMed]
- Ban, C.; Sudaralingam, M. Crystal structure of the self-complementary 5’-purine start decamer d(GCACGCGTGC) in the A-DNA conformation. II. Biophys. J. 1996, 71, 1222–1227. [Google Scholar] [CrossRef]
- Tippin, D.B.; Sundaralingam, M. Structure of d(CCCTAGGG): comparison with nine isomorphous octamer sequences reveals four distinct patterns of sequence-dependent intermolecular interactions. Acta Crystallogr. Sect. D Biol. Crystallogr. 1996, D52, 997–1003. [Google Scholar] [CrossRef] [PubMed]
- Holbrook, S.R.; Dickerson, R.E.; Kim, S.H. Anisotropic thermal-parameter refinement of the DNA dodecamer CGCGAATTCGCG by the segmented rigid-body method. Acta Crystallogr. Sect. D Biol. Crystallogr. 1985, B41, 255–262. [Google Scholar] [CrossRef]
- Goodsell, D.S.; Kopka, M.L.; Cascio, D.; Dickerson, R.E. Crystal structure of CATGGCCATG and its implications for A-tract bending models. Proc. Natl. Acad. Sci. USA. 1993, 90, 2930–2934. [Google Scholar] [CrossRef] [PubMed]
- Malinina, L.; Tereshko, V.; Ivanova, E.; Subirana, J.A.; Zarytova, V.; Nekrasov, Y. Structural variability and new intermolecular interactions of Z-DNA in crystals of d(PCPGPCPGPCPG). Biophys. J. 1998, 74, 2482–2490. [Google Scholar] [CrossRef]
- Venkadesh, S.; Mandal, P.K.; Gautham, N. Crystal structures of d(CACGCG).d(CGCGTG) cocrystallized with MnCl2. To be published.
- Shmueli, U. International Tables for Crystallography, second ed.; Vol. B, Kluwer Academic Publishers: Dordrecht, Netherlands, 2001. [Google Scholar]
- Chapman, H.N.; Fromme, P.; Barty, A.; White, T.A.; Kirian, R.A.; Aquila, A.; Hunter, M.S.; Schulz, J.; DePonte, D.P.; Weierstall, U.; et al. Femtosecond X-ray protein nanocrystallography. Nature 2011, 470, 73–77. [Google Scholar] [CrossRef] [PubMed]
- Nakane, T.; Song, C.; Suzuki, M.; Nango, E.; Kobayashi, J.; Masuda, T.; Inoue, S.; Mizohata, E.; Nakatsu, T.; Tanaka, T.; et al. Native sulfur/chlorine SAD phasing for serial femtosecond crystallography. Acta Crystallogr. Sect. D Biol. Crystallogr. D71, 2519–2525. [CrossRef] [PubMed]
- Lomb, L.; Barends, T.R.M.; Kassemeyer, S.; Aquila, A.; Epp, S.W.; Erk, B.; Foucar, L.; Hartmann, R.; Rudek, B.; Rolles, D.; et al. Radiation damage in protein serial femtosecond crystallography using an x-ray free-electron laser. Phys. Rev. B 2011, 84, 214111. [Google Scholar] [CrossRef] [PubMed]
- Finke, A.D.; Panepucci, E.; Vonrhein, C.; Wang, M.; Bricogne, G.; Olieric, V. Advanced crystaltallographic data colllection protocols for experimental phasing. In Nucleic Acid Crystallography: Methods and Protocols, Methods in Molecular Biology; Ennifar, E., Ed.; Springer Science+Business Media: New York, NY, USA, 2016; pp. 175–191. [Google Scholar]
- Diederichs, K. Quantifying instrument errors in macromolecular X-ray data sets. Acta Crystallogr. Sect. D Biol. Crystallogr. 2010, D66, 733–740. [Google Scholar] [CrossRef] [PubMed]
- Rose, J.P.; Wang, B.C. SAD phasing: history, current impact and future opportunities. Arch. Biochem. Biophys. 2016, 602, 80–94. [Google Scholar] [CrossRef] [PubMed]
- Rose, J.P.; Wang, B.C.; Weiss, M.S. Native SAD is maturing. IUCr J. 2015, 2, 431–440. [Google Scholar] [CrossRef] [PubMed]
- Weinert, T.; Olieric, V.; Waltersperger, S.; Panepucci, E.; Chen, L.; Zhang, H.; Zhou, D.; Rose, J.; Ebihara, A.; Kuramitsu, S. et. al Fast native-SAD phasing for routine macromolecular structure detemination. Nat. Methods 2015, 12, 131–133. [Google Scholar] [CrossRef] [PubMed]
- Liu, Z.J.; Chen, L.; Wu, D.; Ding, W.; Zhang, H.; Zhou, W.; Fu, Z.Q.; Wang, B.C. A multi-dataset data-collection strategy produces better diffraction data. Acta Crystallogr. Sect. A Found. Crystallogr. 2011, A67, 544–549. [Google Scholar] [CrossRef] [PubMed]
- Owen, R.L.; no Piñera, E.R.; Garman, E.F. Experimental determination of the radiation dose limit for cryococryo protein crystals. Proc. Natl. Acad. Sci. USA. 2006, 103, 4912–4917. [Google Scholar] [CrossRef] [PubMed]
- Liu, Q.; Dahmane, T.; Zhang, Z.; Assur, Z.; Brasch, J.; Shapiro, L.; Mancia, F.; Hendrickson, W.A. Structures from anomalous diffraction of native biologicsl macromolecules. Science 2012, 336, 1033–1037. [Google Scholar] [CrossRef] [PubMed]
- Liu, Q.; Liu, Q.; Hendrickson, W.A. Robust structural analysis of native biological macromolecules from multi-crystal anomalous diffraction data. Acta Crystallogr. Sect. D Biol. Crystallogr. 2013, D69, 1314–1332. [Google Scholar] [CrossRef] [PubMed]
- Klinke, S.; Foos, N.; Rinaldi, J.J.; Paris, G.; Goldbaum, F.A.; Legrand, P.; Guimarães, B.G.; Thompson, A. S-SAD phasing of monoclinic histidine kinase from Brucella abortus combining data from multiple crystals and orientations: an example of data-collection strategy and a posteriori analysis of different data combinations. Acta Crystallogr. Sect. D Biol. Crystallogr. 2015, D71, 1433–1443. [Google Scholar] [CrossRef] [PubMed]
- Olieric, V.; Weinert, T.; Finke, A.D.; Anders, C.; Li, D.; Olieric, N.; Borca, C.N.; Steinmetz, M.O.; Caffrey, M.; Jinek, M.; Wang, M. Data-collection strategy for challenging native SAD phasing. Acta Crystallogr. Sect. D Biol. Crystallogr. 2016, D72, 421–429. [Google Scholar] [CrossRef] [PubMed]
- Liebschner, D.; Yamada, Y.; Matsugaki, N.; Senda, M.; Senda, T. On the influence of crystal size and wavelength on native SAD phasing. Acta Crystallogr. Sect. D Biol. Crystallogr. 2016, D72, 728–741. [Google Scholar] [CrossRef] [PubMed]
- Dauter, Z. Data-collection strategies. Acta Crystallogr. Sect. D Biol. Crystallogr. 1999, D55, 1703–1717. [Google Scholar] [CrossRef]
- Cianci, M.; Groves, M.R.; Barford, D.; Schneider, T.R. Data collection with a tailored X-ray beam size at 2.69 Å wavelength (4.6 keV): sulfur SAD phasing of Cdc23Nterm. Acta Crystallogr. Sect. D Biol. Crystallogr. 2016, D72, 403–412. [Google Scholar] [CrossRef] [PubMed]
- Bury, C.S.; McGeehan, J.E.; Antson, A.A.; Carmichael, I.; Gerstel, M.; Shevtsov, M.B.; Garman, E.F. RNA protects a nucleoprotein complex against radiation damage. Acta Crystallogr. Sect. D Biol. Crystallogr. 2016, D72, 648–657. [Google Scholar] [CrossRef] [PubMed]
- Zeldin, O.B.; Gerstel, M.; Garman, E.F. RADDOSE-3D: Time- and space-resolved modelling of dose in macromolecular crystallography. J. Appl. Crystallogr. 2013, 46, 1225–1230. [Google Scholar] [CrossRef]
- Murray, J.W.; Garman, E.F.; Ravelli, R.B.G. X-ray absorption by macromolecular crystals: The effects of wavelength and crystal composition on absorbed dose. J. Appl. Crystallogr. 2004, 37, 513–522. [Google Scholar] [CrossRef]
- Raiber, E.A.; Muray, P.; Chirgadze, D.Y.; Beraldi, D.; Luisi, B.F.; Balasubramanian, S. 5-Formylcytosine alters the structure of the DNA double helix. Nat. Struct. Mol. Bio. 2015, 22, 44–49. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Adams, P.D.; Afonine, P.V.; Bunkoczi, G.; Chen, V.B.; Davis, I.W.; Echols, N.; Headd, J.J.; Hung, L.W.; Kaprai, G.J.; Grosse-Kunstleve, R.W.; et al. PHENIX: a comprehensive Python-based system for macromolecular structure solution. Acta Crystallogr. Sect. D Biol. Crystallogr. 2010, D66, 213–221. [Google Scholar] [CrossRef] [PubMed]
- Gessner, R.V.; Quigley, G.J.; Egli, M. Comparative studies of high resolution Z-DNA crystal structures. Part 1: Common hydration patterns of alternating dG-dC. J. Mol. Biol. 1994, 236, 1154–1168. [Google Scholar] [CrossRef]
- Pallan, P.S.; Prakash, T.P.; Li, F.; Eoff, R.L.; Manoharan, M.; Egli, M. A conformational transition in the structure of a 2’-modified DNA visualized at high resolution. Chem. Commun. 2009, 2017–2019. [Google Scholar] [CrossRef] [PubMed]
- Sheldrick, G.M. XPREP. Bruker AXS: Karlsruhe, Germany, 2003. [Google Scholar]
- Sheldrick, G.M. A short history of SHELX. Acta Crystallogr. Sect. A Found. Crystallogr. 2006, A64, 112–122. [Google Scholar]
- Emsley, P.; Cowtan, K. Coot: model-building tools for molecular grapics. Acta Crystallogr. Sect. D Biol. Crystallogr. 2004, D60, 2126–2132. [Google Scholar] [CrossRef] [PubMed]
- Schrödinger, L. The PyMOL Molecular Graphics System. Version 1.3r1 . Schrödinger LLC: New York, NY, USA,, 2010. [Google Scholar]
- Collaborative Computational Project, N. The CCP4 suite:programs for protein crystallography. Acta Crystallogr. Sect. D Biol. Crystallogr. 1994, D50, 760–763. [Google Scholar] [CrossRef] [PubMed]
- Zwart, P.H. Anomalous signal indicators in protein crystallography. Acta Crystallogr. Sect. D Biol. Crystallogr. 2005, D61, 1437–1448. [Google Scholar] [CrossRef] [PubMed]










| Z-DNA | DDD | 2’-Thio Decamer | |
|---|---|---|---|
| Unit Cell (Å) | |||
| a | 17.863 | 24.873 | 24.768 |
| b | 31.480 | 39.762 | 43.248 |
| c | 44.228 | 65.625 | 45.318 |
| Resolution (Å) | 0.95 (1.04–0.95) | 1.32 (1.41–1.32) | 1.30 (1.39–1.30) |
| No. of reflections | |||
| Measured | 255,194 | 507,675 | 506,771 |
| Unique | 15,976 | 15,756 | 12,553 |
| Completeness (%) | 97.8 (92.2) | 98.6 (98.2) | 99.9 (100.0) |
| Redundancy | 15.6 (5.2) | 29.6 (13.3) | 34.5 (17.4) |
| I/σ (I) | 31.7 (7.5) | 42.46 (3.02) | 37.52 (4.73) |
| Rint | 0.058 (0.183) | 0.046 (0.604) | 0.042 (0.494) |
| Peak Number | 8833 (44.98) | 9700 (29.06) | 8500 (26.99) | 1084 (26.01) | 8(25.58) |
|---|---|---|---|---|---|
| 1 | 6 | 6 | 9 | 6 | 10 |
| 2 | 5 | 9 | 6 | 9 | 6 |
| 3 | 9 | 5 | 5 | 5 | 5 |
| 4 | 8 | 10 | 10 | 10 | 8 |
| 5 | 4 | 2 | 11 | 11 | 9 |
| 6 | 2 | 11 | 8 | 8 | 4 |
| 7 | 12 | 8 | 12 | 12 | 3 |
| 8 | 11 | 12 | 2 | 2 | 12 |
| 9 | 10 | 4 | 3 | 4 | 2 |
| 10 | 3 | 3 | 4 | 3 | 11 |
| Peak Number | Peak Height | B Factor | Base |
|---|---|---|---|
| 1 | 0.9900 | 3.35 | 6 |
| 2 | 0.9683 | 4.09 | 5 |
| 3 | 0.9683 | 3.54 | 9 |
| 4 | 0.9389 | 4.16 | 8 |
| 5 | 0.8936 | 6.81 | 4 |
| 6 | 0.8787 | 4.58 | 2 |
| 7 | 0.8236 | 5.70 | 12 |
| 8 | 0.8181 | 5.26 | 11 |
| 9 | 0.8054 | 4.60 | 10 |
| 10 | 0.7549 | 5.69 | 3 |
| Z-DNA | 2’-Thio Decamer | |
|---|---|---|
| R/Rfree | 0.099/0.108 | 0.152/0.192 |
| No. of Reflections | 242,138 | 11,859 |
| Number of non-hydrogen atoms | ||
| No. of nucleic acid atoms | 240 | 386 |
| No. of heteroatoms | 20 | 43 |
| No. of water atoms | 76 | 76 |
| R.M.S. Deviations | ||
| Bond length (Å) | 0.058 | 0.012 |
| Angle distance (Å) | 0.436 | 0.02 |
| Crystal | Average Bijvoet Signal * | Measurability † (%) |
|---|---|---|
| Z-DNA | 1.21 | 6.55 |
| DDD | 1.37 | 9.55 |
| 2’-thio decamer | 1.31 | 8.43 |
| PDB ID | DNA form | sequence | reference | resolution(Å) |
|---|---|---|---|---|
| 1ZFF | B-DNA | d(CCGAATTCGG) | [66] | 0.94 |
| 1ZF5 | B-DNA | d(CCAGCGTGG) | [66] | 0.99 |
| 440D | A-DNA | d(AGGGGCCCT) | [67] | 1.10 |
| 1DC0 | A/B-DNA | d(CATGGGCCCATG) | [68] | 1.30 |
| 1ZF1 | A-DNA | d(CCGGGCCCGG) | [66] | 1.35 |
| 1D78 | A-DNA | d(GTGTACAC) | [69] | 1.40 |
| 1D79 | A-DNA | d(GTGTACAC) | [69] | 1.45 |
| 1ZNA | Z-DNA | d(CGCG) | [70] | 1.50 |
| 1M6R | Z-DNA | d(CGCGCG) | [71] | 1.54 |
| 2PKV | A/B-DNA | d(GGTATACC) | [72] | 1.60 |
| 118D | A-DNA | d(GTGCGCAC) | [73] | 1.64 |
| 160D | A-DNA | c(CCCGGCCGGG) | [74] | 1.65 |
| 1ZEX | A-DNA | d(CCCGGCCGGG) | [66] | 1.65 |
| 2A7E | A-DNA | d(CCCTAGGG) | [75] | 1.66 |
| 137D | A-DNA | d(GCGGGCCCGC) | [74] | 1.70 |
| 1XJX | A-DNA | d(TCTGCGGTC).d(TGACCCGCAG) | [76] | 1.70 |
| 3F8O | Z-DNA | d(CACGCG).d(CTCGCG) | [77] | 1.72 |
| 1ZFG | B-DNA | d(CCGAGCTCGG) | [66] | 1.75 |
| 138D | A-DNA | d(GCGGGCCCGC) | [78] | 1.80 |
| 1EHV | B-DNA | d(CGCGAATTCGCG) | [79] | 1.80 |
| 3GCY | Z-DNA | d(CACGCG).d(CGCGCG) | [80] | 1.80 |
| 9DNA | A-DNA | d(GCCCGGGC) | [81] | 1.80 |
| 307D | B-DNA | d(CAAAAGAAAAG).d(CTTTTCTTTG) | [82] | 1.85 |
| 3GDA | Z-DNA | d(CACGCG).(CGCGTG) | [83] | 1.88 |
| 1BNA | B-DNA | d(CGCGAATTCGCG) | [84] | 1.90 |
| 260D | A-DNA | d(GCACGCGTGC) | [85] | 1.90 |
| 279D | Z-DNA | d(GCGCGCGCGC) | [85] | 1.90 |
| 317D | A-DNA | d(CCCTAGGG) | [86] | 1.90 |
| 7BNA | B-DNA | d(CGCGAATTCGCG) | [87] | 1.90 |
| 126D | B-DNA | d(CATGGCCATG) | [88] | 2.00 |
| 1XJY | A-DNA | d(TCTGCGGTC).d(TGACCGCAG) | [76] | 2.00 |
| 390D | Z-DNA | d(CGCGCG) | [89] | 2.00 |
| 3G2A | Z-DNA | d(CACGCG).d(CGCCTG) | [90] | 2.00 |
| 1ZFC | B-DNA | d(CCGATATCGG) | [66] | 2.00 |
© 2016 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC-BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Harp, J.M.; Pallan, P.S.; Egli, M. Phosphorus SAD Phasing for Nucleic Acid Structures: Limitations and Potential. Crystals 2016, 6, 125. https://doi.org/10.3390/cryst6100125
Harp JM, Pallan PS, Egli M. Phosphorus SAD Phasing for Nucleic Acid Structures: Limitations and Potential. Crystals. 2016; 6(10):125. https://doi.org/10.3390/cryst6100125
Chicago/Turabian StyleHarp, Joel M., Pradeep S. Pallan, and Martin Egli. 2016. "Phosphorus SAD Phasing for Nucleic Acid Structures: Limitations and Potential" Crystals 6, no. 10: 125. https://doi.org/10.3390/cryst6100125
APA StyleHarp, J. M., Pallan, P. S., & Egli, M. (2016). Phosphorus SAD Phasing for Nucleic Acid Structures: Limitations and Potential. Crystals, 6(10), 125. https://doi.org/10.3390/cryst6100125