Dirac Cones in Graphene, Interlayer Interaction in Layered Materials, and the Band Gap in MoS2
Abstract
:1. Introduction
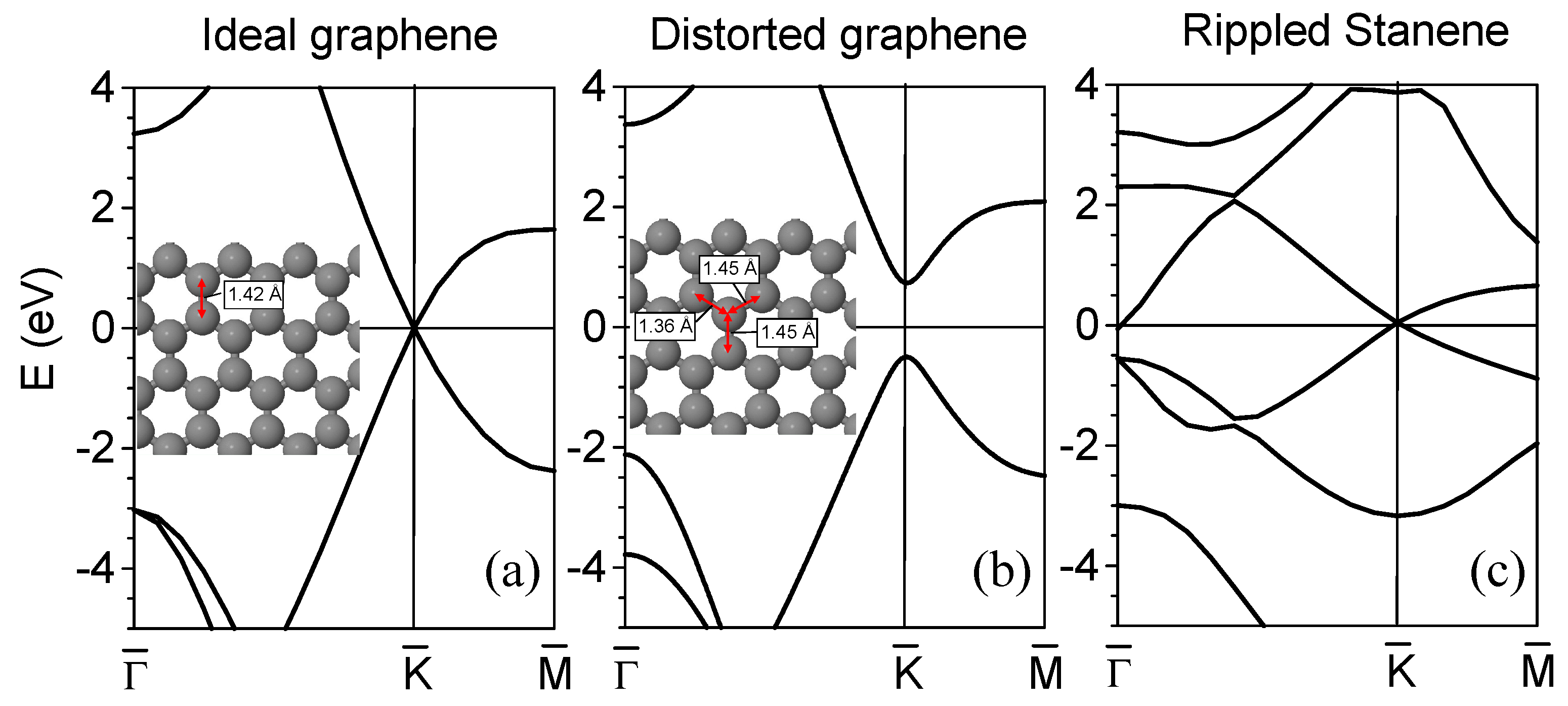
2. Dirac Cones and Buckling in Graphene and Similar Layers
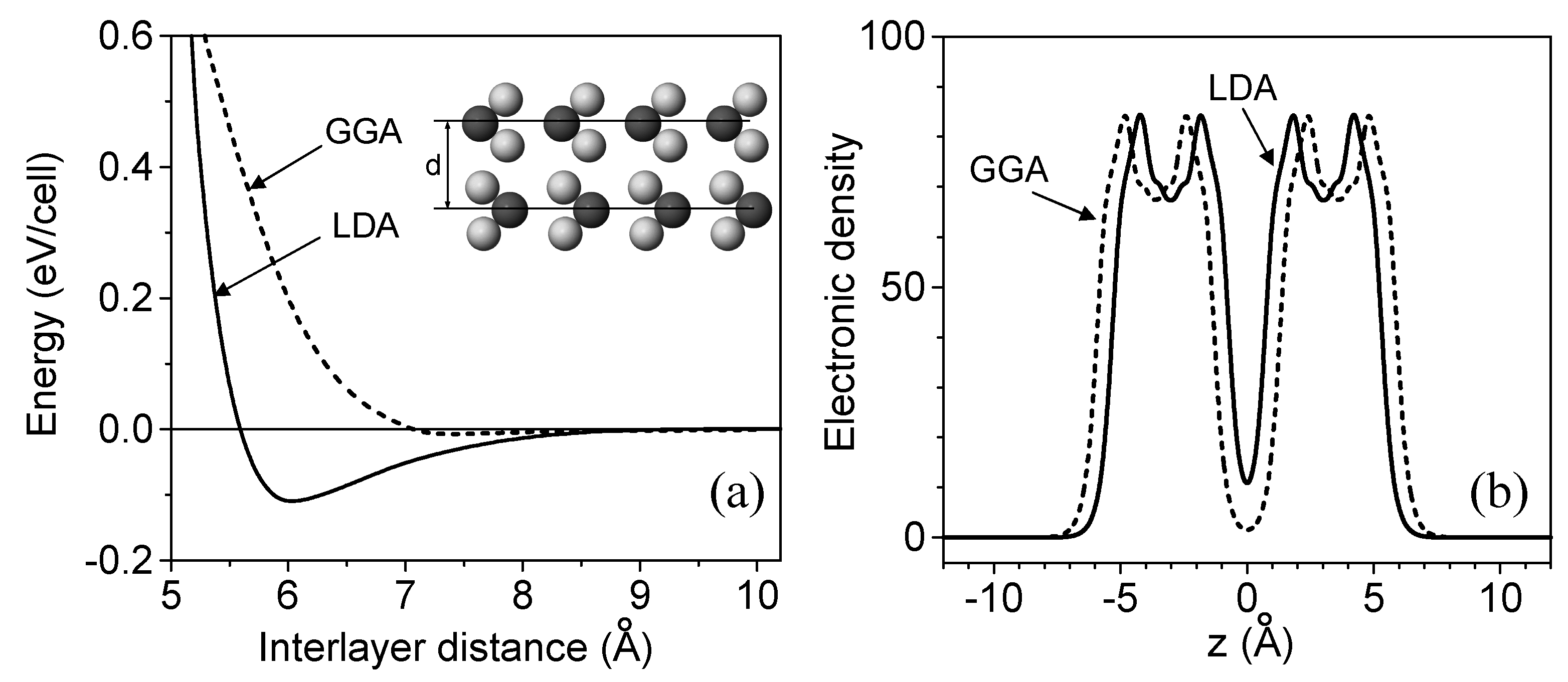
3. The Interlayer Interaction in Layered Crystals
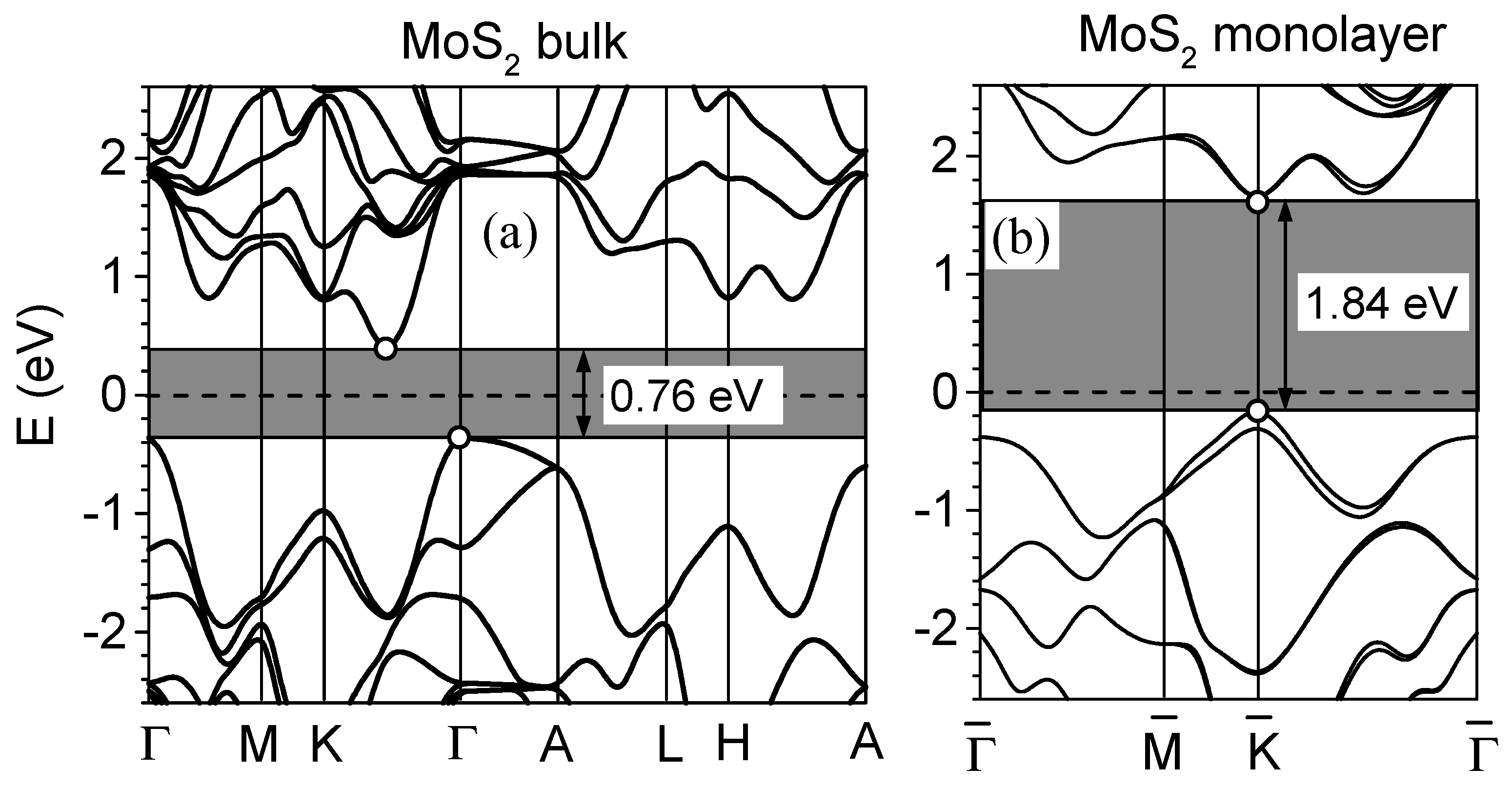
4. Band Gap and Screening in MoS2 Layers
5. Conclusions
Conflicts of Interest
Abbreviations
| DFT | Density Functional Theory |
| LDA | Local Density Approximation |
| GGA | Generalized Gradient Approximation |
| GW | GW quasi-particle Hedin's approach |
| QSGW | Quasiparticle Self-consistent GW approximation |
| BZ | Brillouin Zone |
| vdW | van der Waals |
| HREELS | High Resolution Electron Energy Loss Spectroscopy |
| 2D | 2-Dimensional |
References
- Novoselov, K.S.; Jiang, D.; Schedin, F.; Booth, T.J.; Khotkevich, V.V.; Morozov, S.V.; Geim, A.K. Two-dimensional atomic crystals. Proc. Natl. Acad. Sci. USA 2005, 102, 10451–10453. [Google Scholar] [CrossRef] [PubMed]
- Geim, A.K.; Novoselov, K.S. The rise of graphene. Nat. Mater. 2007, 6, 183–191. [Google Scholar] [CrossRef] [PubMed]
- Geim, A.K. Graphene: Status and Prospects. Science 2009, 324, 1530–1534. [Google Scholar] [CrossRef] [PubMed]
- Castro Neto, A.H.; Guinea, F.; Peres, N.M.R.; Novoselov, K.S.; Geim, A.K. The electronic properties of graphene. Rev. Mod. Phys. 2009, 81, 109. [Google Scholar] [CrossRef]
- Novoselov, K.S.; McCann, E.; Morosov, S.V.; Fal’ko, V.I.; Katsnelson, M.I.; Zeitler, U.; Jiang, D.; Schedin, F.; Geim, A.K. Two-dimensional gas of massless Dirac fermions in graphene. Nature 2005, 438, 192–200. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Do, V.N.; Pham, T.H. Graphene and its one-dimensional patterns: From basic properties towards applications. Adv. Nat. Sci. Nanosci. Nanotechnol. 2010, 1, 033001. [Google Scholar] [CrossRef]
- Wintterlin, J.; Bocquet, M.-L. Graphene on metal surfaces. Surf. Sci. 2009, 603, 1841–1852. [Google Scholar] [CrossRef]
- Lebègue, S.; Eriksson, O. Electronic structure of two-dimensional crystals from ab initio theory. Phys. Rev. B 2009, 79, 115409. [Google Scholar] [CrossRef]
- Nicolosi, V.; Chhowalla, M.; Kanatzidis, M.G.; Strano, M.S.; Coleman, J.N. Liquid Exfoliation of Layered Materials. Science 2013, 340, 1226419. [Google Scholar] [CrossRef]
- Radisavljevic, B.; Radenovic, A.; Brivio, J.; Giacometti, V.; Kis, A. Single-layer MoS2 transistors. Nat. Nanotech. 2011, 6, 147–150. [Google Scholar] [CrossRef] [PubMed]
- Mak, K.F.; Lee, C.; Hone, J.; Shan, J.; Heinz, T.F. Atomically Thin MoS2: A New Direct-Gap Semiconductor. Phys. Rev. Lett. 2010, 105, 136805. [Google Scholar] [CrossRef] [PubMed]
- Splendiani, A.; Sun, L.; Zhang, Y.; Li, T.; Mak, J.; Chim, C.-Y.; Galli, G.; Wang, F. Emerging photoluminescence in monolayer MoS2. Nano Lett. 2010, 10, 1271–1275. [Google Scholar] [CrossRef] [PubMed]
- Eknapakul, T.; King, P.D.; Lombardo, A.; Krupke, R.; Ferrari, A.C.; Avouris, P.; Steiner, M. Electronic structure of a quasi-freestanding MoS2 monolayer. Nano Lett. 2014, 14, 1312–1316. [Google Scholar] [CrossRef] [PubMed]
- Cheiwchanchamnangij, T.; Lambrecht, W.R.L. Quasiparticle band structure calculation of monolayer, bilayer, and bulk MoS2. Phys. Rev. B 2012, 85, 205302. [Google Scholar] [CrossRef]
- Yakovkin, I.N. Interlayer interaction and screening in MoS2. Surf. Rev. Lett. 2014, 21, 1450039. [Google Scholar] [CrossRef]
- Ye, M.; Winslow, D.; Zhang, D.; Pandey, R.; Yap, Y.K. Recent Advancement on the Optical Properties of Two-Dimensional Molybdenum Disulfide (MoS2) Thin Films. Photonics 2015, 2, 288–307. [Google Scholar] [CrossRef]
- Hedin, L. New Method for Calculating the One-Particle Green’s Function with Application to the Electron-Gas Problem. Phys. Rev. 1965, 139, A796. [Google Scholar] [CrossRef]
- Enderlein, C.; Kim, Y.S.; Bostwick, A.; Rotenberg, E.; Horn, K. The formation of an energy gap in graphene on ruthenium by controlling the interface. New J. Phys. 2010, 12, 033014. [Google Scholar] [CrossRef]
- Giovannetti, G.; Khomyakov, P.A.; Brocks, G.; Karpan, V.M.; van den Brink, J.; Kelly, P.J. Doping graphene with metal contacts. Phys. Rev. Lett. 2008, 101, 026803. [Google Scholar] [CrossRef] [PubMed]
- Bostwick, A.; Ohta, T.; McChesney, J.L.; Emtsev, K.V.; Seyller, T.; Horn, K.; Rotenberg, E. Symmetry breaking in few layer graphene films. New J. Phys. 2007, 9, 385. [Google Scholar] [CrossRef]
- Ohta, T.; Bostwick, A.; Seyller, T.; Horn, K.; Rotenberg, E. Controlling the electronic structure of bilayer graphene. Science 2006, 313, 951–954. [Google Scholar] [CrossRef] [PubMed]
- Zhou, S.Y.; Gweon, G.H.; Fedorov, A.V.; First, P.N.; de Heer, W.A.; Lee, D.H.; Guinea, F.; Castro Neto, A.H.; Lanzara, A. Substrate-induced bandgap opening in epitaxial graphene. Nat. Mater. 2007, 6, 770–775. [Google Scholar]
- Skomski, R.; Dowben, P.A.; Sky Driver, M.; Kelber, J.A. Sublattice-induced symmetry breaking and bandgap formation in grapheme. Mater. Horiz. 2014. [Google Scholar] [CrossRef]
- Kumar, P.; Skomski, R.; Manchanda, P.; Kashyap, A.; Dowben, P.A. Effective mass and band gap of strained graphene. Curr. Appl. Phys. 2014, 14, S136. [Google Scholar] [CrossRef]
- Nakada, K.; Fujita, M.; Dresselhaus, G.; Dresselhaus, M.S. Edge state in graphene ribbons: Nanometer size effect and edge shape dependence. Phys. Rev. B 1996, 54, 17954. [Google Scholar] [CrossRef]
- Yin, W.-J.; Xie, Y.-E.; Liu, L.-M.; Wang, R.-Z.; Wei, X.-L.; Lau, L.; Zhong, J.-X.; Chen, Y.-P. R-graphyne: A new two-dimensional carbon allotrope with versatile Dirac-like point in nanoribbons. J. Mater. Chem. A 2013, 1, 5341–5346. [Google Scholar] [CrossRef]
- Pivetta, M.; Patthey, F.; Barke, I.; Hovel, H.; Delley, B.; Schneider, W.-D. Gap opening in the surface electronic structure of graphite induced by adsorption of alkali atoms: Photoemission experiments and density functional calculations. Phys. Rev. B 2005, 71, 165430. [Google Scholar] [CrossRef]
- Petrova, N.V.; Yakovkin, I.N. DFT calculations of the electronic structure and interlayer interaction in the Li-intercalated graphene bilayer. Surf. Rev. Lett. 2016, 24, 1750020. [Google Scholar] [CrossRef]
- Sutter, P.W.; Flege, J.-I.; Sutter, E.A. Epitaxial graphene on ruthenium. Nat. Mater. 2008, 7, 406–411. [Google Scholar] [CrossRef] [PubMed]
- Jiang, D.-E.; Du, M.-H.; Dai, S. First principles study of the graphene/Ru(0001) interface. J. Chem. Phys. 2009, 130, 074705. [Google Scholar] [CrossRef] [PubMed]
- Yakovkin, I.N. Band structure of Au layers on the Ru(0001) and graphene/Ru(0001) surfaces. Eur. Phys. J. B 2012, 85, 61. [Google Scholar] [CrossRef]
- Varykhalov, A.; Sanchez-Barriga, J.; Shikin, A.M.; Biswas, C.; Vescovo, E.; Rybkin, A.; Marchenko, D.; Rader, O. Electronic and magnetic properties of quasifreestanding graphene on Ni. Phys. Rev. Lett. 2008, 101, 157601. [Google Scholar] [CrossRef] [PubMed]
- Pletikosić, I.; Kralj, M.; Pervan, P.; Brako, R.; Coraux, J.; N’Diaye, A.T.; Busse, C.; Michely, T. Dirac Cones and Minigaps for Graphene on Ir(111). Phys. Rev. Lett. 2009, 102, 056808. [Google Scholar] [CrossRef] [PubMed]
- Di Sante, D.; Stroppa, A.; Barone, P.; Whangbo, M.-H.; Picozzi, S. Emergence of ferroelectricity and spin-valley properties in two-dimensional honeycomb binary compounds. Phys. Rev. B 2015, 91, 161401(R). [Google Scholar] [CrossRef]
- Peierls, R.E. Quantum Theory of Solids; Clarendon Press: Oxford, UK, 1955. [Google Scholar]
- Mermin, N.D. Crystalline Order in Two Dimensions. Phys. Rev. 1968, 176, 250–254. [Google Scholar] [CrossRef]
- Lee, S.-H.; Chung, H.-J.; Heo, J.; Yang, H.; Shin, J.; Chung, U.-I.; Seo, S. Band Gap Opening by Two-Dimensional Manifestation of Peierls Instability in Graphene. ACS Nano 2011, 5, 2964–2969. [Google Scholar] [CrossRef] [PubMed]
- Son, Y.-W.; Cohen, M.L.; Louie, S.G. Energy Gaps in Graphene Nanoribbons. Phys. Rev. Lett. 2006, 97, 216803. [Google Scholar] [CrossRef] [PubMed]
- Abanin, D.A.; Shytov, A.V.; Levitov, L.S. Peierls-Type Instability and Tunable Band Gap in Functionalized Graphene. Phys. Rev. Lett. 2010, 105, 086802. [Google Scholar] [CrossRef] [PubMed]
- Batra, I.P. Gapless Peierls transition. Phys. Rev. B 1990, 42, 9162–9165. [Google Scholar] [CrossRef]
- Yakovkin, I.N. Atomic wires. In Encyclopedia of Nanoscience and Nanotechnology; Nalwa, H.S., Ed.; American Scientific Publishers: Valencia, CA, USA, 2004; Volume 1, pp. 169–190. [Google Scholar]
- Yakovkin, I.N. Metallicity of atomic wires. Appl. Surf. Sci. 2006, 252, 6127–6134. [Google Scholar] [CrossRef]
- Bostwick, A.; McChesney, J.L.; Emtsev, K.V.; Seyller, T.; Horn, K.; Kevan, S.D.; Rotenberg, E. Quasiparticle transformation during a metal insulator transition in graphene. Phys. Rev. Lett. 2009, 103, 056404. [Google Scholar] [CrossRef] [PubMed]
- Park, C.-H.; Giustino, F.; Spataru, C.D.; Cohen, M.L.; Louie, S.G. First-principles study of electron linewidths in graphene. Phys. Rev. Lett. 2009, 102, 0768034. [Google Scholar] [CrossRef] [PubMed]
- Kim, S.; Ihm, J.; Choi, H.J.; Son, Y.-W. Origin of anomalous electronic structures of epitaxial graphene on silicon carbide. Phys. Rev. Lett. 2008, 100, 1768024. [Google Scholar] [CrossRef] [PubMed]
- Lennard-Jones, J.E. Processes of adsorption and diffusion on solid surfaces. Trans. Faraday Soc. 1932, 28, 333–359. [Google Scholar] [CrossRef]
- London, F. The general theory of molecular forces. Trans. Faraday Soc. 1937, 33, 8–26. [Google Scholar] [CrossRef]
- Stone, A.J. The Theory of Intermolecular Forces; Clarendon Press: Oxford, UK, 1996. [Google Scholar]
- Berland, K.; Cooper, V.R.; Lee, K.; Schröder, E.; Thonhauser, T.; Hyldgaard, P.; Lundqvist, B.I. Van der Waals forces in density functional theory: A review of the vdW-DF method. Rep. Prog. Phys. 2015, 78, 066501. [Google Scholar] [CrossRef] [PubMed]
- Grimme, S. Density functional theory with London dispersion corrections. WIREs Comput. Mol. Sci. 2011, 1, 211–228. [Google Scholar] [CrossRef]
- Tkatchenko, A.; Romaner, L.; Hofmann, O.T.; Zojer, E.; Ambrosch-Draxl, C.; Scheffler, M. Van der Waals interactions between organic adsorbates and at organic/inorganic interfaces. MRS Bull. 2010, 35, 435–442. [Google Scholar] [CrossRef]
- Klimeš, J.; Michaelides, A. Perspective: Advances and challenges in treating van der Waals dispersion forces in density functional theory. J. Chem. Phys. 2012, 137, 120901. [Google Scholar] [CrossRef] [PubMed]
- Andersson, Y.; Langreth, D.C.; Lundqvist, B.I. van der Waals Interactions in Density-Functional Theory. Phys. Rev. Lett. 1996, 76, 102. [Google Scholar] [CrossRef] [PubMed]
- Dion, M.; Rydberg, H.; Schröder, E.; Langreth, D.C.; Lundqvist, B.I. Van der Waals Density Functional for General Geometries. Phys. Rev. Lett. 2004, 92, 246401. [Google Scholar] [CrossRef] [PubMed]
- Thonhauser, T.; Cooper, V.R.; Li, S.; Puzder, A.; Hyldgaard, P.; Langreth, D.C. Van der Waals density functional: Self-consistent potential and the nature of the van der Waals bond. Phys. Rev. B 2007, 76, 125112. [Google Scholar] [CrossRef]
- Reilly, A.M.; Tkatchenko, A. Understanding the role of vibrations, exact exchange, and many-body van der Waals interactions in the cohesive properties of molecular crystals. J. Chem. Phys. 2013, 139, 024705. [Google Scholar] [CrossRef] [PubMed]
- Silvestrelli, P.L.; Ambrosetti, A. Including screening in van der Waals corrected density functional theory calculations: The case of atoms and small molecules physisorbed on graphene. J. Chem. Phys. 2014, 140, 124107. [Google Scholar] [CrossRef] [PubMed]
- Brako, R.; Sokcević, D.; Lazić, P.; Atodiresei, N. Graphene on the Ir(111) surface: From van der Waals to strong bonding. New J. Phys. 2010, 12, 113016. [Google Scholar] [CrossRef]
- Khomyakov, P.A.; Giovannetti, G.; Rusu, P.C.; Brocks, G.; van den Brink, J.; Kelly, P.J. First-principles study of the interaction and charge transfer between graphene and metals. Phys. Rev. B 2009, 79, 195425. [Google Scholar] [CrossRef]
- Feibelman, P.J. DFT Versus the “Real World” (or, Waiting for Godft). Top. Catal. 2010, 53, 417–422. [Google Scholar] [CrossRef]
- Shulenburger, L.; Baczewski, A.D.; Zhu, Z.; Guan, J.; Tomanek, D. The Nature of the Interlayer Interaction in Bulk and Few-Layer Phosphorus. Nano Lett. 2015, 15, 8170–8175. [Google Scholar] [CrossRef] [PubMed]
- Yakovkin, I.N.; Petrova, N.V. Hydrogen-induced metallicity and strengthening of MoS2. Chem. Phys. 2014, 434, 20–24. [Google Scholar] [CrossRef]
- Petrova, N.V.; Yakovkin, I.N.; Zeze, D.A. Metallization and stiffness of the Li-intercalated MoS2 bilayer. Appl. Surf. Sci. 2015, 353, 333–337. [Google Scholar] [CrossRef] [Green Version]
- Yakovkin, I.N. Band structure of the MoS2 bilayer with adsorbed and intercalated Na. Phys. Status Solidi B 2015, 252, 2693–2697. [Google Scholar] [CrossRef]
- LaShell, S.; McDougall, B.A.; Jensen, E. Spin Splitting of an Au(111) Surface State Band Observed with Angle Resolved Photoelectron Spectroscopy. Phys. Rev. Lett. 1996, 77, 3419. [Google Scholar] [CrossRef] [PubMed]
- Koroteev, Y.M.; Bihlmayer, G.; Gayone, J.E.; Chulkov, E.V.; Blügel, S.; Echenique, P.M.; Hofmann, P. Strong Spin-Orbit Splitting on Bi Surfaces. Phys. Rev. Lett. 2004, 93, 046403. [Google Scholar] [CrossRef] [PubMed]
- Bychkov, Y.A.; Rashba, E.I. Properties of a 2D electron gas with lifted spectral degeneracy. JETP Lett. 1984, 39, 78. [Google Scholar]
- Bihlmayer, G.; Koroteev, Y.M.; Echenique, P.M.; Chulkov, E.V.; Blügel, S. The Rashba-effect at metallic surfaces. Surf. Sci. 2006, 600, 3888–3891. [Google Scholar] [CrossRef]
- Zhu, Z.Y.; Cheng, Y.C.; Schwingenschlögl, U. Giant spin-orbit-induced spin splitting in two-dimensional transition-metal dichalcogenide semiconductors. Phys. Rev. B 2011, 84, 153402. [Google Scholar] [CrossRef]
- Kobayashi, K.; Yamauchi, J. Electronic structure and scanning-tunneling-microscopy image of molybdenum dichalcogenide surfaces. Phys. Rev. B Condens. Matt. 1995, 51, 17085–17095. [Google Scholar] [CrossRef]
- Jin, W.; Yeh, P.-C.; Zaki, N.; Zhang, D.; Sadowski, J.T.; Al-Mahboob, A.; van der Zande, A.M.; Chenet, D.A.; Dadap, J.I.; Herman, I.P. Direct Measurement of the Thickness-Dependent Electronic Band Structure of MoS2 Using Angle-Resolved Photoemmision Spectroscopy. Phys. Rev. Lett. 2013, 111, 106801. [Google Scholar] [CrossRef] [PubMed]
- Yakovkin, I.N.; Dowben, P.A. The problem of the band gap in LDA calculations. Surf. Rev. Lett. 2007, 14, 481–487. [Google Scholar] [CrossRef]
- Kleinman, L.; Lee, S. Gradient expansion of the exchange-energy density functional: Effect of taking limits in the wrong order. Phys. Rev. B 1988, 37, 4634. [Google Scholar] [CrossRef]
- Perdew, J.P.; Burke, K.; Ernzerhof, M. Generalized Gradient Approximation Made Simple. Phys. Rev. Lett. 1996, 77, 3865. [Google Scholar] [CrossRef] [PubMed]
- Yakovkin, I.N.; Petrova, N.V. Influence of the thickness and surface composition on the electronic structure of FeS2 layers. Appl. Surf. Sci. 2016, 377, 184–190. [Google Scholar] [CrossRef]
- Alonso, J.A.; Girifalco, L.A. Nonlocal approximation to the exchange potential and kinetic energy of an inhomogeneous electron gas. Phys. Rev. 1978, 17, 3735. [Google Scholar] [CrossRef]
- Gunnarsson, O.; Jonson, M.; Lundqvist, B.I. Descriptions of exchange and correlation effects in inhomogeneous electron systems. Phys. Rev. B 1979, 20, 3136. [Google Scholar] [CrossRef]
- Ramasubramaniam, A. Large excitonic effects in monolayers of molybdenum and tungsten dichalcogenides. Phys. Rev. B 2012, 86, 115409. [Google Scholar] [CrossRef]
- Qiu, D.Y.; da Jornada, F.H.; Louie, S.G. Optical spectrum of MoS2: Many-body effects and diversity of exciton states. Phys. Rev. Lett. 2013, 111, 216805. [Google Scholar] [CrossRef] [PubMed]
- Ugeda, M.M.; Bradley, A.J.; Shi, S.-F.; da Jornada, F.H.; Zhang, Y.; Qiu, D.Y.; Ruan, W.; Mo, S.-K.; Hussain, Z.; Shen, Z.-X.; et al. Observation of giant bandgap renormalization and excitonic effects in a monolayer transition metal dichalcogenide semiconductor. Nat. Mater 2014, 13, 1091–1095. [Google Scholar] [CrossRef] [PubMed]
- Bradley, A.J.; Ugeda, M.M.; da Jornada, F.H.; Qiu, D.Y.; Ruan, W.; Zhang, Y.; Wickenburg, A.; Riss, S.; Lu, J.; Mo, S.-K.; et al. Probing the Role of Interlayer Coupling and Coulomb Interactions on Electronic Structure in Few-Layer MoSe2 Nanostructures. Nano Lett. 2015, 15, 2594–2599. [Google Scholar] [CrossRef] [PubMed]
- Pelant, I.; Valenta, J. Luminescence Spectroscopy of Semiconductors; Oxford University Press: Oxford, UK, 2012. [Google Scholar]
- Mak, K.F.; He, K.; Lee, C.; Lee, G.H.; Hone, J.; Heinz, T.F.; Shan, J. Tightly bound trions in monolayer MoS2. Nat. Mater. 2013, 12, 207–211. [Google Scholar] [CrossRef] [PubMed]
- Huard, V.; Cox, R.T.; Saminadayar, K.; Arnoult, A.; Tatarenko, S. Bound states in optical absorption of semiconductor quantum wells containing a two-dimensional electron gas. Phys. Rev. Lett. 2000, 84, 187–190. [Google Scholar] [CrossRef] [PubMed]
- Komsa, H.-P.; Krasheninnikov, A.V. Effects of confinement and environment on the electronic structure and exciton binding energy of MoS2 from first principles. Phys. Rev. B 2012, 86, 241201(R). [Google Scholar] [CrossRef]
- Calman, E.V.; Dorow, C.J.; Fogler, M.M.; Butov, L.V.; Hu, S.; Mishchenko, A.; Geim, A.K. Control of excitons in multi-layer van der Waals heterostructures. Appl. Phys. Lett. 2016, 108, 101901. [Google Scholar] [CrossRef]
- Dileep, K.; Sahu, R.; Sarkar, S.; Peter, S.C.; Datta, R. Layer specific optical band gap measurement at nanoscale in MoS2 and ReS2 van der Waals compounds by high resolution electron energy loss spectroscopy. J. Appl. Phys. 2016, 119, 114309. [Google Scholar] [CrossRef]
- Zhang, C.; Johnson, A.; Hsu, C.L.; Li, L.J.; Shih, C.K. Direct Imaging of Band Profile in Single Layer MoS2 on Graphite: Quasiparticle Energy Gap, Metallic Edge States, and Edge Band Bending. Nano Lett. 2014, 14, 2443–2447. [Google Scholar] [CrossRef] [PubMed]
- Ulstrup, S.; Čabo, A.G.; Miwa, J.A.; Riley, J.M.; Grønborg, S.S.; Johannsen, J.C.; Cacho, C.; Alexander, O.; Chapman, R.T.; Springate, E.; et al. Ultrafast Band Structure Control of a Two-Dimensional Heterostructure. ACS Nano 2016, 10, 6315–6322. [Google Scholar] [CrossRef] [PubMed]
- Aziza, Z.B.; Henck, H.; Felice, D.; Di Pierucci, D.; Chaste, J.; Naylor, C.H.; Balan, A.; Dappe, Y.J.; Johnson, A.T.C.; Ouerghi, A. Bandgap inhomogeneity of MoS2 monolayer on epitaxial graphene bilayer in van der Waals p-n junction. Carbon 2016, 110, 396–403. [Google Scholar] [CrossRef]
- Jin, W.; Yeh, P.-C.; Zaki, N.; Chenet, D.; Arefe, G.; Hao, Y.; Sala, A.; Mentes, T.O.; Dadap, J.I.; Locatelli, A.; et al. Tuning the electronic structure of monolayer graphene/MoS2 van der Waals heterostructures via interlayer twist. Phys. Rev. B 2015, 92, 201409(R). [Google Scholar] [CrossRef]
- Diaz, H.C.; Avila, J.; Chen, C.; Addou, R.; Asensio, M.C.; Batzill, M. Direct Observation of Interlayer Hybridization and Dirac Relativistic Carriers in Graphene/MoS2 van der Waals Heterostructures. Nano Lett. 2015, 15, 1135–1140. [Google Scholar] [CrossRef] [PubMed]
- Pierucci, D.; Henck, H.; Avila, J.; Balan, A.; Naylor, C.H.; Patriarche, G.; Dappe, Y.J.; Silly, M.G.; Sirotti, F.; Johnson, A.T.C.; et al. Band Alignment and Minigaps in Monolayer MoS2—Graphene van der Waals Heterostructures. Nano Lett. 2016, 16, 4054–4061. [Google Scholar] [CrossRef] [PubMed]

© 2016 by the author; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC-BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yakovkin, I.N. Dirac Cones in Graphene, Interlayer Interaction in Layered Materials, and the Band Gap in MoS2. Crystals 2016, 6, 143. https://doi.org/10.3390/cryst6110143
Yakovkin IN. Dirac Cones in Graphene, Interlayer Interaction in Layered Materials, and the Band Gap in MoS2. Crystals. 2016; 6(11):143. https://doi.org/10.3390/cryst6110143
Chicago/Turabian StyleYakovkin, Ivan N. 2016. "Dirac Cones in Graphene, Interlayer Interaction in Layered Materials, and the Band Gap in MoS2" Crystals 6, no. 11: 143. https://doi.org/10.3390/cryst6110143
APA StyleYakovkin, I. N. (2016). Dirac Cones in Graphene, Interlayer Interaction in Layered Materials, and the Band Gap in MoS2. Crystals, 6(11), 143. https://doi.org/10.3390/cryst6110143




