Synthesis, Crystal Structure, and Magnetic Properties of Giant Unit Cell Intermetallics R117Co52+δSn112+γ (R = Y, La, Pr, Nd, Ho)

Chai, Ping; Abramchuk, Mykola; Shatruk, Michael

doi:10.3390/cryst6120165

Open AccessArticle

Synthesis, Crystal Structure, and Magnetic Properties of Giant Unit Cell Intermetallics R₁₁₇Co_52+δSn_112+γ (R = Y, La, Pr, Nd, Ho)

by

Ping Chai

,

Mykola Abramchuk

and

Michael Shatruk

^*

Department of Chemistry and Biochemistry, Florida State University, Tallahassee, FL 32306, USA

^*

Author to whom correspondence should be addressed.

Crystals 2016, 6(12), 165; https://doi.org/10.3390/cryst6120165

Submission received: 10 September 2016 / Revised: 7 December 2016 / Accepted: 14 December 2016 / Published: 20 December 2016

(This article belongs to the Special Issue Correlated Electron Crystals)

Download

Browse Figures

Versions Notes

Abstract

:

Ternary intermetallics R₁₁₇Co_52+δSn_112+γ (R = Y, La, Pr, Nd, and Ho) have been prepared by arc-melting followed by annealing at 800 °C. All the compounds belong to the Tb₁₁₇Fe₅₂Ge₁₁₂ structure type (space group Fm

\bar{3}

m) characterized by a complex giant cubic unit cell with a ~ 30 Å. The single-crystal structure determination of Y- and La-containing compounds reveals a significant structural disorder. A comparison of these and earlier reported crystal structures of R₁₁₇Co_52+δSn_112+γ suggests that more extensive disorder occurs for structures that contain larger lanthanide atoms. This observation can be explained by the need to maintain optimal bonding interactions as the size of the unit cell increases. Y₁₁₇Co₅₆Sn₁₁₅ exhibits weak paramagnetism due to the Co sublattice and does not show magnetic ordering in the 1.8–300 K range. Ho₁₁₇Co₅₅Sn₁₀₈ shows ferromagnetic ordering at 10.6 K. Both Pr₁₁₇Co₅₄Sn₁₁₂ and Nd₁₁₇Co₅₄Sn₁₁₁ exhibit antiferromagnetic ordering at 17 K and 24.7 K, respectively, followed by a spin reorientation transition at lower temperature.

Keywords:

intermetallics; crystal structure; giant unit cells; magnetic properties

1. Introduction

Intermetallics with giant unit cells (GUC) that contain hundreds and thousands of atoms represent one of the most interesting topics in the structural inorganic chemistry. The great complexity of these crystal structures stems from the ability of constituent atoms to adopt a range of coordination numbers and a variety of coordination environments, which lead to rather poorly defined rules for the assembly of such structures [1]. Complex intermetallics are also of current interest for potential applications as thermoelectric materials, heterogeneous catalysts, and models for understanding self-organized nanoscale architectures [2,3].

Typical representatives of GUC intermetallics include clathrate compounds [4], Zintl phases [5], Frank-Kasper phases [6,7], Nowotny chimney-ladder phases [8,9], and quasicrystals and their approximants [10]. The realm of these materials can be expanded by slight variation of the compositions that can lead not only to the expansion of the existing isostructural systems but also to the formation of new crystal structures. For instance, in the Al-Cu-Ta system [11,12], Al_56.6Cu_3.9Ta_39.5 crystallizes in the F4

\bar{3}

m space group with the unit cell volume around 93,000 Å3, but a slight compositional change leads to another phase, Al_55.4Cu_5.4Ta_39.1, which exhibits a more complicated crystal structure and has the largest intermetallic unit cell reported to date, with the volume around 365,000 Å3. Another example of such structural complexity is offered by the Tsai-type 2/1 approximant crystal field, where new phases are constantly discovered in a series of adjacent ternary systems, Ca-Au-In, Ca-Au-Ga, and Ca-Au-Sn [13,14,15]. New examples of GUC intermetallics continue to appear, fascinating us with their intricate crystal structures [2,10,16,17,18].

The ternary Tb₁₁₇Fe₅₂Ge₁₁₂ structure type was reported for the first time by Pecharsky et al. in 1987 as a cubic system with the space group Fm

\bar{3}

m and the lattice constant of 28.58 Å [19]. Later, other R₁₁₇Fe₅₂Ge₁₁₂ analogues (R = Pr, Nd, Sm, Gd, Dy, Ho, Er, Tm, Lu, and Y), as well as isostructural Nd₁₁₇Cr₅₂Ge₁₁₂, Sm₁₁₇Cr₅₂Ge₁₁₂, Pr₁₁₇Co₅₂Ge₁₁₂, and Sm₁₁₇Co₅₂Ge₁₁₂, were discovered [20,21]. In recent years, the Tb₁₁₇Fe₅₂Ge₁₁₂-type structure was extended to stannides. To date, the R₁₁₇Co_52+δSn_112+γ phases have been synthesized for all rare-earth elements except Sc, Yb, and Eu [22,23,24,25,26,27,28]. We have recently provided a detailed structural description for these polar intermetallics, using Sm₁₁₇Co_55.6Sn₁₁₆ as an example [23], which was followed by a more comprehensive overview of the entire series by Mudryk et al. [28]. In both works it was concluded that the extensive structural disorder observed in a number of crystallographic positions in R₁₁₇Co_52+δSn_112+γ results in the increase in the Sn/Co ratio as the size of the lanthanide element increases. Understanding the character of the disorder and its relation to the exact composition of these materials requires crystal structure refinement from single-crystal X-ray diffraction data. To date, the results of such refinements have been reported for compounds with R = Pr [25], Sm [23], Gd [27,28], Tb, and Dy [23].

In terms of physical properties, only the basic magnetism studies for R₁₁₇Co_52+δSn_112+γ (R = Pr, Ce, Sm, Tb, Dy) [23,24,25,28] and Pr₁₁₇Co_56.7Ge₁₁₂ [29], plus a relatively complete physical property investigation for Gd₁₁₇Co₅₆Sn₁₁₄ [27,28], have been reported. Given the large concentration of the rare-earth and transition metal elements and the complexity of the crystal structure, one can expect to observe interesting magnetic behavior for these materials. Thus, possible spin reorientation transitions were found for Tb₁₁₇Co₅₉Sn₁₁₁, Dy₁₁₇Co₅₈Sn₁₁₁ [23], and Gd₁₁₇Co₅₆Sn₁₁₄ [28]. The structural complexity might also lead to very low thermal conductivity, as was suggested for Gd₁₁₇Co₅₆Sn₁₁₄ [27]. Therefore, complete and detailed studies of the crystal structures and physical properties of these materials are required, which necessitates the synthesis of pure phases and the growth of representative single crystals.

In this paper, we report the synthesis, crystal structure, and magnetism of five R₁₁₇Co_52+δSn_112+γ compounds (R = Y, La, Pr, Nd, and Ho). The crystal structures of Y- and La-containing compounds were determined by single crystal X-ray diffraction that allows elucidation of the structural disorder model in two more members of the R₁₁₇Co_52+δSn_112+γ series. In addition, the magnetic investigation of the Y-containing compound allows us to demonstrate directly that the Co sublattice in R₁₁₇Co_52+δSn_112+γ does not contribute to magnetic ordering.

2. Results and Discussion

2.1. Synthesis and Analysis

Compounds R₁₁₇Co_52+δSn_112+γ (R = Y, La, Pr, Nd, and Ho) were obtained by arc-melting. Representative single crystals were selected from crashed arc-melted ingots. After homogenizing annealing of arc-melted samples at 1073 K, the products were characterized by powder X-ray diffraction. All of them belong to the Tb₁₁₇Fe₅₂Ge₁₁₂ structure type. The Y-containing sample is highly pure (Figure 1), while the La-containing one contains a small amount of La₂CoSn₄ and a minor unidentified impurity. The Pr-, Nd-, and Ho-containing samples contain minor amounts of Pr₂CoSn₄, Nd₂Co_0.8Sn₄, and Ho₅Sn₃, respectively. The X-ray powder diffraction analysis reveals a gradual decrease in the unit cell parameter a as the atomic number increases (Table 1), in accordance with the lanthanide contraction.

The elemental compositions of Y- and La-containing compounds were established by single-crystal X-ray diffraction analysis as Y₁₁₇Co_55.8(1)Sn_115.11(6) and La_115.78(4)Co_63.1(2)Sn_114.95(6), respectively. The EDX analysis was also used to find elemental compositions for all five compounds studied in this work (Table 1). The compositions observed are very close to the nominal ones, as well as to the earlier reported compositions of these and related Tb₁₁₇Fe₅₂Ge₁₁₂-type stannides [22,23,24,25,26,27,28]. For the sake of simplicity, we will use the approximate formulas Y₁₁₇Co₅₆Sn₁₁₅ and La₁₁₆Co₆₃Sn₁₁₅ in the following discussion.

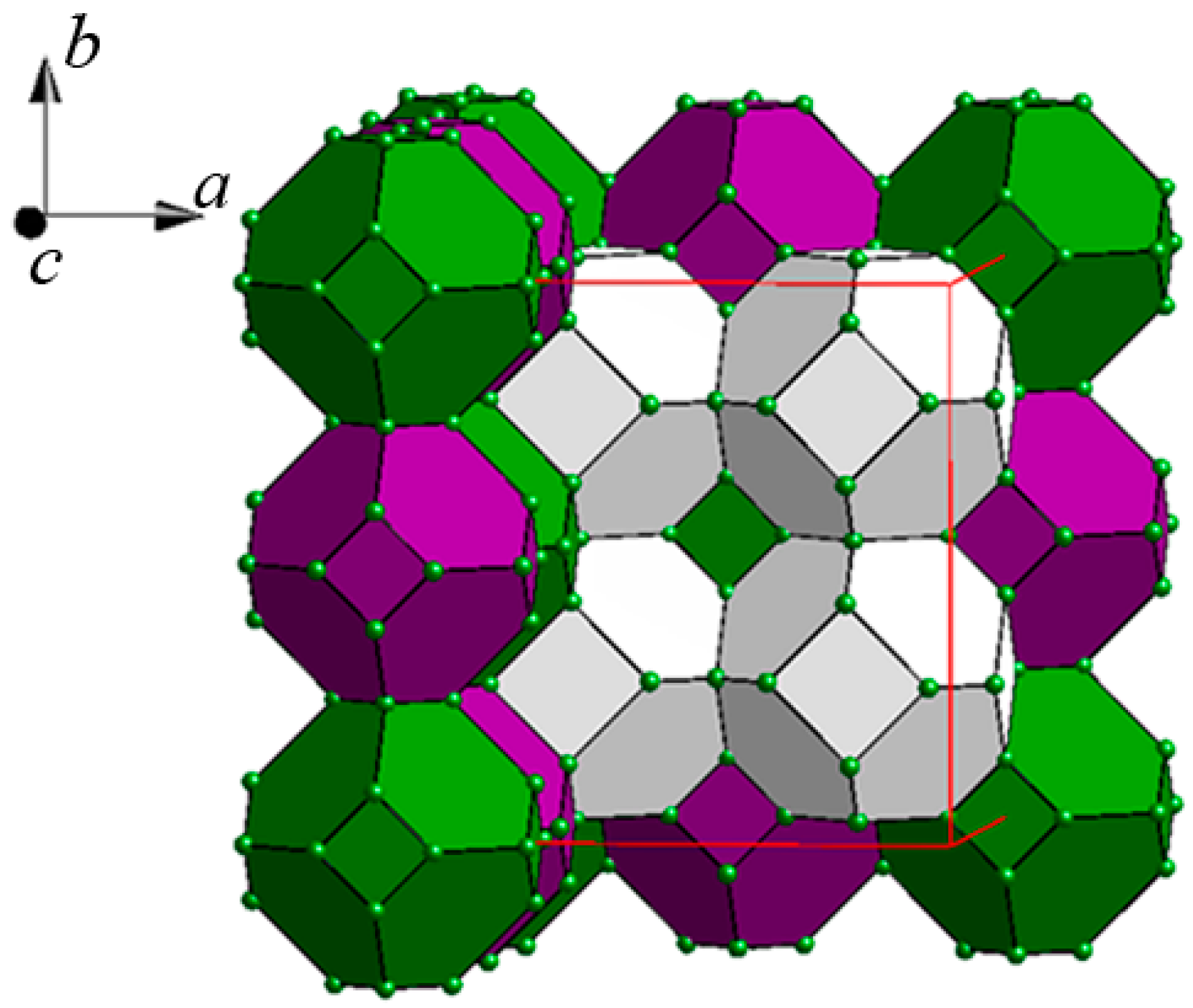
2.2. Crystal Structures

As described by the topological analysis of the Tb₁₁₇Fe₅₂Ge₁₁₂ structure type in our previous paper [23], the crystal structure of R₁₁₇Co_52+δSn_112+γ can be understood as an assembly of multi-shell polyhedra, following the early ideas of Jones [30] and Parthé [31]. Thus, the structure is built of three multi-shell, face-sharing truncated octahedra (TOH), labeled as A, B, and C in Figure 2. Considering only the central atoms of these multi-shell polyhedra, the TOHs B are centered at the origin of the cubic unit cell, while the TOHs A and C occupy, respectively, the (½,0,0) and (¼,¼,¼) crystallographic positions and their symmetry equivalents, thus producing a topological arrangement identical to the crystal structure of the Heusler alloy Cu₂MnAl [32]. The multi-shell polyhedra A, B, and C differ by the centering atom and the nature of endohedral shell enclosed in the outermost TOH shell. The detailed description of the construction for each TOH can be found in our previous paper [23]. In the present contribution, we would like to focus on the analysis of structural disorder found in these complex crystal structures. We will demonstrate how this disorder is dictated by the size of the lanthanide element.

Y₁₁₇Co₅₆Sn₁₁₅, similar to Dy₁₁₇Co₅₇Sn₁₁₂ [24], displays a relatively ordered structure as compared to the reported Sm-, Gd-, and Tb-containing analogues [23,27] (Table 2). All the Y and Sn positions are fully occupied, as opposed to the latter three structures which exhibit partial occupancy or splitting in some of the R and Sn sites. The Co positions in Y₁₁₇Co₅₆Sn₁₁₅ are also less disordered, but one does observe disordered Co2, Co3, and Co6 sites and a mixed Co51/Sn52 site. The Co2 and Co3 sites are located in the yttrium-centered TOH B to build the first cube and second cuboctahedron (CBO) shells, respectively, followed by an octahedron of Sn7 sites (Figure 3a). In this configuration, the distance between two Co2 sites at the apex of CBO is 0.93 Å and the Co2–Co3 distance within the trigonal face of CBO is 1.57 Å; such short separations between cobalt atoms are physically impossible, which explains why both Co2 and Co3 sites show ~50% occupancies. A physically meaningful structure should avoid the coexistence of the cubic apex and its surrounding trigonal apex, so the actual configuration is built of the yttrium-centered distorted cuboctahedron (DCBO) of Co3 sites that is penetrated by a tetrahedron of Co2 sites, where the Co2–Co2 and Co2–Co3 distances are 2.71 and 2.38 Å, respectively (Figure 3b). The disorder of the Co2 and Co3 sites is common to all reported R₁₁₇Co_52+δSn_112+γ compounds. Also common is the mixed occupancy of the 32f Wyckoff positions by cobalt and tin atoms (Co51/Sn52), although in the Dy- and Pr-containing analogues this site was reported to be occupied solely by cobalt [24,25].

Arguably, the most interesting crystallographic changes take place in the TOH A, and these changes are related to the size of the lanthanide atom. In all R₁₁₇Co_52+δSn_112+γ structures, at the center of the TOH A is the Wyckoff site 4b surrounded by a cube of Sn atoms (Figure 4). Interestingly, this site is never occupied in the Tb₁₁₇Fe₅₂Ge₁₁₂-type germanides, which led Mudryk et al. to suggest that the stannides should be considered as a separate Dy₁₁₇Co₅₇Sn₁₁₂ structure type [28], according to the first reported representative of this family [24]. As the radius of the R atom increases upon going from Y to Dy and then to La along the lanthanide series, the increase in the unit cell parameter a causes larger Sn-Sn separation in the cube of Sn atoms that surround the 4b site (Table 3). This increase leads to the variation of other distances between the atoms that surround the cube, and the Co-Sn and R-Sn distances, in general, also increase. The Co atoms that cap the faces of the Sn₈ cube move closer to those faces in order to maintain the effective bonding interactions with Sn atoms, and the Sn₈Co₆ configuration in the La-containing structure resembles a face-centered cube (Figure 4f).

The increase in the volume of the Sn₈ cube has a substantial impact on the arrangement and disorder of the nearby Co atoms. In the structure of Y₁₁₇Co₅₆Sn₁₁₅, where the volume of the cube is the smallest in the series, the 4b site remains vacant (Figure 4a), which is a unique situation among all R₁₁₇Co_52+δSn_112+γ compounds whose structures have been established by single-crystal X-ray diffraction. In the Dy-containing structure, the 4b site is fully occupied by a Co atom, but the face-capping 24e sites are vacant (Figure 4b), while both 4b and 24e sites are occupied in the Tb-containing structure (Figure 4c). The Gd-containing compound represents a borderline at which the Sn₈ cube becomes too large to maintain optimal Co-Sn distances with the central Co atom. As a consequence, the Co atom is displaced from the 4b site and becomes disordered over a 24e site (Figure 4d). The same arrangement of Co atoms is observed for the Sm- and La-containing structures (Figure 4e,f), although the distance between the disordered Co position inside the cube and the Sn atoms in the corners of the cube increases markedly upon going from R = Gd to Sm to La, and in the La-containing structure this distance becomes similar to the distance between the Sn atoms and the Co atom in the central 4b site of the Dy-containing structure (Table 3).

The crystal structure of La₁₁₆Co₆₃Sn₁₁₅ is more disordered as compared to that of Y₁₁₇Co₅₆Sn₁₁₅. The disordered positions in La₁₁₆Co₆₃Sn₁₁₅ include partially occupied Co2, Co61/Co62, Co7, La71, Co72, La8, Co31/Co32, and mixed Co51/Sn52 sites. Particularly notable and important features of the disorder model are as follows:

(i): The Co2 and Co31/Co32 sites correspond to the Co2 and Co3 sites, respectively, in Y₁₁₇Co₅₆Sn₁₁₅. The Co31/Co32 site splitting in La₁₁₆Co₆₃Sn₁₁₅ can be explained by the necessity to maintain optimal interatomic distances while the size of the unit cell increases due to the larger size of La relative to Y. Thus, the Co32 position is located closer to the La8 atom (Figure 3c), resulting in an unreasonably short La-Co distance of 1.61 Å, which in turn causes the partial (83%) occupancy of the La8 site that correlates with the partial (12%) occupancy of the Co32 site.
(ii): The disordered Co61/Co62 site in La₁₁₆Co₆₃Sn₁₁₅, corresponding to the Co6 site in Y₁₁₇Co₅₆Sn₁₁₅, forms an octahedron capping the Sn₈ cube, which in turns encloses the disordered Co7 site, as discussed above (Figure 4f). Thus, the site occupancies of the Co61, Co62, and Co7 sites in the structure of La₁₁₆Co₆₃Sn₁₁₅ are correlated (Table 2).
(iii): The La71 site (s.o.f. = 0.47) is located in the center of the multi-shell polyhedron TOH C. While in the Y-containing structure this central site is fully occupied, in the La-containing structure it is only partially occupied and surrounded by an additional tetrahedron of Co72 atoms (s.o.f. = 0.53) inserted between the La71 site and the rest of the shell (Figure 5a). Such Co72 site was not observed in the corresponding cluster in Y₁₁₇Co₅₆Sn₁₁₅ (Figure 5b). The La₁₁₆Co₆₃Sn₁₁₅ structure is the first example among the Tb₁₁₇Fe₅₂Ge₁₁₂-type structures to exhibit such disorder in the TOH C.

2.3. Magnetic Properties

We have previously reported the magnetic properties of several R₁₁₇Co_52+δSn_112+γ materials (R = Sm, Tb, Dy) [23], suggesting that the magnetic phase transitions arise solely due to the lanthanide sublattice. The availability of the pure polycrystalline sample of Y₁₁₇Co₅₆Sn₁₁₅ now allows us to directly address the role of the Co sublattice in the magnetism of these compounds. The magnetic susceptibility of Y₁₁₇Co₅₆Sn₁₁₅ shows a slow increase upon cooling in the higher-temperature range and then increases faster below ~25 K. The match between the zero-field-cooled (ZFC) and field-cooled (FC) magnetization curves (Figure 6a) indicates the absence of any magnetic phase transitions, suggesting paramagnetic behavior of this material over the entire temperature range. Thus, our earlier assumption of the lack of magnetic ordering in the Co sublattice appears to be well justified. Fitting the high-temperature part of the FC curve to the modified Curie-Weiss law yields a slightly negative Weiss constant θ (Table 4), indicating very weak antiferromagnetic nearest-neighbor interactions between the Co moments. The obtained effective magnetic moment (µ_eff) is 1.62 µ_B per Co atom. The field-dependent magnetization measured at 1.8 K shows a gradual increase with the maximum value of 0.22 µ_B per Co atom at 7 T (Figure 6b), which further supports the paramagnetism of the Co sublattice in Y₁₁₇Co₅₆Sn₁₁₅. Magnetic measurements on the La₁₁₆Co₆₃Sn₁₁₅ sample showed obvious signals from magnetic impurities that were hard to remove. Nevertheless, a paramagnetic behavior is also expected for La₁₁₆Co₆₃Sn₁₁₅ based on the properties of Y₁₁₇Co₅₆Sn₁₁₅, considering that both La³⁺ and Y³⁺ are non-magnetic ions.

The Pr-, Nd-, and Ho-containing compounds exhibit more complicated magnetic behavior as compared to Y₁₁₇Co₅₆Sn₁₁₅. The magnetic susceptibility for all three compounds is nearly temperature-independent in the higher-temperature range (Figure 7a,c,e) and the inverse magnetic susceptibility follows the Curie-Weiss law above 50 K, with the Weiss temperatures of 17, 24.7, and 10 K for R = Pr, Nd, and Ho, respectively (Table 4). Thus, all three compounds exhibit ferromagnetic nearest-neighbor interactions between the lanthanide magnetic moments. To determine the effective magnetic moments, we subtracted the value of 1.62 µ_B per Co atom obtained for Y₁₁₇Co₅₆Sn₁₁₅. This procedure led to the effective moments of 4.9 µ_B/Pr, 3.80 µ_B/Nd, and 10.20 µ_B/Ho, among which only the latter two are close to the theoretical values of 3.58 µ_B/Pr, 3.62 µ_B/Nd, and 10.60 µ_B/Ho.

With decreasing temperature, Pr- and Nd-containing compounds exhibit abrupt increases in magnetic susceptibility below ~30 and ~40 K, respectively, followed by a sharp maximum at T_N = 10.5 and 18.3 K (Figure 7a,c). These features resemble those observed in the FC curves reported for the Gd-, Tb-, and Dy-containing analogues [23,28]. The abrupt increase in the susceptibility agrees with the short-range ferromagnetic correlations indicated by the positive values of the Weiss constant for Pr₁₁₇Co₅₄Sn₁₁₂ and Nd₁₁₇Co₅₄Sn₁₁₁ (Table 4). Nevertheless, the sharp maximum suggests the occurrence of antiferromagnetic ordering in these materials. Additional features observed in the ZFC curves at 5.5 and 11.1 K, respectively, might be indicative of spin reorientation transitions. This assumption is also supported by kinks observed at 7 kOe and 19 kOe, respectively, in the field-dependent magnetization of these materials measured at 1.8 K (Figure 7b,d). These curves do not exhibit saturation, and the maximum magnetization values of 1.49 μ_B per Pr atom and 1.78 μ_B per Nd atom achieved at 7 T are substantially lower than the theoretically expected saturation magnetization of 3.20 μ_B and 3.28 μ_B, respectively, which is also in agreement with the antiferromagnetic ordering in these materials.

The Ho-containing compound shows an abrupt increase in the FC magnetic susceptibility below ~25 K followed by saturation at lower temperatures (Figure 7e). Such behavior, together with the bifurcation of the ZFC and FC magnetization curves, suggests ferromagnetic ordering in this material. The ordering temperature, T_C = 10.6 K, was found as the point of the fastest increase in the FC magnetization as a function of temperature. Consistent with the ferromagnetic ordering, the isothermal magnetization of Ho₁₁₇Co₅₅Sn₁₀₈ at 1.8 K exhibits a fast increase at lower fields followed by a slower increase above ~1.5 T (Figure 7f). Nevertheless, the maximum magnetization value at 7 T is 6.5 µ_B per Ho atom, which is still smaller than the theoretical value of 10.0 µ_B. This observation likely indicates a more complex magnetic structure, which is not surprising taking into account the complexity of the nuclear crystal structure. (Note that the minor impurity of Ho₅Sn₃ observed in this sample was reported to undergo antiferromagnetic ordering at 22 K [33]. We do not observe this feature in our measurements, which suggests that the effect of this minor impurity on the magnetic behavior of Ho₁₁₇Co₅₅Sn₁₀₈ is negligible.)

3. Materials and Methods

3.1. Synthesis

All manipulations during sample preparation were carried out in an argon-filled dry box (content of O₂ < 1 ppm). Powders of yttrium, lanthanum, praseodymium (all 99.9%), cobalt (99.5%), and tin shots (99.99%) were obtained from Alfa Aesar (Haverhill, MA, USA). Powders of neodymium and holmium (both 99.9%) were made by filing the metal bars (Michigan Chem. Corp., Saint Louis, MI, USA) by the aid of stainless steel files. Cobalt powder was additionally purified by heating in a flow of H₂ gas for 5 h at 775 K prior to use. All the samples were synthesized by arc-melting pelletized stoichiometric mixtures of constituent elements on a water-cooled copper hearth. The total mass of each sample was 0.2 mg, and the pellet diameter was 5 mm. The pellets were arc-melted, turned over, and remelted several times to improve homogeneity. The obtained ingots were sealed under vacuum (<10^–2 mbar) in 10 mm i.d. fused silica tubes and annealed at 1073 K for one month. To obtain purer products, several reactions with the ratio of starting elements close to R:Co:Sn = 117:55:115 were tried for each sample, and the optimum loaded compositions are shown in Table 1. For Y- and La-containing compounds, the single crystals were first obtained from the R:Co:Sn = 3:2:3 mixture, and then the bulk samples were prepared by reactions with the nearly stoichiometric compositions determined from the crystal structure analysis, to obtain purer products. All the products are inert to air at room temperature.

3.2. X-Ray Diffraction

Room temperature powder X-ray diffraction was carried out on a X’Pert Pro diffractometer (PANalytical, Almelo, The Netherlands) with an X’Celerator detector using Cu-Kα radiation (λ = 1.54187 Å). The patterns were recorded in the 2θ range of 10° to 80° with a step of 0.017° and the total collection time of two hours. The analysis of powder patterns was carried out with the HighScore Plus software [34].

Single-crystal X-ray diffraction was carried out for Y- and La-containing crystals at room temperature. The single crystal was picked and glued with epoxy cement on the tip of a quartz fiber and mounted on a goniometer of a AXS SMART diffractometer (Bruker, Billerica, MA, USA) equipped with graphite-monochromatied Mo Kα radiation (λ = 0.71073 Å) and with an APEX-II CCD detector. Dataset was recorded as ω-scans at 0.3° step width and integrated with the Bruker SAINT software package [35]. The dataset was indexed in a face-centered cubic unit cell. An analysis of intensity statistics suggested the space group to be Fm

\bar{3}

m (No. 225). The absorption correction was based on fitting a function to the empirical transmission surface sampled by multiple equivalent measurements (SADABS) [36]. Solution and refinement of the crystal structure was performed by using the SHELXTL software package [37]. The structure was solved by direct methods and refined by a full-matrix least-squares method against F_o². Most of the heavy atom positions were located with direct methods, while the other atomic positions were determined according to a combination of displacement parameters, atomic distances, and difference Fourier maps. The occupancy of each position was carefully examined because of the complex disordered features in the structure. The final refinements were carried out with anisotropic atomic displacement parameters for all atoms. The single crystal data collection and structural refinement parameters are listed in Table 5 and the refined positional and isotropic equivalent displacement parameters are given in Table 2.

3.3. Physical Measurements

The elemental analyses were performed on a JEOL 5900 scanning electron microscope (JEOL Ltd., Akishima, Japan) equipped with energy dispersive X-ray (EDX) spectrometer. Lanthanide metals, Sn, and Co were used as internal standards. Multiple locations on different crystallites were probed to establish the statistically averaged composition of each sample. Magnetic measurements were performed with a SQUID magnetometer MPMS-XL (Quantum Design, Inc., San Diego, CA, USA). Direct current (DC) magnetic susceptibility measurements were carried out in both field-cooled (FC) and zero-field-cooled (ZFC) modes under an applied magnetic field of 100 Oe in the 1.8–300 K temperature range. Isothermal field-dependent magnetization was measured at 1.8 K with the field varying from 0 to 7 T.

4. Concluding Remarks

In this work we examined the structural and magnetic behavior of five R₁₁₇Co_52+δSn_112+γ compounds (R = Y, La, Pr, Nd, and Ho). All of them have been reported previously, and the only representatives currently missing from the Dy₁₁₇Co₅₇Sn₁₁₂ structure type are those with R = Sc, Eu, and Yb. Here, for the first time, we revealed the details of crystallographic disorder in the Y- and La-containing crystal structures. These compounds contain the smallest and the largest R elements among crystal structures of R₁₁₇Co_52+δSn_112+γ established by the single-crystal X-ray diffraction thus far. Interestingly, the Y-containing structure represents the first case for which the 4b Wyckoff position in the center of the unit cell is not occupied. It will be of interest to determine single-crystal structures of compounds with R-elements beyond Dy in order to establish whether the lack of a Co atom in the 4b site of R₁₁₇Co_52+δSn_112+γ becomes a general feature for smaller lanthanides.

Our analysis of the crystallographic disorder in the multi-shell polyhedron centered on the 4b site clearly demonstrates that, as the structure expands for the larger lanthanides, the disorder becomes more pronounced. We attribute such an effect to the necessity of optimizing interatomic distances and maintaining efficient bonding interactions throughout the crystal structure. This effect is balanced by the change in the Sn/Co ratio, i.e., as the lanthanide size increases, the mixed Sn/Co sites exhibit a higher population of the larger Sn atoms.

The availability of the highly pure Y₁₁₇Co₅₆Sn₁₁₅ sample obtained in this work also allowed us to address the role of the Co sublattice in the magnetic behavior of R₁₁₇Co_52+δSn_112+γ materials. We did not observe any magnetic phase transitions for the Y-containing sample in the 1.8–300 K range, which suggests the magnetic ordering seen in other compounds of this series is solely due to the lanthanide magnetic moments. The Pr- and Nd-containing compounds exhibit antiferromagnetic ordering followed by spin reorientation at lower temperatures and thus resemble the magnetic behavior of the Gd-, Tb-, and Dy-containing analogues. The Ho-containing compound shows ferromagnetic ordering, similar to the Sm-containing compound.

Acknowledgments

The National Science Foundation is gratefully acknowledged for its support of this research via awards DMR-0955353 and DMR-1507233.

Author Contributions

Ping Chai prepared the compounds, measured X-ray and magnetic data, wrote the paper; Mykola Abramchuk re-collected and interpreting single-crystal X-ray data; Michael Shatruk conceived the project, analyzed single-crystal X-ray and magnetic data, co-wrote and revised the paper.

Conflicts of Interest

The authors declare no conflict of interest.

References

Fredrickson, D.C.; Lee, S.; Hoffmann, R. Interpenetrating polar and nonpolar sublattices in intermetallics: The NaCd₂ structure. Angew. Chem. Int. Ed. 2007, 46, 1958–1976. [Google Scholar] [CrossRef] [PubMed]
Dubois, J.M.; Belin-Ferre, E. (Eds.) Complex Metallic Alloys: Fundamentals and Applications; Wiley-VCH: Weinheim, Germany, 2011.
Feuerbacher, M.; Thomas, C.; Makongo, J.P.A.; Hoffmann, S.; Carrillo-Cabrera, W.; Cardoso, R.; Grin, Y.; Kreiner, G.; Joubert, J.M.; Schenk, T.; et al. The Samson phase, β-Mg₂Al₃, revisited. Z. Kristallogr. 2007, 222, 259–288. [Google Scholar]
Shevelkov, A.V.; Kovnir, K. Zintl phases: Principles and recent developments. Struct. Bonding 2011, 139, 97–142. [Google Scholar]
Samson, S. Crystal structure of NaCd₂. Nature 1962, 195, 259–263. [Google Scholar] [CrossRef]
Frank, F.C.; Kasper, J.S. Complex alloy structures regarded as sphere packings. 1. Definitions and basic principles. Acta Crystallogr. 1958, 11, 184–190. [Google Scholar] [CrossRef]
Frank, F.C.; Kasper, J.S. Complex alloy structures regarded as sphere packing. 2. Analysis and classification of representative structures. Acta Crystallogr. 1959, 12, 483–499. [Google Scholar] [CrossRef]
Fredrickson, D.C.; Lee, S.; Hoffmann, R.; Lin, J.H. The Nowotny chimney ladder phases: Following the c_pseudo clue toward an explanation of the 14 electron rule. Inorg. Chem. 2004, 43, 6151–6158. [Google Scholar] [CrossRef] [PubMed]
Fredrickson, D.C.; Lee, S.; Hoffmann, R. The Nowotny chimney ladder phases: Whence the 14 electron rule? Inorg. Chem. 2004, 43, 6159–6167. [Google Scholar] [CrossRef] [PubMed]
Lin, Q.S.; Corbett, J.D. A chemical approach to the discovery of quasicrystals and their approximant crystals. Struct. Bonding 2009, 133, 1–39. [Google Scholar]
Weber, T.; Dshemuchadse, J.; Kobas, M.; Conrad, M.; Harbrecht, B.; Steurer, W. Large, larger, largest—A family of cluster-based tantalum copper aluminides with giant unit cells. I. Structure solution and refinement. Acta Crystallogr. Sect. B 2009, 65, 308–317. [Google Scholar] [CrossRef] [PubMed]
Conrad, M.; Harbrecht, B.; Weber, T.; Jung, D.Y.; Steurer, W. Large, larger, largest—A family of cluster-based tantalum copper aluminides with giant unit cells. II. The cluster structure. Acta Crystallogr. Sect. B 2009, 65, 318–325. [Google Scholar] [CrossRef] [PubMed]
Lin, Q.S.; Corbett, J.D. Development of the Ca-Au-In icosahedral quasicrystal and two crystalline approximants: Practice via pseudogap electronic tuning. J. Am. Chem. Soc. 2007, 129, 6789–6797. [Google Scholar] [CrossRef] [PubMed]
Lin, Q.S.; Corbett, J.D. Approximant phases and an icosahedral quasicrystal in the Ca-Au-Ga system: The influence of size of gallium versus indium. Inorg. Chem. 2008, 47, 7651–7659. [Google Scholar] [CrossRef] [PubMed]
Lin, Q.L.; Corbett, J.D. Development of an icosahedral quasicrystal and two approximants in the Ca-Au-Sn system: Syntheses and structural analyses. Inorg. Chem. 2010, 49, 10436–10444. [Google Scholar] [CrossRef] [PubMed]
Fredrickson, R.T.; Guo, Y.; Fredrickson, D.C. Epitaxial stabilization between intermetallic and carbide domains in the structures of Mn₁₆SiC₄ and Mn₁₇Si₂C₄. J. Am. Chem. Soc. 2016, 138, 248–256. [Google Scholar] [CrossRef] [PubMed]
Berns, V.M.; Fredrickson, D.C. Structural plasticity: How intermetallics deform themselves in response to chemical pressure, and the complex structures that result. Inorg. Chem. 2014, 53, 10762–10771. [Google Scholar] [CrossRef] [PubMed]
Fan, C.Z.; Weber, T.; Deloudi, S.; Steurer, W. Multiple diffraction in an icosahedral Al-Cu-Fe quasicrystal. Philos. Mag. 2011, 91, 2528–2535. [Google Scholar] [CrossRef]
Pehcarskii, V.K.; Bodak, O.I.; Belskii, V.K.; Starodub, P.K.; Mokra, I.R.; Gladyshevskii, E.I. Crystal structure of Tb₁₁₇Fe₅₂Ge₁₁₂. Kristallografiya 1987, 32, 334–338. [Google Scholar]
Mruz, O.Y. Ph.D. Thesis, L’viv State University, L’viv, Ukraine, 1988.
Morozkin, A.V.; Seropegin, Y.D.; Portnoy, V.K.; Sviridov, I.A.; Leonov, A.V. New ternary compounds R₁₁₇Fe₅₂Ge₁₁₂ (R = Gd, Dy, Ho, Er, Tm) and Sm₁₁₇Cr₅₂Ge₁₁₂ of the Tb₁₁₇Fe₅₂Ge₁₁₂-type structure. Mater. Res. Bull. 1998, 33, 903–908. [Google Scholar] [CrossRef]
Salamakha, P.S. Crystal structures and crystal chemistry of ternary rare-earth germanides. In Handbook on the Physics and Chemistry of Rare Earths; Gschneidner, K.A., Jr., Eyring, L., Eds.; Elsevier: Amsterdam, The Netherlands, 1999; pp. 225–338. [Google Scholar]
Kovnir, K.; Shatruk, M. Magnetism in giant unit cells—Crystal structure and magnetic properties of R₁₁₇Co_52+δSn_112+γ (R = Sm, Tb, Dy). Eur. J. Inorg. Chem. 2011, 2011, 3955–3962. [Google Scholar] [CrossRef]
Salamakha, P.; Sologub, O.; Bocelli, G.; Otani, S.; Takabatake, T. Dy₁₁₇Co₅₇Sn₁₁₂, a new structure type of ternary intermetallic stannides with a giant unit cell. J. Alloys Compd. 2001, 314, 177–180. [Google Scholar] [CrossRef]
He, W.; Zhang, J.; Yan, J.; Fu, Y.; Zeng, L. Crystal structure and magnetic properties of the new ternary compound Pr₁₁₇Co₅₇Sn₁₁₂. J. Alloys Compd. 2010, 491, 49–52. [Google Scholar] [CrossRef]
Cirafici, S.; Canepa, F.; Manfrinetti, P.; Napoletano, M. Physical properties of Ce₂CoSn₂. J. Alloys Compd. 2001, 317–318, 550–555. [Google Scholar] [CrossRef]
Schmitt, D.C.; Haldolaarachchige, N.; Xiong, Y.; Young, D.P.; Jin, R.; Chan, J.Y. Probing the lower limit of lattice thermal conductivity in an ordered extended solid: Gd₁₁₇Co₅₆Sn₁₁₂, a phonon glass-electron crystal system. J. Am. Chem. Soc. 2012, 134, 5965–5973. [Google Scholar] [CrossRef] [PubMed]
Mudryk, Y.; Manfrinetti, P.; Smetana, V.; Liu, J.; Fornasini, M.L.; Provino, A.; Pecharsky, V.K.; Miller, G.J.; Gschneidner, K.A., Jr. Structural disorder and magnetism in rare-earth (R) R₁₁₇Co_54+xSn_112±y. J. Alloys Compd. 2013, 557, 252–260. [Google Scholar] [CrossRef]
Liu, J.; Smetana, V.; Gschneidner, K.A., Jr.; Miller, G.J.; Pecharsky, V.K. The crystal structure and magnetic properties of Pr₁₁₇Co_56.7Ge₁₁₂. J. Appl. Phys. 2013, 113, 17E120. [Google Scholar] [CrossRef]
Bradley, A.J.; Jones, P. An X-ray investigation of the copper-aluminium alloys. J. Inst. Met. 1933, 51, 131–162. [Google Scholar]
Chabot, B.; Cenzual, K.; Parthé, E. Nested polyhedra units: A geometrical concept for describing complicated cubic structures. Acta Crystallogr. Sect. A 1981, 37, 6–11. [Google Scholar] [CrossRef]
Heusler, O. Crystal structure and the iron magnetism of manganese-aluminium-copper alloys. Ann. Phys. 1934, 19, 155–201. [Google Scholar] [CrossRef]
Semitelou, J.P.; Yakinthos, J.K. Commensurate and incommensurate phases in Ho₅Sn₃ compound. J. Magn. Magn. Mater. 2003, 261, 392–398. [Google Scholar] [CrossRef]
HighScorePlus; PANalytical B.V.: Almelo, The Netherlands, 2006.
SMART and SAINT; Bruker AXS Inc.: Madison, WI, USA, 2007.
Sheldrick, G.M. SADABS; University of Gottingen: Gottingen, Germany, 1996. [Google Scholar]
Sheldrick, G.M. A short history of SHELX. Acta Crystallogr. Sect. A 2008, 64, 112–122. [Google Scholar] [CrossRef] [PubMed]

Figure 1. Powder X-ray diffraction patterns of Y₁₁₇Co₅₆Sn₁₁₅: experimental (black) and calculated from the crystal structure established by single-crystal X-ray diffraction (red).

Figure 2. The crystal structure of Y₁₁₇Co₅₆Sn₁₁₅ depicted as a packing of truncated octahedra (TOHs) A (purple), B (green), and C (white). The TOHs in the right front part of the face-centered cubic lattice have been omitted for clarity. The red lines represent unit cell edges.

Figure 3. The first three shells of the multi-shell TOH B in the crystal structures of Y₁₁₇Co₅₆Sn₁₁₅ (a,b) and La₁₁₆Co₆₃Sn₁₁₅ (c). The disordered positions are shown as fully occupied (see the text).

Figure 4. The 4b-centered clusters as the inner shells of TOH A in the crystal structures of Y₁₁₇Co₅₆Sn₁₁₅ (a), Dy₁₁₇Co₅₇Sn₁₁₂ (b), Tb₁₁₇Co₅₉Sn₁₁₆ (c), Gd₁₁₇Co₅₆Sn₁₁₄ (d), Sm₁₁₇Co₅₆Sn₁₁₁ (e), and La₁₁₆Co₆₃Sn₁₁₅ (f). The disordered positions are shown as fully occupied (see the text).

Figure 5. The nearest-neighbor environment of the La71 site in the structure of La₁₁₆Co₆₃Sn₁₁₅ (a) and the Y7 site in the structure of Y₁₁₇Co₅₆Sn₁₁₅ (b).

Figure 6. The zero-field-cooled (ZFC) and field-cooled (FC) magnetic susceptibility at 100 Oe (a) and the field-dependent magnetization at 1.8 K (b) for a powder sample of Y₁₁₇Co₅₆Sn₁₁₅.

Figure 7. The zero-field-cooled (ZFC) and field-cooled (FC) magnetic susceptibility at 100 Oe for Pr₁₁₇Co₅₄Sn₁₁₂ (a), Nd₁₁₇Co₅₄Sn₁₁₁ (c), and Ho₁₁₇Co₅₅Sn₁₀₈ (e); the insets show the enlarged part of the curves at low temperatures. The field-dependent magnetization at 1.8 K for Pr₁₁₇Co₅₄Sn₁₁₂ (b), Nd₁₁₇Co₅₄Sn₁₁₁ (d), and Ho₁₁₇Co₅₅Sn₁₀₈ (f); the red arrows point to the spin-reorientation transitions.

Table 1. Reaction compositions, products, and refined lattice constants for R₁₁₇Co_52+δSn_112+γ (R = Y, La, Pr, Nd, and Ho).

**Table 1.** Reaction compositions, products, and refined lattice constants for R₁₁₇Co_52+δSn_112+γ (R = Y, La, Pr, Nd, and Ho).
Nominal Composition	EDX Analysis	Lattice Constant a (Å)	Impurities
Y₁₁₇Co₅₅Sn₁₁₅	Y₁₁₇₍₉₎Co₅₂₍₁₁₎Sn₁₁₀₍₈₎	29.930(2)	none
La₁₁₇Co₆₁Sn₁₁₅	La₁₁₇₍₇₎Co₆₇₍₉₎Sn₁₁₃₍₆₎	31.334(2)	La₂CoSn₄ + unidentified
Pr₁₁₇Co₅₆Sn₁₁₂	Pr₁₁₇₍₇₎Co₅₄₍₈₎Sn₁₁₂₍₇₎	30.8233(5)	Pr₂CoSn₄
Nd₁₁₇Co₅₆Sn₁₁₆	Nd₁₁₇₍₇₎Co₅₄₍₁₀₎Sn₁₁₁₍₆₎	30.6550(4)	Nd₂Co_0.8Sn₄
Ho₁₁₇Co₅₇Sn₁₁₂	Ho₁₁₇₍₆₎Co₅₅₍₁₂₎Sn₁₀₈₍₈₎	29.7449(5)	Ho₅Sn₃

Table 2. Wyckoff sites and their occupancy factors (s.o.f.), atomic coordinates, and isotropic equivalent atomic displacement parameters in the structures of Y₁₁₇Co₅₆Sn₁₁₅ and La₁₁₆Co₆₃Sn₁₁₅.

**Table 2.** Wyckoff sites and their occupancy factors (s.o.f.), atomic coordinates, and isotropic equivalent atomic displacement parameters in the structures of Y₁₁₇Co₅₆Sn₁₁₅ and La₁₁₆Co₆₃Sn₁₁₅.
Atom	Site	s.o.f.	x	y	z	U_eq
Y₁₁₇Co_55.8(1)Sn_115.11(6)/La_115.78(4)Co_63.1(2)Sn_114.95(6)
Y1/La1	96k	1	0.06778(2)/0.06702(2)	0.06778(2)/0.06702(2)	0.15444(3)/0.15441(2)	0.0073(2)/0.00909(9)
Y2/La2	96k	1	0.17896(2)/0.18021(2)	0.17896(2)/0.18021(2)	0.40537(3)/0.40423(2)	0.0086(2)/0.0101(1)
Y3/La3	96k	1	0.20045(2)/0.20032(2)	0.20045(2)/0.20032(2)	0.06684(3)/0.06818(2)	0.0068(2)/0.00713(9)
Y4/La4	96j	1	0/0	0.24630(3)/0.24595(2)	0.39490(3)/0.39566(2)	0.0068(2)/0.00729(9)
Y5/La5	48i	1	0.5/0.5	0.11983(3)/0.11945(2)	0.11983(3)/0.11945(2)	0.0118(3)/0.0138(1)
Y6/La6	24e	1	0/0	0/0	0.33771(8)/0.34290(3)	0.0187(4)/0.0139(2)
Y7/La71	8c	1/0.470(3)	0.25/0.25	0.25/0.25	0.25/0.25	0.0083(6)/0.0067(5)
–/Co72	32f	–/0.530(3)	–/0.22218(6)	–/0.22218(6)	–/0.22218(6)	–/0.0067(5)
Y8/La8	4a	1/0.84(1)	0/0	0/0	0/0	0.0067(8)/0.0104(9)
Sn1/Sn1	96k	1	0.07276(2)/0.07488(2)	0.07276(2)/0.07488(2)	0.32334(2)/0.32299(2)	0.0059(1)/0.0072(1)
Sn2/Sn2	96k	1	0.10775(2)/0.10868(2)	0.10775(2)/0.10868(2)	0.24000(2)/0.24033(2)	0.0061(1)/0.0078(1)
Sn3/Sn3	48i	1	0.5/0.5	0.20792(2)/0.20859(2)	0.20792(2)/0.20859(2)	0.0075(2)/0.0108(2)
Sn4/Sn4	48h	1	0/0	0.14539(2)/0.14537(2)	0.14539(2)/0.14537(2)	0.0060(2)/0.0074(1)
Sn5/Sn5	48g	1	0.25/0.25	0.25/0.25	0.14034(3)/0.14353(2)	0.0068(2)/0.0087(2)
Sn6/Sn6	32f	1	0.14614(2)/0.14779(2)	0.14614(2)/0.14779(2)	0.14614(2)/0.14779(2)	0.0069(2)/0.0097(2)
Sn7/Sn7	24e	1	0/0	0/0	0.10910(4)/0.10619(3)	0.0061(2)/0.0081(2)
Sn8/Sn8	24e	1	0/0	0/0	0.21602(4)/0.21631(4)	0.0074(2)/0.0119(2)
Sn9/Sn91	32f	1/0.88(3)	0.44652(2)/0.4420(2)	0.44652(2)/0.4420(2)	0.44652(2)/0.4420(2)	0.0191(3)/0.026(1)
–/Sn92	32f	1/0.12(3)	–/0.4340(9)	–/0.4340(9)	–/0.4340(9)	–/0.026(1)
Co1/Co1	96k	1	0.16876(3)/0.16870(2)	0.16876(3)/0.16870(2)	0.23130(4)/0.22973(3)	0.0083(2)/0.0112(2)
Co2/Co2	96k	0.514(4)/0.501(4)	0.07974(5)/0.07930(6)	0.07974(5)/0.07930(6)	0.01571(8)/0.01391(7)	0.0102(7)/0.0218(8)
Co3/Co31	32f	0.521(8)/0.592(8)	0.05746(7)/0.05506(7)	0.05746(7)/0.05506(7)	0.05746(7)/0.05506(7)	0.0073(12)/0.022(1)
–/Co32	32f	–/0.110(5)	–/0.0286(4)	–/0.0286(4)	–/0.0286(4)	–/0.022(1)
Co4/Co4	32f	1	0.39315(4)/0.39159(4)	0.39315(4)/0.39159(4)	0.39315(4)/0.39159(4)	0.0108(4)/0.0191(4)
Co51	32f	0.67(1)/0.630(8)	0.30786(3)/0.2994(1)	0.30786(3)/0.2994(1)	0.30786(3)/0.2994(1)	0.0074(5)/0.0083(10)
Sn52	32f	0.33(1)/0.370(8)	0.30786(3)/0.3077(1)	0.30786(3)/0.3077(1)	0.30786(3)/0.3077(1)	0.0074(5)/0.0083(10)
Co6/Co61	24e	0.25/0.200(9)	0/0	0/0	0.4184(4)/0.4195(7)	0.026(3)/0.018(3)
–/Co62	24e	–/0.31(1)	–/0	–/0	–/0.4394(4)	–/0.018(3)
–/Co7	24e	–/0.185(4)	–/0	–/0	–/0.4816(3)	–/0.029(4)

Table 3. Selected interatomic distances in the multi-shell polyhedron TOH A in the crystal structures of R₁₁₇Co_52+δSn_112+γ (see Figure 4).

**Table 3.** Selected interatomic distances in the multi-shell polyhedron TOH A in the crystal structures of R₁₁₇Co_52+δSn_112+γ (see Figure 4).
Atomic Pair ^a	Interatomic Distance (Å) ^b
Atomic Pair ^a	R = Y ^c	R = Dy [24]	R = Tb [23]	R = Gd [28] ^d	R = Sm [23]	R = La ^c
R–Co_outer	2.41(2)	–	2.370	2.452	2.575	2.71(1)
R–Sn	3.964(4)	3.921	3.900	3.878	3.856	4.041(2)
Sn–Sn	3.201(1)	3.335	3.228	3.328	3.511	3.682(1)
Co_inner–Sn	–	2.888	2.795	2.557	2.756	2.855(12)
Co_outer–Sn	2.416(5)	–	2.416	2.436	2.511	2.782(2)
Co_outer–Sn(cub.face)	0.846	–	0.792	0.630	0.375	0.274

^a The Co_outer and Co_inner indicate the atoms positioned in the 24e site outside the Sn₈ cube and in the 4b or 24e sites inside the Sn₈ cube, respectively. ^b In the case of disordered atomic positions, the average position was used to calculate the distances. ^c This work. ^d The less disordered model reported in the literature was used.

Table 4. Magnetic properties of R₁₁₇Co_52+δSn_112+γ.

**Table 4.** Magnetic properties of R₁₁₇Co_52+δSn_112+γ.
Compound	T_N/T_C (K)	T_SRO (K)	θ (K)	μ_eff (μ_B)	M_max (μ_B) at 7 T
Y₁₁₇Co₅₆Sn₁₁₅	–	–	–4.3(2)	1.62(2)/Co	0.21(1)/Co
Pr₁₁₇Co₅₄Sn₁₁₂	10.5(3)	5.5(4)	17(3)	4.9(3)/Pr	1.49(1)/Pr
Nd₁₁₇Co₅₄Sn₁₁₁	18.3(1)	11.1(2)	24.7(3)	3.80(4)/Nd	1.78(1)/Nd
Ho₁₁₇Co₅₅Sn₁₀₈	10.6(2)	–	10.0(3)	10.20(3)/Ho	6.51(2)/Ho

Table 5. Data collection and structure refinement parameters for R₁₁₇Co_52+δSn_112+γ (R = Y and La) ^a.

**Table 5.** Data collection and structure refinement parameters for R₁₁₇Co_52+δSn_112+γ (R = Y and La) ^a.
Composition	Y₁₁₇Co_55.8(1)Sn_115.11(6)	La_115.78(4)Co_63.1(2)Sn_114.95(6)
T, K	230	230
Space group	Fm $\bar{3}$ m (No. 225)	Fm $\bar{3}$ m (No. 225)
a, Å	29.930(2)	31.334(2)
V, Å³	26810(5)	30763(6)
Z	4	4
ρ_calc, g·cm^–3	6.762	7.232
µ, mm^–1	38.736	28.138
2θ_max, deg	60.72	54.75
Reflections collected	55002	79250
Unique reflections	2027	1788
Parameters refined	101	113
R₁, wR₂ [F_o > 4σ(F_o)]	0.029, 0.054	0.017, 0.031
Goodness-of-fit	1.09	1.17
Diff. peak and hole, e·Å^–3	1.58 and −3.12	3.33 and −2.13

^a Further details of the crystal structure investigation may be obtained from FIZ Karlsruhe, 76344 Eggenstein-Leopoldshafen, Germany (Fax: (+49)7247-808-666; e-mail: [email protected]), on quoting the deposition numbers CSD-431928 and 431929.

© 2016 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC-BY) license (http://creativecommons.org/licenses/by/4.0/).

Share and Cite

MDPI and ACS Style

Chai, P.; Abramchuk, M.; Shatruk, M. Synthesis, Crystal Structure, and Magnetic Properties of Giant Unit Cell Intermetallics R₁₁₇Co_52+δSn_112+γ (R = Y, La, Pr, Nd, Ho). Crystals 2016, 6, 165. https://doi.org/10.3390/cryst6120165

AMA Style

Chai P, Abramchuk M, Shatruk M. Synthesis, Crystal Structure, and Magnetic Properties of Giant Unit Cell Intermetallics R₁₁₇Co_52+δSn_112+γ (R = Y, La, Pr, Nd, Ho). Crystals. 2016; 6(12):165. https://doi.org/10.3390/cryst6120165

Chicago/Turabian Style

Chai, Ping, Mykola Abramchuk, and Michael Shatruk. 2016. "Synthesis, Crystal Structure, and Magnetic Properties of Giant Unit Cell Intermetallics R₁₁₇Co_52+δSn_112+γ (R = Y, La, Pr, Nd, Ho)" Crystals 6, no. 12: 165. https://doi.org/10.3390/cryst6120165

Note that from the first issue of 2016, this journal uses article numbers instead of page numbers. See further details here.

Article Menu