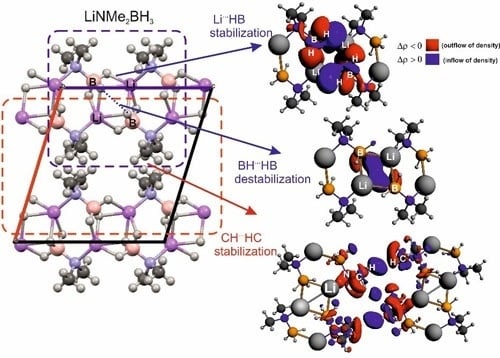
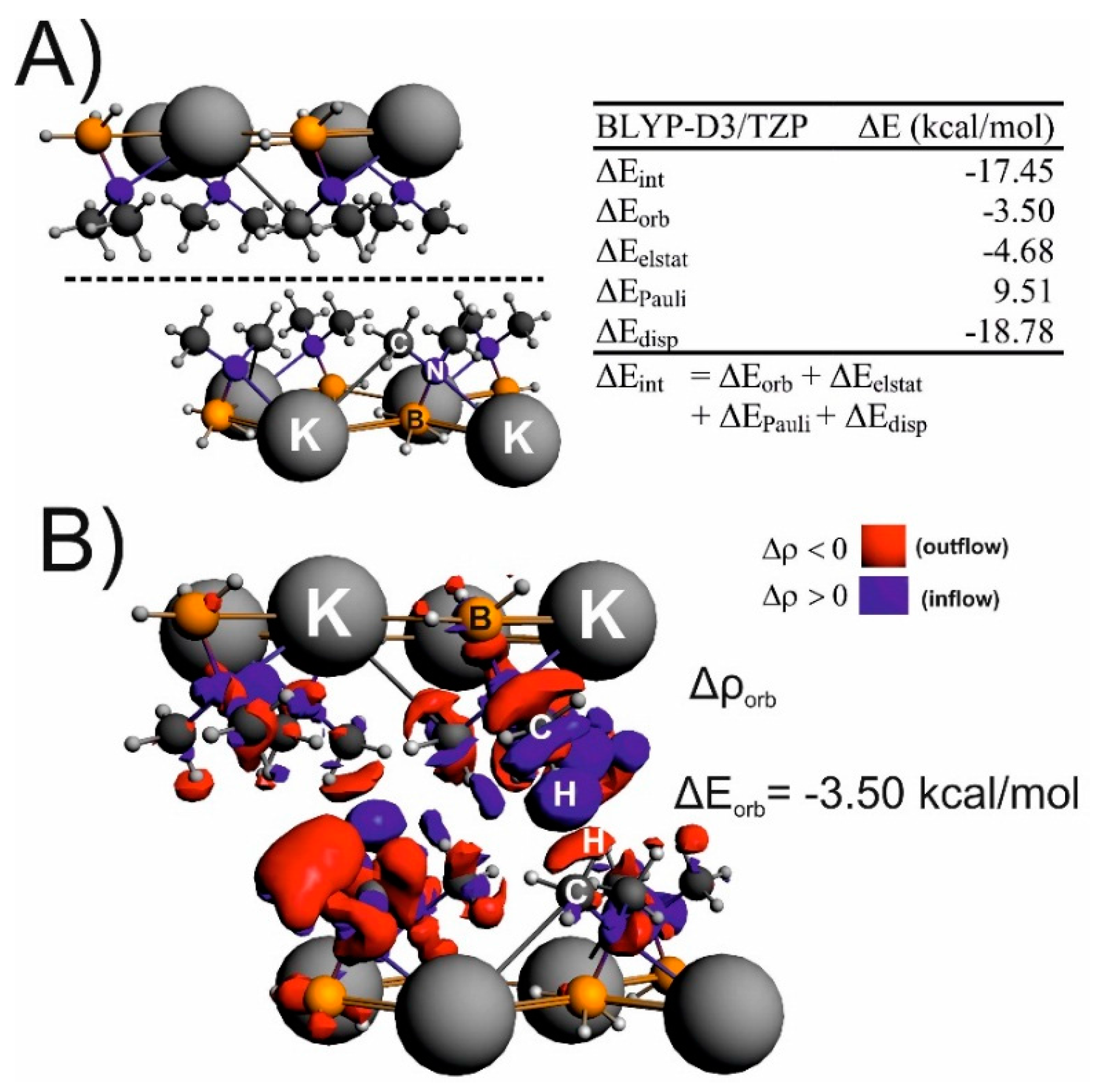
Non-Covalent Interactions in Hydrogen Storage Materials LiN(CH3)2BH3 and KN(CH3)2BH3
Abstract
:1. Introduction
2. Materials and Methods
2.1. ETS-NOCV
2.2. NCI Technique
2.3. IQA (Interacting Quantum Atoms) Energy Decomposition Scheme
2.4. Molecular Electrostatic Potential (MEP)
3. Results and Discussion
4. Conclusions
Supplementary Materials
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Christopher, K.; Dimitrios, R. A review on energy comparison of hydrogen production methods from renewable energy sources. Energy Environ. Sci. 2012, 5, 6640–6651. [Google Scholar]
- Dincer, I.; Acar, C. Review and evaluation of hydrogen production methods for better sustainability. Int. J. Hydrog. Energy 2015, 40, 11094–11111. [Google Scholar]
- Dutta, S. A review on production, storage of hydrogen and its utilization as an energy resource. J. Ind. Eng. Chem. 2014, 20, 1148–1156. [Google Scholar]
- Staubitz, A.; Robertson, A.P.M.; Manners, I. Ammonia-Borane and Related Compounds as Dihydrogen Sources. Chem. Rev. 2010, 110, 4079–4124. [Google Scholar]
- Hamilton, C.W.; Baker, R.T.; Staubitz, A.; Manners, I. B–N compounds for chemical hydrogen storage. Chem. Soc. Rev. 2009, 38, 279–293. [Google Scholar]
- Kim, S.-K.; Han, W.-S.; Kim, T.-J.; Kim, T.-Y.; Nam, S.W.; Mitoraj, M.; Piękoś, Ł.; Michalak, A.; Hwang, S.-J.; Kang, S.O. Palladium Catalysts for Dehydrogenation of Ammonia Borane with Preferential B−H Activation. J. Am. Chem. Soc. 2010, 132, 9954–9955. [Google Scholar]
- Parafiniuk, M.; Mitoraj, M.P. Origin of Binding of Ammonia-Borane to Transition-Metal-Based Catalysts: An Insight from the Charge and Energy Decomposition Method ETS-NOCV. Organometallics 2013, 32, 4103–4113. [Google Scholar]
- Parafiniuk, M.; Mitoraj, M.P. On the origin of internal rotation in ammonia borane. J. Mol. Model. 2014, 20, 2272–2281. [Google Scholar] [CrossRef] [PubMed]
- Huang, Z.; Autrey, T. Boron–nitrogen–hydrogen (BNH) compounds: Recent developments in hydrogen storage, applications in hydrogenation and catalysis, and new syntheses. Energy Environ. Sci. 2012, 5, 9257–9268. [Google Scholar] [CrossRef]
- Umegaki, T.; Yan, J.M.; Zhang, X.B.; Shioyama, H.; Kuriyama, N.; Xu, Q. Boron- and nitrogen-based chemical hydrogen storage materials. Int. J. Hydrog. Energy 2009, 34, 2303–2311. [Google Scholar] [CrossRef]
- Custelcean, R.; Jackson, J.E. Dihydrogen Bonding: Structures, Energetics, and Dynamics. Chem. Rev. 2001, 101, 1963–1980. [Google Scholar] [CrossRef] [PubMed]
- Bakhmutov, V.I. Dihydrogen Bonds: Principles, Experiments and Applications; Wiley-Interscience: Hoboken, NJ, USA, 2008. [Google Scholar]
- Mitoraj, M. Bonding in Ammonia Borane: An Analysis Based on the Natural Orbitals for Chemical Valence and the Extended Transition State Method (ETS-NOCV). J. Phys. Chem. A 2011, 115, 14708–14716. [Google Scholar] [CrossRef] [PubMed]
- Jonas, V.; Frenking, G.; Reetz, M.T. Comparative Theoretical Study of Lewis Acid-Base Complexes of BH3, BF3, BCl3, AlCl3, and SO2. J. Am. Chem. Soc. 1994, 116, 8741–8753. [Google Scholar] [CrossRef]
- Merino, G.; Bakhmutov, V.I.; Vela, A. Do Cooperative Proton-Hydride explain the Gas-Solid Structural Difference of BH3NH3? J. Phys. Chem. A 2002, 106, 8491–8994. [Google Scholar] [CrossRef]
- Popelier, P.L.A. Characterization of a Dihydrogen Bond on the Basis of the Electron Density. J. Phys. Chem. A 1998, 102, 1873–1878. [Google Scholar] [CrossRef]
- Wolstenholme, D.J.; Traboulsee, K.T.; Hua, Y.; Calhoun, L.A.; McGrady, G.S. Thermal desorption of hydrogen from ammonia borane: Unexpected role of homopolar B–H···H–B interactions. Chem. Commun. 2012, 48, 2597–2599. [Google Scholar] [CrossRef] [PubMed]
- Guerra, D.; David, J.; Restrepo, A. (H3N–BH3)4: The ammonia borane tetramer. Phys. Chem. Chem. Phys. 2012, 14, 14892–14897. [Google Scholar] [CrossRef] [PubMed]
- Chen, X.; Yuan, F.; Tan, Y.; Tang, Z.; Yu, X. Improved Dehydrogenation Properties of Ca(BH4)2·nNH3 (n = 1, 2, and 4) Combined with Mg(BH4)2. J. Phys. Chem. C 2012, 116, 21162–21168. [Google Scholar] [CrossRef]
- Wolstenholme, D.J.; Dobson, J.L.; McGrady, G.S. Homopolar dihydrogen bonding in main group hydrides: Discovery, consequences, and applications. Dalton Trans. 2015, 44, 9718–9731. [Google Scholar]
- Wolstenholme, D.J.; Fradsham, E.J.; McGrady, G.S. Supramolecular interactions in boron hydrides: How non-classical bonding directs their crystal architecture. CrystEngComm 2015, 17, 7623–7627. [Google Scholar] [CrossRef]
- Chen, X.; Zhao, J.C.; Shore, S.G. The Roles of Dihydrogen Bonds in Amine Borane Chemistry. Acc. Chem. Res. 2013, 46, 2666–2675. [Google Scholar] [CrossRef] [PubMed]
- Sagan, F.; Piękoś, Ł.; Andrzejak, M.; Mitoraj, M.P. From Saturated BN–compounds to Isoelectronic BN/CC Counterparts—An Insight from Computational Perspective. Chemistry 2015, 21, 15299–15307. [Google Scholar] [CrossRef] [PubMed]
- Grochala, W.; Edwards, P.P. Thermal Decomposition of the Non-Interstitial Hydrides for the Storage and Production of Hydrogen. Chem. Rev. 2004, 104, 1283–1316. [Google Scholar] [CrossRef] [PubMed]
- Dovgaliuk, I.; Le Duff, C.S.; Robeyns, K.; Devillers, M.; Filinchuk, Y. Mild Dehydrogenation of Ammonia Borane Complexed with Aluminum Borohydride. Chem. Mater. 2015, 27, 768–777. [Google Scholar] [CrossRef]
- Orimo, S.; Nakamori, Y.; Eliseo, J.R.; Züttel, A.; Jensen, C.M. Complex Hydrides for Hydrogen Storage. Chem. Rev. 2007, 107, 4111–4132. [Google Scholar] [CrossRef] [PubMed]
- Luoa, J.; Wub, H.; Zhoub, W.; Kang, X.; Fang, Z.; Wang, P. LiBH4·NH3BH3: A new lithium borohydride ammonia borane compound with a novel structure and favorable hydrogen storage properties. Int. J. Hydrog. Energy 2012, 37, 10750–10757. [Google Scholar] [CrossRef]
- Jaroń, T.; Orłowski, P.A.; Wegner, W.; Fijałkowski, K.J.; Leszczyński, P.J.; Grochala, W. Hydrogen Storage Materials: Room-Temperature Wet-Chemistry Approach toward Mixed-Metal Borohydrides. Angew. Chem. Int. Ed. 2015, 54, 1236–1239. [Google Scholar] [CrossRef] [PubMed]
- Wolstenholme, D.J.; Flogeras, J.; Che, F.N.; Decken, A.; McGrady, G.S. Homopolar Dihydrogen Bonding in Alkali Metal Amidoboranes: Crystal Engineering of Low-Dimensional Molecular Materials. J. Am. Chem. Soc. 2013, 135, 2439–2442. [Google Scholar] [CrossRef] [PubMed]
- Bader, R.F.W. Atoms in Molecules: A Quantum Theory; Oxford University Press: Oxford, UK, 1990. [Google Scholar]
- Weinhold, F.; Schleyer, P.R.; McKee, W.C. Bay-Type H–H “Bonding” in cis-2-Butene and Related Species: QTAIM Versus NBO Description. J. Computat. Chem. 2014, 35, 1499–1508. [Google Scholar] [CrossRef] [PubMed]
- Poater, J.; Solà, M.; Bickelhaupt, F.M. Hydrogen–Hydrogen Bonding in Planar Biphenyl, Predicted by Atoms-In-Molecules Theory, Does Not Exist. Chemistry 2006, 12, 2889–2895. [Google Scholar] [CrossRef] [PubMed]
- Grimme, S.; Mück-Lichtenfeld, C.; Erker, G.; Kehr, G.; Wang, H.; Beckers, H.; Willner, H. When Do Interacting Atoms Form a Chemical Bond? Spectroscopic Measurements and Theoretical Analyses of Dideuteriophenanthrene. Angew. Chem. Int. Ed. 2009, 48, 2592–2595. [Google Scholar] [CrossRef] [PubMed]
- Jacobsen, H. Kinetic energy density and covalent bonding—A complementary analysis at the border of bond and no bond. Dalton Trans. 2010, 39, 5426–5428. [Google Scholar] [CrossRef] [PubMed]
- Hancock, R.D.; Nikolayenko, I.V. Do Nonbonded H–H Interactions in Phenanthrene Stabilize It Relative to Anthracene? A Possible Resolution to this Question and Its Implications for Ligands such as 2,2′-Bipyridyl. J. Phys. Chem. A 2012, 116, 8572–8583. [Google Scholar] [CrossRef] [PubMed]
- Cukrowski, I.; de Lange, J.H.; Adeyinka, A.S.; Mangondo, P. Evaluating common QTAIM and NCI interpretations of the electron density concentration through IQA interaction energies and 1D cross-sections of the electron and deformation density distributions. Comput. Theor. Chem. 2015, 1053, 60–76. [Google Scholar] [CrossRef]
- Safin, D.A.; Babashkina, M.G.; Robeyns, K.; Mitoraj, M.P.; Kubisiak, P.; Garcia, Y. Influence of the Homopolar Dihydrogen Bonding CH···HC on Coordination Geometry: Experimental and Theoretical Studies. Chemistry 2015, 21, 16679–16687. [Google Scholar] [CrossRef] [PubMed]
- Cukrowski, I. IQA-embedded fragment attributed molecular system energy change in exploring intramolecular interactions. Comput. Theor. Chem. 2015, 1066, 62–75. [Google Scholar] [CrossRef]
- Cukrowski, I.; Govender, K.K.; Mitoraj, M.P.; Srebro, M. QTAIM and ETS-NOCV Analyses of Intramolecular CH···HC Interactions in Metal Complexes. J. Phys. Chem. A 2011, 115, 12746–12757. [Google Scholar] [CrossRef] [PubMed]
- Cukrowski, I.; de Lange, J.H.; Mitoraj, M.P. Physical Nature of Interactions in ZnII Complexes with 2,2′-Bipyridyl: Quantum Theory of Atoms in Molecules (QTAIM), Interacting Quantum Atoms (IQA), Noncovalent Interactions (NCI), and Extended Transition State Coupled with Natural Orbitals for Chemical Valence (ETS-NOCV) Comparative Studies. J. Phys. Chem. A 2014, 118, 623–637. [Google Scholar] [PubMed]
- Safin, D.A.; Babashkina, M.G.; Kubisiak, P.; Mitoraj, M.P.; Le Duff, C.S.; Robeyns, K.; Garcia, Y. Crucial influence of the intramolecular hydrogen bond on the coordination mode of RC(S)NHP(S)(OiPr)2 in homoleptic complexes with NiII. Eur. J. Inorg. Chem. 2013, 2013, 545–555. [Google Scholar]
- Lyngvi, E.; Sanhueza, I.A.; Schoenebeck, F. Dispersion Makes the Difference: Bisligated Transition States Found for the Oxidative Addition of Pd(PtBu3)2 to Ar-OSO2R and Dispersion-Controlled Chemoselectivity in Reactions with Pd[P(iPr)(tBu2)]2. Organometallics 2015, 34, 805–812. [Google Scholar] [CrossRef]
- Wolters, L.P.; Koekkoek, R.; Bickelhaupt, F.M. Role of Steric Attraction and Bite-Angle Flexibility in Metal-Mediated C–H Bond Activation. ACS Catal. 2015, 5, 5766–5775. [Google Scholar] [CrossRef]
- Bader, R.F.W. Pauli Repulsions Exist Only in the Eye of the Beholder. Chemistry 2006, 12, 2896–2901. [Google Scholar] [CrossRef] [PubMed]
- Hernández-Trujillo, J.; Matta, C.F. Hydrogen–hydrogen bonding in biphenyl revisited. Struct. Chem. 2007, 18, 849–857. [Google Scholar] [CrossRef]
- Matta, C.F.; Sadjadi, S.A.; Braden, D.A.; Frenking, G. The Barrier to the Methyl Rotation in Cis-2-Butene and its Isomerization Energy to Trans-2-Butene, Revisited. J. Comput. Chem. 2016, 37, 143–154. [Google Scholar] [CrossRef] [PubMed]
- Mitoraj, M.P.; Michalak, A. Natural orbitals for chemical valence as descriptors of chemical bonding in transition metal complexes. J. Mol. Model. 2007, 13, 347–355. [Google Scholar] [CrossRef] [PubMed]
- Michalak, A.; Mitoraj, M.P.; Ziegler, T. Bond Orbitals from Chemical Valence Theory. J. Phys. Chem. A 2008, 112, 1933–1939. [Google Scholar] [CrossRef] [PubMed]
- Mitoraj, M.P.; Michalak, A.; Ziegler, T. A Combined Charge and Energy Decomposition Scheme for Bond Analysis. J. Chem. Theory Comput. 2009, 5, 962–975. [Google Scholar] [CrossRef] [PubMed]
- Mitoraj, M.P.; Michalak, A. Theoretical description of halogen bonding—An insight based on the natural orbitals for chemical valence combined with the extended-transition-state method (ETS-NOCV). J. Mol. Model. 2013, 19, 4681–4688. [Google Scholar] [CrossRef] [PubMed]
- Mitoraj, M.P.; Janjic, G.V.; Medakovic, V.B.; Veljkovic, D.Z.; Michalak, A.; Zaric, S.D.; Milcic, M.K. Nature of the Water/Aromatic Parallel Alignment Interactions. J. Comput. Chem. 2015, 36, 171–180. [Google Scholar] [CrossRef] [PubMed]
- Te Velde, G.; Bickelhaupt, F.M.; Baerends, E.J.; Fonseca Guerra, C.; van Gisbergen, S.J.A.; Snijders, J.G.; Ziegler, T. Chemistry with ADF. J. Comput. Chem. 2001, 22, 931–967. [Google Scholar] [CrossRef]
- Bickelhaupt, F.M.; Baerends, E.J. Kohn-Sham Density Functional Theory: Predicting and Understanding Chemistry. Rev. Comput. Chem. 2007, 15, 1–86. [Google Scholar]
- Baerends, E.J.; Autschbach, J.; Bashford, D.; Bérces, A.; Bickelhaupt, F.M.; Bo, C.; Boerrigter, P.M.; Cavallo, L.; Chong, D.P.; Deng, L.; et al. SCM Theoretical Chemistry; ADF2012.01; Vrije Universiteit: Amsterdam, The Netherlands, 2012. [Google Scholar]
- Johnson, E.R.; Keinan, S.; Mori-Sánchez, P.; Contreras-García, J.; Cohen, A.J.; Yang, W. Revealing Noncovalent Interactions. J. Am. Chem. Soc. 2010, 132, 6498–6506. [Google Scholar] [CrossRef] [PubMed]
- Blanco, M.A.; Pendás, A.M.; Francisco, E. Interacting Quantum Atoms: A Correlated Energy Decomposition Scheme Based on the Quantum Theory of Atoms in Molecules. J. Chem. Theory Comput. 2005, 1, 1096–1109. [Google Scholar] [CrossRef] [PubMed]
- Gao, W.; Feng, H.; Xuan, X.; Chen, L. The assessment and application of an approach to noncovalent interactions: The energy decomposition analysis (EDA) in combination with DFT of revised dispersion correction (DFT-D3) with Slater-type orbital (STO) basis set. J. Mol. Model. 2012, 18, 4577–4589. [Google Scholar] [CrossRef] [PubMed]
- Van der Wijst, T.; Fonseca Guerra, C.; Swart, M.; Bickelhaupt, F.M.; Lippert, B. A Ditopic Ion-Pair Receptor Based on Stacked Nucleobase Quartets. Angew. Chem. Int. Ed. 2009, 48, 3285–3287. [Google Scholar] [CrossRef] [PubMed]
- Fonseca Guerra, C.; van der Wijst, T.; Poater, J.; Swart, M.; Bickelhaupt, F.M. Adenine versus guanine quartets in aqueous solution: Dispersion-corrected DFT study on the differences in p-stacking and hydrogen-bonding behavior. Theor. Chem. Acc. 2010, 125, 245–252. [Google Scholar] [CrossRef]
- Grimme, S. Semiempirical GGA-Type Density Functional Constructed with a Long-Range Dispersion Correction. J. Comput. Chem. 2006, 27, 1787–1799. [Google Scholar] [CrossRef] [PubMed]
- Frisch, M.J.; Trucks, G.W.; Schlegel, H.B.; Scuseria, G.E.; Robb, M.A.; Cheeseman, J.R.; Scalmani, G.; Barone, V.; Mennucci, B.; Petersson, G.A.; et al. Gaussian 09; Gaussian Inc.: Wallingford, CT, USA, 2009. [Google Scholar]
- Ziegler, T.; Rauk, A. On the calculation of bonding energies by the Hartree Fock Slater method. Theor. Chim. Acta 1977, 46, 1–10. [Google Scholar] [CrossRef]
- AIMAll, Version 13.05.06 Professional; Todd A. Keith, TK Gristmill Software: Overland Park, KS, USA, 2016.
- Politzer, P.; Murray, J.S.; Clark, T. Halogen bonding: An electrostatically-driven highly directional noncovalent interaction. Phys. Chem. Chem. Phys. 2010, 12, 7748–7757. [Google Scholar] [CrossRef] [PubMed]
- Politzer, P.; Murray, J.S.; Janjić, G.V.; Zarić, S.D. σ-Hole Interactions of Covalently-Bonded Nitrogen, Phosphorus and Arsenic: A Survey of Crystal Structures. Crystals 2014, 4, 12–31. [Google Scholar] [CrossRef]
- Clark, T.; Murray, J.S.; Politzer, P. The Role of Polarization in a Halogen Bond. Aust. J. Chem. 2014, 67, 451–456. [Google Scholar] [CrossRef]
- Politzer, P.; Murray, J.S.; Clark, T. Mathematical modeling and physical reality in noncovalent interactions. J. Mol. Model. 2015, 52, 21–31. [Google Scholar] [CrossRef] [PubMed]
- Schouwink, P.; Hagemann, H.; Embs, J.P.; Anna, V.D.; Černý, R. Di-hydrogen contact induced lattice instabilities and structural dynamics in complex hydride perovskites. J. Phys. Condens. Matter 2015, 27, 265403–265415. [Google Scholar] [CrossRef] [PubMed]
- Černý, R.; Kim, K.C.; Penin, N.; D’Anna, V.; Hagemann, H.; Sholl, D.S. AZn2(BH4)5 (A = Li, Na) and NaZn(BH4)3: Structural Studies. J. Phys. Chem. C 2010, 114, 19127–19133. [Google Scholar] [CrossRef]
- Černý, R.; Ravnsbæk, D.B.; Schouwink, P.; Filinchuk, Y.; Penin, N.; Teyssier, J.; Smrčok, L.; Jensen, T.R. Potassium Zinc Borohydrides Containing Triangular [Zn(BH4)3] and Tetrahedral [Zn(BH4)Cl4]2 Anions. J. Phys. Chem. C 2012, 116, 1563–1571. [Google Scholar] [CrossRef]
- Ravindran, P.; Vajeeston, P.; Vidya, R.; Kjekshus, A.; Fjellvåg, H. Violation of the Minimum H–H Separation “Rule” for Metal Hydrides. Phys. Rev. Lett. 2002, 89, 106403–106407. [Google Scholar]
- Ravnsbæk, D.; Filinchuk, Y.; Cerenius, Y.; Jakobsen, H.J.; Besenbacher, F.; Skibsted, J.; Jensen, T.R. A Series of Mixed-Metal Borohydrides. Angew. Chem. Int. Ed. 2009, 48, 6659–6663. [Google Scholar]
- Demyanov, P.; Polestshuk, P. A Bond Path and an Attractive Ehrenfest Force Do Not Necessarily Indicate Bonding Interactions: Case Study on M2X2 (M = Li, Na, K; X = H, OH, F, Cl). Chemistry 2012, 18, 4982–4993. [Google Scholar] [CrossRef] [PubMed]
- Wang, C.; Danovich, D.; Mo, Y.; Shaik, S. On The Nature of the Halogen Bond. J. Chem. Theory Comput. 2014, 10, 3726–3737. [Google Scholar] [CrossRef] [PubMed]
- Grabowski, S.J. Hydrogen and Halogen Bonds Are Ruled by the Same Mechanisms. Phys. Chem. Chem. Phys. 2013, 15, 7249–7259. [Google Scholar] [CrossRef] [PubMed]
- Mulliken, R.S. Structures of Complexes Formed by Halogen Molecules with Aromatic and with Oxygenated Solvents. J. Am. Chem. Soc. 1950, 72, 600–608. [Google Scholar] [CrossRef]
- Echeverría, J.; Aullón, G.; Danovich, D.; Shaik, S.; Alvarez, S. Dihydrogen contacts in alkanes are subtle but not faint. Nat. Chem. 2011, 3, 323–330. [Google Scholar] [CrossRef] [PubMed]
- Danovich, D.; Shaik, S.; Neese, F.; Echeverría, J.; Aullón, G.; Alvarez, S. Understanding the Nature of the CH···HC Interactions in Alkanes. J. Chem. Theory Comput. 2013, 9, 1977–1991. [Google Scholar] [CrossRef] [PubMed]
- Grimme, S.; Schreiner, P.R. Steric Crowding Can Stabilize a Labile Molecule: Solving the Hexaphenylethane Riddle. Angew. Chem. Int. Ed. 2011, 50, 12639–12642. [Google Scholar] [CrossRef] [PubMed]
- Fokin, A.; Chernish, L.V.; Gunchenko, P.A.; Tikhonchuk, E.Y.; Hausmann, H.; Serafin, M.; Dahl, J.E.P.; Carlson, R.M.K.; Schreiner, P.R. Stable Alkanes Containing Very Long Carbon–Carbon Bonds. J. Am. Chem. Soc. 2012, 134, 13641–13650. [Google Scholar] [CrossRef] [PubMed]
- Zhang, J.; Dolg, M. Dispersion Interaction Stabilizes Sterically Hindered Double Fullerenes. Chemistry 2014, 20, 13909–13912. [Google Scholar] [CrossRef] [PubMed]
- Grabowski, S.J.; Pfitzner, A.; Zabel, M.; Dubis, A.T.; Palusiak, M. Intramolecular H···H Interactions for the Crystal Structures of [4-((E)-But-1-enyl)-2,6-dimethoxyphenyl] pyridine-3-carboxylate and [4-((E)-Pent-1-enyl)-2,6-dimethoxyphenyl] pyridine-3-carboxylate; DFT Calculations on Modeled Styrene Derivatives. J. Phys. Chem. B 2004, 108, 1831–1837. [Google Scholar] [CrossRef]
- Grabowski, S.J. Dihydrogen bond and X–H···σ interaction as sub-classes of hydrogen bond. J. Phys. Org. Chem. 2013, 26, 452–459. [Google Scholar] [CrossRef]
- Grabowski, S.J.; Sokalski, W.A.; Leszczynski, J. Nature of X–H+δ··· −δH–Y dihydrogen bonds and X–H···σ Interactions. J. Phys. Chem. A 2004, 108, 5823–5830. [Google Scholar] [CrossRef]
- Grabowski, S.J.; Sokalski, W.A.; Leszczynski, J. How short can the H···H intermolecular contact can be? New findings that reveal the covalent nature of extremely strong interactions. J. Phys. Chem. A 2005, 109, 4331–4341. [Google Scholar] [CrossRef] [PubMed]
- Krapp, A.; Frenking, G.; Uggerud, E. Nonpolar Dihydrogen Bonds—On a Gliding Scale from Weak Dihydrogen Interaction to Covalent H–H in Symmetric Radical Cations [HnE-H-H-EHn]+. Chemistry 2008, 14, 4028–4038. [Google Scholar] [CrossRef] [PubMed]
- Kim, D.Y.; Singh, N.J.; Lee, H.M.; Kim, K.S. Hydrogen-Release Mechanisms in Lithium Amidoboranes. Chemistry 2009, 15, 5598–5604. [Google Scholar] [CrossRef] [PubMed]
- Lee, T.B.; McKee, M.L. Mechanistic Study of LiNH2BH3 Formation from (LiH)4 + NH3BH3 and Subsequent Dehydrogenation. Inorg. Chem. 2009, 48, 7564–7575. [Google Scholar] [CrossRef] [PubMed]
- Luedtke, A.T.; Autrey, T. Hydrogen Release Studies of Alkali Metal Amidoboranes. Inorg.Chem. 2010, 49, 3905–3910. [Google Scholar] [CrossRef] [PubMed]








| IQA(X∙∙∙Y) | * | ||||||
|---|---|---|---|---|---|---|---|
| Li∙∙∙H(B) | –805.9 | –338.4 | 480.1 | 565.4 | 568.2 | –2.8 | –98.8 |
| (C)H∙∙∙H(C) | –140.6 | –138.2 | 130.8 | 147.2 | 148.6 | –1.4 | –0.80 |
| (B)H∙∙∙H(B) | –198.9 | –198.6 | 119.7 | 327.2 | 330.0 | –2.7 | +49.4 |
© 2016 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons by Attribution (CC-BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Sagan, F.; Filas, R.; Mitoraj, M.P. Non-Covalent Interactions in Hydrogen Storage Materials LiN(CH3)2BH3 and KN(CH3)2BH3. Crystals 2016, 6, 28. https://doi.org/10.3390/cryst6030028
Sagan F, Filas R, Mitoraj MP. Non-Covalent Interactions in Hydrogen Storage Materials LiN(CH3)2BH3 and KN(CH3)2BH3. Crystals. 2016; 6(3):28. https://doi.org/10.3390/cryst6030028
Chicago/Turabian StyleSagan, Filip, Radosław Filas, and Mariusz P. Mitoraj. 2016. "Non-Covalent Interactions in Hydrogen Storage Materials LiN(CH3)2BH3 and KN(CH3)2BH3" Crystals 6, no. 3: 28. https://doi.org/10.3390/cryst6030028
APA StyleSagan, F., Filas, R., & Mitoraj, M. P. (2016). Non-Covalent Interactions in Hydrogen Storage Materials LiN(CH3)2BH3 and KN(CH3)2BH3. Crystals, 6(3), 28. https://doi.org/10.3390/cryst6030028