Numerical Analysis of the Combined Influence of Accelerated Crucible Rotation and Dynamic Crucible Translation on Liquid Phase Diffusion Growth of SiGe
Abstract
:1. Introduction
2. Numerical Simulation
3. Results and Discussions
4. Conclusions
Author Contributions
Conflicts of Interest
References
- Kasper, E. Prospects of SiGe heterodevices. J. Cryst. Growth 1995, 150, 921–925. [Google Scholar] [CrossRef]
- Abrosimov, N.V.; Rossolenko, S.N.; Thieme, W.; Gerhardt, A.; Schröder, W. Czochralski growth of Si- and Ge-rich SiGe single crystals. J. Cryst. Growth 1997, 174, 182–186. [Google Scholar] [CrossRef]
- Deitch, R.H.; Jones, S.H.; Diggers, T.G., Jr. Bulk single crystal growth of silicon-germanium. J. Electron. Mater. 2000, 29, 1074–1078. [Google Scholar] [CrossRef]
- Yildiz, M.; Dost, S.; Lent, B. Growth of bulk SiGe single crystals by liquid phase diffusion. J. Cryst. Growth 2005, 280, 151–160. [Google Scholar] [CrossRef]
- Nakajima, K.; Kodama, S.; Miyashita, S.; Sazaki, G.; Hiyamizu, S. Growth of Ge-rich SixGe1−x single crystal with uniform composition (x = 0.02) on a compositionally graded crystal for use as GaAs solar cells. J. Cryst. Growth 1999, 205, 270–276. [Google Scholar] [CrossRef]
- Azuma, Y.; Usami, N.; Ujihara, T.; Sazaki, G.; Murakami, Y.; Miyashita, S.; Fujiwara, K.; Nakajima, K. Growth of SiGe bulk crystal with uniform composition by directly controlling the growth temperature at the crystal–melt interface using in situ monitoring system. J. Cryst. Growth 2001, 224, 204–211. [Google Scholar] [CrossRef]
- Azuma, Y.; Usami, N.; Ujihara, T.; Fujiwara, K.; Sazaki, G.; Murakami, Y.; Nakajima, K. Growth of SiGe bulk crystals with uniform composition by utilizing feedback control system of the crystal–melt interface position for precise control of the growth temperature. J. Cryst. Growth 2003, 250, 298–304. [Google Scholar] [CrossRef]
- Sekhon, M.; Armour, N.; Dost, S. Numerical and experimental investigation of the effect of crucible translation in liquid phase diffusion growth of SiGe. J. Cryst. Growth 2015, 412, 7–15. [Google Scholar] [CrossRef]
- Scheel, H.J.; Schulz-Dubois, E.O. Flux growth of large crystals by accelerated crucible-rotation technique. J. Cryst. Growth 1971, 8, 304–306. [Google Scholar] [CrossRef]
- Schulz-Dubois, E.O. Accelerated crucible rotation: Hydrodynamics and stirring effect. J. Cryst. Growth 1972, 12, 81–87. [Google Scholar] [CrossRef]
- Capper, P.; Gosney, J.J.G.; Jones, C.L. Application of the accelerated crucible rotation technique to the Bridgman growth of CdxHg1−xTe: Simulations and crystal growth. J. Cryst. Growth 1984, 70, 356–364. [Google Scholar] [CrossRef]
- Coates, W.G.; Capper, P.; Jones, C.L.; Gosney, J.J.G.; Ard, C.K.; Kenworthy, I.; Clark, A. Effect of ACRT rotation parameters on Bridgman grown CdxHg1−xTe crystals. J. Cryst. Growth 1989, 94, 959–966. [Google Scholar] [CrossRef]
- Xu, Y.-B.; Fan, S.-J. Accelerated crucible rotation technique: Bridgman growth of Li2B4O7 single crystal and simulation of the flows in the crucible. J. Cryst. Growth 1993, 133, 95–100. [Google Scholar] [CrossRef]
- Moon, S.J.; Kim, C.-J.; Ro, S.T. Effects of buoyancy and periodic rotation on the melt flow in a vertical Bridgman configuration. Int. J. Heat Mass Transf. 1997, 40, 2105–2113. [Google Scholar] [CrossRef]
- Lan, C.W.; Chian, J.H. Effects of ampoule rotation on vertical zone-melting crystal growth: Steady rotation versus accelerated crucible rotation technique (ACRT). J. Cryst. Growth 1999, 203, 286–296. [Google Scholar] [CrossRef]
- Yeckel, A.; Derby, J.J. Effect of accelerated crucible rotation on melt composition in high-pressure vertical Bridgman growth of cadmium zinc telluride. J. Cryst. Growth 2000, 209, 734–750. [Google Scholar] [CrossRef]
- Okano, Y.; Kondo, H.; Dost, S. Numerical study of interface shape control in the VGF growth of compound semiconductor crystal. J. Cryst. Growth 2002, 237–239, 1769–1772. [Google Scholar] [CrossRef]
- Bloedner, R.U.; Gille, P. Growth of Hg1−xCdxTe single crystals by travelling heater method under accelerated crucible rotation conditions. J. Cryst. Growth 1993, 130, 181–187. [Google Scholar] [CrossRef]
- Brunskill, I.H.; Boutellier, R.; Depmeier, W.; Schmid, H.; Scheel, H.J. High-temperature solution growth of Pb(Fe0.5Nb0.5)O3 and Pb(Mn0.5Nb0.5)O3 crystals. J. Cryst. Growth 1982, 56, 541–546. [Google Scholar] [CrossRef]
- Masalov, V.M.; Emel’chenko, G.A.; Mikhajlov, A.B. Hydrodynamics and oscillation of temperature in single crystal growth from high-temperature solutions with use of ACRT. J. Cryst. Growth 1992, 119, 297–302. [Google Scholar] [CrossRef]
- Barz, R.U.; Sabhapathy, P.; Salcudean, M. A numerical study of convection during THM growth of CdTe with ACRT. J. Cryst. Growth 1997, 180, 566–577. [Google Scholar] [CrossRef]
- Yildiz, M.; Dost, S. A continuum Model for the Liquid Phase Diffusion Growth of Bulk SiGe Single Crystals. Int. J. Eng. Sci. 2005, 43, 1059–1080. [Google Scholar] [CrossRef]
- Sekhon, M.; Lent, B.; Dost, S. Numerical study of liquid phase diffusion growth of SiGe subjected to accelerated crucible rotation. J. Cryst. Growth 2016, 438, 90–98. [Google Scholar] [CrossRef]
- Demirdžić, I.; Perić, M. Space conservation law in finite volume calculations of fluid flow. Int. J. Numer. Methods Fluids 1988, 8, 1037–1050. [Google Scholar] [CrossRef]
- ANSYS Inc. Ansys Fluent 14.5 Theory Guide 2012; ANSYS Inc.: Canonsburg, PA, USA, 2012. [Google Scholar]
- Issa, R.I. Solution of the implicitly discretised fluid flow equations by operator-splitting. J. Comput. Phys. 1986, 62, 40–65. [Google Scholar] [CrossRef]
- ANSYS Inc. Ansys Fluent 14.5 User’s Guide 2012; ANSYS Inc.: Canonsburg, PA, USA, 2012. [Google Scholar]
- Sekhon, M.; Dost, S. Numerical examination of the effect of steady crucible rotation in the liquid phase diffusion growth of SiGe. J. Cryst. Growth 2015, 430, 63–70. [Google Scholar] [CrossRef]


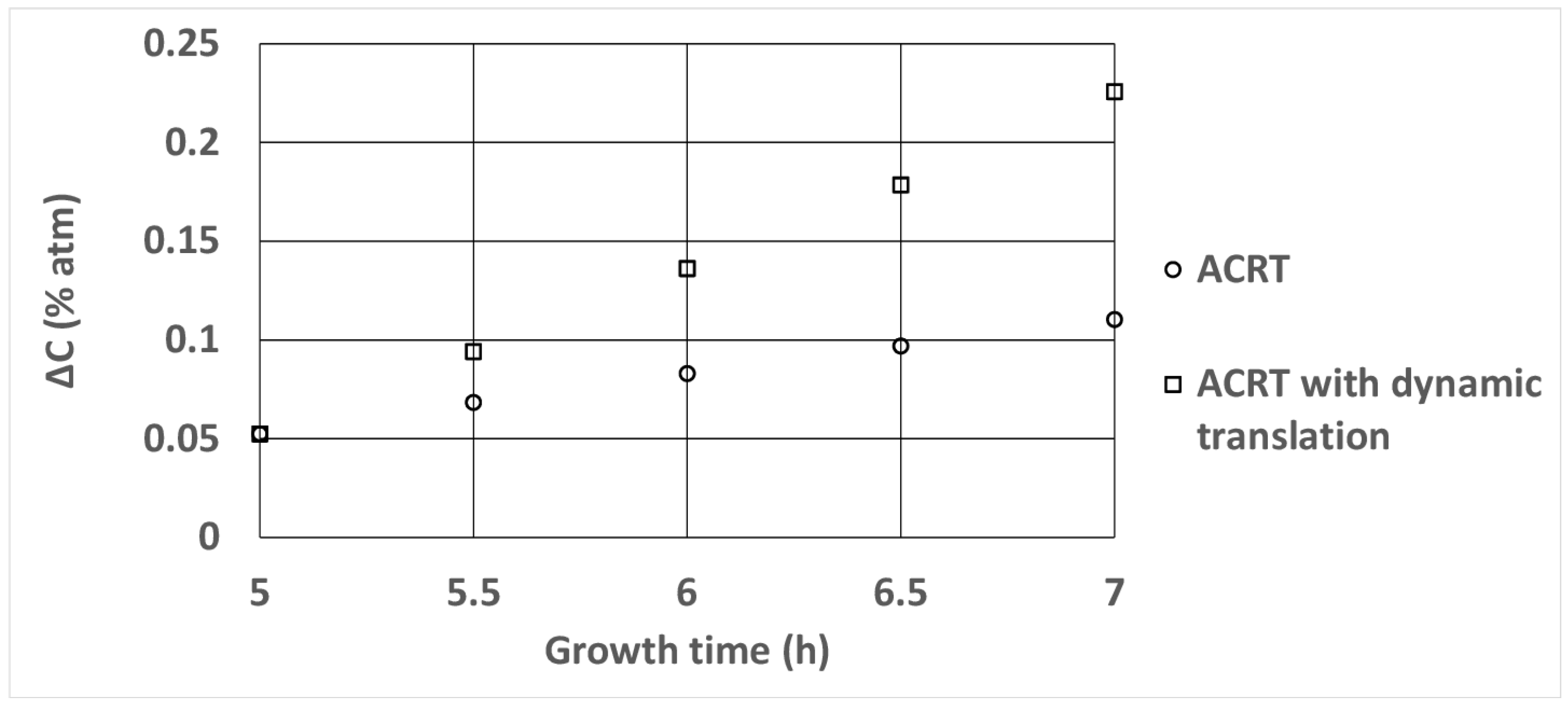
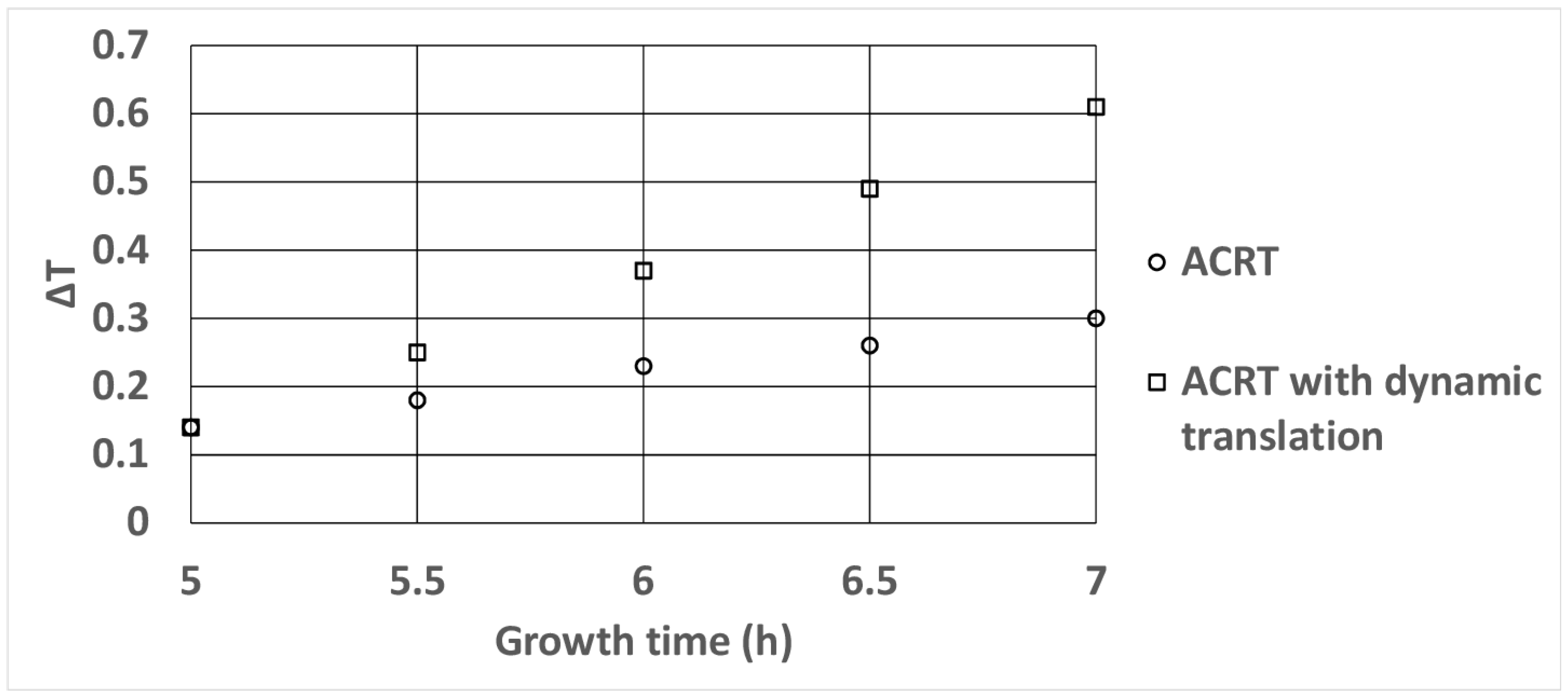
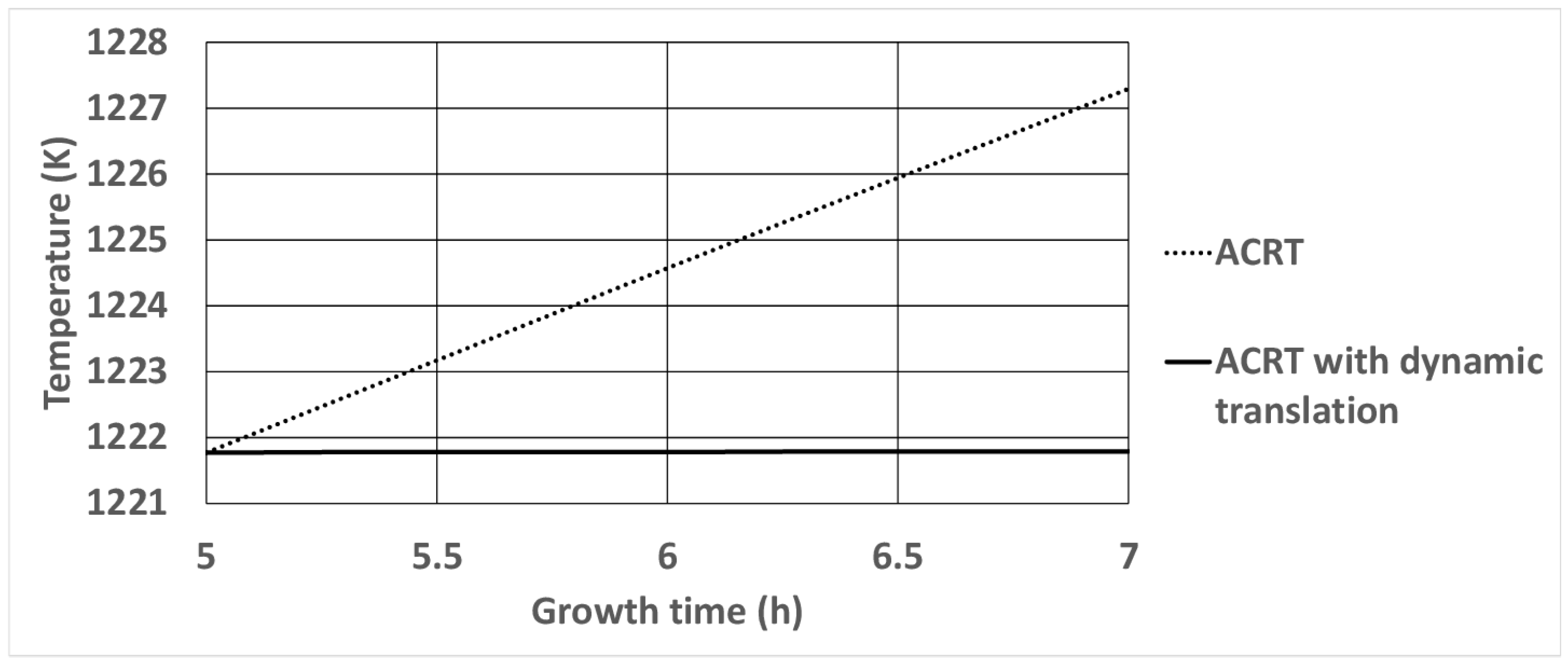




| Growth Time (h) | Growth Velocity (mm/h) at the Centerline (ACRT) (Data from [23]) | Growth Velocity (mm/h) at the Centerline (ACRT with Dynamic Translation) |
|---|---|---|
| 5.5 | 0.760 | 1.328 |
| 6 | 0.763 | 1.613 |
| 6.5 | 0.760 | 2.025 |
| 7 | 0.755 | 2.599 |
© 2016 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC-BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Sekhon, M.; Lent, B.; Ma, Y. Numerical Analysis of the Combined Influence of Accelerated Crucible Rotation and Dynamic Crucible Translation on Liquid Phase Diffusion Growth of SiGe. Crystals 2016, 6, 116. https://doi.org/10.3390/cryst6090116
Sekhon M, Lent B, Ma Y. Numerical Analysis of the Combined Influence of Accelerated Crucible Rotation and Dynamic Crucible Translation on Liquid Phase Diffusion Growth of SiGe. Crystals. 2016; 6(9):116. https://doi.org/10.3390/cryst6090116
Chicago/Turabian StyleSekhon, Mandeep, Brian Lent, and Yanbao Ma. 2016. "Numerical Analysis of the Combined Influence of Accelerated Crucible Rotation and Dynamic Crucible Translation on Liquid Phase Diffusion Growth of SiGe" Crystals 6, no. 9: 116. https://doi.org/10.3390/cryst6090116
APA StyleSekhon, M., Lent, B., & Ma, Y. (2016). Numerical Analysis of the Combined Influence of Accelerated Crucible Rotation and Dynamic Crucible Translation on Liquid Phase Diffusion Growth of SiGe. Crystals, 6(9), 116. https://doi.org/10.3390/cryst6090116







