Next Article in Journal
Nanoindentation-Induced Pile-Up in the Residual Impression of Crystalline Cu with Different Grain Size
Next Article in Special Issue
The Role of Chirality and Helicity between d- and l-Valine Optical Lattices
Previous Article in Journal
Effects of Crystal Orientation on the Crack Propagation of Sapphire by Sequential Indentation Testing
 
 
Search for Articles:
Title / Keyword
Author / Affiliation / Email
Journal
Article Type
 
 
Advanced Search
 
Section
Special Issue
Volume
Issue
Number
Page
 
Journals
Crystals
Volume 8
Issue 1
10.3390/cryst8010010
crystals-logo
Submit to this Journal Review for this Journal Propose a Special Issue
► Article Menu

Article Menu

share Share announcement Help format_quote Cite question_answer Discuss in SciProfiles thumb_up
...
Endorse textsms
...
Comment
first_page
settings
Order Article Reprints
Font Type:
Arial Georgia Verdana
Font Size:
Aa Aa Aa
Line Spacing:
Column Width:
Background:
Article

Structural Basis for the Influence of A1, 5A, and W51W57 Mutations on the Conductivity of the Geobacter sulfurreducens Pili

by
Chuanjun Shu
,
Ke Xiao
and
Xiao Sun
*
State Key Laboratory of Bioelectronics, School of Biological Science and Medical Engineering, Southeast University, Nanjing 210096, China
*
Author to whom correspondence should be addressed.
Crystals 2018, 8(1), 10; https://doi.org/10.3390/cryst8010010
Submission received: 15 November 2017 / Revised: 18 December 2017 / Accepted: 21 December 2017 / Published: 25 December 2017
(This article belongs to the Special Issue Crystal Structures of Amino Acids and Peptides)
Browse Figures
Versions Notes

Abstract

:
The metallic-like conductivity of the Geobacter sulfurreducens pilus and higher conductivity of its mutants reflected that biological synthesis can be utilized to improve the properties of electrically conductive pili. However, the structural basis for diverse conductivities of nanowires remains uncertain. Here, the impacts of point mutations on the flexibility and stability of pilins were investigated based on molecular dynamics simulations. Structures of the G. sulfurreducens pilus and its mutants were constructed by Rosetta. Details of the structure (i.e., electrostatic properties, helical parameters, residue interaction network, distances between amino acids, and salt bridges) were analyzed by PDB2PQR, Rosetta, RING, PyMOL, and VMD, respectively. Changes in stability, flexibility, residue interaction, and electrostatic properties of subunits directly caused wild-type pilin and its mutants assemble different structures of G. sulfurreducens pili. By comparing the structures of pili with different conductivities, the mechanism by which the G. sulfurreducens pilus transfers electron along pili was attributed, at least in part, to the density of aromatic rings, the distances between neighboring aromatic rings, and the local electrostatic environment around aromatic contacts. These results provide new insight into the potential for the biological synthesis of highly electrically conductive, nontoxic nanowires.

1. Introduction

The pili of Geobacter sulfurreducens are biologically electronic materials that can transfer electrons over µm distances with metallic-like conductivity [1,2,3,4,5]. This type of pilus is attractive because it can be generated from sustainable feedstocks, without the need for toxic solvents, or harsh chemical processes, and it can eliminate the presence of toxic components in the final product. Moreover, the conductive pili belong to Type IV pili, which are assembled from thousands of identical subunits known as PilA [3]. The three-dimensional structure of PilA, which is much shorter than other type IV pilins, has been analyzed by nuclear magnetic resonance (NMR) [6]. An understanding of the polymer structure provides important insights into its biological functions [7]; however, the full atomic structure of the G. sulfurreducens pilus remains a challenge because of the insolubility of subunits, its surface appendages, and the heterogeneity of assembly [8]. Therefore, the mechanism of electron transfer for Geobacter pili remains unknown.
Specific mutations in amino acids allow the functions and properties of a protein to be investigated by a rational approach [9]. Furthermore, aromatic amino acids that have redox-active side chains can facilitate electron transfer between distant redox centers [10]. Moreover, there are six aromatic amino acids (F1, F24, Y27, Y32, F51, and Y57) in one subunit of the Geobacter sulfurreducens pilus. Therefore, Vargas et al. investigated the mechanism of electron transfer of conductive pili by site-directed mutagenesis of aromatic residues [11,12]. They found that the genetic substitution of an alanine for each of the three tyrosines (+27, +32 and +57) and two of the phenylalanines (+24 and +51) in PilA (5A mutant) resulted in an assembled pilus with poor conductivity, suggesting the importance of aromatic amino acids in electron transport [11]. The conductivity of the Geobacter sulfurreducens pilus was increased by the genetic substitution of a tryptophan for each of the two aromatic amino acids (+51 tyrosines and +57 phenylalanines) in PilA (W51W57 mutant) [12], since tryptophan facilitates electron transport more effectively than tyrosines or phenylalanines [10,13]. Additionally, other studies also suggested that aromatic amino acids from different subunits were likely packed closely, resulting in π–π interactions that contribute to pili conductivity [3,8,14]. These results indicated that the mechanism for electron transfer in Geobacter has been attributed to the stacking of aromatic amino acids [3,15].
However, Yan et al. provided a different viewpoint [16]. In their study, there was a low calculated value of conductivity of the predicted model for the G. sulfurreducens pilus that suggested that an inter-aromatic chain is an unlikely mechanism of long-distance electron transport [16]. Furthermore, the W51W57 pili were significantly more conductive than the wild-type pili, which was likely because of the change in diameter of the G. sulfurreducens pilus [12]. Point mutations likely influenced conductivity because the structural details of the pilus have changed. Therefore, the role of aromatic residues and the impact of point mutations in the long-distance electron transport for the G. sulfurreducens pilus are not fully established.
Understanding the structures of the G. sulfurreducens pilus and its mutants (5A and W51W57) could provide important insights into their biological functions. However, because of the lack of X-ray crystal or NMR structures for mutant pilins and their polymers, experimental studies regarding this issue are limited. Under this condition, homology modeling and molecular dynamics simulation may be useful to achieve this goal [15]. Furthermore, these techniques have been extensively validated by comparison to experimental results in the past [8,14,15,17].
In this study, we investigated the impacts of 5A and W51W57 mutations on structural details of the G. sulfurreducens pilus, particularly the arrangement of aromatic amino acids, helical parameters, residue interaction networks, and salt bridges. The impact of A1 mutation (F to A mutation of the 1st residue) was also systematically investigated because F1 is probably arranged in a potential electrically conductive pathway in the G. sulfurreducens pilus [8]. Finally, the structures of wild-type and three mutant pili (A1, 5A, and W51W57) were constructed and analyzed. It is hoped that clarifying this issue will lead to a deeper understanding of the mechanism of conductivity of the Geobacter pilus.

2. Materials and Methods

2.1. Molecular Dynamics Simulation

Because the NMR-derived pilin structure was derived from pilin monomers immersed in lipid micelles, the wild-type PilA and its mutants were subjected to molecular dynamics simulation using Amber 12 software (TRII-Biotech, Shanghai, China) [18] with a ff12SB force field [19]. The structure of PilA was obtained from the first frame of 2M7G, which was downloaded from the RCSB protein data bank (RCSB PDB) [20]. The mutants of PilA (A1, 5A, and W51W57) were generated by genetic substitution using the PyMOL package (http://www.pymol.org/) [21]. Topology files for the pilin were created and parameters were assigned to the atoms using Leap [22]. Two Na+ were added to electro neutralize each simulated system. The wild-type PilA and its mutants were placed in a regular octahedron water box of the TIP3P with a 10 Å distance around the protein. The missing hydrogen atoms of the pilin were added using Leap.
Energy minimization, heating and equilibration were performed by the PMEMD (particle mesh Ewald molecular dynamics) program of Amber 12 [23]. The nonbonded interaction cutoff was set as 8 Å. All of the water molecules and hydrogen atoms were minimized when backbone atoms of the protein were constrained by a harmonic constraint potential with 100 kcal·mol−1·Å−2. The whole system was then minimized without any restraint. Each minimization phase was implemented by the steepest descent algorithm (50,000 steps) followed by a conjugate gradient algorithm (20,000 steps). The systems were then gradually heated from 0 to 300 K using a Langevin thermostat with a coupling coefficient of 2 ps−1 in 500 ps molecular simulation (a canonical ensemble NVT). Next, systems were equilibrated for 0.5 ns in the isothermal isobaric ensemble (NPT). During the heating and equilibration, the solute molecules were restrained by applying a constant harmonic force of 50 kcal·mol−1·Å−2 and 5 kcal·mol−1·Å−2, respectively. According to a previous study [24], the systems were subsequently subjected to 20 ns MD (molecular dynamic) simulation in the NPT ensemble at 300 K with a time step of 2 fs. SHAKE algorithm, particle mesh Ewald (PME), periodic boundary conditions, Langevin piston algorithm and Berendsen barostat were used to perform constraint covalent bonds involving hydrogen atoms, treat long range interactions, and avoid edge effects in calculations, temperature, and pressure control. The coordinates were saved every 1 ps and the trajectory files were analyzed every 1 ps using the Cpptraj module implemented in the Amber12 software [25].

2.2. Cross-Correlation Analysis

Cross-correlation analysis was applied to investigate the extent of correlation motions caused by mutations [26]. The cross-correlation matrix C (i, j) represented fluctuations in the coordinates of the Cα atoms to their average positions from the last 20 ns of the molecular simulations. The matrix was determined by the following equation [27]:
C ( i , j ) = 〈 Δ r i × Δ r j 〉 〈 Δ r i 2 〉 〈 Δ r j 2 〉
where   Δ r i reflected the deviation of the Cα atom of the ith residue from its mean position and the angle bracket represented an average over the sampled period. Positive and negative values indicated a correlated motion and anti-correlated motion between the ith and the jth residue, respectively. The values were set from −1 to 1.

2.3. Electrostatic Properties Analysis

To investigate changes in electrostatic properties caused by mutations, adaptive Poisson-Boltzmann solver (APBS) and PDB2PQR were applied to each subunit (http://nbcr-222.ucsd.edu/pdb2pqr_2.1.1/) [28]. Electrostatic interactions played a critical role in the process of pilin assembly [29]. The pqr file of each structure was generated using the PDB2PQR program [30]. The dx file of each structure was generated by utilizing APBS [28]. The pqr file and dx file were then uploaded in VMD to show the molecular surface electrostatic potential map [31]. High-quality 3-D images of the pilin/pilus were drawn by PyMOL [21].

2.4. Constructing a Pilus Structure from Subunit Data with Sparse Constraints

To explore the differences among the structures of pili of G. sulfurreducens and its mutants, structures were constructed using the symmetric docking module of the Rosetta software [8]. The helical parameters were deduced from the homologous biological experiment structure (Neisseria gonorrhoeae pilus structure, PDB ID: 2HIL) since the type IV pilus is a type of helical symmetric protein consisting of thousands of copies of subunits [7,29]. The assembly process included two stages. The first stage was employed to search for potential pili structures from a wide range of sampling spaces (Rotation_angle was set as −180° to 180°). The second stage was employed to produce full atomic models with structure details from a small range of sampling spaces. The rotation angle of the second stage was obtained from convergent models of the first stage. The remaining details of the symmetric files for the two stages were set as follows: Rise (Å) was set as 5 to 15. Radius_to_Com (Å) was set as 15 to 30.
The number of subunits was set as 21. The chain names were set as A, B, C to X. Before assembly, the subunit was aligned along the pilus axis by the align module of PyMOL to define the initial position and facilitate the searching process. During assembly, the proper distance and ambiguous constraints were set between pairs of amino acids (aromatic amino acids and charged amino acids) from neighboring subunits to narrow the sampling time [8,17]. Furthermore, the pair of residue F1/E5 was also set as a constrained pair. Three variables were set in the constraint file; namely, approximation of distance between a pair of atoms, standard deviations of Euclidean Distance between two atoms, and tolerance that represents the acceptable bound of constraints. For aromatic amino acids, restraints were added between the C atoms. For changed amino acids, restraints were added between the N atom of the amino terminal and the O atom of the carboxyl. In two stages, three variables were set as 10, 0.5, 5, and 4, 2, 0.5, respectively. To assemble the data in an appropriate way, clustering (cutoff = 4) and an interfacial energy score were utilized to evaluate models based on the first three consecutive subunits of the models. The “cluster” module in Rosetta was employed to evaluate structural similarity [8].

2.5. Residue Interaction Network

The residue interaction network is an alternative method of representing protein structures in which nodes are residues and arcs physico-chemical interactions. The network has been extensively and successfully employed to analyze mutation effects, domain-domain communication, protein folding, and catalytic activity [32]. The residue interaction networks for pilins and pili were obtained by utilizing the RING web server [32].

2.6. Algorithm for Exploring Potential Electrically Conductive Pathway

Aromatic amino acids that have a redox-active side chain can facilitate electron transfer between redox centers [10]. In the Geobacter pilus, aromatic amino acids from different subunits could pack closely, resulting in a π–π interaction pathway that is likely a mechanism of long-distance electron transport [8]. There is the potential for formation of an electrically conductive pathway if each aromatic amino acid in the pathway could form a π–π interaction with its neighboring aromatic amino acids. A shorter distance between aromatic amino acids was associated with a higher rate of electron transfer [16]. We developed an algorithm that could identify the most efficient electrically conductive pathway, which is the shortest pathway between π-residues, from π–π interacting aromatic amino acids. The algorithm consisted of three steps; namely, identification of π-residues, which are aromatic amino acids capable of forming π–π interactions, extraction of coordinates of π-residues, and calculation of distances between π-residues, searching for and comparing the shortest paths (Figure 1). First, π–π interactions of the Geobacter pilus were obtained by RING, and π-residues were identified by utilizing RING-Viz [32]. An adjacent matrix was then generated to store the interactions between π-residues. In this adjacent matrix, if two π-residues could form a direct π–π interaction, the corresponding value was set as 1, otherwise the value was set as 0. Secondly, the coordinates of all of the C atoms from aromatic rings of π-residues were extracted. The coordinates of the C atoms from the same aromatic ring were averaged to obtain the coordinate of the centroid for a given aromatic ring. The distances between centroids were calculated by the sqrt function using MATLAB software [33]. These distances were stored in a distance matrix. The adjacent/distance matrix consisted of 21 (number of subunit) × M rows and 21 × M columns, where M represents the number of π-residues in every subunit of the Geobacter pilus. The Dijkstra algorithm [34], which is an algorithm for identifying the shortest paths between nodes in a map, was utilized to explore all of the possible potential electrically conductive pathways in a turn of pilus models. A turn of pilus consisted of N subunits, and we searched the potential electrically conductive pathways in the second turn. The start and end node for a potential electrically conductive pathway were set as a special π-residue of subunit p, which is the first subunit of the second turn, and the same special π-residue of subunit p + N, respectively. For example, the start and end node were set as F1p and F1p+N, respectively (color-coded aromatic rings in Figure 1). The shortest pathways for different π-residues were then taken as the potential electrically conductive pathways. By changing the start and corresponding end node (such as F24P&F24P+N/Y27P&Y27P+N), all of the potential electrically conductive pathways were obtained. Finally, potential electrically conductive pathways that consisted of the same order of π-residues were merged into a single pathway. The potential electrically conductive pathways were then visualized directly on a PDB structure using PyMOL.

3. Results

3.1. Structures of Pilins

Structures of the initial mutant pilins were obtained using the mutagenesis module in the PyMOL software package, and then the subunit for each of the four pilins was refined to improve the geometry and structural statistics by utilizing the steepest descent algorithm and the conjugate gradient algorithm [35,36]. A comparison with the wild-type pilin revealed that the root mean square deviations (RMSD) of the A1, 5A, and W51W57 pilins were 0.807, 0.848, and 0.838 Å, respectively. The electrostatic properties of the pilin structure were then calculated using the PDB2PQR server [28,30], and they are shown in Figure 2. Based on the landscapes of the electrostatic potential for the four G. sulfurreducens pilins, the positive potential values were mainly distributed in the N-termini and the negative potential values were primarily distributed in the C-termini. Furthermore, although the net charge for all of the four pilins was −2, the surface electrostatic properties of the four pilins differed because they have different compositions of amino acids and different structures. A comparison with the wild-type revealed that the A1, 5A, and W51W57 mutation increased the area with positive potential value (0−+5) for the N-termini (residues 1–7), the partial fragment of the alpha helix (residues 20–32), and the other partial fragment of the alpha helix (residues 20–40), respectively. Meanwhile, all three of the mutations increased the area with negative potential value (−5–0) for the C-terminal loop domain (residues 50–61) when compared to the wild-type pilin. Furthermore, the hydrophobic values of amino acids A, F, Y, and W were 0.62, 1.19, 0.26, and 0.81, respectively [37]. Because of the special site-directed mutagenesis, the hydrophobic values of the A1, 5A, and W51W57 pilins increased by −0.57, 0.06, and 0.17, respectively, compared with the WT pilin. Meanwhile, detailed secondary structure elements of the WT pilin and its mutants were analyzed. We found that all of the carboxylic ends for WT pilin and its mutants have no alpha helix. There was a turn or 310-helix in the carboxylic ends of WT pilin and its mutants. 310-helix is an intermediary conformation between turn and alpha helix. The difference of structure between the carboxylic ends of the four pilins was probably caused by the process of MD optimization. The pilus is composed of thousands of copies of subunits, and its assembly process can be determined by the electrostatic interactions among subunits and the hydrophobic properties of the subunit [29]. Hence, these results suggested that the point mutations in the pilin could affect the conformation of the pilus.

3.2. Structures of Wild-Type Pilus and Its Mutant Pili for G. Sulfurreducens

Structures of the G. sulfurreducens pilus and its mutants were obtained by utilizing the symmetric docking module of the Rosetta software package [38]. Because the type IV pili have similar structures with a right-hand helical symmetry along their assemblages, the helical parameters of the G. sulfurreducens pili were inferred from the Neisseria gonorrhoeae pilus, which was resolved by combining X-ray crystallography and cryo-electron microscopy [29].
To search potential pilus structures from a wide range of sampling spaces, the rotation angle was set from −180° to 180° in the low resolution stage. After symmetric docking, 3000 low resolution models were obtained for each of the three mutants and the wild-type pilus. The landscapes of the low interfacial energy score (<−10) versus the rotation angle of the subunits are shown in Figure 3. The results indicated that models of WT, A1, 5A, and W51W57 pilus tended to converge into two (rotation angles of 40° to 80° and 120° to 160°), three (rotation angles of 40° to 80°, 90° to 120° and 120° to 160°), four (rotation angles of 30° to 60°, 60° to 90°, 90° to 120° and 130° to 170°) and three (rotation angles of 40° to 80°, 100° to 120° and 130° to 160°) local troughs, respectively. To further narrow the range of sampling, 1000 low-resolution models were obtained for each of these convergent rotation angles. The cluster module in Rosetta was then utilized to cluster these models (cutoff radius = 4.0 Å). Since interfacial energy is an approximation of binding energy that represents the stability of the pilin assemblage [8,17], the convergence phenomenon (Figure 3A–D) and energy scores of the 15 lowest energy models in the biggest cluster for each different range (Figure 3E–H) could be used to help determine the rotation angle for assembling full atomic models. These results suggested that the models that have a rotation angle of 40° to 80° for WT, 90° to 120° for A1, 90° to 120° for 5A, and 40° to 80° for W51W57 had the best convergence phenomenon and the lowest interfacial energy score. Such good convergence suggested a basin of low-energy conformations, within which the native structure tends to situate, to fold efficiently, and retain robustness. Hence, these rotation angles were utilized to assemble full atomic models.
In the second stage, the rotation angle for the WT, A1, 5A, and W51W57 was set as 40° to 80°, 90° to 120°, 90° to 120°, and 40° to 80°, respectively (Figure 3). Next, 1000 full atomic models for each of the three mutants and wild-type pilus were obtained. These full atomic models were clustered using the cluster module of the Rosetta software package (cutoff radius = 4.0 Å) [39]. There were 108, 164, 113, and 314 models in the biggest clusters of the WT, A1, 5A, and W51W57 pili, respectively. The results revealed the convergence of models was impacted by point mutations. The 15 full atomic models with a low interfacial energy score in the largest cluster for each of the four types were selected to analyze the structural basis for diverse conductivity. The helical parameters of the 15 models for each of the four types of pili are shown in Figure 4. The helical parameters of models for the 15 models fluctuated, since the symmetric docking was based on Monte Carlo algorithms that rely on repeated random sampling to obtain numerical results [40]. The values of diameter, axial rise, rotation angle, and subunits per turn for the WT pilus and each of its mutants (A1, 5A, and W51W57 pilus) were around 31.6, 30.3, 32.6, and 23.6 Å; 10.7, 10.9, 7.2, and 10.5 Å; 59.8, 108.4, 106.7 and 52.7°; and 6.0, 3.3, 3.4, and 6.9, respectively. These structural details are close to the experimental values [12]. There were three reasons to explain why these diameters are not same as the experimental values. Namely, the surface of pilus is heterogeneous; the average diameter of the pilus is measured in this study; there are remnants of the buffer solution in the pili environment. The shapes of the four type pili were different, suggesting that the point mutations affected the pilin assembly process, resulting in different structures of the pilus.
To further investigate whether the assembly of pilin was impacted by mutation, salt bridges of the model were found by utilizing the analysis module (salt bridges) in the VMD software (Table 1) [31]. Salt bridges play an important role in the stability of protein structure and functions such as in molecular recognition, domain motions, and electrostatic properties [41,42,43]. Before assembly, none of the four type subunits had salt bridges. In the assembled structure of pili, pairs of neighboring oppositely charged residues often interacted to form salt bridges. For each of the four types of pili, there was only one salt bridge (48E-44K) in the interior of a subunit. However, the salt bridges between subunits were diverse for the four types of pili. For salt bridges between subunits, although 13 of the 15 wild-type pili models shown in Figure 4 had no salt bridge, each one of the three mutant pili models (A1, 5A, and W51W57 pilus) had two or more pairs of salt bridges (Table 1). One subunit in models of the A1, 5A and W51W57 pilus could almost form salt bridges with two, two and four neighboring subunits, respectively. As shown in Table 1, the pilus that consisted of W51W57 subunits had the largest number of salt bridges. These results illustrated that point mutations affected the formation of salt bridges in the pilus, resulting in different pili structures.

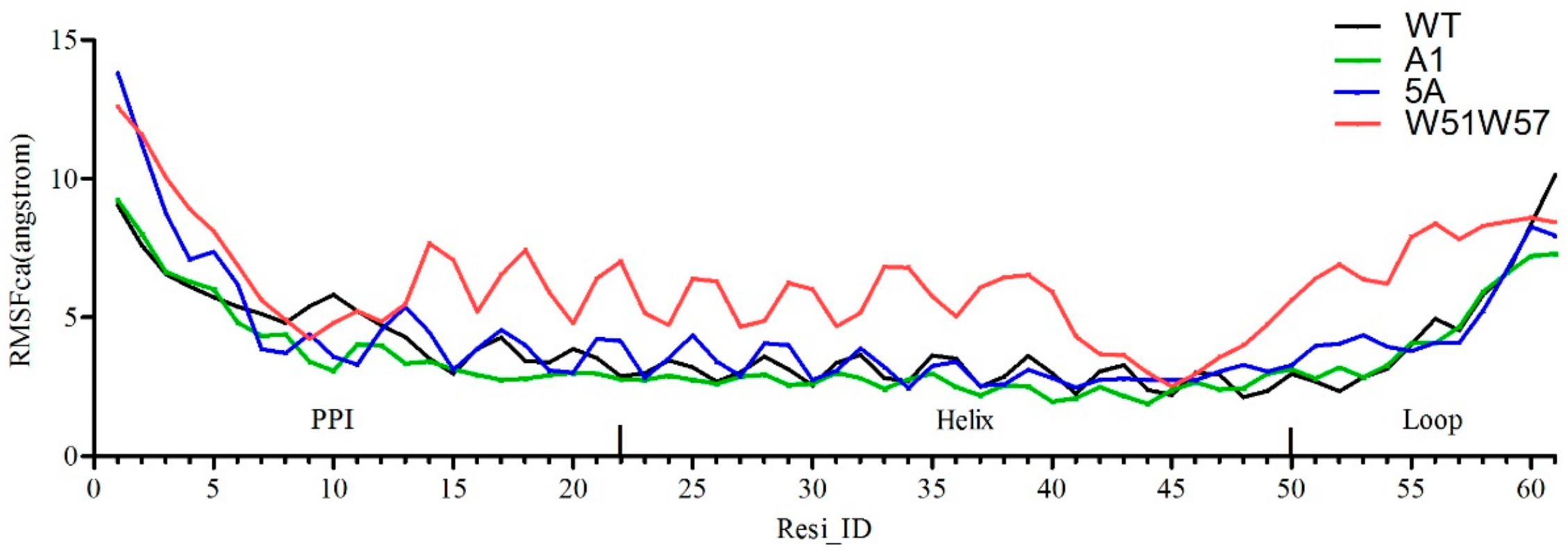
3.3. Structural Changes in Geobacter Pili Were Partly Attributed to More Unstable and More Flexible Pilins

Site-directed mutagenesis and functional studies showed that the most extensive and important contacts, i.e., physico-chemical interactions, which play key roles in pilus assembly, involve the two closest subunits in the pilus [44]. Since the pilus is a flexible polymer that consists of thousands of identical pilins, different characteristics of pilins could be the result of different interactions between neighboring pilins in the pilus [7]. To understand structural changes in the G. sulfurreducens pilus, the stability and flexibility of the wild-type pilin and its mutants were investigated. To ensure the simulated systems reached equilibrium, 20 ns molecular dynamics simulations were conducted for each of the four types of pilins (WT, A1, 5A, and W51W57). The time of simulation was based on the results of a previous study [24]. The RMSDs of backbone Cα atoms from the first frame conformation of molecular dynamics simulations were then computed and described. All of the systems except W51W57 deviated to a similar extent from their first frame after 10 ns. The W51W57 system had larger RMSD values than others when the system reached equilibrium. The average RMSD value of the last 10 ns MD productions for W51W57 was 0.4 Å larger than those of the other three pilins. There was a small difference (0.01–0.15 Å) in the average RMSDs (last 10 ns) among the A1 mutant, the 5A mutant, and WT. The RMSD value of the whole protein was always utilized to represent the flexibility of protein [45]. Therefore, the results suggested that the W51W57 mutant had greater flexibility than the WT and other mutants. There was a small difference in the pilin’s flexibility among the A1 mutant, the 5A mutant, and WT.
To calculate the RMSDs of domains, the pilin was delineated into three subdomains, the PPI (protein-protein interaction) domain (residues 1–22), which is primarily hydrophobic and highly conserved, the Helix domain (residues 23–50), which is amphipathic in character and less conserved in primary structure, and the Loop domain (residues 51–61), which is required for pilin folding and pilus assembly [7,46]. When compared with WT, the W51W57 mutation remarkably influenced the backbone stability of the PPI, Helix, and Loop domains, while the A1 and 5A mutations mainly influenced the backbone stability of the PPI domain (Supplementary information Figure S1). The root-mean-square fluctuations (RMSFs) were utilized to further identify fluctuations in individual residues, determine the flexibility of a domain of pilin, and investigate the conformational changes among the four types of pilins. Figure 5 shows the Cα RMSFs that described the backbone Cα atoms around the average structure for the relevant time interval (20 ns) versus the four models. The result indicated that all three of the mutations (A1, 5A, and W51W57) had a significant effect on flexibility of the PPI domain for the G. sulfurreducens pilin. The fluctuations of residues in the PPI domain for the three mutations differed.
When compared with the RMSFs of WT, the fluctuations of residues in the PPI domain became smaller for the three mutants (residues 6 to 13 and 16 to 21 for the A1 mutant, residues 7 to 11 for the 5A mutant and residues 9 to 10 for the W51W57 mutant), while the fluctuations of residues in the PPI domain became bigger for two mutants (residues 1 to 6 for the 5A mutant and residues 1 to 7 and 14 to 22 for the W51W57 mutant). There was no remarkable difference in fluctuations of residues for the Helix and Loop domain between the A1 mutant and the WT. However, when compared with the WT, the fluctuations of residues 51 to 54 for the A5 mutant were larger. For the W51W57 mutant, the fluctuations of residues in the Helix and Loop domain were bigger than those of other mutants and the WT, except for residues from 44 to 46 and from 60 to 61. These results illustrated that the W51W57 mutation affected the flexibility of the whole G. sulfurreducens pilin, the A5 mutation influenced the flexibility of the PPI and Loop domain, and the A mutation only impacted the flexibility of the PPI domain.
The residues in protein are not only linked through physical contacts, but also through correlated motions [47]. The changes in the extent of correlation motions of residues of pilin could affect the assembly process of the pilus. To further investigate the influence of mutations on the extent of correlation motions for residues in G. sulfurreducens pilin, cross-correlation matrices of Cα atom fluctuations in the 20 ns of the MD productions run were calculated and plotted in Figure 6. In Figure 6A–D, highly positive areas (dark red, value ≥0.8) are associated with strongly correlated motions of special residues, and highly negative areas (dark blue, value <−0.8) represent strong anti-correlation in the special movements of special residues. The landscape indicated there were no highly negative areas for any of the four systems. As shown in Figure 6E–H, absolute values <0.8 were removed to highlight the strong correlation and anti-correlation motions. The highly correlated motions were mainly distributed around the diagonal areas, which indicated the correlation of a residue with itself and neighboring residues. Overall, the correlated motions of the three mutants were stronger than those of the WT (red).
When compared with the WT, all three of the mutations enhanced the extent of correlation motions among residues 1 to 7, while the A1 and W51W57 mutations reduced the highly correlated areas, but increased the extent of correlation motions among residues 21 to 49, and the 5A mutation expanded the highly correlated area among residues 21 to 49. Additionally, the W51W57 mutation enhanced the extent of correlation motions among residues 48 to 61. These findings indicate that the three mutations influenced the extent of correlated motions in pilins and suggest that the mutations impacted the stability, flexibility, and correlation motions among residues of the G. sulfurreducens pilin.

3.4. Structural Basis for Diverse Values of Conductivity

To reveal the structural basis for diverse conductivity of pili, the density of aromatic rings, the electrostatic environment around aromatic amino acids, and π–π interactions in the 15 lowest energy models for each of the four types of pili were analyzed. According to helical parameters (Figure 4), the average density of aromatic rings for the four types of pili was computed by the formula:
  ρ = S   × N π × ( D 2 ) 2 × R
where S represents the number of subunits in one turn, N indicates the number of aromatic rings in one subunit, D is the diameter of pili, and R represents the axial rise of one turn of pili. Tryptophan (W), which has two aromatic rings, promotes electron transport more effectively than phenylalanine (F) or tyrosine (Y) [10]. Other aromatic residues have one aromatic ring.
As shown in Table 2, the W51W57 pilus has the biggest number of aromatic rings (the value is 8) in one subunit, since the amino acid W has one more ring than other aromatic amino acids. Moreover, the W51W57 pilus was found to contain the largest number of subunits (6.9) in one symmetric unit. However, other mutants had fewer aromatic rings than the wild-type. The average density of aromatic rings for the wild-type and its mutants (A1, 5A, and W51W57 pilus) was 4.29, 1.91, 0.57, and 12.02 (1021 cm−3), respectively (Table 2). Meanwhile, the density of aromatic rings had a small fluctuation for the 15 lowest energy models in the same type pili. The result indicated that a big fluctuation of the density of aromatic rings existed between different types of pili. Moreover, the density of aromatic ring was found to be positively correlated with the conductivity of pili. The correlation coefficient (r) of the known conductivities with the corresponding densities of aromatic ring was larger than 0.95. These results illustrated that different aromatic ring densities may explain the different conductivities.
The local electrostatic environment around the aromatic contacts probably influences the rates of electron transfer through the pili [24]. The model with the lowest energy was selected for each type of pili to show the spatial relationship between aromatic residues and charged residues. The pairs of residues that could form a salt bridge in four types of pili (Table 1) were in close proximity (<4 Å) to the aromatic residues (Figure 7). The results indicated that charged amino acids were co-localized with aromatic amino acids. The aromatic amino acids from different subunits could form π–π interactions that contributed to pili conductivity. Salt bridges are formed by a combination of hydrogen bonding and electrostatic interactions [49], while the major contributions to the π–π interaction energy come from the electrostatic and Van der Waals components [50]. Hence, when the two physico-chemical interactions, i.e., salt bridges and π–π interactions, are close (<4 Å), electrostatic interactions of salt bridges could affect the efficiency of electron transfer in π–π interactions [24]. The number of charged residue pairs around the aromatic residues in one subunit of the pilus was one (28R-60E), one (30K-53D), one (28R-39D), and three (39D-41R, 44K-60E, and 5E-41R) for the WT, A1, 5A, and W51W57, respectively. When compared with other pili, the local electrostatic environment around aromatic residues for the W51W57 pilus was the most complicated (Figure 7). These results indicate that mutations changed the local electrostatic environment around the aromatic residues.
The Residue Interaction Network Generator (RING v2.0.1) was utilized to analyze π–πinteractions in pili (interaction type: multiple, node color: type of residue, repulsion: 20, gravity: 0.15, and attraction: 0.7) [32]. When multiple is activated, RING reports multiple interactions per residue pair but only one interaction per interaction type (HBOND, VDW, etc.). When ‘node color’ was set as type of residue, residues was colored by their chemical–physical properties: hydrophobic, polar, charged (negative/positive). Layout parameters of RING includes three aspects, i.e., ‘repulsion’ was utilized to show the strength of the charge; ‘gravity’ was used to show the attraction between nodes; ‘attraction’ was utilized to modify the impact of the links in keeping highly connected nodes close together. The landscape of physico-chemical interactions, including hydrogen bonds, Van der Waals forces, π–π interactions, and ionic bonds, for each of the four pili is shown in Figure 8A–D. The nodes represented residues that could form physico-chemical interactions with other residues. The edges represented physico-chemical interactions. The number of nodes in the residue interaction network of the WT, A1, 5A, and W51W57 pilus was 1176, 1241, 1239, and 1276, while the number of edges was 2569, 2611, 2563, and 2734, respectively. These results indicated that the physico-chemical interactions, including covalent bonds, non-covalent bonds, and π–π stacking, in each of the four pili were different, resulting in different conformations of pili. The residue interaction networks indicated that π–π interactions existed in the three pili (i.e., WT, A1, and W51W57 pili). Furthermore, the red line is mostly continuous in WT and W51W57 pilus, however, sporadic red line between nodes appear for A1 pilus, indicating that only π–π interactions of the WT and W51W57 pilus could construct the continuous electron transfer pathway.

3.5. Potential Electron Transfer Pathway in Geobacter Pili

The spatial distribution of aromatic amino acids showed that all of the models have closely packed aromatic rings. These closely packed aromatic rings from different subunits probably form potential electrically conductive pathways and exhibit a helical distribution in the pilus (Figure 7). Furthermore, although π–π interactions can be identified by RING v 2.0.1, the potential electrically conductive pathway consisting of these aromatic residues, which could form π–π interactions, are unknown (Figure 8). Therefore, the models with the lowest energy were selected for each type of pili to investigate the potential electrically conductive pathway in detail.
Π-residues, which are aromatic amino acids capable of forming π–π interactions, were identified utilizing RING [32]. These aromatic residues in WT and W51W57 were the same, i.e., F1, F24, and Y27 from different pilins. An adjacent and a distance matrix for each of the WT and W51W57 pilus were then constructed. There were 63 (3 × 21) rows and 63 (3 × 21) columns in the distance/adjacent matrix for each of the two pilus models, since each pilus model consisted of 21 subunits and every subunit for each of the two pilus models had three π-residues. The adjacent and distance matrix were input to the Dijkstra algorithm, which is used to identify the shortest paths between nodes in a graph [34]. Since each value of subunits per turn for the WT and W51W57 pilus was six, the start and end nodes for the special pathway of the WT and W51W57 pilus were set at F1p/F24p/Y27p and corresponding F1p+6/F24p+6/Y27p+6, respectively. The p was set to 7, indicating the first subunit of the second turn. After merging the pathways that consisted of the same order of π-residues, potential electrically conductive pathways for the WT and W51W57 pili were obtained (Table 3).
The potential electrically conductive pathways were loaded into each structure of the WT and W51W57 pilus and a continuous chain of aromatic rings was obtained for each pilus (Figure 9A,B). As shown in Table 3 and Figure 9, the potential electrically conductive pathways in the WT and W51W57 pili consisted of the same aromatic residues, F1, F24, and Y27. Furthermore, there were two and zero π-residues in every subunit for the A1 (Y27 and F51) and 5A pilus, respectively, when the extreme distance for the π–π interaction in RING was set as the default (7 Å) [32,51]. Since the number of subunits in one turn for the A1 pilus was three, the start and end node of the potential electrically conductive pathway for the A1 pilus were set as Y27p/F51p and Y27p+3/F51p+3, respectively. The p for the A1 pilus was set at 4, which is the first subunit of the second turn. According to our algorithm, we found that π-residues of the A1 pilus could not construct a continuous π–π interaction chain. These results indicated that there was not a continuous π–π interaction chain in the A1 and 5A pilus. Electrons could be transferred from one aromatic residue to another aromatic residue via electron hopping when distances between centroids of aromatic residues ranged from 7 to 20 Å [52]. Therefore, to identify the continuous aromatic residue chain in the A1 and 5A pilus, the extreme distance was set as 20 Å by manual input for RING. Then, according to our algorithm, a continuous chain of aromatic rings for the A1 and 5A pilus was found (Table 3, Figure 9C,D) that consisted of aromatic residues F24-F51-Y27 and F1, respectively. Furthermore, the distances among aromatic residues in the shortest pathway for A1 and 5A pilus were similar to those in conventional type IV pili, such as N. gonorrhea pili (Table S1). These results suggest that point mutations can directly influence the arrangement of aromatic residues for the Geobacter pilus, resulting in different conductivity of pili.
To further investigate the mechanism for the conductivity of the pilus, the distances between the proximal carbon atoms in neighboring aromatic rings of 15 low energy models for each of the four types of potential electrically conductive pathways are shown in Figure 10. For the WT pili, d (F1, F24), d (F24, Y27), and d (Y27, F1) were around 3.5, 4.0, and 3.5 Å, respectively. The three distances (d (F1, F24), d (F24, Y27), and d (Y27, F1)) of the W51W57 pili were around 3.4, 3.6 and 3.5 Å, while they were around 8.5, 4.8, and 3.5 Å (d (F24, F51), d (F51, Y27), and d (Y27, F24)) in the A1 pili. For the 5A pili, since there was only one aromatic residue in the 5A subunit, the distance (d (F1, F1)) was around 9 Å. The aromatic rings in the WT and W51W57 pilus were closer than in the A1 and 5A pilus. Furthermore, the smallest distance between aromatic rings was observed in the W51W57 pilus. These results illustrated that only aromatic amino acids from the WT and W51W57 pilus could construct a continuous chain of aromatic rings, resulting in π–π interactions that contribute to the high conductivity for pili. The results also suggested that the genetic substitution of a tryptophan for the 51st and 57th amino acids in pilin could change the conformation of the pilus, resulting in closer π–π interactions for other aromatic amino acids (F1, F24, and Y27) (Table 3, Figure 9 and Figure 10). These results could guide further research into the mechanisms involved in extracellular electron transfer along these pili.

4. Discussion

The PPI domain (residues 1–22) is predicted to mediate crucial contacts between subunits involving parallel coiled-coil helix packing [7]. Substitutions in the N-terminal alpha helical spine (PPI and Helix domain) of the type IV pilin could affect the pilus assembly, dynamics, and associated functions [53]. Furthermore, the structurally variable loop is required for pilin folding and pilus assembly, which are involved in pilus–pilus interactions, and predicted to be surface-exposed [6,7]. Therefore, genetic substitutions that occurred in the PPI, Helix, or Loop domain of pilins could affect their physical and chemical properties, resulting in different structures of the pilus. For example, a previous study indicated that substituting a tryptophan for each phenylalanine and tyrosine at the C-terminus of pilin lead to a decrease in the diameter of the pilus [12]. When compared with WT pilin, the stability and flexibility of the PPI domain for A1, 5A, and W51W57 pilin changed remarkably. In addition, WT, A1, 5A, and W51W57 pilin had different extents of correlation motions among residues of the Helix domain. The flexibility and extent of correlation motions among residues of the C-terminal loop domain (residues 51–61) also showed notable changes when genetic substitution occurred in the PilA C-termini (W51W57). Furthermore, the hydrophobic value and surface electrostatic properties of pilin were impacted by the site-directed mutagenesis. These results suggest that these genetic substitutions resulted in different subunit conformations and different electrostatic properties of the pilin surface, which probably resulted in various G. sulfurreducens pilus structures.
It is well known that the structure of a biomolecule determines its function. An understanding of the atomic resolution structure and assembly of the G. sulfurreducens pilus provides important insights into their biological functions, including the mechanism of extracellular electron transfer [54]. Point mutations (A1, 5A, and W51W57) of pilA affected the structural details of G. sulfurreducens pilus, i.e., diameter, axial rise, rotation angle, and subunits per turn. Furthermore, they also influenced the density of aromatic rings and the distance between the proximal carbon atoms in neighboring aromatic rings, which probably impacted the conductivity of the G. sulfurreducens pilus [16,55,56]. The density of aromatic rings in each of the two pili (WT and W51W57) is nearly ten times higher than the previously calculated value [16]. The distances between the proximal carbon atoms in the neighboring aromatic rings for the WT and W51W57 pilus were nearly half of the smallest value of the previous results [16]. These results may help to explain why the previous study thought the inter-aromatic pathway is an unlikely mechanism of conductivity [16]. Furthermore, the conductivity was found to not only be positively correlated with the aromatic ring density, but also positively correlated with the distance between the neighboring aromatic rings for G. sulfurreducens pili. These relationships suggest that aromatic amino acids probably play a decisive role in the magnitude of conductivity. The three aromatic amino acids (F1, F24, and Y27) in each N-terminus of the WT and W51W57 pilin were arranged in a potential electrically conductive geometry in which they were sufficiently close (around 3.5 Å) to account for the experimentally observed metallic-like conductivity of the pili [3,14]. Therefore, the mechanism by which the G. sulfurreducens pilus transfers electrons along pili is attributed, at least in part, to the conjugation of aromatic amino acids (π–π interactions).
Electrostatic interactions are important in protein folding, stability, flexibility, and function [57]. Close-range electrostatic interactions (salt bridges) are formed by spatial pairs of oppositely charged residues in protein structures. Furthermore, for the pilus, the salt bridge in the region in which many aromatic residues exist could affect the configuration of aromatic residues and their reduction potential and then influence the rates of electron transfer [3,58]. Here, we found a co-localization relationship between aromatic and charged amino acids in each of the four G. sulfurreducens pili models. When compared with the WT, the salt bridges of the A1, 5A, and W51W57 pili were changed, indicating that the point mutations affected the local electrostatic environment around the aromatic contacts, and could therefore influence the aromatic configuration to promote efficient electron transfer, resulting in different conductivity of pili.
Furthermore, an approach for exploring the potential electrically conductive pathway for the Geobacter pilus was provided in this study. According to this approach, point mutations were found to affect the arrangement of aromatic residues in the Geobacter pilus, resulting in different potential electrically conductive pathways and conductivities for the WT pilus and its mutants. The distances between centroids of aromatic amino acids can also be calculated by this approach. A larger distance between centroids of aromatic amino acids resulted in a higher energy barrier that needs to be overcome to achieve electron transfer [15]. Moreover, when compared with other distances between the aromatic residues, d (F24, Y27) had the greatest value, suggesting that the highest energy barrier existed between aromatic residue F24 and Y27 for the WT and W51W57 pilus. Therefore, this result could be utilized to guide site-directed mutagenesis to decrease the highest energy barrier and improve nanowire performance.
In conclusion, the three point mutations influenced the flexibility, stability and assembly of the G. sulfurreducens pilin, resulting in different structural details of pili. Moreover, genetic substitution of an alanine for the phenylalanines (+1) in PilA (A1 mutant), the pilus subunit, resulted in assembled pili likely with poor conductivity, further indicating the importance of the local electrostatic environment and aromatic amino acids in electron transport. The conductivity of W51W57 pili became excellent, not only because genetic substitutions increased the conjugation of amino acids, but also because they changed the structural details of the pilus, resulting in higher aromatic ring densities and a smaller distance between neighboring aromatic rings compared to the WT pilus. The number of physico-chemical interactions in W51W57 pilus was greater than that of wild-type pilus. Salt-bridge is most commonly observed to contribute stability to the conformation of proteins. Especially, there were more salt bridges in W51W57 pilus, compared to that of WT pilus. The residues are not only linked through physical contacts, but also through correlated motions. The correlated motions of the W51W57 mutant were stronger than those of the WT. Therefore, more physico-chemical interactions and stronger correlated motions could be resulted in pilins assembled more tightly together. Comparison of the structures and corresponding conductivities of the WT pilus with its mutant pili revealed that the aromatic amino acids and local electrostatic environment around them probably play critical roles in the process of extracellular electron transfer to the G. sulfurreducens pilus. The work described herein provides new insight into the biological synthesis of high conductivity nontoxic electronic materials.

Supplementary Materials

The following are available online at www.mdpi.com/2073-4352/8/1/10/s1, Figure S1: RMSD landscapes of four types of pilins for the PPI, Helix, and Loop domain. (A) The three-dimensional structure of PilA. Three domains, i.e., PPI, Helix, and Loop, are highlighted with red, blue, and yellow, respectively. The aromatic amino acid sites are shown using location and sphere. Time series of RMSDs of backbone Cα atoms to the initial structures for the (B) PPI, (C) Helix, and (D) Loop domain of the wild type and its mutants are computed and plotted. Table S1: The shortest aromatic pathway for GC pili.

Acknowledgments

This research was sponsored by the National Natural Science Foundation of China (No. 61472078), the Key Research and Development Program of Jiangsu Province (BE2016002-3), and the Open Research Fund of the State Key Laboratory of Bioelectronics, Southeast University, China.

Author Contributions

Chuanjun Shu designed the study, carried out the study, and drafted the manuscript; Ke Xiao designed the study and helped write the manuscript; Xiao Sun conceived of the study and was the lead writer of the manuscript. All of the authors have read and approved the final manuscript.

Conflicts of Interest

The authors declare that they have no conflicts of interest regarding the publication of this paper.

References

  1. Reguera, G.; McCarthy, K.D.; Mehta, T.; Nicoll, J.S.; Tuominen, M.T.; Lovley, D.R. Extracellular electron transfer via microbial nanowires. Nature 2005, 435, 1098–1101. [Google Scholar] [CrossRef] [PubMed]
  2. Adhikari, R.Y.; Malvankar, N.S.; Tuominen, M.T.; Lovley, D.R. Conductivity of individual Geobacter pili. RSC Adv. 2016, 6, 8363–8366. [Google Scholar] [CrossRef]
  3. Malvankar, N.S.; Vargas, M.; Nevin, K.; Tremblay, P.L.; Evans-Lutterodt, K.; Nykypanchuk, D.; Martz, E.; Tuominen, M.T.; Lovley, D.R. Structural basis for metallic-like conductivity in microbial nanowires. mBio 2015, 6, e00084-15. [Google Scholar] [CrossRef] [PubMed]
  4. Bond, D.R.; Lovley, D.R. Electricity production by Geobacter sulfurreducens attached to electrodes. Appl. Environ. Microbiol. 2003, 69, 1548–1555. [Google Scholar] [CrossRef] [PubMed]
  5. Leang, C.; Qian, X.; Mester, T.; Lovley, D.R. Alignment of the c-type cytochrome OmcS along pili of Geobacter sulfurreducens. Appl. Environ. Microb. 2010, 76, 4080–4084. [Google Scholar] [CrossRef] [PubMed]
  6. Reardon, P.N.; Mueller, K.T. Structure of the type IVa major pilin from the electrically conductive bacterial nanowires of Geobacter sulfurreducens. J. Biol. Chem. 2013, 288, 29260–29266. [Google Scholar] [CrossRef] [PubMed]
  7. Craig, L.; Pique, M.E.; Tainer, J.A. Type IV pilus structure and bacterial pathogenicity. Nat. Rev. Microbiol. 2004, 2, 363–378. [Google Scholar] [CrossRef] [PubMed]
  8. Xiao, K.; Malvankar, N.S.; Shu, C.; Martz, E.; Lovley, D.R.; Sun, X. Low energy atomic models suggesting a pilus structure that could account for electrical conductivity of Geobacter sulfurreducens pili. Sci. Rep. UK 2016, 6, 23385. [Google Scholar] [CrossRef] [PubMed]
  9. Qin, N.; Shen, Y.; Yang, X.; Su, L.; Tang, R.; Li, W.; Wang, M. Site-directed mutagenesis under the direction of in silico protein docking modeling reveals the active site residues of 3-ketosteroid-Delta1-dehydrogenase from Mycobacterium neoaurum. World. J. Microb. Biotechnol. 2017, 33, 146. [Google Scholar] [CrossRef] [PubMed]
  10. Shih, C.; Museth, A.K.; Abrahamsson, M.; Blanco-Rodriguez, A.M.; Di Bilio, A.J.; Sudhamsu, J.; Crane, B.R.; Ronayne, K.L.; Towrie, M., Jr.; Vlcek, A.; et al. Tryptophan-accelerated electron flow through proteins. Science 2008, 320, 1760–1762. [Google Scholar] [CrossRef] [PubMed]
  11. Vargas, M.; Malvankar, N.S.; Tremblay, P.L.; Leang, C.; Smith, J.A.; Patel, P.; Snoeyenbos-West, O.; Nevin, K.P.; Lovley, D.R. Aromatic amino acids required for pili conductivity and long-range extracellular electron transport in Geobacter sulfurreducens. mBio 2013, 4, e105–e113. [Google Scholar] [CrossRef]
  12. Tan, Y.; Adhikari, R.Y.; Malvankar, N.S.; Pi, S.; Ward, J.E.; Woodard, T.L.; Nevin, K.P.; Xia, Q.; Tuominen, M.T.; Lovley, D.R. Synthetic biological protein nanowires with high conductivity. Small 2016, 12, 4481–4485. [Google Scholar] [CrossRef] [PubMed]
  13. Richter, L.V.; Sandler, S.J.; Weis, R.M. Two isoforms of Geobacter sulfurreducens PilA have distinct roles in pilus biogenesis, cytochrome localization, extracellular electron transfer, and biofilm formation. J. Bacteriol. 2012, 194, 2551–2563. [Google Scholar] [CrossRef] [PubMed]
  14. Shu, C.; Xiao, K.; Yan, Q.; Sun, X. Comparative analysis of Type IV pilin in Desulfuromonadales. Front. Microbiol. 2016, 7, 2080. [Google Scholar] [CrossRef] [PubMed]
  15. Shu, C.; Xiao, K.; Cao, C.; Ding, D.; Sun, X. Predicting and interpreting the structure of type IV pilus of electricigens by molecular dynamics simulations. Molecules 2017, 8, 1342. [Google Scholar] [CrossRef] [PubMed]
  16. Yan, H.; Chuang, C.; Zhugayevych, A.; Tretiak, S.; Dahlquist, F.W.; Bazan, G.C. Inter-aromatic distances in Geobacter sulfurreducens pili relevant to biofilm charge transport. Adv. Mater. 2015, 27, 1908–1911. [Google Scholar] [CrossRef] [PubMed]
  17. Xiao, K.; Shu, C.; Yan, Q.; Sun, X. Predicting homogeneous pilus structure from monomeric data and sparse constraints. BioMed Res. Int. 2015, 2015, 817134. [Google Scholar] [CrossRef] [PubMed]
  18. Case, D.A.; Darden, T.A.; Cheatham, T.E., III; Simmerling, C.L.; Wang, J.; Duke, R.E.; Luo, R.; Walker, R.C.; Zhang, W.; Merz, K.M.; et al. Amber 12; University of California: San Francisco, CA, USA, 2012. [Google Scholar]
  19. Tan, Z.; Spasic, A.; Mathews, D.H. 96 Benchmark of Amber ff12SB force field by comparison of estimated hairpin loop folding stabilities to experiments. J. Biomol. Struct. Dyn. 2015, 33 (Suppl. 1), 61–62. [Google Scholar] [CrossRef] [PubMed]
  20. Chakraborty, S.; Phu, M.; de Morais, T.P.; Nascimento, R.; Goulart, L.R.; Rao, B.J.; Asgeirsson, B.; Dandekar, A.M. The PDB database is a rich source of alpha-helical anti-microbial peptides to combat disease causing pathogens. F1000Research 2014, 3, 295. [Google Scholar] [CrossRef] [PubMed]
  21. McKay, T.; Hart, K.; Bernstein, H.; Tedla-Boyd, W.; Craig, P. Protein function prediction using ProMOL and PyMOL. FASEB J. 2014, 1, 722–725. [Google Scholar]
  22. Choudhury, C.; Deva, P.U.; Sastry, G.N. Molecular dynamics investigation of the active site dynamics of mycobacterial cyclopropane synthase during various stages of the cyclopropanation process. J. Struct. Biol. 2014, 187, 38–48. [Google Scholar] [CrossRef] [PubMed]
  23. Needham, P.J.; Bhuiyan, A.; Walker, R.C. Extension of the AMBER molecular dynamics software to Intel’s Many Integrated Core (MIC) architecture. Comput. Phys. Commun. 2016, 201, 95–105. [Google Scholar] [CrossRef]
  24. Feliciano, G.T.; Steidl, R.J.; Reguera, G. Structural and functional insights into the conductive pili of Geobacter sulfurreducens revealed in molecular dynamics simulations. Phys. Chem. Chem. Phys. 2015, 17, 22217–22226. [Google Scholar] [CrossRef] [PubMed]
  25. Roe, D.R.; Cheatham, T.R. PTRAJ and CPPTRAJ: Software for processing and analysis of molecular dynamics trajectory data. J. Chem. Theory. Comput. 2013, 9, 3084–3095. [Google Scholar] [CrossRef] [PubMed]
  26. Zhao, X.M.; Xia, L.Q.; Yang, X.P.; Peng, X.Y. Flexibility analysis of bacillus thuringiensis Cry1Aa. Biomed. Environ. Sci. 2015, 28, 634–641. [Google Scholar] [PubMed]
  27. Liu, M.; Wang, L.; Sun, X.; Zhao, X. Investigating the impact of Asp181 point mutations on interactions between PTP1B and phosphotyrosine substrate. Sci. Rep. 2014, 4, 5095. [Google Scholar] [CrossRef] [PubMed]
  28. Unni, S.; Huang, Y.; Hanson, R.M.; Tobias, M.; Krishnan, S.; Li, W.W.; Nielsen, J.E.; Baker, N.A. Web servers and services for electrostatics calculations with APBS and PDB2PQR. J. Comput. Chem. 2011, 32, 1488–1491. [Google Scholar] [CrossRef] [PubMed]
  29. Craig, L.; Volkmann, N.; Arvai, A.S.; Pique, M.E.; Yeager, M.; Egelman, E.H.; Tainer, J.A. Type IV pilus structure by cryo-electron microscopy and crystallography: Implications for pilus assembly and functions. Mol. Cell 2006, 23, 651–662. [Google Scholar] [CrossRef] [PubMed]
  30. Dolinsky, T.J.; Czodrowski, P.; Li, H.; Nielsen, J.E.; Jensen, J.H.; Klebe, G.; Baker, N.A. PDB2PQR: Expanding and upgrading automated preparation of biomolecular structures for molecular simulations. Nucleic Acids Res. 2007, 35, W522–W525. [Google Scholar] [CrossRef] [PubMed]
  31. Humphrey, W.; Dalke, A.; Schulten, K. VMD: Visual molecular dynamics. J. Mol. Graph. 1996, 14, 27–28, 33–38. [Google Scholar] [CrossRef]
  32. Piovesan, D.; Minervini, G.; Tosatto, S.C.E. The RING 2.0 web server for high quality residue interaction networks. Nucleic Acids Res. 2016, 44, W367–W374. [Google Scholar] [CrossRef] [PubMed]
  33. Ihlen, E.A.F. Introduction to multifractal detrended fluctuation analysis in Matlab. Front. Physiol. 2012, 3, 141. [Google Scholar] [CrossRef] [PubMed]
  34. Dijkstra, E.W. A note on two problems in connexion with graphs. Numer. Math. 1959, 1, 269–271. [Google Scholar] [CrossRef]
  35. DeLano, W.L. Pymol: An open-source molecular graphics tool. CCP4 Newsl. Protein Crystallogr. 2002, 40, 82–92. [Google Scholar]
  36. Liu, C. Modifications of steepest descent method and conjugate gradient method against noise for ill-posed linear systems. Commun. Numer. Anal. 2012, 2012, cna-00115. [Google Scholar] [CrossRef]
  37. Mandell, A.J.; Selz, K.A.; Shlesinger, M.F. Transformational homologies in amino acid sequences suggest memberships in protein families. J. Stat. Phys. 1998, 93, 673–697. [Google Scholar] [CrossRef]
  38. Yiqing, H.; Qiang, L.X.; Jia, Z. Using evolutionary couplings to optimize dimer prediction with Rosetta SymDock. In Proceedings of the 2013 IEEE International Conference on Bioinformatics and Biomedicine (BIBM), Shanghai, China, 18–21 December 2013; IEEE: Piscataway, NJ, USA, 2013; pp. 65–68. [Google Scholar]
  39. Leaver-Fay, A.; Tyka, M.; Lewis, S.M.; Lange, O.F.; Thompson, J.; Jacak, R.; Kaufman, K.; Renfrew, P.D.; Smith, C.A.; Sheffler, W.; et al. ROSETTA3: An object-oriented software suite for the simulation and design of macromolecules. Methods Enzymol. 2011, 487, 545–574. [Google Scholar] [PubMed]
  40. Das, R.; Baker, D. Macromolecular modeling with Rosetta. Annu. Rev. Biochem. 2008, 77, 363–382. [Google Scholar] [CrossRef] [PubMed]
  41. Kumar, S.; Nussinov, R. Salt bridge stability in monomeric proteins. J. Mol. Biol. 1999, 293, 1241–1255. [Google Scholar] [CrossRef] [PubMed]
  42. Bosshard, H.R.; Marti, D.N.; Jelesarov, I. Protein stabilization by salt bridges: Concepts, experimental approaches and clarification of some misunderstandings. J. Mol. Recognit. 2004, 17. [Google Scholar] [CrossRef] [PubMed]
  43. Min, B.K.; Cheng, S.A.; Logan, B.E. Electricity generation using membrane and salt bridge microbial fuel cells. Water Res. 2005, 39, 1675–1686. [Google Scholar] [CrossRef] [PubMed]
  44. Campos, M.; Cisneros, D.A.; Nivaskumar, M.; Francetic, O. The type II secretion system - a dynamic fiber assembly nanomachine. Res. Microbiol. 2013, 164, 545–555. [Google Scholar] [CrossRef] [PubMed]
  45. Dobbins, S.E.; Lesk, V.I.; Sternberg, M.J.E. Insights into protein flexibility: The relationship between normal modes and conformational change upon protein-protein docking. Proc. Natl. Acad. Sci. USA 2008, 105, 10390–10395. [Google Scholar] [CrossRef] [PubMed]
  46. Giltner, C.L.; Nguyen, Y.; Burrows, L.L. Type IV pilin proteins: Versatile molecular modules. Microbiol. Mol. Biol. Rev. 2012, 76, 740–772. [Google Scholar] [CrossRef] [PubMed]
  47. Fuglestad, B.; Gasper, P.M.; McCammon, J.A.; Markwick, P.R.L.; Komives, E.A. Correlated motions and residual frustration in thrombin. J. Phys. Chem. B 2013, 117, 12857–12863. [Google Scholar] [CrossRef] [PubMed]
  48. Malvankar, N.S.; Vargas, M.; Nevin, K.P.; Franks, A.E.; Leang, C.; Kim, B.C.; Inoue, K.; Mester, T.; Covalla, S.F.; Johnson, J.P.; et al. Tunable metallic-like conductivity in microbial nanowire networks. Nat. Nanotechnol. 2011, 6, 573–579. [Google Scholar] [CrossRef] [PubMed]
  49. Donald, J.E.; Kulp, D.W.; DeGrado, W.F. Salt bridges: Geometrically specific, designable interactions. Proteins 2011, 79, 898–915. [Google Scholar] [CrossRef] [PubMed]
  50. Hunter, C.A.; Sanders, J. The nature of pi-pi interactions. J. Am. Chem. Soc. 1990, 112, 5525–5534. [Google Scholar] [CrossRef]
  51. Sinnokrot, M.O.; Sherrill, C.D. Highly accurate coupled cluster potential energy curves for the benzene dimer: Sandwich, T-shaped, and parallel-displaced configurations. J. Phys. Chem. A 2004, 108, 10200–10207. [Google Scholar] [CrossRef]
  52. Page, C.C.; Moser, C.C.; Chen, X.; Dutton, P.L. Natural engineering principles of electron tunnelling in biological oxidation-reduction. Nature 1999, 402, 47–52. [Google Scholar] [CrossRef] [PubMed]
  53. Aas, F.E.; Winther-Larsen, H.C.; Wolfgang, M.; Frye, S.; Lovold, C.; Roos, N.; van Putten, J.P.M.; Koomey, M. Substitutions in the N-terminal alpha helical spine of Neisseria gonorrhoeae pilin affect type IV pilus assembly, dynamics and associated functions. Mol. Microbiol. 2007, 63, 69–85. [Google Scholar] [CrossRef] [PubMed]
  54. Stoodley, C.J.; Limperopoulos, C. Structure-function relationships in the developing cerebellum: Evidence from early-life cerebellar injury and neurodevelopmental disorders. Semin. Fetal Neonatal Med. 2016, 21, 356–364. [Google Scholar] [CrossRef] [PubMed]
  55. Tan, Y.; Adhikari, R.Y.; Malvankar, N.S.; Ward, J.E.; Woodard, T.L.; Nevin, K.P.; Lovley, D.R. Expressing the Geobacter metallireducens PilA in Geobacter sulfurreducens yields pili with exceptional conductivity. mBio 2017, 8, e2203–e2216. [Google Scholar] [CrossRef] [PubMed]
  56. Walker, D.J.F.; Adhikari, R.Y.; Holmes, D.E.; Ward, J.E.; Woodard, T.L.; Nevin, K.P.; Lovley, D.R. Electrically conductive Pili from pilin genes of phylogenetically diverse microorganisms. ISME J. 2017, 2017, 141. [Google Scholar]
  57. Kumar, S.; Nussinov, R. Close-range electrostatic interactions in proteins. ChemBioChem. 2002, 3, 604–617. [Google Scholar] [CrossRef]
  58. Martinez, C.R.; Iverson, B.L. Rethinking the term “pi-stacking”. Chem. Sci. 2012, 3, 2191–2201. [Google Scholar] [CrossRef]
Crystals 08 00010 g001 550
Figure 1. Workflow for exploring the potential electron transfer pathway. (A) Box and arrow represent data and action. The black dots on the edge and inside of an aromatic ring represent the coordinates of the C atom from an aromatic ring and the coordinates of the centroid for aromatic rings, respectively. (B) An example of the potential electron transfer pathway for the pilus. F1p and F1p+N represent the start and end nodes of a potential electrically conductive pathway. N represents the number of subunits in one turn. The rows indicate the direction of electronic transmission. The grey cartoon is utilized to show the structure of the pilus. The different colors represent the different aromatic amino acids.
Figure 1. Workflow for exploring the potential electron transfer pathway. (A) Box and arrow represent data and action. The black dots on the edge and inside of an aromatic ring represent the coordinates of the C atom from an aromatic ring and the coordinates of the centroid for aromatic rings, respectively. (B) An example of the potential electron transfer pathway for the pilus. F1p and F1p+N represent the start and end nodes of a potential electrically conductive pathway. N represents the number of subunits in one turn. The rows indicate the direction of electronic transmission. The grey cartoon is utilized to show the structure of the pilus. The different colors represent the different aromatic amino acids.
Crystals 08 00010 g001
Crystals 08 00010 g002 550
Figure 2. Electrostatic properties of the G. sulfurreducens pilin and its mutants. The values of electrostatic potential are color-coded. The structures of the pilins are displayed in the rainbow colored cartoons. The main differences between mutations and WT values are circled in red.
Figure 2. Electrostatic properties of the G. sulfurreducens pilin and its mutants. The values of electrostatic potential are color-coded. The structures of the pilins are displayed in the rainbow colored cartoons. The main differences between mutations and WT values are circled in red.
Crystals 08 00010 g002
Crystals 08 00010 g003 550
Figure 3. The landscapes of interfacial energy score versus rotation angle for four pili. (A–D) show the landscapes of the WT, A1, 5A and W51W57 pili. Each dark cyan dot represents one model. These red circles are utilized to highlight the converged troughs. (E–H) indicate the landscapes of the 15 lowest energy models in the biggest cluster for each of the ranges in the WT pilus and its mutants.
Figure 3. The landscapes of interfacial energy score versus rotation angle for four pili. (A–D) show the landscapes of the WT, A1, 5A and W51W57 pili. Each dark cyan dot represents one model. These red circles are utilized to highlight the converged troughs. (E–H) indicate the landscapes of the 15 lowest energy models in the biggest cluster for each of the ranges in the WT pilus and its mutants.
Crystals 08 00010 g003
Crystals 08 00010 g004 550
Figure 4. Helical parameters of models for Geobacter sulfurreducens pilus and its mutants. (A–D) represent the landscapes of diameter, axial rise, rotation angle and subunits per turn for each of the four types of pili (WT, A1, 5A, and W51W57 pilus), respectively. Black, red, blue, and magenta are utilized to highlight the corresponding values for the WT, A1, 5A, and W51W57 models, respectively.
Figure 4. Helical parameters of models for Geobacter sulfurreducens pilus and its mutants. (A–D) represent the landscapes of diameter, axial rise, rotation angle and subunits per turn for each of the four types of pili (WT, A1, 5A, and W51W57 pilus), respectively. Black, red, blue, and magenta are utilized to highlight the corresponding values for the WT, A1, 5A, and W51W57 models, respectively.
Crystals 08 00010 g004
Crystals 08 00010 g005 550
Figure 5. RMSF of residues for wild-type pilin and its mutants. Black, blue, green, and red represent fluctuations of residues for WT, A1, 5A, and W51W57 mutants, respectively.
Figure 5. RMSF of residues for wild-type pilin and its mutants. Black, blue, green, and red represent fluctuations of residues for WT, A1, 5A, and W51W57 mutants, respectively.
Crystals 08 00010 g005
Crystals 08 00010 g006 550
Figure 6. Cross-correlation of Cα atoms during the 20 ns of MD simulation. The extent of correlated motions and anti-correlated motions are color-coded. (A–D) represent the whole landscape of correlation motions for WT, A1, 5A, and W51W57 pilin, respectively. (E–H) show the landscape of strong correlation motions for WT, A1, 5A, and W51W57 pilin, respectively.
Figure 6. Cross-correlation of Cα atoms during the 20 ns of MD simulation. The extent of correlated motions and anti-correlated motions are color-coded. (A–D) represent the whole landscape of correlation motions for WT, A1, 5A, and W51W57 pilin, respectively. (E–H) show the landscape of strong correlation motions for WT, A1, 5A, and W51W57 pilin, respectively.
Crystals 08 00010 g006
Crystals 08 00010 g007 550
Figure 7. The spatial distribution of aromatic and charged residues. In (A–D), the rainbow cartoon, yellow spheres, red sticks, and blue sticks represent the structure of the pilus, aromatic amino acids, positively charged amino acids, and negatively charged amino acids, respectively.
Figure 7. The spatial distribution of aromatic and charged residues. In (A–D), the rainbow cartoon, yellow spheres, red sticks, and blue sticks represent the structure of the pilus, aromatic amino acids, positively charged amino acids, and negatively charged amino acids, respectively.
Crystals 08 00010 g007
Crystals 08 00010 g008 550
Figure 8. The residue interaction networks for each of the four pili. Different colored nodes represent the different types of residue. The different colors on the edge represent different interaction types. The legend is in the middle of the picture. HBOND, VDW, PPSTACK, and IONIC represent hydrogen bonds, Van der Waals forces, π–π interactions, and ionic bonds. (A–D) represent the residue interaction network for the WT, A1, 5A, and W51W57 pilus, respectively.
Figure 8. The residue interaction networks for each of the four pili. Different colored nodes represent the different types of residue. The different colors on the edge represent different interaction types. The legend is in the middle of the picture. HBOND, VDW, PPSTACK, and IONIC represent hydrogen bonds, Van der Waals forces, π–π interactions, and ionic bonds. (A–D) represent the residue interaction network for the WT, A1, 5A, and W51W57 pilus, respectively.
Crystals 08 00010 g008
Crystals 08 00010 g009 550
Figure 9. The continuous chain of aromatic rings in four pili. (A–D) represent the aromatic amino acid chains of the WT, W51W57, A1, and 5A pilus, respectively. Red, green, yellow, and orange spheres indicate the spatial distributions of F1, F24, Y27, and F51 in aromatic amino acid chains, respectively. The gray cartoons represent the structures of the four pili.
Figure 9. The continuous chain of aromatic rings in four pili. (A–D) represent the aromatic amino acid chains of the WT, W51W57, A1, and 5A pilus, respectively. Red, green, yellow, and orange spheres indicate the spatial distributions of F1, F24, Y27, and F51 in aromatic amino acid chains, respectively. The gray cartoons represent the structures of the four pili.
Crystals 08 00010 g009
Crystals 08 00010 g010 550
Figure 10. The distances between proximal carbon atoms in neighboring aromatic rings. (A–D) represent the distances between aromatic rings of aromatic amino acid chains for the four types of pili. As shown in the legends, different color points indicate different distances between the proximal carbon atoms in neighboring aromatic rings.
Figure 10. The distances between proximal carbon atoms in neighboring aromatic rings. (A–D) represent the distances between aromatic rings of aromatic amino acid chains for the four types of pili. As shown in the legends, different color points indicate different distances between the proximal carbon atoms in neighboring aromatic rings.
Crystals 08 00010 g010
Table
Table 1. The inter- and intra-chain salt bridges.
Table 1. The inter- and intra-chain salt bridges.
PilusBefore ✶After-Assembly
Intra ✶✶Inter ⌑-Common ⌑⌑Inter-Different ⌑⌑Number ✦
WT048E-44K028R-60E1, 60E-28R2, 5E-41R3, 41R-5E421
A1048E-44K30K-53D1, 53D-30K2039
5A048E-44K28R-39D1, 39D-28R253D-30K3, 30K-53D438
W51W57048E-44K39D-41R1, 41R-39D2, 44K-60E3, 60E-44K45E-41R5, 41R-5E641
✶ Before represents the number of salt bridges in one subunit prior to assembly. ✶✶ Intra indicates the salt bridges in the subunit of the assembled structure of pili. ⌑ Inter indicates two oppositely charged residues from different subunits can form a salt bridge. ⌑⌑ Inter-common and inter-different illustrate the same and different salt bridges of the 15 lowest energy models for each type of pili, respectively. ✦ Number shows the number of salt bridges in 15 models (consisting of 21 subunits) for each type of pili. The subscript number implies how many subunits are involved in salt bridges for a subunit.
Table
Table 2. The average density of aromatic ring in one symmetric unit of pilus.
Table 2. The average density of aromatic ring in one symmetric unit of pilus.
N ⟡D (Å)R (Å)ρ (1021 cm−3)Conductivity (μs·cm−1)
WT631.610.74.295 [48]
A1530.310.91.91UN ✦
5A132.67.20.57WT*1/100 [11]
W51W57823.610.512.02500*WT [12]
⟡ N represents the number of aromatic rings in one subunit. ✦ UN indicates the conductivity of the pilus was not obtained from a biological experiment.
Table
Table 3. The potential electrically conductive pathways for each of four pili.
Table 3. The potential electrically conductive pathways for each of four pili.
PathwayDistance (Å)
WT(F1p, Y27p+4, F24p+4, F1p+1, Y27p+5, F24p+5, F1p+2, Y27p+6, F24p+6, F1p+3, Y27p+7, F24p+7, F1p+4, Y27p+8, F24p+8, F1p+5, Y27p+9, F24p+9, F1p+6)(5.3, 6.2, 4.3, 5.3, 6.2, 4.3, 5.3, 6.2, 4.3, 5.3, 6.2, 4.3, 5.3, 6.2, 4.3, 5.3, 6.2, 4.3)
W51W57(F1p, Y27p+4, F24p+4, F1p+1, Y27p+5, F24p+5, F1p+2, Y27p+6, F24p+6, F1p+3, Y27p+7, F24p+7, F1p+4, Y27p+8, F24p+8, F1p+5, Y27p+9, F24p+9, F1p+6)(5.1, 6.0, 3.7, 5.1, 6.0, 3.7, 5.1, 6.0, 3.7, 5.1, 6.0, 3.7, 5.1, 6.0, 3.7, 5.1, 6.0, 3.7)
A1(Y27p, F24p, F51p+4, Y27p+1, F24p+1, F51p+5, Y27p+2, F24p+2, F51p+6, Y27p+3)(6.7, 10.3, 4.6, 6.7, 10.3, 4.6, 6.7, 10.3, 4.6)
5A(F1p, F1p+1, F1p+2, F1p+3)(11.3, 11.3, 11.3)

Share and Cite

MDPI and ACS Style

Shu, C.; Xiao, K.; Sun, X. Structural Basis for the Influence of A1, 5A, and W51W57 Mutations on the Conductivity of the Geobacter sulfurreducens Pili. Crystals 2018, 8, 10. https://doi.org/10.3390/cryst8010010

AMA Style

Shu C, Xiao K, Sun X. Structural Basis for the Influence of A1, 5A, and W51W57 Mutations on the Conductivity of the Geobacter sulfurreducens Pili. Crystals. 2018; 8(1):10. https://doi.org/10.3390/cryst8010010

Chicago/Turabian Style

Shu, Chuanjun, Ke Xiao, and Xiao Sun. 2018. "Structural Basis for the Influence of A1, 5A, and W51W57 Mutations on the Conductivity of the Geobacter sulfurreducens Pili" Crystals 8, no. 1: 10. https://doi.org/10.3390/cryst8010010

APA Style

Shu, C., Xiao, K., & Sun, X. (2018). Structural Basis for the Influence of A1, 5A, and W51W57 Mutations on the Conductivity of the Geobacter sulfurreducens Pili. Crystals, 8(1), 10. https://doi.org/10.3390/cryst8010010

Note that from the first issue of 2016, this journal uses article numbers instead of page numbers. See further details here.

Article Metrics

Back to TopTop