Sigma-Holes in Battery Materials Using Iso-Electrostatic Potential Surfaces
Abstract
1. Introduction
2. Methodology
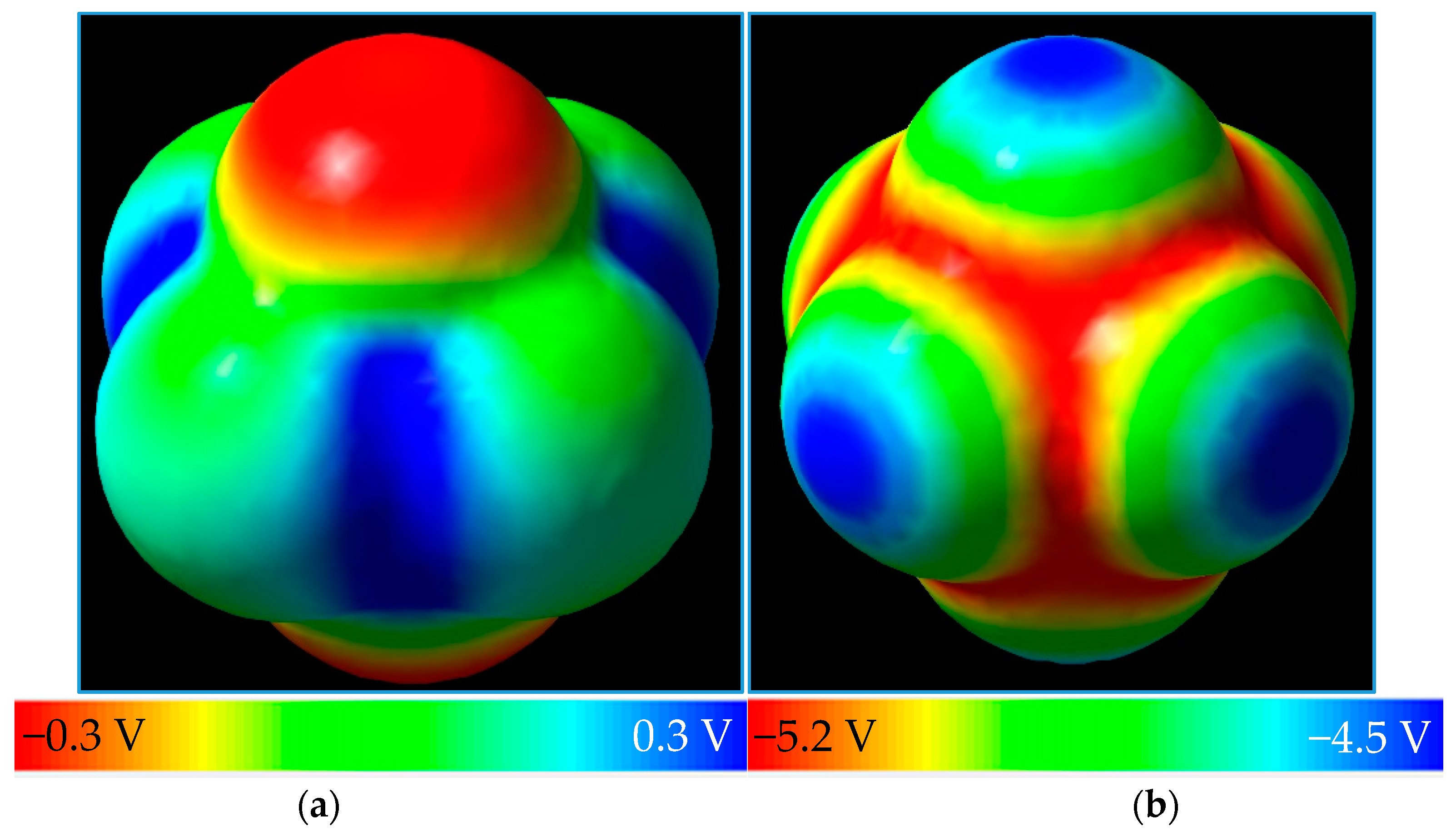
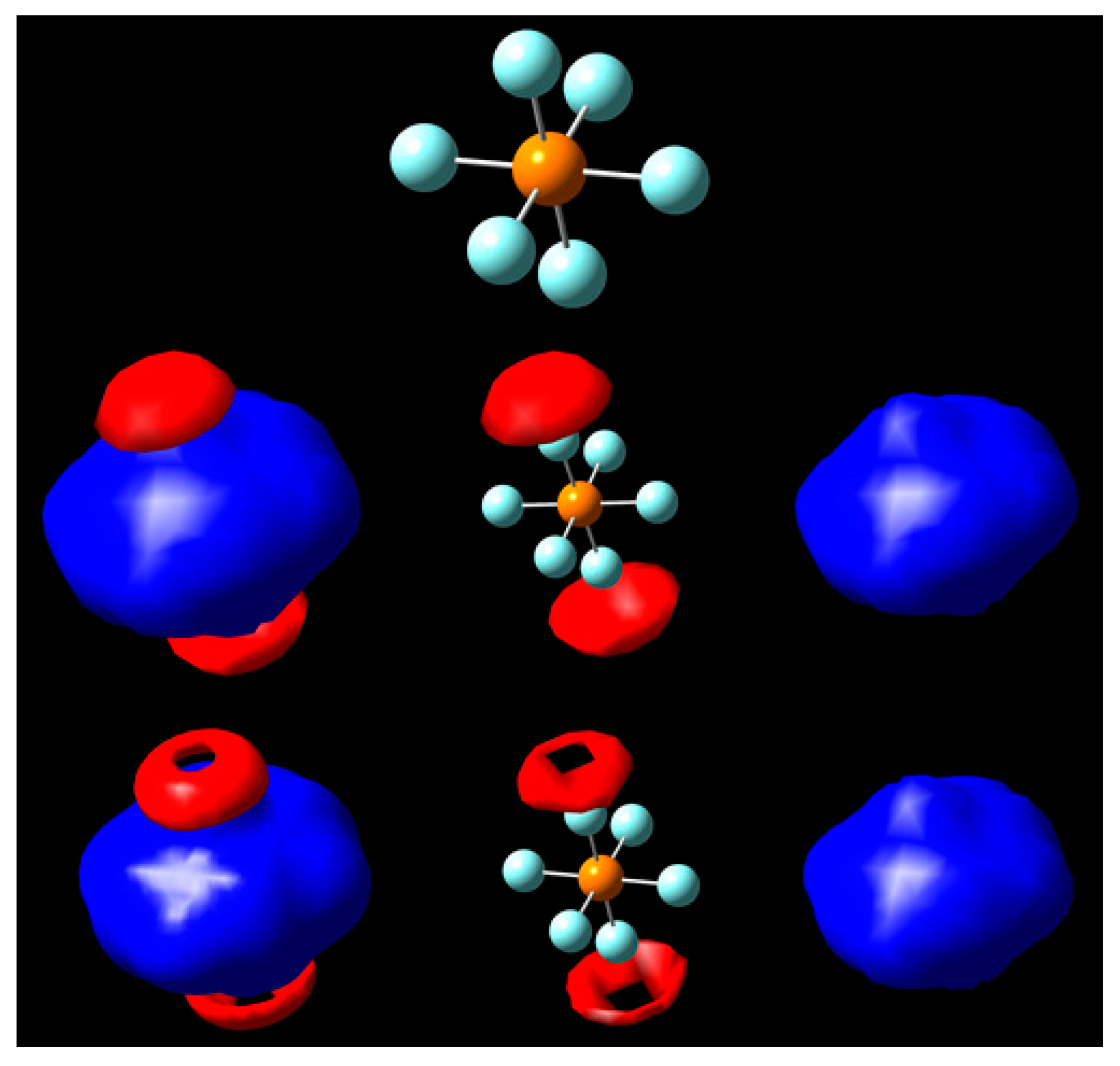
3. Results and Discussion
4. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Chen, H.; Qiu, X.; Zhu, W.; Hagenmuller, P. Synthesis and High Rate Properties of Nanoparticled Lithium Cobalt Oxides as the Cathode Material for Lithium-Ion Battery. Electrochem. Commun. 2002, 4, 488–491. [Google Scholar] [CrossRef]
- Kumar, N.; Seminario, J.M. Lithium-Ion Model Behavior in an Ethylene Carbonate Electrolyte Using Molecular Dynamics. J. Phys. Chem. C 2016, 120, 16322–16332. [Google Scholar] [CrossRef]
- Jorn, R.; Kumar, R.; Abraham, D.P.; Voth, G.A. Atomistic Modeling of the Electrode–Electrolyte Interface in Li-Ion Energy Storage Systems: Electrolyte Structuring. J. Phys. Chem. C 2013, 117, 3747–3761. [Google Scholar] [CrossRef]
- Tao, T.; Lu, S.; Fan, Y.; Lei, W.; Huang, S.; Chen, Y. Anode Improvement in Rechargeable Lithium-Sulfur Batteries. Adv. Mater. 2017, 29. [Google Scholar] [CrossRef] [PubMed]
- Cheng, X.-B.; Zhang, R.; Zhao, C.-Z.; Zhang, Q. Toward Safe Lithium Metal Anode in Rechargeable Batteries: A Review. Chem. Rev. 2017, 117, 10403–10473. [Google Scholar] [CrossRef] [PubMed]
- Jana, A.; García, R.E. Lithium Dendrite Growth Mechanisms in Liquid Electrolytes. Nano Energy 2017, 41, 552–565. [Google Scholar] [CrossRef]
- Wu, B.; Lochala, J.; Taverne, T.; Xiao, J. The Interplay between Solid Electrolyte Interface (Sei) and Dendritic Lithium Growth. Nano Energy 2017, 40, 34–41. [Google Scholar] [CrossRef]
- Benitez, L.; Seminario, J.M. Electron Transport and Electrolyte Reduction in the Solid-Electrolyte Interphase of Rechargeable Lithium Ion Batteries with Silicon Anodes. J. Phys. Chem. C 2016, 120, 17978–17988. [Google Scholar] [CrossRef]
- Soto, F.A.; Martinez de la Hoz, J.M.; Seminario, J.M.; Balbuena, P.B. Modeling Solid-Electrolyte Interfacial Phenomena in Silicon Anodes. Curr. Opin. Chem. Eng. 2016, 13, 179–185. [Google Scholar] [CrossRef]
- Ramos-Sanchez, G.; Soto, F.A.; Martinez de la Hoz, J.M.; Liu, Z.; Mukherjee, P.P.; El-Mellouhi, F.; Seminario, J.M.; Balbuena, P.B. Computational Studies of Interfacial Reactions at Anode Materials: Initial Stages of the Solid-Electrolyte-Interphase Layer Formation. J. Electrochem. Energy Conver. Storage 2016, 13, 031002. [Google Scholar] [CrossRef]
- Soto, F.A.; Ma, Y.; Martinez de la Hoz, J.M.; Seminario, J.M.; Balbuena, P.B. Formation and Growth Mechanisms of Solid-Electrolyte Interphase Layers in Rechargeable Batteries. Chem. Mater. 2015, 27, 7990–8000. [Google Scholar] [CrossRef]
- Benitez, L.; Cristancho, D.; Seminario, J.M.; Martinez de la Hoz, J.M.; Balbuena, P.B. Electron Transfer through Solid-Electrolyte-Interphase Layers Formed on Si Anodes of Li-Ion Batteries. Electrochim. Acta 2014, 140, 250–257. [Google Scholar] [CrossRef]
- Kamaya, N.; Homma, K.; Yamakawa, Y.; Hirayama, M.; Kanno, R.; Yonemura, M.; Kamiyama, T.; Kato, Y.; Hama, S.; Kawamoto, K.; et al. A Lithium Superionic Conductor. Nat. Mater. 2011, 10, 682–686. [Google Scholar] [CrossRef] [PubMed]
- Stallworth, P.E.; Fontanella, J.J.; Wintersgill, M.C.; Scheidler, C.D.; Immel, J.J.; Greenbaum, S.G.; Gozdz, A.S. Nmr, Dsc and High Pressure Electrical Conductivity Studies of Liquid and Hybrid Electrolytes. J. Power Sources 1999, 81–82, 739–747. [Google Scholar] [CrossRef]
- Liu, Z.; Fu, W.; Payzant, E.A.; Yu, X.; Wu, Z.; Dudney, N.J.; Kiggans, J.; Hong, K.; Rondinone, A.J.; Liang, C. Anomalous High Ionic Conductivity of Nanoporous β-Li3PS4. J. Am. Chem. Soc. 2013, 135, 975–978. [Google Scholar] [CrossRef] [PubMed]
- Yubuchi, S.; Teragawa, S.; Aso, K.; Tadanaga, K.; Hayashi, A.; Tatsumisago, M. Preparation of High Lithium-Ion Conducting Li6PS5Cl Solid Electrolyte from Ethanol Solution for All-Solid-State Lithium Batteries. J. Power Sources 2015, 293, 941–945. [Google Scholar] [CrossRef]
- Rangasamy, E.; Liu, Z.; Gobet, M.; Pilar, K.; Sahu, G.; Zhou, W.; Wu, H.; Greenbaum, S.; Liang, C. An Iodide-Based Li7P2S8I Superionic Conductor. J. Am. Chem. Soc. 2015, 137, 1384–1387. [Google Scholar] [CrossRef] [PubMed]
- Kang, J.; Han, B. First-Principles Characterization of the Unknown Crystal Structure and Ionic Conductivity of Li7P2S8I as a Solid Electrolyte for High-Voltage Li Ion Batteries. J. Phys. Chem. Lett. 2016, 7, 2671–2675. [Google Scholar] [CrossRef] [PubMed]
- Brinck, T.; Murray, J.S.; Politzer, P. Surface Electrostatic Potentials of Halogenated Methanes as Indicators of Directional Intermolecular Interactions. Int. J. Quantum Chem 1992, 44, 57–64. [Google Scholar] [CrossRef]
- Murray, J.S.; Paulsen, K.; Politzer, P. Molecular Surface Electrostatic Potentials in the Analysis of Non-Hydrogen-Bonding Noncovalent Interactions. Proc. Indian Acad. Sci. (Chem. Sci.) 1994, 106, 267–275. [Google Scholar]
- Ibrahim, M.A.A. Molecular Mechanical Study of Halogen Bonding in Drug Discovery. J. Comput. Chem. 2011, 32, 2564–2574. [Google Scholar] [CrossRef] [PubMed]
- Clark, T.; Hennemann, M.; Murray, J.S.; Politzer, P. Halogen Bonding: The σ-Hole. J. Mol. Model. 2007, 13, 291–296. [Google Scholar] [CrossRef] [PubMed]
- Politzer, P.; Murray, J.S.; Clark, T. Halogen Bonding and Other σ-Hole Interactions: A Perspective. Phys. Chem. Chem. Phys. 2013, 15, 11178–11189. [Google Scholar] [CrossRef] [PubMed]
- Kolář, M.H.; Hobza, P. Computer Modeling of Halogen Bonds and Other σ-Hole Interactions. Chem. Rev. 2016, 116, 5155–5187. [Google Scholar] [CrossRef] [PubMed]
- Metrangolo, P.; Murray, J.S.; Pilati, T.; Politzer, P.; Resnati, G.; Terraneo, G. The Fluorine Atom as a Halogen Bond Donor, Viz. A Positive Site. CrystEngComm 2011, 13, 6593–6596. [Google Scholar] [CrossRef]
- Metrangolo, P.; Murray, J.S.; Pilati, T.; Politzer, P.; Resnati, G.; Terraneo, G. Fluorine-Centered Halogen Bonding: A Factor in Recognition Phenomena and Reactivity. Cryst. Growth Des. 2011, 11, 4238–4246. [Google Scholar] [CrossRef]
- Politzer, P.; Laurence, P.R.; Jayasuriya, K. Molecular Electrostatic Potentials: An Effective Tool for the Elucidation of Biochemical Phenomena. Environ. Health Perspect. 1985, 61, 191–202. [Google Scholar] [CrossRef] [PubMed]
- Otero-Navas, I.; Seminario, J.M. Molecular Electrostatic Potentials of DNA Base-Base Pairing and Mispairing. J. Mol. Model. 2012, 18, 91–101. [Google Scholar] [CrossRef] [PubMed]
- Cristancho, D.; Seminario, J.M. Polypeptides in Alpha-Helix Conformation Perform as Diodes. J. Chem. Phys. 2010, 132, 065102. [Google Scholar] [CrossRef] [PubMed]
- Jauregui, L.A.; Seminario, J.M. A DNA Sensor for Sequencing and Mismatches Based on Electron Transport through Watson-Crick and Non-Watson-Crick Base Pairs. IEEE Sens. J. 2008, 8, 803–814. [Google Scholar] [CrossRef]
- Salazar-Salinas, K.; Seminario, J.M. Energetics and Vibronics Analyses of the Enzymatic Coupled Electron-Proton Transfer from NfsA Nitroreductase to Trinitrotoluene. IEEE Trans. Nanotechnol. 2010, 9, 543–553. [Google Scholar] [CrossRef]
- Tour, J.M.; Kozaki, M.; Seminario, J.M. Molecular Scale Electronics: A Synthetic/Computational Approach to Digital Computing. J. Am. Chem. Soc. 1998, 120, 8486–8493. [Google Scholar] [CrossRef]
- Seminario, J.M.; Ma, Y.; Tarigopula, V. The Nanocell: A Chemically Assembled Molecular Electronic Circuit. IEEE Sens. J. 2006, 6, 1614–1626. [Google Scholar] [CrossRef]
- Seminario, J.M.; Yan, L. Cascade Configuration of Logical Gates Processing Information Encoded in Molecular Potentials. Int. J. Quantum Chem 2007, 107, 754–761. [Google Scholar] [CrossRef]
- Norma, L.R.; Jorge, M.S. Single Molecule Detection Using Graphene Electrodes. J. Phys. B At. Mol. Opt. Phys. 2010, 43, 115101. [Google Scholar]
- Rangel, N.L.; Seminario, J.M. Nanomicrointerface to Read Molecular Potentials into Current-Voltage Based Electronics. J. Chem. Phys. 2008, 128, 114711. [Google Scholar] [CrossRef] [PubMed]
- Kresse, G.; Hafner, J. Ab Initio. Phys. Rev. B 1993, 47, 558–561. [Google Scholar] [CrossRef]
- Kresse, G.; Hafner, J. Ab Initio. Phys. Rev. B 1994, 49, 14251–14269. [Google Scholar] [CrossRef]
- Kresse, G.; Furthmüller, J. Efficiency of Ab-Initio Total Energy Calculations for Metals and Semiconductors Using a Plane-Wave Basis Set. Comput. Mater. Sci. 1996, 6, 15–50. [Google Scholar] [CrossRef]
- Frisch, M.J.; Trucks, G.W.; Schlegel, H.B.; Scuseria, G.E.; Robb, M.A.; Cheeseman, J.R.; Scalmani, G.; Barone, V.; Mennucci, B.; Petersson, G.A.; et al. Gaussian 09; Gaussian, Inc.: Wallingford, UK, 2009. [Google Scholar]
- Blöchl, P.E. Projector Augmented-Wave Method. Phys. Rev. B 1994, 50, 17953–17979. [Google Scholar] [CrossRef]
- Kresse, G.; Joubert, D. From Ultrasoft Pseudopotentials to the Projector Augmented-Wave Method. Phys. Rev. B 1999, 59, 1758–1775. [Google Scholar] [CrossRef]
- Andersen, O.K. Linear Methods in Band Theory. Phys. Rev. B 1975, 12, 3060–3083. [Google Scholar] [CrossRef]
- Perdew, J.P.; Burke, K.; Ernzerhof, M. Generalized Gradient Approximation Made Simple. Phys. Rev. Lett. 1996, 77, 3865–3868. [Google Scholar] [CrossRef] [PubMed]
- Becke, A.D. A New Mixing of Hartree-Fock and Local Density-Functional Theories. J. Chem. Phys. 1993, 98, 1372–1377. [Google Scholar] [CrossRef]
- Perdew, J. Unified Theory of Exchange and Correlation Beyond the Local Density Approximation. In Electronic Structure of Solids; Ziesche, P., Eschrig, H., Eds.; Akademie Verlag: Berlin, Germangy, 1991; pp. 11–20. [Google Scholar]
- Petersson, G.A.; Bennett, A.; Tensfeldt, T.G.; Al-Laham, M.A.; Shirley, W.A.; Mantzaris, J. A Complete Basis Set Model Chemistry. I. The Total Energies of Closed-Shell Atoms and Hydrides of the First-Row Elements. J. Chem. Phys. 1988, 89, 2193–2218. [Google Scholar] [CrossRef]
- Petersson, G.A.; Al-Laham, M.A. A Complete Basis Set Model Chemistry. II. Open-Shell Systems and the Total Energies of the First-Row Atoms. J. Chem. Phys. 1991, 94, 6081–6090. [Google Scholar] [CrossRef]
- Mooibroek, T.J.; Gamez, P. Halogen···Phenyl Supramolecular Interactions in the Solid State: Hydrogen Versus Halogen Bonding and Directionality. CrystEngComm 2013, 15, 1802–1805. [Google Scholar] [CrossRef]
- Swierczynski, D.; Luboradzki, R.; Dolgonos, G.; Lipkowski, J.; Schneider, H.-J. Non-Covalent Interactions of Organic Halogen Compounds with Aromatic Systems—Analyses of Crystal Structure Data. Eur. J. Org. Chem. 2005, 2005, 1172–1177. [Google Scholar] [CrossRef]
- Kölmel, C.; Palm, G.; Ahlrichs, R.; Bär, M.; Boldyrev, A.I. Ab Initio Study of Structure, Stability and Ionization Potentials of the Anions Pf6− and P2f11−. Chem. Phys. Lett. 1990, 173, 151–156. [Google Scholar] [CrossRef]
- Ponce, V.; Galvez-Aranda, D.E.; Seminario, J.M. Analysis of a Li-Ion Nanobattery with Graphite Anode Using Molecular Dynamics Simulations. J. Phys. Chem. C 2017, 121, 12959–12971. [Google Scholar] [CrossRef]
- Galvez-Aranda, D.E.; Ponce, V.; Seminario, J.M. Molecular Dynamics Simulations of the First Charge of a Li-Ion-Si-Anode Nanobattery. J. Mol. Model. 2017, 23, 120. [Google Scholar] [CrossRef] [PubMed]
- Bauzá, A.; Mooibroek, T.J.; Frontera, A. The Bright Future of Unconventional σ/Π-Hole Interactions. ChemPhysChem 2015, 16, 2496–2517. [Google Scholar] [CrossRef] [PubMed]
- Murray, J.S.; Lane, P.; Politzer, P. Simultaneous σ-Hole and Hydrogen Bonding by Sulfur- and Selenium-Containing Heterocycles. Int. J. Quantum Chem. 2008, 108, 2770–2781. [Google Scholar] [CrossRef]
- Liu, Z.; Balbuena, P.B.; Mukherjee, P.P. Hole Polaron Diffusion in the Final Discharge Product of Lithium—Sulfur Batteries. J. Phys. Chem. C 2017, 121, 17169–17175. [Google Scholar] [CrossRef]
- Liu, Z.; Balbuena, P.B.; Mukherjee, P.P. Revealing Charge Transport Mechanisms in Li2S2 for Li-Sulfur Batteries. J. Phys. Chem. Lett. 2017, 8, 1324–1330. [Google Scholar] [CrossRef] [PubMed]












© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Roman-Vicharra, C.; Franco-Gallo, F.; Alaminsky, R.J.; Galvez-Aranda, D.E.; Balbuena, P.B.; Seminario, J.M. Sigma-Holes in Battery Materials Using Iso-Electrostatic Potential Surfaces. Crystals 2018, 8, 33. https://doi.org/10.3390/cryst8010033
Roman-Vicharra C, Franco-Gallo F, Alaminsky RJ, Galvez-Aranda DE, Balbuena PB, Seminario JM. Sigma-Holes in Battery Materials Using Iso-Electrostatic Potential Surfaces. Crystals. 2018; 8(1):33. https://doi.org/10.3390/cryst8010033
Chicago/Turabian StyleRoman-Vicharra, Cristhian, Franz Franco-Gallo, Ryan J. Alaminsky, Diego E. Galvez-Aranda, Perla B. Balbuena, and Jorge M. Seminario. 2018. "Sigma-Holes in Battery Materials Using Iso-Electrostatic Potential Surfaces" Crystals 8, no. 1: 33. https://doi.org/10.3390/cryst8010033
APA StyleRoman-Vicharra, C., Franco-Gallo, F., Alaminsky, R. J., Galvez-Aranda, D. E., Balbuena, P. B., & Seminario, J. M. (2018). Sigma-Holes in Battery Materials Using Iso-Electrostatic Potential Surfaces. Crystals, 8(1), 33. https://doi.org/10.3390/cryst8010033




