Cellular Automaton Modeling of Silicon Facet Formation during Directional Solidification
Abstract
:1. Introduction
2. Materials and Methods
2.1. LBM Model
2.2. CA Model
2.2.1. Model for the Growth
2.2.2. Model for the Capture
2.3. The Physical Parameters of Silicon Melt
3. Results and Discussion
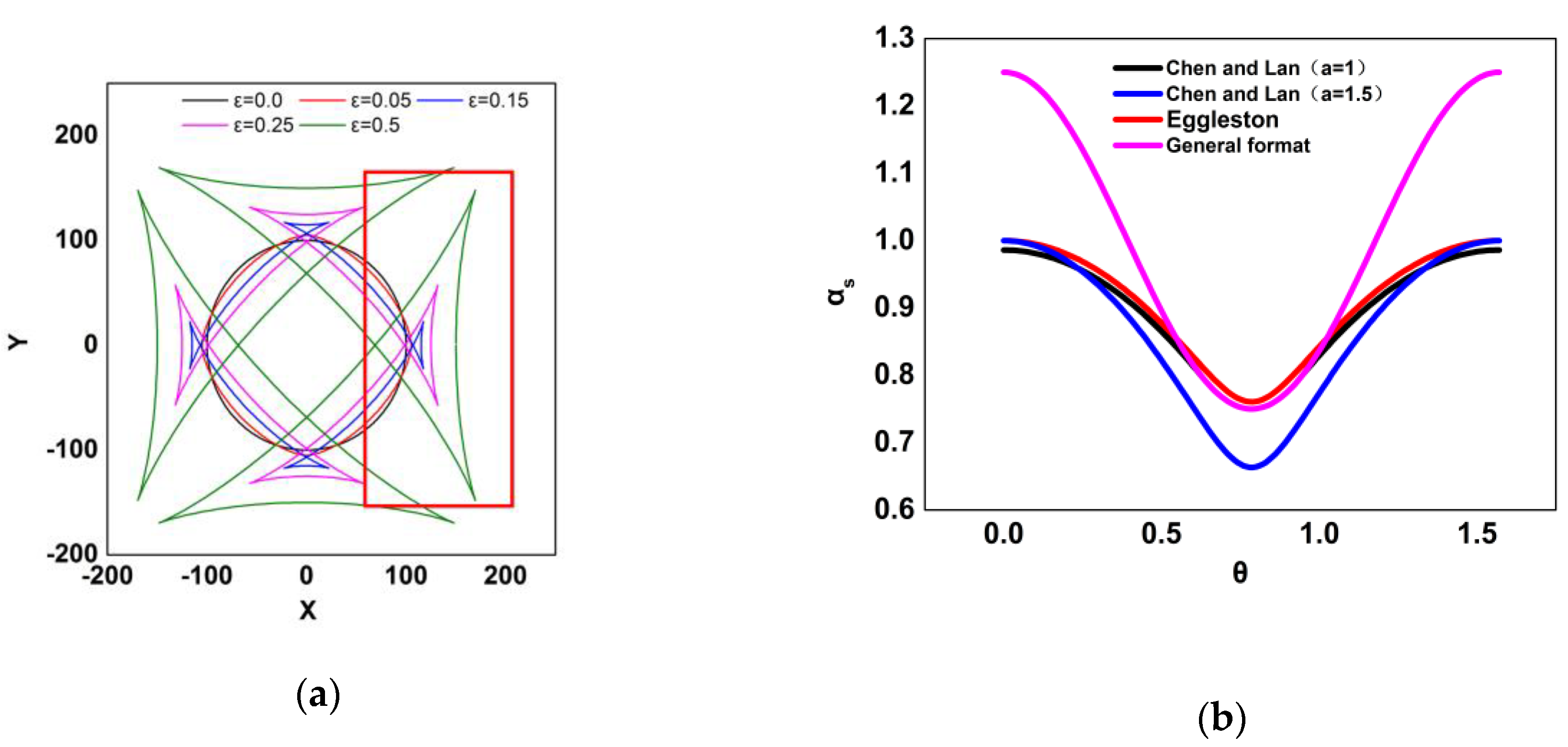
3.1. Anisotropy of Interfacial Free Energy
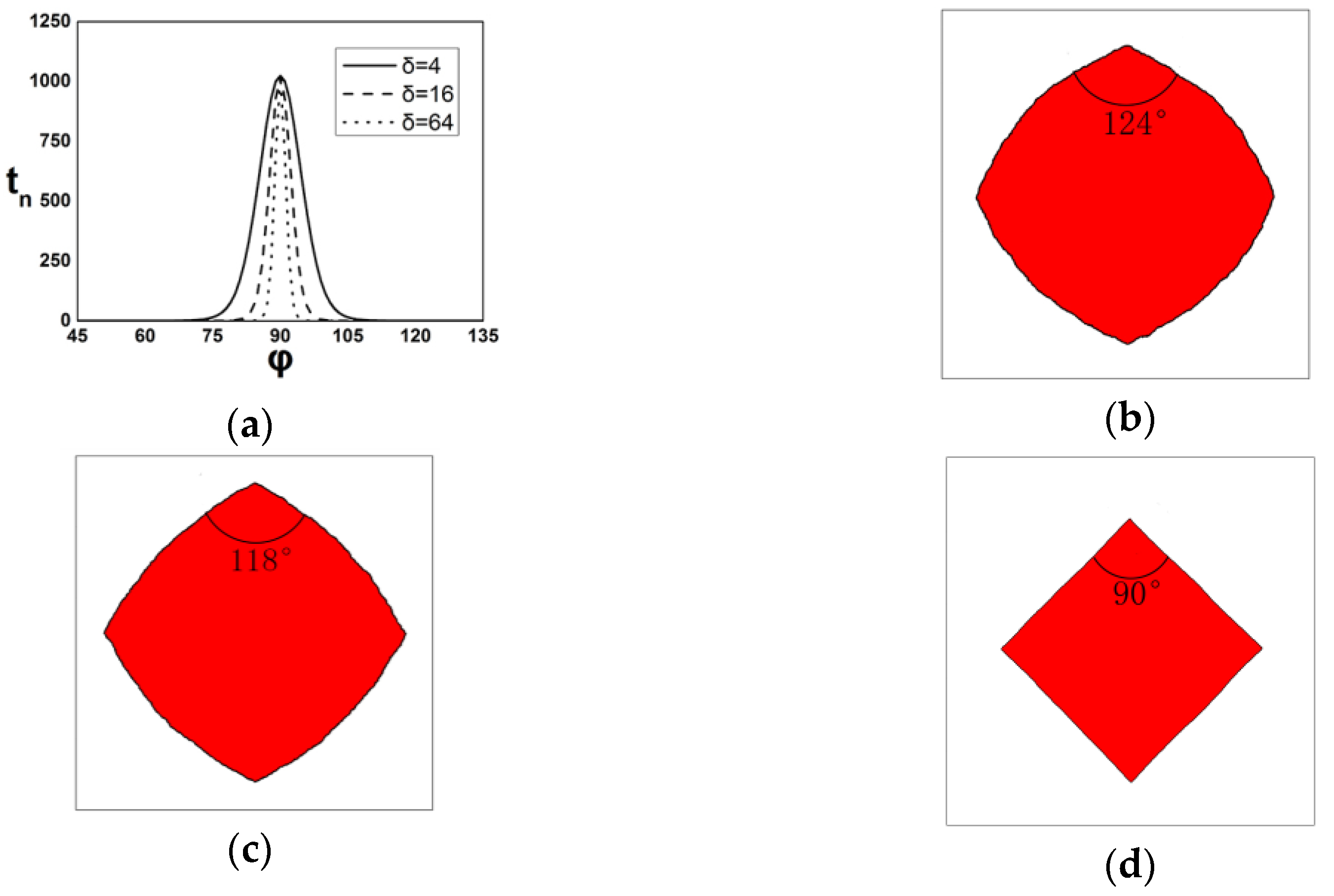
3.2. Anisotropy of Kinetics
3.2.1. Effect of
3.2.2. Effect of
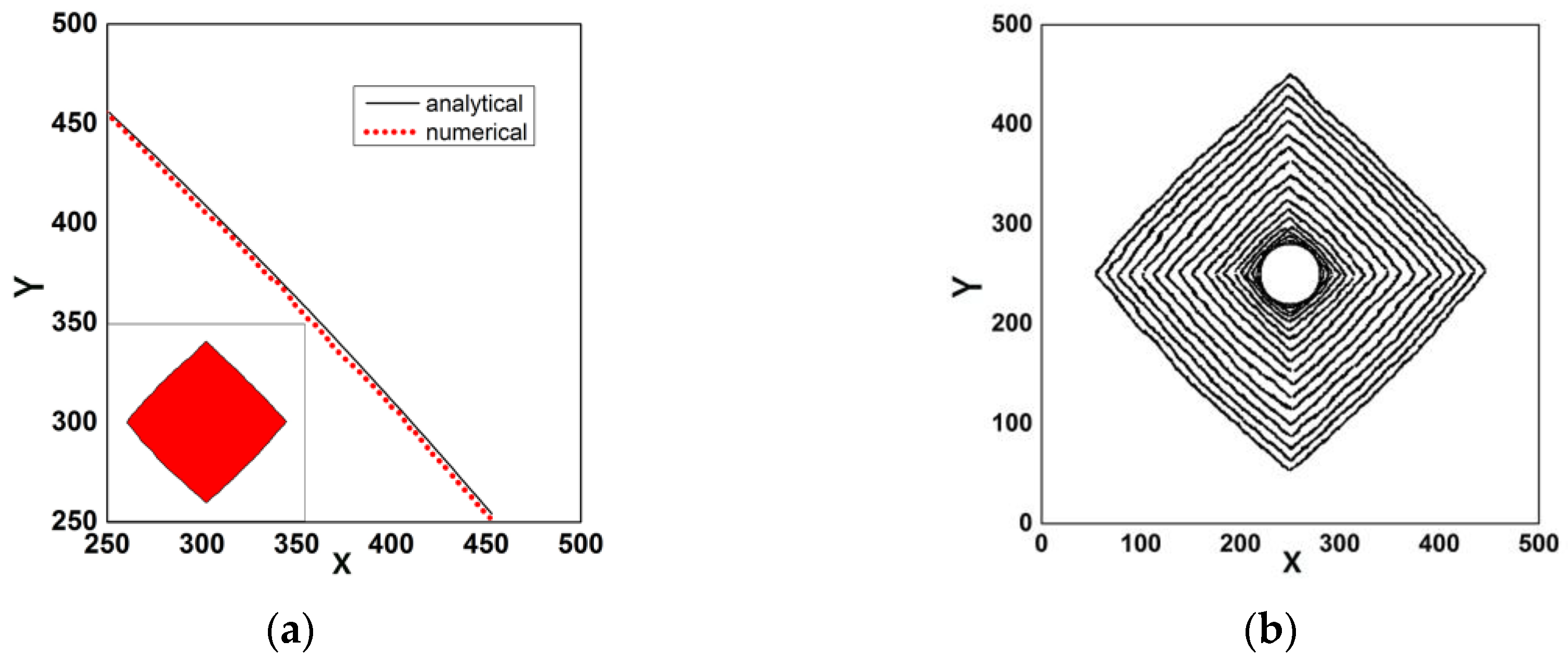
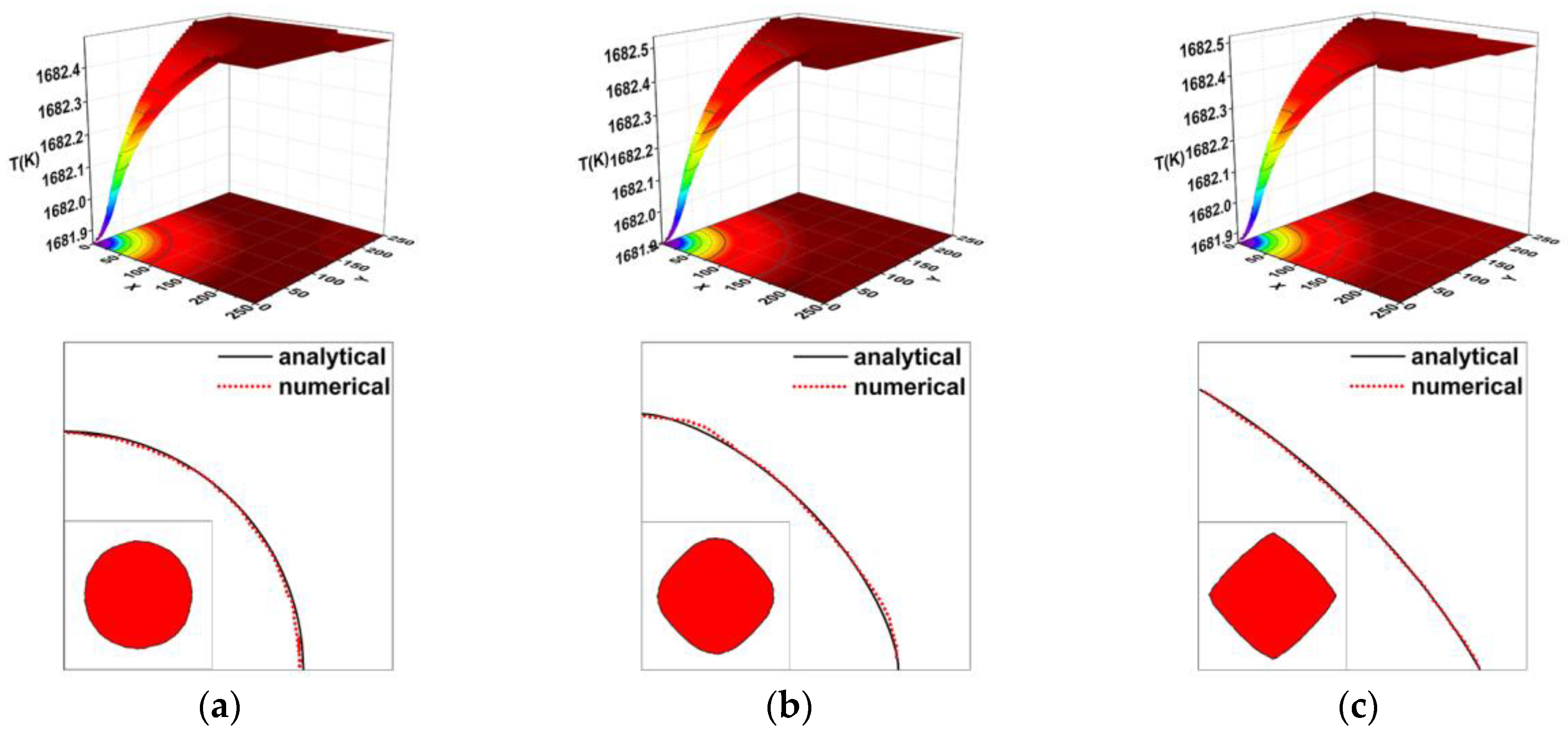
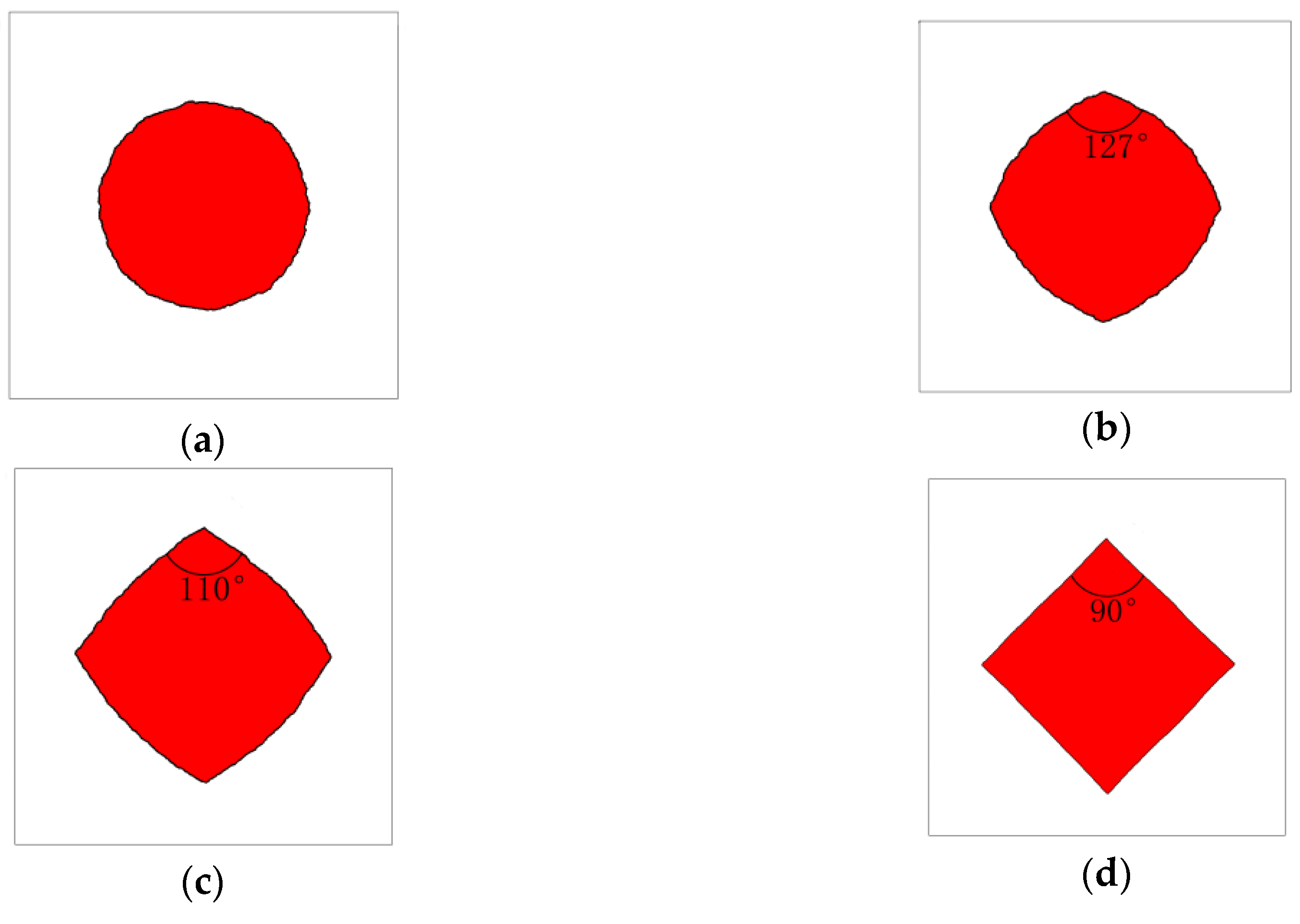
3.3. Simulations for Facet Formation
4. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Jackson, K.A. Crystal growth kinetics. Mater. Sci. Eng. 1984, 65, 7–13. [Google Scholar] [CrossRef]
- Tokairin, M.; Fujiwara, K.; Kutsukake, K.; Kodama, H.; Usami, N.; Nakajima, K. Pattern formation mechanism of a periodically faceted interface during crystallization ofsi. J. Cryst. Growth 2010, 312, 3670–3674. [Google Scholar] [CrossRef]
- Fujiwara, K.; Gotoh, R.; Yang, X.B.; Koizumi, H.; Nozawa, J.; Uda, S. Morphological transformation of a crystal–melt interface during unidirectional growth of silicon. Acta Mater. 2011, 59, 4700–4708. [Google Scholar] [CrossRef]
- Lin, H.K.; Chen, H.Y.; Lan, C.W. Phase field modeling of facet formation during directional solidification of silicon film. J. Cryst. Growth 2014, 385, 134–139. [Google Scholar] [CrossRef]
- Rappaz, M. Modelling of microstructure formation in solidification processes. Int. Mater. Rev. 1989, 34, 93–124. [Google Scholar] [CrossRef]
- Wang, W.; Lee, P.D.; Mclean, M. A model of solidification microstructures in nickel-based superalloys: Predicting primary dendrite spacing selection. Acta Mater. 2003, 51, 2971–2987. [Google Scholar] [CrossRef]
- Yang, X.L.; Dong, H.B.; Wang, W.; Lee, P.D. Microscale simulation of stray grain formation in investment cast turbine blades. Mater. Sci. Eng. A Struct. Mater. 2004, 386, 129–139. [Google Scholar] [CrossRef]
- Sun, D.; Zhu, M.; Pan, S.; Raabe, D. Lattice boltzmann modeling of dendritic growth in a forced melt convection. Acta Mater. 2009, 57, 1755–1767. [Google Scholar] [CrossRef]
- Eggleston, J.J.; Mcfadden, G.B.; Voorhees, P.W. A phase-field model for highly anisotropic interfacial energy. Physica D 2001, 150, 91–103. [Google Scholar] [CrossRef]
- Uehara, T.; Sekerka, R.F. Phase field simulations of faceted growth for strong anisotropy of kinetic coefficient. J. Cryst. Growth 2003, 254, 251–261. [Google Scholar] [CrossRef]
- Weinstein, O.; Brandon, S. Dynamics of partially faceted melt/crystal interfaces i: Computational approach and single step–source calculations. J. Cryst. Growth 2004, 268, 299–319. [Google Scholar] [CrossRef]
- Lian, Q.; Liu, W.; Li, R.; Yan, W.; Liu, C.; Zhang, Y.; Wang, L.; Chen, H. Numerical simulation of multi-crystalline silicon crystal growth using a macro–micro coupled method during the directional solidification process. Appl. Sci. 2016, 7, 21. [Google Scholar] [CrossRef]
- Zhang, Y.X.; Li, R.; Wang, J.; Wang, L.X.; Yan, W.B.; Liu, C.C.; Chen, H.J. Cellular automaton modeling of the transition of multi-crystalline silicon from a planar faceted front to equiaxed growth. Appl. Sci. 2017, 7, 13. [Google Scholar]
- Eshraghi, M.; Jelinek, B.; Felicelli, S.D. Large-scale three-dimensional simulation of dendritic solidification using lattice boltzmann method. JOM 2015, 67, 1786–1792. [Google Scholar] [CrossRef]
- Sun, D.K.; Zhu, M.F.; Pan, S.Y.; Yang, C.R.; Raabe, D. Lattice boltzmann modeling of dendritic growth in forced and natural convection. Comput. Math. Appl. 2011, 61, 3585–3592. [Google Scholar] [CrossRef]
- Pan, S.; Zhu, M. A three-dimensional sharp interface model for the quantitative simulation of solutal dendritic growth. Acta Mater. 2010, 58, 340–352. [Google Scholar] [CrossRef]
- Wei, L.; Lin, X.; Wang, M.; Huang, W. A cellular automaton model for the solidification of a pure substance. Appl. Phys. A 2010, 103, 123–133. [Google Scholar] [CrossRef]
- Fujiwara, K.; Obinata, Y.; Ujihara, T.; Usami, N.; Sazaki, G.; Nakajima, K. Grain growth behaviors of polycrystalline silicon during melt growth processes. J. Cryst. Growth 2004, 266, 441–448. [Google Scholar] [CrossRef]
- Fujiwara, K.; Obinata, Y.; Ujihara, T.; Usami, N.; Sazaki, G.; Nakajima, K. In-situ observations of melt growth behavior of polycrystalline silicon. J. Cryst. Growth 2004, 262, 124–129. [Google Scholar] [CrossRef]
- Karma, A.; Rappel, W.J. Quantitative phase-field modeling of dendritic growth in two and three dimensions. Phys. Rev. E Stat. Phys. Plasmas Fluids Relat. Interdiscip. Top. 1998, 57, 4323–4349. [Google Scholar] [CrossRef]
- Buta, D.; Asta, M.; Hoyt, J.J. Kinetic coefficient of steps at the si(111) crystal-melt interface from molecular dynamics simulations. J. Chem. Phys. 2007, 127, 5262. [Google Scholar] [CrossRef] [PubMed]
- Lei, W.; Xin, L.; Meng, W.; Huang, W. Orientation selection of equiaxed dendritic growth by three-dimensional cellular automaton model. Physica B 2012, 407, 2471–2475. [Google Scholar] [Green Version]
- Qiu, S.; Wen, S.; Fang, M.; Zhang, L.; Gan, C.; Jiang, D.; Tan, Y.; Li, J.; Luo, X. Process parameters influence on the growth rate during silicon purification by vacuum directional solidification. Vacuum 2016, 125, 40–47. [Google Scholar] [CrossRef]
- Desai, P.D. Thermodynamic properties of iron and silicon. J. Phys. Chem. Ref. Date 1986, 15, 967–983. [Google Scholar] [CrossRef]
- Burton, W.K.; Cabrera, N.; Frank, F.C. The growth of crystals and the equilibrium structure of their surfaces. Philos. Trans. R. Soc. Lond. A 1951, 243, 299–358. [Google Scholar] [CrossRef]
- Chen, G.Y.; Lan, C.W. Understanding the facet formation mechanisms of si thin-film solidification through three-dimensional phase-field modeling. J. Cryst. Growth 2017, 474, 166–170. [Google Scholar] [CrossRef]



| Property | Value |
|---|---|
| Melting temperature, | 1683 |
| Density of silicon solid, | 2330 − 2.19 × 10−2T |
| Density of silicon melt, | 2330 − 2.19 × 10−2T − 1.21 × 10−5T2 |
| Thermal diffusivity of silicon solid, | 9.6 × 10−6 |
| Thermal diffusivity of melt, | 2.134 × 10−5 |
| Molar liquid heat capacity, | 26.6 |
| Molar melting entropy, | 29.8 |
| Free interfacial energy, | 0.438 |
| Kinetic coefficient, | 2.4 × 10−4 (Estimated) |
| Molar latent heat, | 4.444 × 104 |
| Liquidus slope, | −0.7637 |
| Tip Angle Comparison | |||
|---|---|---|---|
| 1 | 4 | 10 | |
| Experiment | - | 110° | 90° |
| CA simulation | 127° | 110° | 90° |
| Tip Angle Comparison | |||
|---|---|---|---|
| 4 | 16 | 64 | |
| Phase field | 126° | 108° | 90° |
| CA simulation | 124° | 118° | 90° |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, J.; Li, R.; Li, N.; Yan, W.; Ma, W.; Chen, H. Cellular Automaton Modeling of Silicon Facet Formation during Directional Solidification. Crystals 2018, 8, 399. https://doi.org/10.3390/cryst8110399
Wang J, Li R, Li N, Yan W, Ma W, Chen H. Cellular Automaton Modeling of Silicon Facet Formation during Directional Solidification. Crystals. 2018; 8(11):399. https://doi.org/10.3390/cryst8110399
Chicago/Turabian StyleWang, Jia, Ri Li, Ning Li, Wenbo Yan, Wang Ma, and Hongjian Chen. 2018. "Cellular Automaton Modeling of Silicon Facet Formation during Directional Solidification" Crystals 8, no. 11: 399. https://doi.org/10.3390/cryst8110399
APA StyleWang, J., Li, R., Li, N., Yan, W., Ma, W., & Chen, H. (2018). Cellular Automaton Modeling of Silicon Facet Formation during Directional Solidification. Crystals, 8(11), 399. https://doi.org/10.3390/cryst8110399





