Tetramer Compound of Manganese Ions with Mixed Valence [Mn^II Mn^III Mn^IV] and Its Spatial, Electronic, Magnetic, and Theoretical Studies

Abstract

Using different spectroscopic techniques and computational calculations, we describe the structural and electromagnetic relationship that causes many interesting phenomena within a novel coordination compound with mixed valence manganese (II, III and IV) in its crystal and powder state. The novel compound [Mn^II Mn^III Mn^IV(HL)₂(H₂L)₂(H₂O)₄](NO₃)₂(H₂O) 1 was obtained with the Schiff base (E)-2-((2-hydroxybenzylidene)amine)-2-(hydroximethyl)propane-1,3-diol, (H₄L), and Mn(NO₃)₂.4H₂O. The coordination reaction was promoted by the deprotonation of the ligand by the soft base triethylamine. The paper’s main contribution is the integration of the experimental and computational studies to explain the interesting magnetic behavior that the mixed valence manganese multimetallic core shows. The results presented herein, which are rarely found for Mn(II), (III) and (IV) complexes, will contribute to the understanding of the magnetic communication generated by the valence electrons and its repercussion in the local geometry and in the overall crystalline structure.

1. Introduction

Recently, many types of multimetallic-centered compounds have been extensively studied, especially manganese coordination compounds. This is due to their scientific and technological role as magnetoresistive (GMR or CMR) materials, their biological significance as emulators of catalytic domains, among other properties [1,2,3,4,5,6,7]. Moreover, such complexes exhibit superparamagnetic-like properties as single molecule magnets (SMMs). This type of complex displays slow relaxation of magnetization and can function as a magnet below the blocking temperature [8]. The time frame for the relaxation of magnetization is thermally controlled by the spin ground state and the equatorial anisotropy, D [9,10,11]. As part of the construction of multi Mn, Co, Cu, and Fe [12] complexes with such characteristics, Schiff base ligands acting as brick units have been both widely and successfully used. Interestingly, Schiff base ligands seem to promote the formation of multicenter coordination compounds with mixed valence states due to the diversity of electronegative groups and availability for coordination [13,14,15]. On the other hand, several complexes with low nuclearity of Mn ions have been widely studied [16,17,18]. The coexistence of Mn(II) and Mn(IV) in inorganic complexes has been demonstrated. These compounds have biological relevance due to the presence of the Mn(IV) species, which participate in the oxygen-evolving complex (OEC) that is formed by four Mn ions with a mixture of Mn(III) and Mn(IV), and it is present in around fifty systems in humans [19,20]. Additionally, the photosynthetic process requires four manganese ions to perform the biocatalysis, and it has been observed that Mn(IV) is present during turnover. By these arguments, multi-manganese-centered coordination compounds represent a great area for coordination research [21]. In this work we present the synthesis, structure, electronic, magnetic, and theoretical studies of a mixed valence tetramer compound 1 with [Mn(II)-Mn(III)₂-Mn(IV)] starting from (E)-2-((2-hydroxybenzylidene)amine)-2-(hydroximethyl)propane-1,3-diol, (H₄L), and Mn(NO₃)₂.

2. Experimental Methods

2.1. Equipment and Measurements Conditions

Electronic spectra were measured with a Beckman DU Series 7000 (Beckman Coulter Inc., Brea, CA, USA) equipment on ca 10⁻⁴ M in methanolic solutions at 298 K in the 200–800 nm range. The UV-Vis spectrum in a polycrystalline sample was recorded on a Cary-5E (SpectraLab Scientific Inc., Markham, ON, Canada), Varian spectrophotometer (diffuse reflectance, 40,000–4000 cm⁻¹). A Nicolet Magna-IR 750 spectrophotometer (SpectraLab Scientific Inc., Markham, ON, Canada, Fourier transform infrared (FTIR), transmittance mode, 4000–400 cm⁻¹) was employed to obtain the infrared spectra using KBr. ESR spectra at X-band frequency were obtained with a Bruker ELEXSYS E500 II spectrometer (Bruker, Billerica, MA, USA) from 300 to 80 K on polycrystalline powder samples. The ESR analysis was performed with the simulation program of WINEPR SimFonia (Bruker, Boston, MA, USA). The magnetic g-tensor components needed for simulations were obtained from fitti56ng rigid limit ~9.4641 GHz spectra recorded at 80 K on a powder sample. The sweep width was calibrated at 7996.00 G with a center field of 3998.0 G. We referenced the g values to the common $g_e$ value of 2.0023 and then accurately determined the $g_{xx}$, $g_{yy}$ and $g_{zz}$ values relative to this $g_e$ value from the corresponding spectral splitting. The A-tensor components were obtained from fitting rigid limit ~9.4641 GHz as well. Magnetic measurements were performed in a gelatin capsule using a Physical Property Measurement System (PPMS^®, Quantum Design, Inc., San Diego, CA, USA) from Quantum Design. Measurements were performed in small magnetic fields, from 20 to 200 G, and in the range 2.8–300 K in zero-field-cooling (ZFC). Samples were analyzed using a Surface Science Instruments SSX-100 with operating pressure ~2 × 10⁻⁹ Torr and were measured at each eV in the range from 0 to 1100 eV. Monochromatic Al Kα x rays (1486.6 eV) with 1 mm diameter beam size was used. Photoelectrons were collected at a 55° emission angle. A hemispherical analyzer determined electron kinetic energy, using a pass energy of 150 V for wide/survey scans and the samples were measured at each eV in the range from 0 to 1100 eV. The quantity calculation was performed with CasaXPS software (2009, Casa Software LTD, Teignmouth, UK). Single-crystal X-ray diffraction intensities were collected at 295 K on a Stoe–Stadivari diffractometer, equipped with an Axo microfocus source (AgKα radiation, λ = 0.56083 Å) and a Dectris Pilatus-100K detector [22]. The structure was refined with the software SHELXL (GNU Lesser general public license, Copenhagen, Denmark) [23,24] and deposited with the CCDC (deposition number: CCDC-1848038).

2.2. Computational Details

The calculations were conducted with the program Gaussian 09 [25] using the density functional theory approach. The crystal structure and the proposed models were optimized initially with the functional PBE [26,27] and the basis 6–31g [28,29] with the imposed symmetry C_i. All structures proved to be minima according to frequency calculations with the exception of one model (vide infra). This model was optimized again without any symmetry constriction and a minimum was achieved according to frequency calculations. After verifying that all the resulting structures were minima, we relaxed the models with the functional B3LYP [30] and the basis set 6–31g(d) for lighter atoms and LANL2DZ [31] for Mn atoms with its corresponding effective core potentials. Afterwards, single point calculations with the same functional B3LYP and the slightly larger basis set 6–31g+(d) for lighter atoms and LANL2DZ for Mn atoms were completed for all models.

2.3. Synthesis

Compound 1 was obtained using the methodology previously described [32]. 0.4 mmol of the reported organic ligand H₄L [33] was dissolved in 5 mL of methanol at room temperature under magnetic stirring. 2.8 mmol of the soft base triethylamine was added to promote the deprotonation of the hydroxyl groups present in the ligand and stirred for 0.5 h. Then, 0.04 mmol of Mn(NO₃)₂·4H₂O, previously dissolved in 5 mL of methanol were added to immediately produce a burgundy colored solution. After 0.5 h the reaction was stopped and filtered by gravity at room temperature. The filtered liquid was left for slow evaporation to obtain crystals of 1 suitable for X-ray studies with a yield of 85% and a decomposition temperature of 215 °C. All spectroscopies were conducted from the in situ crystallized compound and were tested at least thrice for each spectroscopy and melting point. In all crystallizations, the same unit cell parameters were verified. In all the reactions made, powder was never obtained. 1 is soluble in methanol, ethanol, DMSO and DMF. Space group: P-1, a = 10.757(33) Å, b = 11.68793(3) Å, c = 13.328(4) Å, α = 98.72(2)°, β = 110.37(2)°, γ = 108.08(4)°, V = 1428.42(7) ų; UV-Vis (λ_max/ε, nm/M⁻¹cm⁻¹, methanol): 388/2317 (MLTC), 500 y 579/778 y 441 (d_xy, _xz, _yz→ d_x²_-y², d_xy, _xz, _yz→ d_z²); IR (cm⁻¹, KBr): 3273 (ν_O–H), 1604 (ν_C=N), 1301 (ν_C–O), 447 (Mn–O); NMR-¹H (500 MHz, DMSO-d₆, δ, ppm): 17.6, 6.7–7.6, 4.1–4.7, 2.99,1–1.5; ESR (crystalline powder, 300 K/90 K, and in DMSO solution, 90 K): $\raisebox{1ex}{$g_{300}$}\!\left/ \!\raisebox{-1ex}{$g_{90}$}\right.=\raisebox{1ex}{$4.9, 3.06, 2.71$}\!\left/ \!\raisebox{-1ex}{$4.8, 3.33, 2.89$}\right.$; $A=8\times {10}^{-4}$ cm⁻¹; ${\chi }_M{T}_{300K}=3.69$ cm³·mol⁻¹·K, ${\chi }_M{T}_{3K}=4.46$ cm³·mol⁻¹·K. Elemental composition by X-ray photoelectron spectroscopy (XPS): C₄₄H₆₀Mn₄N₈O₂₇, C: 40.00%, H 4.35%, N 6.42%, O 32.76%, Mn 16.48%; Calc. C 39.89%, H 4.57%, N 6.34%, O 32.61%, Mn 16.59%.

3. Results and Discussion

3.1. Synthesis

The used methodology gave a mixed-valence tetra-nuclear cluster [Mn^II Mn^III₂ Mn^IV(HL)₂(H₂L)₂(H₂O)₄](NO₃)₂ presenting an oxidation of Mn(II) to Mn(III) and Mn(IV), which were stabilized by different grades of the ligand deprotonation. The redox potential value of the Mn³⁺O₂/Mn²⁺ at pH = 8 is E = +1.79 V with ΔG = −173.28 kJ mol⁻¹, and for Mn⁴⁺O₂/Mn²⁺ at pH = 8, E = +0.99 V with ΔG = −191.81 kJ mol⁻¹, indicating both processes are spontaneous [34]. This oxidation process of Mn(II) was observed by changes in coloration from orange to burgundy. During the establishment of the synthetic methodology, the effect obtained by using different concentrations of base was studied, looking for a larger number of manganese ions in the cluster. We concluded that this parameter is not affected by the O–―H ligand deprotonation. Notably, the temperature, reaction time, and stoichiometric reactants relation were varied one parameter in each assay, and 1 was obtained in a reproducible way.

3.2. Structural Analysis

A burgundy rectangular crystal of 1 was resolved by X-ray crystallography, showing a triclinic cell with space group P-1.

Table 1. Crystallographic Refinement data of 1.

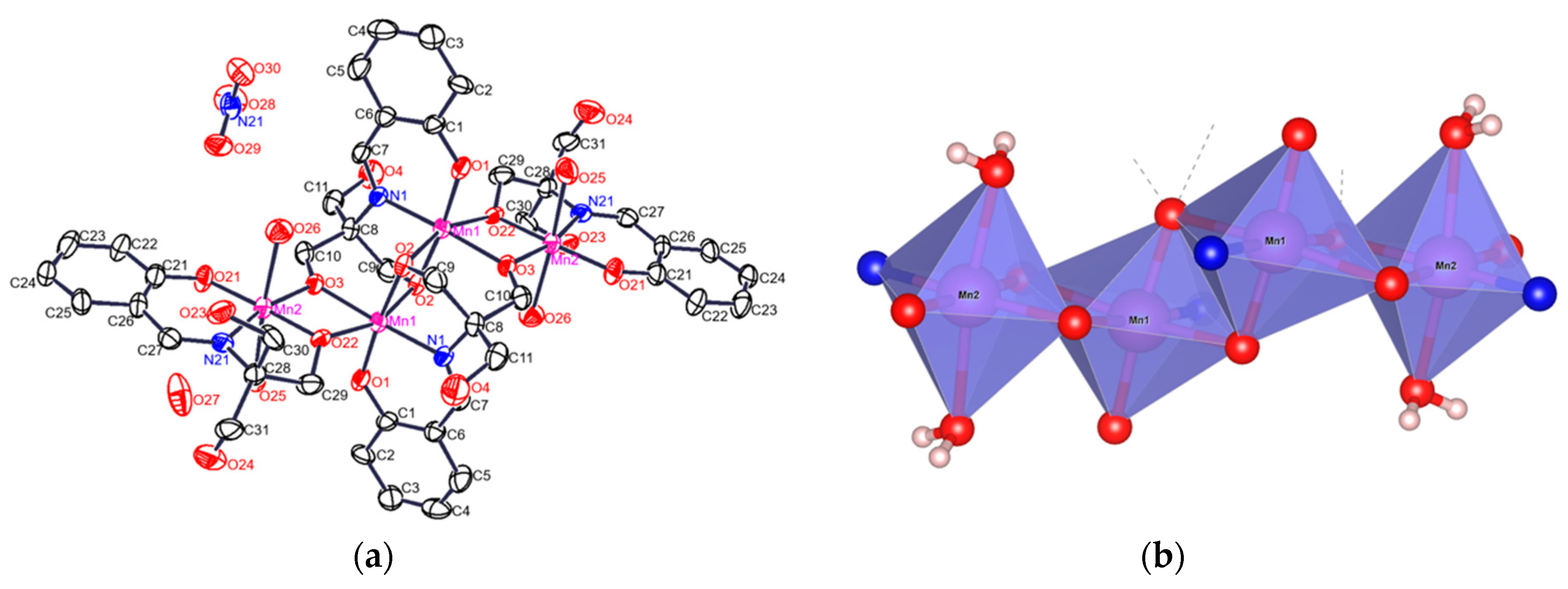
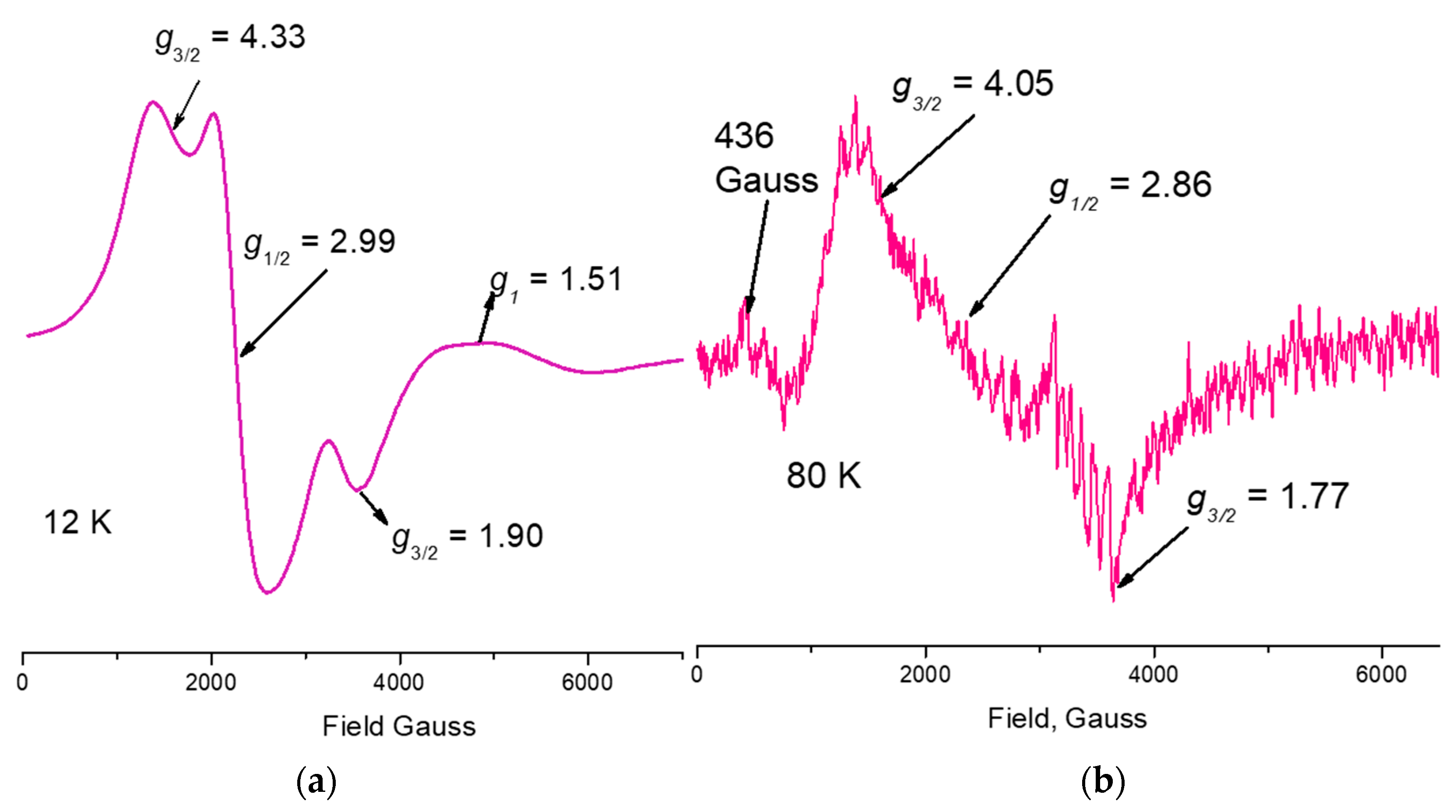
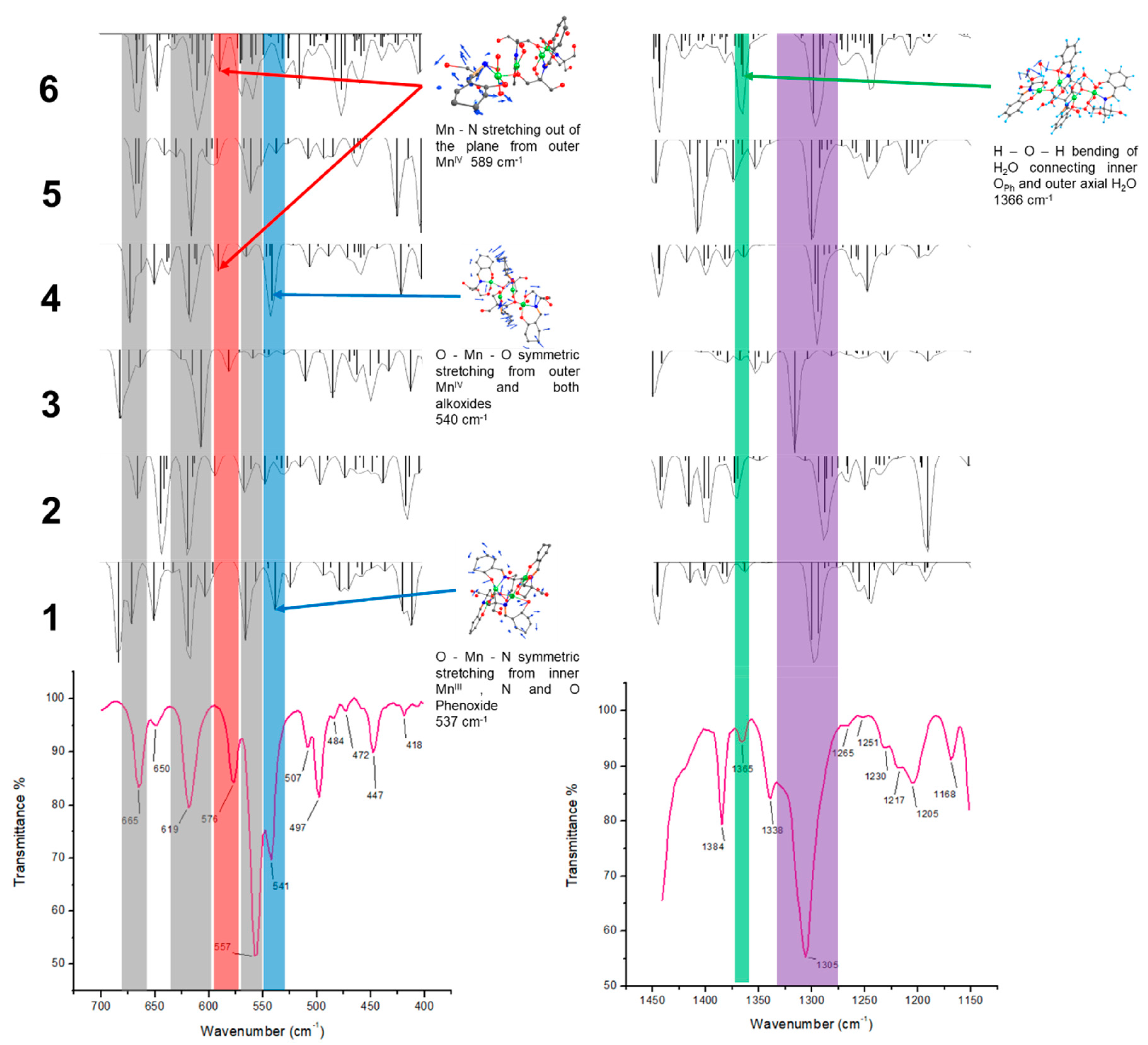
Empirical Formula	C44 H60 Mn4 N6 O27
Formula weight	1324.74
Crystalline system	Triclinic
Space group	P-1
a = 10.757(3) Å	α = 98.72(2)°
b = 11.687(3) Å	β = 110.37(2)°
c = 13.328(4) Å	γ = 108.08(2)°
Volume	1428.4(7) Å3
R-Factor (%)	R = 12.43

summarizes the crystallographic data. Figure 1 shows the structure of 1, which is a centrosymmetric tetramer of manganese ions with mixture valences (II), (III), and (IV). In

Table 2. Bond length [Å] and angles [°] of 1.

Bond Length	(Å)	Angles	(°)	Angles	(°)
Mn1–O1	1.875(10)	O1–Mn1–O2	174.3(4)	O22–Mn2–O21	176.5(4)
Mn1–O2	1.880(10)	O1–Mn1–N1	92.1(4)	O22–Mn2–O3	83.6(4)
Mn1–N1	1.997(11)	O2–Mn1–N1	82.6(4)	O21–Mn2–O3	99.8(4)
Mn1–O3#1	2.023(9)	O1–Mn1–O3#1	92.5(4)	O22–Mn2–N21	83.1(5)
Mn1–O2#1	2.161(10)	O2–Mn1–O3#1	92.8(4)	O21–Mn2–N21	93.5(5)
Mn1–O22#1	2.152(9)	N1–Mn1–O3#1	175.3(5)	O3–Mn2–N21	166.6(4)
		O1–Mn1–O22#1	93.8(4)	O22–Mn2–O26	89.9(4)
Mn2–O3	1.852(9)	O2–Mn1–O22#1	89.6(4)	O21–Mn2–O26	90.0(5)
Mn2–O21	1.868(10)	N1–Mn1–O22#1	103.7(4)	O3–Mn2–O26	85.5(4)
Mn2–O22	1.960(9)	O3#1–Mn1–O22#1	75.0(4)	N21–Mn2–O26	96.5(5)
Mn2–N21	1.976(12)	O1–Mn1–O2#1	95.4(4)	O22–Mn2–O25	90.0(4)
Mn2–O25	2.305(12)	O2–Mn1–O2#1	82.9(4)	O21–Mn2–O25	90.6(5)
Mn2–O26	2.240(11)	N1–Mn1–O2#1	93.4(4)	O3–Mn2–O25	85.9(4)
		O3#1–Mn1–O2#1	87.2(4)	N21–Mn2–O25	92.1(5)
		O22#1–Mn1–O2#1	160.3(3)	O26–Mn2–O25	171.3(4)

Symmetry transformations used to generate equivalent atoms: #1 −x+1, −y+2, −z+1.

the bonds length and angles of interest are summarized.

In Figure 1 the basic nucleus of the crystallographic structure, which denotes all Mn(III) ions according to crystallographic distances (see Computational Details), is shown. Figure 1 shows a primary nucleus [Mn(III)(H₂L)[Mn(III)(HL)]₂Mn(III) (H₂L)]. This molecular nucleus contains four units of [Mn-μ₅−O, μ₁−N] where each manganese ion is bonded to four ligands through one phenolic oxygen atom to two phenolato oxygen atoms, which connect it to the other neighboring manganese ion and to the nitrogen atom of the imino group, which connects a manganese ion with the next manganese ion. One of the four six-coordinated manganese ions, Mn2, is coordinated to one-donor atom of HL³⁻ ligands and to two-donor atoms of HL²⁻ ligands, displaying bond lengths between 1.875–2.161 Å. Mn1 ions are coordinated to four-donor atom of two HL²⁻ ligands, showing the Mn1 bond lengths in the range between 1.852–2.305 Å (Table 2). Nevertheless, the structure of 1 at 295 K, showed an inversion center that would be able to produce the unity [Mn(III)-μ₂-O–N]₄, but the degree of deprotonation of the ligand under the pH conditions of the reaction produces the unity [Mn(II)−, [Mn(III)]₂−, Mn(IV)−μ −O−N]. The unit cell contains two nitrate counter ions (−2), four alkoxide groups (−4), six μ−O (−6), four μ−N and four water molecules for each Mn₄ unity. Each manganese ion is coordinated by five oxygen and one nitrogen atoms, producing an octahedral ligand field with axial elongation with bond lengths >2.15 Å, which lowers the symmetry from O_h to D_4h, with respect to the bond equatorial distances <1.997 Å [35]. The oxygen atoms axially coordinated to the Mn1 ion correspond to –OH group of the ligand (O22#1, Mn1–O2#1); for Mn2 these axially coordinated oxygen atoms belong to two water molecules (O26, O25), which creates an elongated octahedral coordination sphere (Figure 1).

The distances Mn2∙∙∙Mn1#1 and Mn1∙∙∙Mn1#1are ~3 Å and the angles Mn–O–Mn are in the 97.1–100.8° interval. These structural characteristics are in accordance with literature suggesting that the Mn1 and Mn2 have a +3 oxidation state [36,37]. The oxidation states assigned to the manganese ions based on the structural characteristics were different from the interpretation obtained by the ESR studies, discussed in the corresponding section. However, the theoretical calculations of the structure and the ESR results, presented in their respective section, suggest oxidation states of +2, +3, and +4 (Figure 1) [38]. Intermolecular hydrogen bridges build a 2D supramolecular structure (Figure 2). Each manganese ion in 1 is coordinated to five oxygen atoms and one nitrogen atom, with an axially distorted octahedral geometry. This last statement is observed for the axial distances, which are longer than the equatorial distances (Table 2) [36,37]. The deviation of Mn2, with respect to the plane formed by the O21, N21, O22, and O3 atoms is of 0.013 Ǻ, and for Mn2 the deviation from the plane formed for the O3, O22, O2 and N1 is of 0.125 Ǻ. The angles for a perfect octahedral perfect geometry would be of 90° in plane and 180° between the axial positions. Although for 1 these angle values are different, Álvarez et al. [39] have proposed equation 1 to calculate a distortion from O_h symmetry to a distorted D_4h symmetry.

$$S\left(O_h\right)=5.39·{\Delta }^2-0.33·|\Delta |=0.96,$$

(1)

where $\Delta =$ longer distance $-$ shorter distance, taking $S\left(O_h\right)$ a value > 0 for octahedral elongation and a value $S\left(O_h\right)<0$ for a tetragonal distortion. This parameter takes a value of zero for a perfect octahedron. For Mn1 the $S\left(O_h\right)=0.34$ and for Mn2 the $S\left(O_h\right)=0.96$; were the two Mn1, inner ions in Figure 1, show a major distortion towards D_4h symmetry and for Mn2, the outer ions in Figure 1, a $\le O_h$ symmetry [36,37,40,41]. These different environments provide the possible coordination sites for Mn(II) and Mn(IV) for mixed valence compound as described in the DFT section and other studies [42]. When the experimental powder X-ray diffraction (PXRD) was carried out on the polycrystalline grinded sample the crystal size was grinded mechanically and then the typical diffraction pattern of the polycrystalline sample was obtained, which clearly showed the picks corresponding for Mn(II, III and IV) (Figure SI-5-9) [43,44].

The IR interpretation and DFT studies give a plausible explanation for the integrated evidence of three oxidation states for Mn ions. The XPS experiment has been further analyzed to explain how the obtained signals clearly indicate the presence of three oxidation states of manganese ions. Moreover, the reported typical values of the three manganese oxidation states at the NIST database are consistent with the signals obtained for 1 as reported in the supplementary information [45,46,47,48,49,50,51,52,53,54,55,56,57,58].

UV-Vis Spectroscopy

UV–Vis spectroscopy was performed in methanol at room temperature for complex 1. Within the whole curve of the spectrum we were able to solve different transitions by calculating Gaussian deconvolutions [59,60] of the whole spectrum resulting in two d-d forbidden transitions between ${\lambda }_{max}=400-579$ nm. These values fall into the axially distorted octahedral geometry and belong to the $d_{xy, xz, yz}\to d_{x^2-y^{2 }}({}^{4}A_2\to {}^{4}T_2)$ y $d_{xy, xz, yz}\to d_{z^2}({}^{4}A_2\to {}^{4}T_1)$ transitions [61]. Additionally, the electronic transition energies both in polycrystalline powder sample (Figure SI1) and in solution, were in accordance with the presence of a Mn(IV) and Mn(III), which was confirmed by the IR and ESR experiments and computational calculations. Furthermore, the low spin Mn(II) ($s = \frac{1}{2}$) species were not visible due to the Laporte selection rule. Finally, a high energy MLCT was observed at 388 nm, confirming the manganese ions coordination with the organic ligand (

Table 3. UV-Vis data of 1, with the oscillator strength value, f.

Transition	λmax (nm)/ε (M−1·cm−1)	Energy cm−1	f M−1·cm−1
π→π*	211/6143	47,396	0.086
π→π*	237/5086	42,196	0.059
n→π*	269/2561	37,177	0.015
LCT→M	388/2317	25,841	0.0123
d-d	500/778	20,965	0.00139
d-d	579/441	19,158	0.00045

).

Infrared Spectroscopy

The IR analysis of 1 was conducted at room temperature using KBr pellets as a matrix to hold the sample. Comparison of H₄L and 1 shows two main changes, in the O–―H and C=N vibrations that are shifted to lower energies when coordinated to the ionic metals Mn(II), (III) and (IV). The lack of electrons in the oxidized form of Mn ions makes them highly electronegative, affecting the vibration energy by its requirement of electron density from the surrounding atoms. However, the more interesting changes are present at the low energy zone from 1200 to 1500 cm⁻¹. The structure of 1 resolved by X-ray crystallography and the computationally optimized chemical structure, shown in their corresponding sections, imply a lattice built by hydrogen bonds, which affects the C–O frequencies of the phenolate groups in the theoretical IR spectrum, making the assignation of vibration bands of the experimental spectrum possible (Figure 3 and

Table 4. Values of vibrations of C–O_Ph groups coordinated to manganese ions obtained experimentally (Exp) and DFT estimations from models 1-6. Values in cm⁻¹.

Compound	C–O Mn(II)i	C–O Mn(IV)e	C–O Mn(III)i	C–O Mn(III)e
Exp			1305	1308
1			1295	1301
2		1287	1289
3	1304			1316
4		1297	1294
5	1293			1300
6	1295	1291	1294	1300

i, internal manganese central ions; e, outer manganese external ions.

).

Mixed-valence Mn ion complexes have been studied deeply by various spectroscopies [62,63,64]. Many of these reports disregarded the changes in the vibrational information promoted by the differences in the oxidation states. We integrated computational results to the experimental IR spectrum to ensure the assignment of the phenolic C–O bond stretching mode (Figure 3). By deconvolution of the experimental vibration bands, the transitions contained within the envelope were observed and are in agreement with the theoretical estimation of the four vibrational energies for Mn–O bonds (Figure 3). We propose that the energy difference in the C–O stretching vibrational modes between Mn(II)_i and Mn (IV)_e is produced by the electronic effects induced by the different oxidation states of the Mn ions.

Proton Nuclear Magnetic Resonance

Analyzing paramagnetic compounds by NMR spectroscopy is always challenging due to the various phenomena that involve the electron spin momentum interactions with the nuclei, resulting in a distorted base line in the spectrum, making it almost unassignable [65]. In our case, the H₄L NMR-¹H spectrum changes drastically when coordinated to Mn(II), (III), (IV). According to the crystal structure, four molecules of H₄L are coordinated with four manganese ions. The average Mn^…H_aromatic bond distance is 5.46 Å. Thus, all aromatic protons are more distant from the influence of the metallic ions, provoking a loss of the structural symmetry and making them magnetically non-equivalent. Moreover, the multiplicity of the isotropic chemical shifts is also modified with respect to the free ligand, and the signals are shifted to higher energies due to the electronegativity of the metallic ions, as shown in Figure 4.

The integrals estimation for all 16 protons farther from the paramagnetic aromatic center in the molecule was performed in the area between 6 to 11 ppm. Additionally, the signal at 15 ppm (Figure 4b) was assigned to the proton in the H–CN group, with a difference of displacement from the free H₄L of 6.4 ppm. The estimated integral of 4 is in agreement with the number of this type of protons in the whole molecule, and the distance from the manganese is 3.78 Å. Finally, the most affected protons belong to the methyl and hydroxyl groups, which are the closest to the magnetic center with bond distances of 3.5 Å and 4.7 Å, respectively, and appearing now at negative displacement in a range from −11 to −30 ppm. The high electronegativity of the manganese ions withdraws electronic density from the covalent M–L bonds. This group of signals has a broad shape, characteristic of rapid relaxation times due to the highly effective relaxation mechanism induced by the spin-spin interactions [66,67].

The energy range covered by the signal can be used to calculate the real values of the transverse relaxation time. The T₂ parameter, which is ruled mainly by the spin-spin mechanism, is heavily affected by the presence of the manganese ions and its effect on the signal depends on its closeness to the nuclei [66,67]. A summary of the protons’ relaxation times and its dependence to the distance to the metallic ion can be seen in

Table 5. Broad lines of the chemical shifts, relaxation times, and average distances between manganese ions and protons for H₄L and 1.

Protons	Widthline (ppm)	T2 (sec)	Average Distance to Mnn+, (Å)
H4L O–―H	0.4	1.35 × 10−2	n/a
H4L aromatic	0.3	1.35 × 10−2	n/a
H4L C=N and C–H	0.1	2.25 × 10−2	n/a
1, H+ aromatic	1.5	4.16 × 10−4	5.50
1, H+ of the C=N	1.2	3.35 × 10−4	3.78
1, aliphatic C–H	3	1.21 × 10−5	3.06

.

Electron Spin Resonance

Figure 5 shows the ESR spectra of 1 at 300 K and 80 K and its simulation. Figure 6 contains the ESR spectrum of 1 in DMSO solution at 90 K, which shows the hyperfine interactions splitting and zero-field splitting signals, and of the powder sample 1 at 12 K, where the signals show a better resolution [68]. The areas ratio was $\frac{A_{300}}{A_{12}}\sim 2.19 \ll 25 \mathrm{and} \frac{A_{300}}{A_{90}}\sim 2.19 \ll 3.33$, 25 and 2.19 values typical of paramagnetic behaviors [69], where both ratios suggest an antiferromagnetic exchange interaction. The broadlines at different temperatures were ${\Gamma }_{300 \mathrm{K}}=640 \mathrm{G}, {\Gamma }_{90 \mathrm{K}}=660 \mathrm{G}, {\Gamma }_{12 \mathrm{K}}=610 \mathrm{G},$ showing an increase of the dipolar interaction over the magnetic exchange interaction at 90 K; although, at 12 K the value decreases as the exchange interaction is observed over the dipolar interaction [70]. All ESR experiments of 1 are consistent with three different oxidation and spin states for the manganese ions present (Figure 7). 1 contains four manganese ions with a strong ligand field induced by five oxygen and one nitrogen ligand, which stabilize the low spin of Mn(II), $s=\frac{1}{2}$, and of Mn(III), $s=1$, and the high spin of Mn(IV), $s=\frac{3}{2}$ [71,72]. The ESR of Mn(II), Mn(III), and Mn(IV) ions present in 1 is described by the spin Hamiltonian for these $3d^3$, $3d^4$ and $3d^5$ electronic systems in an axial distorted octahedral coordination sphere, $\widehat{H}=g\beta \overrightarrow{H}·\overrightarrow{S}+D\left[{\overrightarrow{S}}_z^2-\frac{1}{3}\overrightarrow{S}\left(\overrightarrow{S}+1\right)\right]+S·D·S-J{S}_1·S_2$, where the axial zero-field splitting is $D\ll h\nu$ at x-band. Coordination compounds with manganese ions in oxidation state Mn(II), $d^5$, with low spin, $s=\frac{1}{2}$, are less frequent that those of a high spin state, and a ²T_2g ground state in an O_h symmetry. The ESR of 1 showed Mn(II) species with a g = 1.87 value corresponding to low spin (Figure 5), in accord with theoretical and experimental reports as typical values $g$ < 2.0023 [68,71,72]. The Mn(III) species of 1 showed a signal with $g$ = 2.760 value. The Mn(III) has d⁴ electrons and a ⁵D configuration for its ground sate, which was considered an ESR silent system due to the shorter relaxation times or to the large zero-field splitting [73]. However, it has been proposed that for systems with $s>\frac{1}{2}$ the magnetic dipole transition is allowed, although not totally, when the Zeeman basal states are mixed by the zero-field Hamiltonian terms. These Zeeman basal state mixes the no-Kramer doublet, $|\pm 2\rangle$ and $|\pm 1\rangle$ states, into $|\pm \frac{1}{2}\rangle$, $|\pm \frac{3}{2}\rangle$ doublets, each formed by the linear states combination. The ESR transition of the $|\pm 1\rangle$ is not totally allowed between the $|\pm 1\rangle$ levels and the $|0\rangle$ level. The $g~2$ values and the shape line for the transitions of Mn(III) ions are different from Fe(III) ESR signals with its $g<2$ value, complement of other signals at low field [74,75]. A $d^3$ Mn(IV) ion in an octahedral symmetry has a ground state ⁴A_2g and should show an isotropic resonance on its ESR spectrum with $g<2$ value [76,77]. Since the four manganese ions in 1 do not have perfect octahedral geometries, they instead show tetragonal distortion and the spin-orbit interaction is present, the two Kramer’s doublets, $=\pm \frac{3}{2},\pm \frac{1}{2}$ ,are splatted by $2\left(D^2+E^2\right)$; where D and E are the axial and rhombic zero-field parameters, respectively. In accord with the UV-Vis, ESR spectra and the X-ray structure the distortion present in 1 is axial and then $\frac{E}{D}=0$. It is important to note that the zero-field split is not observed in the ESR spectra of the solid sample at two temperatures, and we assume that this splitting at the zero-field is smaller than the $h\nu = 0.31\mathrm{c}{\mathrm{m}}^{-1}$ at X-band. Nevertheless, the ESR spectrum and its simulation (Figure 5) gave $g >4 \mathrm{and} g<2$ values characteristic of Mn(IV) species, which is identifiable by the transition at higher field since the $g~2$ signal is weak, which has been observed in other works [78,79,80,81,82,83,84].

The Hamiltonian $\widehat{H}=\widehat{D}\left[{\overrightarrow{S}}_z -\frac{1}{3} \overrightarrow{S}\left(S+1\right)\right]+g\beta \overrightarrow{H}·g_N {\beta }_{N }\overrightarrow{ H}·{\widehat{I}}_z+A{\widehat{I}}_z·{\widehat{S}}_z-J{S}_1·S_2$ corresponds to the ESR spectrum of the solution sample. The ESR spectrum of 1 in solution shows a stronger $g~2$ signal and the signal with $g~4$ shows a lower intensity, observing the ${}^{55}Mn$ hyperfine interaction on the $g~2$ signal. The axial parameter $2D=0.1 \mathrm{c}{\mathrm{m}}^{-1}$ is much less than $h\nu =0.31 \mathrm{c}{\mathrm{m}}^{-1}$, a typical value of ESR spectra with $g~2$ dominant signal with respect to this other with $g~4$. The hyperfine interaction constant values are close to those values for Mn(IV) $A\approx 94\mathrm{and} 100 \mathrm{G}$ in frozen solution, being reported for Mn(III) of $A=94 \mathrm{G}$ and for Mn(II) $A=89 \mathrm{G}$ [85,86].

The χ_MT values for Mn(IV) d³ S = 3/2 is 1.875 BM, while the value for Mn(III) d⁴ S = 2 is 3.000 BM and for Mn(II) d⁵ S = 1/2 is 0.375 BM. The overall spin value of all different oxidation states of manganese is S_T = 4 with a χ_MT = 10.000 BM. In Figure 8,${\chi }_{M }T vs T$ plots for 1 are illustrated and the ${\chi }_{M }{T}_{300 K}$ value is 3.69 cm³ mol⁻¹ K. This value corresponds to $S_T=2$, which is a much lower value than $S_T=4$ if all manganese species are not interacting magnetically. When the temperature decreased, the ${\chi }_{M }{T}_{65 K}\mathrm{value}\mathrm{increases} \mathrm{to} 5.04$ cm³ mol⁻¹ K, and at a lower temperature the ${\chi }_{M }{T}_{3 K}$ value decreases again to 4.46 cm³ mol⁻¹ K. There is a drastic magnetic order change at 65 K and continues during the 65–53 K range with a final value at ${\chi }_{M }{T}_{52.4 K} \mathrm{of} 4.7$ cm³ mol⁻¹. The rearrangement of the magnetic order that starts at 65.5 K can be explained as a change from an antiferromagnetic interaction to a weaker antiferromagnetic interaction measured with J values [85].

The Heisenberg Hamiltonian, Equation (2), was proposed to fit the susceptibility data vs. temperature remembering that the magnetizations studies are bulk and there are no possibilities to distinguish oxidation states of manganese ions. This last consideration led us to consider that the exchange interactions between the Mn2…Mn1 ions of the basic nucleus were equal but different from the exchange interactions between the two central Mn1…Mn1 ions, Figure 9.

$$H=-2J_1(S_1·S_2)-2J_2\left(S_2·S_3\right),$$

(2)

where $J_1$ and $J_2$ are the exchange magnetic constants and $S_i$ are the spin operators [86].

The best data adjustment was made in the two sections with the modified Bleaney–Bowers equation (Equation (3)) [86], giving the following values: $J_1=+115 {\mathrm{cm}}^{-1}$, $J_2=+164 {\mathrm{cm}}^{-1}$, with a $g=2$ value.

$${\chi }_M=\frac{N{\beta }^2{g}^2}{3\left(T-\theta \right)}{\left[1+\frac{1}{3}\exp (-\frac{2J}{kT})\right]}^{-1}\left(1-\rho \right)+\frac{\left(N{\beta }^2{g}^2\right)\rho }{4kT}+N\alpha$$

(3)

As the J’s values were positives and take in account eq 2, the $-2J_1=115{\mathrm{cm}}^{-1}\mathrm{and} -2J_2=164{\mathrm{cm}}^{-1}$ values indeed that exchange interactions are antiferromagnetic [69]. Returning to the ESR area ratio only a small spin population remains turned with the field magnetic, quantified by the ${\chi }_{M }T$ values in the magnetization studies. The oxo-bridges angles >90° in the structure of 1 are consistent with an exchange antiferromagnetic interaction [87]. It is important to note that to quantify the J values, the oxidation states of manganese ions are not considered. Additionally, the two negative charges of the nitrate groups might be on the manganese ions labeled as outer, or only on one of them. Similar to X-ray diffraction, this bulk quantification does not detect the fine-tuning magnetic behavior, which is observed by ESR spectrometry. The magnetic response points towards that at 65.5 K and below the oxo-bridges angles will take values ≫90° and the Mn1 ions will be aligned with the other two outer ions, switching towards a stronger antiferromagnetic coupling with a modified magnetic order, electronic, and spatial arrangement.

Computational Calculations

An optimization of 1 at the crystallographic initial coordinates proved to reproduce the distance pattern of four distances shorter than 2.1 Å forming a plane and two axial distances larger than 2.1 Å (

Table 6. Geometric parameters of the first coordination sphere of Mn in the models optimized with B3LYP/6-31g(d)/LANL2DZ. Values in Å.

M–X Bond		Crystal	1	2	3	4	5	6a*	6b*
Mne,e’	Mn–N	1.976(12)	1.960	1.936	2.000	1.948	1.973	1.990	1.974
	Mn–OPh	1.868(10)	1.838	1.816	1.880	1.823	1.835	1.843	1.858
	Mn–OCH2 A	1.960(9)	1.899	1.847	1.886	1.893	1.873	1.877	1.895
	Mn–OCH2 C1	1.976(12)	1.972	1.917	1.869	1.928	2.011	1.891	1.963
	Mn–OH2O A	2.240(11)	2.348	1.977	2.452	2.147	3.750	1.938	2.273
	Mn–OH2O B	2.305(12)	2.301	2.016	2.334	1.779	2.077	1.877	2.317
Mni,i’	Mn–N	1.997(11)	2.000	1.964	2.174	1.985	2.226	2.225	2.006
	Mn–OPh	1.875(10)	1.869	1.843	2.096	1.857	2.214	2.095	1.850
	Mn–OCH2 B	1.880(10)	1.929	1.944	2.218	1.931	2.169	2.271	1.926
	Mn–OCH2 C1	2.023(9)	1.991	2.048	2.174	2.042	2.201	2.226	1.995
	Mn–OCH2 A	2.152(9)	2.205	2.241	2.181	2.198	2.200	2.161	2.188
	Mn–OCH2 C2	2.161(10)	2.299	2.250	2.088	2.279	2.108	2.184	2.378

* Values a and b correspond to different sides since 6 has no Ci symmetry. Values in bold correspond to Mn where the change of the distances is more than 10% with respect to 1.

). This arrangement showed a spin density on all four Mn cations consistent with a 3d⁴ Mn(III)^III (

Table 7. Mulliken spin populations of Mn atoms in the models considered computationally.

DFT Method/Basis Set	Mn type	1	2	3	4	5	6*
PBE/631g	Inner	3.837	3.804	4.390	3.830	4.533	4.624(3.884)
	Outer	3.844	2.743	4.063	2.817	3.995	3.041(3.860)
B3LYP/631g(d)	Inner	3.850	3.848	4.745	3.856	4.781	4.797(3.858)
	Outer	3.832	2.546	3.840	2.850	3.785	2.906(3.871)
B3LYP/631g+(d)	Inner	4.663	4.709	5.283	4.637	5.366	5.327(4.509)
	Outer	4.270	2.735	4.245	3.096	4.042	3.132(4.280)

* Values in parenthesis are from different sides since 6 has no Ci symmetry. Values in bold correspond to Mn where the change of the spin population varies more than 0.3 electrons and correspond to the gain or loss of one electron.

). Since this interpretation was inconsistent with the ESR results, five more models were explored in order to establish which model could produce a mixture of Mn(II) and Mn(IV).

The first option was a two electron disproportion of the two 1 molecules, which would in turn produce a double oxidized species, [Mn(III)₂ Mn(IV)₂ (H₂L)₂(HL)₂(H₂O)₄]⁴⁺, 2. It would also produce a double reduced species [Mn(III)₂ Mn(II)₂ (H₂L)₂(HL)₂(H₂O)₄], 3. These two molecules show different modifications of the first coordination sphere distances, shortening the axial water molecules distances in the case of 2 and elongating four Mn–X in the case of 3. These distance modifications correspond to changes in the Mulliken spin densities (Table 7) to the formation of two MnIV in the outer Mn cations in the case of 2 and two inner MnII in the case of 3. The free energy difference at B3LYP/6-31g+(d)/LANL2DZ (ΔG_B3LYP) for the process is 274.6 kcal/mol, suggesting this process is not possible at room temperature or below.

The second option corresponds to the transfer of two hydrogen atoms from one 1 molecule to another 1 molecule. In this scenario [Mn(III)₂ Mn(IV)₂ (H₂L)₄(H₂O)₄]²⁺, 4 and [Mn^III₂ Mn^II₂ (H₂L)₂(HL)₂(H₂O)₂(OH)₂]²⁺ , 5 would be produced. Models 4 and 5 produce similar changes to the Mn–X distances and the Mülliken spin densities corresponding to oxidation of the outer Mn and reduction of the inner Mn cations. The ΔG_B3LYP is 62.9 kcal/mol, which is considerably lower in energy than the process to obtain 2 and 3 but still not possible at room temperature.

A third model was attempted with four extra water molecules, [Mn(III)₂ Mn(II) Mn(IV) (H₂L)₂(HL)₂(H₂O)₈]²⁺, 6. The rationale for this model comes from the observation that artificially imposed Mn–X distances corresponding to outer Mn in 2 and inner Mn in 3 induced the oxidation states consistent with the ESR results but introduced great instability to the whole molecule and eventually a restriction-free optimization produced 1 again. To diminish these instabilities, four water molecules were added. The resulting molecule could not be optimized to a minimum with a Ci symmetry. However, this asymmetry induced the observation of the three oxidation states of Mn in the same molecule. The distances and Mulliken spin densities are consistent with this explanation. The ΔG_B3LYP for the reaction where four water molecules are included in the complex is 23.3 kcal/mol, which is still lower in energy than the two other process considered and the most probable explanation from an energy point of view.

Another tool we used to sustain that model 6 is responsible for the ESR signals are the IR vibrational modes. Modifications in the oxidation state of the Mn cations may increase/decrease the energy of certain vibrational modes. We focused our attention on Mn–X stretching modes and phenoxide C–O stretching modes. From DFT calculations some of these vibrational modes could be assigned and compared with experimental IR spectra. The results are shown in Figure 10.

From Figure 10 it can be noticed that the bands at 665, 619, and 557 cm⁻¹ are common to all the models and would not help to discriminate among them. An important band at 576 cm⁻¹, is not present in 1, but it is in 4 and 6. The band at 541 cm⁻¹ is weakly present in 1, but is strongly present in 4 and corresponds to a vibrational mode that includes Mn(IV)^IV. Regarding the band at 1305 cm⁻¹, it distinctively corresponds to the C–O_Ph stretching vibration coordinated to different Mn cations. It can be noticed that a vibrational mode from a single model, as is the case of 1, would not account for the broadening of that band. Furthermore, the charge changes in the Mn cations coordinating the O_Ph would produce the shift observed in those bands. It would increase the energy of C–O_Ph stretching mode when Mn(IV) was coordinated and lower the energy in the case of Mn(II). It is worth mentioning that the protonation state and hydrogen bond networks of O_Ph also play a significant role in the energy of this vibrational mode, in particular in model 6 where all vibrational modes are expected to be present. One particular marker that is distinctive of model 6 is the signal at 1365 cm⁻¹. This signal is barely present in the experimental spectra and only active in model 6. It corresponds to water bending from the extra water molecules. This observation and the values for the free energy variation suggest that model 6 is the responsible for the ESR behavior.

4. Conclusions

The reaction conditions allowed two spontaneous oxidation processes, starting from Mn(II) and stabilizing a mixed valence compound containing different proportions of Mn(II), Mn(III), and Mn(IV). It is not an easy task to identify the different oxidation states in a single molecule structure resolved by single crystal X-ray diffraction (XRD) at 300 K, which shows only Mn(III). In contrast, grinded crystals produced polycrystalline powder and its PXRD pattern showed evidence for the three-oxidation states. UV-Vis spectra, in solid and in solution samples, showed electronic transitions assigned to Mn^{4+, 3+} ions. The experimental IR stretching frequencies of the C–O group were identified with the aid of the DFT calculations, and showed supramolecular effects acting upon specific vibrational modes. Both experimental and theoretical IR spectra are consistent with the vibrational mode changes on the C–O stretching coordinated to Mn ions in different oxidation states. NMR-¹H spectrum showed two zones of proton signals affected for its proximity to paramagnetic ions, which presented shorter relaxation times, with two and three magnitude orders, with respect to the free ligand. The ESR studies at different temperatures developed characteristic transitions for Mn(II) low spin, Mn(III) high spin and Mn(IV). Mn(III) species were detected by the transitions observed at high energy produced among the two split Kramers doublets $|\pm \mathbf{1}/\mathbf{2}\rangle$ and $|\pm \mathbf{3}/\mathbf{2}\rangle$ Mn(II) and Mn(IV) and the no split doublets, $|\pm \mathbf{1}\rangle$ and $|\pm \mathbf{2}\rangle$, which corresponding to Mn(III) spin states, proved the presence of the three manganese oxidation states. Antiferromagnetic exchange interactions through the oxygen atoms established by magnetization studies are consistent with the ESR results, the bond angles between the Mn–O–Mn atoms, and the quantification of the magnetic order. The consistency among the spectroscopic techniques results (either bulk or molecular) demonstrate the coexistence of the manganese three oxidation states obtained.