Design of a Society of Automotive Engineers Regular Curved Retroreflector for Enhancing Optical Efficiency and Working Area

Abstract

A highly efficient regular curved retroreflector is proposed to meet the requirements of the US Society of Automotive Engineers (SAE) regulations. It is demonstrated that 28% higher retroreflection efficiency and 33% more working area can be accomplished with the new designed retroreflector when compared with the commercial ones used in modern vehicles.

1. Introduction

A retroreflector, also called a reflex reflector, can reflect light [1,2,3] back along a vector that is parallel or nearly parallel to but opposite in direction from the light source [4,5], no matter what the incident light angle is [2]. Because of their high tolerance to the direction of incident waves [6], retroreflectors have been used extensively in many applications instead of plane mirrors [2], such as free-space optical communications networks [4], satellites, road signs [7], vehicles [8], and clothing [9,10]. Retroreflectors on cars or clothing increase their visibility in the dark [2], so that traffic accidents can be reduced [6,11,12]. 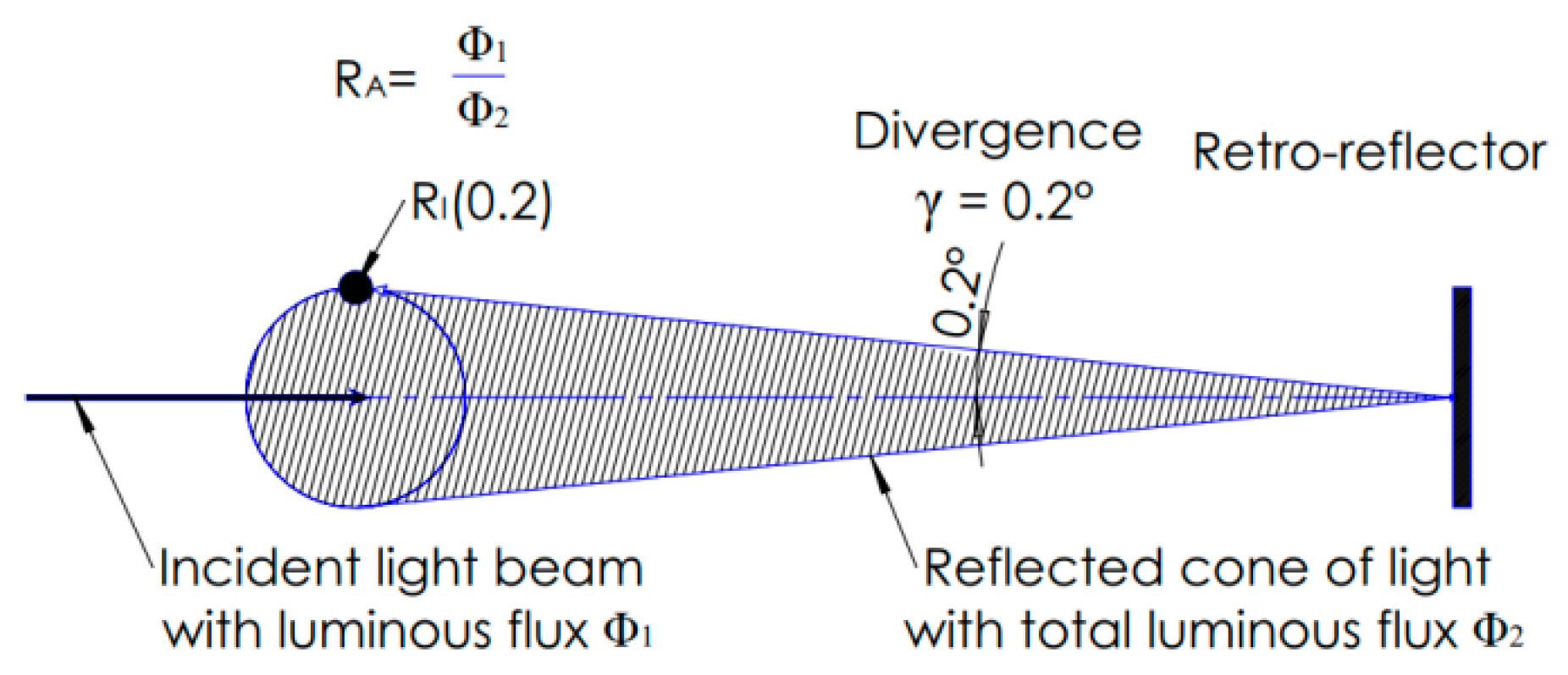Common vehicle signage is composed of cube-corner retroreflectors (CCRs) [13]. According to the regulations of the US Society of Automotive Engineers (SAE), vehicle signage needs to return light back to the observer located 0.2° above the light source [14], and the coefficient of luminous intensity R_I should be more than certain values within a 20° angle of light incidence. The measure of vehicle signage performance R_I is decided by the ratio of the strength of the reflected light (retroreflected light intensity) to the amount of light that falls on the retroreflector (incident light illuminance) [13,14,15], as shown in Figure 1. R_A is the measure of retroreflection efficiency, defined as the ratio of the flux of incident light to the total flux of a reflected cone. Vehicle signage appears brighter as its R_I value increases [10,14,15].

In the design of commercial retroreflectors for modern vehicles, outlook smoothness is usually first considered rather than efficiency. Therefore, it is often necessary for a retroreflector to be made with a curved surface fitting the outlook of the application, such as the corner of a vehicle. However, cube-corner structures are usually distorted or even destroyed to complete the curve, so their effective working area and reflection efficiency are influenced seriously, and that could lead to the retroreflector not complying with SAE regulations [6,16].

Based on pin-bundling technology, the tooling of a reflex reflector mold can be produced, and it can serve as a testing sample or for mass production. In this study, a reflex reflector sample was designed and produced by bundled metal pins for SAE regulations. A curved retroreflector with new cube-corner structure is proposed and demonstrated. By use of genetic algorithms for optimization, the angles and positions of the pins serve as the optimizing parameters to enhance the performance of a curved retroreflector. Compared with conventional retroreflectors, it is found that 28% higher retroreflection efficiency and 33% more working area can be accomplished with our proposed one.

R_A is the measure of retroreflection efficiency, defined as the ratio of the flux of incident light to the total flux of reflected light. R_I (coefficient of luminous intensity) is used to define the reflection efficiency at certain observation angles (upward of 0.2°).

2. Principles

The SAE standard is to reduce deaths and injuries resulting from traffic accidents by providing adequate illumination of roadways and enhancing the conspicuousness of motor vehicles on public roads so that their presence is perceived and their signals understood in both daylight and darkness or other conditions of reduced visibility [14,17]. The value of the standard in each test case is detailed in

Table 1. Minimum mcd (millicandela)/incident lux for a white reflex reflector. SAE, Society of Automotive Engineers.

Observation Angle (°)	US SAE Regulation Requirement	Entrance Angle (°)
		0°	10° Up	10° Down	20° Left	20° Right
0.2	Minimum coefficient of luminous intensity RI (mcd/incident lux)	1680	1120	1120	560	560

[12,15,17].

A corner-cube retroreflector is a kind of reflex reflector and its working mechanism is based on groups of three perpendicular planes, as shown in Figure 2. Usually, the dihedral angle between any pair of reflecting faces is made to be exactly 90°, so that the reflected beam is exactly antiparallel to the incident beam. If the angles differ from 90° by any amount, the reflected beam will be split into multiple beams to achieve the required application.

Through an array of pins, a corner-cube retroreflector can be produced, which is shown in Figure 2. The orientation of each face is given by the unit normal $\widehat{n_1}$, $\widehat{n_2}$, and $\widehat{n_3}$ to each face. The reflection from each face reverses that component of the light’s velocity vector that is normal to the face. Let $\overrightarrow{V}$ and ${\overrightarrow{V}}^{\prime }$ be the directions of a ray before and after reflection, respectively, with the vector V′ given by $\overrightarrow{V^{\prime }}$ = ${\overrightarrow{V}}^{\prime }$ − 2($\overrightarrow{V}$)$\widehat{n}$, where $\widehat{n}$ is the normal to the face. Applying the above formula three times yields the direction of the reflected beam for a particular order of reflection. Formulas for the direction of the reflected rays after the three reflections are given by Chandler’s formula:

$$\overrightarrow{t}=\overrightarrow{q}2\overrightarrow{a}(\mathsf{\alpha }\overrightarrow{a}-\mathsf{\beta }\overrightarrow{b}+\mathsf{\gamma }\overrightarrow{c})$$

(1)

where $\overrightarrow{t}$ is the final direction and $\overrightarrow{q}$ is the original direction; α, β, γ are the small angles by which the angles between the three mirrors exceed right angles, and $\overrightarrow{a}$, $\overrightarrow{b}$, and $\overrightarrow{c}$ are normal to the three mirrors taken in order in a right-hand sense. Equation (1) is valid to the first order when the mirrors are nearly mutually perpendicular. α is the angle between the faces whose normals are $\overrightarrow{b}$ and $\overrightarrow{c}$. The normals may be strictly perpendicular; that is, they do not need to include the small deviations caused by the dihedral-angle offsets. The directions of the reflected rays were computed by applying the law of reflection three times.

The unit normals to the faces can be computed as follows (see Figure 3). Let the normals to the faces without dihedral-angle offsets be the unit vectors $\widehat{ı}$, $\widehat{ȷ}$, and $\widehat{k}$ along the three coordinates x, y, and z, respectively. If the angle between the xz plane and the yz plane is (π/2) + δ, this can be expressed by $\widehat{n_1}$ = $\hat{ı}$ + $\frac{\mathsf{\delta }}{2}\hat{ȷ}$; $\widehat{n_2}$ = $\widehat{ȷ}$ + $\frac{\delta }{2}\widehat{ı}$; $\widehat{n_3}$ = $\widehat{k}$. For small angles δ, these expressions are quite adequate. Offsets in the other two dihedral angles can be similarly represented.

It is desirable to have the unit normals given in the coordinate system of the symmetry axis of the corner cube, since the incidence angle of the laser beam is given with respect to this axis. The symmetry axis is in the direction of the vector x = y = z = 1, as shown in Figure 4; we see that $\cos {\mathsf{\theta }}_A$ = $\frac{1}{\sqrt{2}}$; $\sin {\mathsf{\theta }}_A$ = $\frac{1}{\sqrt{2}}$; $\cos {\mathsf{\lambda }}_A$ = $\frac{\sqrt{2}}{\sqrt{3}}$; $\sin {\mathsf{\lambda }}_A$ = $\frac{1}{\sqrt{3}}$. The normals in the xyz coordinate system can be given in the coordinate system of the symmetry axis by rotating the original coordinate system around the z-axis of θ_A and around the y-axis of –λ_A. This brings the x-axis along the axis of the matrix form, and the total rotation is given by

$$\left(\begin{array}{c}{x}^{\prime }\\ y^{\prime }\\ z^{\prime }\end{array}\right)=\left(\begin{array}{ccc}\cos {\mathsf{\lambda }}_A& 0& \sin {\mathsf{\lambda }}_A\\ 0& 1& 0\\ -\sin {\mathsf{\lambda }}_A& 0& \cos {\mathsf{\lambda }}_A\end{array}\right)\left(\begin{array}{ccc}\cos {\mathsf{\theta }}_A& \sin {\mathsf{\theta }}_A& 0\\ -\sin {\mathsf{\theta }}_A& \cos {\mathsf{\theta }}_A& 0\\ 0& 0& 1\end{array}\right)\left(\begin{array}{c}x\\ y\\ z\end{array}\right)$$

(2)

Substituting the values of the sines and cosines and multiplying the matrices, we get $x^{\prime }$ = $\frac{1}{\sqrt{3}}\left(x+y+z\right)$; $y^{\prime }$ = $\frac{1}{\sqrt{2}}\left(y-x\right)$; $z^{\prime }$ = $\frac{1}{\sqrt{6}}\left(2z-x-y\right)$. In Figure 5, the (x, y, z) axes represent the original coordinate system and the (x′, y′, z′) axes are the rotated coordinates.

The incident beam after reflection at the front face is in a direction given by the angles θ′ and ϕ′ in the (x′, y′, z′) coordinate system (see Figure 6).

A second rotation of the coordinate system must be performed to get the normals to the faces in the coordinate system of the laser beam. By rotating the coordinate system around the x′-axis of θ′ and then around the new z′-axis of ϕ’, we get

$$\left(\begin{array}{c}{x}^{″}\\ y^{″}\\ z^{″}\end{array}\right)=\left(\begin{array}{ccc}\cos \mathsf{\varphi }{}^{\prime }& \sin \mathsf{\varphi }{}^{\prime }& 0\\ -\sin \mathsf{\varphi }{}^{\prime }& \cos \mathsf{\varphi }{}^{\prime }& 0\\ 0& 0& 1\end{array}\right)\left(\begin{array}{ccc}1& 0& 0\\ 0& \cos \mathsf{\theta }{}^{\prime }& \sin \mathsf{\theta }{}^{\prime }\\ 0& -\sin \mathsf{\theta }{}^{\prime }& \cos \mathsf{\theta }{}^{\prime }\end{array}\right)\left(\begin{array}{c}{x}^{\prime }\\ y^{\prime }\\ z^{\prime }\end{array}\right)$$

(3)

The relationship of the (x′, y′, z′) and (x″, y″, z″) coordinate axes is given in Figure 7. The x′ axis is the symmetry axis of the reflector, the y′, z′ plane is parallel to the front face, and the x″ axis is parallel to the beam after it enters the cube corner. In this study, we used a Hollow corner cube, and the reflections can be done for all six possible sequences of reflections by taking the incident beam, given by the vectors x″ = −1, y″ = z″ = 0, and reflecting it from each normal to the faces in the (x″, y″, z″) coordinate system. The y″ and z″ coordinates of the reflected beam give the deviations from the incident direction.

The beam spread at normal incidence when all dihedral angles are offset by an equal amount is given by the formula γ = $\frac{4}{3}\sqrt{6}$ n δ, where δ is the angle by which the dihedral angles exceed 90° and γ is the angle between the incident ray and the reflected ray. Light passes through CCRs and there is a change in the direction of reflection. The direction of the incident beam is determined by θ′ and ϕ′ in the (x′, y′, z′) coordinate system. The values of γ are shown in

Table 2. Angles between incident ray and retroreflected ray γ with respect to δ, which is the dihedral angle of retroreflector corner cube surface with 90° as the reference.

δ (°)	0	0.02	0.03	0.04	0.05	0.06	0.07	0.08	0.09
γ (°)	0	0.05	0.07	0.09	0.13	0.14	0.16	0.19	0.20
δ (°)	0.1	0.11	0.12	0.13	0.14	0.15	0.64	0.7
γ (°)	0.23	0.26	0.28	0.30	0.33	0.35	1.50	1.62

. At δ = 0.09, γ = 0.2° (SAE regulations).

Based on the above computation theory, the optical simulations through TracePro software (Lambda Research Corporation of Littleton, MA, USA) show that CCRs with equal dihedral angles can reflect six beams with equal reflection angle γ with respect to the incident beam, as shown in Figure 8. When the dihedral angle is 90.09°, it can be found that γ becomes 0.2°, which fits SAE regulations and complies with the mathematical analysis shown in Table 2.

The angle between the incident ray and the retroreflected ray γ is closely related to δ, which is the dihedral angle of retroreflector corner cube surface with 90° as the reference. As shown in Table 2, for example, when δ is controlled to be 0.09°, the retroreflected beam angle γ becomes 0.2°, as required by the SAE standards.

3. Optical Setup and Analysis

In order to investigate the properties of a curved reflex reflector, a commercialized one with corner-cube structure for cars was used for testing, shown in Figure 9. The sample is made of PMMA (Poly Methyl Methacrylate) with size 146 mm × 34 mm, provided by Owl Light Automotive Products Mfg. Corp., which has been in mass production for vehicles in the USA. The experimental setup for curved reflex reflector testing is shown in Figure 10. In the optical setup, a semiconductor laser with wavelength 635 nm acted as the light source, and its distance from the curved reflex reflector was set to be 30.5 m to measure the reflected light spot. The laser light with an incident angle of 0° with respect to the car driving direction was incident on the commercialized curved reflex reflector. As a result, several retroreflected light spots could be found on the black screen located 30 m away from the test sample. A Minolta T10 illuminance meter was used to measure the illuminance on the sample and the retroreflected light spot, in order to get the incident light illuminance (in lux) and the retroreflected light intensity (in candela). Coefficient of luminous intensity R_I and retroreflection efficiency R_A of the test sample can thus be worked out. During the experiments, the anterior, central, and posterior regions of the sample were investigated with the car driving direction, and these are presented in Figure 11.

Initially, the laser light was adjusted to be parallel with the driving direction and aimed at the central part of the region. The resulted reflected outputs are shown in Figure 12a–c. While observing the output signals, it was found that the reflected light spots became weaker and weaker as the test region shifted from the front part to the end part of the tested curved corner-cube retroreflector (CCCR). Accordingly, it is evident that its curved shape had an influence on its performance.

In order to improve the poor performance of the commercial CCCR, a single ray antiparallel to the driving direction was set to probe the reflecting surfaces of the posterior region by optical simulations. The labeled input reflecting surface and the resulting ideal reflected light intensity distribution are shown in Figure 13, Figure 14 and Figure 15.

Comparing Figure 12c with Figure 14, it can be seen that reflecting surfaces 1 and 3 in the posterior region did not function, so that four light spots were missed and only two light spots reached the output screen. By means of a genetic algorithm to search for better pin group structures, it could be possible to revive the disabled reflecting surfaces to elevate the coefficient of luminous intensity R_I and reflection efficiency R_A.

4. Optics Design and Verification

In the proposed CCCR structure, two group of pins were connected as a double-pin group, shown in Figure 16, which served as the building element to construct a primary CCCR, as shown in Figure 17. Fifteen pieces of double-pin groups were arranged parallel to the car driving direction to compose the primary CCCR, one pin group touching the curve reference surface and the other one free to translate in the car driving direction. The height differences between the neighboring pins in a group of double pins and the double-pin group are named d_i and D_i, respectively, as shown in Figure 18. In order to further improve the primary CCCR, the add-on ray tracing simulation tool OptisWorks (Optis SAS, La Farlede, France), embedded in SolidWorks mechanical design software, was used to search suitable d_i to elevate its performance and D_i to smoothly fit the reference curve of the outlook of CCCR. The lighting performance of the CCCR, such as intensity distribution, illumination uniformity, and optical efficiency, can be accomplished to meet targets by means of optimization.

The object function f defined by Equation (4) was determined in the optimization process. The optimization process encompassed three fragments.

Object function: The equation that describes the value of the object function of the optimization program established by the genetic algorithm is as follows:

$$f\left(i,j\right)={{\displaystyle \sum }}_{i,j=1}^n\sqrt{w_i{\left(m_i-t_i\right)}^2+w_j{\left(m_j-t_j\right)}^2}$$

(4)

where w_i is the level of curvature of a curved retroreflector that has 15 variables from w₁ to w₁₅, and the constraint of each variable is determined by the curvature of the CCCR surface; m_j is the value of the measured target, which is determined by the intensity sensor through each optimal loop when running the program; and t_j is the optimization target defined with a value corresponding to the retroreflective light intensity on the retroreflector plane.

Luminous intensity function: We searched for an approximation of the luminous intensity (R_I) I (Φ, a, b, c) at the polar angle of Φ in the form:

$$\mathrm{I}(\mathsf{\phi },x,y,z)={\mathrm{I}}_{\max }{{\displaystyle \sum }}_{k=1}^k{x}_{k}co{s}^{z_k}(\mathsf{\phi }-y_k)$$

(5)

Here, K is the number of functions to sum and x_k, y_k, z_k are the function coefficients that we expect. For brevity, coefficients are written as vectors x = (x₁, x₂, …, x_K), y = (y₁,y₂, …, y_K), z = (z₁,z₂, …, z_K). The interval range of the coefficients is a = [0,0.81], b = [−1,1], c = [0,100]. Discrete optimization algorithms will work on finite subsets where the possible values will be x* ϵ {0, 0.001, 0.002, …, 0.81}, y* ϵ {−1, 0.9,0.8,0.7, …, -1}, z* ϵ {0, 1, 2, …, 100}.

The components in OptisWorks were configured to incorporate light source, intensity sensor, and CCCR. The space between the CCCR and the surface source was set to fit the required testing conditions of SAE standards.

In the initial CCCR building, there were 15 groups of double pins, so it comprised 15 variables d_i (from d₁ to d₁₅), illustrated in Figure 18. The constraint of each variable d_i is determined by the curvature of the CCCR surface. Each variable has a non-identical limitation of height values and is dependent on the surface curve. The resulting merit fluctuated 0.01–0.81 mm. The territory of CCCR with extreme curvature will have the highest altitude value. Our focus was on improving the reflection properties of the end area.

In order to set the target value of the optimization, we conducted a simulation experiment with a flat regular CCR to find the reflected light power as referenced by 1000 lumen incident beam. The resulting reflected light power was 850 lm, and it was used as the target for subsequent searches for optimized CCCR. Through running the scheme in the optimization process, the best results were determined in the step 25. The recorded data of intensity sensor versus running cycles are shown in Figure 19. The final intensity sensor data was shown as 737.52 lm, which was also the output power of the optimized CCCR.

In the initial optimization process, the mathematical equation for the intensity distribution of reflected light was entered into the program that is expressed in the measurement value of the intensity sensor. The luminous intensity R_I is defined by I(φ, a, b, c) at the polar angle of φ shown in Equation (5). The target of the optimization process was defined with a value corresponding to the retroreflective light intensity on the retroreflector plane. During the optimization, to have the CCCR meet the requirements of SAE standards at 0.2° and maximum reflection efficiency, the values of δ and d_i were found through the workflows shown in Figure 20 and Figure 21, respectively.

Before optimization, the d_i values shown in

Table 3. Height variable d_i before and after optimization.

di (mm)	d1	d2	d3	d4	d5	d6	d7	d8	d9	d10	d11	d12	d13	d14	d15
Region	Anterior Region					Central Region					Posterior Region
Min (mm)	0.01	0.05	0.1	0.15	0.18	0.3	0.5	0.55	0.6	0.65	0.7	0.7	0.73	0.74	0.75
Max (mm)	0.15	0.2	0.25	0.3	0.4	0.6	0.7	0.75	0.78	0.78	0.81	0.81	0.81	0.81	0.81

were selected by a random process from the height difference constraint by the optics design software. The constraints of each variable d_i were determined by the surface curve of the commercial reflex reflector shown in Figure 10. As shown in

Table 4. Constraints of height variable d_i in optimization process.

d (mm)	d1	d2	d3	d4	d5	d6	d7	d8	d9	d10	d11	d12	d13	d14	d15
Region	Anterior Region					Central Region					Posterior Region
Before optimization	0.15	0.2	0.25	0.3	0.4	0.6	0.7	0.75	0.78	0.78	0.81	0.81	0.81	0.81	0.81
After optimization	0.11	0.18	0.14	0.23	0.28	0.56	0.62	0.70	0.68	0.78	0.77	0.74	0.78	0.80	0.80

, each variable has a different limitation of height values in the range of 0.01 mm to about 0.81 mm. As the optimization was executed and terminated by the program, the optimized CCCR with the same curve of the commercial one was produced. The d_i and D_i of the optimized CCCR (after optimization) and those of the primary CCCR (before optimization) are listed in Table 4 and

Table 5. Height variable Di before and after optimization.

Di (mm)	D1	D2	D3	D4	D5	D6	D7	D8	D9	D10	D11	D12	D13	D14	D15
Region	Anterior Region					Central Region					Posterior Region
Before optimization	0.17	0.3	0.45	0.75	0.89	1.37	1.66	1.88	2	2.13	2.26	2.57	2.74	3.15	3.43
After optimization	0.07	0.12	0.31	0.52	0.61	0.81	1.04	1.18	1.32	1.35	1.49	1.83	1.96	2.35	2.63

, respectively.

After ending the solution search, the optimized CCCR was analyzed to compare with the commercial one by simulations. The distance from the light source to the CCCR was 30 m, CCCR was kept in the car driving direction, 0°, 10° (up, down) vertical and 20° (left, right) horizontal with the incident light, to proceed with optical tests of SAE regulations. The resulting intensity distributions by 0° light incident to anterior, central, and posterior regions sequentially are shown in Figure 22, which demonstrate that R_I and R_A increased significantly in all regions, and more retroreflection working area was accomplished through the new design. With 0°, 10° (up, down) vertical and 20° (left, right) horizontal incident light, the retroflection results for R_I and R_A achieved by the optimized CCCR, the primary CCCR, and the commercial CCCR were calculated and are shown in Figure 23 and Figure 24 individually for comparison.

In order to demonstrate that the optimized CCCR can really meet SAE requirements and perform better than the commercial sample, it was prototyped and tested in practical experiments, shown in Figure 25. Through the proposed experimental setup in Figure 10, the retroreflected outputs on screen by the commercial CCCR and the optimized CCCR are presented in Figure 26, and the resulting R_I at rotational angles of 0°, 10° U, 10° D, 20° L, and 20° R were calculated and are shown in Figure 27.

5. Discussion of the Results

In the study, a curved retroreflector with 120 mm × 28 mm reflecting area was built by 15 arrays of double-pin groups, and each pin cross-section size was 5.56 mm. It was demonstrated that the CCCR could retroreflect one incident beam as six beams, as shown in Figure 12. In the optimization process, the height differences d_i among the pin groups were set as variables. In order to find the optimal height difference under the limit of computer memory, only 15 sets of d_i were used. Therefore, the retroreflector structure was controlled and could be adjusted in one dimension only, resulting in the annoying staircase effect. However, if the height of all double-pin groups was allowed to change independently during the optimization procedure, we believe that the staircase effect can be diminished and more complex curved retroreflector design can be accomplished. If the CCCR has a curved outlook, the height between each pin group due to surface curvature would affect optical characteristics, leading to lower reflection efficiency and even failing to pass SAE regulations. By using double-pin groups to build the primary CCCR, reflection efficiency can be improved. Through OptisWorks software to produce the optimized CCCR, R_I can be increased further, but sacrificing reflection efficiency R_A, as shown in Figure 23 and Figure 24.

6. Conclusions

Serving as an efficient working area ratio, reflection efficiency R_A and coefficient of luminous intensity R_I as evaluation indices for a commercial CCCR and a proposed new design are compared. It can be concluded that the optimized CCCR redistributed the reflected light beam energy of the primary CCCR, which shared more energy in the 0.2° up-reflected beam by taking energy from the other five reflected beams. After computer simulations and optical experiments, it was demonstrated that the proposed CCCR not only exceeded SAE standards, listed in Table 1, but also had 33% more working area and much better reflection efficiency than the commercial one, whose posterior region was not effective at all, as shown in Figure 26 and Figure 27. Based on the data in Figure 27, it can be computed that the ratio of average R_I of the optimized CCCR to that of the commercial CCCR is (13419/9470, 0°), (5900/4263, 10° U), (3916/2832, 10° D), (4218/2983, 20° L), and (4354/3080, 20° D), which means 29.43% (0°), 27.75% (10° U), 27.67% (10° D), 29.27% (20° L), and 29.26% (20° R) higher retroreflection efficiency can be accomplished by the proposed CCCR.