Next Article in Journal
Selective and Recyclable Sensing of Aqueous Phase 2,4,6-Trinitrophenol (TNP) Based on Cd(II) Coordination Polymer with Zwitterionic Ligand
Next Article in Special Issue
Two 1-D Coordination Polymers Containing Zinc(II) Hexaborates: [Zn(en){B6O7(OH)6}]·2H2O (en = 1,2-diaminoethane) and [Zn(pn){B6O7(OH)6}]·1.5H2O (pn = 1,2-diaminopropane)
Previous Article in Journal
Thickness Study of Er-Doped Magnesium Zinc Oxide Diode by Spray Pyrolysis
Previous Article in Special Issue
Self-Assembly of a Carboxyl-Functionalized BODIPY Dye via Hydrogen Bonding
 
 
Search for Articles:
Title / Keyword
Author / Affiliation / Email
Journal
Article Type
 
 
Advanced Search
 
Section
Special Issue
Volume
Issue
Number
Page
 
Journals
Crystals
Volume 8
Issue 12
10.3390/cryst8120455
crystals-logo
Submit to this Journal Review for this Journal Propose a Special Issue
► Article Menu

Article Menu

share Share announcement Help format_quote Cite question_answer Discuss in SciProfiles thumb_up
...
Endorse textsms
...
Comment
first_page
settings
Order Article Reprints
Font Type:
Arial Georgia Verdana
Font Size:
Aa Aa Aa
Line Spacing:
Column Width:
Background:
Article

The Importance of CH···X (X = O, π) Interaction of a New Mixed Ligand Cu(II) Coordination Polymer: Structure, Hirshfeld Surface and Theoretical Studies

by
Saikat Kumar Seth
Department of Physics, Jadavpur University, Kolkata 700032, India
Crystals 2018, 8(12), 455; https://doi.org/10.3390/cryst8120455
Submission received: 22 October 2018 / Revised: 3 December 2018 / Accepted: 5 December 2018 / Published: 7 December 2018
(This article belongs to the Special Issue Self-Assembled Supramolecular Polymers via Strong H Bonding)
Browse Figures
Versions Notes

Abstract

:
In this study, a new equimolar (1:1:1) mixed ligand Cu(II) polymer, [Cu(IDA)(ImP)]n (1) with iminodiacetato (IDA) and imidazo[1,2-a]-pyridine (ImP) was synthesized and characterized by single crystal X-ray diffraction analysis. X-ray crystallography reveals that compound (1) consists of polymeric zigzag chain along [010] the carboxylate carbonyl oxygen atom by two-fold symmetry screw axis. The solid-state structure is stabilized through C–H···O hydrogen bonds and C–H···π interactions that lead the molecules to generate two-dimensional supramolecular assemblies. The intricate combinations of hydrogen bonds and C–H···π interactions are fully described along with computational studies. A thorough analysis of Hirshfeld surface and fingerprint plots elegantly quantify the interactions involved within the structure. The binding energies associated with the noncovalent interactions observed in the crystal structure and the interplay between them were calculated using theoretical DFT calculations. Weak noncovalent interactions were analyzed and characterized using Bader’s theory of ‘‘atoms-in-molecules’’ (AIM). Finally, the solid-state supramolecular assembly was characterized by the “Noncovalent Interaction” (NCI) plot index.

Graphical Abstract

1. Introduction

Coordination polymers (CPs) and/or metal-organic framework (MOFs) [1,2,3] represent multi-dimensional periodic structures of metal ions that are interconnected by organic bridging ligands, and have attracted great interest from scientists in the fields of crystal engineering, materials science, and supramolecular chemistry [4,5]. The rational design of CPs has increased significantly, owing to their fascinating structural architectures and their emerging application areas, including gas adsorption/separation, catalysis, magnetism, luminescence, sensors, etc. [6,7,8,9]. The most effective route to construct CPs is to use metal ions with mixed bridging ligands, especially with the bridging ligands containing O/N atoms [10,11,12]. In the construction of CPs, carboxylates and N-donor ligands have been widely chosen [13,14,15] as building blocks mainly due to two aspects: (i) They can exhibit rich coordination modes and (ii) they can participate in hydrogen bonding interactions by acting as donors and/or acceptors. The rational design of CPs is the control of linkage between the metal ions that allows the construction of particular structural motifs and the chemical properties of the crystalline solids [16,17]. Though there are suitable ligands and metal ions to obtain CPs, it is still a prodigious task to predict the final structure, depending on reaction conditions in the self-assembly [18,19]. The interconnectivity of organic spacers and the presence of ancillary ligands plays a substantial role in estimating the final structures [18,20]. Moreover, CPs can organize their final solid-state structure by employing a variety of non-bonded interactions such as electrostatic attraction, hydrogen bonding, interactions involving π-ring [21,22,23,24]. In this respect, C–H···π [25,26,27], π-stacking [28,29,30,31], anion···π [32,33,34,35] and lone pair···π [36,37] interactions have been successfully used in building supramolecular networks [38]. A proper understanding of these forces is extremely significant, since the problem of prediction is often limited to the recognition patterns or supramolecular synthons of different functional groups. The control of the topology of crystal packing through covalent and noncovalent interactions is the main goal of crystal engineering. Therefore, proper understanding of noncovalent forces is crucial to design and predict new supramolecular entities based on mono-dimensional coordination polymers.
Keeping this in mind, a new Cu(II) polymer [Cu(IDA)(ImP)]n (1) (H2IDA = Iminodiacetic acid and ImP = Imidazo[1-a]-pyridine]), has been synthesized (see Scheme 1) and characterized by single crystal X-ray diffraction. The title 1D polymer is stabilized through hydrogen bonds and C–H···π interaction in building 2D layered structures. The structural descriptions have been corroborated with theoretical calculations. The weak noncovalent interactions observed in the title polymer have been analyzed both energetically and using Bader’s theory of “atoms in molecules” by means of Density Functional theory (DFT) calculations.

2. Materials and Methods

2.1. Materials and Measurements

The reaction was carried out in aerobic conditions and in an aqueous medium. Iminodiacetic acid (Aldrich, St. Louis, Missouri, United States), basic copper(II) nitrate trihydrate (Sigma, St. Louis, Missouri, United States), and Imidazo[1,2-a]-pyridine (Aldrich, St. Louis, Missouri, United States) were used as received. Double distilled and then freshly boiled water was used throughout. IR spectra (KBr disk) was performed on a Perkin-Elmer RXI FT-IR spectrophotometer (Perkin Elmer Inc.,Waltham, MA, USA). Elemental analysis was carried out on a Perkin-Elmer 240C elemental analyzer.

2.2. Synthesis

Basic copper(II) nitrate trihydrate [purum ≥ 98.0%], Cu(NO3)2·3H2O (0.483 g, 2.0 mmol), was reacted with iminodiacetic acid [purum ≥ 98.0%] (0.266 g, 2.0 mmol) in water (25 mL) nearly at 70 °C until a clear solution resulted in an open glassware. A warm (∼40 °C) aqueous solution (20 mL) of Imidazo[1,2-a]-pyridine [purum ∼ 99.0%] (0.236 g, 2.0 mmol) was then added dropwise to the above solution with continuous stirring for about an hour at normal laboratory temperature (∼30 °C). The solution mixture was then left undisturbed for a few days when block shaped; light blue crystals suitable for X-ray diffraction analysis were obtained. The crystals were collected by filtration, washed with cold water, and dried in air (yield = 60%). Anal. Calcd. for C11H11CuN3O4 (MW = 312.74): C, 42.24; H, 3.54; N, 13.43%. Found: C, 46.21; H, 3.51; N, 13.46%. FT–IR (cm−1): 3185 (b), 3120 (s), 3081 (s), 3046 (s), 2922 (b), 1657 (s), 1615 (s), 1503 (s), 1435 (s), 1411 (s), 1375 (s), 1338 (s), 1315 (s), 1288 (s), 1238 (s), 1164 (s), 1127 (s), 1109 (s), 1026 (s), 1011 (s), 959 (s), 905 (s), 870 (s), 788 (s), 762 (s), 747 (s), 727 (s), 663 (s), 637 (s), 608 (s), 580 (s), 556 (s), 506 (s), 456 (s).

2.3. X-ray Crystallography Study

The single crystal X-ray diffraction intensity data of the title compound was collected at 293(2) K using a Bruker APEX-II CCD diffractometer equipped with graphite monochromated MoKα radiation (λ = 0.71073 Å). Data reduction was carried out using the Bruker SAINT [39] program and an empirical absorption correction was applied based on the multi-scan method [40]. The structure of the title compound was solved by the direct method and refined by the full-matrix least-square technique on F2 using the programs SHELXS-14 [41] and SHELXL-18 [42], respectively. All the hydrogen atoms were placed at their geometrically idealized positions and refined isotropically. All calculations were carried out using the WinGX system V2014.1 [43] and PLATON [44]. A summary of crystal data and relevant refinement parameters are given in Table 1. CCDC 1,868,166 contain the supplementary crystallographic data of this paper.

2.4. Hirshfeld Surface Analysis

The molecular Hirshfeld surface [45,46,47,48,49] is created based on the electron distribution of a molecule and has been calculated as the sum of spherical atom electron densities [50,51]. For a given crystal structure and set of spherical atomic electron densities, the Hirshfeld surface is unique [52]. The normalized contact distance (dnorm) calculated by Equation (1) was used to locate both inner and outer intermolecular interactions simultaneously on a single Hirshfeld surface [45]. Where, de is the distance from the point to the nearest nucleus external to the surface, di is the distance to the nearest nucleus internal to the surface; rivdw and revdw are the internal and external van der Walls (vdW) radii of the two atoms to the surface, respectively. The 2D fingerprint plot provides a summary of intermolecular contacts in the crystal [52,53,54,55,56]. The Hirshfeld surface presented here was generated using Crystal Explorer 3.1. [57].
d n o r m = d i − r i v d w r i v d w + d e − r e v d w r e v d w

2.5. Theoretical Methods

The energies of the title compound included in this study were performed using Gaussian 09 calculation package [58] at the B3LYP level with a large basis set 6-311++G(d,p). The visualization of the results is accomplished with GaussView 5.0. The B3LYP method of DFT is quite reliable for the prediction of geometric and electronic properties of neutral [59] and charged species [60], ranging from simple molecular to polymer structures [61]. For the theoretical analysis of the noncovalent interactions present in the solid state, we have used crystallographic coordinates. The Bader’s “Atoms in molecules” theory [62] has been used to analyze the interactions studied herein by means of the AIMall calculation package [63]. The topological properties of the charge density (ρ(r)) characterized by their critical points (CPs) and its Laplacian, which is expressed in terms of L(r) = −∇2 (ρ(r)), were calculated using the Atom In Molecule (AIM) theory [64]. It is noted that electron density is concentrated where ∇2 (ρ(r)) < 0 and it is depleted where ∇2 (ρ(r)) > 0. The calculations for the wave function analysis have been performed using Gaussian09 calculation package [58]. The NCI is a visualization index based on the electron density and its derivatives [65]. Since the noncovalent interactions are represented using isosurfaces instead of critical points, it enables their efficient visualization and identification. The isosurfaces may correspond to either favorable or unfavorable interactions, which are differentiated by the signs of the second density Hessian eigenvalues and defined by the isosurface color. NCI plot facilitates the assessment of host-guest complementarity and the extent to which weak interactions stabilize a complex. However, the information delivered by NCI plots is fundamentally qualitative, i.e., which molecular regions are interacting. The color scheme is a red-yellow-green-blue scale with red for ρ+cut (repulsive) and blue for ρ−cut (attractive). Yellow and green surfaces correspond to weak repulsive and weak attractive interactions, respectively [65].

3. Results and Discussion

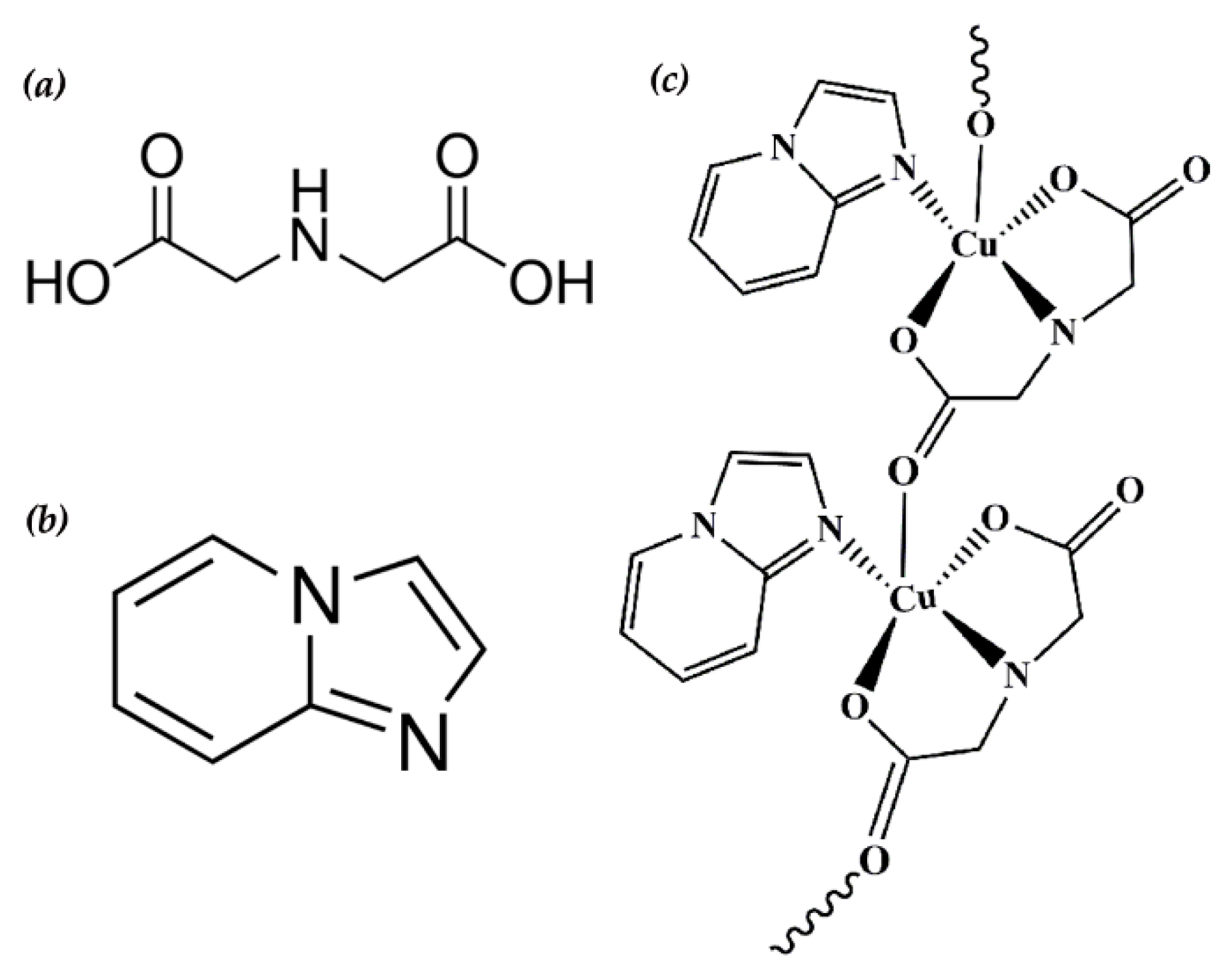
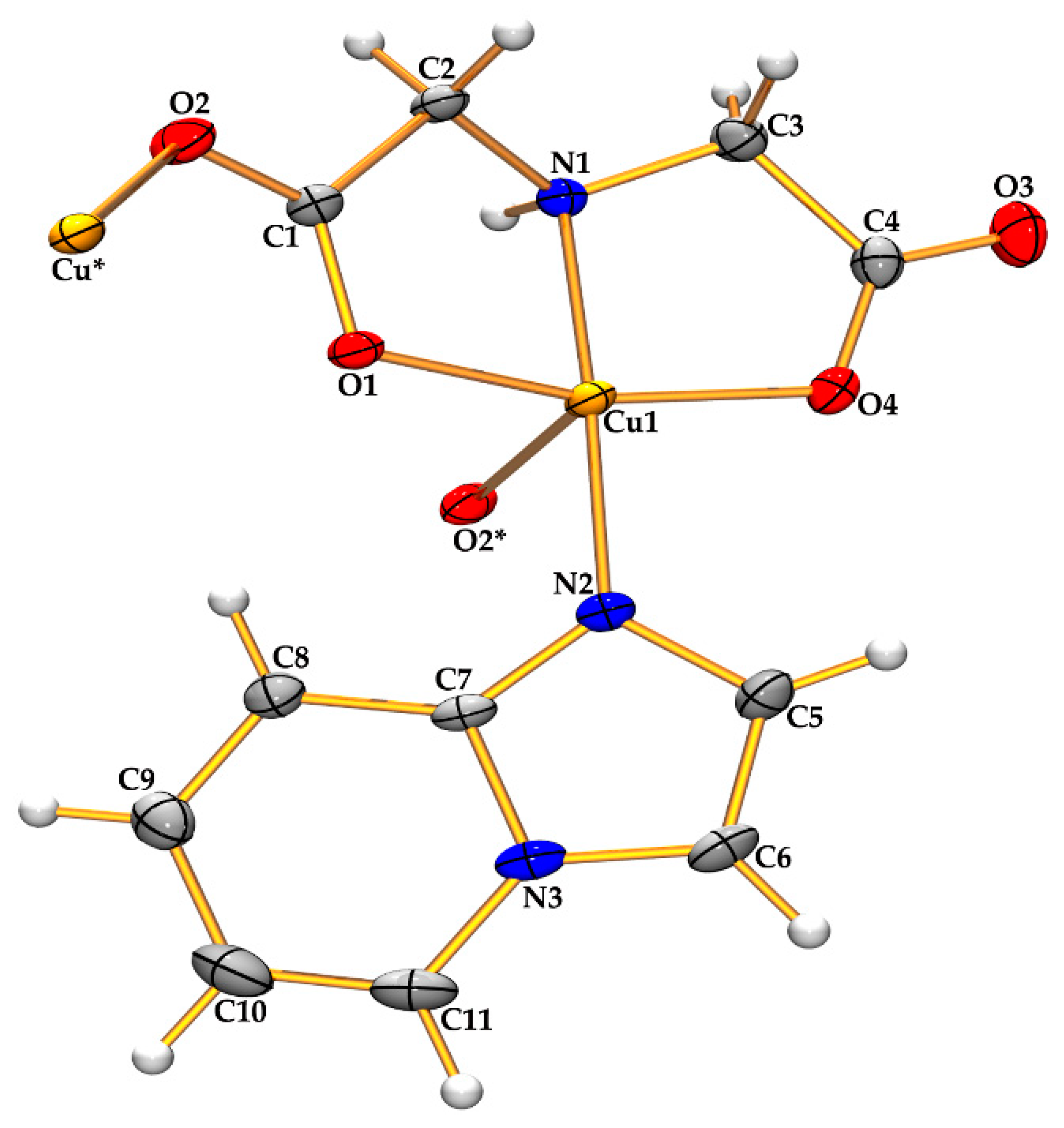
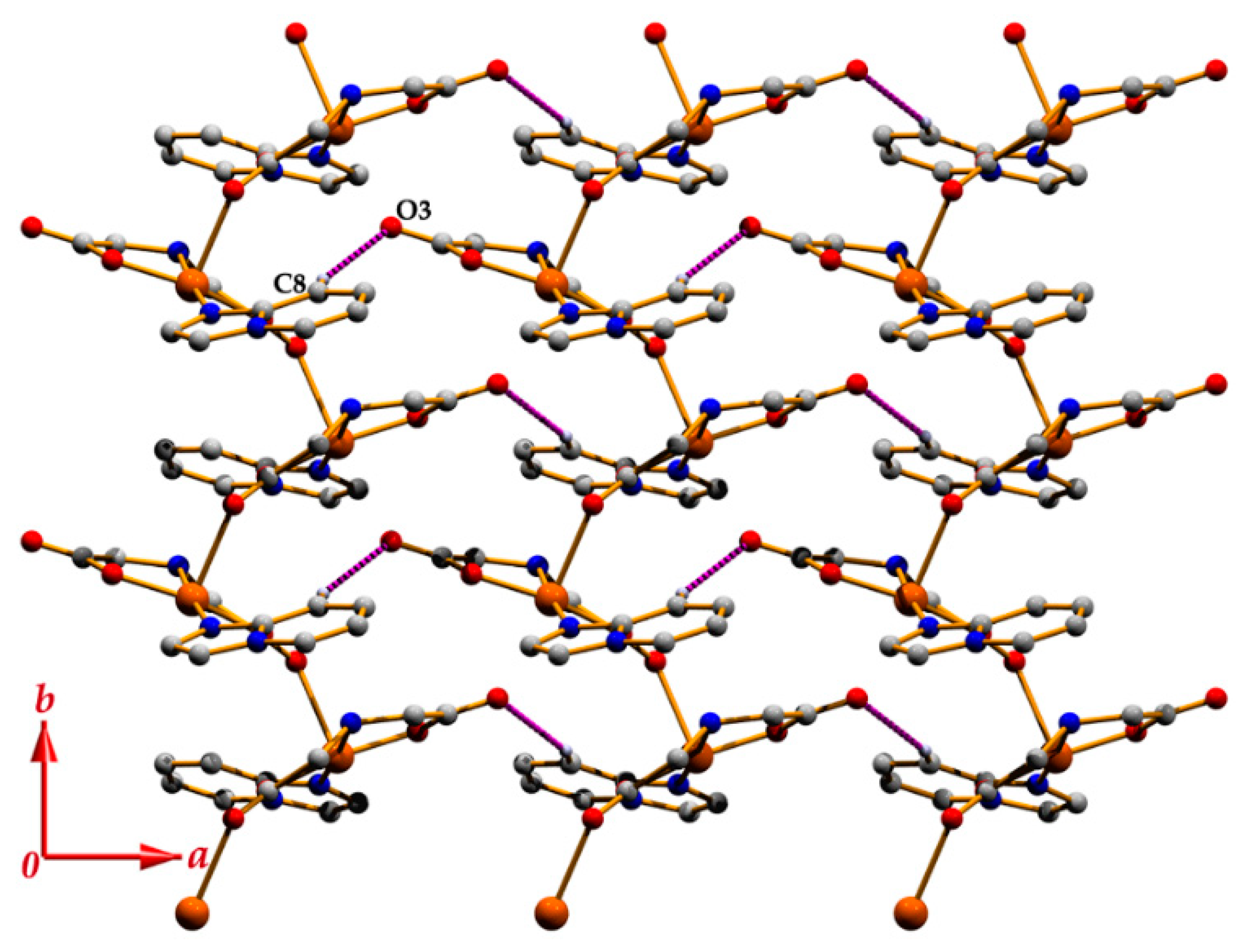
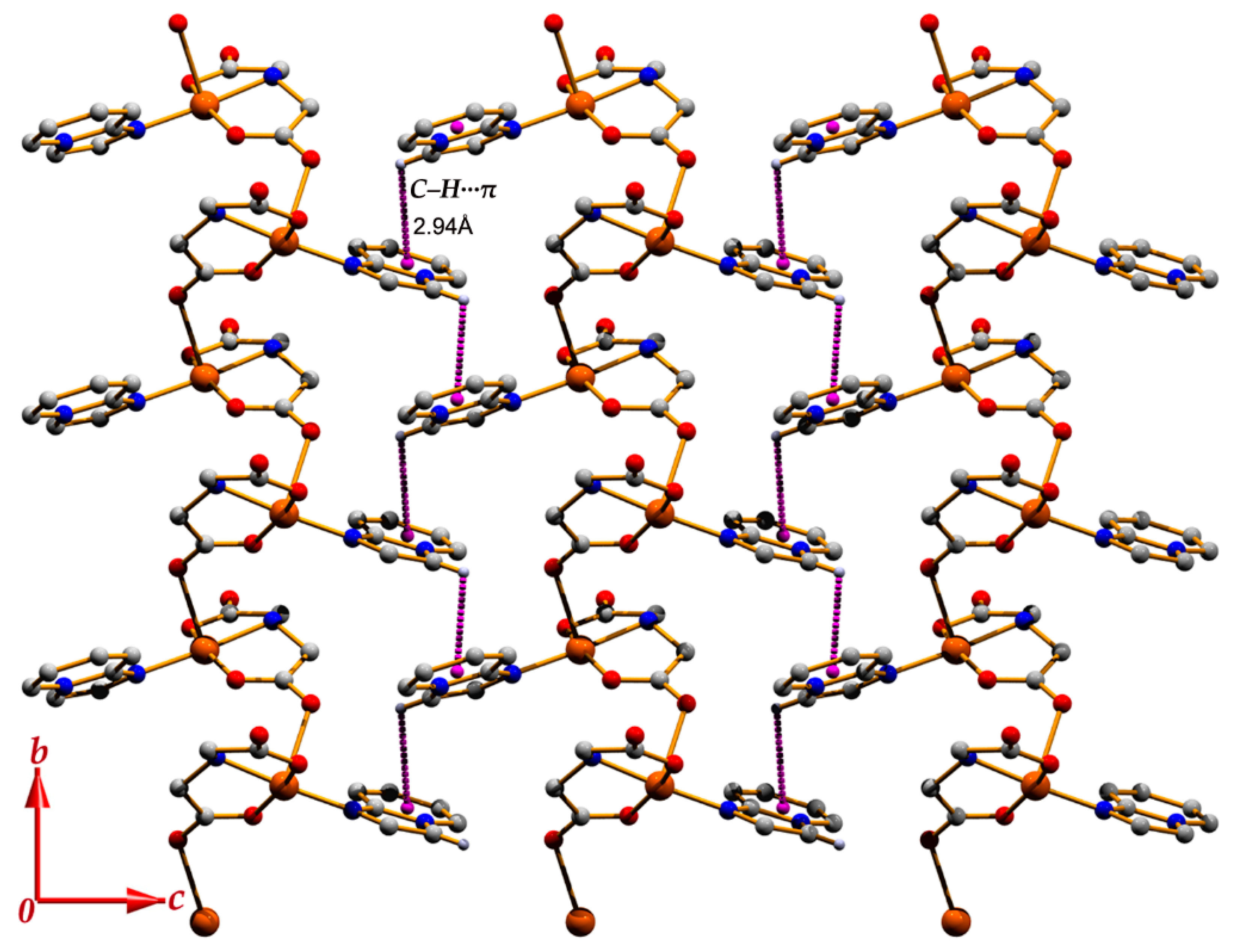
3.1. Structural Description

Crystal structure analysis reveals that compound (1) is a one-dimensional metal-organic coordination polymer constructed from Cu(II) ion, iminodiacetic acid, and imidazo[1,2-a]-pyridine. An ORTEP drawing is presented in Figure 1 with atom numbering scheme. Two carboxylate oxygen atoms and one nitrogen atom of the IDA ligand and one nitrogen atom of the ImP molecule define a distorted square base coordination geometry. The Cu(II) atom is displaced only 0.051(1) Å from the mean plane P(1) generated through the atoms (O1-O4-N1-N2). The Cu(II) is displaced towards the fifth donor atom O2i (symmetry code i = 2 − x, 1/2 + y, 1 − z) of the adjacent IDA ligand that is related to the former molecule by two-fold symmetry screw axis. The Cu(II) atom lies in a rather common distorted square base pyramidal environment of the type (4 + 1) and therefore, the Cu-O2i bond-length is typically longer in comparison to other four coordination bonds (Table S1). The imidazo[1,2-a]-pyridine is strictly planar and Cu(II) atom lies 0.082 Å out from this plane P(2) that defines a dihedral angle of 36.29° with plane P(1). The percentage of trigonal distortion of the square pyramidal stereochemistry [66], obtained from trans angles θ = N(1)-Cu(1)-N(2) and ρ = O(1)-Cu(1)-O(4), is τ = 100(θ − ρ)/60 = 19.5. This value is comparable with the reported analogous five-coordinated compounds [Cu(IDA) (4-aminopyridine)(H2O)] [36] and [Cu(IDA)(5MeImH) [67] and significantly higher than [[Cu(MIDA) (ImH)] [68] and low value compare to the compound [Cu(IDA)(ImH)(H2O)]·H2O [69]. Again, the dihedral angle between the mean planes for the two Cu-glycinate five-membered rings (φ = 22.30°) shows almost coplanar conformation of the five-membered chelate rings of Cu(IDA) moiety. This structural feature agrees well with the nearly coplanar chelate rings in the Cu(IDA) moiety of the 1:1:1 Cu/IDA/N-heterocyclic donor compounds reported earlier [36,67,68,70].
In compound (1), the molecules are propagating along [010] direction through coordination-bonding mode and generating a 1-D coordination polymer (See Figure 2). The solid-state structure of (1) comprises a combination of N–H···O, C–H···O hydrogen bonds and C–H···π interactions (Table 2). The [Cu(IDA)(ImP)] units are interconnected to generate the polymeric chain through the coordination bonding in between parent Cu(1) atom and carbonyl oxygen atom O(2) of the partner molecule (Figure 2). The 1D polymeric chain network is further strengthened by N–H···O hydrogen bonding contacts, where the nitrogen atom N(1) acts as a donor to the carboxylate oxygen atom O(1) in the molecule at (2 − x, 1/2 + y, 1 − z) (See Figure S1). The ring carbon atom C(8) acted as a donor to the carbonyl oxygen atom O(3) of the parallel chain structure in the molecule at (1 + x, y, z), thereby generating a two-dimensional layer network in (110) plane (Figure 2).
In another substructure, the molecules are self-assembled through two C–H···O bonding interactions. Interconnection in between carbon atoms C(8) and C(6) with carbonyl oxygen atoms O(3) and O(2) in the molecule at (1 + x, y, z) and (x, y, 1 + z) respectively, leads the molecules to generate a two-dimensional supramolecular network in (101) plane (Figure 3).
In the final substructure, the 1-D parallel chain is juxtaposed through self-complementary C–H···π interactions. The carbon atom C(6) in the molecule at (x, y, z) acts as a donor to the π-cloud of the pyridine ring at (2 − x, 1/2 + y, 2 − z) (Table 2); therefore generating a two-dimensional supramolecular self-assembled structure in (011) plane (Figure 4). Consequently, this entire assembly as a whole produces a supramolecular combination of C–H···π interactions that illustrates the occurrence of a self-assembled two-dimensional supramolecular layered structure of a polymeric compound.

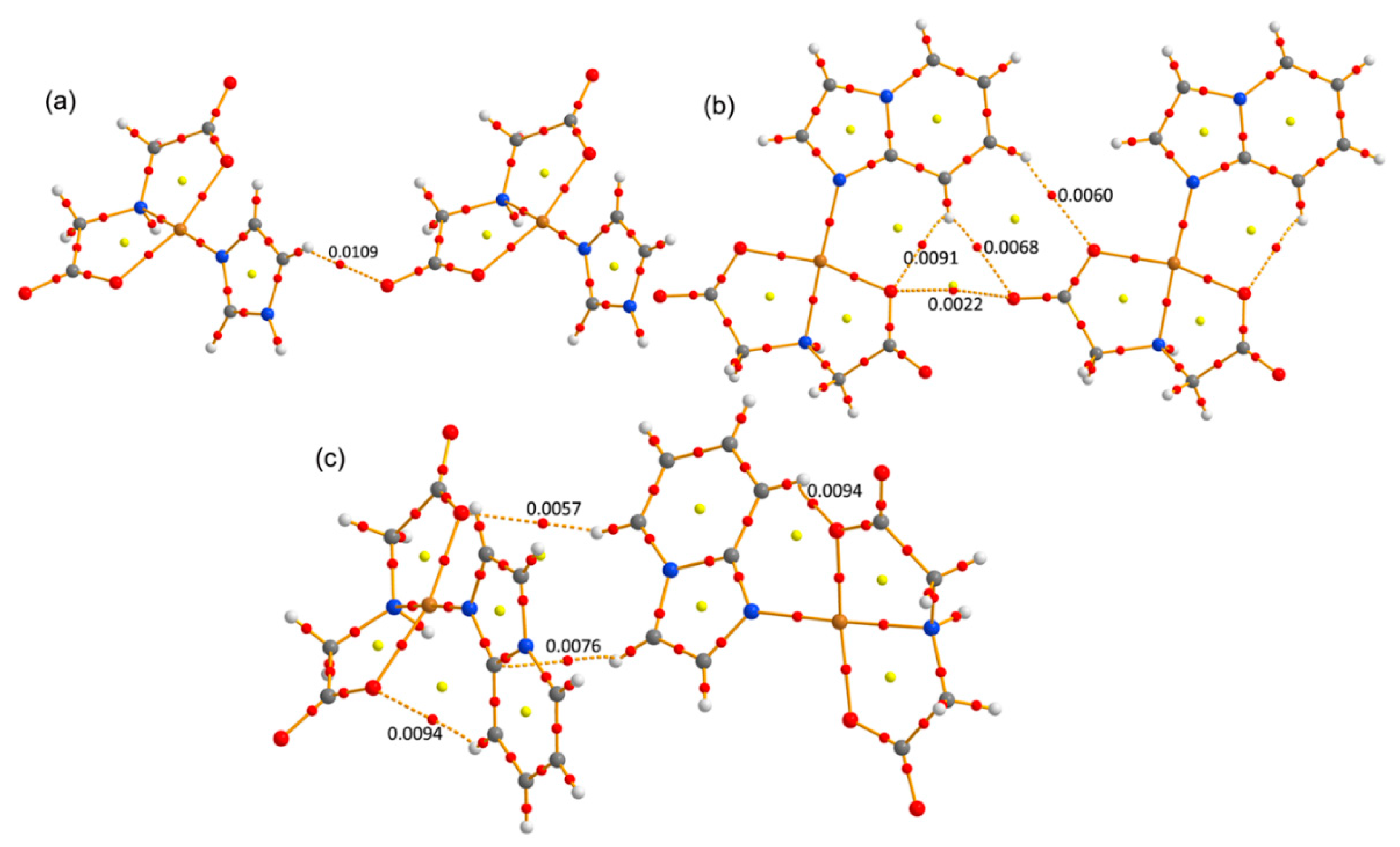
3.2. Hirshfeld Surface

The Hirshfeld surface [45,46,47,48,49] emerged from a unique attempt to define the space occupied by a molecule in a crystal to partition the crystal electron density into molecular fragments [50,51]. In this study, the contacts that are responsible in the crystal packing are estimated with respect to their contribution to the crystal structure. The Hirshfeld surface of the title compound is illustrated in Figure 5 showing surfaces that have been mapped over dnorm and de. The information concerning intermolecular interactions that are presented in Table 2 are noticeable by the spots on the dnorm surface. The large circular depression (deep red) on the dnorm surface, which is evident just above the metal ion, designate the Cu···O bonding contacts. Other light-colored depressions on the dnorm surface are an indicator of weaker contacts. Fingerprint plots are the key tools for the calculation of the density of intermolecular contacts present in a crystal and can be decomposed to quantify individual contributions of intermolecular interactions related to each structure. The combination of de and di in the form of a 2D fingerprint plot [52,53,54,55,56] provides a summary of the intermolecular contacts in the crystal, where one molecule acts as a donor (de > di) and other as an an acceptor (di > de). The Cu···O/O···Cu contacts are evidenced by two distinct spikes in the (di, de) region (1.262 Å, 1.171 Å) of the fingerprint plot that comprised 4.8% of the total Hirshfeld surface area of the molecule (Figure S2). The N···H/H···N contacts are evidenced by the scattered points on the fingerprint plot (Figure S2), where N···H interaction contributed more [2.4%; (di = 1.818, de = 1.242)] compared to the H···N counterpart [1.8%; de = 1.188, di = 1.242)]. The O···H/H···O interactions contributed 29.6% and are evidenced by the distinct spikes in the (di, de) region of (1.171 Å, 0.831 Å) (Figure 6). The C···H/H···C interactions appear as two spikes in the fingerprint plot, where the proportion of C···H/H···C interactions comprise 18.4% of the total Hirshfeld surface area of (1). The C···H interactions are represented by the spike in the bottom right region (di = 1.552 Å, de = 1.056 Å), whereas the H···C spike is located at (de = 1.562 Å, di = 1.056 Å) and comprises 10.7% and 7.7%, respectively (Figure 6).
Apart from the hydrogen bonding contacts, the structure is stabilized through C–H···π interaction and is visible on the de surface as well as in the fingerprint plot. The ‘bright-orange’ spot and consequently a large depression on the de surface above the π-cloud of the aryl ring indicates the existence of a C–H···π interaction (Figure 5). Moreover, the C–H···π interaction is also evidenced by a pair of ‘wings’ in the fingerprint plot, where the left wing region (di < de) correspond to the points on the surface around the C–H donor and the right wing region (de < di) corresponds to the points around the π-acceptor. From Hirshfeld surface calculations, it is not possible to individuate the C···H/H···C contacts for hydrogen bond and C–H···π interactions. The decomposed dnorm plots corresponding to each type of interactions involved within the structure are included in Figure S3. The decomposed fingerprint plots corresponding to various interactions that contributed more than 5% are included in Figure 6, whereas the others are included in Figure S1. A detailed analysis of intermolecular contacts reveals that the title compound comprises C···O/O···C, C···N/N···C and N···O/O···N contacts that comprised only 1.5%, 1.9% and 1.0%, respectively (Figure S2). Significant molecular interactions of the title compound in terms of O···O and C···C contacts are reflected in the distribution of scattered points in the region of (di = de = 1.805 Å) and (di = de = 1.813 Å) respectively (Figure S2). Moreover, the distribution of scattered points in the fingerprint plot that spread only up to (di = de = 1.101 Å) designate H···H contacts that comprises 33.9% (Figure 6) of the total Hirshfeld surface area of compound (1).

3.3. Theoretical Calculations

Computational studies are included herein to analyze the noncovalent interactions using theoretical DFT calculation. This study mainly focused on two issues: First, the energetic features of the interactions are studied and second, the interplay of noncovalent interactions are characterized by Bader’s theory of “atoms-in-molecules” (AIM). The crystallographic coordinates have been used in the computational studies. To evaluate formation energies, few models were prepared following self-assembled X-ray structure (Figure 7 and Figure 8). Following the X-ray fragment (Figure 7a), the imidazo[1,2-a]-pyridine moiety is simplified (see the black arrow in Figure 7b) to avoid the short contact in between the pyridine ring carbon atom and the carbonyl oxygen atom. In this model (model-1), the formation energy of the C–H···O hydrogen bond is ΔE1 = −5.6 Kcal/mol. Following Figure 2 and Figure 3, we are interested to evaluate the formation energy of the C8–H8···O3 hydrogen bond. In model-2 (Figure 7c), it is observed that another pyridine ring carbon atom C9 is in contact with the carboxylate oxygen atom O4 (see red dotted line). Mutual interactions displayed the formation energy of ΔE2 = −3.5 Kcal/mol.
Again, following an X-ray structure (Figure 8a), we carried out formation energy of C–H···π interaction in some models; the results are included in Figure 8b–d. In model-3, we computed the interaction energy using two uncoordinated imidazo[1,2-a]-pyridine moieties (Figure 8b). As a result, the interaction energy is modest (ΔE3 = −0.9 Kcal/mol). In another model, we analyzed the effect of metal coordination, including IDA moiety, keeping other imidazo[1,2-a]-pyridine moiety fixed (Figure 8c). As a result, the interaction energy increases to ΔE4 = −2.2 Kcal/mol, therefore confirming the reinforcement of the C–H···π interaction due to the metal coordinated moiety. In the fifth model, we studied the effect of the coordination mode in both moieties to analyze the strength of the interaction. It is expected to have a stronger effect on the strength of the interaction. As expected, the interaction energy of the theoretical model (Figure 8d) is ΔE5 = −3.0 Kcal/mol, which is much more favorable than ΔE3 = −0.9 Kcal/mol.
We performed the Bader’s theory of atoms in molecules (AIM) analysis of compound (1) by using the models described above. The AIM analysis has been included for visualization and characterization of the noncovalent interactions following the distribution of the critical points and bond paths. The existence of a bond critical point (CP) and bond path connecting two atoms designate the interaction between those two atoms [62]. The hydrogen bonding interactions are characterized by the distribution of CPs and bond paths of the models used for compound (1) (see Figure 9). In Figure 9a, the hydrogen bonding interaction is characterized by the presence of a bond critical point that is represented by a red sphere and corresponding bond path between the hydrogen atom of the parent ring carbon atom and carbonyl oxygen atom of the partner molecule. The ρ(r) value (0.0109 a.u.) of the bond CP is also analyzed to verify the strength of the interaction. In the second model, the hydrogen bonding is characterized by the bond CP (ρBCP = 0.0068 a.u.) and bond path connecting hydrogen atom of the pyridine ring and carbonyl oxygen atom. As discussed earlier (red dotted lines in Figure 7c), another interaction is evidenced by CP (ρBCP = 0.0060 a.u.) and the corresponding bond path. Therefore, a ring CP is generated due to the formation of a ring motif and is represented by a yellow sphere.
The intramolecular C–H···O bonding and O···O contacts are also evidenced in AIM analysis and are characterized by the bond CPs, 0.0091 a.u and 0.0022 a.u, respectively (Figure 9b). The inspection of the results indicates that the values of ρ(r) are larger in model 1 (0.0109 a.u.) than model 2 (0.0068 a.u.), in good agreement with the energetic analysis commented above. Furthermore, we analyzed the C–H···π interaction, depicted in Figure 9c. The bond CP (ρBCP = 0.0076 a.u.) and bond path connecting hydrogen atom of the imidazo ring carbon atom and carbon atom of the pyridine ring characterized the C–H···π interaction in (1). Finally, we further characterized the C–H···π interaction using the NCI index. The representation of NCI plot obtained for dimer that highlights the C–H···π interaction of compound (1) is shown in Figure 10. The π-facial noncovalent interaction involving the C-H donor of the ring carbon atoms is characterized by the extended green isosurface. The green isosurface has been identified over the rings of the imidazo[1,2-a]-pyridine ligand and directed towards the C-H bond, thus characterizing the C–H···π interaction. Moreover, the small blue-green isosurfaces characterize the hydrogen bonding interactions in between ring carbon atoms and carboxylate oxygen atoms and are in agreement with the energetic study.

4. Conclusions

In summary, the title polymeric compound reported herein exhibit C–H···O and C–H···π interactions in the solid state that have been characterized using Hirshfeld surface and high-level theoretical calculation. Noncovalent interactions play a decisive role in building supramolecular self-assemblies that have been evaluated by DFT calculations, AIM and NCI plot analyses. The contribution of noncovalent interactions in the self-assembly process was estimated by providing individual energy values through computational studies. The results reported herein are expected to be useful to understand the solid-state structure of coordination polymers and have possible importance for research studies in supramolecular chemistry and crystal engineering.

Supplementary Materials

The following are available online at https://www.mdpi.com/2073-4352/8/12/455/s1, One crystallographic file (CIF), CCDC-1868166; Table S1: Selected Bond-lengths (Å) and angles (°). Figures S1–S4: N–H···O bonded motif; Decomposed fingerprint plots; Decomposed plots of dnorm surface and PXRD.

Funding

This research received no external funding.

Conflicts of Interest

The author declares no conflict of interest. This research received no external funding and the Editor fully waived the APC since it was an invited article.

References

  1. Furukawa, H.; Cordova, K.E.; O’Keeffe, M.; Yaghi, O.M. The Chemistry and Applications of Metal-Organic Frameworks. Science 2013, 341, 1230444. [Google Scholar] [CrossRef]
  2. Zhou, H.-C.; Long, J.R.; Yaghi, O.M. Introduction to Metal–Organic Frameworks. Chem. Rev. 2012, 112, 673–674. [Google Scholar] [CrossRef] [PubMed]
  3. Batten, S.R.; Champness, N.R.; Chen, X.-M.; Garcia-Martinez, J.; Kitagawa, S.; Ohrstrom, L.; O’Keeffe, M.; Suh, M.P.; Reedijk, J. Coordination polymers, metal–organic frameworks and the need for terminology guidelines. CrystEngComm 2012, 14, 3001–3004. [Google Scholar] [CrossRef] [Green Version]
  4. Li, J.-R.; Sculley, J.; Zhou, H.-C. Metal–Organic Frameworks for Separations. Chem. Rev. 2012, 112, 869–932. [Google Scholar] [CrossRef] [PubMed]
  5. Liu, J.; Thallapally, P.K.; McGrail, B.P.; Brown, D.R.; Liu, J. Progress in adsorption-based CO2 capture by metal–organic frameworks. Chem. Soc. Rev. 2012, 41, 2308–2322. [Google Scholar] [CrossRef]
  6. He, H.; Song, Y.; Sun, F.; Bian, Z.; Gao, L.; Zhu, G. A porous metal–organic framework formed by a V-shaped ligand and Zn(II) ion with highly selective sensing for nitroaromatic explosives. J. Mater. Chem. A 2015, 3, 16598–16603. [Google Scholar] [CrossRef]
  7. Carlucci, L.; Ciani, G.; Proserpio, D.M.; Mitina, T.G.; Blatov, V.A. Entangled two-dimensional coordination networks: A general survey. Chem. Rev. 2014, 114, 7557–7580. [Google Scholar] [CrossRef]
  8. Nagarkar, S.S.; Joarder, B.; Chaudhari, A.K.; Mukherjee, S.; Ghosh, S.K. Highly Selective Detection of Nitro Explosives by a Luminescent Metal–Organic Framework. Angew. Chem. Int. Ed. 2013, 52, 2881–2885. [Google Scholar] [CrossRef]
  9. Liu, Y.-Y.; Wang, Z.-H.; Yang, J.; Liu, B.; Liu, Y.-Y.; Ma, J.-F. A series of coordination polymers based on reduced Schiff base multidentate anions and bis(imidazole) ligands: Syntheses, structures and photoluminescence. CrystEngComm 2011, 13, 3811–3821. [Google Scholar] [CrossRef]
  10. Du, M.; Li, C.P.; Liu, C.S.; Fang, S.M. Design and construction of coordination polymers with mixed-ligand synthetic strategy. Coord. Chem. Rev. 2013, 257, 1282–1305. [Google Scholar] [CrossRef]
  11. Li, M.-X.; Zhang, Y.-F.; He, X.; Shi, X.-M.; Wang, Y.-P.; Shao, M.; Wang, Z.-X. Diverse Structures and Ferro-/Ferri-/Antiferromagnetic Interactions of Pyridyltetrazole Coordination Polymers with Polycarboxylate Auxiliary Ligands. Cryst. Growth Des. 2016, 16, 2912–2922. [Google Scholar] [CrossRef]
  12. Li, Y.-L.; Zhao, D.; Zhao, Y.; Wang, P.; Wang, H.-W.; Sun, W.-Y. Synthesis, structure, and magnetic and catalytic properties of metal frameworks with 2,2′-dinitro-4,4′-biphenyldicarboxylate and imidazole-containing tripodal ligands. Dalton Trans. 2016, 45, 8816–8823. [Google Scholar] [CrossRef] [PubMed]
  13. Zhou, H.-C.; Kitagawa, S. Metal–Organic Frameworks (MOFs). Chem. Soc. Rev. 2014, 43, 5415–5418. [Google Scholar] [CrossRef]
  14. Amayuelas, E.; Fidalgo-Marijuan, A.; Barandika, G.; Bazán, B.; Urtiaga, M.K.; Arriortua, M.I. Mother structures related to the hexagonal and cubic close packing in Cu24 clusters: Solvent-influenced derivatives. CrystEngComm 2015, 17, 3297–3304. [Google Scholar] [CrossRef]
  15. Du, M.; Li, C.-P.; Liu, C.-S.; Fang, S.-M. Design and construction of coordination polymers with mixed-ligand synthetic strategy. Chem. Rev. 2013, 257, 1282–1305. [Google Scholar]
  16. Farrusseng, D. Metal-Organic Frameworks: Applications from Catalysis to Gas Storage, 1st ed.; Wiley-VCH: Weinheim, Germany, 2011. [Google Scholar]
  17. Tranchemontagne, D.J.; Mendoza-Cortés, J.L.; O’Keeffe, M.; Yaghi, O.M. Secondary Building Units, Nets and Bonding in the Chemistry of Metal-Organic Frameworks. Chem. Soc. Rev. 2009, 38, 1257–1283. [Google Scholar] [CrossRef] [PubMed]
  18. Erer, H.; Yesilel, O.Z.; Arıcı, M. A Series of Zinc(II) 3D → 3D Interpenetrated Coordination Polymers Based On Thiophene-2,5-dicarboxylate and Bis(Imidazole) Derivative Linkers. Cryst. Growth Des. 2015, 15, 3201–3211. [Google Scholar] [CrossRef]
  19. Zhou, L.; Wang, C.; Zheng, X.; Tian, Z.; Wen, L.; Qu, H.; Li, D. New metal–organic frameworks based on 2,5-thiophenedicarboxylate and pyridine- or imidazole-based spacers: Syntheses, topological structures, and properties. Dalton Trans. 2013, 42, 16375–16386. [Google Scholar] [CrossRef]
  20. Yaghi, O.M.; O’keeffe, M.; Ockwig, N.W.; Chae, H.K.; Eddaoudi, M.; Kim, J. Reticular synthesis and the design of new materials. Nature 2003, 423, 705–714. [Google Scholar] [CrossRef]
  21. Mitra, M.; Manna, P.; Das, A.; Seth, S.K.; Helliwell, M.; Bauzá, A.; Choudhury, S.R.; Frontera, A.; Mukhopadhyay, S. On the Importance of Unprecedented Lone Pair–Salt Bridge Interactions in Cu(II)–Malonate–2-Amino-5-Chloropyridine–Perchlorate Ternary System. J. Phys. Chem. A 2013, 117, 5802–5811. [Google Scholar] [CrossRef]
  22. Mitra, M.; Manna, P.; Seth, S.K.; Das, A.; Meredith, J.; Helliwell, M.; Bauzá, A.; Choudhury, S.R.; Frontera, A.; Mukhopadhyay, S. Salt-bridge–π (sb–π) interactions at work: Associative interactions of sb–π, π–π and anion–π in Cu(II)-malonate–2-aminopyridine–hexafluoridophosphate ternary system. CrystEngComm 2013, 15, 686–696. [Google Scholar] [CrossRef]
  23. He, Y.C.; Yang, J.; Kan, W.Q.; Zhang, H.M.; Liu, Y.Y.; Ma, J.F. A New Microporous Anionic Metal-Organic Framework as a Platform for Highly Selective Adsorption and Separation of Organic Dyes. J. Mater. Chem. A 2015, 3, 1675–1681. [Google Scholar] [CrossRef]
  24. Yan, W.; Han, L.J.; Jia, H.L.; Shen, K.; Wang, T.; Zheng, H.G. Three Highly Stable Cobalt MOFs Based on ″Y″-Shaped Carboxylic Acid: Synthesis and Absorption of Anionic Dyes. Inorg. Chem. 2016, 55, 8816–8821. [Google Scholar] [CrossRef]
  25. Seth, P.; Bauzá, A.; Frontera, A.; Massera, C.; Gamez, P.; Ghosh, A. Analysis of the contribution of the π-acidity of the s-tetrazine ring in the crystal packing of coordination polymers. CrystEngComm 2013, 15, 3031–3039. [Google Scholar] [CrossRef]
  26. Seth, S.K. Exploration of supramolecular layer and bi-layer architecture in M(II)–PPP complexes: Structural elucidation and Hirshfeld surface analysis [PPP = 4-(3-Phenylpropyl)pyridine, M = Cu(II), Ni(II)]. J. Mol. Struct. 2014, 1070, 65–74. [Google Scholar] [CrossRef]
  27. Maity, T.; Mandal, H.; Bauza, A.; Samanta, B.C.; Frontera, A.; Seth, S.K. Quantifying conventional C–H···π(aryl) and unconventional C–H···π(chelate) interactions in dinuclear Cu(II) complexes: Experimental observations, Hirshfeld surface and theoretical DFT study. New J. Chem. 2018, 42, 10202–10213. [Google Scholar] [CrossRef]
  28. Bloom, J.W.G.; Wheeler, S.E. Taking the Aromaticity out of Aromatic Interactions. Angew. Chem. Int. Ed. 2011, 50, 7847–7849. [Google Scholar] [CrossRef]
  29. Seth, S.K.; Sarkar, D.; Kar, T. Use of π–π forces to steer the assembly of chromone derivatives into hydrogen bonded supramolecular layers: Crystal structures and Hirshfeld surface analyses. CrystEngComm 2011, 13, 4528–4535. [Google Scholar] [CrossRef]
  30. Seth, S.K.; Manna, P.; Singh, N.J.; Mitra, M.; Jana, A.D.; Das, A.D.; Choudhury, S.R.; Kar, T.; Mukhopadhyay, S.; Kim, K.S. Molecular architecture using novel types of noncovalent π-interactions involving aromatic neutrals, aromatic cations and π-anions. CrystEngComm 2013, 15, 1285–1288. [Google Scholar] [CrossRef]
  31. Manna, P.; Seth, S.K.; Mitra, M.; Das, A.; Singh, N.J.; Choudhury, S.R.; Kar, T.; Mukhopadhyay, S. A successive layer-by-layer assembly of supramolecular frameworks driven by a novel type of face-to-face π+–π+ interactions. CrystEngComm 2013, 15, 7879–7886. [Google Scholar] [CrossRef]
  32. Frontera, A.; Gamez, P.; Mascal, M.; Mooibroek, T.J.; Reedijk, J. Putting Anion–π Interactions into Perspective. Angew. Chem. Int. Ed. 2011, 50, 9564–9583. [Google Scholar] [CrossRef] [PubMed]
  33. Manna, P.; Seth, S.K.; Mitra, M.; Choudhury, S.R.; Bauzá, A.; Frontera, A.; Mukhopadhyay, S. Experimental and Computational Study of Counterintuitive ClO4−···ClO4− Interactions and the Interplay between π+···π and Anion···π+ Interactions. Cryst. Growth Des. 2014, 14, 5812–5821. [Google Scholar] [CrossRef]
  34. Manna, P.; Seth, S.K.; Bauzá, A.; Mitra, M.; Choudhury, S.R.; Frontera, A.; Mukhopadhyay, S. pH Dependent Formation of Unprecedented Water–Bromide Cluster in the Bromide Salts of PTP Assisted by Anion···π Interactions: Synthesis, Structure, and DFT Study. Cryst. Growth Des. 2014, 14, 747–755. [Google Scholar] [CrossRef]
  35. Mitra, M.; Manna, P.; Bauzá, A.; Ballester, P.; Seth, S.K.; Choudhury, S.R.; Frontera, A.; Mukhopadhyay, S. 3-Picoline Mediated Self-Assembly of M(II)–Malonate Complexes (M = Ni/Co/Mn/Mg/Zn/Cu) Assisted by VariousWeak Forces Involving Lone Pair···π, π–π, and Anion···π–Hole Interactions. J. Phys. Chem. B 2014, 118, 14713–14726. [Google Scholar] [CrossRef] [PubMed]
  36. Seth, S.K.; Saha, I.; Estarellas, C.; Frontera, A.; Kar, T.; Mukhopadhyay, S. Supramolecular Self-Assembly of M-IDA Complexes Involving Lone-Pair···π Interactions: Crystal Structures, Hirshfeld Surface Analysis, and DFT Calculations [H2IDA = iminodiacetic acid, M = Cu(II), Ni(II)]. Cryst. Growth Des. 2011, 11, 3250–3265. [Google Scholar] [CrossRef]
  37. Manna, P.; Seth, S.K.; Das, A.; Hemming, J.; Prendergast, R.; Helliwell, M.; Choudhury, S.R.; Frontera, A.; Mukhopadhyay, S. Anion Induced Formation of Supramolecular Associations Involving Lone pair···π and Anion···π Interactions in Co(II) Malonate Complexes: Experimental Observations, Hirshfeld Surface Analyses and DFT Studies. Inorg. Chem. 2012, 51, 3557–3571. [Google Scholar] [CrossRef]
  38. Steed, J.W.; Turner, D.R.; Wallace, K.J. Core Concepts in Supramolecular Chemistry and Nanochemistry; John Wiley & Sons, Ltd.: Chichester, UK, 2007; pp. 194–228. [Google Scholar]
  39. Bruker. SAINT, Version 6.36a; Bruker-AXS Inc.: Madison, WI, USA, 2002. [Google Scholar]
  40. Bruker. SMART, Version 5.625 and SADABS, Version 2.03a; Bruker AXS Inc.: Madison, WI, USA, 2001. [Google Scholar]
  41. Sheldrick, G.M. A short history of SHELX. Acta Crystallogr. A 2008, 64, 112–122. [Google Scholar] [CrossRef]
  42. Sheldrick, G.M. Crystal structure refinement with SHELXL. Acta Crystallogr. C 2015, 71, 3–8. [Google Scholar] [CrossRef] [PubMed]
  43. Farrugia, L.J. WinGX suit for small-molecule single-crystal crystallography. J. Appl. Crystallogr. 1999, 32, 837–838. [Google Scholar] [CrossRef]
  44. Spek, A.L. Single-crystal structure validation with the program PLATON. J. Appl. Crystallogr. 2003, 36, 7–13. [Google Scholar] [CrossRef]
  45. Spackman, M.A.; McKinnon, J.J. Fingerprinting intermolecular interactions in molecular crystals. CrystEngComm 2002, 4, 378–392. [Google Scholar] [CrossRef]
  46. McKinnon, J.J.; Jayatilaka, D.; Spackman, M.A. Towards quantitative analysis of intermolecular interactions with Hirshfeld surfaces. Chem. Commun. 2007, 37, 3814–3816. [Google Scholar] [CrossRef]
  47. Seth, S.K.; Bauzá, A.; Frontera, A. Screening polymorphism in a NiIJII) metal–organic framework: Experimental observations, Hirshfeld surface analyses and DFT studies. CrystEngComm 2018, 20, 746–754. [Google Scholar] [CrossRef]
  48. Seth, S.K. Structural characterization and Hirshfeld surface analysis of a CoII complex with imidazo[1,2-a]-pyridine. Acta Crystallogr. E 2018, 74, 600–606. [Google Scholar] [CrossRef] [PubMed]
  49. Seth, S.K.; Bauzá, A.; Mahmoudi, G.; Stilinović, V.; López-Torres, E.; Zaragoza, G.; Keramidas, A.D.; Frontera, A. On the importance of Pb⋯X (X = O, N, S, Br) tetrel bonding interactions in a series of tetra- and hexa-coordinated Pb(II) compounds. CrystEngComm 2018, 20, 5033–5044. [Google Scholar] [CrossRef]
  50. Spackman, M.A.; Byrom, P.G. A novel definition of a molecule in a crystal. Chem. Phys. Lett. 1997, 267, 215–220. [Google Scholar] [CrossRef]
  51. McKinnon, J.J.; Mitchell, A.S.; Spackman, M.A. Hirshfeld Surfaces: A New Tool for Visualising and Exploring Molecular Crystals. Chem. Eur. J. 1998, 4, 2136–2141. [Google Scholar] [CrossRef]
  52. McKinnon, J.J.; Spackman, M.A.; Mitchell, A.S. Novel tools for visualizing and exploring intermolecular interactions in molecular crystals. Acta Crystallogr. B 2004, 60, 627–668. [Google Scholar] [CrossRef]
  53. Rohl, A.L.; Moret, M.; Kaminsky, W.; Claborn, K.; Mckinnon, J.J.; Kahr, B. Hirshfeld Surfaces Identify Inadequacies in Computations of Intermolecular Interactions in Crystals: Pentamorphic 1,8-Dihydroxyanthraquinone. Cryst. Growth Des. 2008, 8, 4517–4525. [Google Scholar] [CrossRef]
  54. Seth, S.K.; Sarkar, D.; Roy, A.; Kar, T. Insight into supramolecular self-assembly directed by weak interactions in acetophenone derivatives: Crystal structures and Hirshfeld surface analyses. CrystEngComm 2011, 13, 6728–6741. [Google Scholar] [CrossRef]
  55. Seth, S.K.; Sarkar, D.; Jana, A.D.; Kar, T. On the Possibility of Tuning Molecular Edges To Direct Supramolecular Self-Assembly in Coumarin Derivatives through Cooperative Weak Forces: Crystallographic and Hirshfeld Surface Analyses. Cryst. Growth Des. 2011, 11, 4837–4849. [Google Scholar] [CrossRef]
  56. Seth, S.K. Structural elucidation and contribution of intermolecular interactions in O-hydroxy acyl aromatics: Insights from X-ray and Hirshfeld surface analysis. J. Mol. Struct. 2014, 1064, 70–75. [Google Scholar] [CrossRef]
  57. Wolff, S.K.; Grimwood, D.J.; McKinnon, J.J.; Jayatilaka, D.; Spackman, M.A. CrystalExplorer 3.1; University of Western Australia: Perth, Australia, 2007. [Google Scholar]
  58. Frisch, M.J.; Trucks, G.W.; Schlegel, H.B.; Scuseria, G.E.; Robb, M.A.; Cheeseman, J.R.; Scalmani, G.; Barone, V.; Petersson, G.A.; Nakatsuji, H.; et al. Gaussian 09, Revision C.01; Gaussian, Inc.: Wallingford, CT, USA, 2009. [Google Scholar]
  59. Nisa, R.U.; Ayub, K. Mechanism of Zn(OTf)2 catalyzed hydroamination–hydrogenation of alkynes with amines: Insight from theory. New J. Chem. 2017, 41, 5082–5090. [Google Scholar] [CrossRef]
  60. Mahmood, T.; Kosar, N.; Ayub, K. DFT study of acceleration of electrocyclization in photochromes under radical cationic conditions: Comparison with recent experimental data. Tetrahedron 2017, 73, 3521–3528. [Google Scholar] [CrossRef]
  61. Bibi, S.; Ullah, H.; Ahmad, S.M.; Ali Shah, A.-U.-H.; Bilal, S.; Tahir, A.A.; Ayub, K. Molecular and electronic structure elucidation of polypyrrole gas sensors. Phys. Chem. C 2015, 119, 15994–16003. [Google Scholar] [CrossRef]
  62. Bader, R.F.W. A quantum theory of molecular structure and its applications. Chem. Rev. 1991, 91, 893–928. [Google Scholar] [CrossRef]
  63. Keith, T.A. AIMAll, Version 13.05.06; TK Gristmill Software: Overland Park, KS, USA, 2013. [Google Scholar]
  64. Bader, R.F.W. Atoms in Molecules, a Quantum Theory; Oxford University Press: New York, NY, USA, 1990. [Google Scholar]
  65. Contreras-García, J.; Johnson, E.R.; Keinan, S.; Chaudret, R.; Piquemal, J.-P.; Beratan, D.N.; Yang, W. NCIPLOT: A Program for Plotting Noncovalent Interaction Regions. J. Chem. Theory Comput. 2011, 7, 625–632. [Google Scholar] [CrossRef] [PubMed] [Green Version]
  66. Hathaway, B.J.; Wilkinson, G.; Gillard, R.D.; McCleverty, J.A. (Eds.) Comprehensive Coordination Chemistry; Pergamon Press: Oxford, UK, 1987; Volume 5, Chapter 53; p. 612. [Google Scholar]
  67. Castiñeiras Campos, A.; Busnot, A.; Abarca García, M.E.; Sicilia Zafra, A.G.; González Pérez, J.M.; Niclós Gutiérrez, J. Mixed-ligand copper(II) complexes with iminodiacetato and 2- or 4-methylimidazole: Molecular and crystal structure of the ‘remote’ isomer iminodiacetato(5-methylimidazole)copper(II) monohydrate, [Cu(IDA)(5MeImH)]·H2O. Inorg. Chim. Acta 1994, 215, 73–78. [Google Scholar] [CrossRef]
  68. Castiñeiras Campos, A.; Sicilia Zafra, A.G.; González Pérez, J.M.; Niclós Gutiérrez, J.; Chinea, E.; Mederos, A. Mixed-ligand copper(II) complexes with N-methyl derivatives of iminodiacetato or imidazole: Crystal structures of (N-methyliminodiacetato) (imidazole) copper(II), [Cu(MIDA) (ImH)] and diaqua (iminodiacetato) (N-methyl-imidazole) copper(II) monohydrate, [Cu(IDA) (1MelmH) (H2O)2]·H2O. Inorg. Chim. Acta 1996, 241, 39–45. [Google Scholar]
  69. Castiñeiras, A.; Tercero, J.M.; Matilla, A.; González, J.M.; Sicilia, A.G.; Niclós, J. Structures and properties of copper(II) complexes with iminodiacetato and imidazole or related ligands. I. crystal structure of aqua(imidazole)(iminodiaceato)copper(II) monohydrate and (imidazole)(N-carboxymethyl-d,l-Threoninato)copper(II). J. Coord. Chem. 1995, 35, 61–72. [Google Scholar] [CrossRef]
  70. Dung, N.H.; Viossat, B.; Busnot, A.; González Pérez, J.M.; Niclós Gutiérrez, J.; Gardette, F. Additional contribution to the study of iminodiacetate (IDA) and imidazole (ImH) mixed-ligand copper(II) complexes; crystal structure of [Cu(IDA)(ImH)(CH3OH)]·0.37H2O. Inorg. Chim. Acta 1990, 174, 145–148. [Google Scholar]
Crystals 08 00455 sch001 550
Scheme 1. Chemical diagrams of the primary ligand (a), secondary ligand (b) and the title metal compound (c).
Scheme 1. Chemical diagrams of the primary ligand (a), secondary ligand (b) and the title metal compound (c).
Crystals 08 00455 sch001
Crystals 08 00455 g001 550
Figure 1. An ORTEP view (ellipsoids of thermal oscillations with 30% probabilities) with atom numbering scheme of compound (1). The atoms that are labelled with (*) are generated through symmetry operation (2 − x, 1/2 + y, 1 − z).
Figure 1. An ORTEP view (ellipsoids of thermal oscillations with 30% probabilities) with atom numbering scheme of compound (1). The atoms that are labelled with (*) are generated through symmetry operation (2 − x, 1/2 + y, 1 − z).
Crystals 08 00455 g001
Crystals 08 00455 g002 550
Figure 2. 1D polymeric chains are interconnected through C–H···O hydrogen bond to generate a layered assembly in (110) plane.
Figure 2. 1D polymeric chains are interconnected through C–H···O hydrogen bond to generate a layered assembly in (110) plane.
Crystals 08 00455 g002
Crystals 08 00455 g003 550
Figure 3. Perspective view of the supramolecular network generated through hydrogen bonds.
Figure 3. Perspective view of the supramolecular network generated through hydrogen bonds.
Crystals 08 00455 g003
Crystals 08 00455 g004 550
Figure 4. Formation of supramolecular layer network in (011) plane.
Figure 4. Formation of supramolecular layer network in (011) plane.
Crystals 08 00455 g004
Crystals 08 00455 g005 550
Figure 5. Hirshfeld surface of compound (1) mapped with dnorm (a) and de (b).
Figure 5. Hirshfeld surface of compound (1) mapped with dnorm (a) and de (b).
Crystals 08 00455 g005
Crystals 08 00455 g006 550
Figure 6. Fingerprint plots: Full (a) and resolved into O···H/H···O (b); C···H/H···C (c) and H···H (d) interactions showing percentages of contacts (more than 5%) to the total Hirshfeld surface area of the molecules.
Figure 6. Fingerprint plots: Full (a) and resolved into O···H/H···O (b); C···H/H···C (c) and H···H (d) interactions showing percentages of contacts (more than 5%) to the total Hirshfeld surface area of the molecules.
Crystals 08 00455 g006
Crystals 08 00455 g007 550
Figure 7. (a) X-ray fragment. (b,c) theoretical models used to estimate the formation energies.
Figure 7. (a) X-ray fragment. (b,c) theoretical models used to estimate the formation energies.
Crystals 08 00455 g007
Crystals 08 00455 g008 550
Figure 8. (a) X-ray fragment. (b–d) Theoretical models used to estimate the C–H···π interaction.
Figure 8. (a) X-ray fragment. (b–d) Theoretical models used to estimate the C–H···π interaction.
Crystals 08 00455 g008
Crystals 08 00455 g009 550
Figure 9. AIM analysis of different models (a–c). Red and yellow spheres represent bond and ring critical points, respectively. The bond paths connecting bond critical points are shown as dashed lines. The values of ρ(r) at the bond critical points are given in atomic units (a.u.).
Figure 9. AIM analysis of different models (a–c). Red and yellow spheres represent bond and ring critical points, respectively. The bond paths connecting bond critical points are shown as dashed lines. The values of ρ(r) at the bond critical points are given in atomic units (a.u.).
Crystals 08 00455 g009
Crystals 08 00455 g010 550
Figure 10. NCI plot of the self-assembled dimer in (1). The NCI plots only show the intermolecular interactions.
Figure 10. NCI plot of the self-assembled dimer in (1). The NCI plots only show the intermolecular interactions.
Crystals 08 00455 g010
Table
Table 1. Crystal data and structure refinement parameters for title compound.
Table 1. Crystal data and structure refinement parameters for title compound.
Empirical formula(C11H11CuN3O4)n
Formula weight312.77
Temperature293(2) K
Wavelength0.71073 Å
Crystal system, space groupMonoclinic, P21
Unit cell dimensionsa = 8.178(3) Å; α = 90°
b = 7.155(2) Å; β = 102.324(3)°
c = 10.118(3) Å; γ = 90°
Volume578.5(3) Å3
Z, Calculated density2, 1.796 Mg/m3
Absorption coefficient1.902 mm−1
F(000)318
Crystal size0.12 × 0.07 × 0.04 mm
θ range for data collection2.060 to 24.998°
Limiting indices−9 ≤ h ≤ 9, −8 ≤ k ≤ 8, −11 ≤ l ≤ 12
Reflections collected/unique5093/1883 [R(int) = 0.0244]
Completeness to θ100.0%
Absorption correctionSemi-empirical from equivalents
Max. and min. transmission0.93 and 0.85
Refinement methodFull-matrix least-squares on |F|2
Data/parameters1883/174
Goodness-of-fit on F21.092
Flack parameter0.051(18)
Absolute structure parameter0.051(18)
Extinction coefficient0.012(2)
Final R indices [I > 2σ(I)]R1 = 0.0186, wR2 = 0.0489
R indices (all data)R1 = 0.0191, wR2 = 0.0496
Largest diff. peak and hole0.192 and −0.181 e·Å−3
R1 = ∑||Fo|–|Fc||/∑|Fo|, wR2 = [∑{(Fo2–Fc2)2}/∑{w(Fo2)2}]1/2, w = 1/{σ2(Fo2) + (aP)2 + bP}, where a = 0.0087 and b = 0.1805 for the title structure.
Table
Table 2. Relevant Hydrogen Bonding Parameters in (1).
Table 2. Relevant Hydrogen Bonding Parameters in (1).
D–H···AD–HH···AD···AD–H···ASymmetry
N(1)–H(1)···O(1)0.982.052.910(4)1462 − x, 1/2 + y, 1 − z
C(2)–H(2B)···O(3)0.972.573.057(5)1111 − x, 1/2 + y, 1 − z
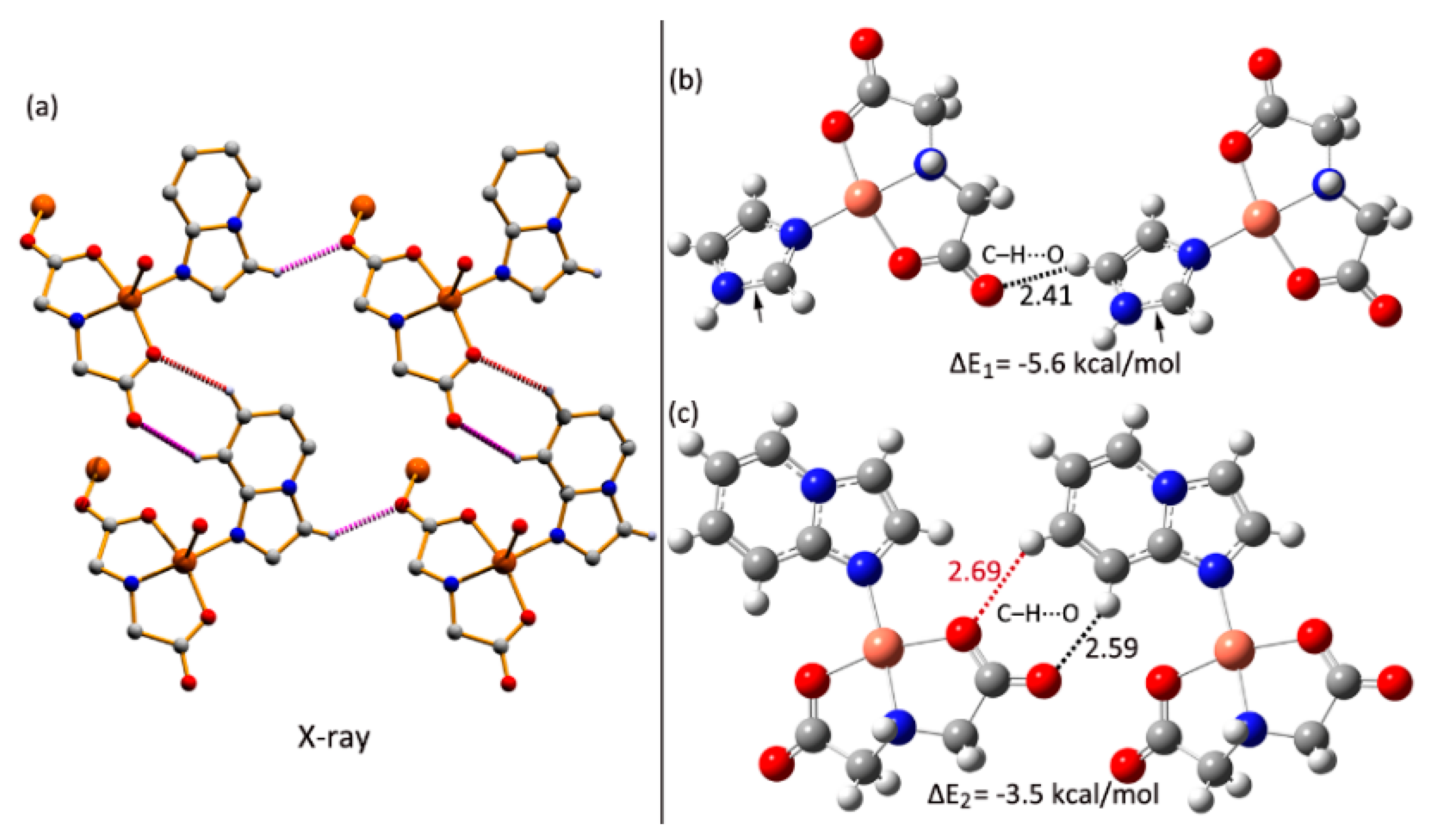
C(6)–H(6)···O(2)0.932.413.175(4)139x, y, 1 + z
C(8)–H(8)···O(1)0.932.493.089(4)122---
C(8)–H(8)∙∙∙O(3)0.932.593.405(5)1461 + x, y, z
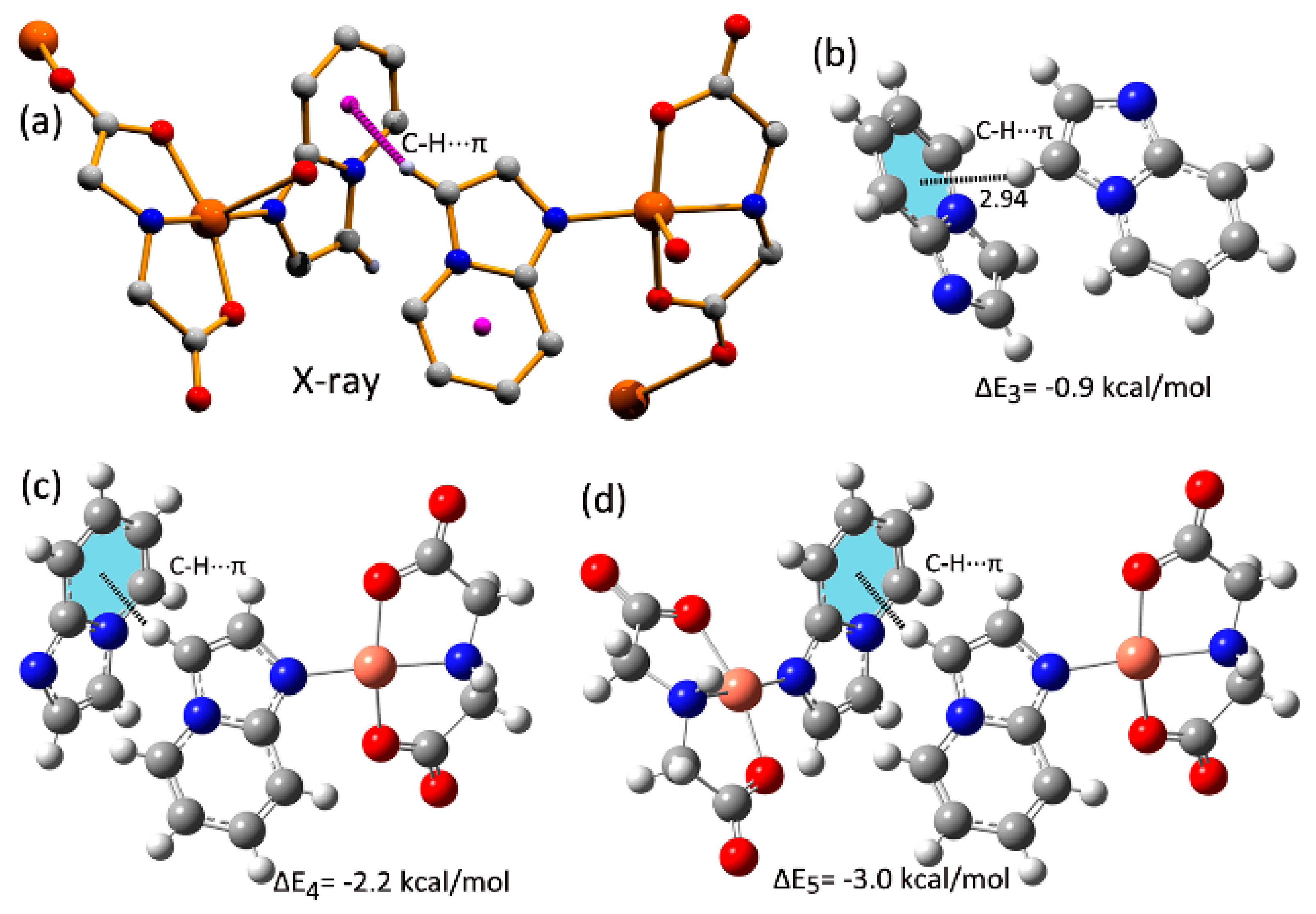
C(6)–H(6)∙∙∙Cg(4)0.932.943.424(4)1142 − x, 1/2 + y, 2 − z
Cg(4) is the centroid of the (N3/C7–C11) ring.

Share and Cite

MDPI and ACS Style

Seth, S.K. The Importance of CH···X (X = O, π) Interaction of a New Mixed Ligand Cu(II) Coordination Polymer: Structure, Hirshfeld Surface and Theoretical Studies. Crystals 2018, 8, 455. https://doi.org/10.3390/cryst8120455

AMA Style

Seth SK. The Importance of CH···X (X = O, π) Interaction of a New Mixed Ligand Cu(II) Coordination Polymer: Structure, Hirshfeld Surface and Theoretical Studies. Crystals. 2018; 8(12):455. https://doi.org/10.3390/cryst8120455

Chicago/Turabian Style

Seth, Saikat Kumar. 2018. "The Importance of CH···X (X = O, π) Interaction of a New Mixed Ligand Cu(II) Coordination Polymer: Structure, Hirshfeld Surface and Theoretical Studies" Crystals 8, no. 12: 455. https://doi.org/10.3390/cryst8120455

APA Style

Seth, S. K. (2018). The Importance of CH···X (X = O, π) Interaction of a New Mixed Ligand Cu(II) Coordination Polymer: Structure, Hirshfeld Surface and Theoretical Studies. Crystals, 8(12), 455. https://doi.org/10.3390/cryst8120455

Note that from the first issue of 2016, this journal uses article numbers instead of page numbers. See further details here.

Article Metrics

Back to TopTop