Rhombohedral Distortion of the Cubic MgCu2-Type Structure in Ca2Pt3Ga and Ca2Pd3Ga
Abstract
:1. Introduction
2. Materials and Methods
2.1. Electronic Structure Calculations
2.2. Synthesis
2.3. Powder X-ray Diffraction
2.4. Single Crystal X-ray Diffraction
3. Results
3.1. Phase Analysis
3.2. Structure Determination
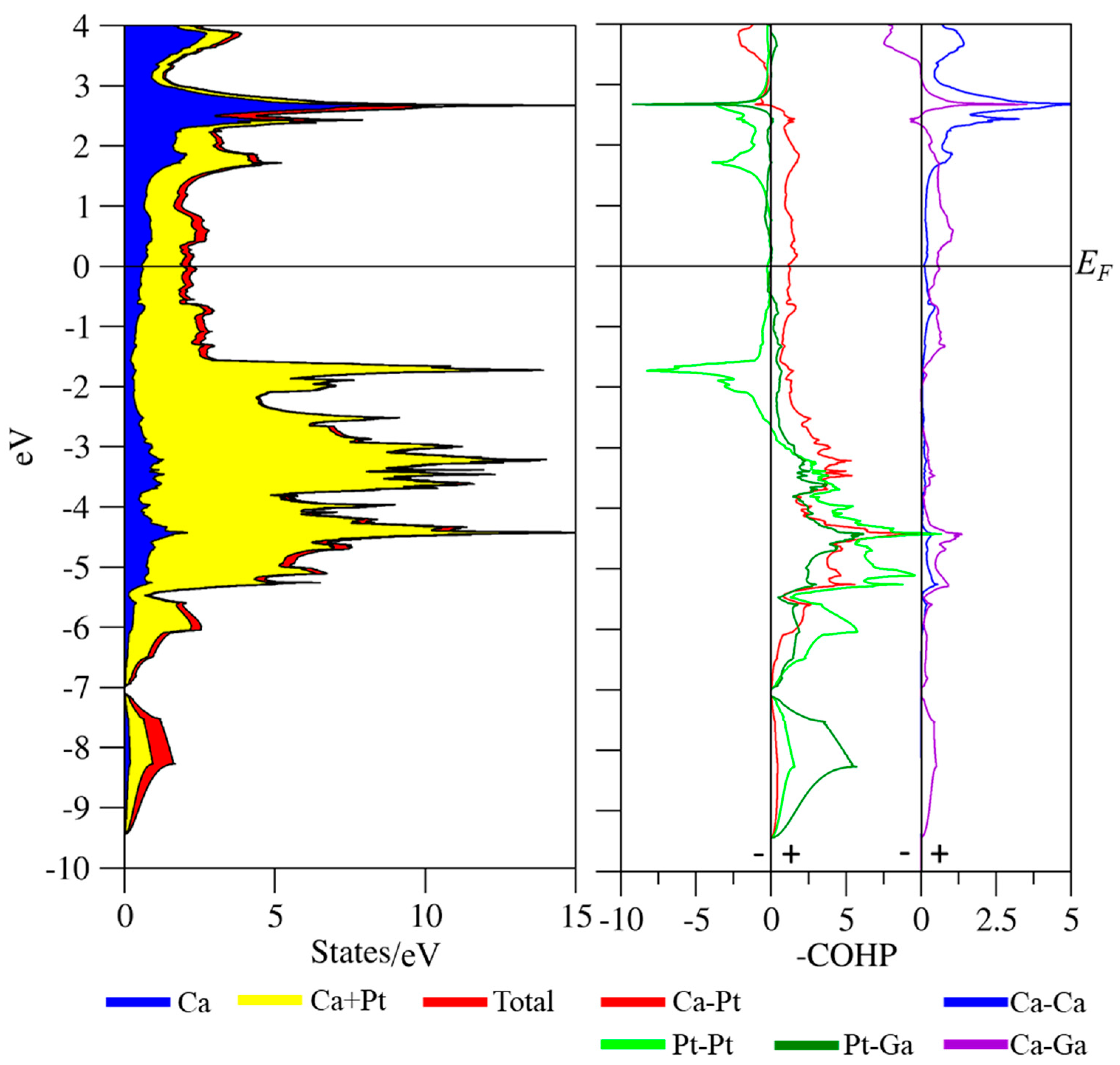
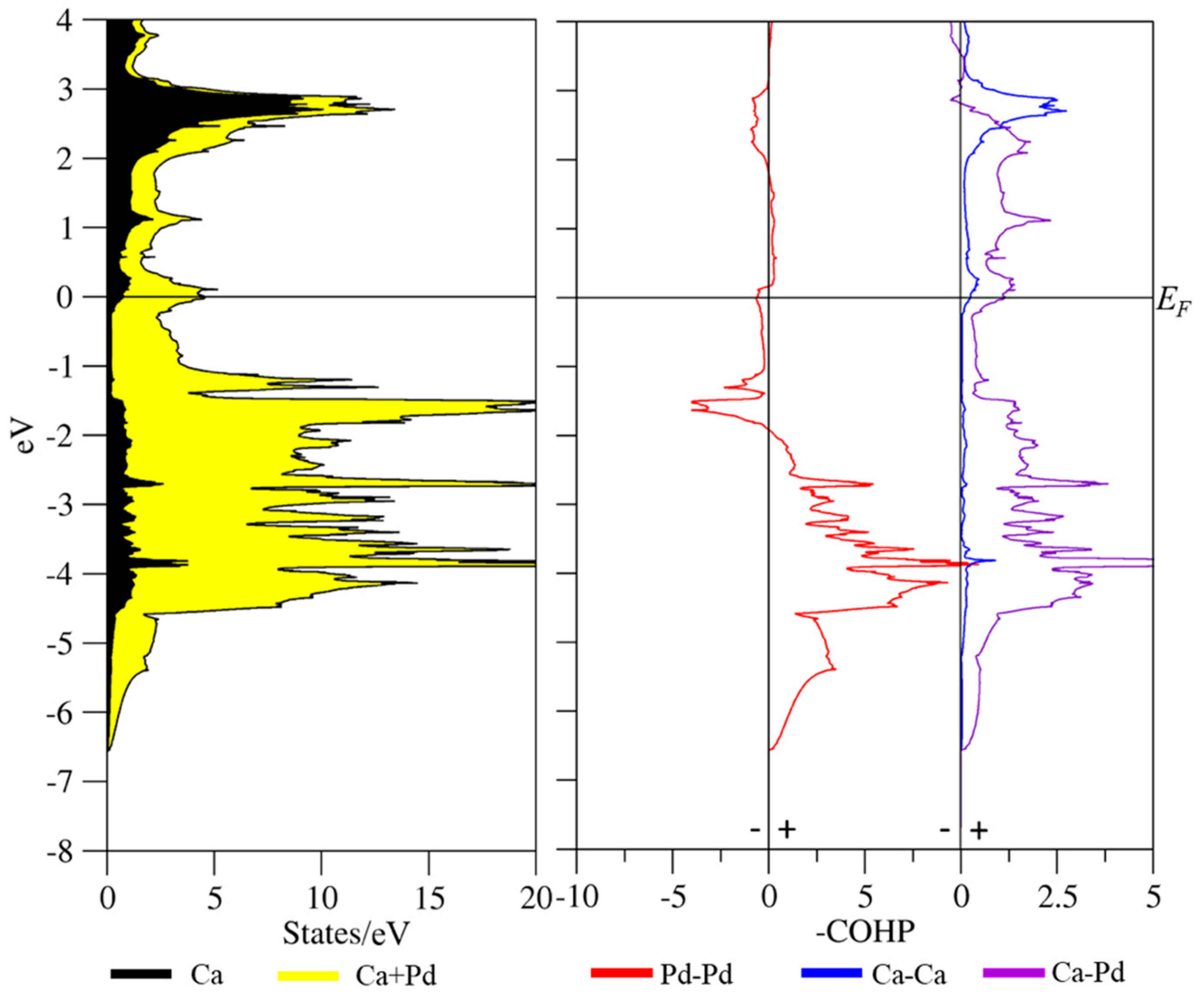
3.3. Coloring Models and Electronic Structure Calculations
4. Conclusions
Supplementary Materials
Author Contributions
Acknowledgments
Conflicts of Interest
References
- Jansen, M. Effects of relativistic motion of electrons on the chemistry of gold and platinum. Solid State Sci. 2005, 7, 1464–1474. [Google Scholar] [CrossRef]
- Siggelkow, L.; Hlukhyy, V.; Faessler, T.F. The Influence of the Valence Electron Concentration on the Structural Variation of the Laves Phases MgNi2−xGex. Z. Anorg. Allg. Chem. 2017, 643, 1424–1430. [Google Scholar] [CrossRef]
- Doverbratt, I.; Ponou, S.; Lidin, S. Ca2Pd3Ge, a new fully ordered ternary Laves phases structure. J. Solid State Chem. 2013, 197, 312–316. [Google Scholar] [CrossRef]
- Stein, F.; Palm, M.; Sauthoff, G. Structure and stability of Laves phases. Part I—Critcal assessment of factors controlling Laves phase stability. Intermetallics 2004, 12, 713–720. [Google Scholar] [CrossRef]
- Osters, O.; Nilges, T.; Schöneich, M.; Schmidt, P.; Rothballer, J.; Pielnhofer, F.; Weihrich, R. Cd4Cu7As, The First Representative of a Fully Ordered, Orthorhombically Distorted MgCu2 Laves Phases. Inorg. Chem. 2012, 51, 8119–8127. [Google Scholar] [CrossRef] [PubMed]
- Murtaza, A.; Yang, S.; Zhou, C.; Song, X. Influence of Tb on easy magnetization direction and magnetostriction of ferromagnetic Laves phase GdFe compounds. Chin. Phys. B 2016, 25, 096107. [Google Scholar] [CrossRef]
- Manickam, K.; Grant, D.M.; Walker, G.S. Optimization of AB2 type alloy composition with superior hydrogen storage properties for stationary applications. Int. J. Hydrogen Energy 2015, 40, 16288–16293. [Google Scholar] [CrossRef]
- Nash, C.P.; Boyden, F.M.; Whittig, L.D. Intermetallic compounds of alkali metals with platinum. A novel preparation of a colloidal platinum hydrogenation catalyst. J. Am. Chem. Soc. 1960, 82, 6203–6204. [Google Scholar] [CrossRef]
- Xiao, C.; Wang, L.; Maligal-Ganesh, R.V.; Smetana, V.; Walen, H.; Thiel, P.A.; Miller, G.J.; Johnson, D.D.; Huang, W. Intermetallic NaAu2 as a Heterogeneous Catalyst for Low-Temperature CO Oxidation. J. Am. Chem. Soc. 2013, 135, 9592–9595. [Google Scholar] [CrossRef] [PubMed]
- Thimmaiah, S.; Miller, G.J. Influence of Valence Electron Concentration on Laves Phases: Structures and Phase Stability of Pseudo-Binary MgZn2−xPdx. Z. Anorg. Allg. Chem. 2015, 641, 1486–1494. [Google Scholar] [CrossRef]
- Seidel, S.; Janka, O.; Benndorf, C.; Mausolf, B.; Haarmann, F.; Eckert, H.; Heletta, L.; Pöttgen, R. Ternary rhombohedral Laves phases RE2Rh3Ga (RE = Y, La-Nd, Sm, Gd-Er). Z. Naturforsch. 2017, 72, 289–303. [Google Scholar] [CrossRef]
- Dwight, A.E.; Kimball, C.W. A rhombohedral Laves phase. Terbium-ron (TbFe2). Acta Cryst. Sect. B 1974, 30, 2791–2793. [Google Scholar] [CrossRef]
- Burdett, J.K.; Canadell, E.; Hughbanks, T. Symmetry control of the coloring problem: The electronic structure of MB2C2 (M = calcium, lanthanum, …). J. Am. Chem. Soc. 1986, 108, 3971–3976. [Google Scholar] [CrossRef]
- Jepsen, O.; Andersen, O.K. TB-LMTO, version 47; Max-Planck-Institut für Festkörperforshcung: Stuttgart, Germany, 2000. [Google Scholar]
- Von Barth, U.; Hedin, L. Local exchange-correlation potential for the spin-polarized case. J. Phys. C 1972, 5, 1629. [Google Scholar] [CrossRef]
- Koelling, D.D.; Harmon, B.N. A technique for relative spin-polarized calculations. J. Phys. C 1977, 10, 3107–3114. [Google Scholar] [CrossRef]
- Kresse, G.; Hafner, J. Ab initio molecular dynamics for liquid metals. Phys. Rev. B 1993, 47, 558. [Google Scholar] [CrossRef]
- Kreese, G.; Furthmüller, J. Efficient iterative schemes for ab initio total-energy calculations using a plane-wave basis set. Phys. Rev. B 1996, 54, 11169–11186. [Google Scholar] [CrossRef]
- Blöchl, P.E. Projector augmented-wave method. Phys. Rev. B 1994, 50, 17953–17979. [Google Scholar] [CrossRef]
- Perdew, J.P.; Burke, K.; Wang, Y. Gerneralized gradient approximation for the exchange-correlation hole of a many-electron system. Phys. Rev. B 1996, 54, 16533–16539. [Google Scholar] [CrossRef]
- Monkhorst, H.J.; Pack, J.D. Special points for Brillouin-zone integrations. Phys. Rev. B 1976, 13, 5188. [Google Scholar] [CrossRef]
- Blöchl, P.E.; Jepsen, O.; Andersen, O.K. Improved tetrahedron method for Brillouin-zone integrations. Phys. Rev. B 1994, 49, 16223–16233. [Google Scholar] [CrossRef]
- PowderCell, version 2.3; Federal Institute for Materials Research and Testing: Berlin, Germany, 2000.
- APEX-II; Bruker AXS Inc.: Madison, WI, USA, 2013.
- SAINT-V8.27; Bruker AXS Inc.: Madison, WI, USA, 2013.
- SHELXTL-v2008/4; Bruker AXS Inc.: Madison, WI, USA, 2013.
- Brandenburg, K. Diamond, version 3.2; Crystal Impact GbR: Bonn, Germany, 2011. [Google Scholar]
- Petricek, V.; Dusek, M.; Palatinus, L. Structure Determination Software Programs; Institute of Physics: Praha, Czech Republic, 2006. [Google Scholar]
- Cenzual, K.; Chabot, B.; Parthe, E. Yttrium rhodium germanide (Y2Rh3Ge), a rhombohedral substitution variant of the MgCu2 type. J. Solid State Chem. 1987, 70, 229–234. [Google Scholar] [CrossRef]
- Burdett, J.K.; McLarnan, T.J. Geometrical and electronic links among the structures of MX2 solids: Structural enumeration and electronic stability of pyritelike systems. Inorg. Chem. 1982, 21, 1119–1128. [Google Scholar] [CrossRef]
- Xie, W.; Miller, G.J. β-Mn-Type Co8+xZn12−x as a Defect Cubic Laves Phase: Site Preferences, Magnetism, and Electronic Structure. Inorg. Chem. 2013, 52, 9399–9408. [Google Scholar] [CrossRef] [PubMed]
- Wells, A.F. Structural Inorganic Chemistry, 5th ed.; Clarendon Press: Oxford, UK, 1984. [Google Scholar]
- Pearson, R.G. Absolute Electronegativity and Hardness: Application to Inorganic Chemistry. Inorg. Chem. 1988, 27, 734–740. [Google Scholar] [CrossRef]
- Johnston, R.; Hoffmann, R. Structure-Bonding Relationships in the Laves Phases. Z. Anorg. Allg. Chem. 1992, 616, 105–120. [Google Scholar] [CrossRef]
- Ormeci, A.; Simon, A.; Grin, Y. Structural Topology and Chemical Bonding in Laves Phases. Angew. Chem. 2010, 49, 8997–9001. [Google Scholar] [CrossRef] [PubMed]
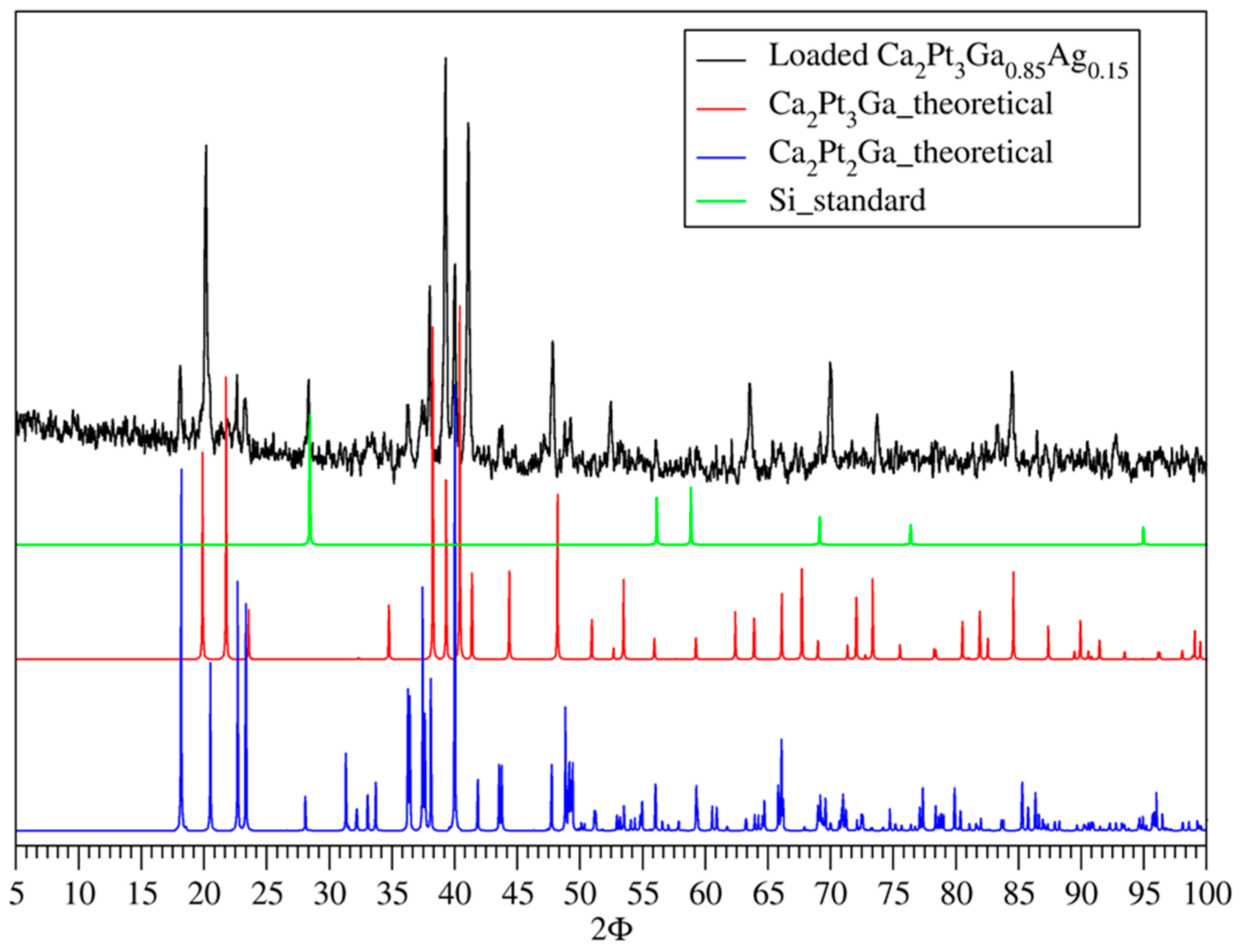
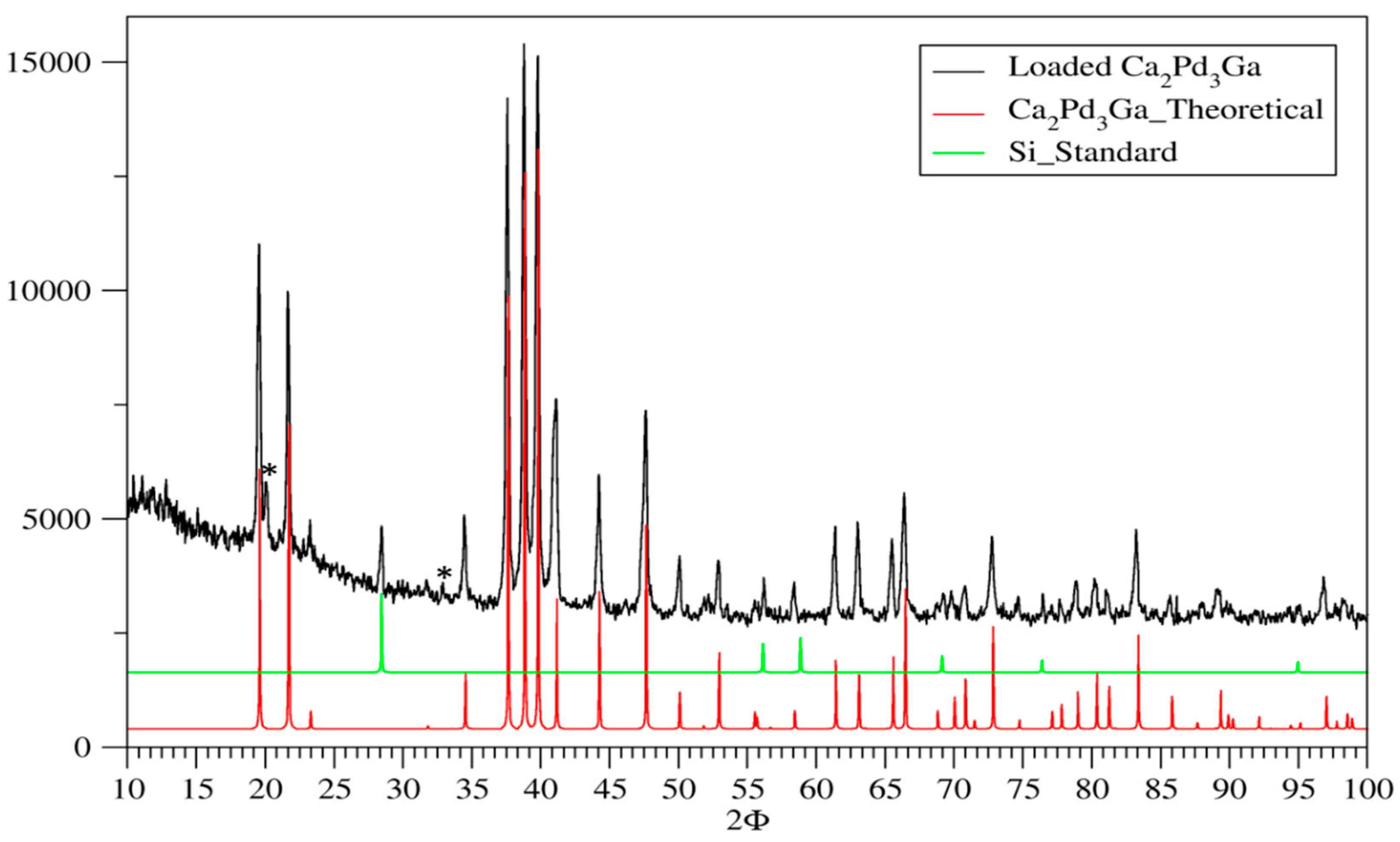
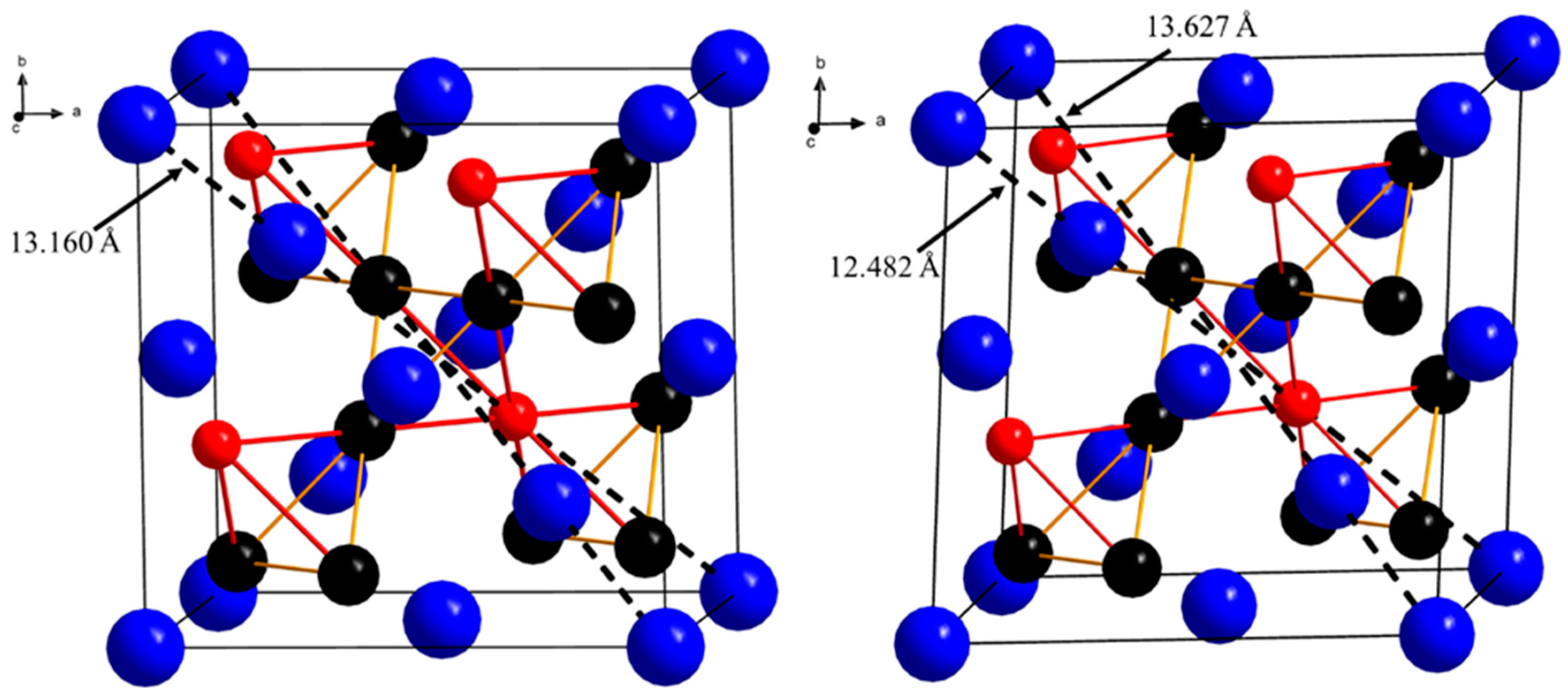
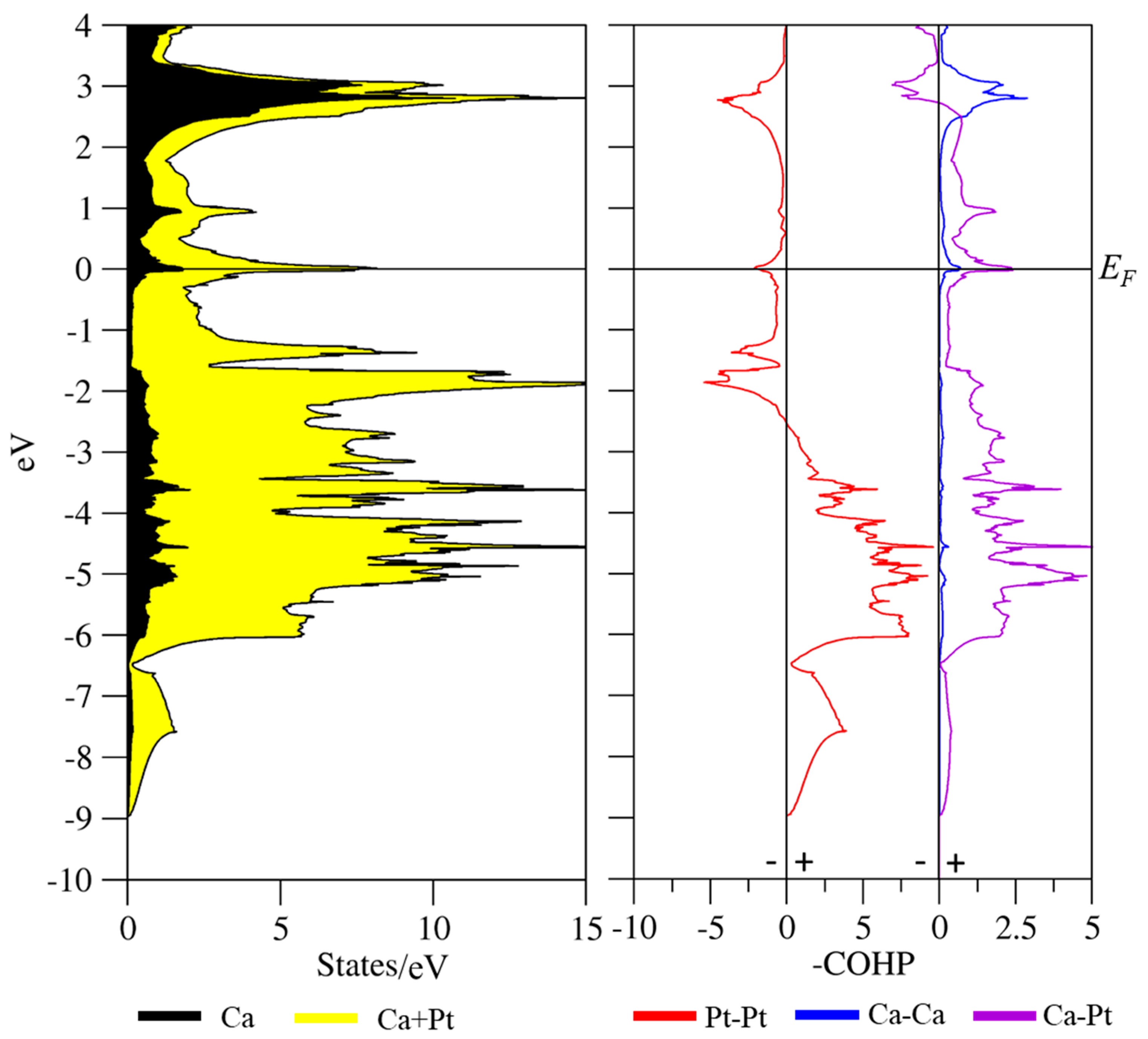

| Sample | Ca2Pt3Ga | Ca2Pd3Ga |
|---|---|---|
| Space Group | R-3m | R-3m |
| Unit Cell Dim. | a = 5.576(1) Å c = 12.388(3) Å | a = 5.6326(8) Å c = 12.300(2) Å |
| Volume | 333.6(2) Å3 | 337.9(1) Å3 |
| Z | 3 | 3 |
| Theta range for data collection | 4.530 to 28.922° | 4.495 to 49.319° |
| Index ranges | −7 ≤ h ≤ 7, −7 ≤ k ≤ 7, −16 ≤ l ≤ 16 | −11 ≤ h ≤ 11, −11 ≤ k ≤ 11, −26 ≤ l ≤ 26 |
| Reflections Collected | 1321 | 4878 |
| Independent Reflections | 126 [R(int) = 0.0485 | 460 [R(int) = 0.0585] |
| Data/restraints/parameters | 126/0/11 | 460/0/11 |
| Goodness-of-fit | 1.078 | 1.091 |
| Final R indices [I > 2sigma(l)] | R1 = 0.0179, wR2 = 0.0403 | R1 = 0.0208, wR2 = 0.0403 |
| R indices (all data) | R1 = 0.0179, wR2 = 0.0403 | R1 = 0.0251, wR2 = 0.0414 |
| Extinction Coefficient | 0.0008(1) | 0.0036(3) |
| Largest diff. peak and hole | 3.366 and −2.052 e·Å−3 | 1.697 and −2.657 e·Å−3 |
| Ca2Pt3Ga | Ca2Pd3Ga | ||||||
|---|---|---|---|---|---|---|---|
| Model | Ga-Ga Distance (Å) | meV Non-Optimized | meV Optimized | # Ga-Ga Interactions | meV Optimized | meV Non-Optimized | Ga-Ga Distance (Å) |
| Alpha | 5.276 | 0 | 0 | 0 | 0 | 0 | 5.282 |
| Beta | 2.755 | +38.5 | +78.8 | 1 | +68.1 | +30.5 | 2.732 |
| Delta | 2.811 | +62.1 | +121.8 | 2 | +121.8 | +59.3 | 2.775 |
| Epsilon | 2.808 | +50.8 | +95.7 | 1 | +73.0 | +36.0 | 2.800 |
| Gamma | 4.738 | +140.7 | +56.0 | 0 | +26.0 | +92.0 | 4.791 |
| Iota | 2.931 | +70.5 | +113.4 | 2 | +104.7 | +61.2 | 2.922 |
| Mu | 4.709 | +37.6 | +71.0 | 0 | +66.5 | +13.3 | 4.653 |
| Theta | 2.950 | +203.0 | +289.4 | 6 | +256.6 | +155.5 | 2.909 |
| Zeta | 2.824 | +97.6 | +168.6 | 3 | +150.0 | +81.1 | 2.798 |
| 2 CaPd2 | + Ga | → | Ca2Pd3Ga | + Pd | ΔE = −0.599 eV | |
| (1) | 2 CaPd2 | + Ga | → | Ca2Pd3Ga * | + Pd | ΔE = −0.258 eV |
| (2) | Ca2Pd3Ga * | → | Ca2Pd3Ga ** | ΔE = −0.042 eV | ||
| (3) | Ca2Pd3Ga ** | → | Ca2Pd3Ga | ΔE = −0.299 eV | ||
| 2 CaPt2 | + Ga | → | Ca2Pt3Ga | + Pt | ΔE = −0.297 eV | |
| (1) | 2 CaPt2 | + Ga | → | Ca2Pt3Ga * | + Pt | ΔE = +0.115 eV |
| (2) | Ca2Pt3Ga * | → | Ca2Pt3Ga ** | ΔE = −0.088 eV | ||
| (3) | Ca2Pt3Ga ** | → | Ca2Pt3Ga | ΔE = −0.324 eV |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Toombs, A.; Miller, G.J. Rhombohedral Distortion of the Cubic MgCu2-Type Structure in Ca2Pt3Ga and Ca2Pd3Ga. Crystals 2018, 8, 186. https://doi.org/10.3390/cryst8050186
Toombs A, Miller GJ. Rhombohedral Distortion of the Cubic MgCu2-Type Structure in Ca2Pt3Ga and Ca2Pd3Ga. Crystals. 2018; 8(5):186. https://doi.org/10.3390/cryst8050186
Chicago/Turabian StyleToombs, Asa, and Gordon J. Miller. 2018. "Rhombohedral Distortion of the Cubic MgCu2-Type Structure in Ca2Pt3Ga and Ca2Pd3Ga" Crystals 8, no. 5: 186. https://doi.org/10.3390/cryst8050186
APA StyleToombs, A., & Miller, G. J. (2018). Rhombohedral Distortion of the Cubic MgCu2-Type Structure in Ca2Pt3Ga and Ca2Pd3Ga. Crystals, 8(5), 186. https://doi.org/10.3390/cryst8050186




