Note that, among the following subsections, results are repeated in a few instances. This is only to simplify the comparative analysis, and will be explicitly remarked on when done so.
3.2. He–C Interaction
Consider now the He–C interaction. While the importance of corrugation has been considered before (either directly (e.g., [
14]) or indirectly), thorough quantitative details are considered here.
The phase diagram calculated with each of the three He–C potentials under consideration (
Section 2) is shown in
Figure 5. The corresponding data is reported in
Table 2.
The liquid curves are qualitatively similar for the isotropic and anisotropic potentials. That of the atom–bond though is different. Quantitatively, each potential has a different relative depth at the minimum (the equilibrium liquid density). From the low-density side, and from shallowest to deepest, are the curves for the anisotropic, isotropic, and atom–bond potentials. On the high-density side, the isotropic and anisotropic curves increase in energy significantly. The atom–bond potential, however, does not. There are also differences in the equilibrium liquid densities among the potentials. The anisotropic one results in the lowest density, whereas that of the atom–bond is just a bit higher than that of the isotropic one. Therefore, while the atom–bond potential looks qualitatively different, this could be related to the higher equilibrium liquid density shifting the entire curve higher.
The (relative) energies of the solid phase are significantly different for the three potentials. For the isotropic one (
Figure 5a), the energy of the
structure and the liquid at the equilibrium density are nearly within error bars (
Table 2); therefore, the latter is stable (approximately) only at a single point. The anisotropic potential (
Figure 5b), however, significantly lowers the energy of the
structure; the solid is unambiguously the ground state. These results are in good agreement with previous calculations [
5,
6,
7,
8,
9,
10], but with using a different He–He potential. The atom–bond potential, however, raises the energy of the
structure above that of the liquid. Note that a probable contribution to this is the shallow increase in energy of the high(er)-density liquid (as discussed above).
To understand the above, it is necessary to consider the quantitative properties of these potentials. Of particular importance is their corrugation, herein defined to be the relative difference in potential between the high-symmetry sites over the graphene plane (
Figure 1b). This can be seen by
, the He–C potential for a single helium atom as a function of its height
z over the carbon surface.
The potentials
over the sites in
Figure 1b for each of the He–C potentials are shown in
Figure 6. Qualitatively, they are similar. The well depths increase from top and bridge to the hollow sites for each. In addition, the (relative) well depths for the bridge and top sites are comparable. Quantitatively however, those for the hollow sites are noticeably different. That for the anisotropic potential is largest, whereas that for the atom–bond potential is comparable to the other sites.
Looking at the He–C potential across the entire carbon surface and for all z alone however is insufficient to explain the observed properties of the phase diagram. Additional information is needed, in particular the separation of He atoms from the surface. For the purpose of this discussion, it turns out to be sufficient to consider only the equilibrium (most probable) separation .
The separation of He atoms and their distribution is calculable directly from the simulations (and presented below). It is insightful, however, to first consider a single-body Schrödinger equation, with a potential obtained as a lateral () average (i.e., at each z) of over the entire graphene plane.
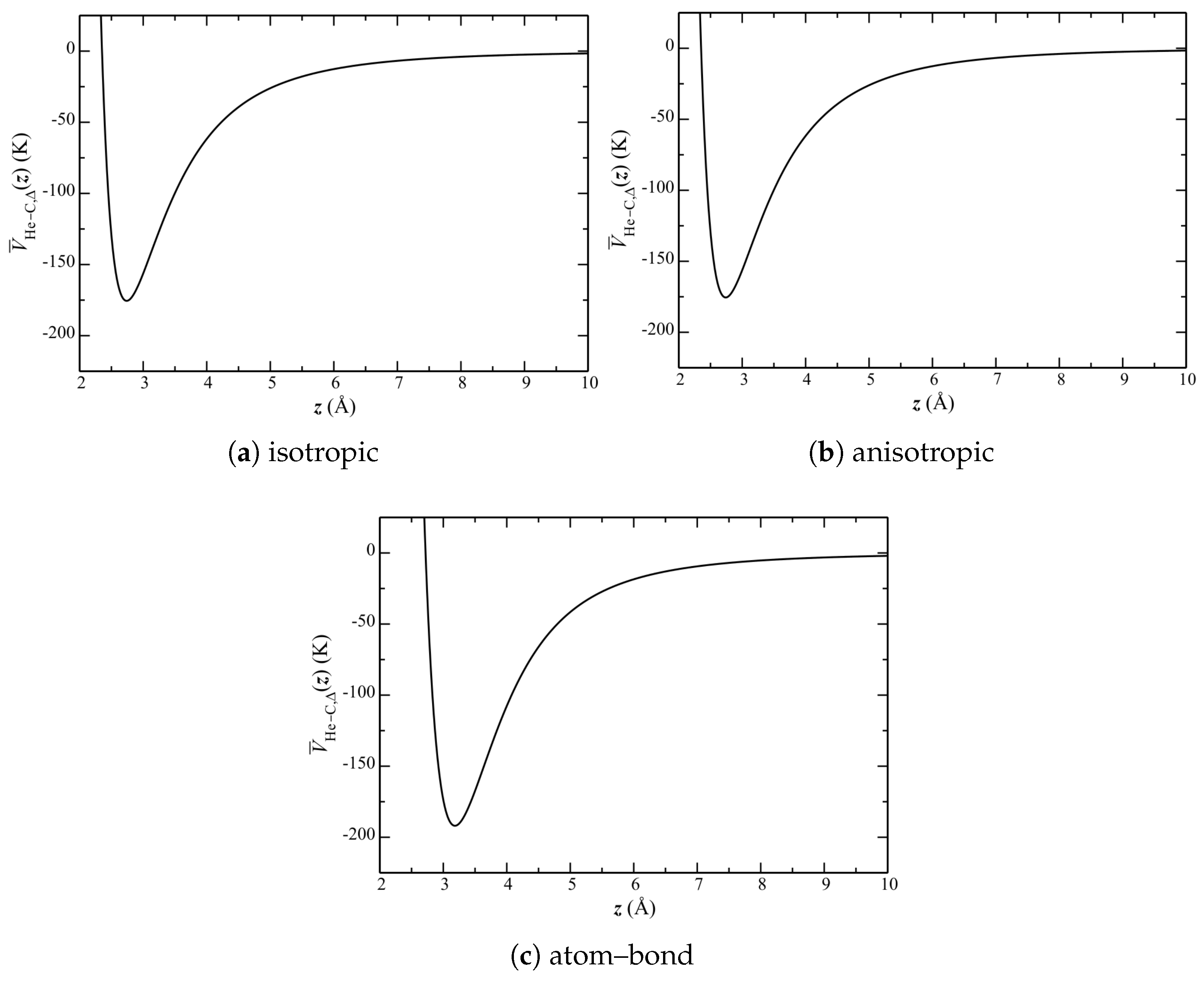
Lateral-averaged potentials are shown in
Figure 7. This side-by-side comparison shows that the isotropic and anisotropic potentials are qualitatively similar. The atom–bond potential, however, exhibits a much larger well depth, with a minimum at a much higher
z.
The solutions to the aforementioned Schrödinger equation for each of the potentials are shown in
Figure 8. Shown also are full-simulation results, calculated at the equilibrium liquid densities (
Table 2); note that the same
resulted also from calculating at the density of the
structure (start of
Section 3). The corresponding
and full width at half maximum (FWHM) are reported in
Table 3.
First compare the single-body to full-simulation results. The latter are significantly more narrow (quantitatively, given by the FWHM).
Figure 8 shows that the distributions are also (the most) different for
.
, however, as calculated by the two methods, are nearly identical. Consider now the difference between potentials. Interestingly, the FWHM is identical among them. This suggests that the shapes of the average potential wells (at least near the minima) are similar; and, hence, so is the average corrugation.
is also the same for the isotropic and anisotropic potentials. It is significantly larger, however, for the atom–bond potential.
Consider now though the potential
(
) (i.e., at the equilibrium separation) over the three symmetric sites (
Figure 1b). The relative difference in potential at each of these sites represents the corrugation (defined above) felt by a
He atom. These values are reported in
Table 4, and differences relative to the lateral averages are shown in
Table 5. There is a clear trend revealed by this table. The atom–bond potential is the least corrugated, followed by the isotropic and then (most significantly) anisotropic ones.
Finally, consider these results in the context of the phase diagram (
Figure 5). Stronger corrugation leads to a lower equilibrium liquid density (
Table 2). Regarding the stability of the
structure, the deeper the (relative) well depth at an adsorption site (the hollow site; see
Section 1), the harder it is to remove an atom (i.e., the more stable the solid). In this context, the results in
Table 4 are also consistent with
Figure 5. Differences on the order of kelvins therefore lead to significant quantitative changes in the phase diagram. This is despite the fact that well depths (at other
z) are much deeper. Note that making more quantitative statements based only on
is probably not possible.
For the remainder of (this)
Section 3, results based on the isotropic He–C potential are shown (unless otherwise stated). In
Section 4, it is argued that this potential is the most accurate, though caution is needed.
3.3. Graphite
Nearly all experimental studies of
He adsorbed on or scattered from a carbon surface are for graphite. All of the results presented earlier in this section, however, were for graphene. It is natural to ask whether these results can therefore be compared to experiment (as will be done in
Section 4). It is also natural to ask the converse, of whether a He–C potential developed for graphite (such as the isotropic and anisotropic ones; see
Section 2) might be inaccurate for studying adsorption on graphene.
He adsorbed on graphite has been considered in prior calculations [
5,
6,
11,
12,
13,
14,
15]. Because of this, and the fact that changing the He–He interaction will likely lead only to minor quantitative changes in the phase diagram (
Section 3.1), results for these potentials are not (re-)reported in this section. Instead, quantitative details about the corrugation of the isotropic potential (only; see the remarks at the end of
Section 3.2) are considered in the context of this prior work. This, however, motivates once more consideration of the atom–bond potential. Note that throughout this section, for one graphene layer,
, the results are repeated from
Section 3.2. Note also that
is referred to as “graphite”.
A representative and recent prior study using the isotropic potential is that of [
5]. Therein, it was found that the phase diagrams of graphene and graphite are qualitatively similar.
In order to understand this result, consider the changes in corrugation when going from graphene to graphite.
Figure 9 shows the change in He–C potential over the three symmetric sites of the top graphene layer (
Figure 1b), as the number of layers is increased. Qualitatively, the potential appears to uniformly decrease.
For the equilibrium separations reported in
Table 6, more quantitative results are reported in
Table 7 and
Table 8. There are two significant observations to make from these tables. One is that the potentials at the symmetric sites all become stronger relative to the lateral average (
Table 8), with increased repulsion at the bridge and top sites and attraction at the hollow one, with an increasing number of layers. That is, the corrugation becomes stronger. The other is that the relative well depth at the hollow site increases significantly more than the repulsion at either of the other two sites.
Despite the above, there is relatively little change in the equilibrium separation of atoms (
Table 6). This might be due to that there are more bridge and top sites, as compared to hollow ones.
Increasing corrugation suggests that the solid phase will possibly become (more) stabilized relative to the liquid. This would have the most significant (qualitative) change for the atom–bond potential (see
Section 3.2).
Motivated by this suggestion, the phase diagram calculated with the atom–bond potential, for an increasing number of layers, is shown in
Figure 10. Corresponding data is reported in
Table 9. As suspected, the increased corrugation acts to stabilize the solid. Whereas for graphene the liquid remains the ground state at the density of the solid, the addition of even one layer causes the energies to be within error bars. Note that this situation then does not change (e.g., the solid eventually becoming the ground state), with an increasing number of layers, within the uncertainties of the calculations. The interpretation (for this He–C potential) could be that the liquid is stable as the ground-state on graphite, until reaching the density of the solid, where they are then in equilibrium.