Influence of Dislocations in Transition Metal Oxides on Selected Physical and Chemical Properties
Abstract
:1. Introduction
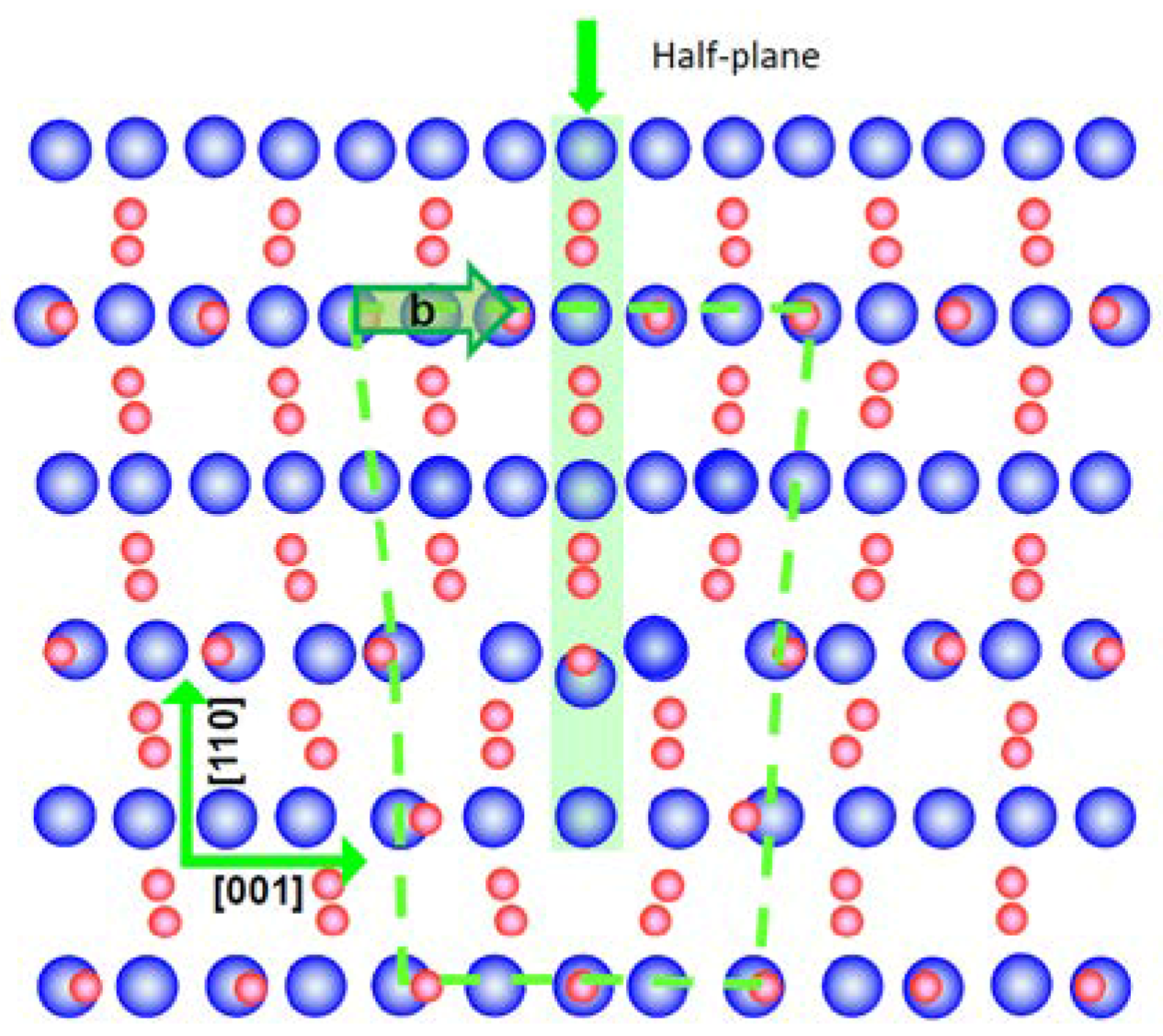
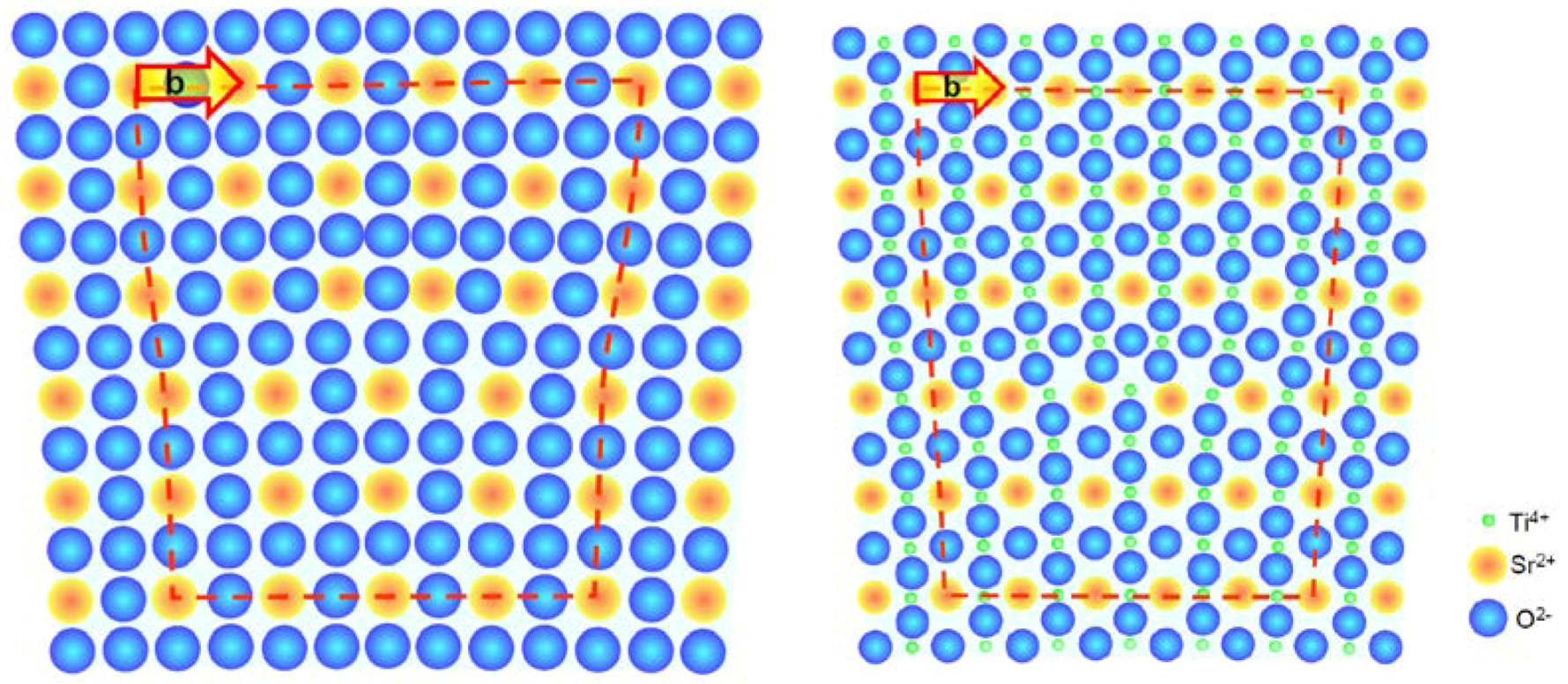
2. Edge Dislocations in TiO2 and SrTiO3
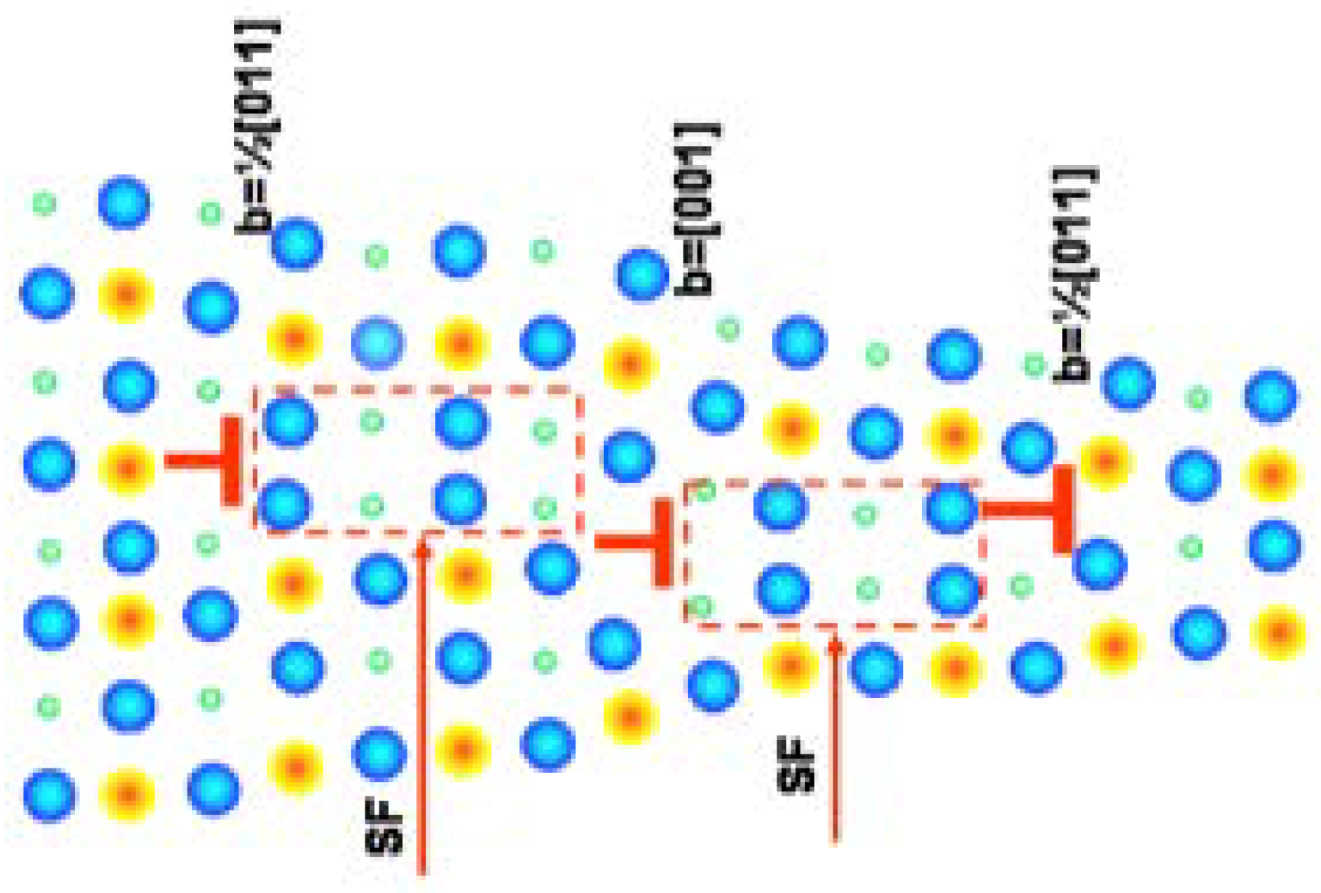
3. Arrangement of Dislocations
4. Annihilations or Multiplications of Dislocations
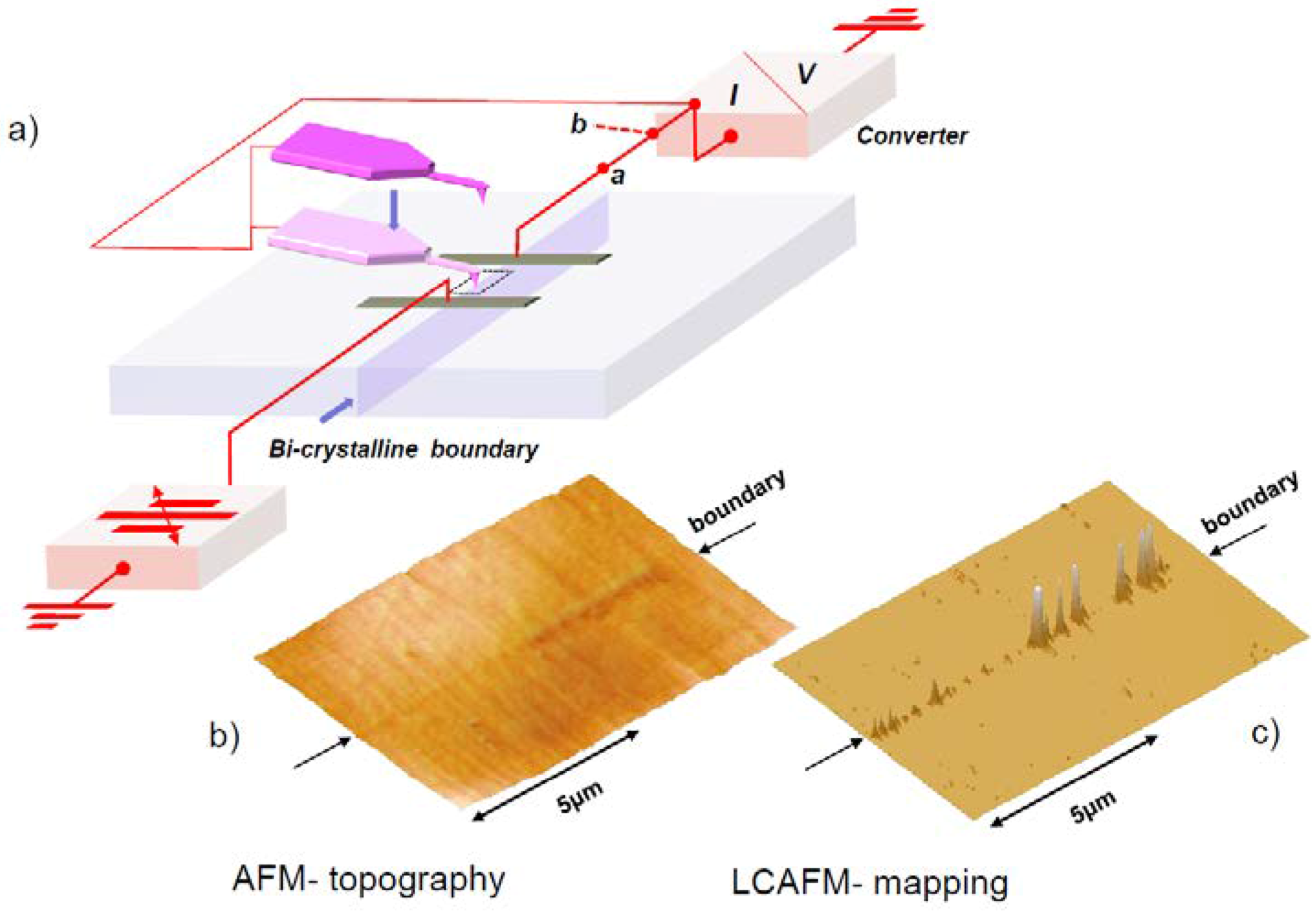
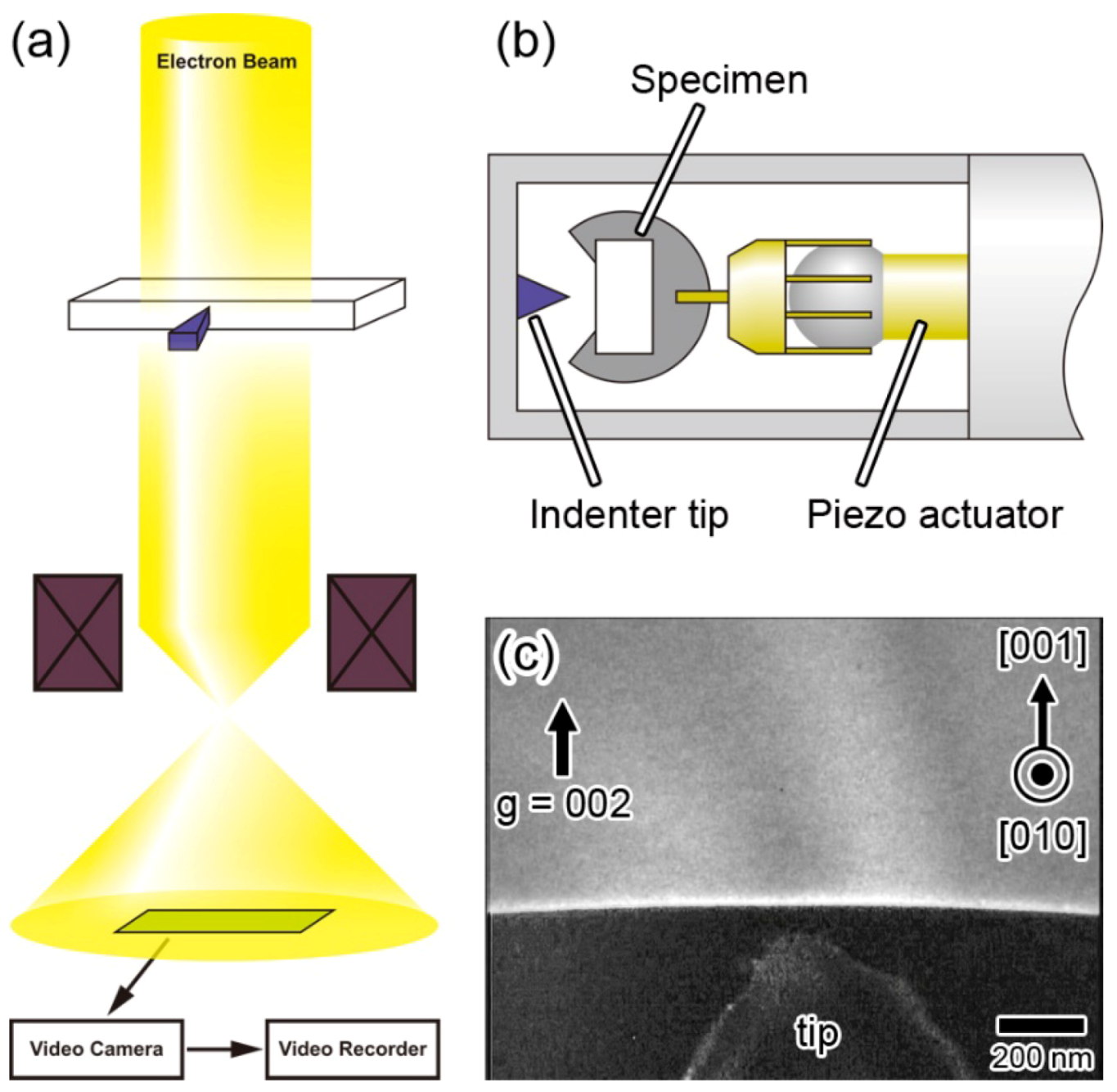
5. Experimental Techniques for the Investigation of Dislocations in Real Oxides Crystals
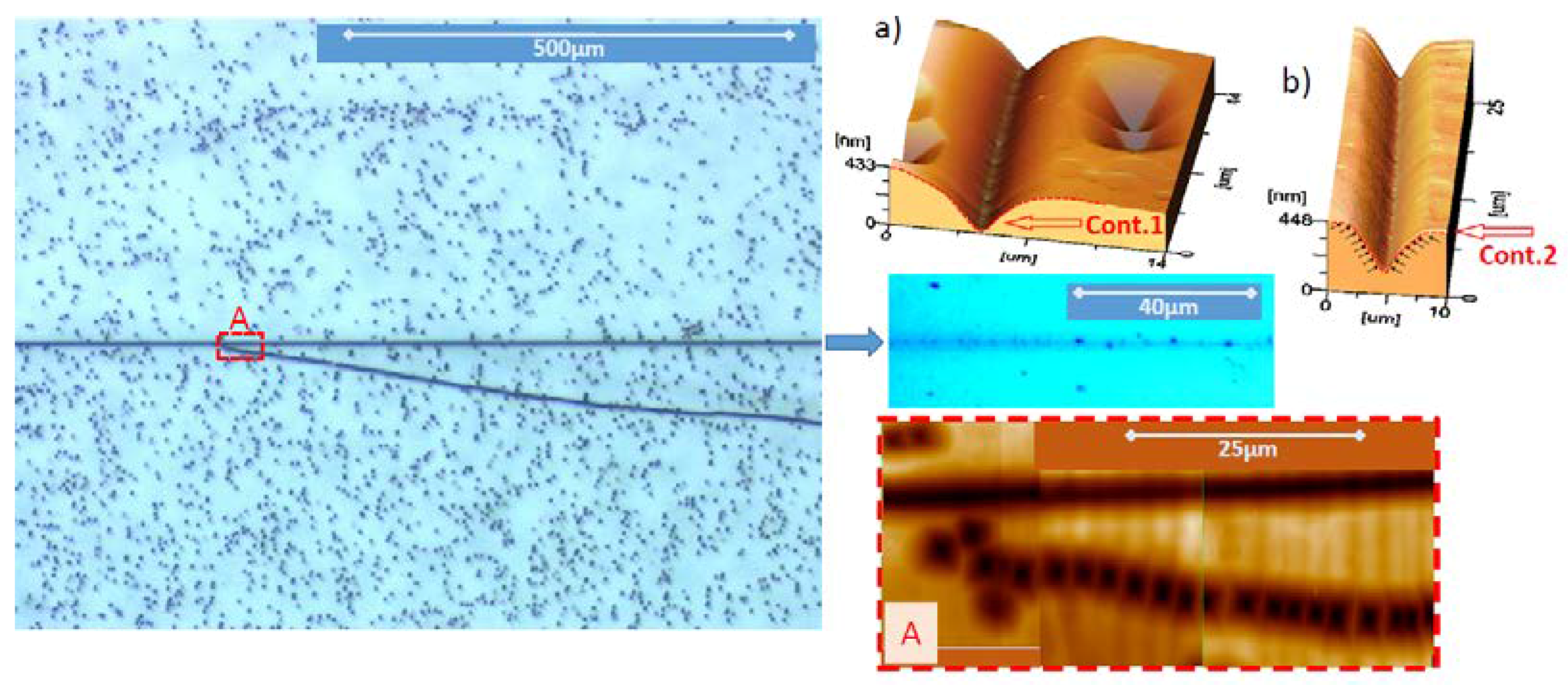
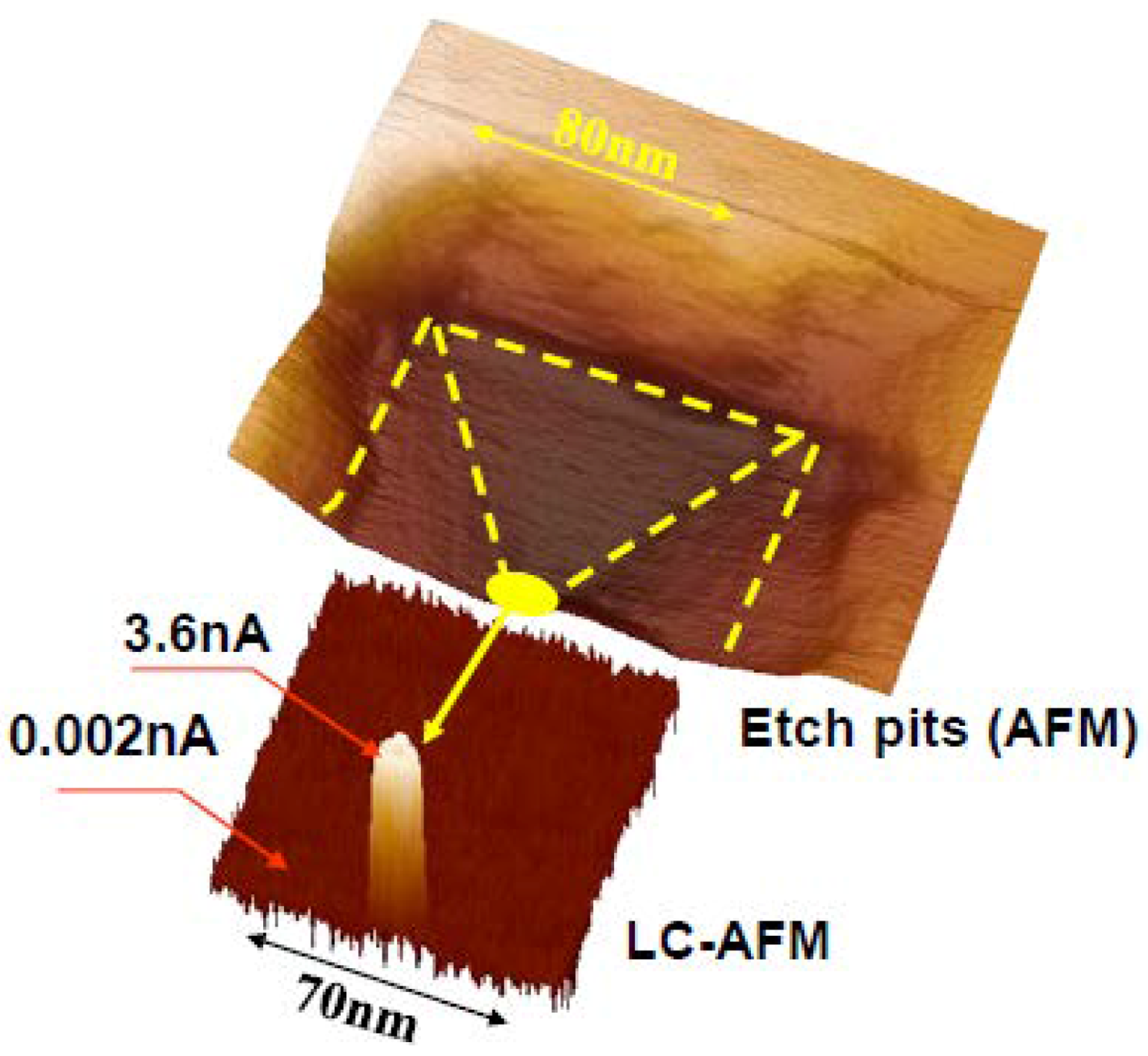
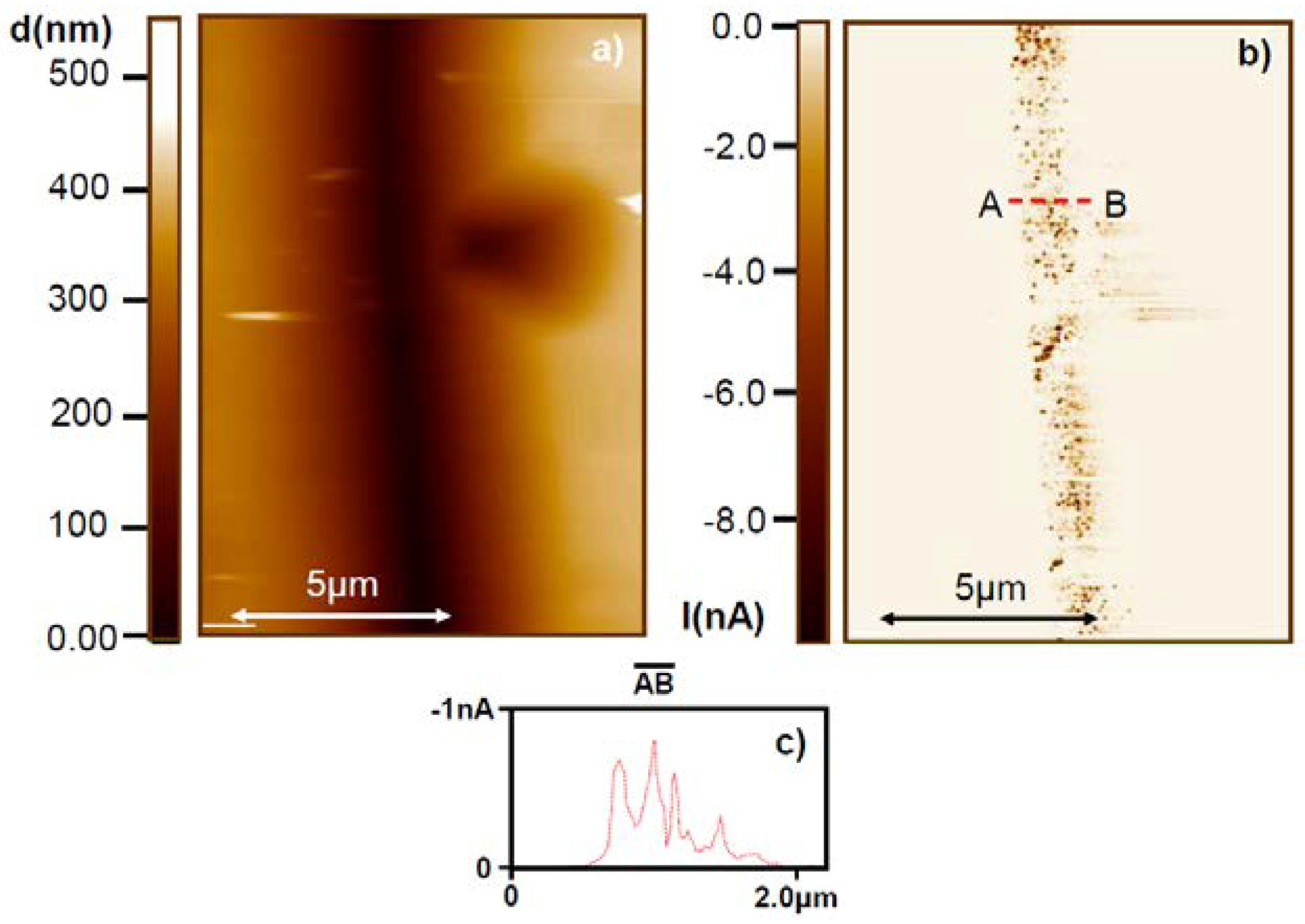
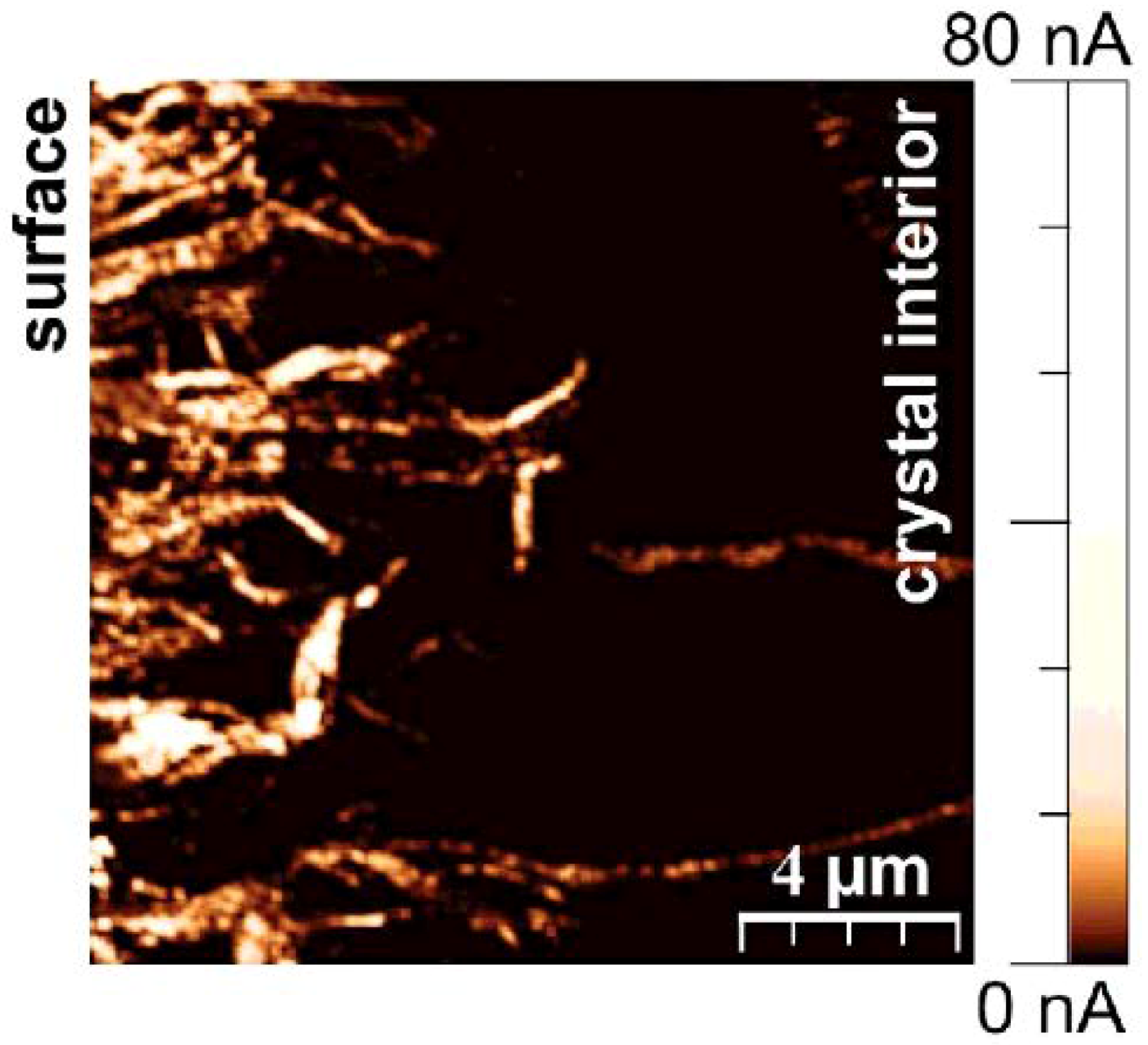
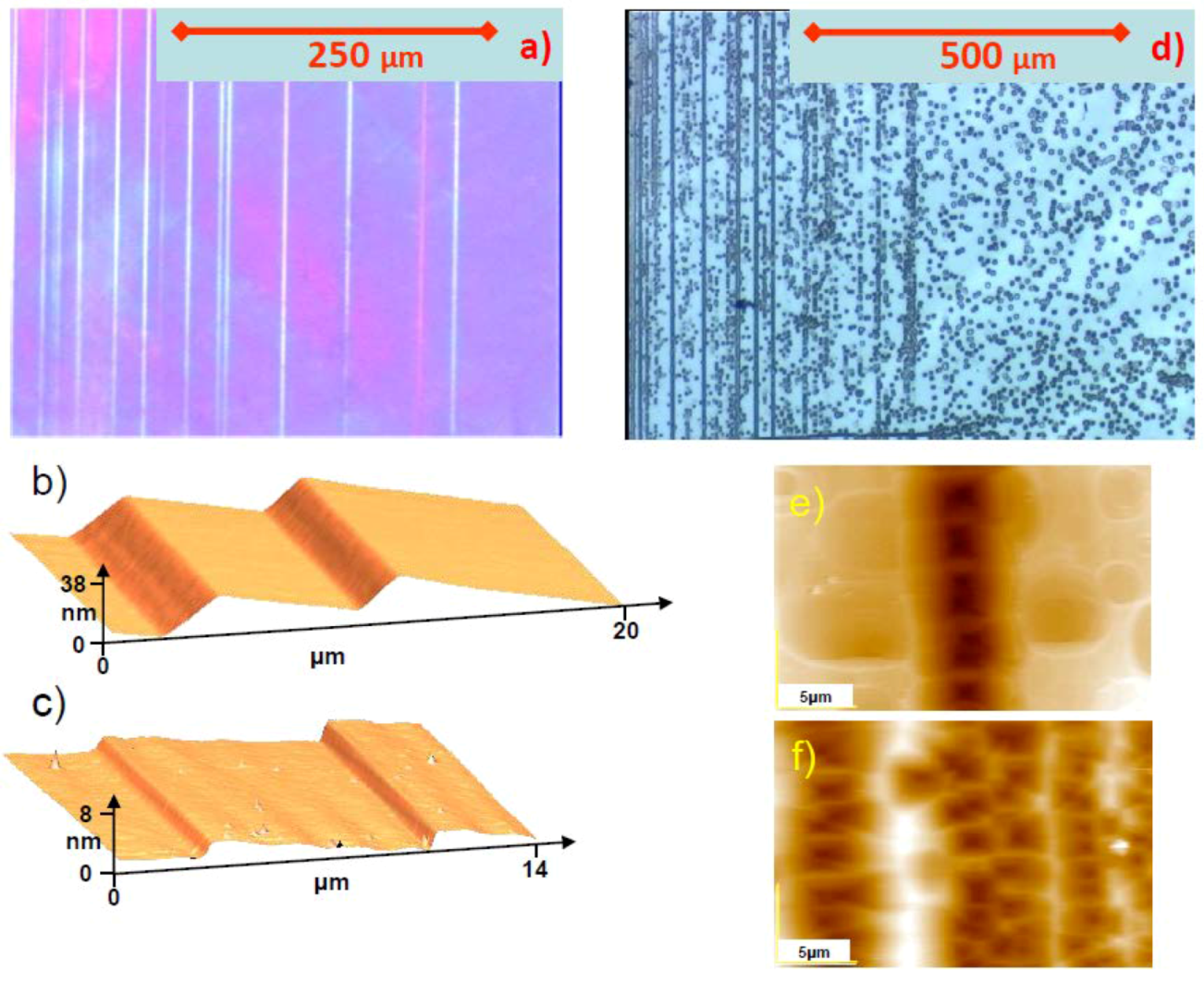
5.1. Etch Pits Technique (Optical, SEM and AFM Investigation)
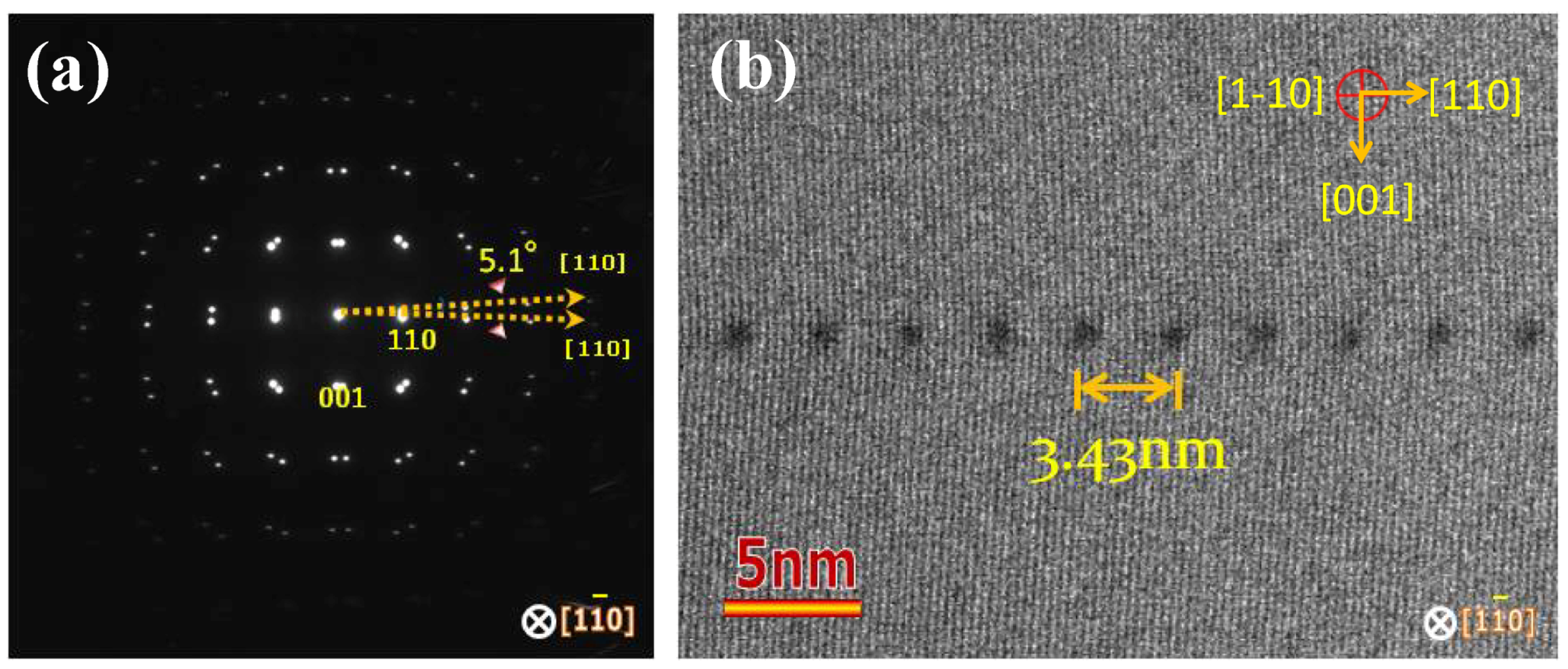
5.2. X-ray Topography
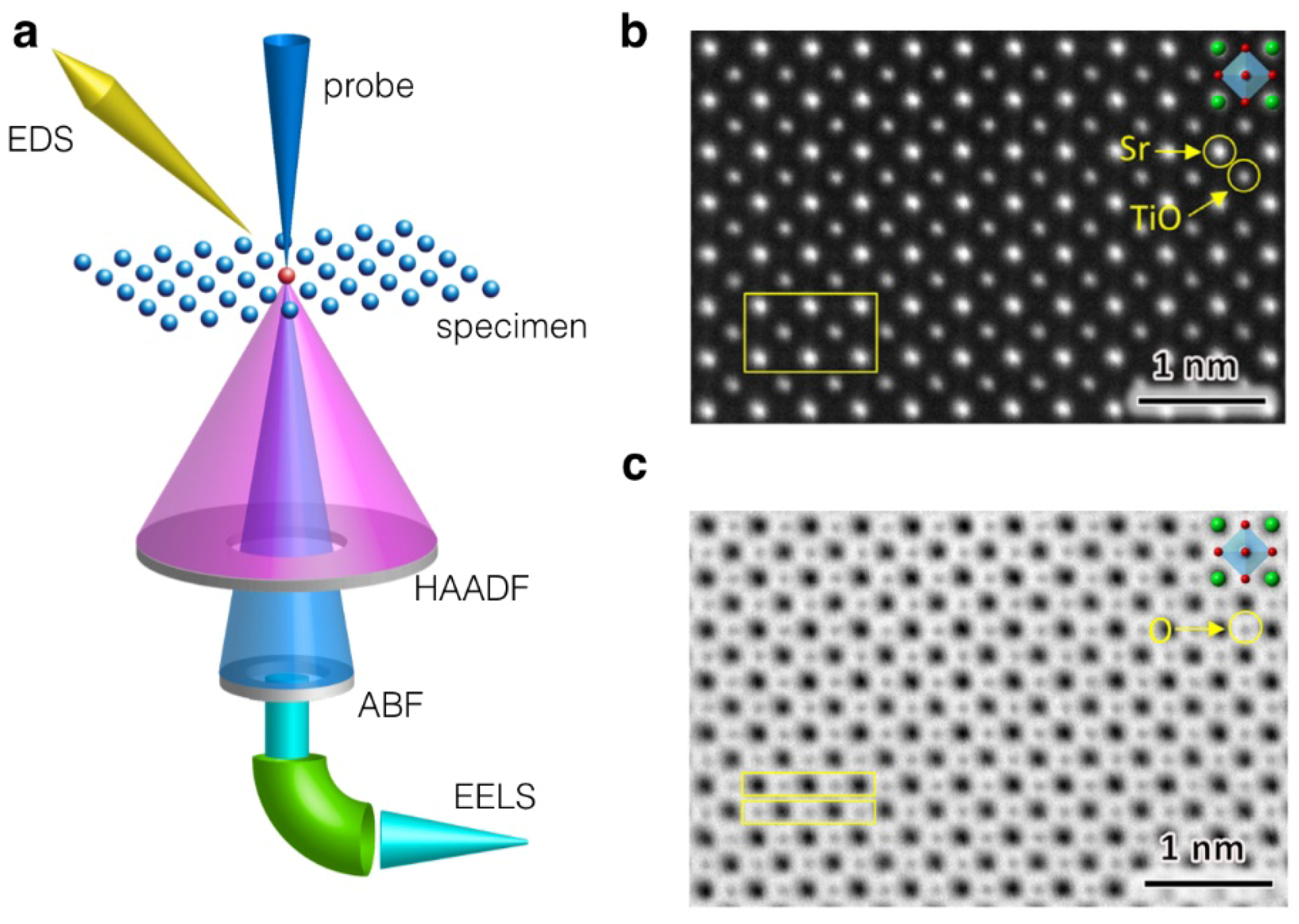
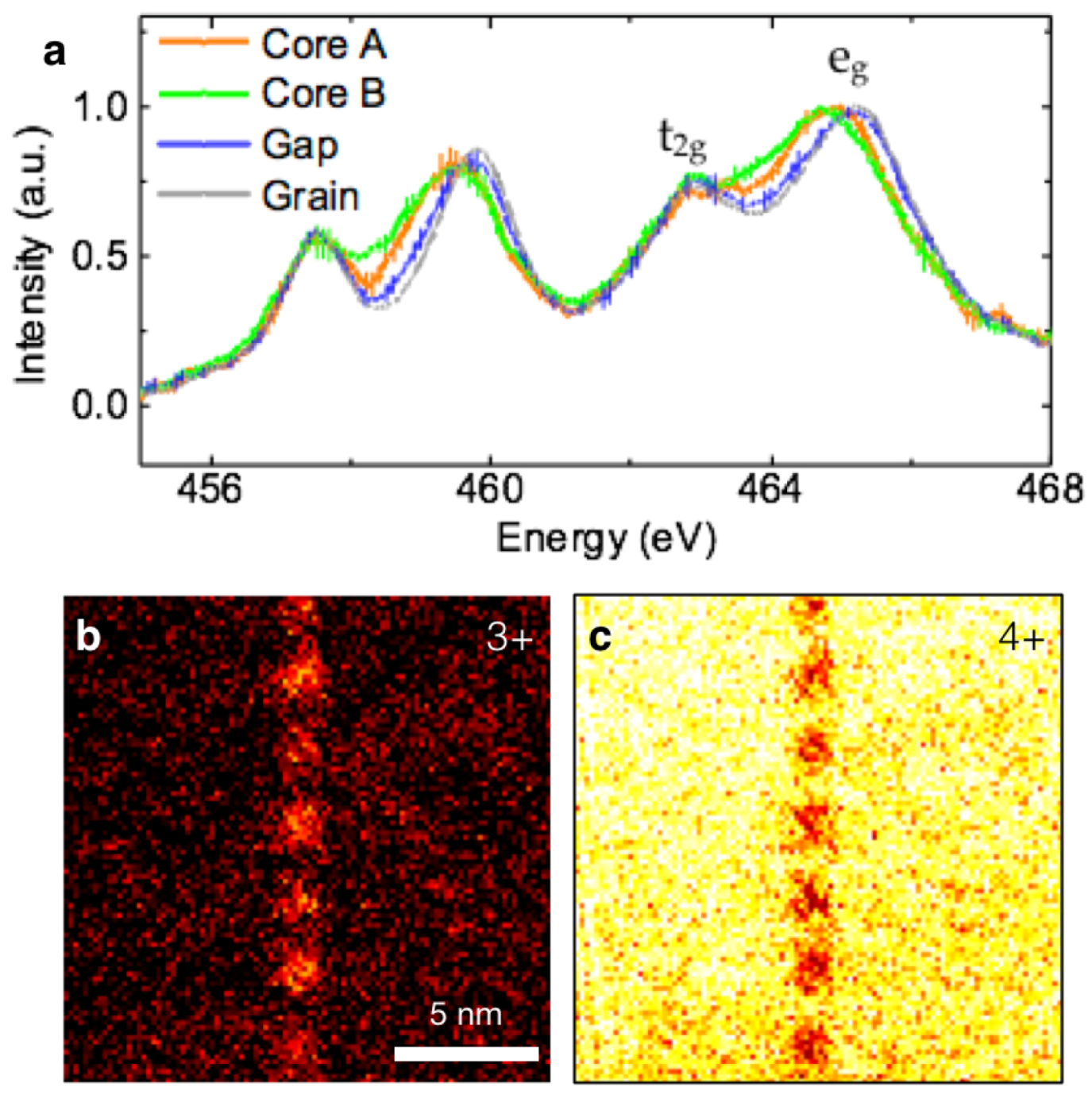
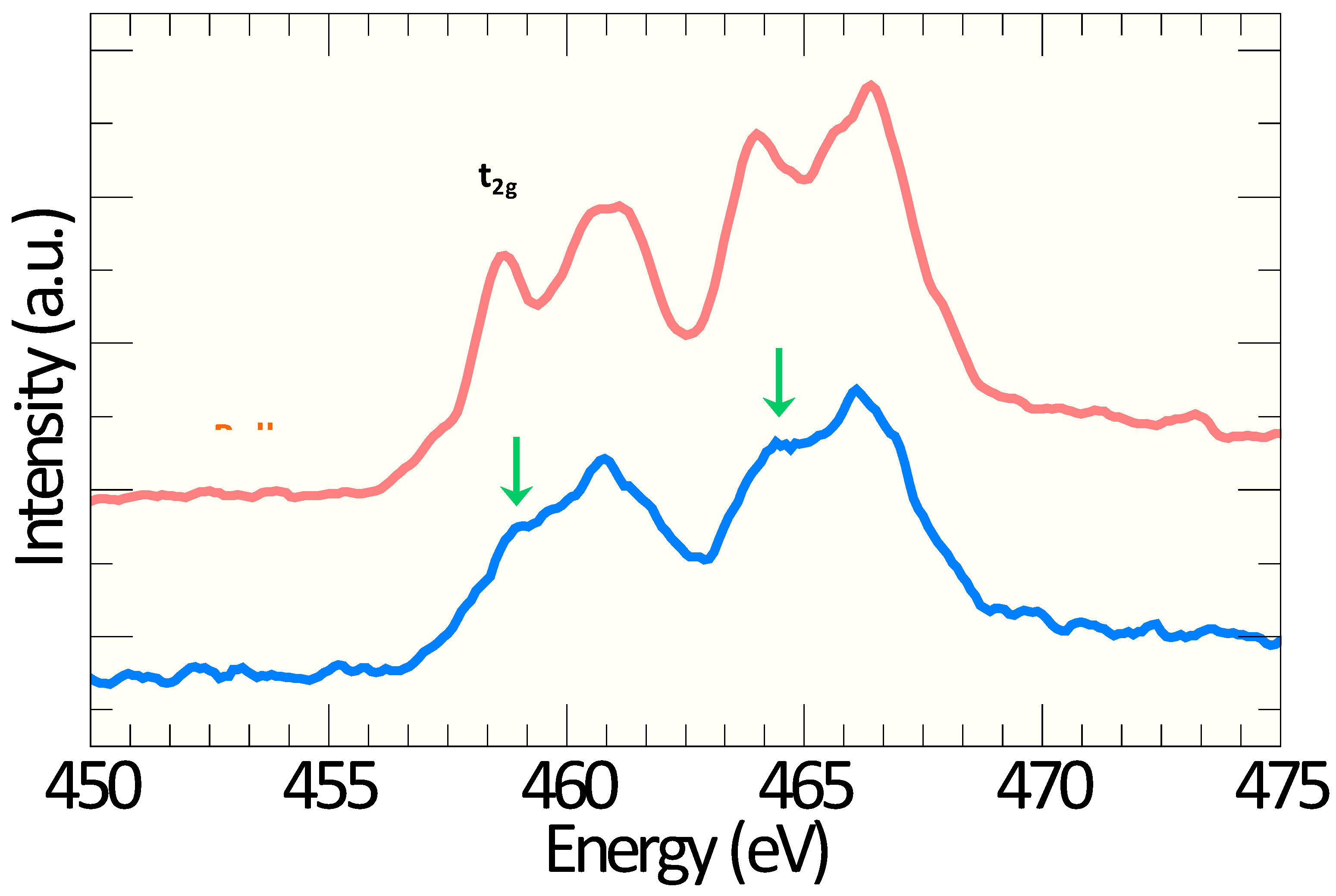
5.3. Imaging and Spectroscopy by Atomic-Resolution STEM
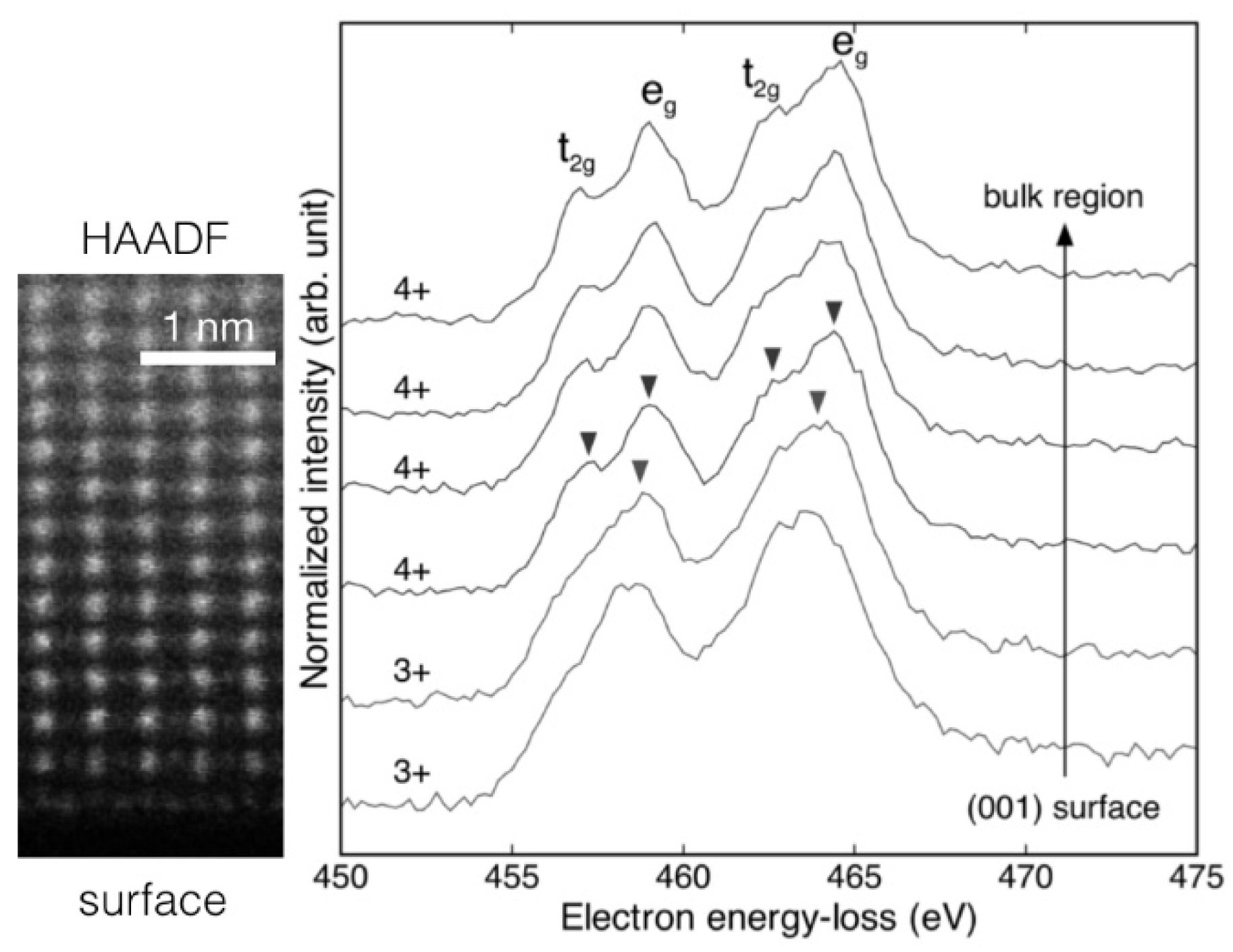
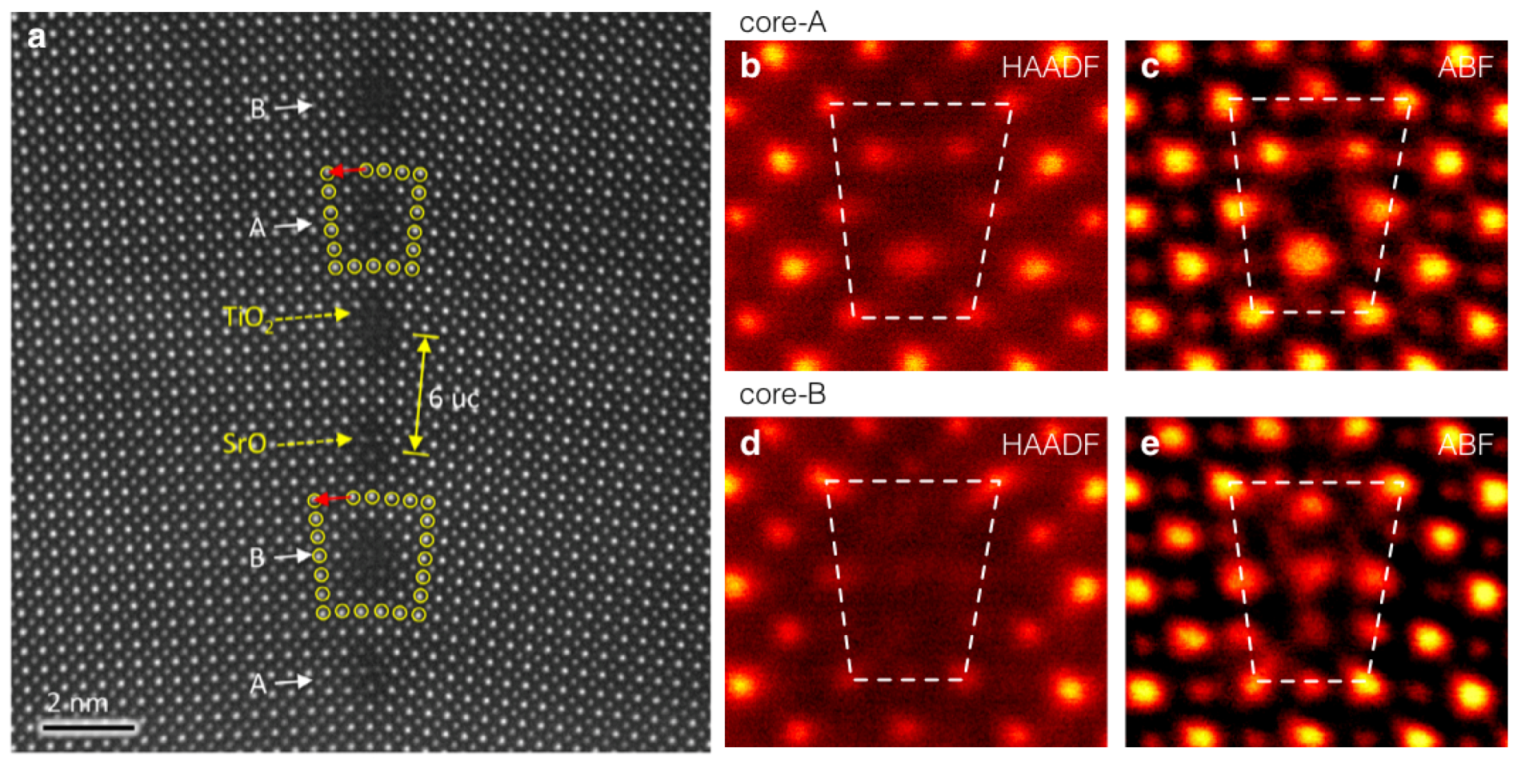
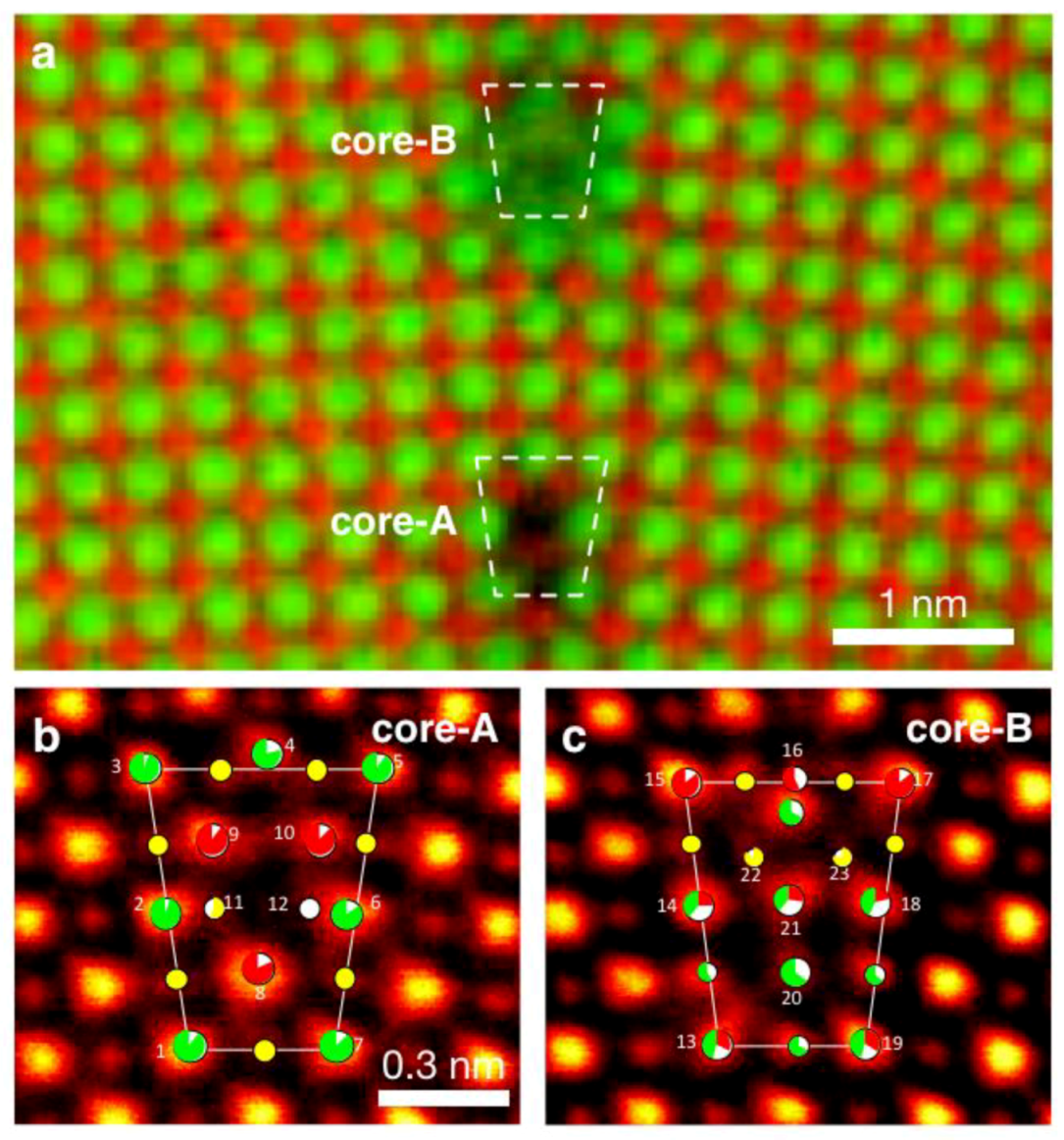
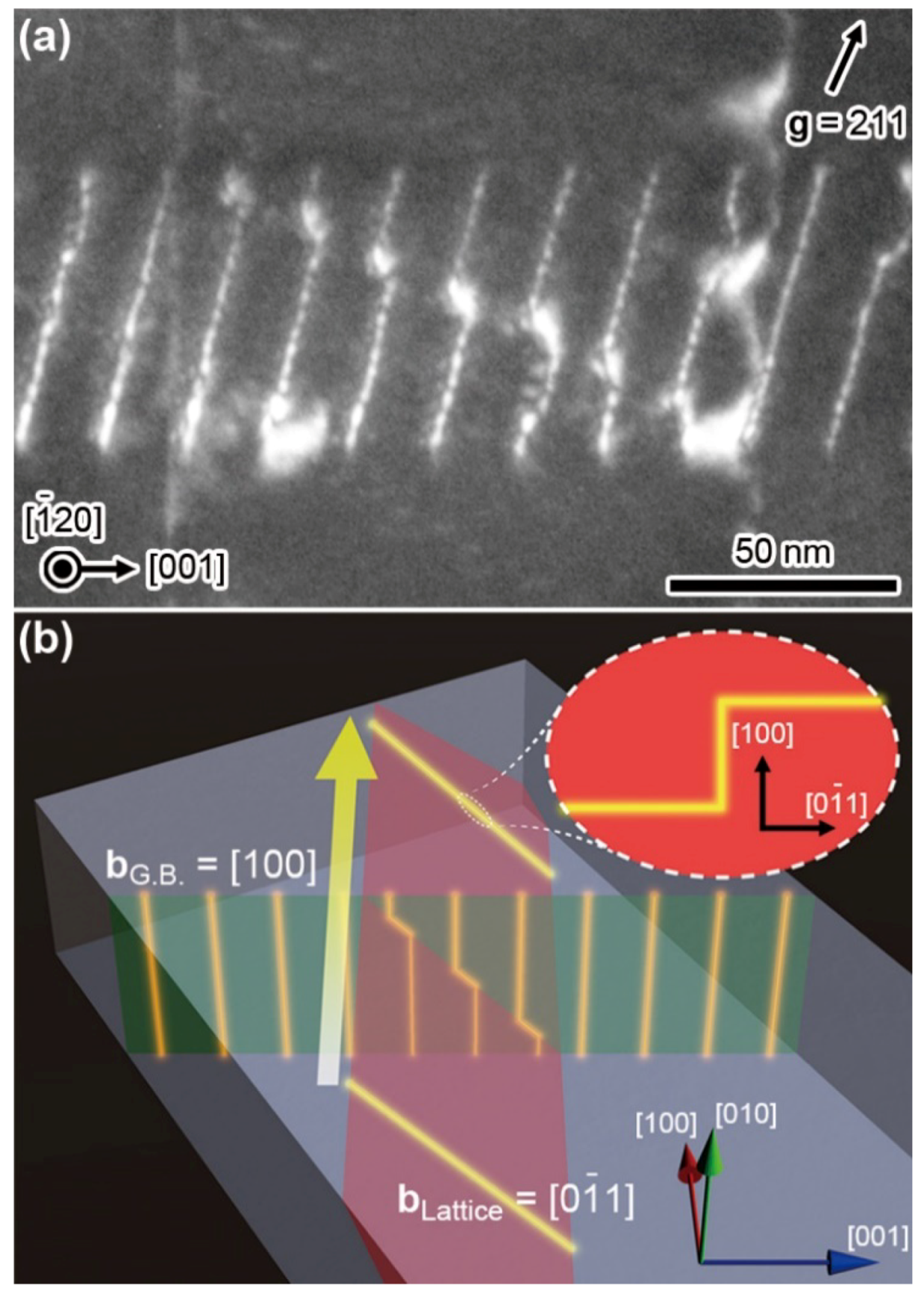
5.3.1. Dislocation Structure and Chemistry in the Grain Boundary of SrTiO3
5.3.2. Dislocation Structure and Chemistry of Titanium Dioxide (TiO2)
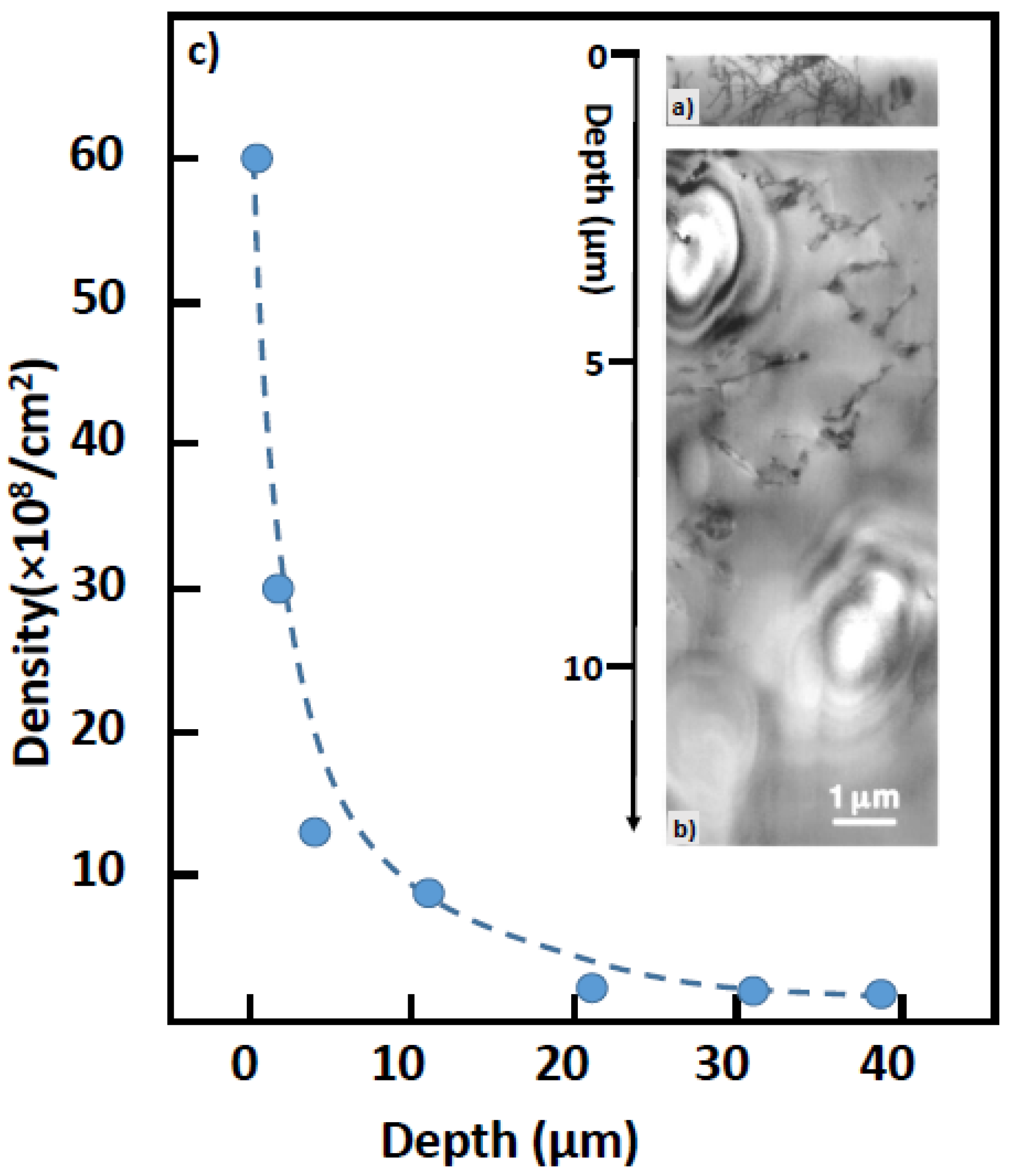
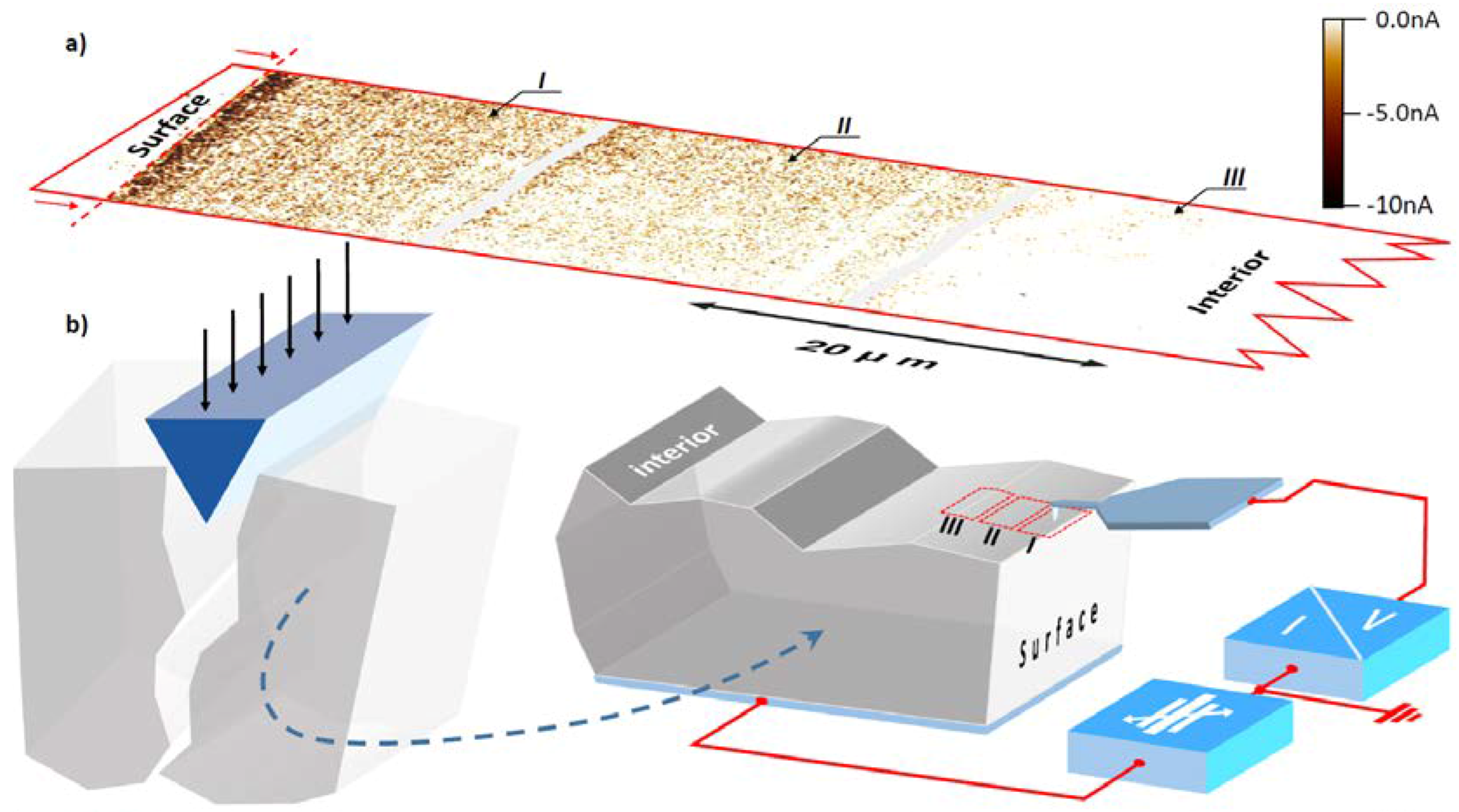
5.3.3. Hierarchical Distribution of Dislocations in the Surface Layer of SrTiO3
5.4. Electron Channeling Contrast Imaging (ECCI)
5.5. Electron Holography
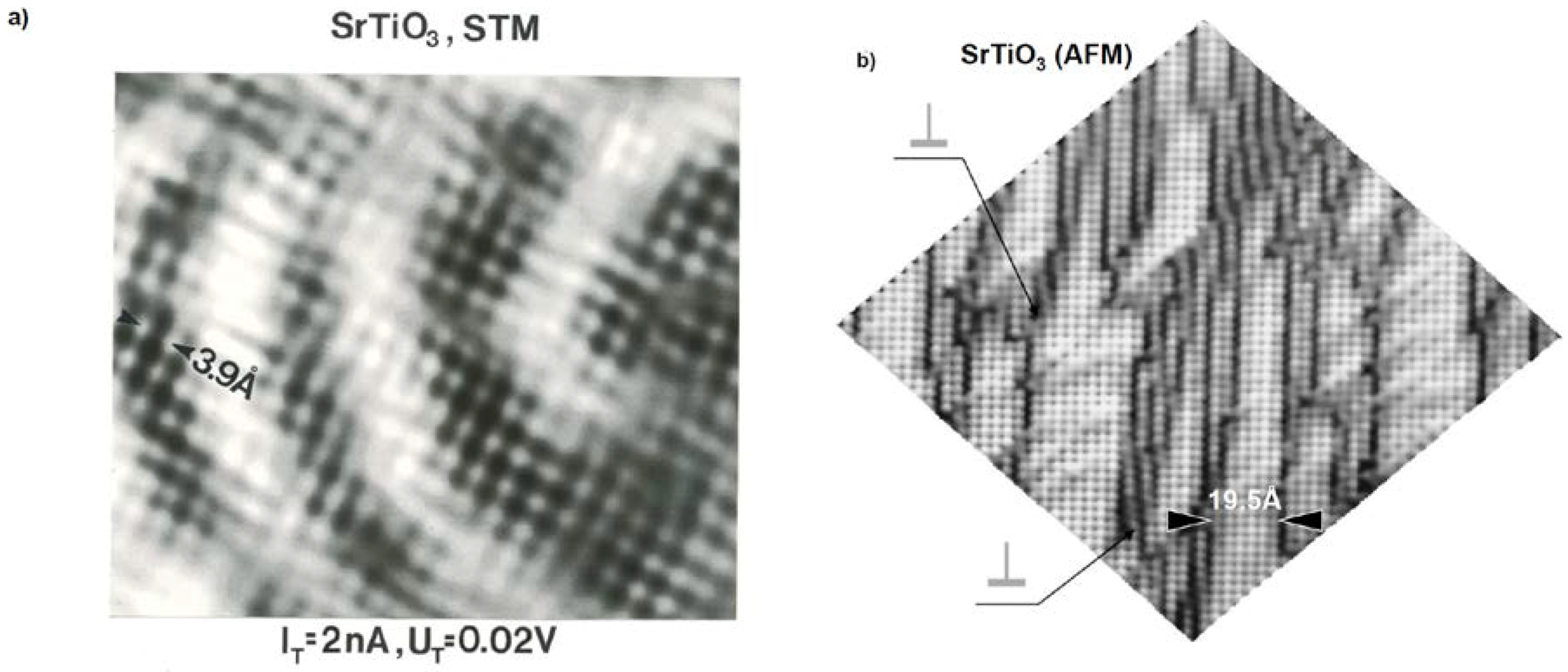
5.6. AFM STM Study on Dislocations in TiO2 and SrTiO3 Crystals with Atomic Resolution
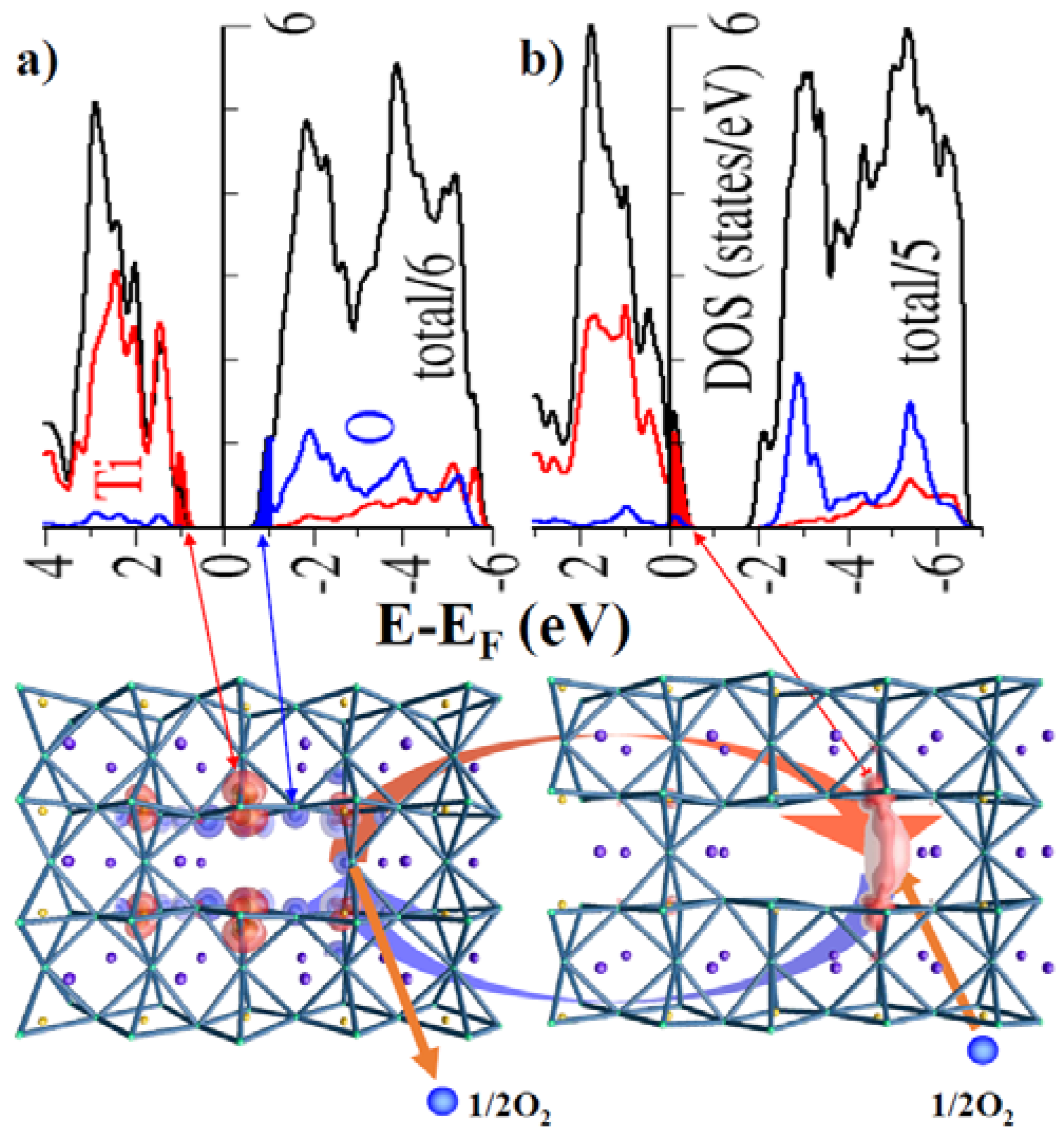
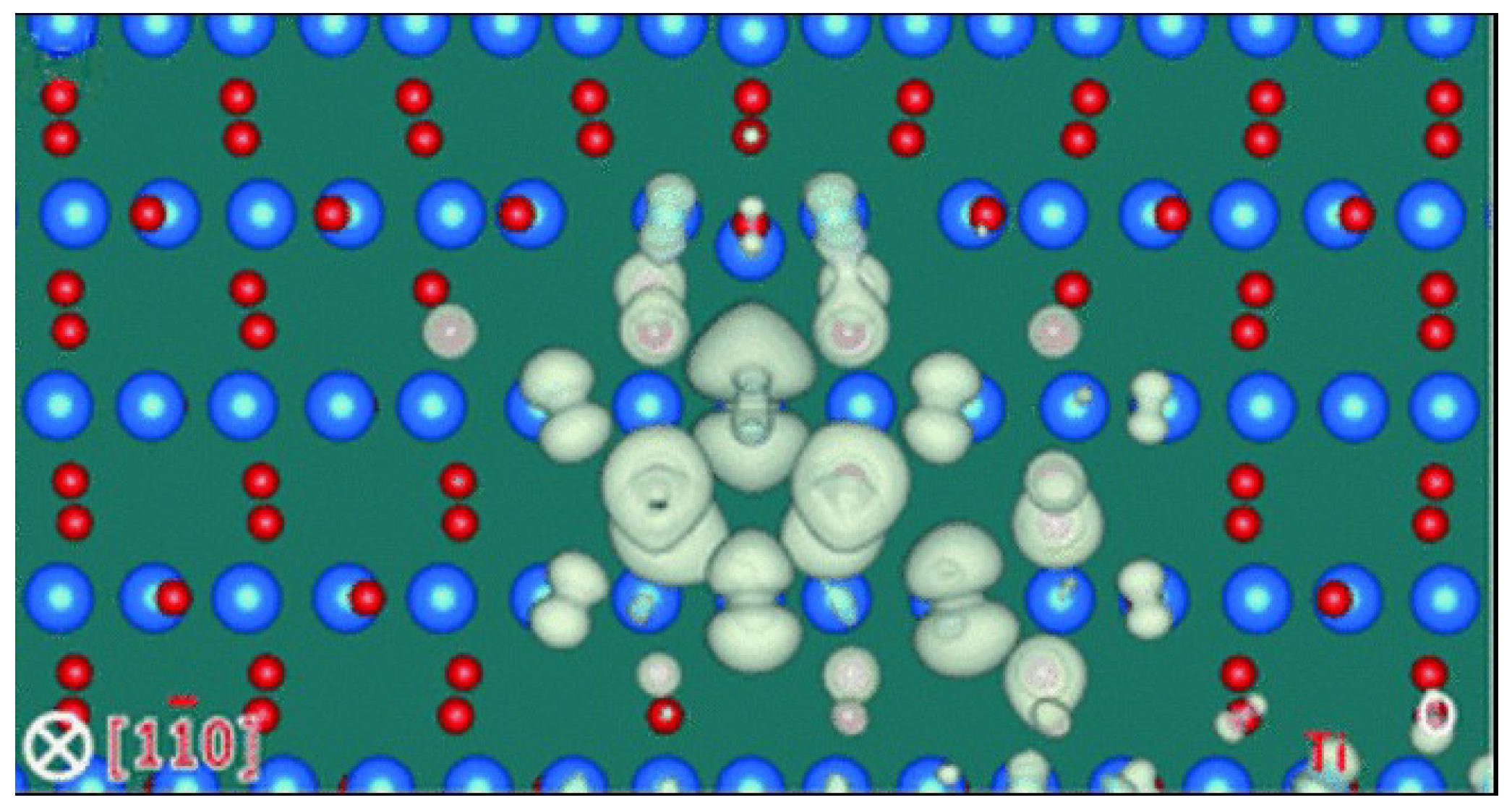
6. Calculations of the Electronic Structure and Molecular Atomic Modelling of the Cores of Dislocations in TiO2 or SrTiO3 Crystals
6.1. DFT Calculation and Atomic Simulations
6.2. Molecular Atomic Simulation
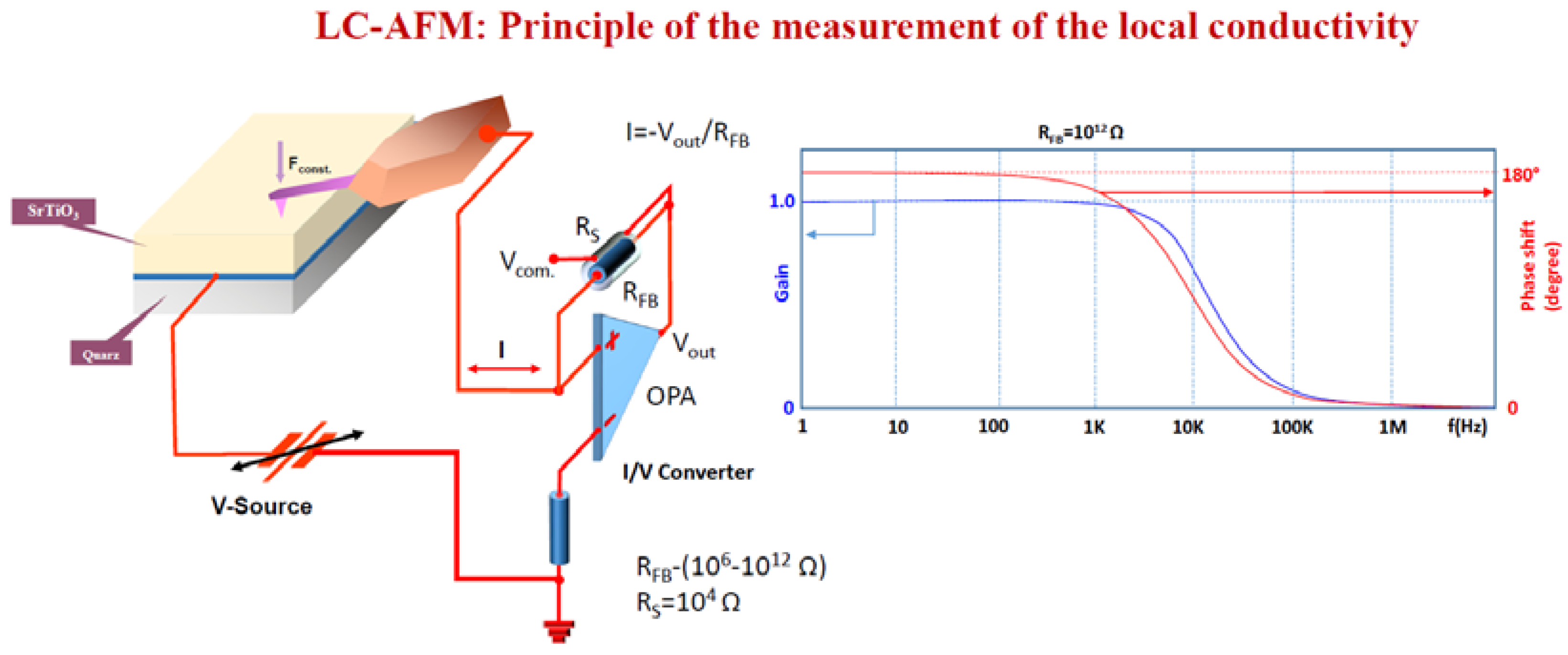
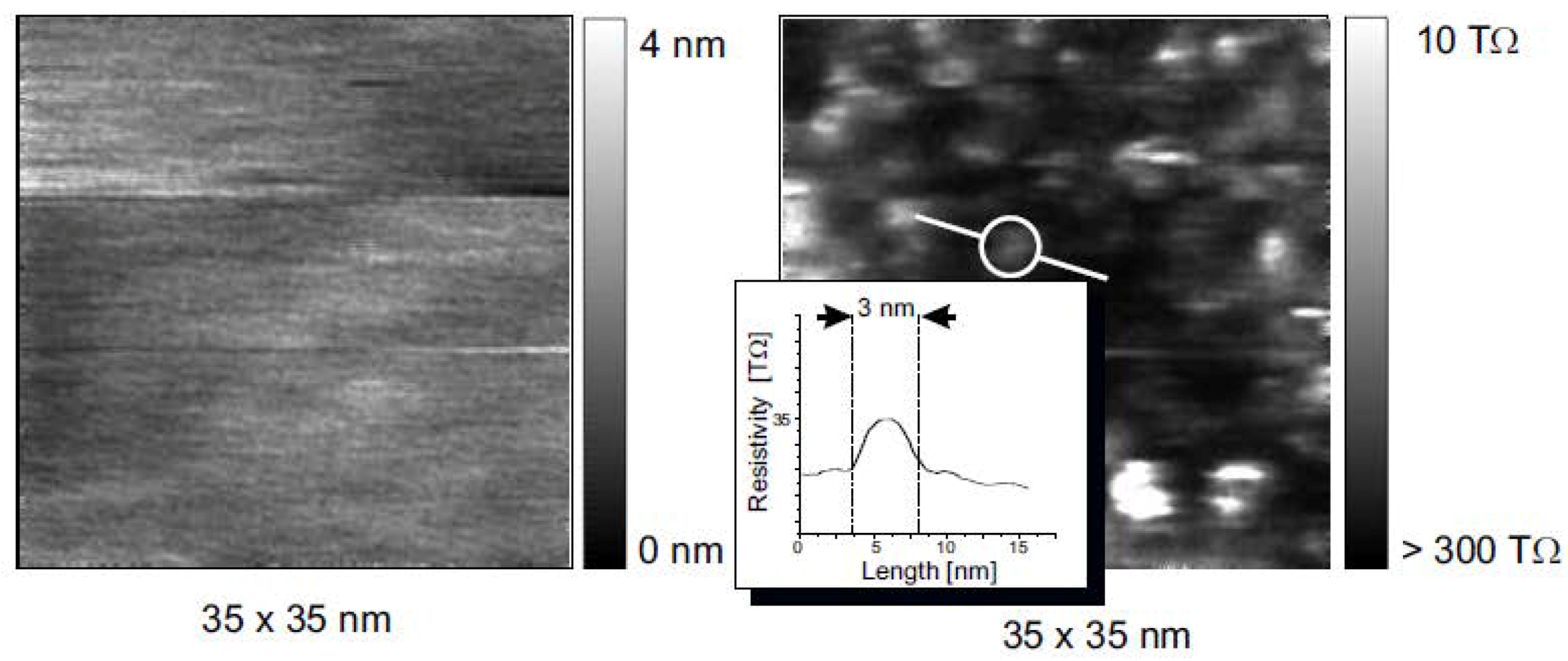
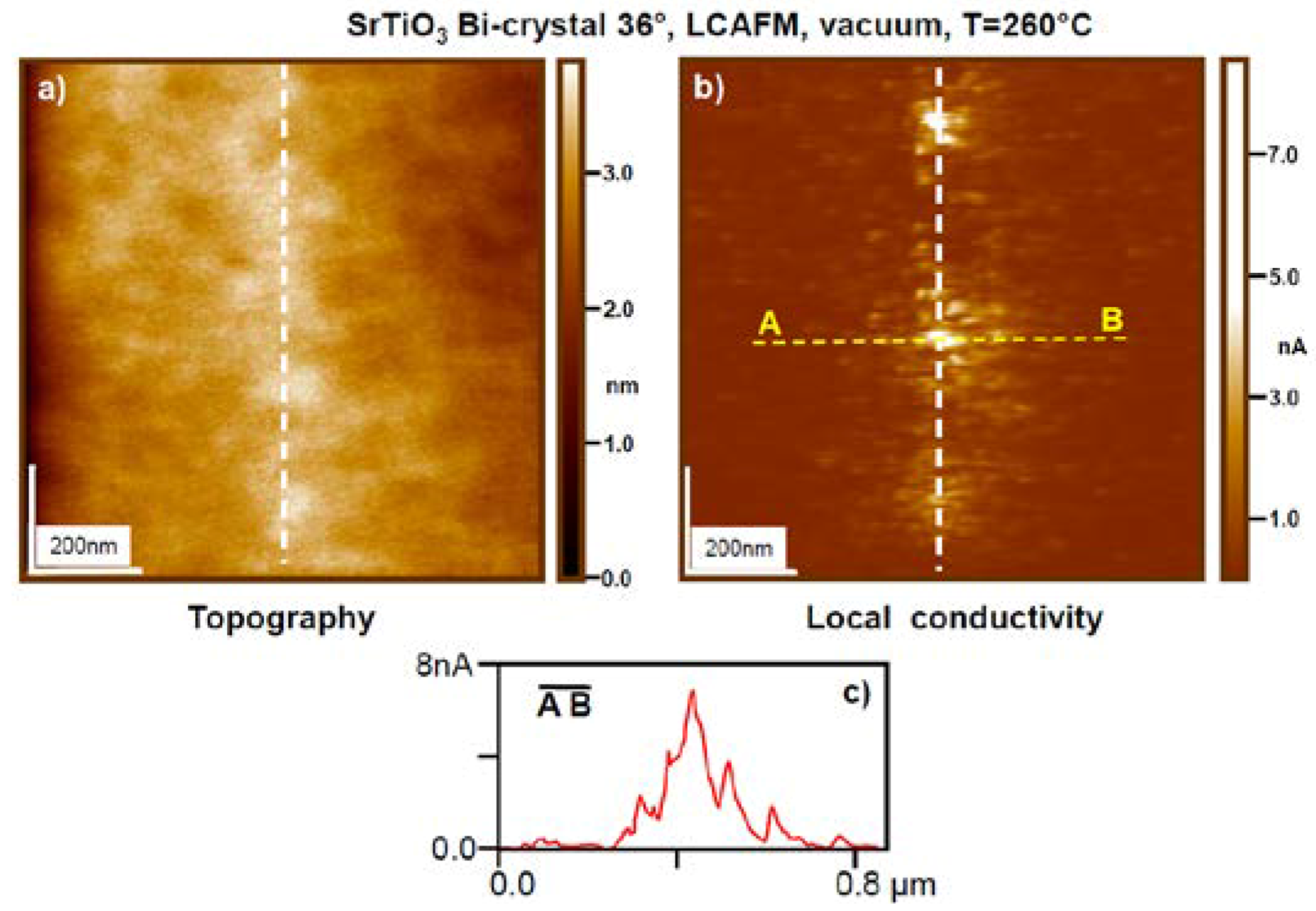
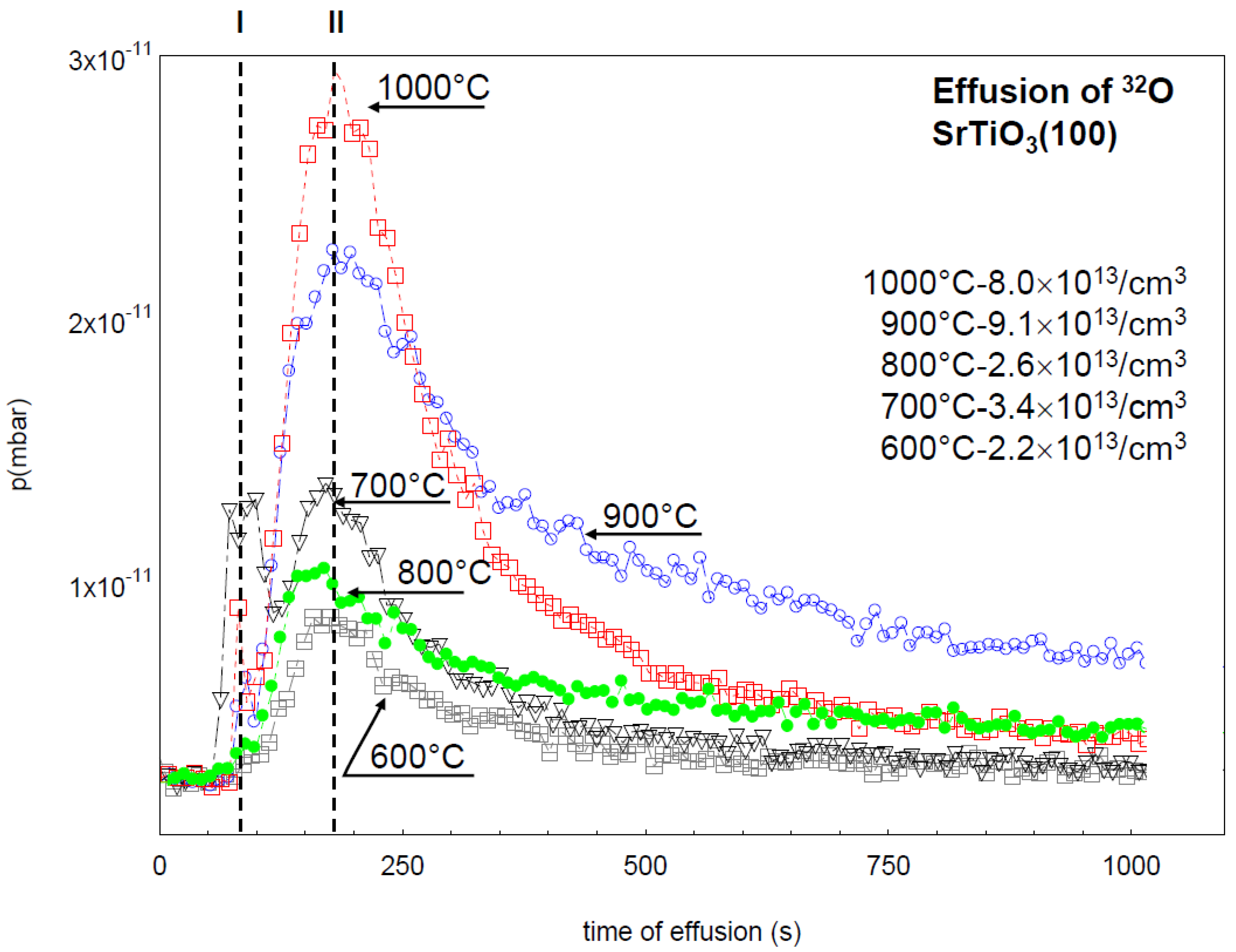
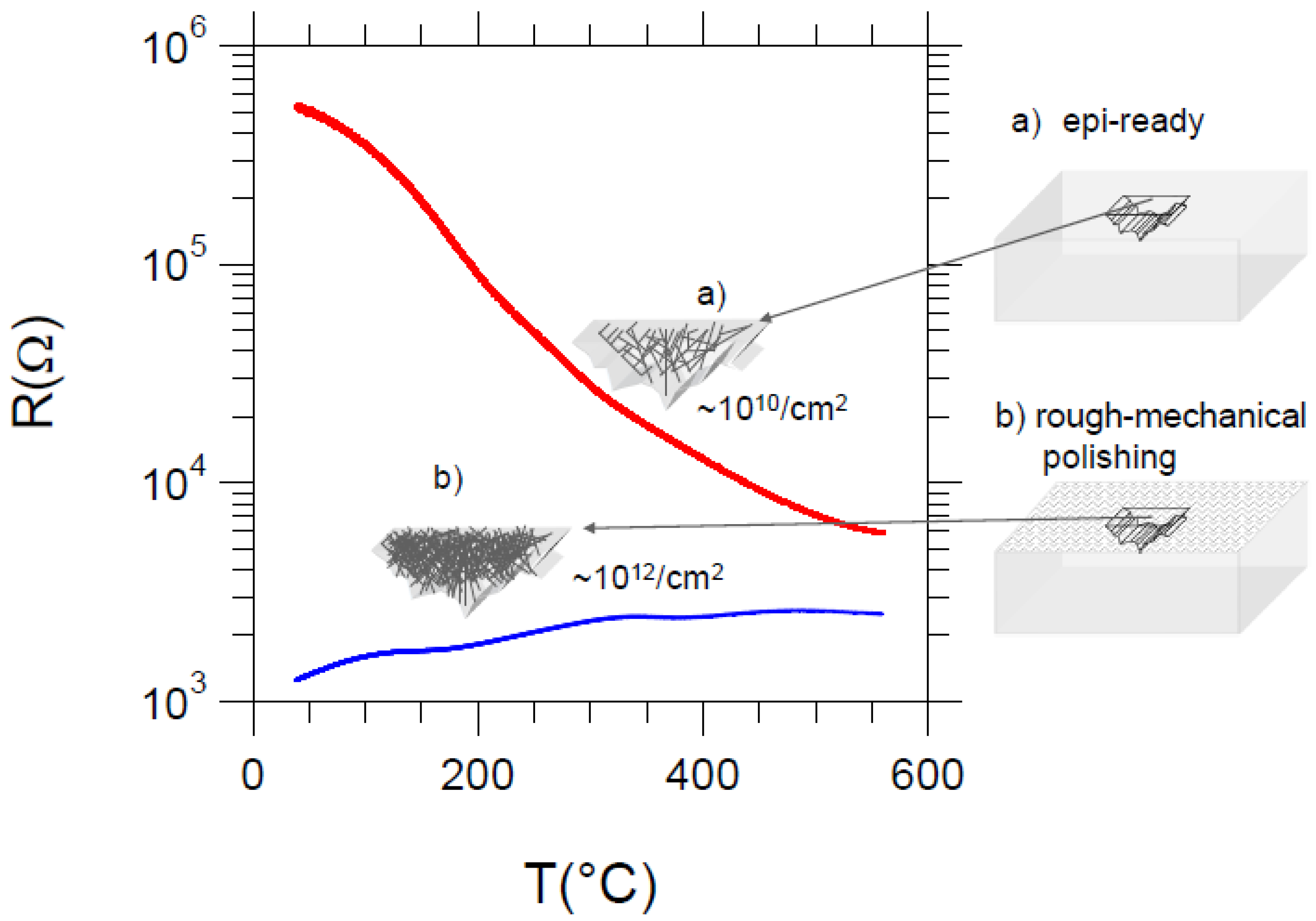
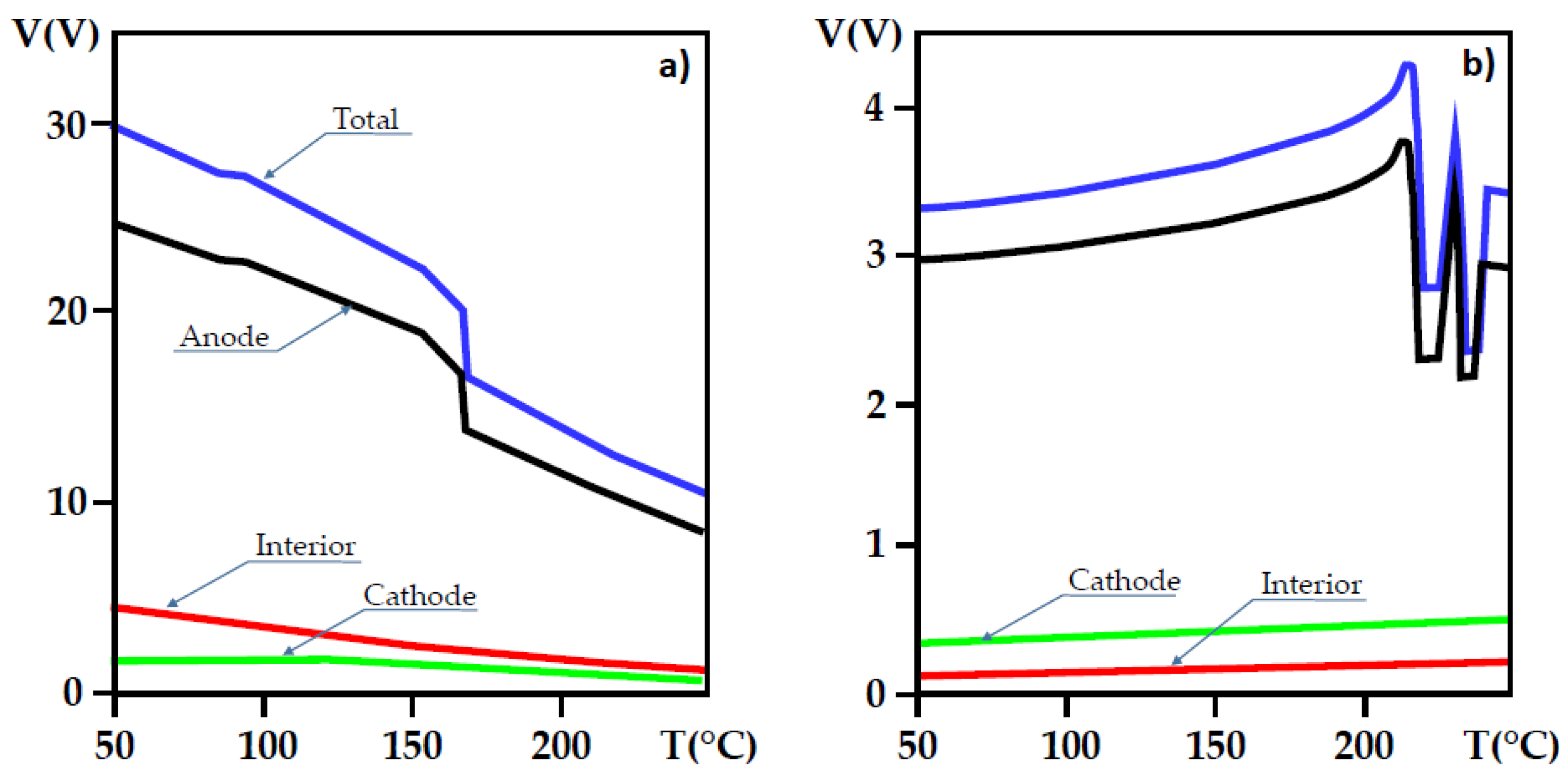
7. Electrical Properties of the Dislocations in TiO2 and SrTiO3
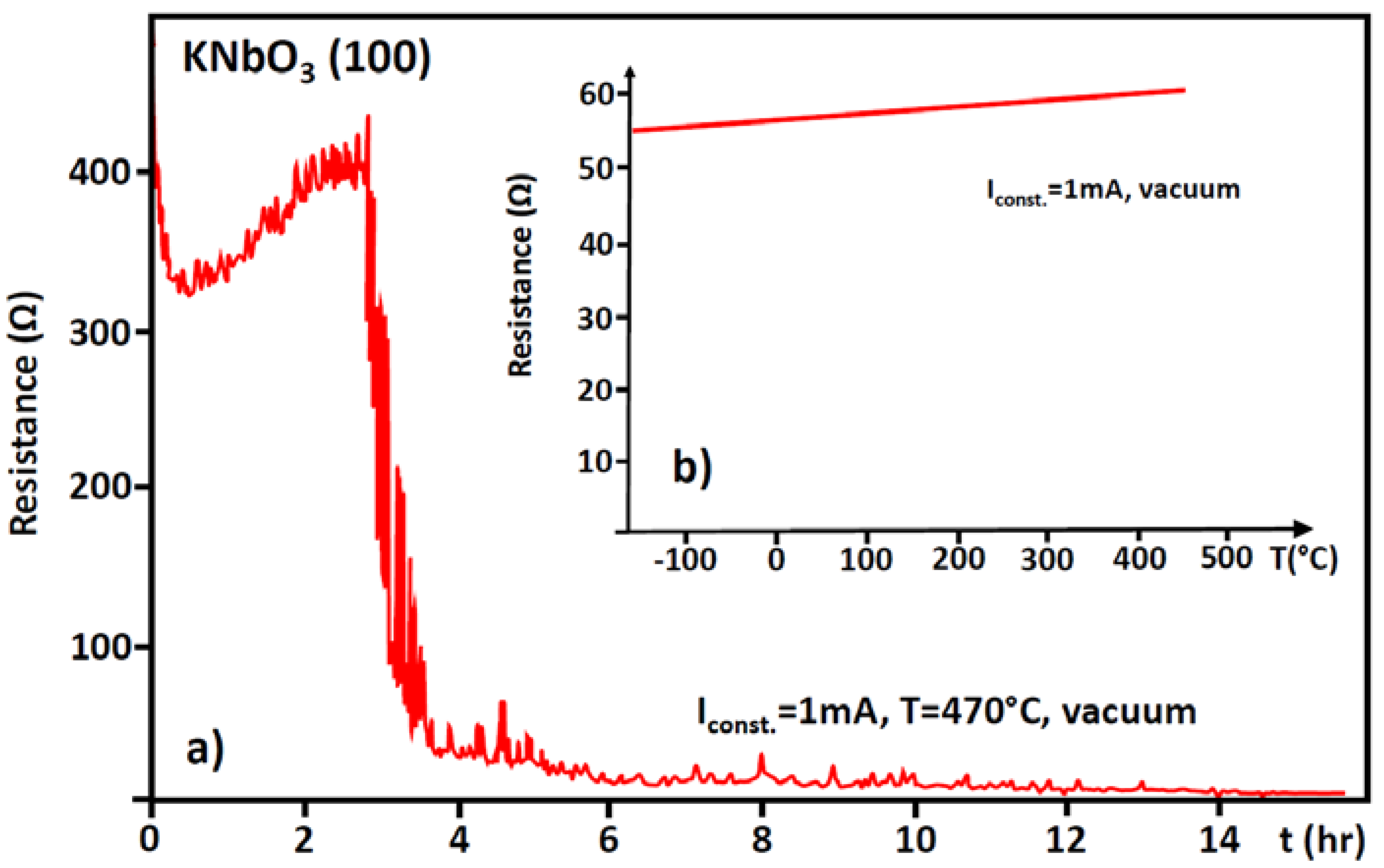
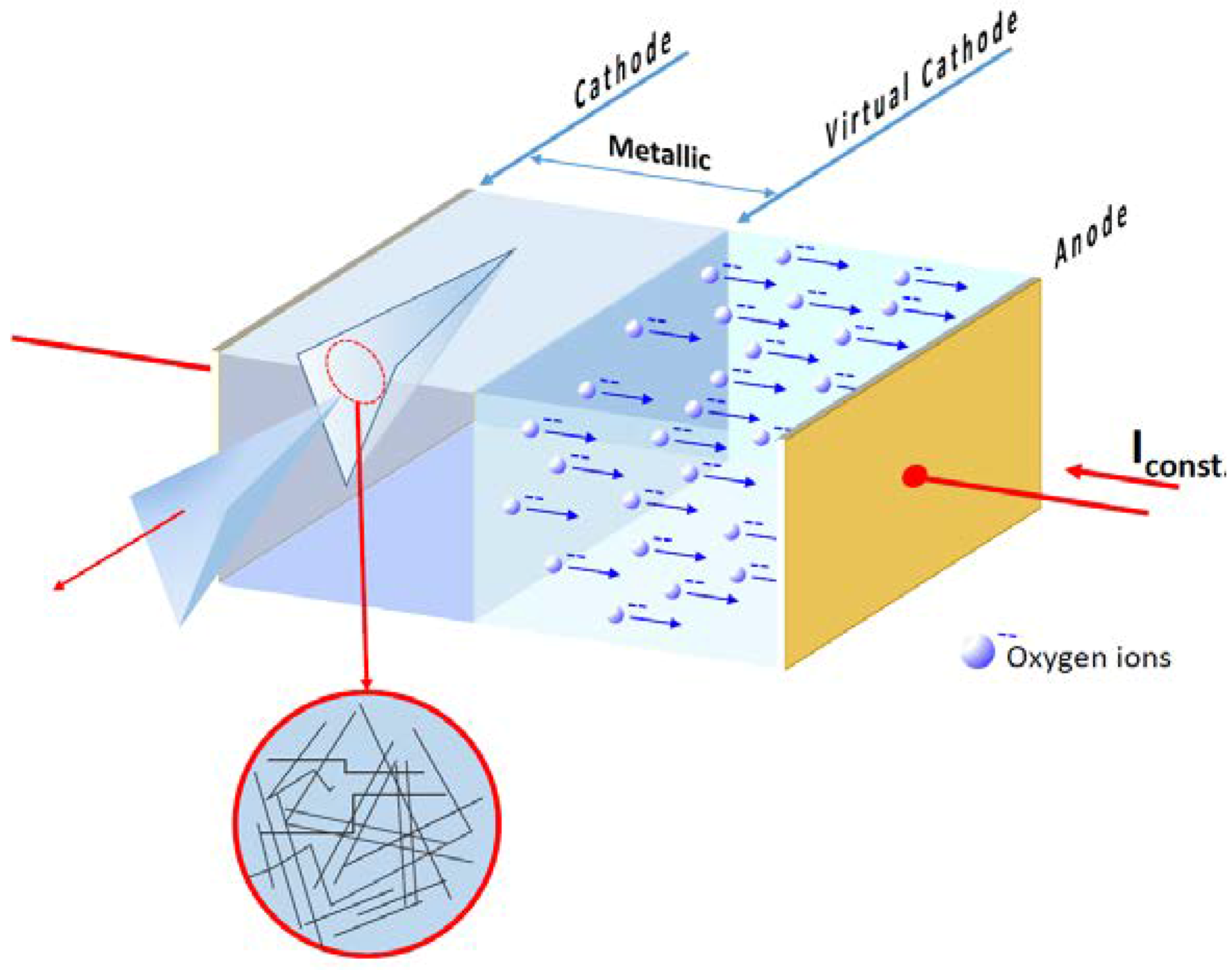
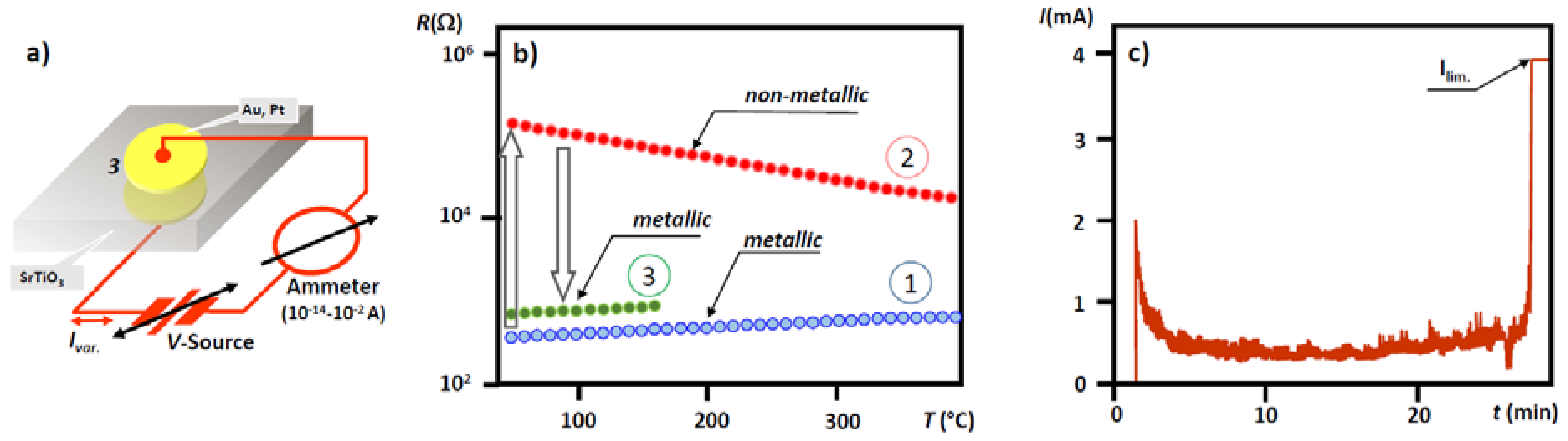
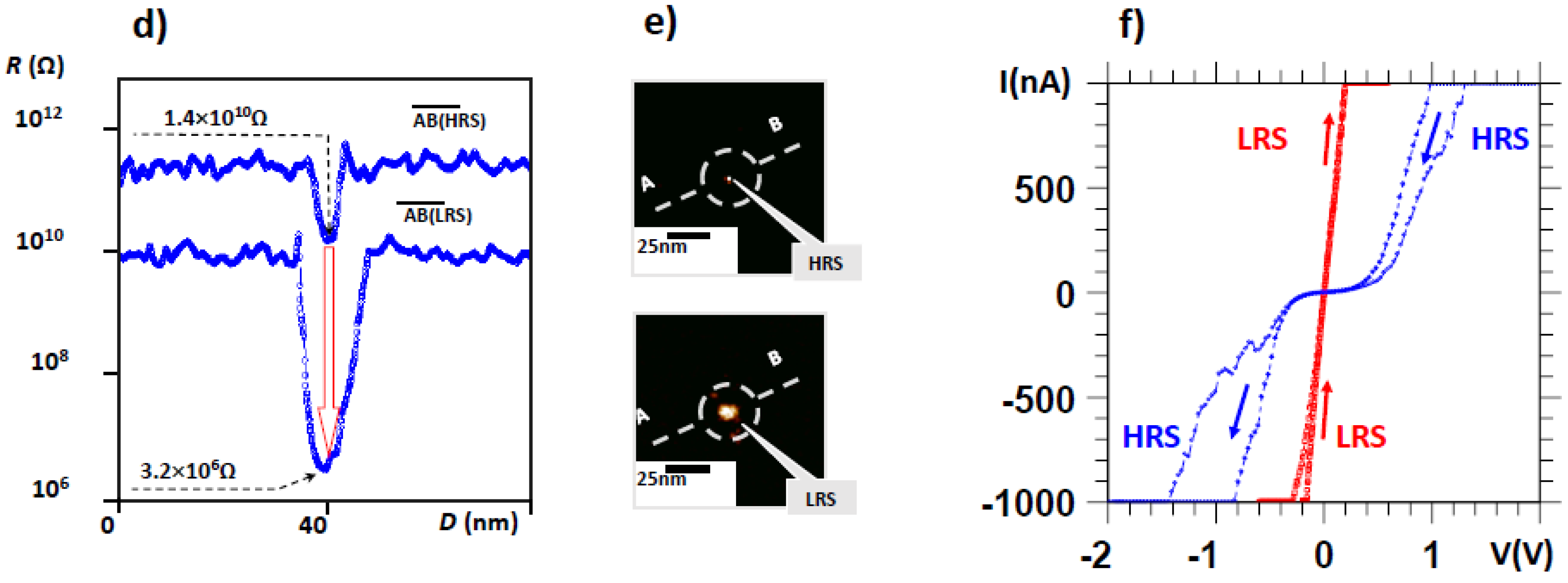
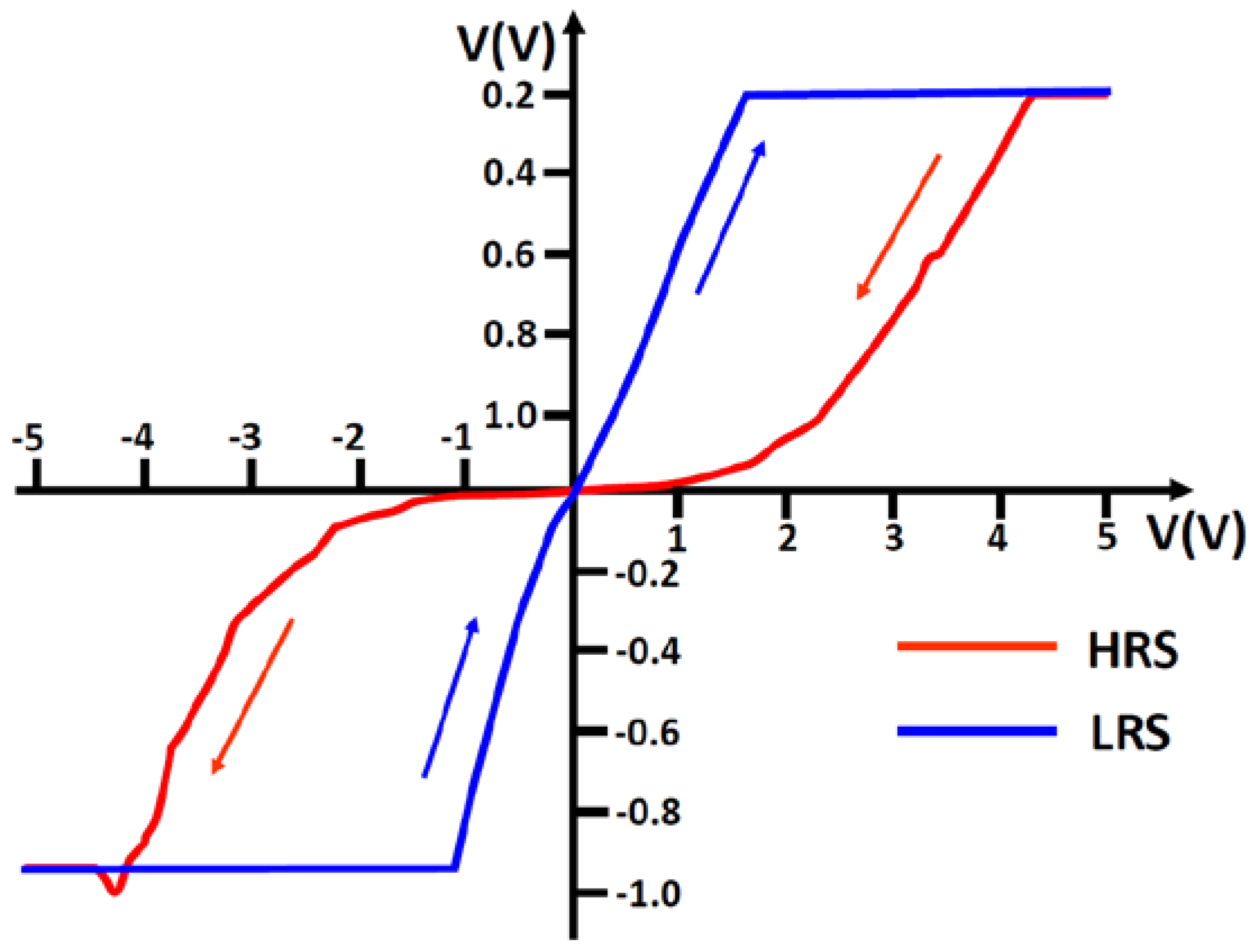
8. Role of Dislocations in Resistive Switching of TiO2 and SrTiO3 Crystals
- the polarization (negative or positive) of the tip,
- the voltage, i.e., local strength of the electrical field, and
- the low oxygen partial pressure available in the AFM microscope.
9. Mechanical Properties versus Dislocations
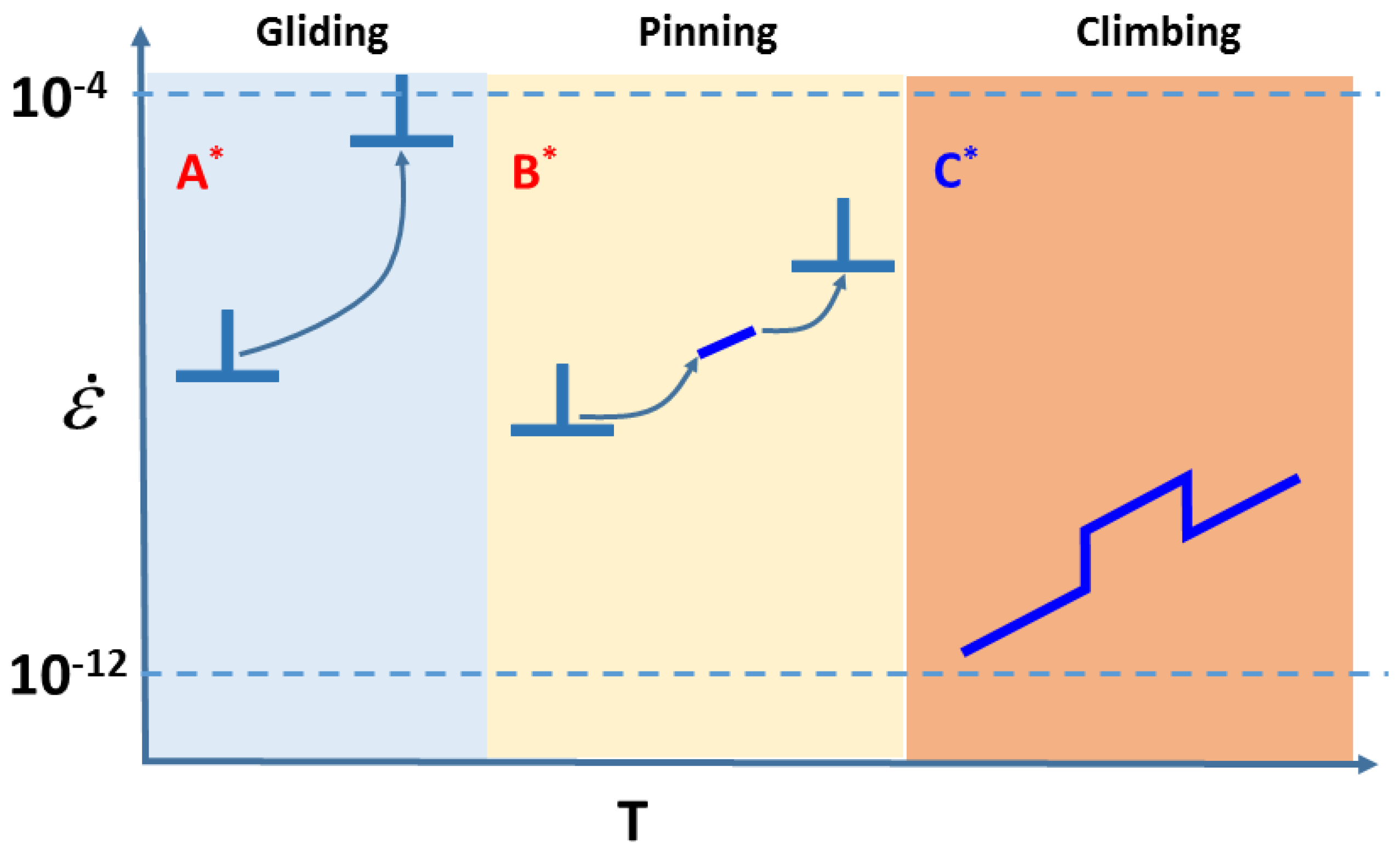
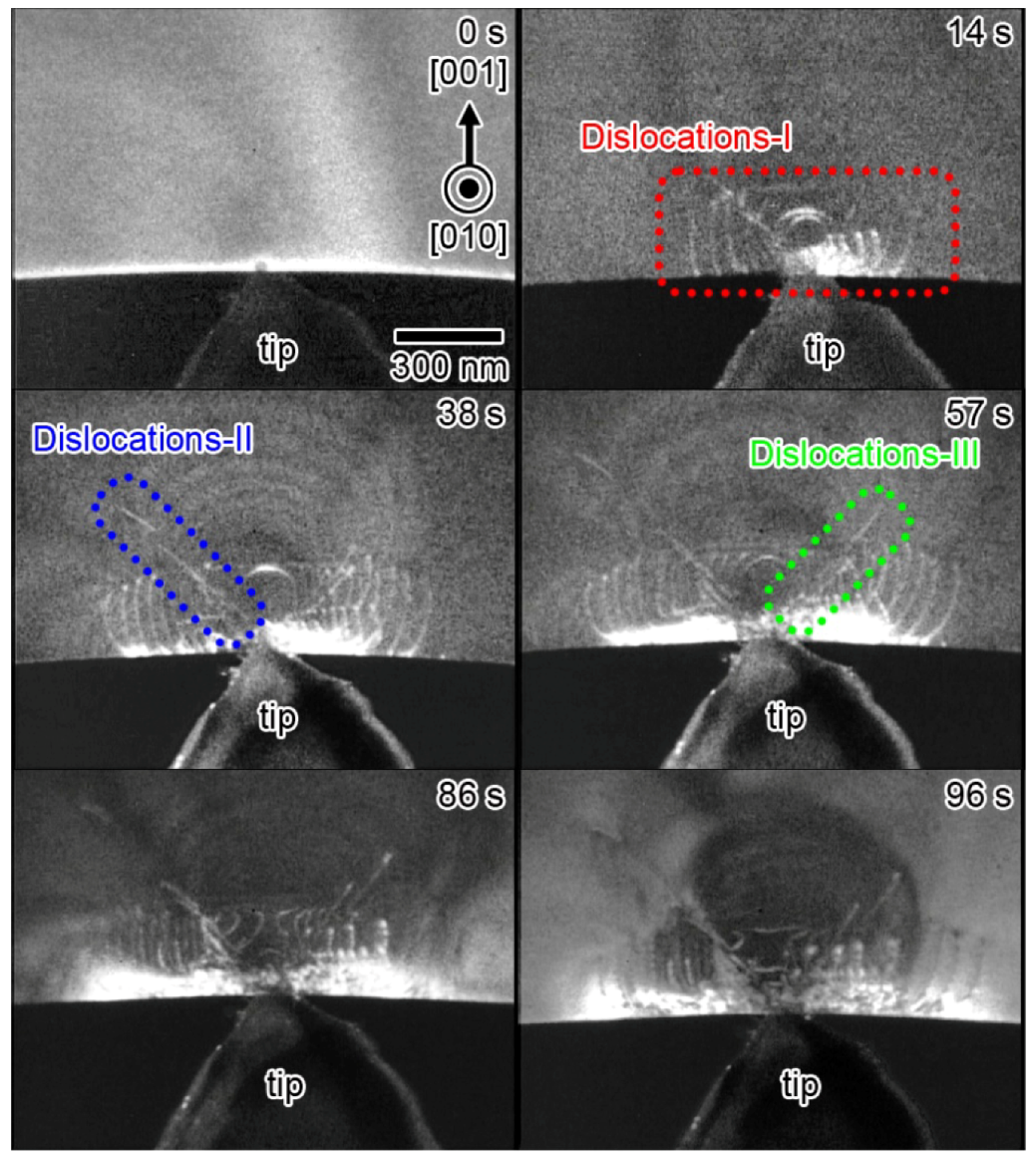
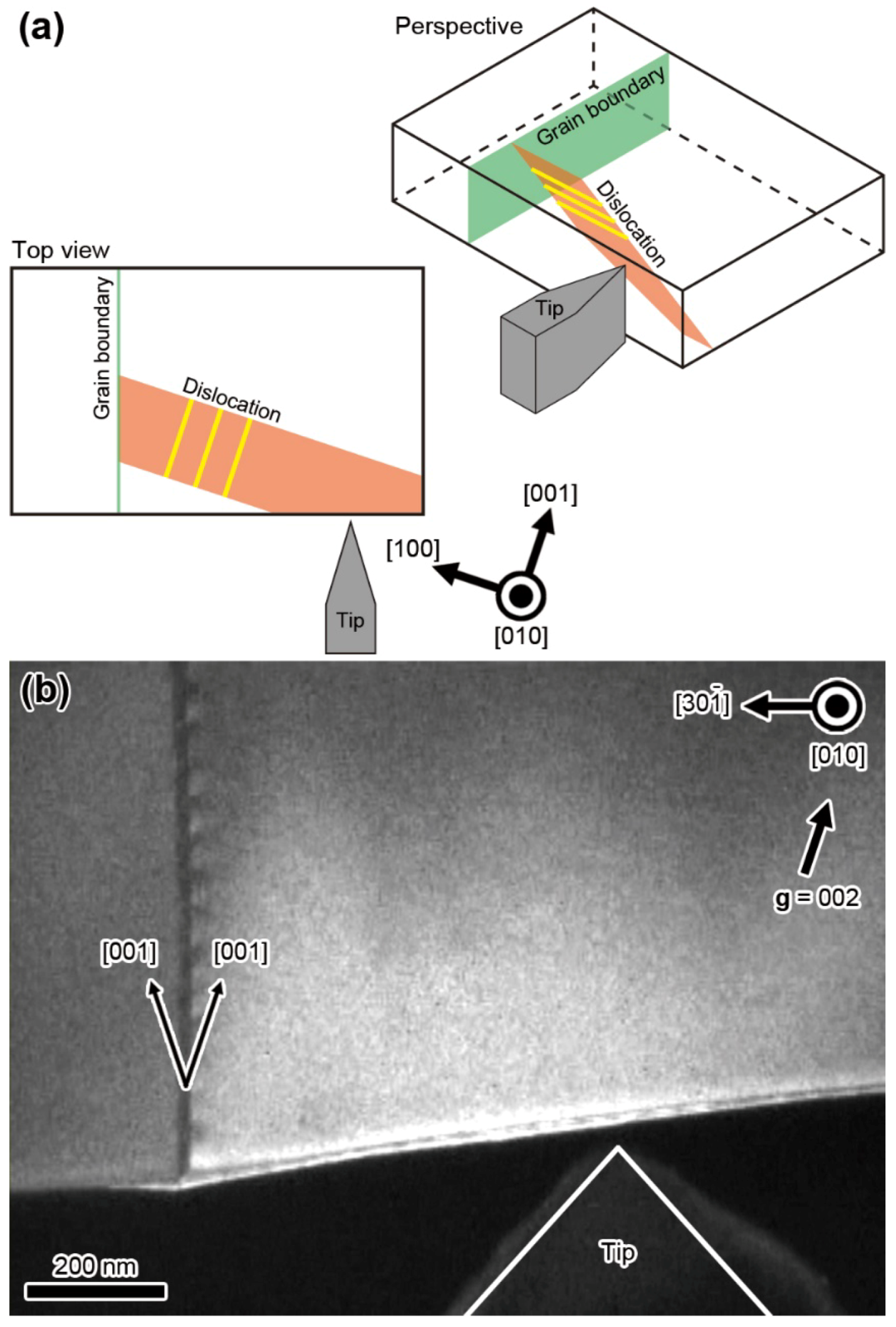
10. Dynamic Behavior of Dislocations in SrTiO3 by In Situ Nanoindentation Experiments inside TEM
11. Conclusions
Author Contributions
Acknowledgments
Conflicts of Interest
References
- Veyssiere, P. Dislocation-Structure in Non-Stoichiometric Oxides. Radiat. Eff. 1983, 74, 1–15. [Google Scholar] [CrossRef]
- Doukhan, N.; Doukhan, J.C. Dislocations in Perovskites BaTiO3 and CaTiO3. Phys. Chem. Miner. 1986, 13, 403–410. [Google Scholar]
- Nakamura, A.; Matsunaga, K.; Tohma, J.; Yamamoto, T.; Ikuhara, Y. Conducting nanowires in insulating ceramics. Nat. Mater. 2003, 2, 453–456. [Google Scholar] [CrossRef] [PubMed]
- Shibata, N.; Chisholm, M.F.; Nakamura, A.; Pennycook, S.J.; Yamamoto, T.; Ikuhara, Y. Nonstoichiometric dislocation cores in α-alumina. Science 2007, 316, 82–85. [Google Scholar] [CrossRef] [PubMed]
- Arredondo, M.; Ramasse, Q.M.; Weyland, M.; Mahjoub, R.; Vrejoiu, I.; Hesse, D.; Browning, N.D.; Alexe, M.; Munroe, P.; Nagarajan, V. Direct Evidence for Cation Non-Stoichiometry and Cottrell Atmospheres Around Dislocation Cores in Functional Oxide Interfaces. Adv. Mater. 2010, 22, 2430–2434. [Google Scholar] [CrossRef] [PubMed]
- Shimada, T.; Xu, T.; Araki, Y.; Wang, J.; Kitamura, T. Multiferroic Dislocations in Ferroelectric PbTiO3. Nano Lett. 2017, 17, 2674–2680. [Google Scholar] [CrossRef] [PubMed]
- Nagarajan, V.; Jia, C.L.; Kohlstedt, H.; Waser, R.; Misirlioglu, I.B.; Alpay, S.P.; Ramesh, R. Misfit dislocations in nanoscale ferroelectric heterostructures. Appl. Phys. Lett. 2005, 86, 192910. [Google Scholar] [CrossRef] [Green Version]
- De Souza, R.A.; Fleig, J.; Maier, J.; Kienzle, O.; Zhang, Z.L.; Sigle, W.; Rühle, M. Electrical and structural characterization of a low-angle tilt grain boundary in iron-doped strontium titanate. J. Am. Ceram. Soc. 2003, 86, 922–928. [Google Scholar] [CrossRef]
- Mao, Z.; Knowles, K.M. Dissociation of lattice dislocations in SrTiO3. Philos. Mag. A 1996, 73, 699–708. [Google Scholar] [CrossRef]
- Wang, R.H.; Zhu, Y.M.; Shapiro, S.M. Structural defects and the origin of the second length scale in SrTiO3. Phys. Rev. Lett. 1998, 80, 2370–2373. [Google Scholar] [CrossRef]
- Zhang, Z.L.; Sigle, W.; Kurtz, W.; Rühle, M. Electronic and atomic structure of a dissociated dislocation in SrTiO3. Phys. Rev. B 2002, 66, 214112. [Google Scholar] [CrossRef]
- Zhang, Z.L.; Sigle, W.; Rühle, M. Atomic and electronic characterization of the a[100] dislocation core in SrTiO3. Phys. Rev. B 2002, 66, 094108. [Google Scholar] [CrossRef]
- Chen, J.; Sekiguchi, T.; Li, J.Y.; Ito, S. Investigation of dislocations in Nb-doped (100) SrTiO3 single crystals and their impacts on resistive switching. Superlattices Microstruct. 2016, 99, 182–185. [Google Scholar] [CrossRef]
- Sun, H.P.; Tian, W.; Pan, X.Q.; Haeni, J.H.; Schlom, D.G. Evolution of dislocation arrays in epitaxial BaTiO3 thin films grown on (100) SrTiO3. Appl. Phys. Lett. 2004, 84, 3298–3300. [Google Scholar] [CrossRef]
- Brunner, D.; Taeri-Baghbadrani, S.; Sigle, W.; Rühle, M. Surprising results of a study on the plasticity in strontium titanate. J. Am. Ceram. Soc. 2001, 84, 1161–1163. [Google Scholar] [CrossRef]
- Gumbsch, P.; Taeri-Baghbadrani, S.; Brunner, D.; Sigle, W.; Rühle, A. Plasticity and an inverse brittle-to-ductile transition in strontium titanate. Phys. Rev. Lett. 2001, 87, 085505. [Google Scholar] [CrossRef] [PubMed]
- Metlenko, V.; Ramadan, A.H.H.; Gunkel, F.; Du, H.C.; Schraknepper, H.; Hoffmann-Eifert, S.; Dittmann, R.; Waser, R.; De Souza, R.A. Do dislocations act as atomic autobahns for oxygen in the perovskite oxide SrTiO3? Nanoscale 2014, 6, 12864–12876. [Google Scholar] [CrossRef] [PubMed]
- Wang, Z.C.; Karato, S.; Fujino, K. High-Temperature Creep of Single-Crystal Strontium-Titanate (SrTiO3)—A Contribution to Creep Systematics in Perovskites. Phys. Earth Planet. Inter. 1993, 79, 299–312. [Google Scholar] [CrossRef]
- Adepalli, K.K.; Kelsch, M.; Merkle, R.; Maier, J. Influence of Line Defects on the Electrical Properties of Single Crystal TiO2. Adv. Funct. Mater. 2013, 23, 1798–1806. [Google Scholar] [CrossRef]
- Adepalli, K.K.; Kelsch, M.; Merkle, R.; Maier, J. Enhanced ionic conductivity in polycrystalline TiO2 by “one-dimensional doping”. Phys. Chem. Chem. Phys. 2014, 16, 4942–4951. [Google Scholar] [CrossRef] [PubMed]
- Anderson, J.S.; Hyde, B.G. On Possible Role of Dislocations in Generating Ordered and Disordered Shear Structures. J. Phys. Chem. Solids 1967, 28, 1393–1408. [Google Scholar] [CrossRef]
- Ashbee, K.H.G.; Smallman, R.E. Plastic Deformation of Titanium Dioxide Single Crystals. Proc. R. Soc. Lond. Ser. A Math. Phys. Sci. 1963, 274, 195–205. [Google Scholar] [CrossRef]
- Ashbee, K.H.G.; Smallman, R.E. The Fracture of Titanium Dioxide Single Crystals with Particular Reference to Non-Stoichiometry. Phys. Status Solidi 1964, 4, 289–298. [Google Scholar] [CrossRef]
- Barber, D.J.; Wenk, H.-R.; Hirth, G.; Kohlstedt, H.L. Chapter 95 Dislocations in Minerals. Dislocat. Solids 2010, 16, 171–232. [Google Scholar]
- Blanchin, M.G.; Fontaine, G. Transmission Electron-Microscope Observations of Deformed Rutile (TiO2). Phys. Status Solidi A 1975, 29, 491–501. [Google Scholar] [CrossRef]
- Bursill, L.A.; Smith, D.J. Interaction of Small and Extended Defects in Nonstoichiometric Oxides. Nature 1984, 309, 319–321. [Google Scholar] [CrossRef]
- Hirthe, W.M.; Brittain, J.O. Dislocations in Rutile as Revealed by the Etch-Pit Technique. J. Am. Ceram. Soc. 1962, 45, 546–554. [Google Scholar] [CrossRef]
- Hirthe, W.M.; Brittain, J.O. High-Temperature Steady-State Creep in Rutile. J. Am. Ceram. Soc. 1963, 46, 411–417. [Google Scholar] [CrossRef]
- Lenser, C.; Connell, Z.; Kovacs, A.; Dunin-Borkowski, R.; Kohl, A.; Waser, R.; Dittmann, R. Identification of screw dislocations as fast-forming sites in Fe-doped SrTiO3. Appl. Phys. Lett. 2013, 102, 183504. [Google Scholar] [CrossRef]
- De Souza, R.A.; Fleig, J.; Maier, J.; Zhang, Z.L.; Sigle, W.; Rühle, M. Electrical resistance of low-angle tilt grain boundaries in acceptor-doped SrTiO3 as a function of misorientation angle. J. Appl. Phys. 2005, 97, 053502. [Google Scholar] [CrossRef]
- Marrocchelli, D.; Sun, L.X.; Yildiz, B. Dislocations in SrTiO3: Easy To Reduce but Not so Fast for Oxygen Transport. J. Am. Chem. Soc. 2015, 137, 4735–4748. [Google Scholar] [CrossRef] [PubMed]
- Sun, R.; Wang, Z.C.; Shibata, N.; Ikuhara, Y. A dislocation core in titanium dioxide and its electronic structure. RSC Adv. 2015, 5, 18506–18510. [Google Scholar] [CrossRef]
- Sigle, W.; Sarbu, C.; Brunner, D.; Rühle, M. Dislocations in plastically deformed SrTiO3. Philos. Mag. 2006, 86, 4809–4821. [Google Scholar] [CrossRef]
- Motohashi, Y.; Blanchin, M.G.; Vicario, E.; Fontaine, G.; Otake, S. Elastic Parameters, Elastic Energy, and Stress-Fields of Dislocations in TiO2 Rutile Crystals. Phys. Status Solidi A 1979, 54, 355–364. [Google Scholar] [CrossRef]
- Ohno, T.; Ii, S.; Shibata, N.; Matsunaga, K.; Ikuhara, Y.; Yamamoto, T. High resolution Microscopy study for [001] symmetric tilt boundary with a tilt angle of 66 degrees in rutile-type TiO2 bicrystal. Mater. Trans. 2004, 45, 2117–2121. [Google Scholar] [CrossRef]
- Stephens, D.L.; Alford, W.J. Dislocation Structures in Single-Crystal Al2O3. J. Am. Ceram. Soc. 1964, 47, 81–86. [Google Scholar] [CrossRef]
- Suzuki, K.; Ichihara, M.; Takeuchi, S. High-Resolution Electron-Microscopy of Lattice-Defects in TiO2 and SnO2. Philos. Mag. A 1991, 63, 657–665. [Google Scholar] [CrossRef]
- Wang, Z.C.; Tsukimoto, S.; Saito, M.; Ikuhara, Y. Individual charge-trapping dislocations in an ionic insulator. Appl. Phys. Lett. 2009, 95, 184101. [Google Scholar] [CrossRef]
- Jia, C.L.; Thust, A.; Urban, K. Atomic-scale analysis of the oxygen configuration at a SrTiO3 dislocation core. Phys. Rev. Lett. 2005, 95, 225506. [Google Scholar] [CrossRef] [PubMed]
- Buban, J.P.; Chi, M.F.; Masiel, D.J.; Bradley, J.P.; Jiang, B.; Stahlberg, H.; Browning, N.D. Structural variability of edge dislocations in a SrTiO3 low-angle [001] tilt grain boundary. J. Mater. Res. 2009, 24, 2191–2199. [Google Scholar] [CrossRef]
- Hirth, J.P.; Lothe, J. Theory of Dislocations; Krieger Publishing Company: Malabar, FL, USA, 1992. [Google Scholar]
- Jin, L.; Guo, X.; Jia, C.L. TEM study of -type 35.26 degrees dislocations specially induced by polishing of SrTiO3 single crystals. Ultramicroscopy 2013, 134, 77–85. [Google Scholar] [CrossRef] [PubMed]
- McGibbon, M.M.; Browning, N.D.; Chisholm, M.F.; Mcgibbon, A.J.; Pennycook, S.J.; Ravikumar, V.; Dravid, V.P. Direct Determination of Grain-Boundary Atomic-Structure in SrTiO3. Science 1994, 266, 102–104. [Google Scholar] [CrossRef] [PubMed]
- Paladino, A.E.; Rubin, L.G.; Waugh, J.S. Oxygen Ion Diffusion in Single Crystal SrTiO3. J. Phys. Chem. Solids 1965, 26, 391–397. [Google Scholar] [CrossRef]
- Szot, K.; Speier, W.; Carius, R.; Zastrow, U.; Beyer, W. Localized metallic conductivity and self-healing during thermal reduction of SrTiO3. Phys. Rev. Lett. 2002, 88, 075508. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Zhang, Z.L.; Sigle, W.; Kurtz, W. HRTEM and EELS study of screw dislocation cores in SrTiO3. Phys. Rev. B 2004, 69, 144103. [Google Scholar] [CrossRef]
- Kwon, J.; Sharma, A.A.; Bain, J.A.; Picard, Y.N.; Skowronski, M. Oxygen Vacancy Creation, Drift, and Aggregation in TiO2-Based Resistive Switches at Low Temperature and Voltage. Adv. Funct. Mater. 2015, 25, 2876–2883. [Google Scholar] [CrossRef]
- Rogala, M.; Bihlmayer, G.; Speier, W.; Klusek, Z.; Rodenbücher, C.; Szot, K. Resistive Switching of a Quasi-Homogeneous Distribution of Filaments Generated at Heat-Treated TiO2 (110)-Surfaces. Adv. Funct. Mater. 2015, 25, 6382–6389. [Google Scholar] [CrossRef]
- Strukov, D.B.; Snider, G.S.; Stewart, D.R.; Williams, R.S. The missing memristor found. Nature 2008, 453, 80–83. [Google Scholar] [CrossRef] [PubMed]
- Waser, R.; Aono, M. Nanoionics-based resistive switching memories. Nat. Mater. 2007, 6, 833–840. [Google Scholar] [CrossRef] [PubMed]
- Waser, R.; Dittmann, R.; Staikov, G.; Szot, K. Redox-Based Resistive Switching Memories—Nanoionic Mechanisms, Prospects, and Challenges. Adv. Mater. 2009, 21, 2632–2663. [Google Scholar] [CrossRef]
- Kim, K.M.; Jeong, D.S.; Hwang, C.S. Nanofilamentary resistive switching in binary oxide system; a review on the present status and outlook. Nanotechnology 2011, 22, 254002. [Google Scholar] [CrossRef] [PubMed]
- Szot, K.; Rogala, M.; Speier, W.; Klusek, Z.; Besmehn, A.; Waser, R. TiO2-a prototypical memristive material. Nanotechnology 2011, 22, 254001. [Google Scholar] [CrossRef] [PubMed]
- Jeong, D.S.; Thomas, R.; Katiyar, R.S.; Scott, J.F.; Kohlstedt, H.; Petraru, A.; Hwang, C.S. Emerging memories: Resistive switching mechanisms and current status. Rep. Prog. Phys. 2012, 75, 076502. [Google Scholar] [CrossRef] [PubMed]
- Szot, K.; Speier, W.; Bihlmayer, G.; Waser, R. Switching the electrical resistance of individual dislocations in single-crystalline SrTiO3. Nat. Mater. 2006, 5, 312–320. [Google Scholar] [CrossRef] [PubMed]
- Watanabe, Y.; Bednorz, J.G.; Bietsch, A.; Gerber, C.; Widmer, D.; Beck, A.; Wind, S.J. Current-driven insulator-conductor transition and nonvolatile memory in chromium-doped SrTiO3 single crystals. Appl. Phys. Lett. 2001, 78, 3738–3740. [Google Scholar] [CrossRef]
- Kwon, D.H.; Kim, K.M.; Jang, J.H.; Jeon, J.M.; Lee, M.H.; Kim, G.H.; Li, X.S.; Park, G.S.; Lee, B.; Han, S.; et al. Atomic structure of conducting nanofilaments in TiO2 resistive switching memory. Nat. Nanotechnol. 2010, 5, 148–153. [Google Scholar] [CrossRef] [PubMed]
- Wojtyniak, M.; Szot, K.; Wrzalik, R.; Rodenbücher, C.; Roth, G.; Waser, R. Electro-degradation and resistive switching of Fe-doped SrTiO3 single crystal. J. Appl. Phys. 2013, 113, 083713. [Google Scholar] [CrossRef] [Green Version]
- Szot, K.; Speier, W.; Eberhardt, W. Microscopic Nature of the Metal to Insulator Phase-Transition Induced through Electroreduction in Single-Crystal KNbO3. Appl. Phys. Lett. 1992, 60, 1190–1192. [Google Scholar] [CrossRef]
- Urban, K.W. Studying atomic structures by aberration-corrected transmission electron microscopy. Science 2008, 321, 506–510. [Google Scholar] [CrossRef] [PubMed]
- Matsunaga, T.; Saka, H. Transmission electron microscopy of dislocations in SrTiO3. Philos. Mag. Lett. 2000, 80, 597–604. [Google Scholar] [CrossRef]
- Jia, C.L.; Mi, S.B.; Urban, K.; Vrejoiu, I.; Alexe, M.; Hesse, D. Effect of a Single Dislocation in a Heterostructure Layer on the Local Polarization of a Ferroelectric Layer. Phys. Rev. Lett. 2009, 102, 117601. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Nishigaki, J.; Kuroda, K.; Saka, H. Electron-Microscopy of Dislocation-Structures in SrTiO3 Deformed at High-Temperatures. Phys. Status Solidi A 1991, 128, 319–336. [Google Scholar] [CrossRef]
- Yang, G.Y.; Finder, J.M.; Wang, J.; Wang, Z.L.; Yu, Z.; Ramdani, J.; Droopad, R.; Eisenbeiser, K.W.; Ramesh, R. Study of microstructure in SrTiO3/Si by high-resolution transmission electron microscopy. J. Mater. Res. 2002, 17, 204–213. [Google Scholar] [CrossRef]
- Du, H.C.; Jia, C.L.; Houben, L.; Metlenko, V.; De Souza, R.A.; Waser, R.; Mayer, J. Atomic structure and chemistry of dislocation cores at low-angle tilt grain boundary in SrTiO3 bicrystals. Acta Mater. 2015, 89, 344–351. [Google Scholar] [CrossRef]
- Diebold, U. The surface science of titanium dioxide. Surf. Sci. Rep. 2003, 48, 53–229. [Google Scholar] [CrossRef]
- Fukui, K.; Onishi, H.; Iwasawa, Y. Atom-resolved image of the TiO2(110) surface by noncontact atomic force microscopy. Phys. Rev. Lett. 1997, 79, 4202–4205. [Google Scholar] [CrossRef]
- Szot, K.; Bihlmayer, G.; Speier, W. Nature of the Resistive Switching Phenomena in TiO2 and SrTiO3: Origin of the Reversible Insulator-Metal Transition. Solid State Phys. 2014, 65, 353–559. [Google Scholar]
- Jia, C.L.; Lentzen, M.; Urban, K. Atomic-resolution imaging of oxygen in perovskite ceramics. Science 2003, 299, 870–873. [Google Scholar] [CrossRef] [PubMed]
- Bieger, T.; Maier, J.; Waser, R. Optical Investigation of Oxygen Incorporation in SrTiO3. Solid State Ion. 1992, 53, 578–582. [Google Scholar] [CrossRef]
- Bieger, T.; Maier, J.; Waser, R. Kinetics of Oxygen Incorporation in SrTiO3 (Fe-Doped)—An Optical Investigation. Sens. Actuators B Chem. 1992, 7, 763–768. [Google Scholar] [CrossRef]
- Ferre, D.; Carrez, P.; Cordier, P. Modeling dislocation cores in SrTiO3 using the Peierls-Nabarro model. Phys. Rev. B 2008, 77, 014106. [Google Scholar] [CrossRef]
- Clinard, F.W.; Hobbs, L.W. Radiation effects in non-metals. In Physics of Radiation Effects in Crystals; Johnson, R.A., Orlov, A.N., Eds.; North-Holland Physics Publishing: Amsterdam, The Nederlands, 1986. [Google Scholar]
- Furushima, Y.; Arakawa, Y.; Nakamura, A.; Tochigi, E.; Matsunaga, K. Nonstoichiometric [012] dislocation in strontium titanate. Acta Mater. 2017, 135, 103–111. [Google Scholar] [CrossRef]
- Weertman, J.; Weertman, J.R. Elementary Dislocation Theory; Oxford University Press Oxford: New York, NY, USA, 1992. [Google Scholar]
- Kofstad, P. Note on Defect Structure of Rutile (TiO2). J. Less Common Met. 1967, 13, 635–638. [Google Scholar] [CrossRef]
- Kofstad, P. Electrical Conductivity and Diffusion in Binary Metal Oxides; Wiley: New York, NY, USA, 1972. [Google Scholar]
- Marucco, J.F.; Gautron, J.; Lemasson, P. Thermogravimetric and Electrical Study of Nonstoichiometric Titanium-Dioxide TiO2−x between 800 and 1100 °C. J. Phys. Chem. Solids 1981, 42, 363–367. [Google Scholar] [CrossRef]
- Marucco, J.F.; Poumellec, B.; Gautron, J.; Lemasson, P. Thermodynamic Properties of Titanium-Dioxide, Niobium Dioxide and Their Solid-Solutions at High-Temperature. J. Phys. Chem. Solids 1985, 46, 709–717. [Google Scholar] [CrossRef]
- Millot, F.; Blanchin, M.G.; Tetot, R.; Marucco, J.F.; Poumellec, B.; Picard, C.; Touzelin, B. High-Temperature Nonstoichiometric Rutile TiO2−x. Prog. Solid State Chem. 1987, 17, 263–293. [Google Scholar] [CrossRef]
- Balachandran, U.; Eror, N.G. Electrical-Conductivity in Non-Stoichiometric Titanium-Dioxide at Elevated-Temperatures. J. Mater. Sci. 1988, 23, 2676–2682. [Google Scholar] [CrossRef]
- Bak, T.; Burg, T.; Kang, S.J.L.; Nowotny, J.; Rekas, M.; Sheppard, L.; Sorrell, C.C.; Vance, E.R.; Yoshida, Y.; Yamawaki, M. Charge transport in polycrystalline titanium dioxide. J. Phys. Chem. Solids 2003, 64, 1089–1095. [Google Scholar] [CrossRef]
- Bak, T.; Nowotny, J.; Rekas, M.; Sorrell, C.C. Defect chemistry and semiconducting properties of titanium dioxide: III. Mobility of electronic charge carriers. J. Phys. Chem. Solids 2003, 64, 1069–1087. [Google Scholar] [CrossRef]
- Yamada, H.; Miller, G.R. Point-Defects in Reduced Strontium-Titanate. J. Solid State Chem. 1973, 6, 169–177. [Google Scholar] [CrossRef]
- Chan, N.H.; Sharma, R.K.; Smyth, D.M. Non-Stoichiometry in SrTiO3. J. Electrochem. Soc. 1981, 128, 1762–1769. [Google Scholar] [CrossRef]
- Smyth, D.M. Defects and Order in Perovskite-Related Oxides. Annu. Rev. Mater. Sci. 1985, 15, 329–357. [Google Scholar] [CrossRef]
- Eror, N.G.; Balachandran, U. Electrical-Conductivity in Strontium-Titanate with Nonideal Cationic Ratio. J. Solid State Chem. 1982, 42, 227–241. [Google Scholar] [CrossRef]
- Waser, R. Bulk Conductivity and Defect Chemistry of Acceptor-Doped Strontium-Titanate in the Quenched State. J. Am. Ceram. Soc. 1991, 74, 1934–1940. [Google Scholar] [CrossRef]
- Smyth, D.M. Oxidative Nonstoichiometry in Perovskite Oxides. In Properties and Application of Perovskite-Type Oxides; Tejuca, L.G., Fierro, J.L.G., Eds.; CRC Press: New York, NY, USA, 1993; p. 63. [Google Scholar]
- Ravikumar, V.; Rodrigues, R.P.; Dravid, V.P. Direct Imaging of Spatially Varying Potential and Charge across Internal Interfaces in Solids. Phys. Rev. Lett. 1995, 75, 4063–4066. [Google Scholar] [CrossRef] [PubMed]
- Ravikumar, V.; Rodrigues, R.P.; Dravid, V.P. An investigation of acceptor-doped grain boundaries in SrTiO3. J. Phys. D Appl. Phys. 1996, 29, 1799–1806. [Google Scholar] [CrossRef]
- Von Alfthan, S.; Benedek, N.A.; Chen, L.; Chua, A.; Cockayne, D.; Dudeck, K.J.; Elsässer, C.; Finnis, M.W.; Koch, C.T.; Rahmati, B.; et al. The Structure of Grain Boundaries in Strontium Titanate: Theory, Simulation, and Electron Microscopy. Annu. Rev. Mater. Res. 2010, 40, 557–599. [Google Scholar] [CrossRef]
- Wang, Y.G.; Dravid, V.P. Determination of electrostatic characteristics at a 24 degrees, [001] tilt grain boundary in a SrTiO3 bicrystal by electron holography. Philos. Mag. Lett. 2002, 82, 425–432. [Google Scholar] [CrossRef]
- Kalinin, S.V.; Bonnell, D.A. Surface potential at surface-interface junctions in SrTiO3 bicrystals. Phys. Rev. B 2000, 62, 10419–10430. [Google Scholar] [CrossRef]
- Gao, P.; Ishikawa, R.; Feng, B.; Kumamoto, A.; Shibata, N.; Ikuhara, Y. Atomic-scale structure relaxation, chemistry and charge distribution of dislocation cores in SrTiO3. Ultramicroscopy 2018, 184, 217–224. [Google Scholar] [CrossRef] [PubMed]
- Yang, S.F.; Xiong, L.M.; Deng, Q.; Chen, Y.P. Concurrent atomistic and continuum simulation of strontium titanate. Acta Mater. 2013, 61, 89–102. [Google Scholar] [CrossRef]
- Yang, S.F.; Chen, Y.P. Concurrent atomistic and continuum simulation of bi-crystal strontium titanate with tilt grain boundary. Proc. R. Soc. A Math. Phys. Eng. Sci. 2015, 471, 20140758. [Google Scholar] [CrossRef] [PubMed]
- Seltzer, M.S.; Wilcox, B.A.; Clauer, A.H. The Influence of Stoichiometric Defects on the Creep of Oxides with the Fluorite Structure. In Defects and Transport in Oxides; Jaffee, R.I., Ed.; Springer: Berlin, Germany, 1973; pp. 443–457. [Google Scholar]
- Yamanaka, J.; Yoshimura, J.; Kimura, S. Characterization of lattice defects in strontium titanate single crystals by X-ray topography and transmission electron microscopy. J. Electron Microsc. 2000, 49, 89–92. [Google Scholar] [CrossRef]
- Yoshimura, J.; Sakamoto, T.; Yamanaka, J. X-ray double-crystal diffractometry of Verneuil-grown SrTiO3 crystals. Jpn. J. Appl. Phys. 2001, 40, 6536–6542. [Google Scholar] [CrossRef]
- Yoshimura, J.; Yamanaka, J.; Iwamoto, T.; Kimura, S. X-ray topographic observation of lattice defects in heat-treated SrTiO3 crystals. Mater. Trans. JIM 2000, 41, 559–562. [Google Scholar] [CrossRef]
- Yamanaka, J. High-resolution electron microscopy of a subgrain boundary in strontium titanate single crystal. Mater. Trans. 2001, 42, 1131–1134. [Google Scholar] [CrossRef]
- Yoshimura, J.; Sakamoto, T.; Usui, S.; Kimura, S. X-ray perfection study of Verneuil-grown SrTiO3 crystals. J. Cryst. Growth 1998, 191, 483–491. [Google Scholar] [CrossRef]
- Nabokin, P.I.; Souptel, D.; Balbashov, A.M. Floating zone growth of high-quality SrTiO3 single crystals. J. Cryst. Growth 2003, 250, 397–404. [Google Scholar] [CrossRef]
- Hirel, P.; Carrez, P.; Cordier, P. From glissile to sessile: Effect of temperature on <110> dislocations in perovskite materials. Scr. Mater. 2016, 120, 67–70. [Google Scholar] [CrossRef]
- Hirel, P.; Carrez, P.; Clouet, E.; Cordier, P. The electric charge and climb of edge dislocations in perovskite oxides: The case of high-pressure MgSiO3 bridgmanite. Acta Mater. 2016, 106, 313–321. [Google Scholar] [CrossRef]
- Szot, K.; Speier, W. Verfahren zur Herstellung eines ABO3 Substrates mit einer Stufe. Patent DE19808778 C2, 9 December 1999. [Google Scholar]
- Kondo, S.; Shibata, N.; Mitsuma, T.; Tochigi, E.; Ikuhara, Y. Dynamic observations of dislocation behavior in SrTiO3 by in situ nanoindentation in a transmission electron microscope. Appl. Phys. Lett. 2012, 100, 181906. [Google Scholar] [CrossRef]
- Yang, K.H.; Ho, N.J.; Lu, H.Y. Kink-Pair Mechanism in <001> SrTiO3 Single Crystal Compression-Deformed at Room Temperature. Jpn. J. Appl. Phys. 2011, 50, 105601. [Google Scholar]
- Prabhumirashi, P.; Dravid, V.P.; Lupini, A.R.; Chisholm, M.F.; Pennycook, S.J. Atomic-scale manipulation of potential barriers at SrTiO3 grain boundaries. Appl. Phys. Lett. 2005, 87, 121917. [Google Scholar] [CrossRef]
- Mizoguchi, T.; Sato, Y.; Buban, J.P.; Matsunaga, K.; Yamamoto, T.; Ikuhara, Y. Sr vacancy segregation by heat treatment at SrTiO3 grain boundary. Appl. Phys. Lett. 2005, 87, 241920. [Google Scholar] [CrossRef]
- Zhang, Z.; Yates, J.T. Defects on TiO2—Key Pathways to important surface processes. In Defects at Oxide Surfaces; Jupille, J., Thorton, G., Eds.; Springer: Berlin, Germany, 2015; p. 86. [Google Scholar]
- Javaid, F.; Stukowski, A.; Durst, K. 3D Dislocation structure evolution in strontium titanate: Spherical indentation experiments and MD simulations. J. Am. Ceram. Soc. 2017, 100, 1134–1145. [Google Scholar] [CrossRef]
- Hanzig, J.; Abendroth, B.; Hanzig, F.; Stocker, H.; Strohmeyer, R.; Meyer, D.C.; Lindner, S.; Grobosch, M.; Knupfer, M.; Himcinschi, C.; et al. Single crystal strontium titanate surface and bulk modifications due to vacuum annealing. J. Appl. Phys. 2011, 110, 064107. [Google Scholar] [CrossRef]
- Guo, X.; Zhang, Z.L.; Sigle, W.; Wachsman, E.; Waser, R. Schottky barrier formed by network of screw dislocations in SrTiO3. Appl. Phys. Lett. 2005, 87, 162105. [Google Scholar] [CrossRef] [Green Version]
- Anderson, S.; Jahnberg, L. Crystal structure studies on the homologous series TinO2n−1, VnO2n−1 and Tin−2Cr2O2n−1. Ark. Kemi 1963, 21, 413. [Google Scholar]
- Bursill, L.A.; Hyde, B.G. Crystallographic shear in the higher titanium oxides: Structure, texture, mechanisms and thermodynamics. Prog. Solid State Chem. 1972, 7, 177–253. [Google Scholar] [CrossRef]
- Bursill, L.A.; Peng, J.; Fan, X. Structure and reactivity of atomic surfaces of barium-titanate under electron-irradiation. Ferroelectrics 1989, 97, 71–84. [Google Scholar] [CrossRef]
- Szot, K.; Pawelczyk, M.; Herion, J.; Freiburg, C.; Albers, J.; Waser, R.; Hulliger, J.; Kwapulinski, J.; Dec, J. Nature of the surface layer in ABO3-type Perovskites at elevated temperatures. Appl. Phys. A 1996, 62, 335–343. [Google Scholar] [CrossRef]
- Szot, K.; Speier, W. Surfaces of reduced and oxidized SrTiO3 from atomic force microscopy. Phys. Rev. B 1999, 60, 5909–5926. [Google Scholar] [CrossRef]
- Lee, W.; Yoo, S.; Yoon, K.J.; Yeu, I.W.; Chang, H.J.; Choi, J.H.; Hoffmann-Eifert, S.; Waser, R.; Hwang, C.S. Resistance switching behavior of atomic layer deposited SrTiO3 film through possible formation of Sr2Ti6O13 or Sr1Ti11O20 phases. Sci. Rep. 2016, 6, 20550. [Google Scholar] [CrossRef] [PubMed]
- Meyer, D.C.; Levin, A.A.; Leisegang, T.; Gutmann, E.; Paufler, P.; Reibold, M.; Pompe, W. Reversible tuning of a series of intergrowth phases of the Ruddlesden-Popper type SrO(SrTiO3)n in an (001) SrTiO3 single-crystalline plate by an external electric field and its potential use for adaptive X-ray optics. Appl. Phys. A 2006, 84, 31–35. [Google Scholar] [CrossRef]
- Szot, K.; Speier, W.; Breuer, U.; Meyer, R.; Szade, J.; Waser, R. Formation of micro-crystals on the (100) surface of SrTiO3 at elevated temperatures. Surf. Sci. 2000, 460, 112–128. [Google Scholar] [CrossRef]
- Van Landuyt, J. Shear structures and crystallographic shear propagation. J. Phys. Colloq. 1974, 35, C7–C35. [Google Scholar] [CrossRef]
- Vogel, F.L.; Pfann, W.G.; Corey, H.E.; Thomas, E.E. Observations of Dislocations in Lineage Boundaries in Germanium. Phys. Rev. 1953, 90, 489–490. [Google Scholar] [CrossRef]
- Barber, D.J.; Tighe, N.J. Observations of Dislocations and Surface Features in Corundum Crystals by Electron Transmission Microscopy. J. Res. Natl. Bur. Stand. Sect. A Phys. Chem. 1965, A69, 271. [Google Scholar] [CrossRef]
- Sangwal, K. Etching of the Crystals; North-Holland: Amsterdam, The Netherlands, 1987. [Google Scholar]
- Ashbee, K.A.G.; Smallman, R.E.; Williamson, G.K. Stacking Faults and Dislocations in Titanium Dioxide, with Special Reference to Non-Stoichiometry. Proc. R. Soc. Lond. Ser. A Math. Phys. Sci. 1963, 276, 542–552. [Google Scholar] [CrossRef]
- Barber, D.J.; Farabaug, E.N. Dislocations and Stacking Faults in Rutile Crystals Grown by Flame-Fusion Methods. J. Appl. Phys. 1965, 36, 2803–2806. [Google Scholar] [CrossRef]
- Bell, H.; Jones, J.T.; Krishnam, V. Recovery of High-Temperature Creep-Resistant Substructure in Rutile. J. Am. Ceram. Soc. 1972, 55, 6–10. [Google Scholar] [CrossRef]
- Fleischauer, P.D.; Chase, A.B. Coordination Chemistry and Kinetics of Preferential Etching on Surfaces of TiO2 (Rutile). J. Phys. Chem. Solids 1974, 35, 1211–1219. [Google Scholar] [CrossRef]
- Bright, E.; Readey, D.W. Dissolution Kinetics of TiO2 in Hf-HCl Solutions. J. Am. Ceram. Soc. 1987, 70, 900–906. [Google Scholar] [CrossRef]
- Gorokhovsky, A.V.; Escalante-García, J.I.; Sánchez-Monjarás, T.; Gutiérrez-Chavarría, C.A. Synthesis of potassium polytitanate precursors by treatment of TiO2 with molten mixtures of KNO3 and KOH. J. Eur. Ceram. Soc. 2004, 24, 3541–3546. [Google Scholar] [CrossRef]
- Zaremba, T. Investigation on synthesis and microstructure of potassium tetratitanate. J. Therm. Anal. Calorim. 2008, 91, 911–913. [Google Scholar] [CrossRef]
- Waugh, J.S.; Paladino, A.E.; Dibenedetto, B.; Wantman, R. Effect of Dislocations on Oxidation and Reduction of Single-Crystal SrTiO3. J. Am. Ceram. Soc. 1963, 46, 60. [Google Scholar] [CrossRef]
- Rhodes, W.H. Etching and Chemical Polishing of Single-Crystal SrTiO3. J. Am. Ceram. Soc. 1966, 49, 110–112. [Google Scholar] [CrossRef]
- Spalding, G.; Murphy, W.I.; Davidsmeier, T.M.; Elenewski, J. Faceting of single-crystal SrTiO3 during wet chemical etching. In Substrate Engineering: Paving the Way to Epitaxy; Norton, D., Schlom, D.G., Newman, N., Matthiesen, D., Eds.; Materials Research Society: Warrendale, PA, USA, 1999. [Google Scholar]
- Yamamoto, T.; Oba, F.; Ikuhara, Y.; Sakuma, T. Current-voltage characteristics across small angle symmetric tilt boundaries in Nb-doped SrTiO3 bicrystals. Mater. Trans. 2002, 43, 1537–1541. [Google Scholar] [CrossRef]
- Raghothamachar, B.; Dhanaraj, G.; Bai, J.; Dudley, M. Defect analysis in crystals using X-ray topography. Microsc. Res. Tech. 2006, 69, 343–358. [Google Scholar] [CrossRef] [PubMed]
- Moore, M. White-beam X-ray topography. Crystallogr. Rev. 2012, 18, 205–233. [Google Scholar] [CrossRef]
- Tanner, B.K. Contrast of defects in X-ray diffraction topographs. X-Ray Neutron Dyn. Diffr. 1996, 357, 147–166. [Google Scholar]
- Rozhestrevenskaya, M.B.; Kazurov, K. The growth of SrTiO3 single crystals using the melt method in a flame and X-ray graphic studies of the degree of their perfection. In Kristallizatsiia i Fazovye Prevrashcheniia; Sirota, N.N., Ed.; Akademii Nauk SSSR Nauchnyi Sov. Pol., Nauka i tekhnika: Minsk, Russia, 1971; p. 267. [Google Scholar]
- Mochizuki, S.; Fujishiro, F.; Shibata, K.; Ogi, A.; Konya, T.; Inaba, K. Optical, electrical, and X-ray-structural studies on verneuil-grown SrTiO3 single crystal: Annealing study. Physica B 2007, 401, 433–436. [Google Scholar] [CrossRef]
- Haider, M.; Uhlemann, S.; Schwan, E.; Rose, H.; Kabius, B.; Urban, K. Electron microscopy image enhanced. Nature 1998, 392, 768–769. [Google Scholar] [CrossRef]
- Krivanek, O.L.; Dellby, N.; Lupini, A.R. Towards sub-angstrom electron beams. Ultramicroscopy 1999, 78, 1–11. [Google Scholar] [CrossRef]
- Morishita, S.; Ishikawa, R.; Kohno, Y.; Sawada, H.; Shibata, N.; Ikuhara, Y. Attainment of 40.5 pm spatial resolution using 300 kV scanning transmission electron microscope equipped with fifth-order aberration corrector. Microsopy 2017, in press. [Google Scholar]
- Kimoto, K.; Asaka, T.; Nagai, T.; Saito, M.; Matsui, Y.; Ishizuka, K. Element-selective imaging of atomic columns in a crystal using STEM and EELS. Nature 2007, 450, 702–704. [Google Scholar] [CrossRef] [PubMed]
- Bosman, M.; Keast, V.J.; Garcia-Munoz, J.L.; D’Alfonso, A.J.; Findlay, S.D.; Allen, L.J. Two-dimensional mapping of chemical information at atomic resolution. Phys. Rev. Lett. 2007, 99, 086102. [Google Scholar] [CrossRef] [PubMed]
- Muller, D.A.; Kourkoutis, L.F.; Murfitt, M.; Song, J.H.; Hwang, H.Y.; Silcox, J.; Dellby, N.; Krivanek, O.L. Atomic-scale chemical imaging of composition and bonding by aberration-corrected microscopy. Science 2008, 319, 1073–1076. [Google Scholar] [CrossRef] [PubMed]
- D’Alfonso, A.J.; Freitag, B.; Klenov, D.; Allen, L.J. Atomic-resolution chemical mapping using energy-dispersive X-ray spectroscopy. Phys. Rev. B 2010, 81, 100101. [Google Scholar] [CrossRef]
- Chu, M.W.; Liou, S.C.; Chang, C.P.; Choa, F.S.; Chen, C.H. Emergent Chemical Mapping at Atomic-Column Resolution by Energy-Dispersive X-Ray Spectroscopy in an Aberration-Corrected Electron Microscope. Phys. Rev. Lett. 2010, 104, 196101. [Google Scholar] [CrossRef] [PubMed]
- Pennycook, S.J.; Nellist, P.D. Scanning Transmission Electron Microscopy Imaging and Analysis; Springer: New York, NY, USA, Dordrecht, The Netherlands; Heidelberg, Germany; 2011. [Google Scholar]
- Crewe, A.V. Scanning Electron Microscopes—Is High Resolution Possible. Science 1966, 154, 729–738. [Google Scholar] [CrossRef] [PubMed]
- Crewe, A.V.; Wall, J.; Langmore, J. Visibility of Single Atoms. Science 1970, 168, 1338–1340. [Google Scholar] [CrossRef] [PubMed]
- Pennycook, S.J.; Boatner, L.A. Chemically Sensitive Structure-Imaging with a Scanning-Transmission Electron-Microscope. Nature 1988, 336, 565–567. [Google Scholar] [CrossRef]
- Krivanek, O.L.; Chisholm, M.F.; Nicolosi, V.; Pennycook, T.J.; Corbin, G.J.; Dellby, N.; Murfitt, M.F.; Own, C.S.; Szilagyi, Z.S.; Oxley, M.P.; et al. Atom-by-atom structural and chemical analysis by annular dark-field electron microscopy. Nature 2010, 464, 571–574. [Google Scholar] [CrossRef] [PubMed]
- Krivanek, O.L.; Lovejoy, T.C.; Dellby, N.; Aoki, T.; Carpenter, R.W.; Rez, P.; Soignard, E.; Zhu, J.T.; Batson, P.E.; Lagos, M.J.; et al. Vibrational spectroscopy in the electron microscope. Nature 2014, 514, 209. [Google Scholar] [CrossRef] [PubMed]
- Mukai, M.; Okunishi, E.; Ashino, M.; Omoto, K.; Fukuda, T.; Ikeda, A.; Somehara, K.; Kaneyama, T.; Saitoh, T.; Hirayama, T.; et al. Development of a monochromator for aberration-corrected scanning transmission electron microscopy. Microscopy 2015, 64, 151–158. [Google Scholar] [CrossRef] [PubMed]
- Ishikawa, R.; Lupini, A.R.; Findlay, S.D.; Pennycook, S.J. Quantitative Annular Dark Field Electron Microscopy Using Single Electron Signals. Microsc. Microanal. 2014, 20, 99–110. [Google Scholar] [CrossRef] [PubMed]
- Shibata, N.; Kohno, Y.; Findlay, S.D.; Sawada, H.; Kondo, Y.; Ikuhara, Y. New area detector for atomic-resolution scanning transmission electron microscopy. J. Electron Microsc. 2010, 59, 473–479. [Google Scholar] [CrossRef] [PubMed]
- Shibata, N.; Seki, T.; Sanchez-Santolino, G.; Findlay, S.D.; Kohno, Y.; Matsumoto, T.; Ishikawa, R.; Ikuhara, Y. Electric field imaging of single atoms. Nat. Commun. 2017, 8, 15631. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Yang, H.; Rutte, R.N.; Jones, L.; Simson, M.; Sagawa, R.; Ryll, H.; Huth, M.; Pennycook, T.J.; Green, M.L.H.; Soltau, H.; et al. Simultaneous atomic-resolution electron ptychography and Z-contrast imaging of light and heavy elements in complex nanostructures. Nat. Commun. 2016, 7, 12532. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Kirkland, E.J. Advanced Computing in Electron Microscopy; Springer: New York, NY, USA, 2010. [Google Scholar]
- Pennycook, S.J.; Jesson, D.E. High-Resolution Incoherent Imaging of Crystals. Phys. Rev. Lett. 1990, 64, 938–941. [Google Scholar] [CrossRef] [PubMed]
- Pennycook, S.J.; Jesson, D.E. High-Resolution Z-Contrast Imaging of Crystals. Ultramicroscopy 1991, 37, 14–38. [Google Scholar] [CrossRef]
- Gao, P.; Kumamoto, A.; Ishikawa, R.; Lugg, N.; Shibata, N.; Ikuhara, Y. Picometer-scale atom position analysis in annular bright-field STEM imaging. Ultramicroscopy 2018, 184, 177–187. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- LeBeau, J.M.; Findlay, S.D.; Allen, L.J.; Stemmer, S. Standardless Atom Counting in Scanning Transmission Electron Microscopy. Nano Lett. 2010, 10, 4405–4408. [Google Scholar] [CrossRef] [PubMed]
- Van Aert, S.; De Backer, A.; Martinez, G.T.; Goris, B.; Bals, S.; Van Tendeloo, G.; Rosenauer, A. Procedure to count atoms with trustworthy single-atom sensitivity. Phys. Rev. B 2013, 87, 064107. [Google Scholar] [CrossRef]
- Jones, L.; MacArthur, K.E.; Fauske, V.T.; van Helvoort, A.T.J.; Nellist, P.D. Rapid Estimation of Catalyst Nanoparticle Morphology and Atomic-Coordination by High-Resolution Z-Contrast Electron Microscopy. Nano Lett. 2014, 14, 6336–6341. [Google Scholar] [CrossRef] [PubMed]
- Ishikawa, R.; Lupini, A.R.; Findlay, S.D.; Taniguchi, T.; Pennycook, S.J. Three-Dimensional Location of a Single Dopant with Atomic Precision by Aberration-Corrected Scanning Transmission Electron Microscopy. Nano Lett. 2014, 14, 1903–1908. [Google Scholar] [CrossRef] [PubMed]
- Findlay, S.D.; Shibata, N.; Sawada, H.; Okunishi, E.; Kondo, Y.; Yamamoto, T.; Ikuhara, Y. Robust atomic resolution imaging of light elements using scanning transmission electron microscopy. Appl. Phys. Lett. 2009, 95, 191913. [Google Scholar] [CrossRef]
- Findlay, S.D.; Shibata, N.; Sawada, H.; Okunishi, E.; Kondo, Y.; Ikuhara, Y. Dynamics of annular bright field imaging in scanning transmission electron microscopy. Ultramicroscopy 2010, 110, 903–923. [Google Scholar] [CrossRef] [PubMed]
- Findlay, S.D.; LeBeau, J.M. Detector non-uniformity in scanning transmission electron microscopy. Ultramicroscopy 2013, 124, 52–60. [Google Scholar] [CrossRef] [PubMed]
- Findlay, S.D.; Huang, R.; Ishikawa, R.; Shibata, N.; Ikuhara, Y. Direct visualization of lithium via annular bright field scanning transmission electron microscopy: A review. Microscopy 2017, 66, 3–14. [Google Scholar] [CrossRef] [PubMed]
- Huang, R.; Ikuhara, Y.H.; Mizoguchi, T.; Findlay, S.D.; Kuwabara, A.; Fisher, C.A.J.; Moriwake, H.; Oki, H.; Hirayama, T.; Ikuhara, Y. Oxygen-Vacancy Ordering at Surfaces of Lithium Manganese(III,IV) Oxide Spinel Nanoparticles. Angew. Chem. Int. Ed. 2011, 50, 3053–3057. [Google Scholar] [CrossRef] [PubMed]
- Findlay, S.D.; Saito, T.; Shibata, N.; Sato, Y.; Matsuda, J.; Asano, K.; Akiba, E.; Hirayama, T.; Ikuhara, Y. Direct Imaging of Hydrogen within a Crystalline Environment. Appl. Phys. Express 2010, 3, 116603. [Google Scholar] [CrossRef]
- Ishikawa, R.; Okunishi, E.; Sawada, H.; Kondo, Y.; Hosokawa, F.; Abe, E. Direct imaging of hydrogen-atom columns in a crystal by annular bright-field electron microscopy. Nat. Mater. 2011, 10, 278–281. [Google Scholar] [CrossRef] [PubMed]
- Egerton, R.F. Electron Energy-Loss Spectroscopy in the Electron Microscope; Springer: New York, NY, USA, 2011. [Google Scholar]
- Matsukawa, M.; Ishikawa, R.; Hisatomi, T.; Moriya, Y.; Shibata, N.; Kubota, J.; Ikuhara, Y.; Domen, K. Enhancing Photocatalytic Activity of LaTiO2N by Removal of Surface Reconstruction Layer. Nano Lett. 2014, 14, 1038–1041. [Google Scholar] [CrossRef] [PubMed]
- Ishikawa, R.; Shimbo, Y.; Sugiyama, I.; Lugg, N.R.; Shibata, N.; Ikuhara, Y. Room-temperature dilute ferromagnetic dislocations in Sr1−xMnxTiO3−δ. Phys. Rev. B 2017, 96, 024440. [Google Scholar] [CrossRef]
- Sugiyama, I.; Shibata, N.; Wang, Z.C.; Kobayashi, S.; Yamamoto, T.; Ikuhara, Y. Ferromagnetic dislocations in antiferromagnetic NiO. Nat. Nanotechnol. 2013, 8, 266–270. [Google Scholar] [CrossRef] [PubMed]
- Chen, Z.; Weyland, M.; Sang, X.; Xu, W.; Dycus, J.H.; LeBeau, J.M.; D’Alfonso, A.J.; Allen, L.J.; Findlay, S.D. Quantitative atomic resolution elemental mapping via absolute-scale energy dispersive X-ray spectroscopy. Ultramicroscopy 2016, 168, 7–16. [Google Scholar] [CrossRef] [PubMed]
- Chen, M.S.; Goodman, D.W. The structure of catalytically active gold on titania. Science 2004, 306, 252–255. [Google Scholar] [CrossRef] [PubMed]
- Chen, X.B.; Liu, L.; Yu, P.Y.; Mao, S.S. Increasing Solar Absorption for Photocatalysis with Black Hydrogenated Titanium Dioxide Nanocrystals. Science 2011, 331, 746–750. [Google Scholar] [CrossRef] [PubMed]
- Rodriguez, J.A.; Ma, S.; Liu, P.; Hrbek, J.; Evans, J.; Perez, M. Activity of CeOx and TiOx nanoparticles grown on Au(111) in the water-gas shift reaction. Science 2007, 318, 1757–1760. [Google Scholar] [CrossRef] [PubMed]
- Diguna, L.J.; Shen, Q.; Kobayashi, J.; Toyoda, T. High efficiency of CdSe quantum-dot-sensitized TiO2 inverse opal solar cells. Appl. Phys. Lett. 2007, 91, 023116. [Google Scholar] [CrossRef]
- Gai, Y.Q.; Li, J.B.; Li, S.S.; Xia, J.B.; Wei, S.H. Design of Narrow-Gap TiO2: A Passivated Codoping Approach for Enhanced Photoelectrochemical Activity. Phys. Rev. Lett. 2009, 102, 036402. [Google Scholar] [CrossRef] [PubMed]
- Wendt, S.; Sprunger, P.T.; Lira, E.; Madsen, G.K.H.; Li, Z.S.; Hansen, J.O.; Matthiesen, J.; Blekinge-Rasmussen, A.; Laegsgaard, E.; Hammer, B.; et al. The role of interstitial sites in the Ti3d defect state in the band gap of Titania. Science 2008, 320, 1755–1759. [Google Scholar] [CrossRef] [PubMed]
- Nakano, Y.; Morikawa, T.; Ohwaki, T.; Taga, Y. Electrical characterization of band gap states in C-doped TiO2 films. Appl. Phys. Lett. 2005, 87, 052111. [Google Scholar] [CrossRef]
- Ahn, H.S.; Han, S.; Hwang, C.S. Pairing of cation vacancies and gap-state creation in TiO2 and HfO2. Appl. Phys. Lett. 2007, 90, 252908. [Google Scholar] [CrossRef]
- Li, H.; Bradt, R.C. Knoop Microhardness Anisotropy of Single-Crystal Rutile. J. Am. Ceram. Soc. 1990, 73, 1360–1364. [Google Scholar] [CrossRef]
- Basu, S.; Elshrief, O.A.; Coward, R.; Anasori, B.; Barsoum, M.W. Microscale deformation of (001) and (100) rutile single crystals under spherical nanoindentation. J. Mater. Res. 2012, 27, 53–63. [Google Scholar] [CrossRef]
- Ikuhara, Y.; Nishimura, H.; Nakamura, A.; Matsunaga, K.; Yamamoto, T.; Lagerlof, K.P.D. Dislocation structures of low-angle and near-Σ3 grain boundaries in alumina bicrystals. J. Am. Ceram. Soc. 2003, 86, 595–602. [Google Scholar] [CrossRef]
- Tochigi, E.; Shibata, N.; Nakamura, A.; Mizoguchi, T.; Yamamoto, T.; Ikuhara, Y. Structures of dissociated <1 0 0> dislocations and {1 0 0} stacking faults of alumina (α-Al2O3). Acta Mater. 2010, 58, 208–215. [Google Scholar] [CrossRef]
- Stoyanov, E.; Langenhorst, F.; Steinle-Neumann, G. The effect of valence state and site geometry on Ti L-3,L-2 and O K electron energy-loss spectra of TixOy phases. Am. Mineral. 2007, 92, 577–586. [Google Scholar] [CrossRef]
- Morin, P.; Pitaval, M.; Besnard, D.; Fontaine, G. Electron-channelling imaging in scanning electron-microscopy. Philos. Mag. A 1979, 40, 511–524. [Google Scholar] [CrossRef]
- Czernuszka, J.T.; Long, N.J.; Boyes, E.D.; Hirsch, P.B. Imaging of dislocations using backscattered electrons in a scanning electron-microscope. Philos. Mag. Lett. 1990, 62, 227–232. [Google Scholar] [CrossRef]
- Kamaladasa, R.J.; Liu, F.; Porter, L.M.; Davis, R.F.; Koleske, D.D.; Mulholland, G.; Jones, K.A.; Picard, Y.N. Identifying threading dislocations in GaN films and substrates by electron channelling. J. Microsc. 2011, 244, 311–319. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Kuwano, N.; Itakura, M.; Nagatomo, Y.; Tachibana, S. Scanning electron microscope observation of dislocations in semiconductor and metal materials. J. Electron Microsc. 2010, 59, S175–S181. [Google Scholar] [CrossRef] [PubMed]
- Kamaladasa, R.J.; Jiang, W.K.; Picard, Y.N. Imaging Dislocations in Single-Crystal SrTiO3 Substrates by Electron Channeling. J. Electron. Mater. 2011, 40, 2222–2227. [Google Scholar] [CrossRef]
- Lichte, H.; Lehmann, M. Electron holography—Basics and applications. Rep. Prog. Phys. 2008, 71, 016102. [Google Scholar] [CrossRef]
- Jones, R.O. Density functional theory: Its origins, rise to prominence, and future. Rev. Mod. Phys. 2015, 87, 897–923. [Google Scholar] [CrossRef]
- Shanthi, N.; Sarma, D.D. Electronic structure of electron doped SrTiO3: SrTiO3−δ and Sr1−xLaxTiO3. Phys. Rev. B 1998, 57, 2153–2158. [Google Scholar] [CrossRef]
- Ricci, D.; Bano, G.; Pacchioni, G.; Illas, F. Electronic structure of a neutral oxygen vacancy in SrTiO3. Phys. Rev. B 2003, 68, 224105. [Google Scholar] [CrossRef]
- He, J.; Behera, R.K.; Finnis, M.W.; Li, X.; Dickey, E.C.; Phillpot, S.R.; Sinnott, S.B. Prediction of high-temperature point defect formation in TiO2 from combined ab initio and thermodynamic calculations. Acta Mater. 2007, 55, 4325–4337. [Google Scholar] [CrossRef]
- Carrasco, J.; Illas, F.; Lopez, N.; Kotomin, E.A.; Zhukovskii, Y.F.; Piskunov, S.; Maier, J.; Hermansson, K. First-principles calculations of the atomic and electronic structure of F centers in the bulk and on the (001) surface of SrTiO3. Phys. Status Solidi 2005, 2, 153–158. [Google Scholar] [CrossRef]
- Alexandrov, V.E.; Kotomin, E.A.; Maier, J.; Evarestov, R.A. First-principles study of bulk and surface oxygen vacancies in SrTiO3 crystal. Eur. Phys. J. B 2009, 72, 53–57. [Google Scholar] [CrossRef]
- Lin, C.; Demkov, A.A. Electron Correlation in Oxygen Vacancy in SrTiO3. Phys. Rev. Lett. 2013, 111, 217601. [Google Scholar] [CrossRef] [PubMed]
- Park, S.G.; Magyari-Köpe, B.; Nishi, Y. Electronic correlation effects in reduced rutile TiO2 within the LDA+U method. Phys. Rev. B 2010, 82, 115109. [Google Scholar] [CrossRef]
- Cuong, D.D.; Lee, B.; Choi, K.M.; Ahn, H.S.; Han, S.; Lee, J. Oxygen vacancy clustering and electron localization in oxygen-deficient SrTiO3: LDA+U study. Phys. Rev. Lett. 2007, 98, 115503. [Google Scholar] [CrossRef] [PubMed]
- Park, S.G.; Magyari-Köpe, B.; Nishi, Y. Impact of Oxygen Vacancy Ordering on the Formation of a Conductive Filament in TiO2 for Resistive Switching Memory. IEEE Electr. Device Lett. 2011, 32, 197–199. [Google Scholar] [CrossRef]
- Le Bacq, O.; Salinas, E.; Pisch, A.; Bernard, C.; Pasturel, A. First-principles structural stability in the strontium-titanium-oxygen system. Philos. Mag. 2005, 86, 2283. [Google Scholar] [CrossRef]
- Jia, C.L.; Mi, S.B.; Urban, K.; Vrejoiu, I.; Alexe, M.; Hesse, D. Atomic-scale study of electric dipoles near charged and uncharged domain walls in ferroelectric films. Nat. Mater. 2008, 7, 57–61. [Google Scholar] [CrossRef] [PubMed]
- Rahmanizadeh, K.; Wortmann, D.; Bihlmayer, G.; Blugel, S. Charge and orbital order at head-to-head domain walls in PbTiO3. Phys. Rev. B 2014, 90, 115104. [Google Scholar] [CrossRef]
- Basletic, M.; Maurice, J.L.; Carretero, C.; Herranz, G.; Copie, O.; Bibes, M.; Jacquet, E.; Bouzehouane, K.; Fusil, S.; Barthelemy, A. Mapping the spatial distribution of charge carriers in LaAlO3/SrTiO3 heterostructures. Nat. Mater. 2008, 7, 621–625. [Google Scholar] [CrossRef] [PubMed]
- Hirel, P.; Mrovec, M.; Elsässer, C. Atomistic simulation study of <1 1 0> dislocations in strontium titanate. Acta Mater. 2012, 60, 329–338. [Google Scholar] [CrossRef]
- Vollman, M.; Waser, R. Grain-Boundary Defect Chemistry of Acceptor-Doped Titanates—Space-Charge Layer Width. J. Am. Ceram. Soc. 1994, 77, 235–243. [Google Scholar] [CrossRef]
- Vollmann, M.; Hagenbeck, R.; Waser, R. Grain-boundary defect chemistry of acceptor-doped titanates: Inversion layer and low-field conduction. J. Am. Ceram. Soc. 1997, 80, 2301–2314. [Google Scholar] [CrossRef]
- Hagenbeck, R.; Waser, R. Influence of temperature and interface charge on the grain-boundary conductivity in acceptor-doped SrTiO3 ceramics. J. Appl. Phys. 1998, 83, 2083–2092. [Google Scholar] [CrossRef]
- Dudler, R.; Albers, J.; Muser, H.E. Dielectric Behavior of Pure BaTiO3 at Ultralow Frequencies. Ferroelectrics 1978, 21, 381–383. [Google Scholar] [CrossRef]
- Waser, R.; (Forschungszentrum Jülich, Jülich, Germany). Personal communication, 2018.
- Rodenbücher, C.; Bihlmayer, G.; Speier, W.; Kubacki, J.; Wojtyniak, M.; Rogala, M.; Wrana, D.; Krok, F.; Szot, K. Detection of confined paths on oxide surfaces by local-conductivity atomic force microscopy with atomic resolution. arXiv, 2016; arXiv:1611.07773. [Google Scholar]
- Psiuk, B.; Szade, J.; Schroeder, H.; Haselier, H.; Mlynarczyk, M.; Waser, R.; Szot, K. Photoemission study of SrTiO3 surface layers instability upon metal deposition. Appl. Phys. A Mater. 2007, 89, 451–455. [Google Scholar] [CrossRef]
- Szot, K.; Otto, R.; Herion, J. Strom-Spannungswandler zur Erfassung eines Tunnelstroms eines Rastertunnelmikroskops. Patent DE4438960, 31 October 1994. [Google Scholar]
- Szot, K.; Dittmann, R.; Speier, W.; Waser, R. Nanoscale resistive switching in SrTiO3 thin films. Phys. Status Solidi Rapid Res. Lett. 2007, 1, R86–R88. [Google Scholar] [CrossRef]
- Wrana, D.; Rodenbücher, C.; Belza, W.; Szot, K.; Krok, F. In situ study of redox processes on the surface of SrTiO3 single crystals. Appl. Surf. Sci. 2018, 432, 46–52. [Google Scholar] [CrossRef]
- Rodenbücher, C.; Speier, W.; Bihlmayer, G.; Breuer, U.; Waser, R.; Szot, K. Cluster-like resistive switching of SrTiO3: Nb surface layers. New J. Phys. 2013, 15, 103017. [Google Scholar] [CrossRef]
- Pilch, M. Role of the La Doping in SrTiO3 Crystals. Ph.D. Thesis, University of Silesia, Kattowice, Poland, 2010. [Google Scholar]
- Reichenberg, B.; Szot, K.; Schneller, T.; Breuer, U.; Tiedke, S.; Waser, R. Inhomogeneous local conductivity induced by thermal reduction in BaTiO3 thin films and single crystals. Integr. Ferroelectr. 2004, 61, 43–49. [Google Scholar] [CrossRef]
- Szot, K.; Reichenberg, B.; Peter, F.; Waser, R.; Tiedke, S. Electrical Characterization of Perovskite Nanostructures. In Scanning Probe Microscopy; Kalinin, S., Gruverman, A., Eds.; Springer: New York, NY, USA, 2007. [Google Scholar]
- Jankowska-Sumara, I.; Szot, K.; Majchrowski, A.; Roleder, K. Effect of resistive switching and electrically driven insulator-conductor transition in PbZrO3 single crystals. Phys. Status Solidi A Appl. Mater. Sci. 2013, 210, 507–512. [Google Scholar] [CrossRef]
- Kubacki, J.; Molak, A.; Rogala, M.; Rodenbücher, C.; Szot, K. Metal-insulator transition induced by non-stoichiometry of surface layer and molecular reactions on single crystal KTaO3. Surf. Sci. 2012, 606, 1252–1262. [Google Scholar] [CrossRef]
- Molak, A.; Szot, K.; Kania, A.; Friedrich, J.; Penkalla, H.J. Insulator-metal transition in Mn-doped NaNbO3 induced by chemical and thermal treatment. Phase Transit. 2008, 81, 977–986. [Google Scholar] [CrossRef]
- Molak, A.; Szot, K. Insulator-semiconductor-metallic state transition induced by electric fields in Mn-doped NaNbO3. Phys. Status Solidi Rapid Res. Lett. 2009, 3, 127–129. [Google Scholar] [CrossRef]
- Markiewicz, E.; Szot, K.; Hilczer, B.; Pietraszko, A.A. BiFeO3 single crystal as resistive switching element for application in microelectronic devices. Phase Transit. 2013, 86, 284–289. [Google Scholar] [CrossRef]
- Choi, B.J.; Jeong, D.S.; Kim, S.K.; Rohde, C.; Choi, S.; Oh, J.H.; Kim, H.J.; Hwang, C.S.; Szot, K.; Waser, R.; et al. Resistive switching mechanism of TiO2 thin films grown by atomic-layer deposition. J. Appl. Phys. 2005, 98, 033715. [Google Scholar] [CrossRef] [Green Version]
- Menke, T.; Meuffels, P.; Dittmann, R.; Szot, K.; Waser, R. Separation of bulk and interface contributions to electroforming and resistive switching behavior of epitaxial Fe-doped SrTiO3. J. Appl. Phys. 2009, 105, 066104. [Google Scholar] [CrossRef]
- Muenstermann, R.; Dittmann, R.; Szot, K.; Mi, S.B.; Jia, C.L.; Meuffels, P.; Waser, R. Realization of regular arrays of nanoscale resistive switching blocks in thin films of Nb-doped SrTiO3. Appl. Phys. Lett. 2008, 93, 023110. [Google Scholar] [CrossRef]
- Menke, T.; Dittmann, R.; Meuffels, P.; Szot, K.; Waser, R. Impact of the electroforming process on the device stability of epitaxial Fe-doped SrTiO3 resistive switching cells. J. Appl. Phys. 2009, 106, 114507. [Google Scholar] [CrossRef]
- Peter, F.; Rudiger, A.; Dittmann, R.; Waser, R.; Szot, K.; Reichenberg, B.; Prume, K. Analysis of shape effects on the piezoresponse in ferroelectric nanograins with and without adsorbates. Appl. Phys. Lett. 2005, 87, 082901. [Google Scholar] [CrossRef] [Green Version]
- Chen, J.; Sekiguchi, T.; Li, J.Y.; Ito, S.; Yi, W.; Ogura, A. Investigation of dislocations in Nb-doped SrTiO3 by electron-beam-induced current and transmission electron microscopy. Appl. Phys. Lett. 2015, 106, 102109. [Google Scholar] [CrossRef]
- Jiang, W.; Evans, D.; Bain, J.A.; Skowronski, M.; Salvador, P.A. Electron beam induced current investigations of interfaces exposed to chemical and electrical stresses. Appl. Phys. Lett. 2010, 96, 092102. [Google Scholar] [CrossRef]
- Kim, D.C.; Seo, S.; Ahn, S.E.; Suh, D.S.; Lee, M.J.; Park, B.H.; Yoo, I.K.; Baek, I.G.; Kim, H.J.; Yim, E.K.; et al. Electrical observations of filamentary conductions for the resistive memory switching in NiO films. Appl. Phys. Lett. 2006, 88, 202102. [Google Scholar] [CrossRef]
- Zhang, K.; Lanza, M.; Shen, Z.Y.; Fu, Q.; Hou, S.M.; Porti, M.; Nafria, M. Analysis of Factors in the Nanoscale Physical and Electrical Characterization of High-K Materials by Conductive Atomic Force Microscope. Integr. Ferroelectr. 2014, 153, 1–8. [Google Scholar] [CrossRef]
- Son, J.Y.; Shin, Y.H. Direct observation of conducting filaments on resistive switching of NiO thin films. Appl. Phys. Lett. 2008, 92, 222106. [Google Scholar] [CrossRef]
- Rodenbücher, C.; Luysberg, M.; Schwedt, A.; Havel, V.; Gunkel, F.; Mayer, J.; Waser, R. Homogeneity and variation of donor doping in Verneuil-grown SrTiO3:Nb single crystals. Sci. Rep. 2016, 6, 32250. [Google Scholar] [CrossRef] [PubMed]
- Kim, Y.; Disa, A.S.; Babakol, T.E.; Fang, X.Y.; Brock, J.D. Strain and oxygen vacancy ordering in SrTiO3: Diffuse X-ray scattering studies. Phys. Rev. B 2015, 92, 064105. [Google Scholar] [CrossRef]
- Mott, N.F. Metal-Insulator Transition. Rev. Mod. Phys. 1968, 40, 677. [Google Scholar] [CrossRef]
- Frederikse, H.P.R.; Thurber, W.R.; Hosler, W.R. Electronic Transport in Strontium Titanate. Phys. Rev. 1964, 134, A442. [Google Scholar] [CrossRef]
- Calvani, P.; Capizzi, M.; Donato, F.; Lupi, S.; Maselli, P.; Peschiaroli, D. Observation of a Midinfrared Band in SrTiO3−y. Phys. Rev. B 1993, 47, 8917–8922. [Google Scholar] [CrossRef]
- Spinelli, A.; Torija, M.A.; Liu, C.; Jan, C.; Leighton, C. Electronic transport in doped SrTiO3: Conduction mechanisms and potential applications. Phys. Rev. B 2010, 81, 155110. [Google Scholar] [CrossRef]
- Lin, X.; Rischau, C.W.; Buchauer, L.; Jaoui, A.; Fauque, B.; Behnia, K. Metallicity without quasi-particles in room-temperature strontium titanate. npj Quantum Mater. 2017, 2, 41. [Google Scholar] [CrossRef]
- Pergament, A.; Stefanovich, G.; Markova, N. The Mott criterion: So simple and yet so complex. arXiv, 2014; arXiv:1411.4372. [Google Scholar]
- Lehovec, K.; Shirn, G.A. Conductivity Injection and Extraction in Polycrystalline Barium Titanate. J. Appl. Phys. 1962, 33, 2036–2044. [Google Scholar] [CrossRef]
- Lin, Y.H.; Chen, Y.; Goldman, A.M. Indications of superconductivity at somewhat elevated temperatures in strontium titanate subjected to high electric fields. Phys. Rev. B 2010, 82, 172507. [Google Scholar] [CrossRef]
- Pilch, M.; Szot, K. Resistive switching in Sr1−0.05La0.05TiO3. In Proceedings of the 2012 International Symposium on Applications of Ferroelectrics Held Jointly with 11th IEEE ECAPD and IEEE PFM (ISAF/ECAPD/PFM), Aveiro, Portugal, 9–13 July 2012. [Google Scholar]
- Szot, K.; Rytz, D.; Lazar, I.; Kajewki, D.; Roleder, K. The macro- and nanoscale phenomena in BaTiO3 single crystals (inv. talk). In Proceedings of the International Meeting on Ferroelectricity (IFM), San Antonio, TX, USA, 4–8 September 2017. [Google Scholar]
- Van Landuyt, J.; Amelinckx, S. Generation Mechanism for Shear Planes in Shear Structures. J. Solid State Chem. 1973, 6, 222–229. [Google Scholar] [CrossRef]
- Sakaguchi, I.; Komastu, M.; Watanabe, A.; Haneda, H. Oxygen diffusion along the short-circuit paths in bicrystal SrTiO3. J. Mater. Res. 2000, 15, 2598–2601. [Google Scholar] [CrossRef]
- Szot, K.; Rodenbücher, C. Insulator-Metal Transition Associated with Resistive Switching in Real SrTiO3 and TiO2 Crystals. In Proceedings of the 2015 Joint IEEE International Symposium on the Applications of Ferroelectric, International Symposium on Integrated Functionalities and Piezoelectric Force Microscopy Workshop (ISAF/ISIF/PFM), Singapore, 24–27 May 2015; pp. 143–146. [Google Scholar]
- Menzel, S.; Waters, M.; Marchewka, A.; Bottger, U.; Dittmann, R.; Waser, R. Origin of the Ultra-nonlinear Switching Kinetics in Oxide-Based Resistive Switches. Adv. Funct. Mater. 2011, 21, 4487–4492. [Google Scholar] [CrossRef]
- Jiang, W.; Kamaladasa, R.J.; Lu, Y.M.; Vicari, A.; Berechman, R.; Salvador, P.A.; Bain, J.A.; Picard, Y.N.; Skowronski, M. Local heating-induced plastic deformation in resistive switching devices. J. Appl. Phys. 2011, 110, 054514. [Google Scholar] [CrossRef]
- Kamaladasa, R.J.; Noman, M.; Chen, W.; Salvador, P.A.; Bain, J.A.; Skowronski, M.; Picard, Y.N. Dislocation impact on resistive switching in single-crystal SrTiO3. J. Appl. Phys. 2013, 113, 234510. [Google Scholar] [CrossRef]
- Kim, G.H.; Lee, J.H.; Seok, J.Y.; Song, S.J.; Yoon, J.H.; Yoon, K.J.; Lee, M.H.; Kim, K.M.; Lee, H.D.; Ryu, S.W.; et al. Improved endurance of resistive switching TiO2 thin film by hourglass shaped Magneli filaments. Appl. Phys. Lett. 2011, 98, 262901. [Google Scholar]
- Bobeth, M.; Farag, N.; Levin, A.A.; Meyer, D.C.; Pompe, W.; Romanov, A.E. Reversible electric field-induced structure changes in the near-surface region of strontium titanate. J. Ceram. Soc. Jpn. 2006, 114, 1029–1037. [Google Scholar] [CrossRef]
- Kamaladasa, R.J.; Sharma, A.A.; Lai, Y.T.; Chen, W.H.; Salvador, P.A.; Bain, J.A.; Skowronski, M.; Picard, Y.N. In Situ TEM Imaging of Defect Dynamics under Electrical Bias in Resistive Switching Rutile-TiO2. Microsc. Microanal. 2015, 21, 140–153. [Google Scholar] [CrossRef] [PubMed]
- Cooper, D.; Baeumer, C.; Bernier, N.; Marchewka, A.; La Torre, C.; Dunin-Borkowski, R.E.; Menzel, S.; Waser, R.; Dittmann, R. Anomalous Resistance Hysteresis in Oxide ReRAM: Oxygen Evolution and Reincorporation Revealed by In Situ TEM. Adv. Mater. 2017, 29, 1700212. [Google Scholar] [CrossRef] [PubMed]
- Meuffels, P.; Soni, R. Fundamental Issues and Problems in the Realization of Memristors. arXiv, 2012; arXiv:1207.7319. [Google Scholar]
- Baeumer, C.; Schmitz, C.; Marchewka, A.; Mueller, D.N.; Valenta, R.; Hackl, J.; Raab, N.; Rogers, S.P.; Khan, M.I.; Nemsak, S.; et al. Quantifying redox-induced Schottky barrier variations in memristive devices via in operando spectromicroscopy with graphene electrodes. Nat. Commun. 2016, 7, 12398. [Google Scholar] [CrossRef] [PubMed]
- Menzel, S.; Bottger, U.; Wimmer, M.; Salinga, M. Physics of the Switching Kinetics in Resistive Memories. Adv. Funct. Mater. 2015, 25, 6306–6325. [Google Scholar] [CrossRef]
- Ikuhara, Y.; Suzuki, T.; Kubo, Y. Transmission Electron-Microscopy Insitu Observation of Crack-Propagation in Sintered Alumina. Philos. Mag. Lett. 1992, 66, 323–327. [Google Scholar] [CrossRef]
- Oh, S.H.; Legros, M.; Kiener, D.; Dehm, G. In situ observation of dislocation nucleation and escape in a submicrometre aluminium single crystal. Nat. Mater. 2009, 8, 95–100. [Google Scholar] [CrossRef] [PubMed]
- Kiener, D.; Hosemann, P.; Maloy, S.A.; Minor, A.M. In situ nanocompression testing of irradiated copper. Nat. Mater. 2011, 10, 608–613. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Minor, A.M.; Asif, S.A.S.; Shan, Z.W.; Stach, E.A.; Cyrankowski, E.; Wyrobek, T.J.; Warren, O.L. A new view of the onset of plasticity during the nanoindentation of aluminium. Nat. Mater. 2006, 5, 697–702. [Google Scholar] [CrossRef] [PubMed]
- De Hosson, J.T.M.; Soer, W.A.; Minor, A.M.; Shan, Z.W.; Stach, E.A.; Asif, S.A.S.; Warren, O.L. In situ TEM nanoindentation and dislocation-grain boundary interactions: A tribute to David Brandon. J. Mater. Sci. 2006, 41, 7704–7719. [Google Scholar] [CrossRef]
- Kondo, S.; Mitsuma, T.; Shibata, N.; Ikuhara, Y. Direct observation of individual dislocation interaction processes with grain boundaries. Sci. Adv. 2016, 2, e1501926. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Hirsch, P.B.; Howie, A.; Nicholson, R.B.; Pashley, D.W.; Whelan, M.J. Electron Microscopy of Thin Crystals, 2nd ed.; Krieger: New York, NY, USA, 1977. [Google Scholar]
- Yang, K.H.; Ho, N.J.; Lu, H.Y. Deformation Microstructure in (001) Single Crystal Strontium Titanate by Vickers Indentation. J. Am. Ceram. Soc. 2009, 92, 2345–2353. [Google Scholar] [CrossRef]
- Yang, K.H.; Ho, N.J.; Lu, H.Y. Plastic Deformation of <001> Single-Crystal SrTiO3 by Compression at Room Temperature. J. Am. Ceram. Soc. 2011, 94, 3104–3111. [Google Scholar] [CrossRef]
- Ravikumar, V.; Dravid, V.P. Atomic-Structure of Undoped Σ5 Symmetrical Tilt Grain-Boundary in Strontium-Titanate. Ultramicroscopy 1993, 52, 557–563. [Google Scholar] [CrossRef]
- Imaeda, M.; Mizoguchi, T.; Sato, Y.; Lee, H.S.; Findlay, S.D.; Shibata, N.; Yamamoto, T.; Ikuhara, Y. Atomic structure, electronic structure, and defect energetics in [001](310) Σ5 grain boundaries of SrTiO3 and BaTiO3. Phys. Rev. B 2008, 78, 245320. [Google Scholar] [CrossRef]
- Lim, L.C.; Raj, R. Continuity of Slip Screw and Mixed-Crystal Dislocations across Bicrystals of Nickel at 573-K. Acta Metall. 1985, 33, 1577–1583. [Google Scholar] [CrossRef]
- Priester, L. On the accommodation of extrinsic dislocations in grain boundaries. Interface Sci. 1997, 4, 2005–2219. [Google Scholar] [CrossRef]
- Sutton, A.P.; Balluffi, R.W. Interfaces in Crystalline Materials; Oxford University Press: New York, NY, USA, 1995. [Google Scholar]
- Hirth, J.P.; Pond, R.C.; Lothe, J. Spacing defects and disconnections in grain boundaries. Acta Mater. 2007, 55, 5428–5437. [Google Scholar] [CrossRef]
- Shockley, W. Do Dislocations Hold Technological Promise. Solid State Technol. 1983, 26, 75–78. [Google Scholar]







































© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Szot, K.; Rodenbücher, C.; Bihlmayer, G.; Speier, W.; Ishikawa, R.; Shibata, N.; Ikuhara, Y. Influence of Dislocations in Transition Metal Oxides on Selected Physical and Chemical Properties. Crystals 2018, 8, 241. https://doi.org/10.3390/cryst8060241
Szot K, Rodenbücher C, Bihlmayer G, Speier W, Ishikawa R, Shibata N, Ikuhara Y. Influence of Dislocations in Transition Metal Oxides on Selected Physical and Chemical Properties. Crystals. 2018; 8(6):241. https://doi.org/10.3390/cryst8060241
Chicago/Turabian StyleSzot, Kristof, Christian Rodenbücher, Gustav Bihlmayer, Wolfgang Speier, Ryo Ishikawa, Naoya Shibata, and Yuichi Ikuhara. 2018. "Influence of Dislocations in Transition Metal Oxides on Selected Physical and Chemical Properties" Crystals 8, no. 6: 241. https://doi.org/10.3390/cryst8060241
APA StyleSzot, K., Rodenbücher, C., Bihlmayer, G., Speier, W., Ishikawa, R., Shibata, N., & Ikuhara, Y. (2018). Influence of Dislocations in Transition Metal Oxides on Selected Physical and Chemical Properties. Crystals, 8(6), 241. https://doi.org/10.3390/cryst8060241





