Next Article in Journal
Simultaneously Improve White LED Omni-Directional Package Efficacy and Spatial Color Uniformity on Scattered Photon Extraction Technology
Previous Article in Journal
Anion Influence on Spin State in Two Novel Fe(III) Compounds: [Fe(5F-sal2333)]X
Previous Article in Special Issue
Fabrication of Novel ZIF-8@BiVO4 Composite with Enhanced Photocatalytic Performance
 
 
Search for Articles:
Title / Keyword
Author / Affiliation / Email
Journal
Article Type
 
 
Advanced Search
 
Section
Special Issue
Volume
Issue
Number
Page
 
Journals
Crystals
Volume 9
Issue 1
10.3390/cryst9010020
crystals-logo
Submit to this Journal Review for this Journal Propose a Special Issue
► Article Menu

Article Menu

share Share announcement Help format_quote Cite question_answer Discuss in SciProfiles thumb_up
...
Endorse textsms
...
Comment
first_page
settings
Order Article Reprints
Font Type:
Arial Georgia Verdana
Font Size:
Aa Aa Aa
Line Spacing:
Column Width:
Background:
Article

Modulating and Orienting an Anisotropic Zn-Based Metal Organic Framework for Selective CH4/CO2 Gas Separation

by
Luke Huelsenbeck
†,
Karl S. Westendorff
†,
Yuntao Gu
,
Silvia Marino
,
Sangeun Jung
,
William S. Epling
and
Gaurav Giri
*
Department of Chemical Engineering, University of Virginia, Charlottesville, VA 22904-4741, USA
*
Author to whom correspondence should be addressed.
†
These authors contributed equally to this work.
Crystals 2019, 9(1), 20; https://doi.org/10.3390/cryst9010020
Submission received: 13 November 2018 / Revised: 25 December 2018 / Accepted: 26 December 2018 / Published: 29 December 2018
(This article belongs to the Special Issue Synthesis, Modeling, Characterization and Applications of Metal-Organic Frameworks)
Browse Figures
Versions Notes

Abstract

:
This work investigates the morphological control of the anisotropic [Zn2(NDC)2(DABCO)]n MOF (Metal organic framework) and the subsequent adsorption characteristics for CO2/CH4 gas separation. Morphology of the MOF crystals is controlled by the use of modulators. The addition of acetic acid or pyridine successfully produce rod or plate morphologies, respectively, with each morphology possessing a different major surface pore aperture. Single-component equilibrium and kinetic adsorption data for CO2 and CH4 were collected. Equilibrium analysis indicates a slight selectivity towards CO2 whereas kinetic data unexpectedly shows lower diffusion time constants for CO2 compared to CH4. Mass transfer resistances on each species is discussed. Finally, a coating technique termed solution shearing is used to orient different morphologies on substrates as a film. An increase in film orientation is observed for the rod morphology, indicating that this MOF morphology is a promising candidate to create large area, thin-film applications.

1. Introduction

The efficient separation of CO2 from CH4 is critical for the technoeconomic success of the natural and biogas industries, however current industrial separation techniques are energy intensive or require high capital and operational expenses [1,2]. Common separation processes such as cryogenic distillation require a significant amount of energy and do not align with “green” chemistry practices, highlighting the need to find alternative approaches [1,2]. Recent attempts at making these separations more efficient involve the use of polymer membranes. While these membrane systems require a lower energy input, a lower concentration of feed CO2 is required to prevent the membrane from plasticizing [3]. Other approaches use zeolites, but these materials are often synthesized with non-ideal particle morphologies, offer a limited range of pore sizes and chemistry, and can require energy and capital-intensive synthesis conditions [4]. An ideal separation platform would use easily synthesized and easily tunable materials, and would be effective regardless of intake quantities and concentrations.
Metal organic frameworks (MOFs) are novel materials and could potentially fulfill these requirements. MOFs consist of metal ion clusters bound together by coordinating organic linkers to form a porous, periodic structure [5,6]. Their key features include high surface areas (>1000 m2/g), chemical customizability, and relatively easy and low temperature synthesis, which enable their application in a wide range of areas including catalysis, fuel cell development, drug delivery, data storage, and gas separations [5,7,8,9,10,11].
MOFs have shown promise as selective gas separators due to their ability to sterically and chemically restrict the species that pass through their pores. MOFs have previously been used in combination with a polymer matrix to demonstrate a high selectivity in a CO2/CH4 gas mixture [2]. It was hypothesized that the selective permeation was due to the well-defined sorption properties of the microporous, crystalline MOF [2]. Additionally, it has been shown that the unmodulated [Cu2(NDC)2(DABCO)]n MOF can separate gases in a CO2/CH4 system where CO2 and CH4 have differing kinetic diameters of 3.3 Å and 3.8 Å, respectively [12,13]. This system is interesting for gas sorption kinetics due to its different lattice dimensions leading to anisotropic pore sizes (a = b = 10.819 Å, c = 9.635 Å).
Recent studies have shown that these gas adsorption capabilities can be further enhanced through the introduction of modulators during MOF synthesis, by altering the overall crystal growth process [14]. In anisotropic MOFs, such as those in the M2(dicarboxylate)2(N-ligand) series, the modulator-based growth control is dramatic and can significantly alter crystal aspect ratios [15,16,17]. The introduction of modulators during synthesis can target either the carboxylate (h00, 0k0) or the amino (00l) planes, inhibiting crystal growth along these planes and directing MOF crystal growth along unmodulated axes (Figure 1) [15,16,17]. Previous work has demonstrated the [Cu2(NDC)2(DABCO)]n (NDC = 1,4-naphthalene dicarboxylate; DABCO = 1,4-diazabicyclo[2.2.2]-octane) member of the [M2(dicarboxylate)2(N-ligand)]n MOF series can be modulated to obtain rod or plate morphologies with the use of acetic acid (carboxylate) or pyridine (amino) modulators [18].
The intrinsic anisotropy of the unit cell, combined with modifying the crystal aspect ratio, exposes pore apertures of different dimensions on the crystal surface. The choice of modulator determines which pore aperture is exposed as the major pore aperture on the crystal surface, allowing for selection of the surface pore dimension, as well as the total internal channel length of each pore type. For example, the use of an amino modulator creates a plate morphology where a carboxylate-carboxylate aperture predominates on the crystal surface, while the use of a carboxylate modulator creates a rod morphology where more of the carboxylate-amino aperture is present on the surface of the crystal. These morphologies can be used to create and tune molecular sieves for specific separation applications within the same topology.
While many examples of the effect of modulators on individual MOF crystal growth have been studied, controlling the overall orientation of these crystals for membrane applications is also important. Previous work has shown that MOF crystals can be oriented on mixed matrix membrane post-synthesis, which then show an increased performance in separation applications [19]. Ghorbanpour et al. [20] have also shown that MOF crystals can be oriented post-synthesis through a solution shearing technique to form highly ordered thin films. These are highly desirable qualities for gas separation membranes, as oriented thin films, along with controlled crystal aspect ratios, allow for a higher flux than packed beds while retaining performance [21].
In this work, we synthesized and characterized the [Zn2(NDC)2(DABCO)]n MOF and controlled its morphology using pyridine and acetic acid as modulators to form plates and rods, respectively. We then demonstrated the change in steric separation selectivity using these two crystal morphologies in a single component adsorption system for both CO2 and CH4. We tested this performance in a competitive adsorption environment. Finally, using solution shearing and drop casting, we show differing thin film orientation of the modulated crystals for future applications as thin film separation membranes.

2. Materials and Methods

2.1. Materials

The following chemicals were purchased from Sigma Aldrich (St. Louis, MO, USA): dimethyl formamide (DMF, ≥99.8%), acetone (≥99.9%), Zn(CH3COO)2·2H2O (≥99.0%), and DABCO (≥99%). 1,4-napthalenedicarboxylic acid (98+%) was purchased from Alfa Chemistry (Ronkonkoma, NY, USA), while pyridine (ACS grade), acetic acid (ACS grade), toluene (99.9%), and isopropyl alcohol (laboratory grade) were purchased from Fisher Chemical (Hampton, NH, USA). Quartz tubes were purchased from Quartz Scientific, Inc (Fairport Harbor, OH, USA). CO2 (99.99%), CH4 (99.97%), and N2 (99.999%) gases were purchased from Praxair Inc (Danbury, CT, USA).

2.2. Synthesis of [Zn2(NDC)2(DABCO)]n MOFs

In a typical unmodulated MOF synthesis, a solution with 0.050 g of DABCO, 0.196 g of 1,4-NDC and 13.20 g of DMF was added to a solution of 0.277 g of Zn(CH3COO)2·2H2O and 19.82 g of DMF for a final molar ratio of Zn/DABCO/1,4-NDC/DMF of 2.8:2:1:400. The total mixture was stirred for 25 min, after which it was poured into a 50 mL Teflon lined acid digestion vessel (Parr Instruments, Moline, IL, USA) and heated at 100 °C for 24 h.
The same process was applied to synthesizing [Zn2(NDC)2(DABCO)]n rod and plate morphologies with the addition of a modulator. To synthesize rods, a solution with 0.045 g of DABCO, 0.171 g of 1,4-NDC and 11.80 g of DMF was added to a solution of 0.247 g of Zn(CH3COO)2·2H2O, 3.37 g of acetic acid, and 17.70 g of DMF for a final molar ratio of Zn/DABCO/1,4-NDC/acetic acid/DMF of 2.8:1:2:125:400. To synthesize plates, a solution consisting of, 0.022 g of DABCO, 4.36 g of pyridine, and 0.086 g of 1,4-NDC, and 11.56 g of DMF was added to a solution of 0.120 g of Zn(CH3COO)2·2H2O and 17.34 g of DMF for a final molar ratio of Zn/DABCO/1,4-NDC/pyridine/DMF of 2.8:1:2:250:800.
After cooling for 1 h, the precipitate was centrifuged and washed once with fresh DMF and twice with EtOH. The resulting product was then heated to 80 °C under ~3 kPa vacuum overnight and stored as a powder under vacuum.

2.3. Characterization

All X-ray diffraction (XRD) patterns were recorded on a PANalytical Empyrean X-ray diffractometer (Malvern Panalytical, Egham, UK) with a Cu K-α beam (λ = 1.54 Å). Scans were completed from 2θ of 7° to 70° with a step size of 0.0035°. For Brunauer, Emmet, Teller isotherm (BET) analysis, MOF samples of 15–25 mg were degassed at 70 °C until a pressure of 1.3 × 10−3 kPa was obtained, after which the samples were heated at 80 °C for 8 h. BET surface areas were measured using nitrogen adsorption isotherms collected on a Micromeritics ASAP 2020 instrument (Micromeritics, Norcross, GA, USA) at a relative pressure range of 0.01–0.05 relative to the nitrogen saturation pressure at 77 K. SEM micrographs were collected with a FEI Quanta 650 at 3 kV with a spot size of 4 at various magnifications.

2.4. CO2 and CH4 Kinetic and Equilibrium Experiments

Single-component adsorption equilibrium and kinetics of CO2 and CH4 were measured volumetrically using a Micromeritics ASAP 2020 Surface Area and Porosity Analyzer using the Rate of Adsorption Software (ROA v1.02, Micromeritics, Norcross, GA, USA) at 273.15 K with pressures up to 105 kPa. Initially, 100–400 mg of MOF sample was degassed using the same process outlined for BET isotherms. Samples were degassed between subsequent runs by holding a pressure of 1.3 × 10−3 kPa for minimum of 5 h at room temperature and stored under nitrogen atmosphere. Kinetic data was taken at pressures of ~53 kPa and ~93 kPa. At these pressures, adsorbate was dosed into the sample chamber nominally at 5 cm3/g and the resulting change in pressure was recorded and converted to an uptake volume as a function of time. The first 1 s of data was discarded to account for valve switching time and gas expansion into the sample chamber. The final adsorption amount at 1.05 atm was used as the equilibrium quantity.
For multi-component adsorption experiments, MOF samples were sieved to particle sizes between 250 and 600 µm, after which 30–70 mg of sieved material was gently mixed with 105 mg of crushed cordierite sieved to the same size. The mixture was loaded between quartz wool in a quartz tube reactor (inner diameter: 6.35 mm, length: 457 mm). The tube was set into a Lindbergh Mini-Mite furnace for temperature control. Gas concentrations and flows were controlled using MKS mass flow controllers. The adsorption experiments were initiated by generating a step change of the adsorbate concentrations in the reactor [22]. Prior to the multi-component adsorption experiment, the quartz tube reactor was heated to 60 °C and nitrogen gas was passed over the sample for a minimum of 20 min to remove any residual water. After cooling to room temperature, separation tests were run by introducing a gas mixture of ~1000 ppm CO2, ~1000 ppm CH4, balanced by N2, flowrates were adjusted based on the mass of MOF samples to keep a constant space velocity. Controls were taken of an empty reactor and a reactor containing only cordierite to determine dead volume effects on measurements. The composition of the downstream was analyzed every second by an MKS MultiGas 2030 (MKS Instruments, Inc., Andover, MA, USA).

2.5. Solution Shearing of [Zn2(NDC)2(DABCO)]n Particles

A solution shearing procedure previously outlined by Ghorbanpour et al. was used to make thin films from particle suspension [20]. Solution shearing was conducted on 1 cm × 1 cm silicon wafers washed thoroughly with toluene, acetone, and isopropyl alcohol prior to the deposition of 20 µL of 5 wt./wt. % MOF/EtOH solution on the silicon wafer substrate. The substrate was heated to 60 °C, and the shearing blade was translated at speeds of 0.1, 0.25, and 0.5 mm/s for each morphology. Drop-cast samples were created by depositing 20 µL of 5 wt. % MOF/EtOH solution on silicon wafers substrates heated to temperatures of 60 °C. The orientation of the solution sheared MOF thin film was quantified by dividing the intensity of the (110) peak by the (001) peak intensity in the XRD.

3. Results and Discussion

3.1. Characterization of Modulated [Zn2(NDC)2(DABCO)]n

By extending the rationale developed by Pham et al., rod and plate morphologies of the [Zn2(NDC)2(DABCO)]n MOF can be created with the use of acetic acid (carboxylate) or pyridine (amine) modulators, respectively [18]. Figure 2 shows scanning electron microscope (SEM) images of particles synthesized with no modulator, 1.6 M acetic acid as modulator, and 1.6 M pyridine as modulator. Compared to the unmodulated synthesis, the modulated syntheses show larger crystals. The acetic acid modulator shows the formation of rod-like crystals, and the pyridine modulator shows the formation of plate-like crystals. This confirms that modulating for different coordination modes in a MOF composed of two distinct linkers can yield drastically different morphologies. It should be noted that at similar modulator concentrations, the [Zn2(NDC)2(DABCO)]n MOF was found to produce single crystals which are a magnitude greater in size than the previously reported [Cu2(NDC)2(DABCO)]n MOF [18]. Aspect ratios of these crystals are described in Table 1 showing both modulators increase the aspect ratio of their respective morphologies. The unmodulated MOF shows slight preferential growth to a rod-like morphology. While the major axis for the rod morphology is in the [001] direction, the major axes for the plate morphology are in the [100] and [010] directions (Figure 1). It should be noted the major planes on each particle (i.e., the surfaces parallel to the major axis or axes) are associated with the carboxylate-carboxylate or carboxylate-amine pore aperture as a result of the anisotropic crystal structure.
Figure 3 shows powder x-ray diffraction (PXRD) data collected for [Zn2(NDC)2(DABCO)]n MOF synthesis with and without the presence of the amine and carboxylate modulators compared to a simulated diffraction pattern. These patterns show that the modulators do not alter the crystal structure. It should be noted that texture in the bulk powder sample is observed. Differing relative intensities in the peaks, specifically in those matching the (001) and (110) planes, are recorded for different morphologies. Since particle orientation affects the relative intensity of diffraction peaks, these patterns indicate a preferential crystal orientation for a bulk powder. This is likely due to particle morphology influencing packing, orienting particles along their major axes and with respect to the substrate [23]. This effect is highlighted in Figure 2c, where plates are observed to orient in stacks.

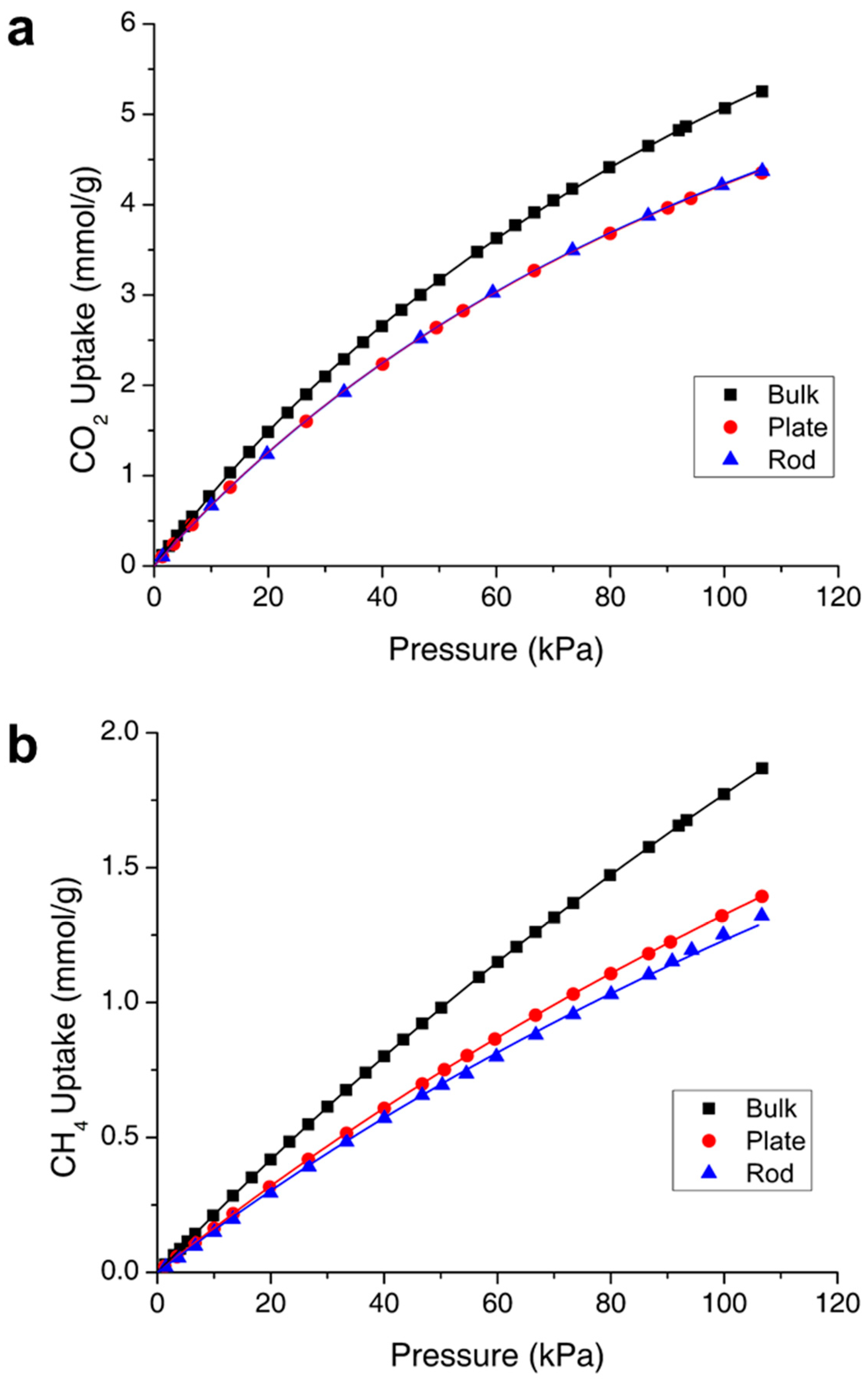
3.2. Adsorption Isotherms

Nitrogen isotherms of the synthesized [Zn2(NDC)2(DABCO)]n MOF were used to verify the microporosity of the synthesized material for the bulk and modulated samples (Figure S1). The BET surface area (Table 2) and isotherms are comparable to that of reported values for the Zn and Cu analog of [M2(NDC)2(DABCO)]n (M = Zn,Cu) [15,18]. Experiments show that the [Zn2(NDC)2(DABCO)]n surface area measurements are highly sensitive to the drying procedure (Table S1). The sensitivity is likely due to solvent stabilization effects observed in the [Zn2(dicarboxylate)2(N-ligand)]n MOF family [15]. Previous results have shown that a MOF with a similar zinc-based topology had reduced crystallinity after activation, indicating a partial collapse of the framework [15]. Given this information, it is difficult to ascertain surface area contributions from defects due to modulation (i.e., defect engineering) or degradation from activation for the different modulated syntheses. However, a similarity in measured surface area between morphologies shows that any effect is similar in all three cases.
Figure 4 shows the single-component isotherms for CO2 and CH4 of [Zn2(NDC)2(DABCO)] at 273 K for different morphologies. The total uptake of each species follows the same trend as BET surface area measurements, where lower quantities of CO2 and CH4 are adsorbed by lower surface area morphologies. This behavior is expected for physisorption as the quantity adsorbed is a function of the accessible surface area. The Langmuir isotherm model (Equation (1)) provides an accurate approximation of the adsorption with fitting parameters listed in Table 3.
q = a m b P 1 + b P
where q is the quantity adsorbed per mass of adsorbate, am is the maximum adsorbed quantity per adsorbate mass to form a complete monolayer, b is the affinity or Langmuir constant and P is the dosing pressure.
The product of am and b yield another constant termed Henry’s constant (K), which provides a linear approximation of the adsorption isotherm. The ratio of Henry’s constants for CO2 and CH4 provides an equilibrium selectivity, α.
[Zn2(NDC)2(DABCO)] demonstrates moderate selectivity towards CO2 compared to CH4. This value is comparable to selectivity for other MOFs under similar conditions such as the ZIF family (3.9–10.1) [26], MIL-101 (3–5) [27] and MOF-177 (4.43) [28]. The higher affinity of CO2 to adsorb on the surface is likely due to a higher quadrupole moment [27,29]. Both modulated morphologies (amine and carboxylate) show a moderate increase in selectivity compared to the bulk. This may be because more defect sites are preferentially interacting with CO2 [30], however more work is required to confirm this interaction.

3.3. Surface Pore Aperture and CO2/CH4 Kinetic Selectivity

As previously mentioned, the major surface for each crystal morphology, defined as the surfaces parallel to the crystal major axes, is associated with a crystallographic plane. More specifically, the plate morphology will have a major surface with a pore entrance aperture defined by the carboxylate-carboxylate frame, whereas the rod morphology will have a major surface with a pore entrance aperture defined by the carboxylate-amine frame (Figure 1). Each pore aperture is expected to present different mass transfer resistances [31]. Therefore, diffusional differences between carboxylate-carboxylate and carboxylate-amine pore apertures will exist and variation in kinetic selectivity between morphologies can be expected for the differently sized adsorbates CO2 and CH4. Given the high aspect ratio of each morphology, a significant portion of diffusion is expected to occur through the major surface pore.
Figure 5 shows representative data taken for the uptake of CO2 and CH4 for the bulk morphology. CH4 is adsorbed more quickly, reaching 90% of the total uptake at around 50 s compared to about 125 s for the CO2. This contradicts other work in microporous MOFs, which determined the diffusion of CO2 is much quicker than CH4 due to the difference in kinetic diameter [32]. However, such a trend agrees with the Knudsen diffusion model, which states molecules with larger mass will diffuse more slowly in pores with a diameter below that of the mean free path, as is the case for gas in microporous materials. To better understand the diffusion of each species with respect to morphologies, we apply a single-component adsorption micropore diffusion control model developed by Ruthven et al. [33] to adsorption rate data collected for CO2 and CH4 that has successfully been applied to several MOF particle systems [27,34].
m m ∞ ≈ 6 π D c t r c 2 − 3 D c t r c 2
where m / m ∞ is the mass uptake relative to the equilibrium uptake mass, Dc is the intracrystalline diffusivity, rc is the crystal radius, and t is time. It should be noted Equation (2) is valid for m m ∞ < 0.85 [33]. This model assumes the intracrystalline diffusion resistances are much greater than macroporous resistances in particle aggregates, diffusion is constant within the crystalline material, and the concentration of adsorbate is constant outside of the particle. All of these assumptions are valid given that the free diffusivity of gases in macropores are much greater than those in the micropores [33], the gases do not condense in the micropores under the sampling conditions, and the sample tube volume can be approximated as an infinite reservoir compared to the volume adsorbed.
Table 4 shows the diffusion time constants, Dc/rc2, found by fitting Equation (2) to multiple uptake curves for each gas species and morphology at 94 kPa (700 mmHg). Kinetic selectivity was found by dividing the diffusion time constant for CO2 by the diffusion time constant for CH4. It can be seen that kinetic selectivity exists for CO2/CH4 as a function of morphology. Interestingly, the CO2 diffusion time constant remains relatively constant across the different morphologies. This implies that the diffusional resistances on CO2 within the framework are not highly dependent on diffusion direction (i.e., the pore aperture size or frame chemistry) and may be dominated by more complex electrostatic interactions with the framework [35,36]. A two-fold increase in diffusion time constant is observed for CH4 between the plate and rod, suggesting the different pore apertures have a significant effect on diffusion through the framework. These data show the diffusion through the carboxylate-amine frame (rod) is nearly twice as fast as the carboxylate-carboxylate frame (plate). Since CH4 is thought to have little chemical or intermolecular interactions with the framework, the diffusion is likely determined by pore aperture size [37]. Given the linker geometry and bond rotation of 1,4-naphthalenedicarboxylate, the pore aperture in the carboxylate-carboxylate frame may be significantly smaller than the carboxylate-amine frame. Such a geometry could explain why the diffusion is faster through the carboxylate-amine frame, however more work is required to understand the chemistry and structure around each pore aperture.
Attempting to replicate these results in a competitive adsorption environment showed the rod morphology adsorbs 2–4 times as much CO2 and CH4 than other tested morphologies at equilibrium (Table S2). We hypothesize that the MOF is unstable which results in the disparity in equilibrium values compared to those for the single-component isotherms. Follow up XRD data taken of samples run in the multi-component reactor showed significant degradation in crystallinity, confirming [Zn2(NDC)2(DABCO)]n is not stable under ambient conditions (Figure S2). Given the differing equilibrium uptakes, we hypothesize each morphology degrades at a different rate, and that the stability of anisotropic MOFs may depend on morphology and major surface bond mode.

3.4. Orientation of [Zn2(NDC)2(DABCO)]n Particle Films

Previous studies by our group have shown that well faceted MOF morphologies can be utilized in combination with flow coating techniques to control the crystal orientation of MOF thin films [20]. Orienting MOFs, to obtain selected pore apertures on substrates is desirable for high performance separations membranes [38,39]. Solution shearing is a meniscus guided flow coating technique where a particle suspension or solution can be deposited on a substrate using a blade [40,41]. As the blade is translated across the substrate at a prescribed speed, an evaporation front develops such that the crystalline material is deposited as a film in a controlled manner. The evaporation rate and fluid dynamics during deposition can be controlled by tuning the substrate temperature, blade speed, wetting properties of the substrate, or the solvent used for the suspension. Given our previous results with aligning faceted MOF particles and the well-faceted, high aspect ratio of the MOF used in this study, we identified the [Zn2(NDC)2(DABCO)]n morphologies as good candidates for creating oriented thin films.
The different [Zn2(NDC)2(DABCO)]n morphologies are drop cast and solution sheared with varied blade speeds, and the orientation of the solution sheared MOF thin films are measured by evaluating the orientation number, defined as the ratio of the intensities of the (110) and (001) peaks for each sample. As previously mentioned, the relative intensity of peaks can be used to determine the degree of orientation of a crystalline sample. It should be noted this method is not a precise measure of the orientation as peak intensity is a function of many factors in a polydisperse crystalline systems [42], however it can show the deviation of crystal texture from an isotropically distributed powder. Table 5 shows the orientation number for each morphology with varying film deposition techniques. The further an orientation number is from the ratio of intensities scattered by the (110) and the (001) planes for an isotropic powder (orientation number = 2.98), the more oriented the film. For lower orientation numbers, the (001) peak intensity increases and therefore the (001) crystal plane is preferentially oriented with respect to the substrate. For higher orientation numbers, the (110) peak increases, indicating that the (100) and (010) planes are preferentially oriented with respect to the substrate.
As previously mentioned, powder XRD scans show slight preferential orientation likely due to morphology influencing packing [24]. Drop cast films have a measurable degree of orientation compared to an isotropic film. The rod and bulk morphologies show preferential orientation for the (100) and (010) to be parallel to the substrate, which is enhanced by solution shearing and drop casting the particle suspensions. The observed orientation is expected for the rod morphology, as the major surfaces are defined by the (100) and (010) plane and are expected to lay flat with the substrate due to shear alignment forces during convective deposition processes [43]. Furthermore, this result agrees with other convective deposition techniques used to orient rod-like particles [43]. It should be noted the (001) peak was not observed on the diffraction patterns for solution sheared rods. To quantify the orientation, we took the standard deviation of the signal noise as the maximum possible peak value for the (001) (Table 5). As previously mentioned, the bulk material gave a lower aspect ratio, rod-like morphology, which is likely why preferential orientation similar to the higher aspect ratio rods is observed.
The plate morphology shows a modest orientation number with preferential orientation of the (001) plane parallel to the substrate. This corresponds to the major surface of the plate morphology laying on the substrate. The lower degree of orientation for the plates may be explained by the stacking observed in SEM images taken of the plate morphology. In this case, shear alignment forces that orient particles during deposition would be reduced for a lower aspect ratio cluster or a mixture of clusters and plates [43].
It should be noted this result differs from our previous study in that solution shearing enhanced particle orientation compared to drop cast samples. This difference is likely due to the large particle size and high aspect ratios of [Zn2(NDC)2(DABCO)]n (3–10 µm and 7–10, respectively) compared to UiO-66 in our previous study (<1 µm and 1, respectively) [20]. In this case the larger size is not as greatly affected by the flow coating region during shearing or shear alignment forces exerted on large, high aspect ratio particles are comparable for the solution shearing and drop casting processes. However, more work is required to elucidate the importance of particle morphology and fluid forces on orientation.

4. Conclusions

The anisotropic MOF [Zn2(NDC)2(DABCO)]n in the [M2(NDC)2(DABCO)]n (M = metal) family can be modulated in a similar fashion to other metal analogs. Modulation yielded high aspect ratio crystals with different pore apertures on the major surface of a given morphology. Additionally, the modulation of the [Zn2(NDC)2(DABCO)]n MOF produced larger single crystals than other MOFs in this family, thereby indicating modulators may be used to control crystal size while maintaining morphology within a MOF family. XRD and BET characterization showed modulation had little effect on the crystallinity and microporosity of the resulting materials. Furthermore, it was demonstrated [Zn2(NDC)2(DABCO)]n has a moderate equilibrium selectivity of around 4 for all morphologies, which is comparable to other MOFs. Kinetic selectivity experiments showed the diffusion of CH4 into the framework as measured by a diffusion time constant was much faster than CO2. We hypothesize this may be due to other interactions controlling the CO2 diffusion as the diffusion constant did not change appreciably between different morphologies (i.e., pore apertures). We further hypothesized the pore aperture defined by the carboxylate-amine frame may be larger, as it allows for faster diffusion of CH4. Finally, oriented films were fabricated using a convective deposition technique termed solution shearing, which can be used for creating high performance selective membranes of oriented thin film MOFs.

Supplementary Materials

The following are available online at https://www.mdpi.com/2073-4352/9/1/20/s1, Figure S1: Representative nitrogen isotherms for varied morphologies of [Zn2(NDC)2(DABCO)]n, Figure S2: PXRD patterns for MOF material pre and post-competitive gas adsorption procedure showing peak broadening for all samples, indicating sample degradation, Figure S3: PXRD patterns for powder, drop cast and solution sheared MOFs. XRDs were taken with the same XRD geometry reported in the main text, with no revolution during the scans. Additionally, these XRDs were taken parallel to the shearing direction of the material. (a) are the bulk material XRDs, while (b) and (c) are the rod and plate morphologies’ XRDs, respectively, Table S1: BET Surface Areas and standard error of [Zn2(NDC)2(DABCO)]n with differing drying procedures, Table S2: Equilibrium adsorption quantities in competitive adsorption environment, Table S3: Diffusion time constant data for CO2 and CH4 at 700 mmHg and 273 K for multiple trials.

Author Contributions

Conceptualization, L.H., K.S.W. and G.G.; Formal analysis, L.H. and K.S.W.; Funding acquisition, G.G.; Investigation, L.H., K.S.W., Y.G., S.M. and S.J.; Methodology, L.H., K.S.W., Y.G., S.M., S.J., W.S.E. and G.G.; Project administration, G.G.; Supervision, W.S.E. and G.G.; Validation, L.H., K.S.W., Y.G., S.M. and S.J.; Visualization, L.H. and K.S.W.; Writing—original draft, L.H. and K.S.W.; Writing—review & editing, L.H., K.S.W., W.S.E. and G.G.

Funding

This research received funding through a Harrison Grant provided through the Office for Undergraduate Research at the University of Virginia, the University of Virginia Center for Global Inquiry and Innovation, the Virginia Space Grant Consortium, and the Thomas F. and Kate Miller Jeffress Memorial Trust, Bank of America, Trustee.

Acknowledgments

The authors would like to acknowledge Arian Ghorbanpour for his initial work in the study.

Conflicts of Interest

The authors declare no conflict of interest.

References

  1. Sholl, D.S.; Lively, R.P. Seven chemical separations to change the world. Nature 2016, 532, 435–437. [Google Scholar] [CrossRef] [PubMed] [Green Version]
  2. Kertik, A.; Wee, L.H.; Pfannmöller, M.; Bals, S.; Martens, J.A.; Vankelecom, I.F.J. Highly selective gas separation membrane using in situ amorphised metal-organic frameworks. Energy Environ. Sci. 2017, 10, 2342–2351. [Google Scholar] [CrossRef]
  3. Suleman, M.S.; Lau, K.K.; Yeong, Y.F. Plasticization and Swelling in Polymeric Membranes in CO2 Removal from Natural Gas. Chem. Eng. Technol. 2016, 39, 1604–1616. [Google Scholar] [CrossRef]
  4. Rangnekar, N.; Mittal, N.; Elyassi, B.; Caro, J.; Tsapatsis, M. Zeolite membranes—A review and comparison with MOFs. Chem. Soc. Rev. 2015, 44, 7128–7154. [Google Scholar] [CrossRef] [PubMed]
  5. Li, J.R.; Kuppler, R.J.; Zhou, H.C. Selective gas adsorption and separation in metal-organic frameworks. Chem. Soc. Rev. 2009, 38, 1477–1504. [Google Scholar] [CrossRef] [PubMed]
  6. Yuan, S.; Feng, L.; Wang, K.; Pang, J.; Bosch, M.; Lollar, C.; Sun, Y.; Qin, J.; Yang, X.; Zhang, P.; et al. Stable Metal-Organic Frameworks: Design, Synthesis, and Applications. Adv. Mater. 2018, 30, 1704303. [Google Scholar] [CrossRef] [PubMed]
  7. Wang, H.; Zhu, Q.-L.; Zou, R.; Xu, Q. Metal-Organic Frameworks for Energy Applications. Chem 2017, 2, 52–80. [Google Scholar] [CrossRef]
  8. Al Haydar, M.; Abid, H.R.; Sunderland, B.; Wang, S. Metal organic frameworks as a drug delivery system for flurbiprofen. Drug Des. Dev. Ther. 2017, 11, 2685–2695. [Google Scholar] [CrossRef] [Green Version]
  9. Worrall, S.D.; Bissett, M.A.; Hirunpinyopas, W.; Attfield, M.P.; Dryfe, R.A.W. Facile fabrication of metal–organic framework HKUST-1-based rewritable data storage devices. J. Mater. Chem. C 2016, 4, 8687–8695. [Google Scholar] [CrossRef] [Green Version]
  10. Farha, O.K.; Eryazici, I.; Jeong, N.C.; Hauser, B.G.; Wilmer, C.E.; Sarjeant, A.A.; Snurr, R.Q.; Nguyen, S.T.; Yazaydın, A.Ö.; Hupp, J.T. Metal–Organic Framework Materials with Ultrahigh Surface Areas: Is the Sky the Limit? J. Am. Chem. Soc. 2012, 134, 15016–15021. [Google Scholar] [CrossRef]
  11. Gangu, K.K.; Maddila, S.; Mukkamala, S.B.; Jonnalagadda, S.B. A review on contemporary Metal-Organic Framework materials. Inorg. Chim. Acta 2016, 446, 61–74. [Google Scholar] [CrossRef]
  12. Bétard, A.; Bux, H.; Henke, S.; Zacher, D.; Caro, J.; Fischer, R.A. Fabrication of a CO2-selective membrane by stepwise liquid-phase deposition of an alkylether functionalized pillared-layered metal-organic framework [Cu2L2P]n on a macroporous support. Microporous Mesoporous Mater. 2012, 150, 76–82. [Google Scholar] [CrossRef]
  13. Ismail, A.F.; Khulbe, K.C.; Matsuura, T. Gas Separation Membrane Materials and Structures. In Gas Separation Membranes: Polymeric and Inorganic; Springer: Cham, Switzerland, 2015. [Google Scholar] [CrossRef]
  14. Hu, Z.; Castano, I.; Wang, S.; Wang, Y.; Peng, Y.; Qian, Y.; Chi, C.; Wang, X.; Zhao, D. Modulator Effects on the Water-Based Synthesis of Zr/Hf Metal–Organic Frameworks: Quantitative Relationship Studies between Modulator, Synthetic Condition, and Performance. Cryst. Growth Des. 2016, 16, 2295–2301. [Google Scholar] [CrossRef]
  15. Sakata, Y.; Furukawa, S.; Kim, C.; Kitagawa, S. Formation of Nanocrystals of a Zinc Pillared-layer Porous Coordination Polymer Using Microwave-assisted Coordination Modulation. Chem. Lett. 2012, 41, 1436–1438. [Google Scholar] [CrossRef] [Green Version]
  16. Tsuruoka, T.; Furukawa, S.; Takashima, Y.; Yoshida, K.; Isoda, S.; Kitagawa, S. Nanoporous Nanorods Fabricated by Coordination Modulation and Oriented Attachment Growth. Angew. Chem. Int. Ed. 2009, 48, 4739–4743. [Google Scholar] [CrossRef] [PubMed]
  17. Masoomi, M.Y.; Beheshti, S.; Morsali, A. Shape Control of Zn (II) Metal-Organic Frameworks by Modulation Synthesis and Their Morphology-Dependent Catalytic Performance. Cryst. Growth Des. 2015, 15, 2533–2538. [Google Scholar] [CrossRef]
  18. Pham, M.-H.; Vuong, G.-T.; Fontaine, F.-G.; Do, T.-O. Rational Synthesis of Metal-Organic Framework Nanocubes and Nanosheets Using Selective Modulators and Their Morphology-Dependent Gas-Sorption Properties. Cryst. Growth Des. 2012, 12, 3091–3095. [Google Scholar] [CrossRef]
  19. Shete, M.; Kumar, P.; Bachman, J.E.; Ma, X.; Smith, Z.P.; Xu, W.; Mkhoyan, K.A.; Long, J.R.; Tsapatsis, M. On the direct synthesis of Cu (BDC) MOF nanosheets and their performance in mixed matrix membranes. J. Memb. Sci. 2018, 549, 312–320. [Google Scholar] [CrossRef]
  20. Ghorbanpour, A.; Huelsenbeck, L.D.; Smilgies, D.-M.; Giri, G. Oriented UiO-66 thin films through solution shearing. Cryst. Eng. Comm. 2018, 20, 294–300. [Google Scholar] [CrossRef]
  21. Selyanchyn, R.; Fujikawa, S. Membrane thinning for efficient CO2 capture. Sci. Technol. Adv. Mater. 2017, 18, 816–827. [Google Scholar] [CrossRef]
  22. Gu, Y.; Epling, W.S. Passive NOx Adsorber: An Overview of Catalyst Performance and Reaction Chemistry. Appl. Catal. A Gen. 2018. [Google Scholar] [CrossRef]
  23. Wang, Z.L.; Mohamed, M.B.; Link, S.; El-Sayed, M.A. Crystallographic facets and shapes of gold nanorods of different aspect ratios. Surf. Sci. 1999, 440, L809–L814. [Google Scholar] [CrossRef]
  24. Furukawa, S.; Hirai, K.; Nakagawa, K.; Takashima, Y.; Matsuda, R.; Tsuruoka, T.; Kondo, M.; Haruki, R.; Tanaka, D.; Sakamoto, H.; et al. Heterogeneously Hybridized Porous Coordination Polymer Crystals: Fabrication of Heterometallic Core-Shell Single Crystals with an In-Plane Rotational Epitaxial Relationship. Angew. Chem. Int. Ed. 2009, 48, 1766–1770. [Google Scholar] [CrossRef]
  25. Chun, H.; Dybtsev, D.N.; Kim, H.; Kim, K. Synthesis, X-ray Crystal Structures, and Gas Sorption Properties of Pillared Square Grid Nets Based on Paddle-Wheel Motifs: Implications for Hydrogen Storage in Porous Materials. Chem. A Eur. J. 2005, 11, 3521–3529. [Google Scholar] [CrossRef] [PubMed]
  26. Phan, A.; Doonan, C.J.; Uribe-Romo, F.J.; Knobler, C.B.; Okeeffe, M.; Yaghi, O.M. Synthesis, structure, and carbon dioxide capture properties of zeolitic imidazolate frameworks. Acc. Chem. Res. 2010, 43, 58–67. [Google Scholar] [CrossRef]
  27. Lin, Y.; Kong, C.; Chen, L. Direct synthesis of amine-functionalized MIL-101 (Cr) nanoparticles and application for CO2 capture. RSC Adv. 2012, 2, 6417–6419. [Google Scholar] [CrossRef]
  28. Saha, D.; Bao, Z.; Jia, F.; Deng, S. Adsorption of CO2, CH4, N2O, and N2 on MOF-5, MOF-177 and zeolite 5A. Environ. Sci. Technol. 2010, 44, 1820–1826. [Google Scholar] [CrossRef] [PubMed]
  29. Graham, C.; Imrie, D.A.; Raab, R.E. Measurement of the electric quadrupole moments of CO2, CO, N2, Cl2 and BF3. Mol. Phys. Int. J. Interface Chem. Phys. 1998, 1, 49–56. [Google Scholar] [CrossRef]
  30. Jiang, Z.R.; Wang, H.; Hu, Y.; Lu, J.; Jiang, H.L. Polar Group and Defect Engineering in a Metal-Organic Framework: Synergistic Promotion of Carbon Dioxide Sorption and Conversion. Chem. Sustain. Energy Mater. 2015, 8, 878–885. [Google Scholar] [CrossRef]
  31. Heinke, L.; Gu, Z.; Wöll, C. The surface barrier phenomenon at the loading of metal-organic frameworks. Nat. Commun. 2014, 5, 4562. [Google Scholar] [CrossRef] [Green Version]
  32. Bao, Z.; Alnemrat, S.; Yu, L.; Vasiliev, I.; Ren, Q.; Lu, X.; Deng, S. Kinetic separation of carbon dioxide and methane on a copper metal-organic framework. J. Colloid Interface Sci. 2011, 2, 504–509. [Google Scholar] [CrossRef] [PubMed]
  33. Ruthven, D.M. Principles of Adsorption and Adsorption Processes; Wiley: New York, NY, USA, 1984; ISBN 0471866067. [Google Scholar]
  34. Bao, Z.; Yu, L.; Ren, Q.; Lu, X.; Deng, S. Adsorption of CO2 and CH4 on a magnesium-based metal organic framework. J. Colloid Interface Sci. 2011, 2, 549–556. [Google Scholar] [CrossRef] [PubMed]
  35. Karra, J.R.; Walton, K.S. Molecular simulations and experimental studies of CO2, CO, and N2 adsorption in metal-organic frameworks. J. Phys. Chem. C 2010, 114, 15735–15740. [Google Scholar] [CrossRef]
  36. Cmarik, G.E.; Kim, M.; Cohen, S.M.; Walton, K.S. Tuning the adsorption properties of UiO-66 via ligand functionalization. Langmuir 2012, 28, 15606–15613. [Google Scholar] [CrossRef] [PubMed]
  37. Schneider, D.; Mehlhorn, D.; Zeigermann, P.; Kärger, J.; Valiullin, R. Transport properties of hierarchical micro-mesoporous materials. Chem. Soc. Rev. 2016, 12, 3439–3467. [Google Scholar] [CrossRef] [PubMed]
  38. Caro, J.; Noack, M. Zeolite membranes-Recent developments and progress. Microporous Mesoporous Mater. 2008, 3, 215–333. [Google Scholar] [CrossRef]
  39. Lai, Z.; Bonilla, G.; Diaz, I.; Nery, J.G.; Sujaoti, K.; Amat, M.A.; Kokkoli, E.; Terasaki, O.; Thompson, R.W.; Tsapatsis, M.; et al. Microstructural optimization of a zeolite membrane for organic vapor separation. Science 2003, 300, 456–460. [Google Scholar] [CrossRef]
  40. Giri, G.; Li, R.; Smilgies, D.M.; Li, E.Q.; Diao, Y.; Lenn, K.M.; Chiu, M.; Lin, D.W.; Allen, R.; Reinspach, J.; et al. One-dimensional self-confinement promotes polymorph selection in large-area organic semiconductor thin films. Nat. Commun. 2014, 5, 3573. [Google Scholar] [CrossRef] [Green Version]
  41. Guthrie, S.M.; Smilgies, D.M.; Giri, G. Controlling Polymorphism in Pharmaceutical Compounds Using Solution Shearing. Cryst. Growth Des. 2018, 18, 602–606. [Google Scholar] [CrossRef]
  42. Scardi, P.; Leoni, M. Diffraction line profiles from polydisperse crystalline systems. Acta Crystallogr. Sect. A Found. Crystallogr. 2001, 57, 604–613. [Google Scholar] [CrossRef] [Green Version]
  43. Lin, Z. Evaporative Self-Assembly of Ordered Complex Structures. Evaporative Self-Assembly Ordered Complex Struct; World Scientific Publishing Company, Inc.: Singapore, 2012. [Google Scholar] [CrossRef]
Crystals 09 00020 g001 550
Figure 1. Schematic of the modulation process for the [Zn2(NDC)2(DABCO)]n MOF. Acetic acid (red pyramids) competitively coordinates with 1,4-naphthalene dicarboxylate (red rods) to direct growth in the [001] direction, while pyridine (blue pyramids) competitively coordinates with DABCO (blue spheres) to direct growth in the [100] and [010] direction.
Figure 1. Schematic of the modulation process for the [Zn2(NDC)2(DABCO)]n MOF. Acetic acid (red pyramids) competitively coordinates with 1,4-naphthalene dicarboxylate (red rods) to direct growth in the [001] direction, while pyridine (blue pyramids) competitively coordinates with DABCO (blue spheres) to direct growth in the [100] and [010] direction.
Crystals 09 00020 g001
Crystals 09 00020 g002 550
Figure 2. SEM image of [Zn2(NDC)2(DABCO)] (a) unmodulated resulting in bulk morphology (b) 1.6 M acetic acid as a modulator resulting in rod morphology and (c) 1.6 M pyridine as a modulator resulting in plate morphology. Scale bars are 5 µm.
Figure 2. SEM image of [Zn2(NDC)2(DABCO)] (a) unmodulated resulting in bulk morphology (b) 1.6 M acetic acid as a modulator resulting in rod morphology and (c) 1.6 M pyridine as a modulator resulting in plate morphology. Scale bars are 5 µm.
Crystals 09 00020 g002
Crystals 09 00020 g003 550
Figure 3. Powder XRD Data for synthesized [Zn2(NDC)2(DABCO)]n MOFs. Simulated XRD patterns were obtained from Furukawa et al. [24].
Figure 3. Powder XRD Data for synthesized [Zn2(NDC)2(DABCO)]n MOFs. Simulated XRD patterns were obtained from Furukawa et al. [24].
Crystals 09 00020 g003
Crystals 09 00020 g004 550
Figure 4. Adsorption isotherms for bulk, plate and rod morphologies of [Zn2(NDC)2(DABCO)]n at 273 K for (a) CO2 and (b) CH4.
Figure 4. Adsorption isotherms for bulk, plate and rod morphologies of [Zn2(NDC)2(DABCO)]n at 273 K for (a) CO2 and (b) CH4.
Crystals 09 00020 g004
Crystals 09 00020 g005 550
Figure 5. Fractional uptake versus time for the bulk morphology of [Zn2(NDC)2(DABCO)]n at 273 K for CO2 and CH4.
Figure 5. Fractional uptake versus time for the bulk morphology of [Zn2(NDC)2(DABCO)]n at 273 K for CO2 and CH4.
Crystals 09 00020 g005
Table
Table 1. Minor axis, major axis, and aspect ratio measurements for different morphologies of [Zn2(NDC)2(DABCO)]n.
Table 1. Minor axis, major axis, and aspect ratio measurements for different morphologies of [Zn2(NDC)2(DABCO)]n.
MorphologyMinor Axis (µm)Major Axis (µm)Aspect RatioMajor Surface Plane(s)
Bulk0.3 ± 0.10.6 ± 0.32.1 ± 1.1N/A
Rod1.2 ± 0.510.5 ± 5.410.1 ± 5.3(100), (010)
Plate0.4 ± 0.12.7 ± 0.46.9 ± 2.5(001)
Table
Table 2. BET surface areas and standard error calculated from nitrogen isotherms at 77 K for three (3) samples of the bulk morphology and four (4) samples of the plate-like and rod-like morphologies of [Zn2(NDC)2(DABCO)]n and a reference value.
Table 2. BET surface areas and standard error calculated from nitrogen isotherms at 77 K for three (3) samples of the bulk morphology and four (4) samples of the plate-like and rod-like morphologies of [Zn2(NDC)2(DABCO)]n and a reference value.
MorphologyBET Surface Area (m2/g)
Zn2(NDC)2(DABCO) Bulk [25]1000
Bulk1226 ± 16
Rod1100 ± 68
Plate946 ± 127
Table
Table 3. Langmuir isotherm fitting parameters (am and b), Henry’s constant (K) and CO2/CH4 selectivity for different morphologies of [Zn2(NDC)2(DABCO)]n.
Table 3. Langmuir isotherm fitting parameters (am and b), Henry’s constant (K) and CO2/CH4 selectivity for different morphologies of [Zn2(NDC)2(DABCO)]n.
MorphologyAdsorbateam (mmol/g)b (kPa−1)K (mmol/g kPa)CO2/CH4 Selectivity, α
BulkCO212.780.00660.08423.85
CH49.380.00230.0219
RodCO210.350.00690.07164.46
CH45.260.00310.0161
PlateCO210.210.00700.07194.26
CH46.160.00270.0169
Table
Table 4. Diffusion time constants from fitting Equation (2) to kinetic adsorption data of CO2 and CH4 and kinetic selectivity for varied morphologies. Individual trial data can be found in supplemental materials (Table S3).
Table 4. Diffusion time constants from fitting Equation (2) to kinetic adsorption data of CO2 and CH4 and kinetic selectivity for varied morphologies. Individual trial data can be found in supplemental materials (Table S3).
MorphologyCO2 Dc/rc(s−1) × 10−3CH4 Dc/rc(s−1) × 10−3CO2/CH4 Kinetic Selectivity
Bulk1.57 ± 0.075.24 ± 0.440.300 ± 0.028
Rod1.73 ± 0.138.75 ± 0.740.197 ± 0.022
Plate1.88 ± 0.154.72 ± 0.270.399 ± 0.039
Table
Table 5. Orientation number for different morphologies for different film deposition techniques, where orientation number is the ratio of (110)/(001) peak intensities for each XRD. An orientation number of 2.98 represents a uniformly isotropic powder. PXRD patterns of sheared samples can be found in supplemental materials (Figure S3).
Table 5. Orientation number for different morphologies for different film deposition techniques, where orientation number is the ratio of (110)/(001) peak intensities for each XRD. An orientation number of 2.98 represents a uniformly isotropic powder. PXRD patterns of sheared samples can be found in supplemental materials (Figure S3).
MorphologyIsotropic PowderPowderDropcastSolution Sheared at 0.25 mm/s
Bulk2.984.114.054.67
Rod2.987.7540.6343.50
Plate2.982.191.111.23

Share and Cite

MDPI and ACS Style

Huelsenbeck, L.; Westendorff, K.S.; Gu, Y.; Marino, S.; Jung, S.; Epling, W.S.; Giri, G. Modulating and Orienting an Anisotropic Zn-Based Metal Organic Framework for Selective CH4/CO2 Gas Separation. Crystals 2019, 9, 20. https://doi.org/10.3390/cryst9010020

AMA Style

Huelsenbeck L, Westendorff KS, Gu Y, Marino S, Jung S, Epling WS, Giri G. Modulating and Orienting an Anisotropic Zn-Based Metal Organic Framework for Selective CH4/CO2 Gas Separation. Crystals. 2019; 9(1):20. https://doi.org/10.3390/cryst9010020

Chicago/Turabian Style

Huelsenbeck, Luke, Karl S. Westendorff, Yuntao Gu, Silvia Marino, Sangeun Jung, William S. Epling, and Gaurav Giri. 2019. "Modulating and Orienting an Anisotropic Zn-Based Metal Organic Framework for Selective CH4/CO2 Gas Separation" Crystals 9, no. 1: 20. https://doi.org/10.3390/cryst9010020

APA Style

Huelsenbeck, L., Westendorff, K. S., Gu, Y., Marino, S., Jung, S., Epling, W. S., & Giri, G. (2019). Modulating and Orienting an Anisotropic Zn-Based Metal Organic Framework for Selective CH4/CO2 Gas Separation. Crystals, 9(1), 20. https://doi.org/10.3390/cryst9010020

Note that from the first issue of 2016, this journal uses article numbers instead of page numbers. See further details here.

Article Metrics

Back to TopTop