Intermolecular Interactions in Molecular Organic Crystals upon Relaxation of Lattice Parameters
Abstract
:1. Introduction
2. Materials and Methods
3. Results
3.1. Calculated Lattice Energies for the X23 Benchmark Set
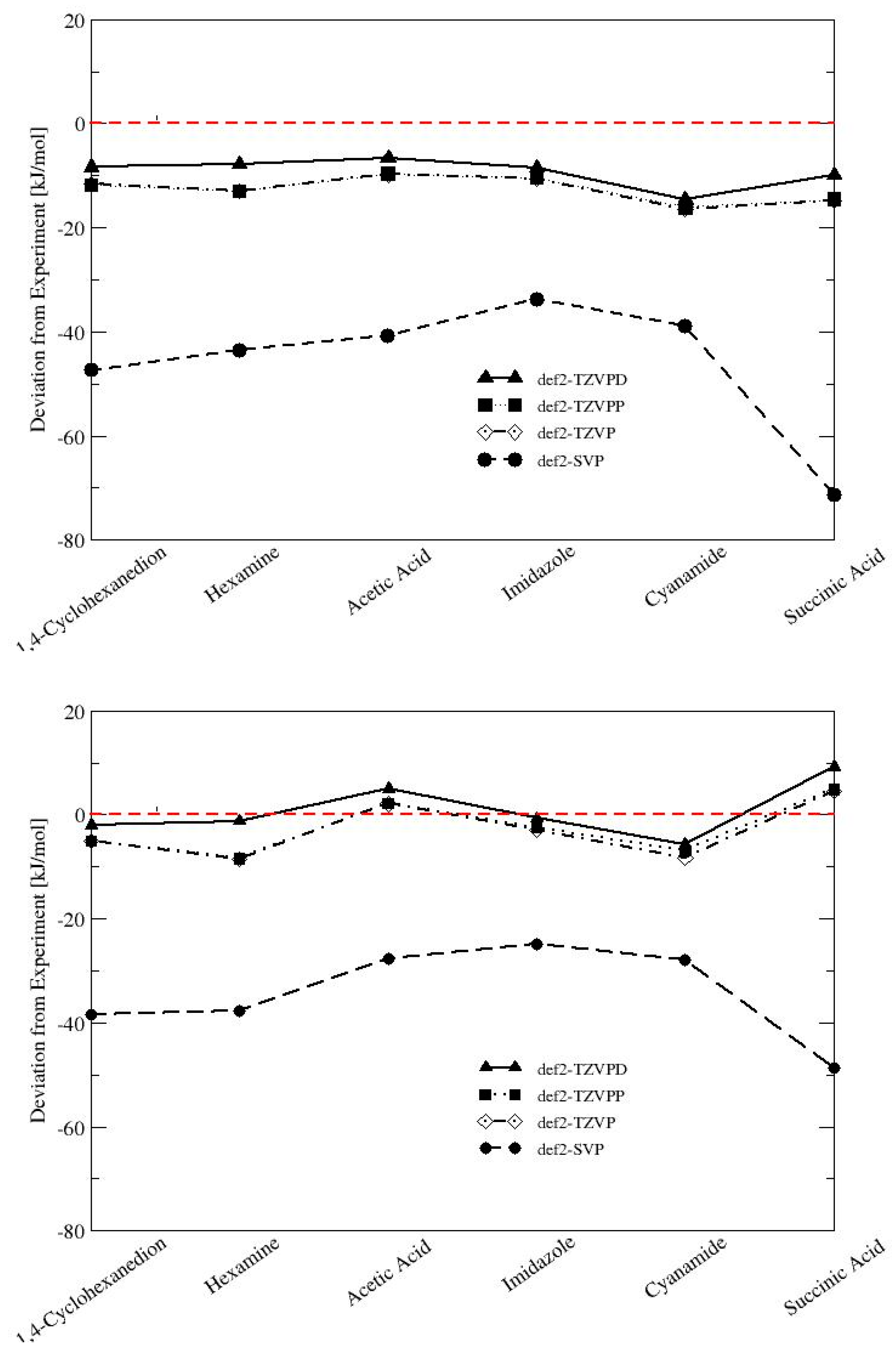
3.2. Convergence of Lattice Energies with Basis Set
3.3. Optimization of Unit Cell Parameters
3.3.1. Changes of Unit Cell Volumes and Lattice Parameters
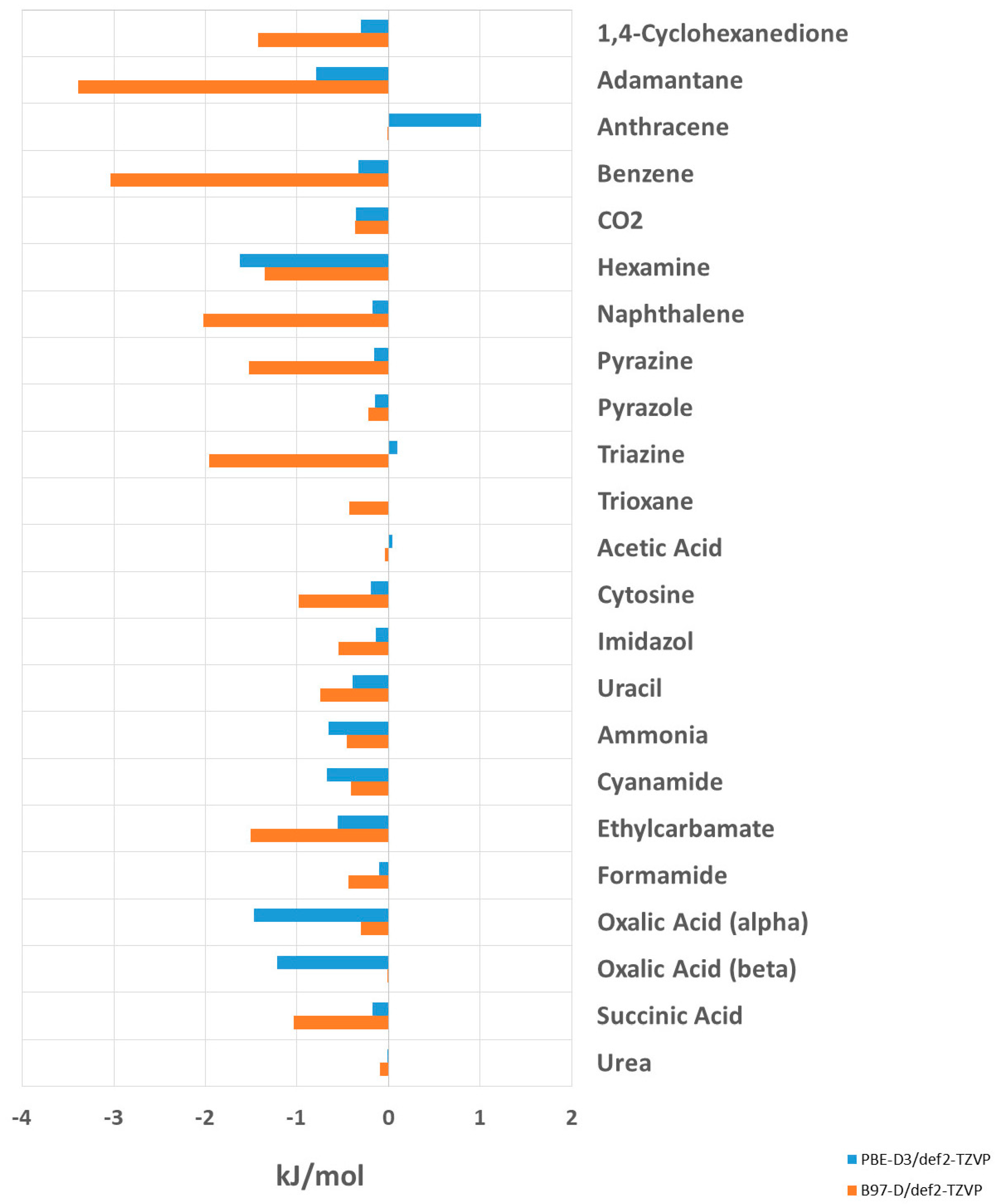
3.3.2. Lattice Energies after Unit Cell Optimization
4. Conclusions
Supplementary Materials
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Food and Drug Administration. FDA’s policy statement for the development of new stereoisomeric drugs. Chirality 1992, 4, 338–340. [Google Scholar] [CrossRef] [PubMed]
- De Camp, W.H. Chiral drugs: The FDA perspective on manufacturing and control. J. Pharm. Biomed. Anal. 1993, 11, 1167–1172. [Google Scholar] [CrossRef]
- Brooks, W.H.; Guida, W.C.; Daniel, K.G. The significance of chirality in drug design and development. Curr. Top. Med. Chem. 2011, 11, 760–770. [Google Scholar] [CrossRef] [PubMed]
- Hylton, R.K.; Tizzard, G.J.; Threlfall, T.L.; Ellis, A.L.; Coles, S.J.; Seaton, C.C.; Schulze, E.; Lorenz, H.; Seidel-Morgenstern, A.; Stein, M.; et al. Are the crystal structures of enantiopure and racemic mandelic acids determined by kinetics or thermodynamics? J. Am. Chem. Soc. 2015, 137, 11095–11104. [Google Scholar] [CrossRef] [Green Version]
- Lorenz, H.; Seidel-Morgenstern, A. Processes to separate enantiomers. Angew. Chem. Int. Ed. 2014, 53, 1218–1250. [Google Scholar] [CrossRef]
- Cruz-Cabeza, A.J.; Reutzel-Edens, S.M.; Bernstein, J. Facts and fictions about polymorphism. Chem. Soc. Rev. 2015, 44, 8619–8635. [Google Scholar] [CrossRef]
- Gavezzotti, A.; Rizzato, S. Are racemic crystals favored over homochiral crystals by higher stability or by kinetics? Insights from comparative studies of crystalline stereoisomers. J. Org. Chem. 2014, 79, 4809–4816. [Google Scholar] [CrossRef]
- Nyman, J.; Day, G.M. Static and lattice vibrational energy differences between polymorphs. CrystEngComm 2015, 17, 5154–5165. [Google Scholar] [CrossRef] [Green Version]
- Buchholz, H.K.; Hylton, R.K.; Brandenburg, J.G.; Seidel-Morgenstern, A.; Lorenz, H.; Stein, M.; Price, S.L. Thermochemistry of racemic and enantiopure organic crystals for predicting enantiomer separation. Cryst. Growth Des. 2017, 17, 4676–4686. [Google Scholar] [CrossRef]
- Beran, G.J.O. Modeling polymorphic molecular crystals with electronic structure theory. Chem. Rev. 2016, 116, 5567–5613. [Google Scholar] [CrossRef]
- Deringer, V.L.; George, J.; Dronskowski, R.; Englert, U. Plane-wave density functional theory meets molecular crystals: Thermal ellipsoids and intermolecular interactions. Acc. Chem. Res. 2017, 50, 1231–1239. [Google Scholar] [CrossRef] [PubMed]
- Stohr, M.; Van Voorhis, T.; Tkatchenko, A. Theory and practice of modeling van der waals interactions in electronic-structure calculations. Chem. Soc. Rev. 2019, 48, 4118–4154. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Hoja, J.; Reilly, A.M.; Tkatchenko, A. First-principles modeling of molecular crystals: Structures and stabilities, temperature and pressure. Wiley Interdiscip. Rev. Comput. Mol. Sci. 2017, 7, e1294. [Google Scholar] [CrossRef]
- Kronik, L.; Tkatchenko, A. Understanding molecular crystals with dispersion-inclusive density functional theory: Pairwise corrections and beyond. Acc. Chem. Res. 2014, 47, 3208–3216. [Google Scholar] [CrossRef]
- Price, S.L. Computational prediction of organic crystal structures and polymorphism. Int. Rev. Phys. Chem. 2008, 27, 541–568. [Google Scholar] [CrossRef]
- Price, S.L. Predicting crystal structures of organic compounds. Chem. Soc. Rev. 2014, 43, 2098–2111. [Google Scholar] [CrossRef] [Green Version]
- Moellmann, J.; Grimme, S. Dft-D3 study of some molecular crystals. J. Phys. Chem. C 2014, 118, 7615–7621. [Google Scholar] [CrossRef]
- Brandenburg, J.G.; Grimme, S. Dispersion corrected Hartree-Fock and density functional theory for organic crystal structure prediction. Top. Curr. Chem. 2014, 345, 1–23. [Google Scholar]
- Otero-de-la-Roza, A.; Johnson, E.R. A benchmark for non-covalent interactions in solids. J. Chem. Phys. 2012, 137, 054103. [Google Scholar] [CrossRef] [Green Version]
- Reilly, A.M.; Tkatchenko, A. Understanding the role of vibrations, exact exchange, and many-body van der waals interactions in the cohesive properties of molecular crystals. J. Chem. Phys. 2013, 139, 024705. [Google Scholar] [CrossRef] [Green Version]
- Dovesi, R.; Orlando, R.; Erba, A.; Zicovich-Wilson, C.M.; Civalleri, B.; Casassa, S.; Maschio, L.; Ferrabone, M.; De La Pierre, M.; D’Arco, P.; et al. Crystal14: A program for the ab initio investigation of crystalline solids. Int. J. Quantum Chem. 2014, 114, 1287–1317. [Google Scholar] [CrossRef]
- Kudin, K.N.; Scuseria, G.E. Linear-scaling density-functional theory with gaussian orbitals and periodic boundary conditions: Efficient evaluation of energy and forces via the fast multipole method. Phys. Rev. B 2000, 61, 16440–16453. [Google Scholar] [CrossRef] [Green Version]
- Buchholz, H.K.; Stein, M. Accurate lattice energies of organic molecular crystals from periodic Turbomole calculations. J. Comput. Chem. 2018, 39, 1335–1343. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Perdew, J.P.; Burke, K.; Ernzerhof, M. Generalized gradient approximation made simple. Phys. Rev. Lett. 1996, 77, 3865–3868. [Google Scholar] [CrossRef] [Green Version]
- Perdew, J.P.; Wang, Y. Accurate and simple analytic representation of the electron-gas correlation energy. Phys. Rev. B 1992, 45, 13244–13249. [Google Scholar] [CrossRef]
- Grimme, S.; Antony, J.; Ehrlich, S.; Krieg, H. A consistent and accurate ab initio parametrization of density functional dispersion correction (DFT-D) for the 94 elements H-Pu. J. Chem. Phys. 2010, 132, 154104. [Google Scholar] [CrossRef] [Green Version]
- Grimme, S. Semiempirical GGA-type density functional constructed with a long-range dispersion correction. J. Comput. Chem. 2006, 27, 1787–1799. [Google Scholar] [CrossRef]
- Becke, A.D. Density-functional thermochemistry. V. Systematic optimization of exchange-correlation functionals. J. Chem. Phys. 1997, 107, 8554–8560. [Google Scholar] [CrossRef]
- Antony, J.; Grimme, S. Density functional theory including dispersion corrections for intermolecular interactions in a large benchmark set of biologically relevant molecules. Phys. Chem. Chem. Phys. 2006, 8, 5287–5293. [Google Scholar] [CrossRef]
- Mardirossian, N.; Head-Gordon, M. Thirty years of density functional theory in computational chemistry: An overview and extensive assessment of 200 density functionals. Mol. Phys. 2017, 115, 2315–2372. [Google Scholar] [CrossRef]
- Raiteri, P.; Martoňák, R.; Parrinello, M. Exploring polymorphism: The case of benzene. Angew. Chem. Int. Ed. 2005, 44, 3769–3773. [Google Scholar] [CrossRef]
- Reilly, A.M.; Cooper, R.I.; Adjiman, C.S.; Bhattacharya, S.; Boese, A.D.; Brandenburg, J.G.; Bygrave, P.J.; Bylsma, R.; Campbell, J.E.; Car, R.; et al. Report on the sixth blind test of organic crystal structure prediction methods. Acta Crystallogr. Sect. B 2016, 72, 439–459. [Google Scholar] [CrossRef]
- Nyman, J.; Day, G.M. Modelling temperature-dependent properties of polymorphic organic molecular crystals. Phys. Chem. Chem. Phys. 2016, 18, 31132–31143. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Whittleton, S.R.; Otero-de-la-Roza, A.; Johnson, E.R. Exchange-hole dipole dispersion model for accurate energy ranking in molecular crystal structure prediction. J. Chem. Theory Comput. 2017, 13, 441–450. [Google Scholar] [CrossRef]
- Whittleton, S.R.; Otero-de-la-Roza, A.; Johnson, E.R. Exchange-hole dipole dispersion model for accurate energy ranking in molecular crystal structure prediction ii: Nonplanar molecules. J. Chem. Theory Comput. 2017, 13, 5332–5342. [Google Scholar] [CrossRef]
- Price, S.L. Is zeroth order crystal structure prediction (csp_0) coming to maturity? What should we aim for in an ideal crystal structure prediction code? Faraday Discuss. 2018, 211, 9–30. [Google Scholar] [CrossRef] [Green Version]
- Burow, A.M.; Sierka, M. Linear scaling hierarchical integration scheme for the exchange-correlation term in molecular and periodic systems. J. Chem. Theory Comput. 2011, 7, 3097–3104. [Google Scholar] [CrossRef]
- Łazarski, R.; Burow, A.M.; Grajciar, L.; Sierka, M. Density functional theory for molecular and periodic systems using density fitting and continuous fast multipole method: Analytical gradients. J. Comput. Chem. 2016, 37, 2518–2526. [Google Scholar] [CrossRef]
- Becker, M.; Sierka, M. Density functional theory for molecular and periodic systems using density fitting and continuous fast multipole method: Stress tensor. J. Comput. Chem. 2019, 40, 2563–2570. [Google Scholar] [CrossRef]
- Furche, F.; Ahlrichs, R.; Hattig, C.; Klopper, W.; Sierka, M.; Weigend, F. Turbomole. Wiley Interdiscip. Rev. Comput. Mol. Sci. 2014, 4, 91–100. [Google Scholar] [CrossRef]
- Turbomole v7.3. 2018, a Development of University of Karlsruhe and Forschungszentrum Karlsruhe GmbH, 1989–2007, since 2007; Turbomole GmbH: Karlsruhe, Germany, 2017; Available online: http://www.turbomole.com (accessed on 9 December 2019).
- Weigend, F.; Ahlrichs, R. Balanced basis sets of split valence, triple zeta valence and quadruple zeta valence quality for h to rn: Design and assessment of accuracy. Phys. Chem. Chem. Phys. 2005, 7, 3297. [Google Scholar] [CrossRef] [PubMed]
- Eichkorn, K.; Treutler, O.; Ohm, H.; Haser, M.; Ahlrichs, R. Erratum to: Auxiliary basis-sets to approximate coulomb potentials (240, pg 283, 1995). Chem. Phys. Lett. 1995, 242, 652–660. [Google Scholar] [CrossRef]
- Eichkorn, K.; Weigend, F.; Treutler, O.; Ahlrichs, R. Auxiliary basis sets for main row atoms and transition metals and their use to approximate coulomb potentials. Theor. Chem. Acc. 1997, 97, 119–124. [Google Scholar] [CrossRef]
- Łazarski, R.; Burow, A.M.; Sierka, M. Density functional theory for molecular and periodic systems using density fitting and continuous fast multipole methods. J. Chem. Theory Comput. 2015, 11, 3029–3041. [Google Scholar] [CrossRef]
- Grajciar, L. Low-memory iterative density fitting. J. Comput. Chem. 2015, 36, 1521–1535. [Google Scholar] [CrossRef]
- Burow, A.M.; Sierka, M.; Mohamed, F. Resolution of identity approximation for the coulomb term in molecular and periodic systems. J. Chem. Phys. 2009, 131, 214101. [Google Scholar] [CrossRef]
- Thomas, S.P.; Spackman, P.R.; Jayatilaka, D.; Spackman, M.A. Accurate lattice energies for molecular crystals from experimental crystal structures. J. Chem. Theory Comput. 2018, 14, 1614–1623. [Google Scholar] [CrossRef] [Green Version]
- Dolgonos, G.A.; Hoja, J.; Boese, A.D. Revised values for the X23 benchmark set of molecular crystals. Phys. Chem. Chem. Phys. 2019, 21, 24333–24344. [Google Scholar] [CrossRef]
- Boese, A.D. Density functional theory and hydrogen bonds: Are we there yet? ChemPhysChem 2015, 16, 978–985. [Google Scholar] [CrossRef]
- Carter, D.J.; Rohl, A.L. Benchmarking calculated lattice parameters and energies of molecular crystals using van der waals density functionals. J. Chem. Theory Comput. 2014, 10, 3423–3437. [Google Scholar] [CrossRef]
- LeBlanc, L.M.; Weatherby, J.A.; Otero-de-la-Roza, A.; Johnson, E.R. Non-covalent interactions in molecular crystals: Exploring the accuracy of the exchange-hole dipole moment model with local orbitals. J. Chem. Theory Comput. 2018, 14, 5715–5724. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Boese, R.; Niederprüm, N.; Bläser, D.; Maulitz, A.; Antipin, M.Y.; Mallinson, P.R. Single-crystal structure and electron density distribution of ammonia at 160 k on the basis of x-ray diffraction data. J. Phys. Chem. B 1997, 101, 5794–5799. [Google Scholar] [CrossRef]
- Simon, A.; Peters, K. Single-crystal refinement of the structure of carbon dioxide. Acta Crystallogr. Sect. B 1980, 36, 2750–2751. [Google Scholar] [CrossRef] [Green Version]
- Heit, Y.N.; Beran, G.J.O. How important is thermal expansion for predicting molecular crystal structures and thermochemistry at finite temperatures? Acta Crystallogr. Sect. B 2016, 72, 514–529. [Google Scholar] [CrossRef] [Green Version]
- Bučko, T.; Lebègue, S.; Gould, T.; Ángyán, J.G. Many-body dispersion corrections for periodic systems: An efficient reciprocal space implementation. J. Phys. Condens. Matter 2016, 28, 045201. [Google Scholar] [CrossRef]
- Caldeweyher, E.; Bannwarth, C.; Grimme, S. Extension of the D3 dispersion coefficient model. J. Chem. Phys. 2017, 147, 034112. [Google Scholar] [CrossRef]
- Irmler, A.; Burow, A.M.; Pauly, F. Robust periodic fock exchange with atom-centered Gaussian basis sets. J. Chem. Theory Comput. 2018, 14, 4567–4580. [Google Scholar] [CrossRef]
- Otero-de-la-Roza, A.; LeBlanc, L.M.; Johnson, E.R. Dispersion XDM with hybrid functionals: Delocalization error and halogen bonding in molecular crystals. J. Chem. Theory Comput. 2019, 15, 4933–4944. [Google Scholar] [CrossRef]
- Zhang, I.Y.; Grüneis, A. Coupled cluster theory in materials science. Front. Mater. 2019, 6, 123. [Google Scholar] [CrossRef] [Green Version]
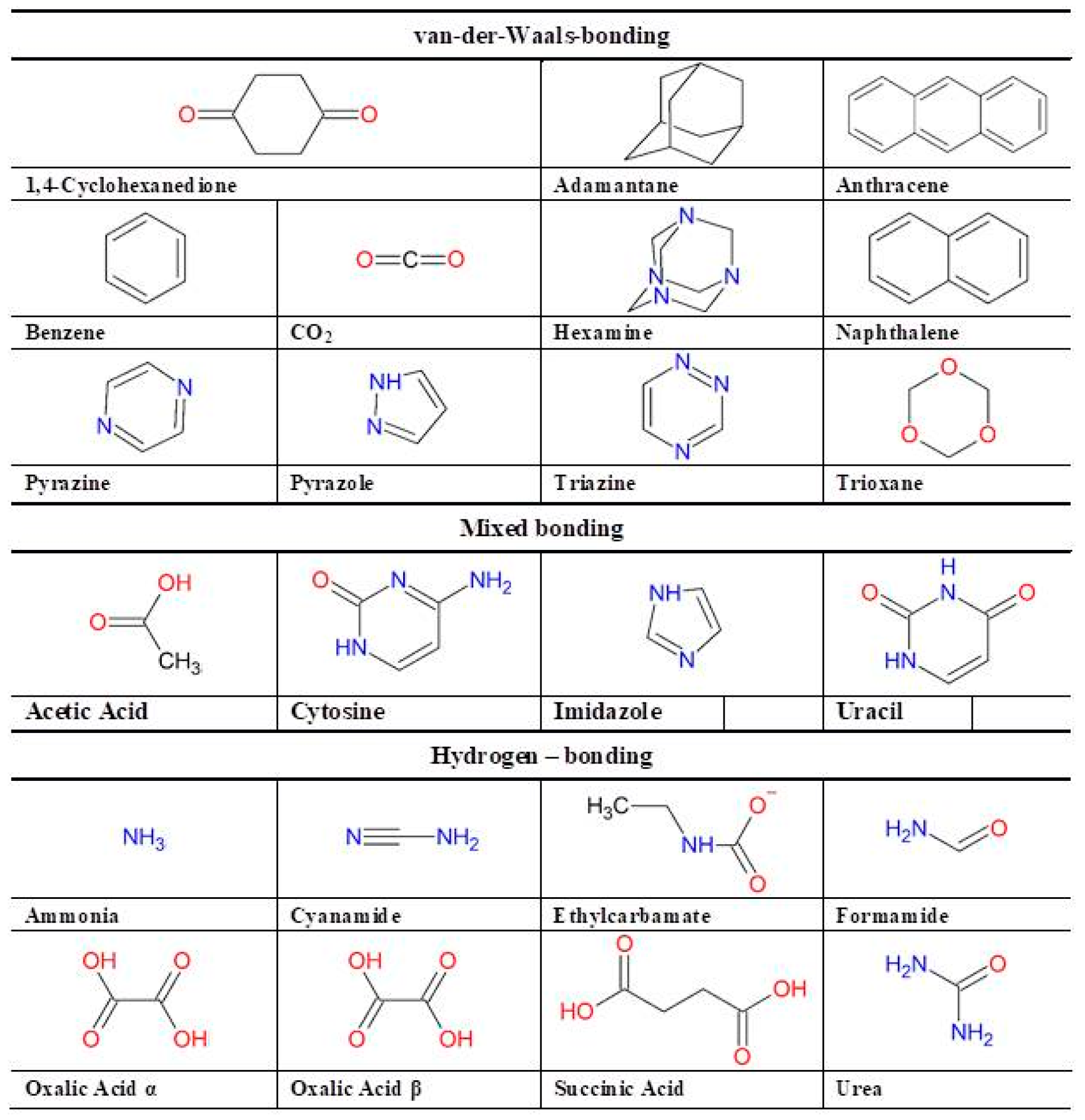



| Compound | Calc. Elatt (kJ/mol) | Exp. (kJ/mol) | Deviation (kJ/mol) | Rel. Deviation (%) |
|---|---|---|---|---|
| 1,4-Cyclohexanedione | −93.55 | −88.6 | −4.95 | 5.59 |
| Adamantane | −74.50 | −69.4 | −5.10 | 7.36 |
| Anthracene | −118.88 | −112.7 | −6.18 | 5.48 |
| Benzene | −59.08 | −55.3 | −3.78 | 6.84 |
| CO2 | −23.04 | −28.4 | 5.36 | 18.86 |
| Hexamine | −94.79 | −86.2 | −8.59 | 9.97 |
| Naphtalene | −87.13 | −83.1 | −4.03 | 4.85 |
| Pyrazine | −66.01 | −61.3 | −4.71 | 7.68 |
| Pyrazole | −81.01 | −77.7 | −3.31 | 4.26 |
| Triazine | −60.70 | −61.7 | 1.00 | 1.62 |
| Trioxane | −63.34 | −66.4 | 3.06 | 4.61 |
| Acetic Acid | −70.75 | −72.8 | 2.05 | 2.82 |
| Cytosine | −159.39 | −162.8 | 3.41 | 2.09 |
| Imidazole | −89.90 | −86.8 | −3.10 | 3.57 |
| Uracil | −132.99 | −135.7 | 2.71 | 2.00 |
| Ammonia | −45.36 | −37.2 | −8.16 | 21.94 |
| Cyanamide | −86.98 | −79.7 | −7.28 | 9.14 |
| Ethylcarbamate | −87.00 | −86.3 | −0.70 | 0.81 |
| Formamide | −79.90 | −79.2 | −0.70 | 0.88 |
| Oxalic Acid (alpha) | −89.50 | −96.3 | 6.80 | 7.06 |
| Oxalic Acid (beta) | −92.03 | −96.1 | 4.07 | 4.24 |
| Succinic Acid | −125.69 | −130.3 | 4.61 | 3.54 |
| Urea | −108.21 | −102.5 | −5.71 | 5.57 |
| Interaction Type | PBE-D3 | B97-D | ||||||
|---|---|---|---|---|---|---|---|---|
| NRMSE (%) | RMSE (kJ/mol) | MSE (kJ/mol) | MAE (kJ/mol) | NRMSE (%) | RMSE (kJ/mol) | MSE (kJ/mol) | MAE (kJ/mol) | |
| vdW | 9.76 | 7.34 | −5.69 | 5.90 | 8.21 | 4.91 | −2.84 | 4.55 |
| Mixed | 10.16 | 9.67 | −9.58 | 9.58 | 2.70 | 2.86 | 1.27 | 2.28 |
| H-bonding | 17.91 | 12.54 | −12.12 | 12.12 | 9.20 | 5.45 | −0.88 | 4.75 |
| total | 13.32 | 9.84 | −8.60 | 8.70 | 7.94 | 4.82 | −1.14 | 4.32 |
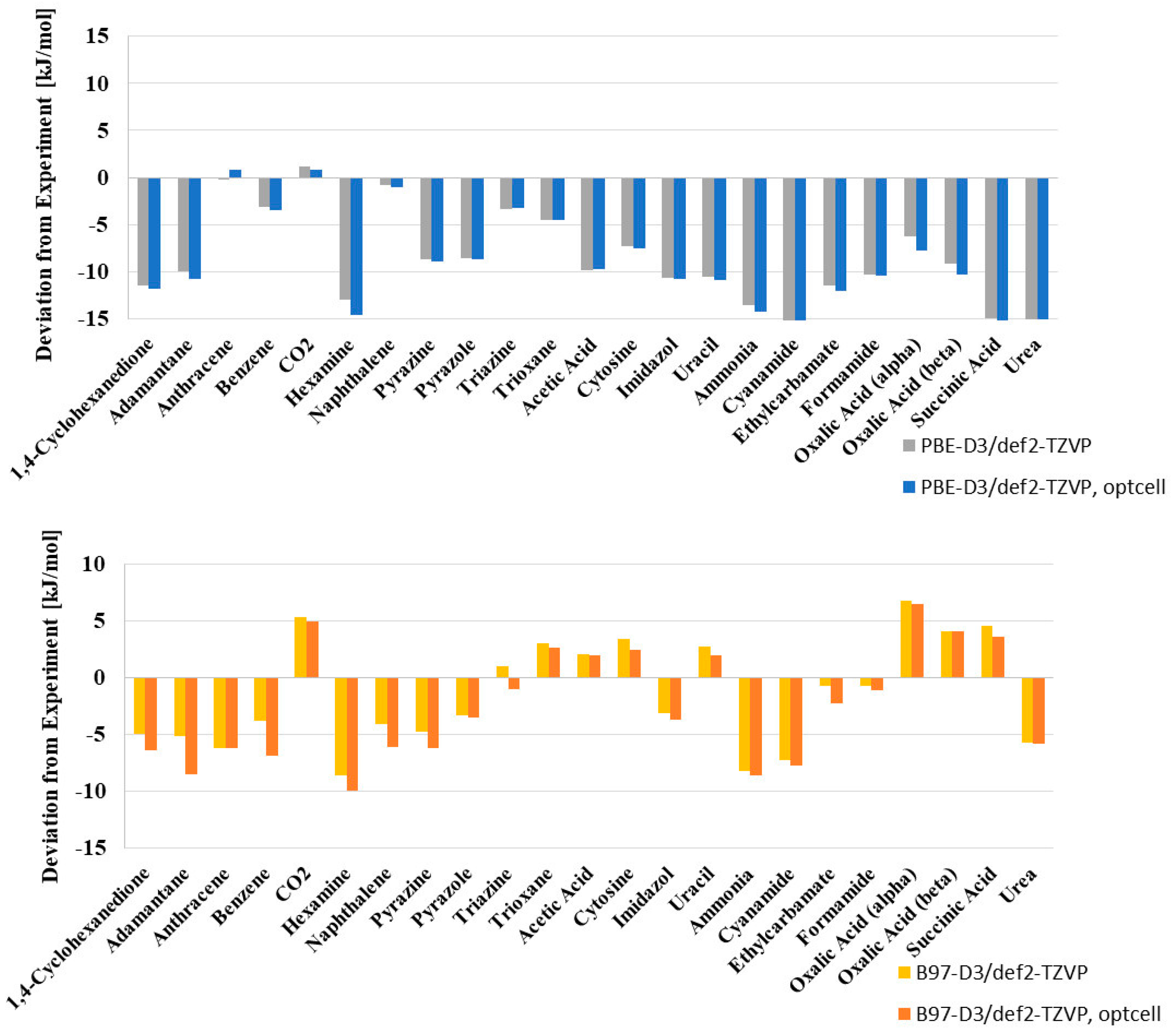
| PBE-D3 | B97-D | |||||
|---|---|---|---|---|---|---|
| Elatt,calc. (kJ/mol) | Δ(Ecalc-exp) (kJ/mol) | Δ(Ecalc-exp) (%) | Elatt,calc. (kJ/mol) | Δ(Ecalc-exp) (kJ/mol) | Δ(Ecalc-exp) (%) | |
| 1,4-Cyclohexanedione | −88.60 | −11.81 | 13.33 | −94.98 | −6.38 | 7.20 |
| Adamantane | −69.40 | −10.72 | 15.44 | −77.90 | −8.50 | 12.25 |
| Anthracene | −112.70 | 0.81 | −0.72 | −118.88 | −6.18 | 5.48 |
| Benzene | −55.30 | −3.44 | 6.22 | −62.12 | −6.82 | 12.33 |
| CO2 | −28.40 | 0.78 | −2.73 | −23.41 | 4.99 | −17.56 |
| Hexamine | −86.20 | −14.61 | 16.95 | −96.14 | −9.94 | 11.54 |
| Naphthalene | −83.10 | −1.02 | 1.23 | −89.15 | −6.05 | 7.28 |
| Pyrazine | −61.30 | −8.86 | 14.45 | −67.53 | −6.23 | 10.16 |
| Pyrazole | −77.70 | −8.73 | 11.23 | −81.24 | −3.54 | 4.55 |
| Triazine | −61.70 | −3.29 | 5.33 | −62.66 | −0.96 | 1.56 |
| Trioxane | −66.40 | −4.49 | 6.76 | −63.76 | 2.64 | −3.97 |
| Acetic Acid | −72.80 | −9.75 | 13.40 | −70.79 | 2.01 | −2.77 |
| Cytosine | −162.80 | −7.54 | 4.63 | −160.37 | 2.43 | −1.49 |
| Imidazole | −86.80 | −10.82 | 12.46 | −90.45 | −3.65 | 4.20 |
| Uracil | −135.70 | −10.89 | 8.02 | −133.74 | 1.96 | −1.45 |
| Ammonia | −37.20 | −14.20 | 38.17 | −45.82 | −8.62 | 23.16 |
| Cyanamide | −79.70 | −16.98 | 21.30 | −87.39 | −7.69 | 9.65 |
| Ethylcarbamate | −86.30 | −12.01 | 13.92 | −88.50 | −2.20 | 2.55 |
| Formamide | −79.20 | −10.37 | 13.09 | −80.33 | −1.13 | 1.43 |
| Oxalic Acid α | −96.30 | −7.77 | 8.07 | −89.80 | 6.50 | −6.75 |
| Oxalic Acid β | −96.10 | −10.31 | 10.73 | −92.04 | 4.06 | −4.23 |
| Succinic Acid | −130.30 | −15.12 | 11.60 | −126.73 | 3.57 | −2.74 |
| Urea | −102.50 | −15.09 | 14.72 | −108.31 | −5.81 | 5.66 |
| PBE-D3 | B97-D | |||||||
|---|---|---|---|---|---|---|---|---|
| NRMSE (%) | RMSE (kJ/mol) | MAE (kJ/mol) | MSE (kJ/mol) | NRMSE (%) | RMSE (kJ/mol) | MSE (kJ/mol) | MAE (kJ/mol) | |
| vdW | 10.27 | 7.79 | 6.23 | −5.94 | 9.63 | 6.16 | −4.27 | 5.66 |
| Mixed | 10.26 | 9.84 | 9.75 | −9.75 | 2.72 | 2.60 | 0.69 | 2.51 |
| H-bonding | 18.73 | 13.06 | 12.73 | −12.73 | 9.62 | 5.53 | −1.41 | 4.95 |
| total | 13.81 | 10.26 | 9.10 | −8.97 | 8.82 | 5.47 | −2.41 | 4.86 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Stein, M.; Heimsaat, M. Intermolecular Interactions in Molecular Organic Crystals upon Relaxation of Lattice Parameters. Crystals 2019, 9, 665. https://doi.org/10.3390/cryst9120665
Stein M, Heimsaat M. Intermolecular Interactions in Molecular Organic Crystals upon Relaxation of Lattice Parameters. Crystals. 2019; 9(12):665. https://doi.org/10.3390/cryst9120665
Chicago/Turabian StyleStein, Matthias, and Madalen Heimsaat. 2019. "Intermolecular Interactions in Molecular Organic Crystals upon Relaxation of Lattice Parameters" Crystals 9, no. 12: 665. https://doi.org/10.3390/cryst9120665
APA StyleStein, M., & Heimsaat, M. (2019). Intermolecular Interactions in Molecular Organic Crystals upon Relaxation of Lattice Parameters. Crystals, 9(12), 665. https://doi.org/10.3390/cryst9120665