The Effect of Pressure on Magnetic Properties of Prussian Blue Analogues

Abstract

We present the review of pressure effect on the crystal structure and magnetic properties of Cr(CN)₆-based Prussian blue analogues (PBs). The lattice volume of the fcc crystal structure space group Fm$\overline{3}$m in the Mn-Cr-CN-PBs linearly decreases for p ≤ 1.7 GPa, the change of lattice size levels off at 3.2 GPa, and above 4.2 GPa an amorphous-like structure appears. The crystal structure recovers after removal of pressure as high as 4.5 GPa. The effect of pressure on magnetic properties follows the non-monotonous pressure dependence of the crystal lattice. The amorphous like structure is accompanied with reduction of the Curie temperature (T_C) to zero and a corresponding collapse of the ferrimagnetic moment at 10 GPa. The cell volume of Ni-Cr-CN-PBs decreases linearly and is isotropic in the range of 0–3.1 GPa. The Raman spectra can indicate a weak linkage isomerisation induced by pressure. The Curie temperature in Mn²⁺-Cr^III-PBs and Cr²⁺-Cr^III-PBs with dominant antiferromagnetic super-exchange interaction increases with pressure in comparison with decrease of T_C in Ni²⁺-Cr^III-PBs and Co²⁺-Cr^III-PBs ferromagnets. T_C increases with increasing pressure for ferrimagnetic systems due to the strengthening of magnetic interaction because pressure, which enlarges the monoelectronic overlap integral S and energy gap ∆ between the mixed molecular orbitals. The reduction of bonding angles between magnetic ions connected by the CN group leads to a small decrease of magnetic coupling. Such a reduction can be expected on both compounds with ferromagnetic and ferrimagnetic ordering. In the second case this effect is masked by the increase of coupling caused by the enlarged overlap between magnetic orbitals. In the case of mixed ferro–ferromagnetic systems, pressure affects μ(T) by a different method in Mn²⁺–N≡C–Cr^III subsystem and Cr^III–C≡N–Ni²⁺ subsystem, and as a consequence T_comp decreases when the pressure is applied. The pressure changes magnetization processes in both systems, but we expect that spontaneous magnetization is not affected in Mn²⁺-Cr^III-PBs, Ni²⁺-Cr^III-PBs, and Co²⁺-Cr^III-PBs. Pressure-induced magnetic hardening is attributed to a change in magneto-crystalline anisotropy induced by pressure. The applied pressure reduces saturated magnetization of Cr²⁺-Cr^III-PBs. The applied pressure p = 0.84 GPa induces high spin–low spin transition of cca 4.5% of high spin Cr²⁺. The pressure effect on magnetic properties of PBs nano powders and core–shell heterostructures follows tendencies known from bulk parent PBs.

1. Introduction

The main interest for reinvestigation of PBs was dominantly driven by the vision of new molecule-based magnetic materials with a temperature of magnetic ordering higher than 300 K and simultaneously very sensitive to external parameters like high pressure or light. Huge versatility in tuning its physical properties using external perturbations-stimuli, confirmed in many papers [1], opened the possibility of applications in various research branches. We will mention several of the most popular topics active at the present time.

A very sound application possibility is connected with the use of Prussian blue, its analogues, and derivatives as electrodes for alkali ion batteries. This application possibility is based on the fact that Prussian blue analogues with large three dimensional networks have large spaces to host large alkali ions, such as Li⁺, Na+, and K+. When applied to rechargeable batteries, its large channels and interstices in the open framework make PB a prominent candidate for cathode materials with long cycle life and fast charge transfer kinetics. Additionally, the easy preparation process and composition variety of PB serves as a good basis for the complex metal oxides employed as catalysts for metal-air batteries [2,3].

As it is generally known that oxygen oxidation eases 142 kJ/g, that means much less energy than the amount obtained from gasoline (47.5 kJ/g). It is thus not surprising that the hydrogen is considered as an alternative to fossil fuel derivatives. The advantage of hydrogen is that it can be produced from water cleavage and its oxidation by-product is water. On the other hand, the classical fossil fuel derivatives release carbon dioxide, which is undoubtedly responsible for global warming and corresponding climate changes. One of the hydrogen storage means is H₂ adsorption in nanoporous solids. The transition metal centres, located at the surface of cavities, are supposed to act as prototype materials for H₂ storage, and PBs belong to this group of materials as well [4,5,6].

A very successful story is related to application of Prussian blue and its derivatives as biosensors, defined as “self-contained integrated devices, which are capable of providing specific quantitative or semi-quantitative analytical information using a biological recognition element (biochemical receptor), which is retained in direct spatial contact with an electrochemical transduction element” [7]. During the last decade, PBs-modified biosensors have been successfully applied to blood, serum, and urine samples [8].

Prussian blue analogues are sensitive to different external physical impulses, such as light and pressure. There are several mechanisms to explain the effect of the pressure on magnetic properties of selected PBs. The first mechanism is connected with the intermetallic charge transfer reported on few PBs transition metal systems, e.g., Co^II _x[Fe^III(CN)₆]_y·zH₂O and its alkali-doped analogues were reported to undergo photo-caused magnetization and thermally-caused demagnetization [9] and pressure-caused structural phase transitions [10]—all of which are the result of an externally driven electron transfer between the Co and Fe sites. PBs are materials, in which one can observe the switching between electronic states within the use of an external stimulus, may be referred to as switchable or tuneable. The switching phenomena reported on selected PBs develop as a result of molecular instability [11]. Magnetic measurements obtained by Mösbauer spectroscopy on the series of Co-Fe PBs have revealed how the presence of an alkali ion in the lattice affects pressure driven electron transfer between Co and Fe [12]. The study of the charge transfer effects, as well as spin and magnetic order induced by high hydrostatic pressure, which was applied to the two bimetallic multifunctional PBs, K_0.1Co₄[Fe(CN)₆]_2.7·18H₂O and K_0.5Mn₃[Fe(CN)₆]₂.₁₄·6H₂O, was reported in [13]. The goal of the investigation was comparison of two opposite tendencies of variation in magnetic properties under pressure: (i) the magnetization reduction and magnetic order disappearing for the K_0.1Co₄[Fe(CN)₆]_2.7·18H₂O magnets and (ii) an enhancement of the magnetization and variation of the sign of exchange coupling for the K_0.5Mn₃[Fe(CN)₆]₂.₁₄·6H₂O material. Magnetization measurements under pressure pointed out that the external hydrostatic pressure considerably enlarges the ferrimagnetic Curie temperature, T_C, for A₂Mn[Mn(CN)₆] (A = K, Rb, Cs). For this monoclinic system with A = K and Rb, dT_C/dp amounts are 21.2 and 14.6 K GPa⁻¹, respectively. The cubic A = Cs compound also exhibits a monotonous enlargement with an initial rate of 4.22 K GPa⁻¹ and about 11.4 K GPa⁻¹ above 0.6 GPa. The enlargement in T_C we associate with deformation of the structure, such that the Mn^II−N≡C angle reduces with increasing pressure. The smaller the alkali cation, the greater the reduction in the Mn^II−N≡C angle caused by pressure and the larger the enlargement of T_C/dp. The large rise in T_C for the A = K compound is the highest class among several cyano-bridged metal complexes. The tuning of the transition temperature by pressure may result in additional applications, such as switching devices [14].

The pressure as a very efficient tool for tuning of magnetic properties in Prussian blue analogues was confirmed to be responsible for linkage isomerization [15], for magnetic pole inversion [16], and influenced spin crossover in [17,18]. In our paper, we will concentrate on the general mechanism present for the pressure effect on superexchange interaction in TM-Cr(CN)₆−PBs and K-M-Cr(CN)₆−PBs, where TM = Mn, Ni, Co, Cr, and M = Mn, Ni.

2. Magnetic Prussian Blue Analogues

The history of Prussian blue itself goes back to 18th century, when draper Diesbach synthesized Prussian blue (ferric hexacyanoferrate) as the first known synthetic blue pigment, which was more easily available and cheaper than other blue pigments available in that time. The first record in literature about that fact was published in [19]. Prussian blue was not only used for paintings but also for coloring of fabrics, and it is still used for this purpose when sold under the commercial name iron blue [20]. Since the discovery, its chemical stoichiometric composition became an intricate puzzle for chemists. The first ideas concerning its crystal structure were published by Keggin and Miles in [21]. Buser et al. in 1970 published a detailed crystal structure and confirmed the composition as Fe₄[Fe(CN)₆]₃.zH₂O (z = 14–16) in [22]. They concluded that PB formed a perovskite-like disordered structure with cubic unit cell dimensions of 10.2 Å. The cubic symmetry and the existence of a disordered structure lead to the fact that the lattice can accommodate wide variety of ions. When both positions of iron in the lattice are replaced by different ions, the resultant compound belongs to the family of Prussian blue analogues (PBs). Prussian blue and its analogues form a large family of compounds due to the fact that it is easy to modify the synthetic conditions and consequently to obtain compound of desired stoichiometric composition, shape, and size. Versatility in tuning its physical properties using external perturbations-stimuli opened the possibility of applications in various research branches.

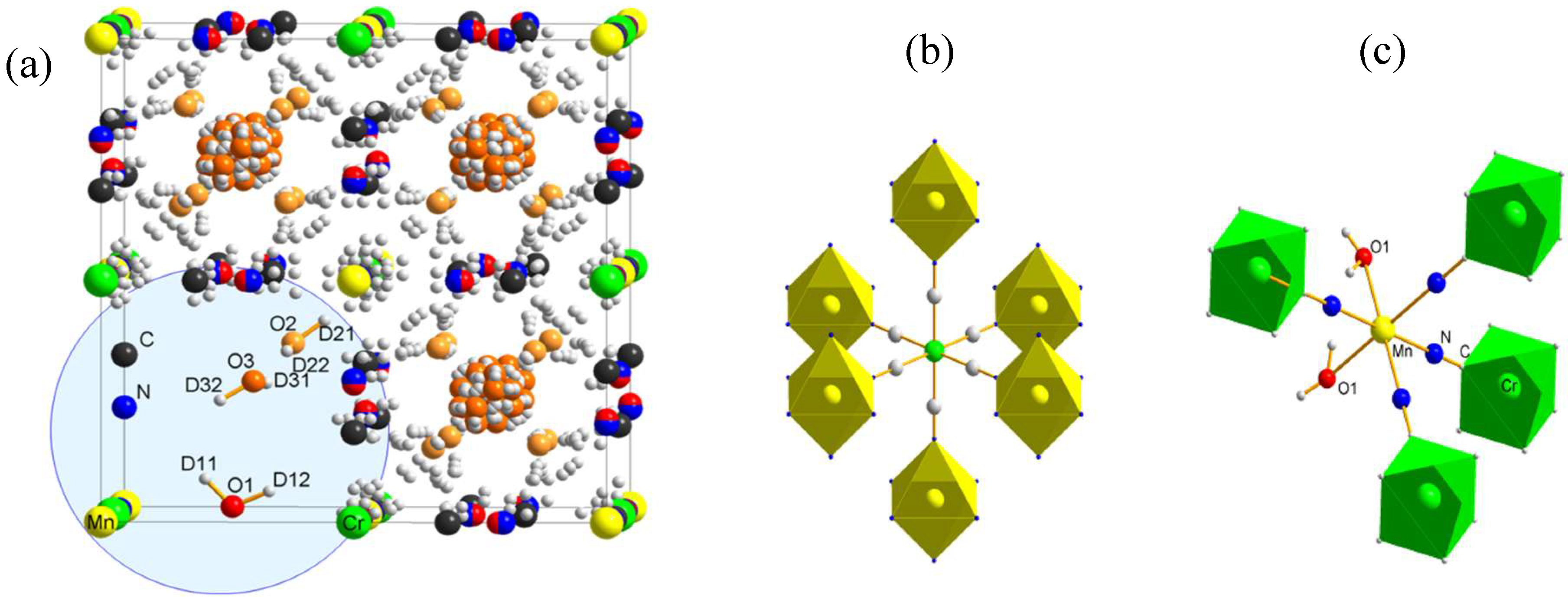
2.1. Crystal Structure of Prussian Blue Analogues

The formulas of Prussian Blue and its analogues are often written as M_xA[B(CN)₆]_z·nH₂O, where M is an alkali metal [1]. For z = 1, the face-centred cubic (fcc) structure with unit cells comprising eight octants, with the interiors referred to as interstitial, tetrahedral, or cuboctahedral sites, are adopted by the Prussian Blue analogues (PBs). Two different types of octahedral metal sites are present in the lattice: C6 strong ligand-field sites and N6 weak ligand-field sites. For z < 1, it was determined that the B sites are fractionally occupied, and that the A centres surrounding the vacant sites are randomly filled with one or more water molecules in their coordination spheres. As the water in the lattice is present also at interstitial sites (crystal water), the structure of PBs is supposed to be stabilized by the hydrogen bond network as well [1].

The Prussian Blue Fe^II₄[Fe^III(CN)₆]₃·14H₂O crystallizes in a cubic structure where the space group is Fm$\overline{3}$m; when taking into account also the weak reflections, the space group is changed to Pm$\overline{3}$m. The crystallization conditions strongly influence distribution of the [Fe(CN)₆] vacancies in the lattice. They can be either disordered in the crystal, giving an apparent high-symmetry structure with a fractional occupancy (3/4) of the [Fe(CN)₆] sites, or ordered, thereby lowering the symmetry. Due to the stoichiometric reasons, the presence of vacancies in the lattice is intrinsic to PBs whenever z < 1. The structure of PBs resembles a typical perovskite structure ABO₃ that means the structure, as such, is CaTiO₃. There are, however, at least two important differences between PBs and classical perovskite materials. The first evident difference is the different chemical composition of links between metal ions; instead of oxygen atoms, the octahedral metal centres are connected by cyanide bridges to form the cubic framework. The second difference is the fact that the [B(CN)₆]p– units in the solid are the same as the hexacyanometalate reactant used in the synthesis [B(CN)₆]p– units, which are stable as well in solution. The fact that Prussian blue and its analogues can be synthesized directly from prebuilt molecular precursors results in the fact that they can be considered as molecule-based materials. The ideal structural model of Prussian blue contains a linear A–N≡C–B unit and the geometries of metal atoms in the A and B sites are perfectly octahedral. In reality, it is however a rare situation. The X-ray diffraction Rietveld analyses show that the [B(CN)₆] units are often tilted (Figure 1). The tilting results in A–N≡C angles that are less than 180°. There are many reasons for tilting and distortions, starting with conditions of synthesis as well as effect of external perturbations. Observed distortions were, not surprisingly, found to have significant impact on the overlap of local wave functions, and thus on the efficiency of the exchange interaction pathway.

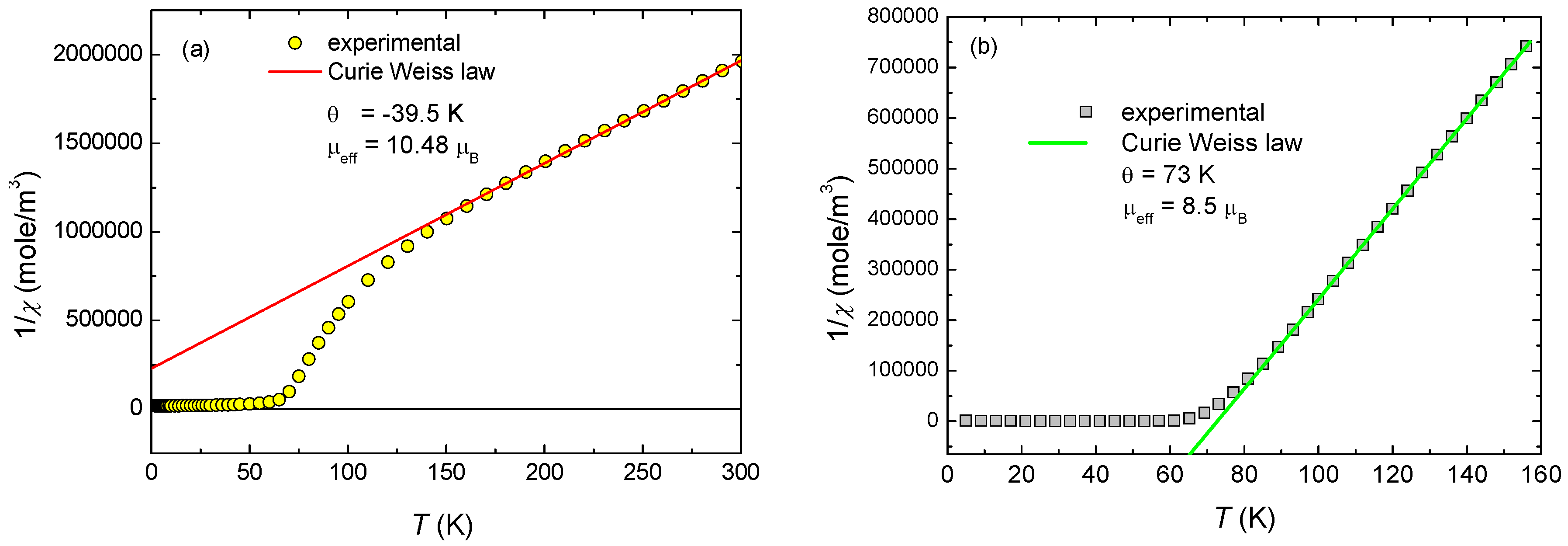
2.2. Magnetic Properties

Despite the fact that the first paper dealing with magnetic properties of Prussian blue showed very low ordering temperature T_C = 5.6 K, nearly 10 years later, T_C reached room temperature for some of its analogues, also with the help of external stimuli [23]. Early work of Bozorth et al. clearly demonstrated the direct relationship between magnetic ordering temperatures and type of paramagnetic TM centers, as demonstrated by the rather low magnetic ordering temperature of Prussian Blue, in which only half the TM ions are paramagnetic [24]. The pronounced increase in the Curie temperature of PBs is referred to in the 1980s, when Babel et al. discovered CsMn[Cr(CN)₆], a ferrimagnet with T_N = 90 K, and proposed a superexchange mechanism to account for the magnetic properties of PBs [25]. Superexchange refers to the magnetic coupling of next-to-nearest paramagnetic neighbors through a non-magnetic anion. Superexchange interactions are usually explained in the terms of the Goodenough-Kanamori-Anderson rules and are typically indirect interactions between 3d metal ions [26,27,28]. On the basis of these rules, a magnetic ion-ligand-magnetic ion, including an angle of 90°, where the singly occupied d-orbitals of the paramagnetic ions are orthogonal to one another and there is zero orbital overlap, is anticipated to give rise to weak ferromagnetic exchange interactions, which are assigned as a potential exchange mechanism. For a magnetic ion-ligand-magnetic ion, including an angle of 180°, the singly occupied d-orbitals of the paramagnetic ions are non-orthogonal to one another and there is direct orbital overlap. Consequently, the unpaired electrons of the magnetic ions align antiparallel to one another, giving rise to strong antiferromagnetic exchange interactions in a superexchange mechanism, known as kinetic exchange. In the case of PBs, the metal d orbitals split into t_2g and e_g sets by the CN ligands. The magnetic interactions in these materials are given by the super-exchange interaction between metal ions A²⁺ and B^III interposed through a three-dimensional network of C≡N bridges, as resultant 3D magnetic ordering with Curie temperatures T_C up to 376 K depending on the nature of the metal ions is created [27]. Magnetic features of Prussian Blue analogues are usually interpreted taking into account two assumptions: (1) the super-exchange coupling only between next A²⁺ metal ion and B^III (A²⁺–N≡C–B^III) ion; (2) in the case when the magnetic orbital symmetries of the metal ions are identical, the dominant super-exchange coupling is antiferromagnetic (J_AF) and on the other hand the super-exchange coupling is ferromagnetic (J_F) for magnetic orbitals with different symmetries. The B^III ion, surrounded by the carbon atoms of six cyanide ligands, experiences a large ligand field. Consequently, all familiar [B^III(CN)₆] units are invariably low spin and have electrons only in the t_2g orbitals. A²⁺ ions in Prussian Blue are usually high spin and can have both e_g and t_2g magnetic orbitals. When A has only e_g magnetic orbitals, all the exchange coupling with the t_2g magnetic orbitals of the [B(CN)₆] will be ferromagnetic. When only t_2g magnetic orbitals are present on A, all the exchange interactions with the t_2g magnetic orbitals present on [B(CN)₆] will be antiferromagnetic. When both t_2g and e_g magnetic orbitals are simultaneously present on A, ferromagnetic and antiferromagnetic interactions with the t_2g magnetic orbitals on [B(CN)₆] coexist and compete. The conclusions are straightforward: the t_2g(B)–e_g(A) pathways lead to ferromagnetic (F) interactions; the t_2g(B)–t_2g(A) pathways lead to antiferromagnetic (AF) interactions [1].

It cannot be overlooked that the huge variety of interesting physical phenomena in the family of PBs are closely related to the fact that the cubic symmetry of the lattice can accommodate a lot of transition metal ions as hexacyanometalate anions. Therefore, the Prussian Blue analogues can be prepared with a number of metals in the B sites [1]. As examples of paramagnetic ions, according to [1] we can mention:

• [B(CN)₆]⁴⁻ for B = V^II, Mn^II
• [B(CN)₆]³⁻ for B = Ti^III, Cr^III, Mn^III, Fe^III
• [B(CN)₆]²⁻ for B = Mn^IV

All above-mentioned paramagnetic anions are low spin due to the large ligand field splitting induced by the cyanide ligand, with anions spins varying from S = 1/2 for the Ti^III, Mn^II, and Fe^III derivatives, to S = 1 for the Mn^III derivative, up to S = 3/2 for the V^II, Cr^III, and Mn^IV derivatives. The paramagnetic ions placed in the A site are usually high spin due to the fact that N-coordinated cyanide and water molecules are weak field ligands. As examples of the ions placed on the A positions in the lattice, V^II, Cr^II, Mn^II, Fe^II, Co^II, Ni^II, Cu^II, and Fe^III ions can be mentioned. Corresponding spin values range from S = 1/2 for Cu^II to S = 5/2 for Mn^II and Fe^III [1].

3. Probing of Magnetocrystalline Correlations Using External Pressure

This simple model mentioned above has already been tested on the TM²⁺₃[Cr^III(CN)₆]₂·zH₂O and KM²⁺[Cr(CN)₆] systems, where TM²⁺ = Cr²⁺, Mn²⁺, Ni²⁺, Co²⁺, and M²⁺ = Mn²⁺, Ni²⁺ [29,30,31,32,33,34,35,36,37,38,39,40]. Our paper is focused on the pressure effect on crystal structure and magnetic properties.

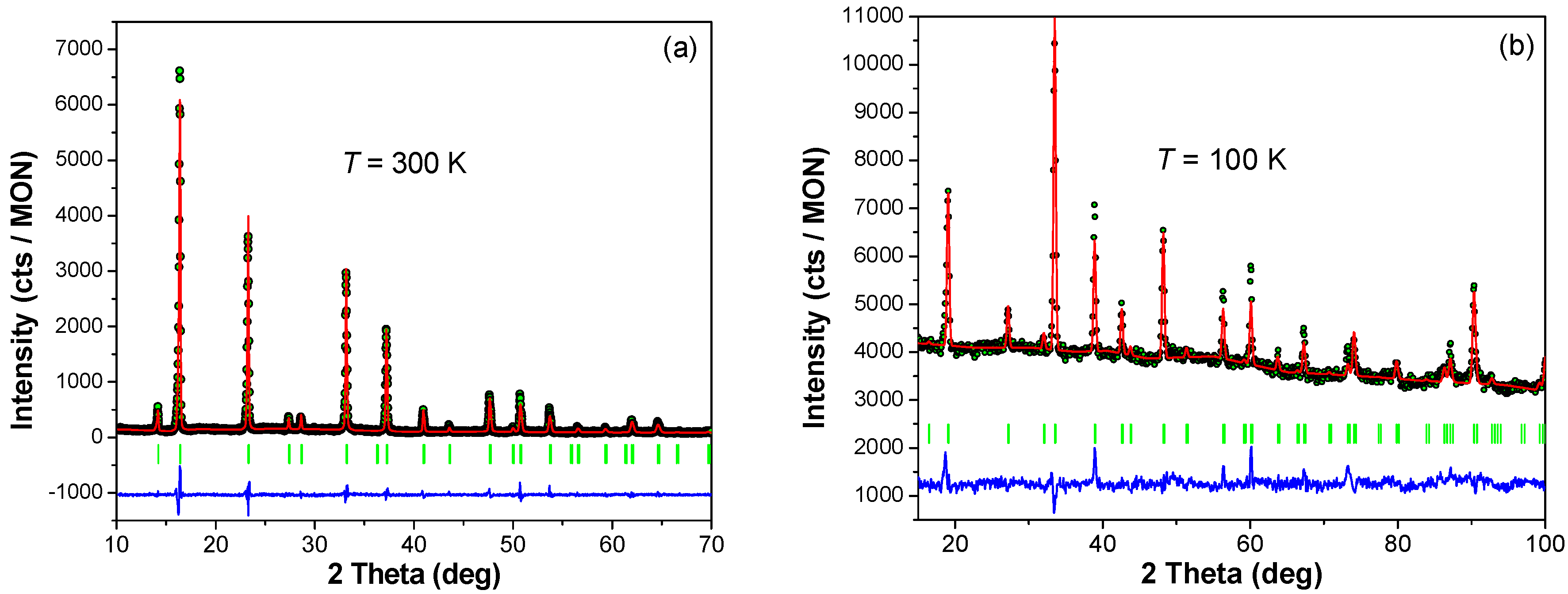
3.1. Crystal Structure of TM²⁺-Cr^III-PBs

The crystal structure of selected PBs was investigated by X-ray and neutron powder diffraction techniques. We studied (Ni_xMn_1−x)₃[Cr(CN)₆]₂·zD₂O (x = 0, 0.38 and 1) materials by powder neutron diffraction techniques in temperature ranges higher or lower than the Curie temperature T_C [30]. Our study enabled us to determine the entire crystal structure, including D-sites. We determined the crystal lattice of Mn₃[Cr(CN)₆]₂·zH₂O and Ni₃[Cr(CN)₆]₂·zH₂O molecular magnets with the help of the Rietveld technique by application software program FullProf, and the crystal structure was confirmed as a cubic space group Fm$\overline{3}$m (No 225) with lattice parameters a = 10.754 04(6) Å and a = 10.4341(3) Å [30]. However the lattice parameter of Co₃[Cr(CN)₆]₂·10H₂O are as follows: a = 1.04905(3) nm and a = 1.03805(9) nm for Cr₃[Cr(CN)₆]₂·2H₂O [33]. Doping with Ni for Mn leads to the reduction in the volume of elementary cells, which is approximately equal to 3.8 percent compared to Mn₃[Cr(CN)₆]₂ material [34], and (Ni_xMn_1−x)₃[Cr(CN)₆]₂ compound follows Vegard’s law and the enlargement of x results in a progressive reduction of the lattice parameter [34]. Lattice parameters decrease nearly linearly with substitution of Cu for Mn in the case (Cu_xMn_1−x)₃[Cr(CN)₆]₂·zH₂O metalo-complexes: a = 10.51909 Å, 10.49812 Å, 10.50418 Å, 10.49833 Å, 10.4887 Å, 10.3851 Å for x = 0.2, 0.25, 0.3, 0.35, 0.4, and 1.0, respectively [36]. Both KMn[Cr(CN)₆] and KNi[Cr(CN)₆] crystallizes in the fcc system, with lattice constants a = 10.786793 Å and a = 10.48679(5) Å, respectively [39,40]. The examples of x-ray diffraction and neutron diffraction patterns are displayed in Figure 2.

Neutron powder diffraction (ND) patterns were obtained on two different samples of (Ni_xMn_1−x)₃[Cr(CN)₆]₂·zD₂O mixed ferri-ferromagnetic material. The H atoms were substituted by D in the process of samples synthesis. The z number varies between 12 and 15, but in most events is equal to 12. The higher amount of background present in ND measurements points to the fact that D₂O molecules are replaced by H₂O molecules in the process of the ageing of the samples and incoherent scattering from H supplies to background (Figure 2b). The incoherent scattering caused pronounced enlargement of the time of measurement, but finally we obtained good statistics and the crystal structure, including D-sites, was completely described by the Rietveld refinement procedure. Prior to the neutron experiment, we left the experimental material in wet conditions to elude the aging, e.g., substitution of D₂O by H₂O. Our procedure resulted in a lower background but a second phase (ice made of D₂O) was indicated at low temperature [30]. Determination of the positions of building elements (CrC₆ octants, D₂O molecules, and other atoms were considered as isolated) in the cell was calculated by the direct-space method by application of reverse Monte-Carlo approach (Figure 3). The incoherent scattering led to extension of the experimental time, but in the end a good statistic was reached and the crystal structure, including D-sites, was determined by the Rietveld refinement.

3.2. Effect of Pressure on the Crystal Structure of TM²⁺-Cr^III-PBs

Effects of pressure on the structure and magnetic properties of 3-D cyanide bridged bimetallic coordination polymer magnets, Mn²⁺Cr^III ferrimagnet [Mn(en)]₃[Cr(CN)₆]₂·4H₂O (a en = ethylenediamine), Ni²⁺Cr^III ferromagnet [Ni(dipn)]₃[Cr(CN)₆]₂·3H₂O (b dipn = N, N-di(3-aminopropyl)amine were methodically studied in hydrostatic pressure up to 4.7 GPa by application of a piston-cylinder-type pressure cell and a diamond anvil cell [41,42]. The lattice of the ferrimagnet (a) was reduced in an isotropic manner for p ≤ 1.7 GPa, and the lattice volume linearly decreased. At higher pressure, the bc frame and total volume decreased only slightly, but the stacking along the a axis tended to tilt with the expansion of the a axis anisotropically. The reduction of lattice size saturated with a total volume reduction of about 9% at 3.2 GPa. An amorphous structure was observed at above 4.2 GPa. The pressure induced reduction of the lattice size is completely reversible. The original crystal structure recovered after releasing 4.5 GPa, indicating sufficient elasticity of Cr-CN-Mn. The compound (b) showed a different response to pressure. The cell volume decreased linearly and isotropically in the range 0–3.1 GPa with about 15% compression at 4.7 GPa, extending of the vertexes, and no amorphization, which demonstrated the structural strength. The shrinkage ratio of (b) is twice as large as that of (a) [42].

The pressure-caused change of crystal structure can be identified indirectly from the variation of pressure effect on T_C [43]. The first dT_C/dp = 25 K/GPa of Mn₃[Cr(CN)₆]₂·zH₂O PBs was alike to the amounts published in the study at pressures below 1 GPa [29]. At higher pressures, an essential but nonlinear increase in T_C from 63 K at ambient pressure to a maximum T_C = 93 K at 3.2 GPa pressure was found. This reflects an enlargement of the superexchange coupling between the transition metal cations as the bonds to cyanide are reduced by hydrostatic pressure. The ferrimagnetic moment falls down as T_C is enlarged, which may point to the higher degree of tilting of the Mn(CN)₆ and Cr(NC)₆ octants. At pressures above 3.2 GPa, the magnetic transition is broader, and T_C is reduced to zero near 10 GPa, with a correspondent break down of the ferrimagnetic moment. The finding coincides with a pressure-caused amorphisation of the material, as was reported on similar PBs [42].

Reference [44] resumes 0 to 0.6 GPa neutron diffraction data obtained on a nickel hexacyanochromate PBs K_0.25Ni[Cr(CN)₆]_0.75(D₂O)_0.25·2.1D₂O having fcc Prussian blue structure. Small thermal contraction is a characteristic feature of this material. On the other hand, pressure causes pronounced consequences on the top positions, enabling determination of the bulk modulus, K = −VdV/dp. The 110 K phase exhibits a variation from 10.477 Å at ambient pressure to 10.410 Å at high pressure, such that K = 31.43 GPa. In like manner, at 5 K the usage of pressure causes a reduction from 10.468 to 10.413 Å that leads to almost the same amount of K = 31.94 GPa. The assumption of linear volume reduction with pressure is evidenced by the alike K amounts for 0.5 and 0.6 GPa. Second, the widths of the peaks provide information about particle size and strain, and these results exhibit pressure-caused anisotropic widening. Third, the strength of the tops provides information about the fractional coordinates of atoms within the unit cell and their positional distributions. A real-space visualization of how pressure varies the ND scattering length density (SLD) identifies an antisymmetric change rising near the Cr sites while, simultaneously reducing by a similar value at the Ni site. The isomerization of cyanide linker from C bonding to Cr to C bonding to Ni makes these data clear. However, a shift of the coordinated water and the cyanide linker will also multiply an antisymmetric change in SLD between the metal ions [44].

The effect of pressure on Raman spectra of molecule-based magnets KNiCr(CN)₆ and KMnCr(CN)₆ was studied in [40]. The M–N≡C–Cr linkages M = Ni, Mn form the fcc lattice that may contain vacancies. It is generally accepted that the cyanide bridge can be extra susceptible to its surroundings, including the oxidation state and the spin state of the magnetic ions in the lattice. We reported on the effect of pressure on the ν [C≡N] vibration band, which is placed into the 2100–2200 cm⁻¹ spectral region [40]. The location of the band passes under pressure nonlinearly beginning at 2162.7 cm⁻¹ for 6.50 GPa for KMnCr(CN)₆ (Figure 4a). The CN frequency of KNiCr(CN)₆ falls down at first from 2195.7 cm⁻¹ for zero applied pressure to 2189.1 cm⁻¹ for 0.23 GPa, and then rises to 2211.9 cm⁻¹ for 6.2 GPa (Figure 4b). A thin arm (an arrow in Figure 4b) happens to be visible in the pressure region from 0.23 to 2.3 GPa, moving its location from 2188.4 cm⁻¹ to 2193.9 cm⁻¹, with rising pressure pointing to the existence of two different CN bridge neighbourhoods. The hydrostatic pressure-susceptible arm can point to the linkage isomerisation, suggesting that Cr^III–N≡C–Ni^II fragments grow at the expense of the original C^rIII–C≡N–Ni^II units [44,45]. However, the effect can also be superimposed by other contributions, such as the presence of surface non-bridging cyanides or coupling between alkali cations.

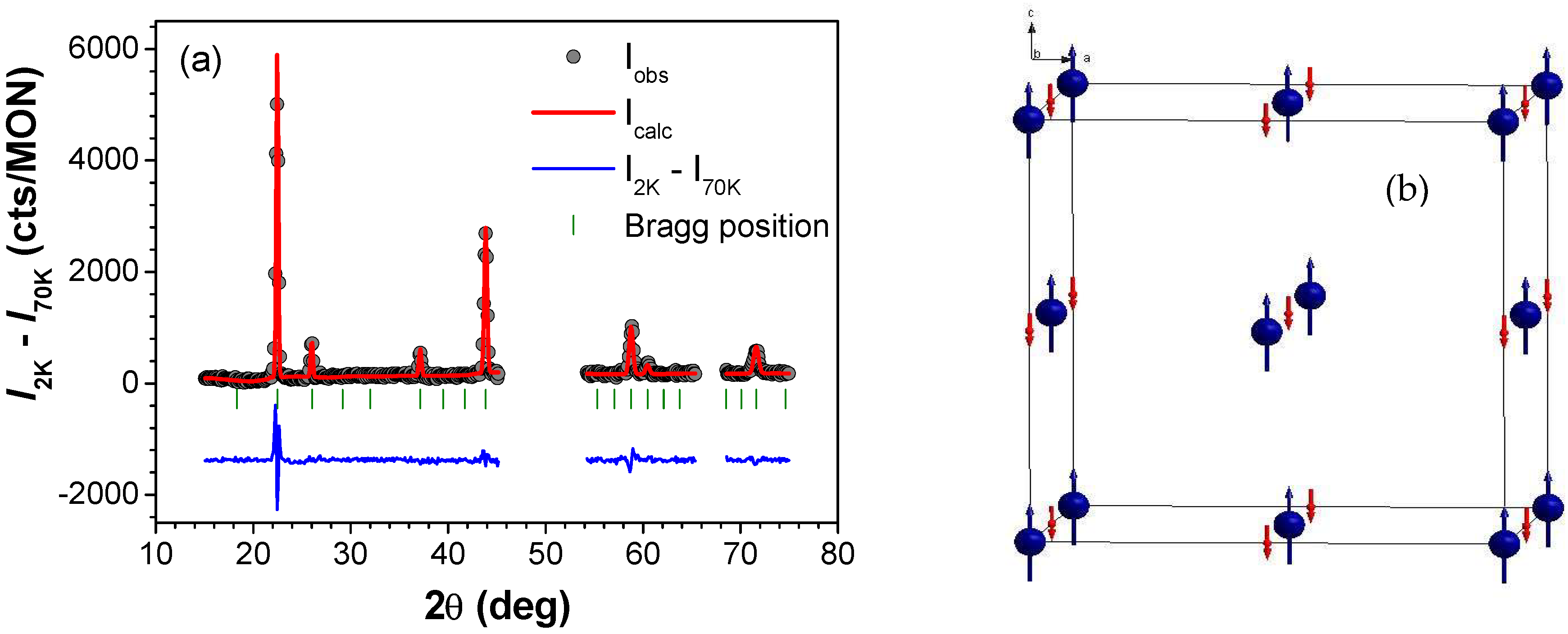
3.3. Magnetic Structure of TM²⁺-Cr^III-PBs

Magnetic structure was determined by powder ND experiment, which was performed on two samples of (Ni_xMn_1−x)₃[Cr(CN)₆]₂·zD₂O on E9 (λ = 1.79734 Å, HZ-Berlin) for z = 0, 1 at T = 2 K, 100 K and on G4.1 (λ = 2.42500 Å, LLB Saclay) for z = 0, 0.38, and 1 at different temperatures below T = 70 K. The pronounced magnetic contribution we found only in the case of the Mn₃[Cr(CN)₆]₂ magnet, and in this study we focused merely on the mentioned material [30]. A very poor magnetic signal was detected on Ni₃[Cr(CN)₆]₂ contribution at 1.6 K, perhaps because of a distribution of magnetically ordered domains [30,44]. Magnetization measurements of (Ni_0.38Mn_0.62)₃[Cr(CN)₆]₂ mixed ferro-ferri magnet indicated a maximum at about 60 K and low value of M at T = 2 K [34]. ND measurements undertaken on this material at 60 K pointed out an almost weak indication of magnetic signal. A strong magnetic signal was detected on Mn₃[Cr(CN)₆]₂ under 60 K and emerged only on allowed nuclear peaks—no additional signal was detected on forbidden nuclear Bragg summits. Diffraction apexes (222), (400), (422), and (440), with magnetic signal compared to experimental error, were excluded from refinement of magnetic contribution I_2K -I_70K (Figure 5a). Magnetization measurements and elastic ND of Mn₃[Cr(CN)₆]₂ clearly point out a magnetic structure consisting of Mn and Cr sublattices, with antiparallel magnetic moments µ_Mn = 3.790 µ_B and µ_Cr = −1.375 µ_B leading to overall ferromagnetic ordering below the Curie temperature T_C = 63 K. The simplified model of possible ferrimagnetic ordering of Mn₃[Cr(CN)₆]₂·zD₂O is plotted in Figure 5b. On the other hand, the magnetic structure of the Dy[Fe(CN)₆]·4D₂O molecule-based magnet with the orthorhombic crystal structure (Cmcm space group) was refined using Rietveld technique [46,47]. ND indicated that the magnetic structure is formed by Fe and Dy sublattices, which are merged antiferromagnetically, leading to overall ferrimagnetic arrangement with the magnetic phase transition at T_C = 3.7 K. While in the case of Fe-atoms the y-component of magnetic moment is large and the z-component is nominal, in the case of Dy-atoms, the x-and the y-magnetic moment components are large and the ordering of magnetic moments on Dy-sublattice is non-collinear [47].

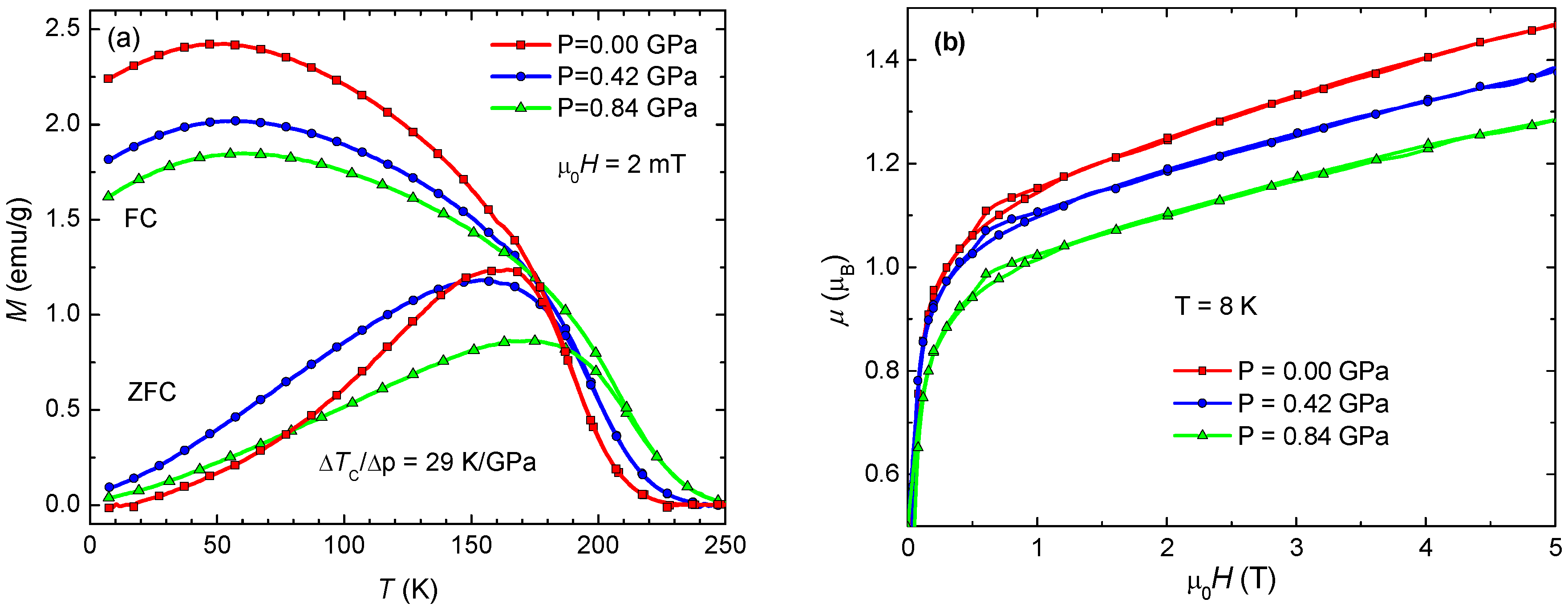
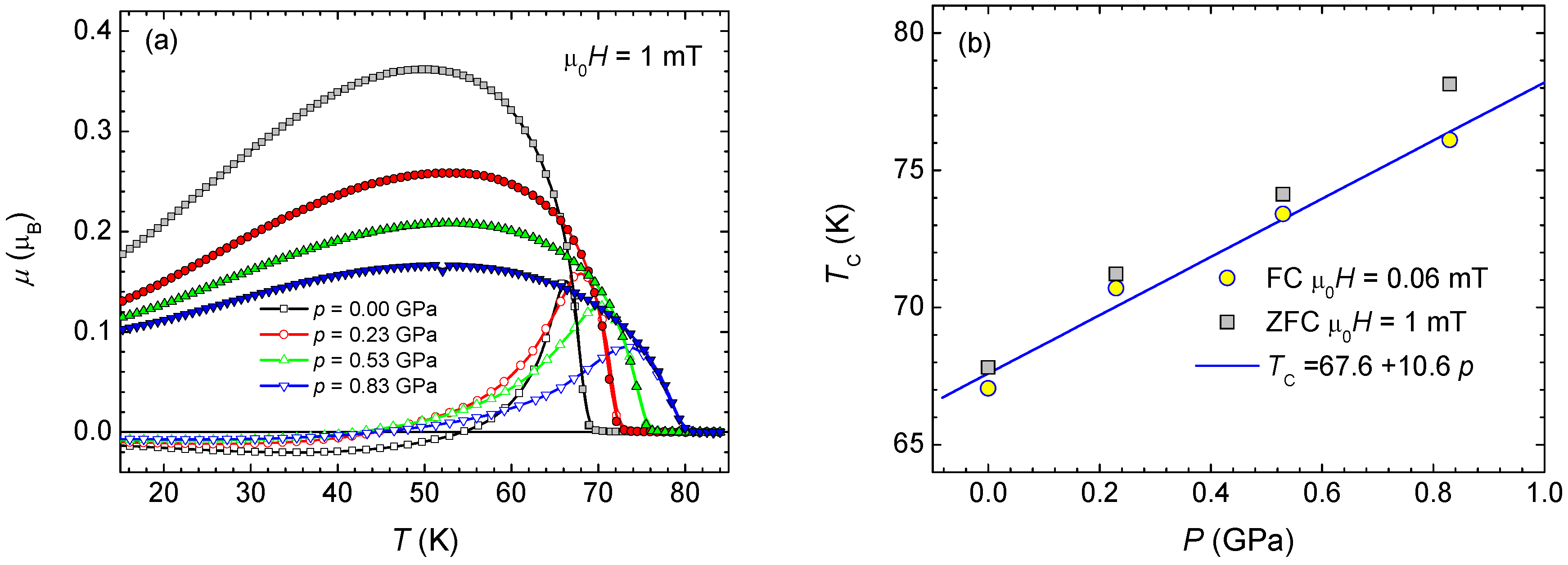
3.4. Pressure Effect on Magnetic Properties of Polycrystaline Samples

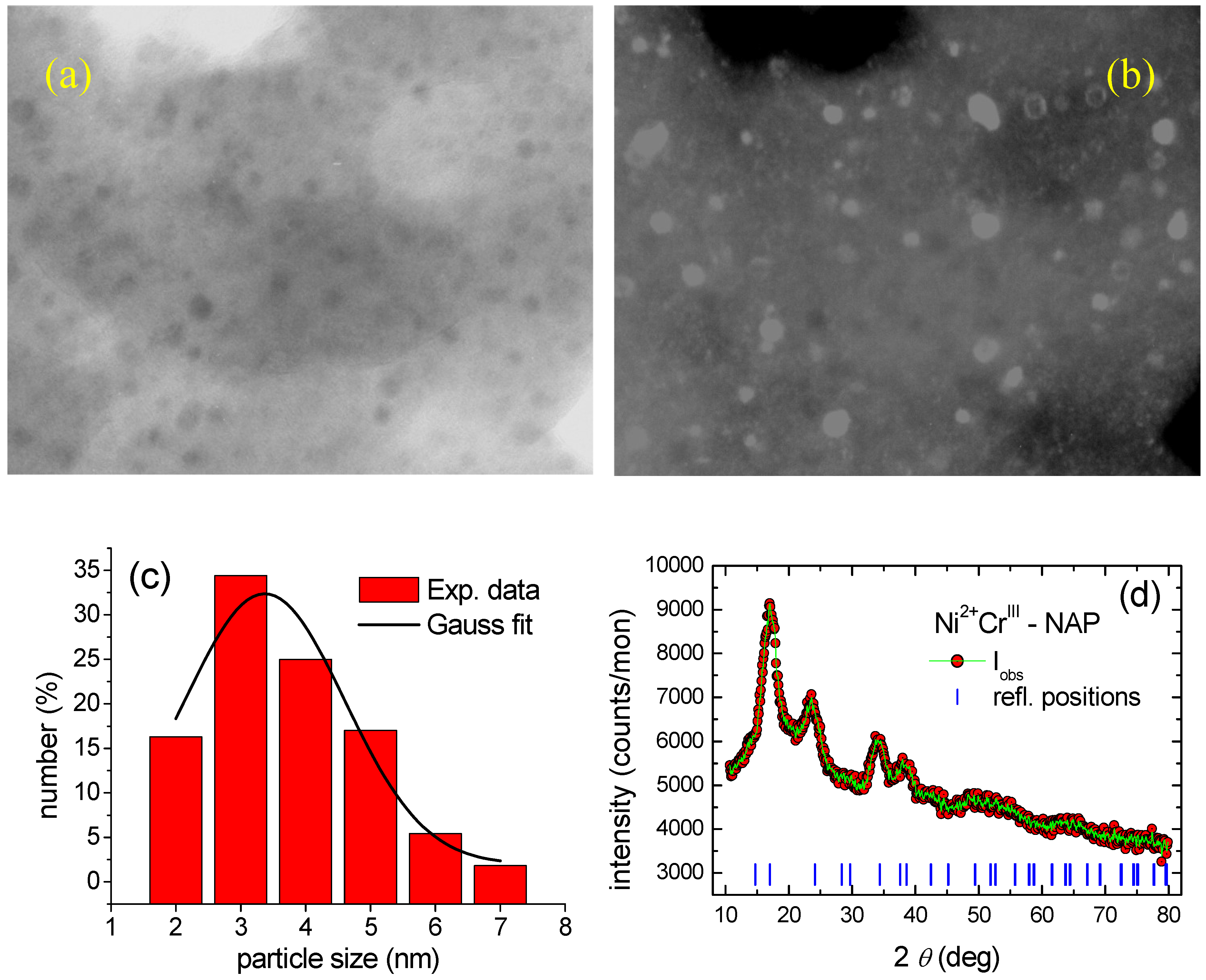
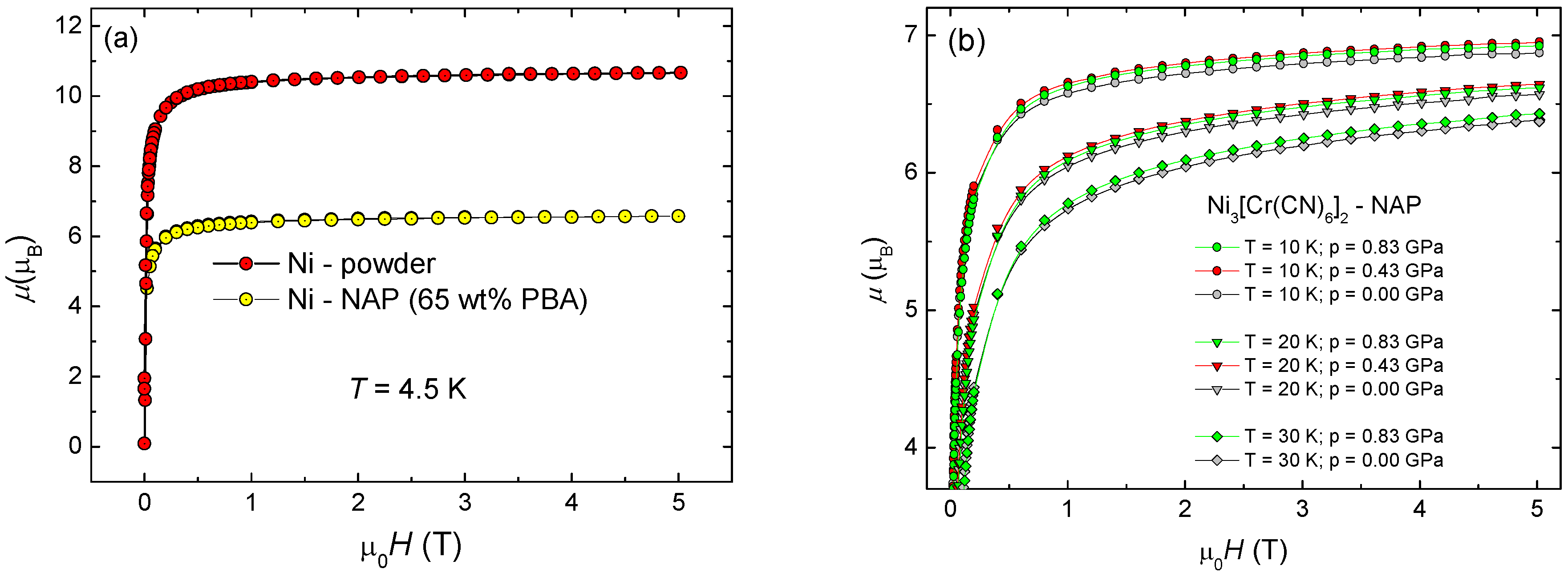
The above-mentioned magnetic model was tested on the TM⁺²₃[Cr^III(CN)₆]₂·zH₂O system [29,30,31,32,33,34,35,36,37,38] and KTM²⁺Cr(CN₎₆ [39,40], where TM²⁺ is a 3d ion and the following papers [29,32,34,38,39,40] are focused on the pressure effect on magnetic properties of these two types of PBs. The Cr^III in the low spin anion [Cr^III(CN)₆]³⁻ has (t_2g)³ orbital resulting in six ferromagnetic (FM) and nine antiferromagnetic (AFM) pathways, with (t_2g)³(e_g)² orbitals of Mn²⁺ leading to J_AF interaction. Compared to the (t_2g)³ orbital of Cr^III, we have six F pathways with (e_g)² orbitals of Ni²⁺ leading to overall J_F interaction (Figure 6).

Measurements of magnetic susceptibility (Figure 7) indicate a ferrimagnetic ordering below T_C ~ 65 K for the Mn-sample with μ_eff = 10.48 μ_B and θ = −39.5 K. The magnetic moment μ_s saturates to an amount of 8 μ_B/f.u. at T = 2K and μ₀H = 5 T. The Ni-sample orders ferromagnetically below T_C ~ 56 K, μ_eff = 8.6 μ_B, θ = 72 K. The magnetic moment saturates to a higher value of μ_s = 10.3 μ_B/f.u at T = 2K and μ₀H = 5 T [29,30].

Figure 8a shows magnetic isotherms for Mn²⁺-Cr^III-PBs obtained by measurements at various pressures [29]. The magnetic transition at T_C was defined as the inflection point of M(T) curve in this region. Magnetization as a function of hydrostatic pressure saturates in a very steep way, already reaching independence on the applied magnetic field for the values higher than µ₀H = 200 mT (Figure 8a). There is no magnetic hysteresis, with very small remnant magnetization µ_r and coercive field H_c. The effect of applied pressure on magnetization curves is pronounced only in the region of small magnetic fields. It was observed that the shape of magnetic isotherms changes and magnetization saturates at higher magnetic fields, as it is supposed that effective barriers for domain wall motion induced under pressure negatively influence its free motion in the irreversible part of magnetic hysteresis [29,44]. The second possible explanation for the effect of applied pressure on magnetic isotherms can be ascribed to the change in magneto crystalline anisotropy [44], as its shape resembles magnetization curves typical for the hard magnetization axis. Both magnetic ions are placed in octahedral positions, and therefore magnetic moments are aligned along the axes of octahedron. Even without applied external pressure, the octahedrons are tilted (Figure 1). Hydrostatic pressure enlarges the extent of tilting and octants are deformed. Both effects influence the efficiency of the magnetic exchange pathway and lead to magnetic anisotropy and reduction of the magnetic moment. The magnetic isotherms of Ni²⁺-Cr^III-PBs measured for various applied pressures [29] are plotted in Figure 8b. The magnetization saturates at a higher magnetic field, even at ambient pressure. In the region of small magnetic fields below µ₀H = 5 mT, initial magnetization increases linearly, followed by a steeper S-shape increase and consequently showing almost linear dependence again above µ₀H = 1T. The remnant magnetization and coercive field are small but more pronounced. It is expected that the hydrostatic pressure leaves spontaneous magnetization unchanged, and the magnetization processes are strongly changed only at low temperatures below 8 K. The magnetization saturates in a higher magnetic field, the interval of linearity for initial magnetization extends to µ₀H = 10 mT and the remnant magnetization M_r is a little bit higher. Pressurization of the crystal lattice results in deformation, including small rotation of octants leading to reorientation of magnetic moments of 3d magnetic ions followed by decrease of magnetization in the saturated state.

The effect of applied pressure on the temperature of the transition to magnetically ordered state—the Curie temperature T_C is shown in the Figure 9. The Curie temperature T_C, defined as the inflection point of the M(T) curve, increases almost linearly in the whole range of applied pressures. The pressure = coefficient ΔT_C/Δp = 25.5 K/GPa is one of the highest positive changes of T_C with pressure so far published for any PBs [29]. The positive pressure coefficients ΔT_C/Δp ≈ 13 K/GPa and ΔT_C/Δp ≈ 11 K/GPa were reported for [Mn(en)]₃[Cr(CN)₆]₂·4H₂O [41,42] and for Mn₃²⁺[Mn^III(CN)₆]₂·12H₂O·1.7(CH₃OH) [48] Mn-based PB ferromagnetic materials. The typical property of majority PBs, hysteretic behaviour between ZFC and FC magnetization for small magnetic fields, is shown for Mn²⁺-Cr^III-PBs in Figure 9. ZFC and FC magnetization curves merge very well in the range above the magnetic phase transition and show hysteretic behaviour below the bifurcation temperature T_b. The hysteretic behaviour between ZFC and FC regimes defines an interval where irreversible magnetization processes determine shape of magnetization curve. A small maximum below T_C in the region where ZFC and FC regimes have large hysteresis is very often accompanied with freezing temperature T_f of the cluster-glass system, which is often present in PBs. The hydrostatic pressure enlarges this hysteretic behaviour, which is observed for ZFC and FC regimes. Smaller magnetization M(T) observed on the ZFC curve points to the variation in magneto-crystalline anisotropy caused by pressure. It points out to the fact that the cluster-glass-like feature is enhanced under applied pressure.

The real part of AC susceptibility χ’(T) for the Mn-sample, which we obtained for non-DC magnetic field, modulation with the amplitude of 3 Oe and frequency f = 0.4 Hz confirmed very similar behaviour to the one described earlier on the M(T) measurements under pressure in ZFC regime (Figure 10a). The pronounced maximum in the imaginary part of susceptibility χ’’(T) at about T_C indicates an energy-dissipative process, which is connected with forming of a magnetically-ordered state (Figure 10b). Hydrostatic pressure gradually shifts the peak at T_C to higher temperatures, which indicates the enlargement of T_C. The gradient of the T_C rises with pressure, estimated from a steep rise of χ’(T) or as a peak of χ’’(T), is similar to ΔTc/Δp = 25.5 K/GPa, determined from M(T) measurements. Mn²⁺ has five unpaired d-electrons (t_2g)³(e_g)² with S = 5/2 and Cr^III has three d-electrons (t_2g)³ with S = 3/2 in the Mn²⁺-Cr^III-PBs. In the ligand-field model, each t_2g orbital (a) of Mn²⁺ can find t_2g orbital (b) in Cr^III, which it can strongly interact with in a three-dimensional network [1]. The super-exchange interaction of this pair will be antiferromagnetic. From the extended Hückel calculations follows that the antiferromagnetic contribution to the magnetic coupling J is determined approximately by the expression 2 S (∆2 − δ2)1/2, where δ is the energy gap between the (unmixed) a and b orbitals, ∆ is the energy gap between the molecular orbitals formed by them, and S is the mono-electronic overlap integral between a and b. The antiferromagnetic term can be rewritten as (∆² − δ²) = (∆ − δ) (∆ + δ); the strength of the interaction is gauged by the term (∆ − δ) and the stabilization of charge-transfer states, in which an electron being transferred from one magnetic orbital to the other is gauged by the term ∆ + δ. The most general effect of applied pressure, namely shortening of the distance between the magnetic ions in the lattice, leads to the increase of the amount of the overlap integral S. The enlargement of T_C in Mn²⁺-Mn^III-PBs can, therefore, be ascribed to an enlargement of the overlap integrals between d_π (Mn^III) and π*(CN⁻) and d_π (Mn²⁺) and π*(CN⁻). The hydrostatic pressure enlarges ∆, resulting in an enlargement of both expressions (∆ − δ), (∆ + δ) and gives rise to the enhancement of the antiferromagnetic interactions. The term (∆² − δ²) can be determined for number of TM²⁺ and TM^III, with the precondition that the spacing between magnetic ions is identical. In the case that the coupling between a single pair of orbitals is known, one can sum all the combinations presented by a three-dimensional network to obtain the consequential contribution. In Mn²⁺-Cr^III-PBs with nine AF and six F pathways, the antiferromagnetic coupling will be preferred. The rise of T_C caused by hydrostatic pressure was associated with a rise of super-exchange coupling J, determined by the enlargement of S and ∆ in Mn²⁺-Cr^III-PBs.

However, the situation is different for the case of Ni²⁺-Cr^III-PBs, where magnetization and AC susceptibility measurements indicate a slight decrease in T_C with pressure ΔT_C/Δp = −3.0 K/GPa, and later more detailed experiments have shown that the T_C is not modified prominently under hydrostatic pressure [29]. Ni²⁺ has two unpaired d-electrons (e_g)² with S = 1 and six paired d-electrons (t_2g)⁶, which do not contribute to magnetic coupling. Magnetic interactions between the (e_g) orbital of Ni and (t_2g) of Cr are therefore dominantly ferromagnetic, the overlap of t_2g and e_g orbitals is practically equal to 0 (∆ = 0), the pressure does not change J, and we do not expect any change in magnetic coupling. The hydrostatic pressure subtly affects bonding angles between magnetic ions interposed by the CN group. A slight deviation from perfect 180° of the bonding angle reduces the power of magnetic interactions, and consequently, T_C decreases.

Our study [29] revealed principally separate effects of pressure on the magnetic phase transition in Mn²⁺-Cr^III-PBs with prevailing antiferromagnetic super-exchange coupling and a Ni²⁺-Cr^III-PBs compound with prevailing ferromagnetic coupling. The applied pressure powered the super-exchange antiferromagnetic coupling J_AF. The Curie temperature T_C increased with the hydrostatic pressure, ΔT_C/Δp = 25.5 K/GPa, for the ferrimagnetic Mn₃[Cr(CN)₆]₂ compound as a result of powered magnetic interaction determined by enlarged amount of the monoelectronic overlap integral S and energy gap ∆ between the mixed molecular orbitals. However, the hydrostatic pressure does not change J_F exchange magnetic coupling in the Ni₃[Cr(CN)₆]₂ ferromagnetic material. The bonding angle between magnetic ions differs from the perfect amount of 180° for any Prussian Blue analogue. The hydrostatic pressure affects bonding angles between magnetic ions interposed by the cyano-bridge and reduces the strength of magnetic interaction. Reduction of the magnetic coupling due to variations of bonding angle is general feature for both types of molecule magnets.

However, the enhanced exchange interaction of Mn₃[Cr(CN)₆]₂ caused by enhanced overlapping between magnetic orbitals masks this effect. The magnetization processes are modified by the pressure in both magnets, but we expect that the hydrostatic pressure does not affect the spontaneous magnetization. Pressure-induced magnetic hardening can be interpreted as a variation of magneto-crystalline anisotropy due to pressure. The mentioned effect was observed mainly for Ni₃[Cr(CN)₆]₂, where saturated magnetization µ_s decreased in the entire temperature range, while µ_s remains unchanged for Mn₃[Cr(CN)₆]₂ at low temperatures. The enlargement of µ_s for Mn²⁺-Cr^III-PBs near to T_C was associated with the increase of magnetic interactions [29].

The applied pressure linearly shifts T_C of Co²⁺-Cr^III-PBs down in the used interval of hydrostatic pressures (Figure 11a) with the determined negative coefficient ΔT_C/Δp = −1.8 K/GPa. The overlap of t_2g and e_g orbitals is principally zero and J_F is not changed by pressure. The hydrostatic pressure slightly affects bonding angles between magnetic ions mediated by the cyano-bridge, and this is the reason for reduction of T_C. Magnetization of Co²⁺-Cr^III-PBs is reduced only weakly (Figure 11b). We expect that the spontaneous magnetization is unaffected hydrostatically by hydrostatic pressure, and only the magnetization processes are strongly affected even at low temperatures. The hydrostatic pressure increases the degree of deformation in the crystal structure, which leads to miss-orientation of magnetic moments placed on magnetic ions and to reduction of saturated magnetization [32].

In the Prussian blue analogue Cr₃[Cr(CN)₆]₂·2H₂O the anion [Cr^III(CN)₆]³⁻ has only (t_2g)³ orbitals and there are 3 ferromagnetic (F) and 9 antiferromagnetic (AF) pathways with (t_2g)³(e_g)² orbitals of Cr²⁺ in high spin state leading to overall J_AF interaction. On the other hand, the (t_2g)³ orbitals of Cr^III have 6 AF pathways with (t_2g)² orbitals of Cr²⁺ in low spin state leading to overall J_AF interaction (Figure 12). The transition to a magnetically ordered state is accompanied by a steep increase in M(T) (Figure 13). The hydrostatic pressure shifts T_C of Cr²⁺-Cr^III-PBs to higher temperatures almost linearly in this range of applied pressures. The estimated positive coefficient ΔT_C/Δp = 29 K/GPa is the highest positive change of T_C with pressure which has so far been published for any PBs [32]. The applied pressure reduces the length of exchange path Cr²⁺–N≡C–Cr^III and increases overlap integral S. The hydrostatic pressure increases ∆ resulting in the enlargement of both terms (∆ − δ) and (∆ + δ) powers the antiferromagnetic coupling [1]. The variance between M(T) determined for ZFC and FC measurements identifies the temperature range where irreversible magnetization processes take place (Figure 13a). A flat peak near to T_C in the range where large differences between ZFC and FC magnetic curves take place is very often attributed to freezing temperature T_f of the cluster glass system, which is a very common feature of the majority of PBs. The pressure enlarges the gap between magnetization obtained in ZFC and FC regimes for Cr²⁺-Cr^III-PBs. Reduced value of magnetization M(T) in ZFC regime indicates a change in ligand field leading to change of magnetocrystalline anisotropy.

The magnetic isotherms of Cr²⁺-Cr^III-PBs determined at various pressures are present in Figure 13b. Magnetization goes up at first very steeply, at very low field starts to saturate, and above µ₀H = 1 T the magnetization grows almost by a linear way. The applied pressure reduces saturated magnetization of Cr²⁺-Cr^III-PBs. The Cr^III in anion [Cr^III(CN)₆]³⁻ is low spin and exhibits only (t_2g)³ orbital and the spin S = 3/2. However, we suppose for cation Cr²⁺ two possibilities: at first Cr²⁺ is high spin, having S = 2 and magnetic orbitals are (t_2g)³(e_g)¹, implying three F and nine AF pathways, or another opportunity when Cr²⁺ is low spin S = 1 and magnetic orbitals are (t_2g)², implying six AF pathways [1]. In the case that all Cr²⁺ are high spin, the expected theoretical amount of spontaneous magnetization μ_s = g[3S(Cr²⁺) − 2S(Cr^III)] = 6 μ_B; g = 2 is the Lande factor. The experimentally estimated amount μ_s(exp) = 1.73 μ_B [32] is widely less than theoretical one, pointing out that a portion of Cr²⁺ is low spin (S = 1), yielding total compensation of spins μ_s = 0 μ_B. It seems that only approximately 30% of Cr²⁺ is high spin. The applied pressure p = 0.84 GPa causes high spin–low spin transition of cca 4.5% of high spin Cr²⁺.

Magnetic properties of mixed ferro-ferrimagnet (Ni_xMn_1-x)₃[Cr(CN)₆]₂·zH₂O and the compensation temperature T_comp for different amounts of x were first mentioned and interpreted by molecular field theory in [49]. This happened because the negative magnetization due to the Mn²⁺–N≡C–Cr^III subsystem with dominant J_AF and the positive magnetizations due to Cr^III–C≡N–Ni²⁺ subsystem with dominant J_F have different temperature dependences of magnetization μ(T), and at T_comp, which is below T_C, the sign of the magnetization is reversed [50]. The possibility that the spontaneous magnetization might change sign at particular T_comp was envisaged by Néel in the classical theory of ferrimagnets [51,52].

The effect of pressure on magnetization features of (Ni₃₈Mn₆₂)₃[Cr(CN)₆]₂·zH₂O was studied in pressures up to 0.8 GPa [34]. Both ferrimagnetic J_AF and ferromagnetic coupling J_F are present in this type of magnet and magnetization inversion is observed at the compensation temperature T_comp. Our study revealed that J_AF is prevailing in this material. The Curie temperature T_C of the magnet rises with hydrostatic pressure, dT_C/dp = 10.6 KGPa⁻¹, due to enhancement of J_AF. The rise of J_AF is associated with an enlarged amount of the single electron overlapping integral S and an energy gap ∆ between the mixed molecular orbitals t_2g (Mn²⁺) and t_2g (Cr^III) caused by pressure. Magnetization process is also influenced by pressure—magnetization saturates at a higher magnetic field and saturated magnetization decreases with pressure. The compensation temperature T_comp falls down under hydrostatic pressure. The μ(T) curves plotted in Figure 14a were obtained on the material with the very low amount of μ_s compared to parent compounds [34]. The same sample were used for high pressure measurements. The smooth shape of ZFC and FC magnetization curves together with nearly the same compensation temperature T_comp ~ 12 K for both ZFC and FC regimes confirm the high quality of the sample. Magnetic susceptibility follows the Curie–Weiss law above 100 K, with the effective magnetic moment μ_eff = 9.32 μ_B and the paramagnetic Curie temperature θ = −18.8 K (Figure 14b). The negative value of θ indicates that J_AF is dominant but the shape of 1/χ(T) below 100 K points out to ferrimagnetic ordering.

The magnetic phase transition at 67.6 K of this mixed ferri-ferro magnet takes place at a higher temperature than for both Ni₃[Cr(CN)₆]₂·zH₂O (T_C = 56 K) and Mn₃[Cr(CN)₆]₂·zH₂O (T_C = 65 K). Simultaneously, with increase of Ni for Mn substitution, the decrease of lattice parameters was observed. The increase of T_C correlates with the chemical pressure induced by this substitution. An unusually high value of magnetic Grűneisen parameter ε in the range 9.03–9.97, which was reported for PBs [46], points to a very strong magneto-structural correlation in PBs. The material-dependent parameter ε can be, in accordance to the definition in a phenomenological model, ascribed to the intersite distances, and consequently to the interaction strength J.

The general tendencies of the hydrostatic pressure effect on T_C remain the same. The magnetic phase transition is shifted to higher temperature (Figure 15a) but dT_C/dp = 10.6 K/GPa (Figure 15b) is significantly decreased compared to Mn₃[Cr(CN)₆]₂.zH₂O, where dT_C/dp = 25.5 K/GPa) [29]. Despite weakening of the effect, the interpretation is again related to changes of electronic structure, as in Mn²⁺–N≡C–Cr^III. The single electron overlapping integral S, as well the energy gap ∆ of the mixed molecular orbitals t_2g (Mn²⁺) and t_2g (Cr^III) become enhanced, and J_AF interaction is more effective [1,29]. On the contrary, the ferromagnetic Cr^III–C≡N–Ni²⁺ subsystem is weakly affected due to no overlap of magnetic orbitals, and therefore J is given Mn²⁺–N≡C–Cr^III -part. The number of exchange paths sensitive to pressure is reduced in this ferri-ferro-mixed magnet, resulting in the lower value of dT_C/dp in (Ni_0.38Mn_0.62)₃[Cr(CN)₆]₂.

The characteristic feature of ZFC and FC curves, the compensation temperature T_comp, appears because the algebraic sum of μ(T) of Mn²⁺–N≡C–Cr^III part and Cr^III–C≡N–Ni²⁺ part is 0 at T_comp [51]. It seems that T_comp is not an intrinsic property of the system and depends on treatment. Heat treatment removes T_comp from FC curves but not from ZFC curves [34]. The hydrostatic pressure p₁= 0.23 GPa reduces T_comp. The application of higher pressure does not have any effect on T_com (Figure 15a).

Both types of magnetic ions (Mn²⁺, Ni²⁺) and (Cr^III) are located in the octants, which are basic motives of the crystal structure. A very stable octant around Cr^III is formed from six CN groups and coordinated to Cr^III via C atom. The coordination of Mn²⁺, Ni² ions via N and H atoms is realized by four CN and two H₂O groups forming the octahedrons that can be deformed easier. Both types of octants can rotate and can be tilted, as it was shown for vanadium-based PBs [1,33]. As a consequence, the bonding angle between magnetic ions deviates from 180 degrees, and that is why J_AF will be reduced. Simultaneously, this reduction of J_AF competes with an increase of J_AF resulting from the enhanced value of S and ∆ induced by pressure, leading to the smaller value of dT_C/dp. In these two cases the octants are tilted, the alignment of moments on magnetic ions is not strictly parallel or anti-parallel, and as a consequence μ saturates at a higher magnetic field (Figure 16a). The number of domain barriers, like [Cr^III(CN)₆] vacancies, which are not filled by H₂O, can be reduced by pressure. and the lower coercive force is expected for a system with a smaller number of domains (Figure 16b).

Both magnetic isotherms and thermo-magnetic curves of KMnCr(CN)₆ are affected by hydrostatic pressure, as it was demonstrated in our paper [39]. Our results confirmed that the applied hydrostatic pressure raises the enhancement of magnetic coupling in this material, because a linear increase of T_C was observed under pressure (Figure 17a). A step on μ(T) in the vicinity of magnetic phase transition was generated by the applied pressure (Figure 17a) and dμ(T)/dT curve shows two minima associated with two magnetic transitions. Corresponding pressure coefficients of the two magnetic phases were estimated as ∆T_C1/∆p =18.18 KGPa⁻¹ and ∆T_C2/∆p = 26.62 KGPa⁻¹. The basic magnetic characteristics are very similar to those earlier mentioned for Mn₃[Cr(CN)₆]₂ compound. Magnetization reached saturation at low temperatures for low magnetic fields μ₀H = 200 mT. Remnant magnetization μ_r and coercive field H_c are close to zero. This situation is changed under the pressure. The magnetic isotherms alter their curve with the hydrostatic pressure (Figure 17b) and magnetization saturates at a higher magnetic field. The hydrostatic pressure does not change the saturated magnetization μ_s, remnant magnetization μ_r, and coercive force H_c at low temperatures in a pronounced way.

Our study of KMnCr(CN)₆ and KNiCr(CN)₆ molecule-based magnets presented in the paper [39] confirmed the main differences in pressure effect on T_C between Mn-PBs with prevailing antiferromagnetic magnetic interaction and Ni-PBs showing ferromagnetic properties. In the case of of the KMnCr(CN)₆ magnet, the pressure enhances the super-exchange antiferromagnetic coupling J_AF and that is why T_C simultaneously increases, due to enlarged monoelectronic overlap integral S and energy gap ∆ between the mixed molecular orbitals. The hydrostatic pressure does not affect J_F exchange interaction in KNiCr(CN)₆ and the magnetic phase transition does not change. The bonding angle between magnetic ions differs a little from the ideal value of 180° in real systems.

The bonding angle between magnetic ions represented by the CN group softly decreases with pressure, which leads to reduction of the magnetic coupling. This effect is present on both types of magnets, but it is masked on ferromagnetic materials because pressure strengthens exchange interaction resulting from enlarged overlapping of magnetic orbitals. The magnetization processes are influenced by the pressure in both systems, but the spontaneous magnetization does not change. Pressure-induced magnetic hardening was ascribed to variations in magneto-crystalline anisotropy induced by pressure. The rise of µ_s in Mn²⁺-Cr^III-PBs near T_C was associated with the enhancement of magnetic interactions.

3.5. Magnetic Properties of Magnetic Nanoparticles

In the last few years, there has been considerable interest in preparation and investigation of magnetic nanoparticles (NAP) because of their potential applications in high density recording media, but also for the reasons of macroscopic tunnelling [53] and quantum computing [54]. After discovery of single–molecule magnet behaviour in Mn₁₂-acetate with highest spin ground state S = 51/2 [55], one of the important issues of magnetism is the study of objects with magnetic moments intermediately between this value and the value of metallic NAP with S ≥ 1000 [56]. NAP based on Prussian blue analogues (PBs) prepared by reverse micelle technique with S < 1000 are promising candidates. The first report on application of this technique for preparation of NAP based on PBs has been made by Vaucher in [57]. Later in works [58,59], authors referred to preparation of cyanide bridged Cr^III-Ni²⁺ nanoparticles. The reverse micelle technique described in [56] was used [37,38]. The content of organic surfactants in the samples was estimated to about 22 wt.% Ni-NAP and 28 wt.% Mn-NAP. The average size of about 4.5 nm determined from X-ray measurements corresponds with TEM results (Figure 18).

We expect that both systems Ni-NAP and Mn-NAP behave as systems of strongly interacting magnetic particles. The super-exchange interaction is dominant in intra-NAP magnetic interaction. The dipole-dipole interaction is dominant in inter-NAP magnetic interaction. The dispersion of NAP into an organic matrix leads to a dilution of the mother PBs, and consequently the Curie temperature is reduced from T_C = 56 K for Ni-PBs to T_C = 21 K for Ni-NAP system and from T_C = 65 K for Mn-PBs to T_C = 38 K for Mn-NAP system. In the case of Mn-NAP, we found two satellite minima in dM/dT. Each of these minima indicates T_C of Mn-PBs sub-systems and represents two extra regions with different concentration of magnetic NAP [37]. Pressure induced changes of the saturated magnetization μ_s and the Curie temperature T_C are reversible. We expect that pressure affects inter-NAP distance (high compressibility of an organic matrix) and changes magnetic properties of NAP. The applied pressure strengthens the magnetic super-exchange interaction of Mn-NAP with the increased overlapping of magnetic orbitals [38]. As it is shown in Figure 19b, pressure decreases T_C (dT_C = dp = −3 K/GPa) for the system of Ni-NAP with dominant JF, which is mainly attributed to less effective magnetic coupling due to the reduction in the bonding angle Ni²⁺–N≡C–Cr^III from an ideal value of 180°. Figure 20a demonstrates a dilution effect. The shape of the magnetization curve for Ni-NAP is the same as for Ni-PBs and the reduction of the saturated magnetization μ_s is mainly due to reduced ratio of mother PBs (only 65 wt.%) in the system. The applied pressure increases the magnetic moment μ_s (Figure 20b). This behavior is opposite to the behavior of the mother Ni-PBs and is attributed to the reduction of inter-NAP distances by compression of the organic matrix [38].

3.6. Cr^III-PBs Core–Shell Heterostructures under Pressure

Magnetic studies on the PBs with chemical formula Li_xCu_y[Fe(CN)₆]_z·zH₂O (LiCuFe–PBs) and Li_jNi_k[Cr(CN)₆]_l·zH₂O (LiNiCr–PBs), as well as LiCuFe@LiNiCr–PBs core–shell heterostructures, have been conducted under pressures ranging from ambient to ≈1.4 GPa and at temperatures of 2–90 K. The results for the single component CuFe–PBs indicate robust magnetic properties under the range of pressures studied, where a T_C = 20 K was observed at all pressures [60]. Pressure studies of single component NiCr–PBs are consistent with previously published results by other workers below 1.0 GPa. However, at pressures above 1.0 GPa, the decrease in magnetization is accompanied by a decrease in the T_C, an indication of changes in the superexchange value. The results obtained with the single component samples can be mapped onto the observations of the heterostructures [60].

Cubic core@shell particles of Prussian blue analogues, composed of a shell (≈80 nm thick) of ferromagnetic K_0.3Ni[Cr(CN)₆]_0.8·1.3H₂O (A), T_C ≈ 70 K, surrounding a bulk (≈350 nm) core of photoactive ferrimagnetic Rb_0.4Co[Fe(CN)₆]_0.8·1.2H₂O (B), T_C ≈ 20 K, have been studied [61]. Below nominally 70 K, these CoFe@NiCr samples exhibit a persistent photo induced decrease in low-field magnetization, and these results resemble data from other BA core@shell particles and analogous ABA heterostructured films [44]. This net decrease suggests that the photo induced lattice expansion in the B layer generates a strain-induced decrease in the magnetization of the NiCr layer, similar to a pressure-induced decrease observed in a similar, pure NiCr material and in CoFe@NiCr cubes [10]. Upon further examination, the data also reveal a significant portion of the NiCr shell whose magnetic superexchange, J, is perturbed by the photo induced strain from the CoFe constituent [61].

The photo and thermal responses of the magnetism of CoFe@CrCr-PBs core@shell nanoparticles were investigated down to 5 K and up to 0.5 GPa in 100 G in a home-made, anvil pressure-cell, which was adapted to a probe suitable for use with a commercial magnetometer. The effect of pressure on the Curie temperatures of the CoFe-PBs core (≈25 K) and the CrCr-PBs shell (≈200 K) together with a change of the relaxation temperature of the photo-CTIST (charge-transfer-induced spin-transition) of the CoFe-PBs core (≈125 K) were alike to the operation already presented for the single-phase materials. Specifically, although the magnetic ordering temperature of the CrCr-PBs shell shifts to higher temperatures, the relaxation temperature of the photo-CTIST of the CoFe-PBs core goes down to lower temperatures when the pressure was enlarged, thereby lowering the temperature range in which the CrCr-PBs component is photo switchable [62].

4. Conclusions

The isotropic contract of the Mn-Cr-CN-PBs lattice with the linear reduction of the volume was observed for p ≤ 1.7 GPa. The additional enlargement of the pressure leads to almost no decrease of the volume. The reduction of the crystal lattice size saturates at about 3.2 GPa reaching a volume decrease of approximately 9%. The evidence of an amorphous structure was obtained at above 4.2 GPa. The pressure does not induce any linkage isomerisation. The pressure induced reduction of the lattice size is completely reversible and the original crystal structure recovered if the pressure 4.5 GPa was released, which indicates that the framework extended by Cr-CN-Mn linkages had sufficient elasticity. The effect of pressure on magnetic properties follows the non-monotonous pressure dependence of crystal lattice. At pressures above 3.2 GPa the magnetic transition becomes much broader and T_C is suppressed to zero near 10 GPa, with a corresponding collapse of the ferrimagnetic moment. This is consistent with a pressure-induced amorphous structure of the sample, as was observed in a similar PBs.

On the other hand, Ni-Cr-CN Prussian Blue analogue has a quite different response to pressure. The volume of elementary cell narrows by linear way and isotropic in the range of 0–3.1 GPa, reaching compression of about 15% at 4.7 GPa, which is accompanied by broadening of the peaks, but the crystal character is unaffected. The applied pressure-sensitive shoulder in the Raman spectra can point to the linkage isomerisation, indicating that Cr^III–N≡C–Ni^II fragments grow at the expense of the original Cr^III–N≡C–Ni^II units. However, the effect can be superimposed also by other contributions, such as the presence of surface non-bridging cyanides or shift of the coordinated water.

The comprehensive study of magnetic properties under hydrostatic pressure on PBs revealed principally different behaviour in Mn²⁺-Cr^III-PBs and Cr²⁺-Cr^III-PBs, with prevailing antiferromagnetic super-exchange interaction J_AF compared to Ni²⁺-Cr^III-PBs and Co²⁺-Cr^III-PBs with prevailing ferromagnetic interaction J_F. The strengthened magnetic coupling determined by enhanced values of the monoelectronic overlap integral S and energy gap ∆ between the mixed molecular orbitals under hydrostatic pressure leads to the enlargement of J_AF and the Curie temperature T_C rises. On the contrary, J_F does not change with pressure. In this case, no overlap of magnetic orbitals is present, and that is why the elastic contraction of crystal lattice does not change the overlap. The hydrostatic pressure slightly changes tilting of Cr^IIIC₆ and TM²⁻N4(OH)₂ octants, which leads to a small change of the bonding angle and reorientation of magnetic moments. Both effects reduce T_C and saturated magnetic moment. This small reduction of basic magnetic characteristics was observed in samples with prevailing J_F, but is present even in samples with dominant J_AF; in this case, the effect is masked by a large increase of J_AF due to the enhanced overlapping of magnetic orbitals.

The pressure affects magnetization processes in systems with prevailing J_AF coupling as well as with prevailing J_F interaction, but we expect that pressure does not change the spontaneous magnetization in Mn²⁺-Cr^III-PBs, Ni²⁺-Cr^III-PBs, and Co²⁺-Cr^III-PBs. Pressure-induced magnetic hardening we attribute to variations of magneto-crystalline anisotropy. The enlargement of the saturated magnetization µ_s of Mn²⁺-Cr^III-PBs near T_C was associated with the enhancement of magnetic interactions. The compensation temperature T_comp appears because the algebraic sum of μ(T) for Mn²⁺–N≡C–Cr^III subsystem and Cr^III–C≡N–Ni²⁺ subsystem is zero at T_comp. Pressure affects μ(T) by different ways in these two subsystems, and as a consequence T_comp decreases when the pressure is applied. The applied pressure reduces saturated magnetization of Cr²⁺-Cr^III-PBs. We can assume for cation Cr²⁺ two possibilities: at first Cr²⁺ is high spin, or the second possibility when Cr²⁺ is low spin. It seems that only approximately 30% of Cr²⁺ is high spin. The applied pressure p = 0.84 GPa induces high spin–low spin transition of cca 4.5% of high spin Cr²⁺.

The pressure effect on magnetic properties of PB nano-powders and core–shell heterostructures follows tendencies known from bulk parent PBs. We expect that both systems Ni-NAP and Mn-NAP behave as systems of strongly interacting magnetic particles. The super-exchange interaction is dominant intra-NAP magnetic interaction. The dipole-dipole interaction is dominant inter-NAP magnetic interaction. The dispersion of NAP into an organic matrix leads to a dilution of the mother PBs and consequently the Curie temperature is reduced. The applied pressure strengthens magnetic super-exchange interaction of Mn-NAP with dominant J_AF and increases T_C and pressure decreases T_C for system of Ni-NAP with dominant J_F, which is mainly attributed to less effective magnetic coupling due to the reduction in the bonding angle. The applied pressure increases magnetic moment μ_s. This behaviour is opposite to the behaviour of the mother PBs and is attributed to the reduction of inter-NAP distances by compression of the organic matrix.

A persistent photo-induced reduction in low-field magnetization is a characteristic feature of CoFe@NiCr artificial structures resembling already-known results from PBs core@shell particles and analogical heterostructured coatings. The plain reduction in low-field magnetization for CoFe@NiCr heterostructures indicates that the photo induced lattice expansion resembles a pressure-induced reduction observed on related net NiCr material. The pressure effect on the Curie temperature of the CoFe-PBs core and the CrCr-PBs shell together with a change of the relaxation temperature of the photo-CTIST of the CoFe-PBs core resembles the behaviors known from the single-phase materials. Despite the Curie temperature of the CrCr-PBs shell shifting to higher temperatures, the relaxation temperature of the photo-CTIST of the CoFe-PBs core decreases to lower temperatures when the pressure rises, thereby lowering the temperature region in which the CrCr-PBs part is photo switchable.