Numerical Simulation of Temperature and Fluid Fields in Solidification Process of Ferritic Stainless Steel under Vibration Conditions
Abstract
:1. Introduction
2. Mathematical Model
2.1. Fundamental Equations
2.2. Simulation Parameters Determination
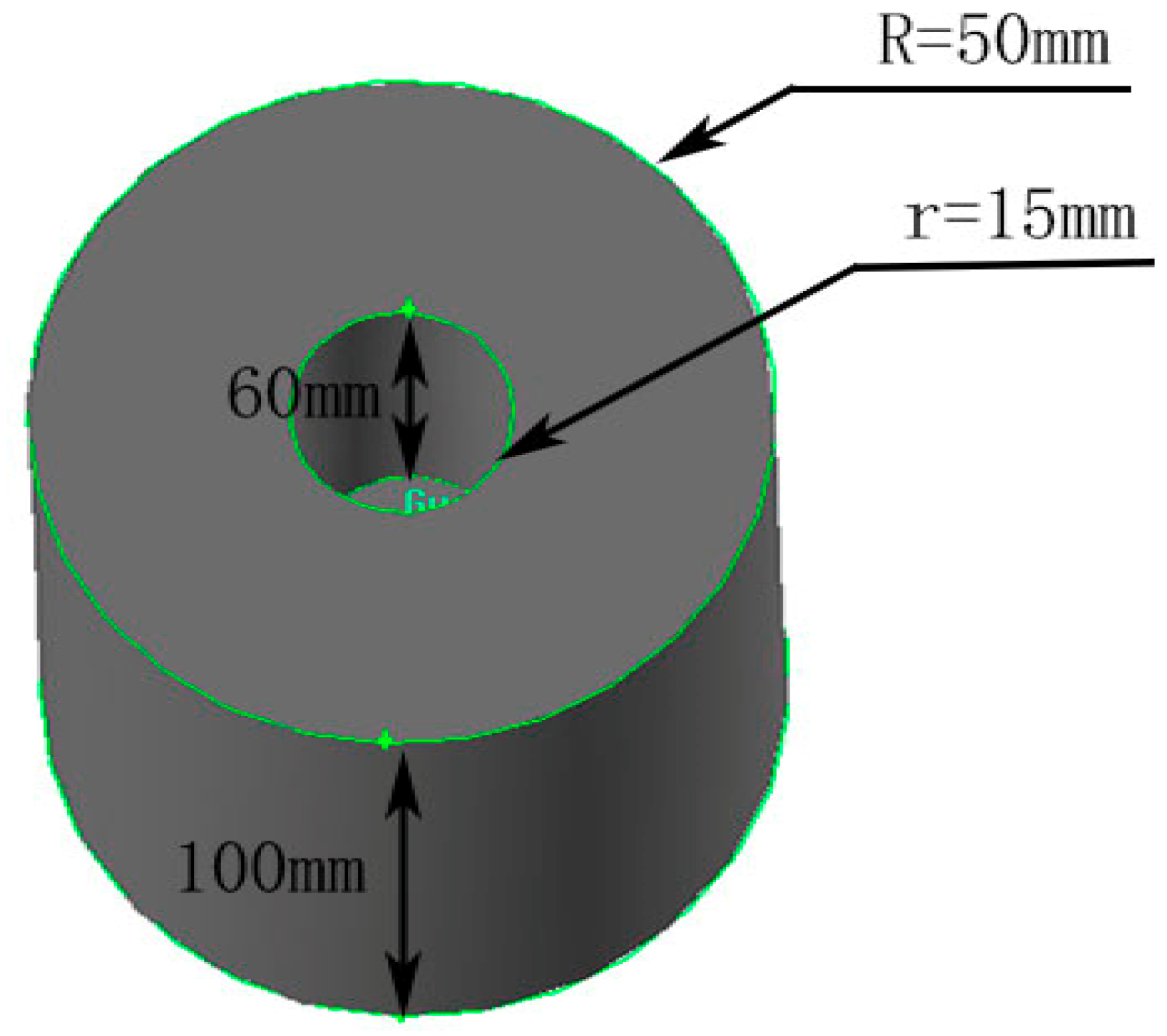
3. Simulation Process
4. Results and Discussion
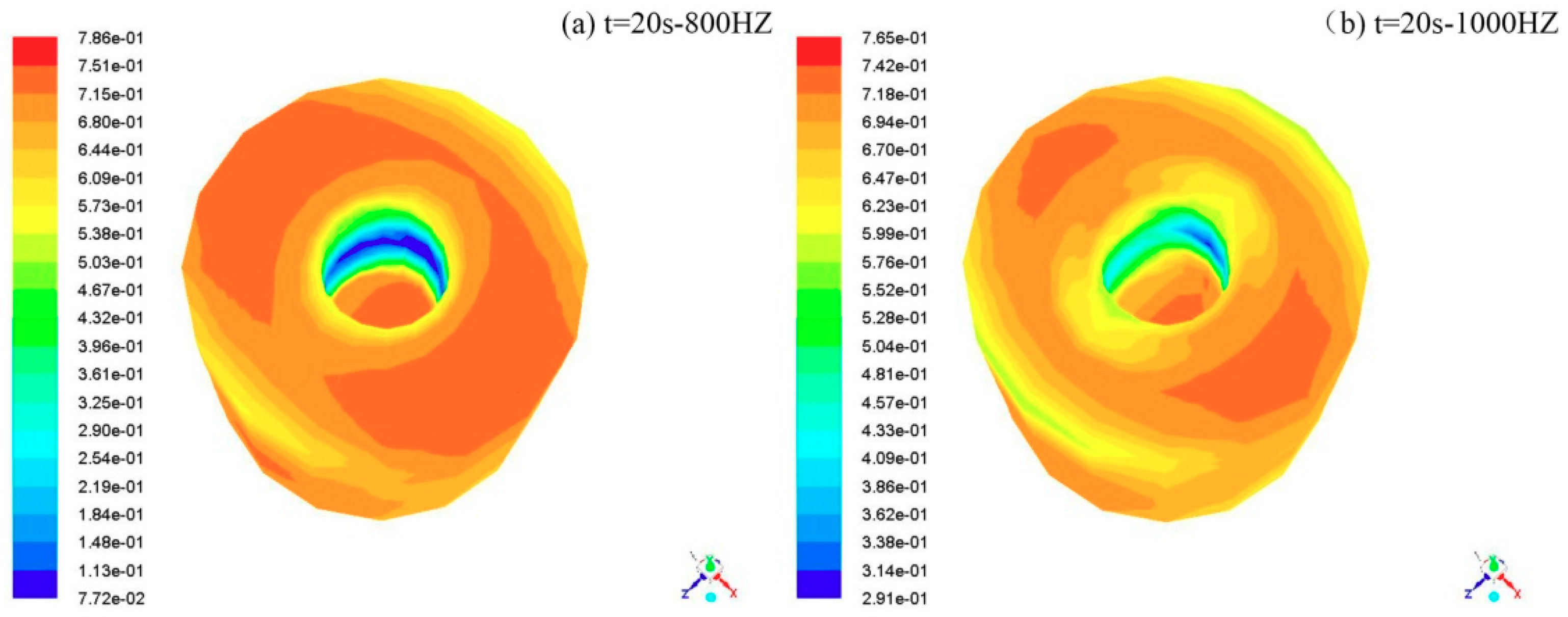
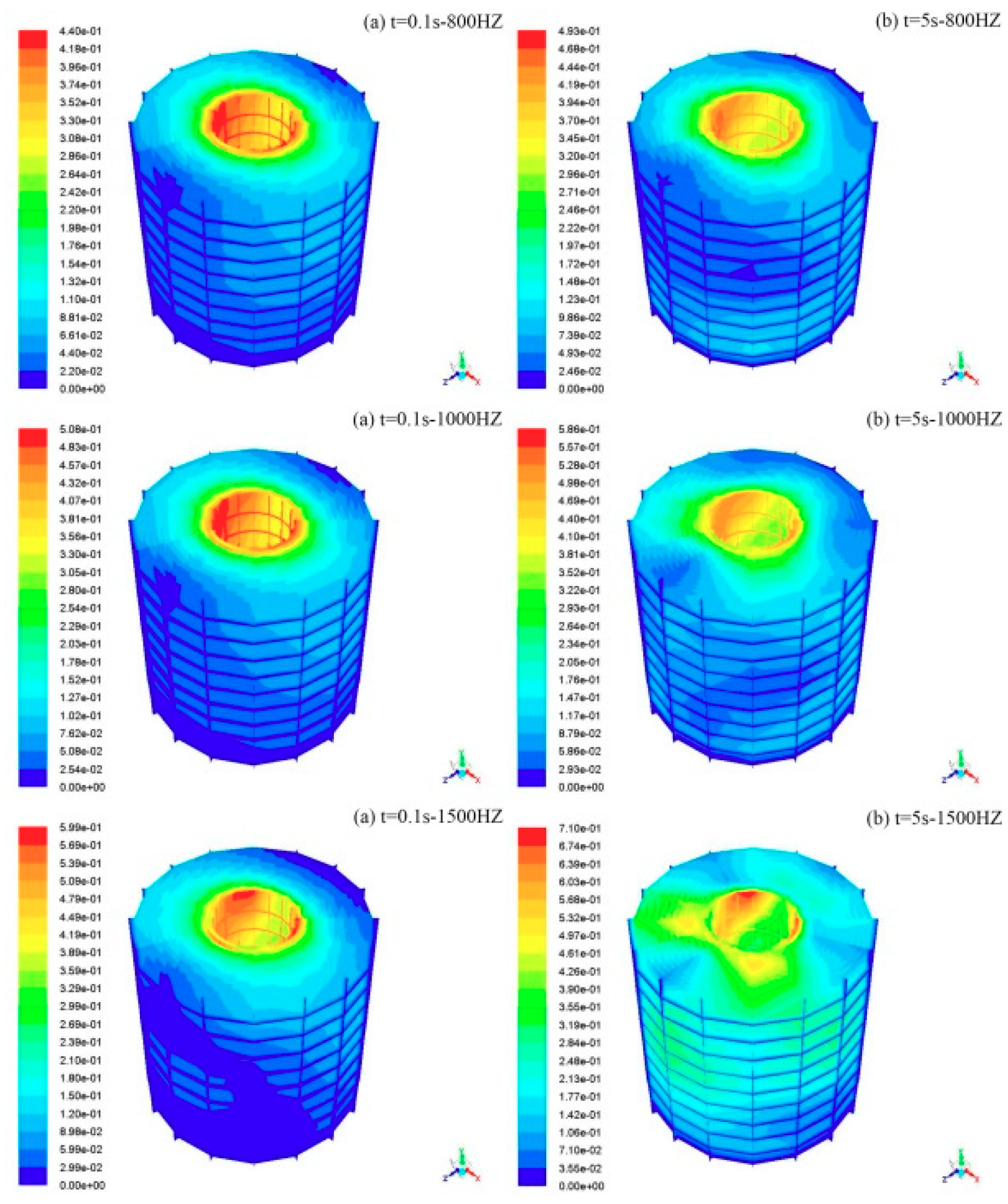
4.1. Temperature Field Distribution
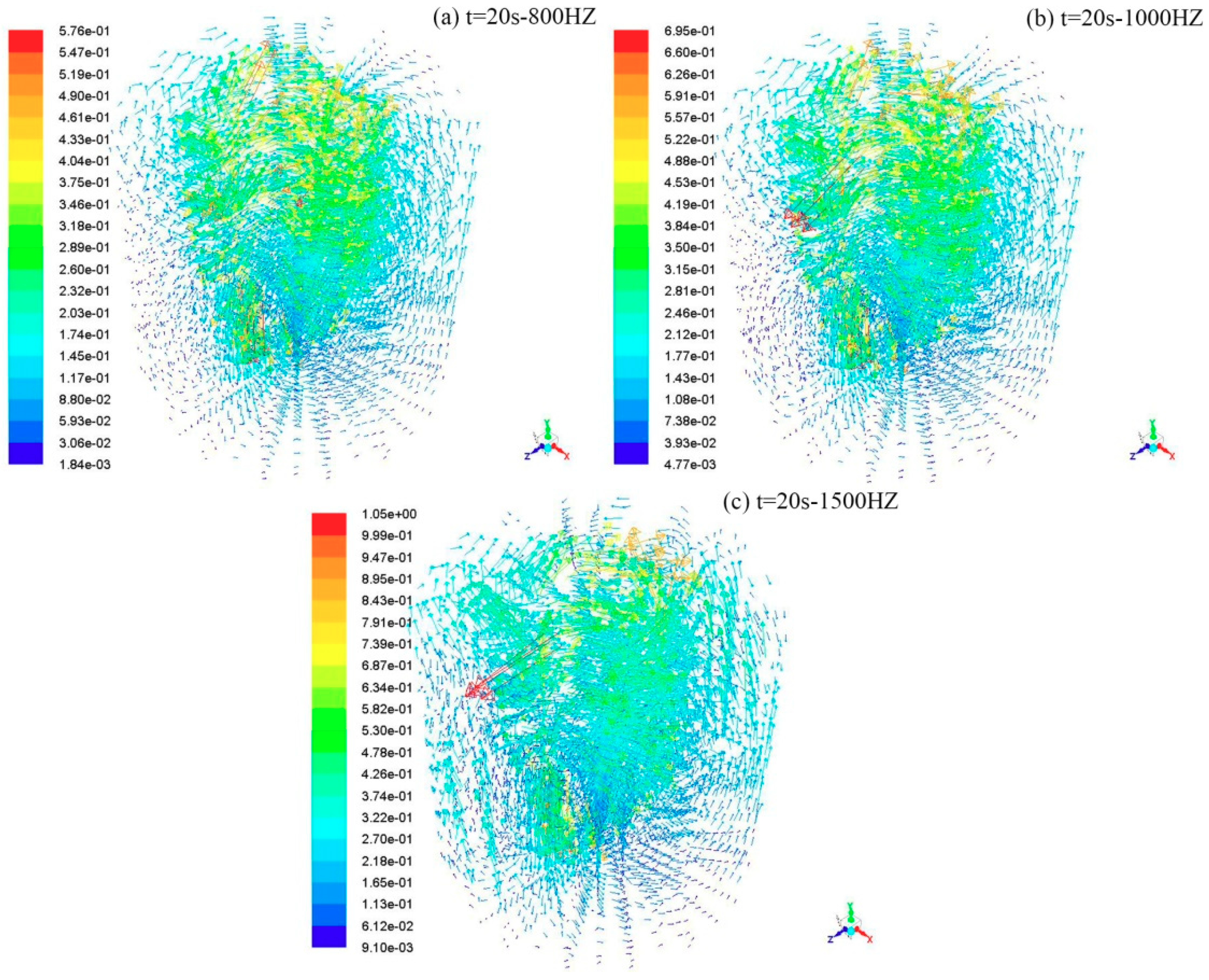
4.2. Flow Field Distribution
5. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Appendix
References
- Gan, Y.; Zhao, P.; Wang, M.; Zhao, H.Z.; Tao, H.B.; Yan, C. Physical analogue of liquid metal original position nucleation stirred by vibration. J. Iron Steel Res. 2006, 18, 9–13. (In Chinese) [Google Scholar]
- Zhang, H.; Tao, H.; Li, F.; Wang, M.; Huang, W.; Zhao, P. Research on mechanism of nucleation in liquid metal excited by vibration. Steel 2008, 43, 20–24. (In Chinese) [Google Scholar]
- Johnson, D.R.; Inui, H.; Muto, S.; Omiya, Y.; Yamanaka, T. Microstructural development during directional solidification of α-seeded TiAl alloys. Acta Mater. 2006, 54, 1077–1085. [Google Scholar] [CrossRef]
- Charbon, C.; Jacot, A.; Rappaz, M. 3D stochastic modelling of equiaxed solidification in the presence of grain movement. Acta Metal. Mater. 1994, 42, 3953–3966. [Google Scholar] [CrossRef]
- Dong, H.; Lee, P. Simulation of the columnar-to-equiaxed transition in directionally solidified Al-Cu alloys. Solid State Phenom. 2005, 139, 129–134. [Google Scholar] [CrossRef]
- Liao, D.; Cao, L.; Sun, F.; Chen, T. Research status and prospect on numerical simulation technology of casting macroscopic process. Acta Metall. 2017, 54, 161–173. (In Chinese) [Google Scholar]
- Kuo, J.K.; Huang, P.H.; Guo, M.J. Removal of CrMo alloy steel components from investment casting gating system using vibration-excited fatigue failure. Int. J. Adv. Manuf. Technol. 2016, 89, 1–11. [Google Scholar] [CrossRef]
- Lyubimov, D.V.; Lyubimova, T.P.; Parshakova, Y.N.; Roux, B.; Lan, C.-W.; Yu, W.-C. Effect of high-frequency vibrations on oriented crystallization of binary alloys. J. Surface Investig. X-ray Synchrotron Neutron Tech. 2009, 3, 116–120. [Google Scholar] [CrossRef]
- Lyubimova, T.P.; Parshakova, Y.N. Numerical investigation of heat and mass transfer during vertical Bridgman crystal growth under rotational vibrations. J. Cryst. Growth 2014, 385, 82–87. [Google Scholar] [CrossRef]
- Su, Y.J.; Liu, X.H.; Wu, Y.F.; Huang, H.-Y.; Xie, J.-X. Numerical simulation of temperature field in horizontal core-filling continuous casting for copper cladding aluminum rods. Inter. J. Miner. Metal. Mater. 2013, 20, 684–692. [Google Scholar] [CrossRef]
- Ko, E.Y.; Yi, K.W.; Park, J.K.; Cho, J.W.; Shin, H.-J. Numerical modeling and analysis of the thermal behavior of copper molds in continuous casting. Met. Mater. Int. 2010, 16, 281–288. [Google Scholar] [CrossRef]
- Xia, Y.J.; Wang, F.M.; Wang, J.L.; Li, G.-Z. Simulation of the continuous casting process in a mold of free-cutting steel 38MnVS based on a MiLE method. Int. J. Miner. Metal. Mater. 2011, 18, 562–569. [Google Scholar] [CrossRef]
- Gandin, C.A.; Rappaz, M. A coupled finite element-cellular automaton model for the prediction of dendritic grain structures in solidification processes. Acta Metal. Mater. 1994, 42, 2233–2246. [Google Scholar] [CrossRef]
- Wang, J.L.; Wang, F.M.; Li, C.R.; Zhang, J.-M. Effects of carbon and phosphor contents on microstructure of a free-cutting steel 9SMn28. Trans. Mater. Heat Treat. 2010, 31, 60–64. [Google Scholar]
- Wang, J.; Wang, F.; Li, C.; Zhang, J. Simulation of solidification microstructure and columnar to equiaxed transition in free-cutting steel 9SMn28 based on a CAFE method. Steel Res. Int. 2010, 81, 150–157. [Google Scholar] [CrossRef]
- Pedlosky, J.; Leibovich, S. Geophysical Fluid Dynamics; Springer: New York, NY, USA, 1987. [Google Scholar]
- Yang, X.; Li, M.; Ma, W.H.; Lv, G.Q.; Luo, T.; Wang, Y.F. Numerical simulation on the heat transfer performance of multicrystalline silicon in directional solidification process. Appl. Mech. Mater. 2013, 444–445, 1412–1416. [Google Scholar] [CrossRef]
- Mills, K.C.; Su, Y.; Li, Z.; Brooks, R.F. Equations for the calculation of the thermophysical properties of stainless steel. ISIJ Intern. 2007, 44, 1661–1668. [Google Scholar] [CrossRef]
- Liu, L.; Nakano, S.; Kakimoto, K. Dynamic simulation of temperature and iron distributions in a casting process for crystalline silicon solar cells with a global model. J. Cryst. Growth 2006, 292, 515–518. [Google Scholar] [CrossRef]







| Specific Heat/ | Viscosity/ | Thermal Conductivity/ | ||
|---|---|---|---|---|
| 293 | 7700 | 460 | 0.00225 | 35.100 |
| 1813 | 6800 | 715 | 0.007307 | 34.669 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, W.; Chen, J.; Li, M.; Wang, A.; Su, M. Numerical Simulation of Temperature and Fluid Fields in Solidification Process of Ferritic Stainless Steel under Vibration Conditions. Crystals 2019, 9, 174. https://doi.org/10.3390/cryst9030174
Wang W, Chen J, Li M, Wang A, Su M. Numerical Simulation of Temperature and Fluid Fields in Solidification Process of Ferritic Stainless Steel under Vibration Conditions. Crystals. 2019; 9(3):174. https://doi.org/10.3390/cryst9030174
Chicago/Turabian StyleWang, Wenli, Jing Chen, Miaomiao Li, Along Wang, and Mengyao Su. 2019. "Numerical Simulation of Temperature and Fluid Fields in Solidification Process of Ferritic Stainless Steel under Vibration Conditions" Crystals 9, no. 3: 174. https://doi.org/10.3390/cryst9030174
APA StyleWang, W., Chen, J., Li, M., Wang, A., & Su, M. (2019). Numerical Simulation of Temperature and Fluid Fields in Solidification Process of Ferritic Stainless Steel under Vibration Conditions. Crystals, 9(3), 174. https://doi.org/10.3390/cryst9030174




