Flexible Photonic Nanojet Formed by Cylindrical Graded-Index Lens
Abstract
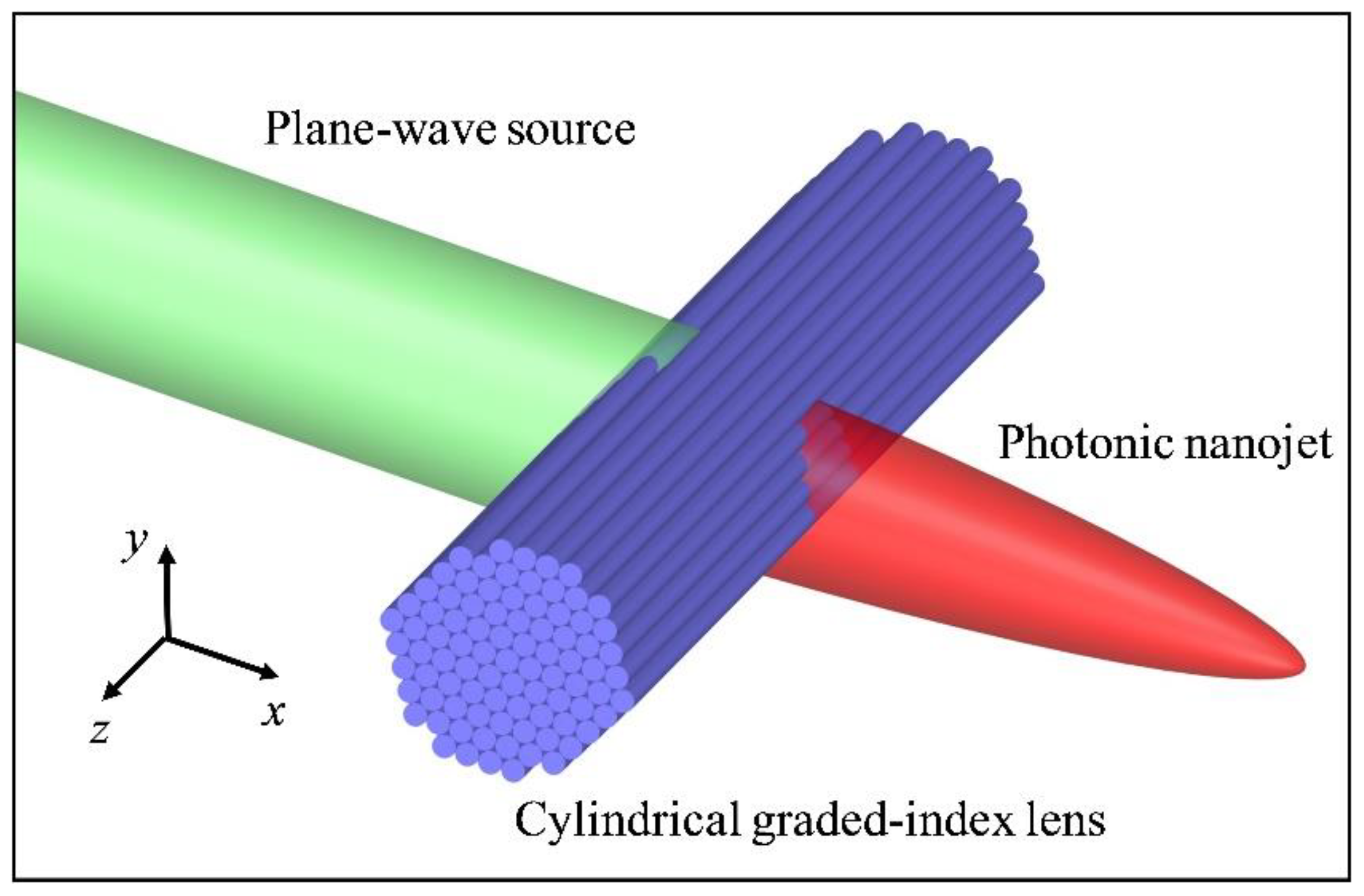
:1. Introduction
2. Physical Modeling
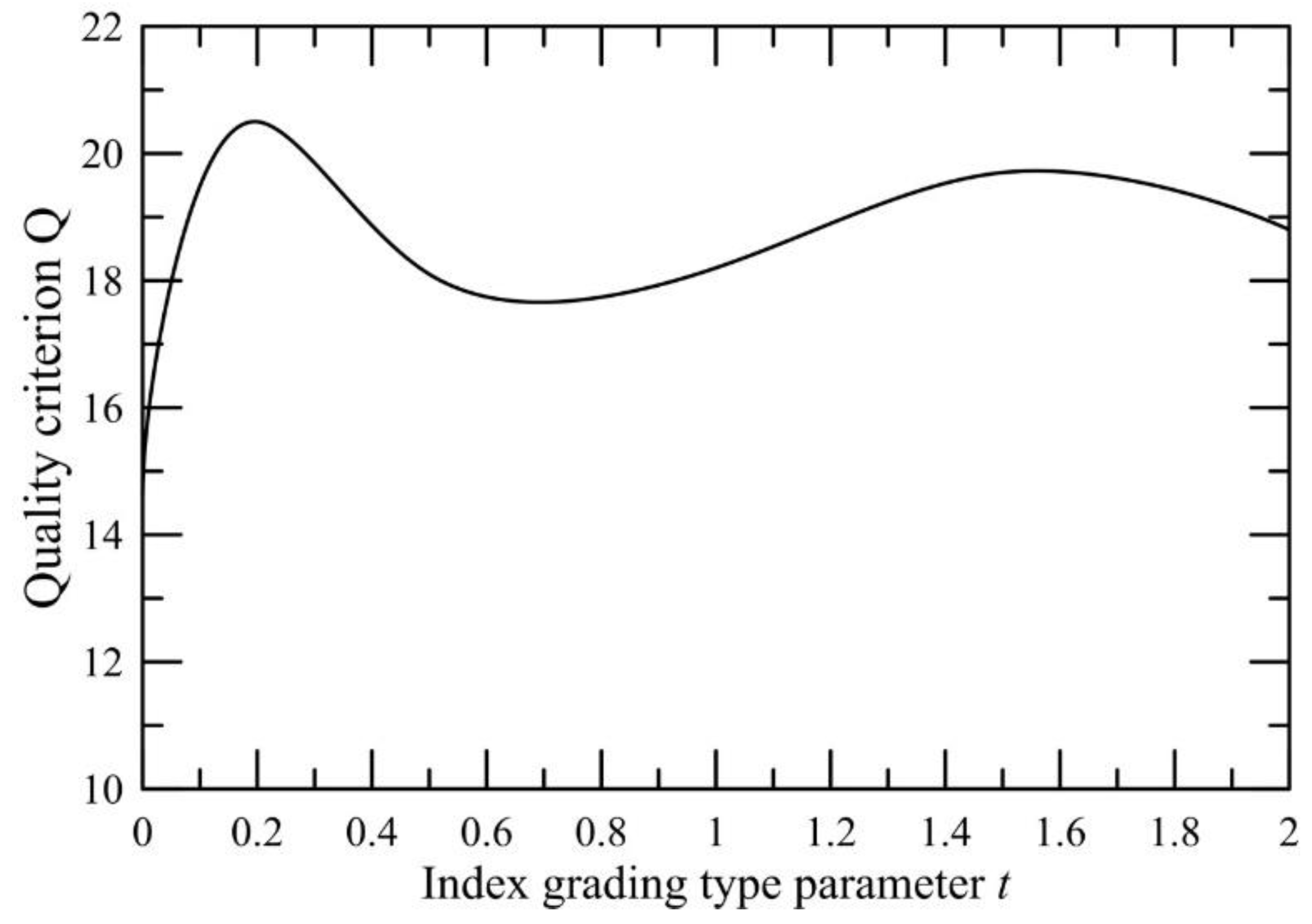
3. Results and Discussion
4. Conclusions
Funding
Acknowledgments
Conflicts of Interest
References
- Wang, Z.; Guo, W.; Li, L.; Lukyanchuk, B.; Khan, A.; Liu, Z.; Chen, Z.; Hong, M. Optical virtual imaging at 50 nm lateral resolution with a white-light nanoscope. Nat. Commun. 2011, 2, 218. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Upputuri, P.; Pramanik, M. Microsphere-aided optical microscopy and its applications for super-resolution imaging. Opt. Commun. 2017, 404, 32–41. [Google Scholar] [CrossRef]
- Li, Y.; Xin, H.; Liu, X.; Zhang, Y.; Lei, H.; Li, B. Trapping and detection of nanoparticles and cells using a parallel photonic nanojet array. ACS Nano 2016, 10, 5800–5808. [Google Scholar] [CrossRef] [PubMed]
- Shakhov, A.; Astaflev, A.; Nadtochenko, V. Microparticle manipulation using femtosecond photonic nanojet-assisted laser cavitation. Opt. Lett. 2018, 43, 1858–1861. [Google Scholar] [CrossRef]
- Wu, W.; Katsnelson, A.; Memis, O.G.; Mohseni, H. A deep sub-wavelength process for the formation of highly uniform arrays of nanoholes and nanopillars. Nanotechnology 2007, 18, 485302. [Google Scholar] [CrossRef] [Green Version]
- Jacassi, A.; Tantussi, F.; Dipalo, M.; Biagini, C.; Maccaferri, N.; Bozzola, A.; Angelis, F. Scanning probe photonic nanojet lithography. ACS Appl. Mater. Interfaces 2017, 9, 32386–32393. [Google Scholar] [CrossRef] [PubMed]
- Li, X.; Chen, Z.; Taflove, A.; Backman, V. Optical analysis of nanoparticles via enhanced backscattering facilitated by 3-D photonic nanojets. Opt. Express. 2005, 13, 526–533. [Google Scholar] [CrossRef] [PubMed]
- Kong, S.; Sahakian, A.V.; Heifetz, A.; Taflove, A.; Backman, A. Robust detection of deeply subwavelength pits in simulated optical data-storage disks using photonic jets. Appl. Phys. Lett. 2008, 92, 211102. [Google Scholar] [CrossRef]
- Betzig, E.; Trautman, J.K. Near-field optics: Microscopy, spectroscopy, and surface modification beyond the diffraction limit. Science 1992, 257, 189–195. [Google Scholar] [CrossRef] [PubMed]
- Chen, Z.; Taflove, A.; Backman, V. Photonic nanojet enhancement of backscattering of light by nanoparticles: a potential novel visible-light ultramicroscopy technique. Opt. Express 2004, 12, 1214–1220. [Google Scholar] [CrossRef]
- Ferrand, P.; Wenger, J.; Devilez, A.; Pianta, M.; Stout, B.; Bonod, N.; Popov, E.; Rigneault, H. Direct imaging of photonic nanojets. Opt. Express 2008, 16, 6930–6940. [Google Scholar] [CrossRef]
- Kim, M.; Scharf, T.; Mühlig, S.; Rockstuhl, C.; Herzig, H. Engineering photonic nanojets. Opt. Express 2011, 19, 10206–10220. [Google Scholar] [CrossRef] [PubMed]
- Darafsheh, A.; Walsh, G.; Dal Negro, L.; Astratov, V. Optical super-resolution by high-index liquid-immersed microspheres. Appl. Phys. Lett. 2012, 101, 141128. [Google Scholar] [CrossRef]
- Liu, C.; Wang, Y. Real-space observation of photonic nanojet in microspheres. Phys. E 2014, 61, 141–147. [Google Scholar] [CrossRef]
- Darafsheh, A.; Bollinger, D. Systematic study of the characteristics of the photonic nanojets formed by dielectric microcylinders. Opt. Commun. 2017, 402, 270–275. [Google Scholar] [CrossRef]
- Darafsheh, A. Influence of the background medium on imaging performance of microsphere-assisted super-resolution microscopy. Opt. Lett. 2017, 42, 735–738. [Google Scholar] [CrossRef] [PubMed]
- Jalalia, T.; Ernib, D. Highly confined photonic nanojet from elliptical particles. J. Mod. Opt. 2014, 61, 1069–1076. [Google Scholar] [CrossRef]
- Wu, M.; Huang, B.; Chen, R.; Yang, Y.; Wu, J.; Ji, R.; Chen, X.; Hong, M. Modulation of photonic nanojets generated by microspheres decorated with concentric rings. Opt. Express 2015, 23, 20096–20103. [Google Scholar] [CrossRef] [PubMed]
- Wu, M.; Chen, R.; Soh, J.; Shen, Y.; Jiao, L.; Wu, J.; Chen, X.; Ji, R.; Hong, M. Super-focusing of center-covered engineered microsphere. Sci. Rep. 2016, 6, 31637. [Google Scholar] [CrossRef] [Green Version]
- Liu, C.; Lin, F. Geometric effect on photonic nanojet generated by dielectric microcylinders with non-cylindrical cross-sections. Opt. Commun. 2016, 380, 287–296. [Google Scholar] [CrossRef]
- Wu, M.; Chen, R.; Ling, J.; Chen, Z.; Chen, X.; Ji, R.; Hong, M. Creation of a longitudinally polarized photonic nanojet via an engineered microsphere. Opt. Lett. 2017, 42, 1444–1447. [Google Scholar] [CrossRef] [PubMed]
- Yang, J.; Twardowski, P.; Gerard, P.; Duo, Y.; Fontaine, J.; Lecler, S. Ultra-narrow photonic nanojets through a glass cuboid embedded in a dielectric cylinder. Opt. Express 2018, 26, 3723–3731. [Google Scholar] [CrossRef]
- Zhou, Y.; Gao, H.; Teng, J.; Luo, X.; Hong, M. Orbital angular momentum generation via a spiral phase microsphere. Opt. Lett. 2018, 43, 34–37. [Google Scholar] [CrossRef]
- Chen, L.; Zhou, Y.; Wu, M.; Hong, M. Remote-mode microsphere nano-imaging: new boundaries for optical microscopes. Opto-Electron. Adv. 2018, 1, 170001. [Google Scholar] [CrossRef]
- Kong, S.; Taflove, A.; Backman, V. Quasi one-dimensional light beam generated by a graded-index microsphere. Opt. Express 2009, 17, 3722–3731. [Google Scholar] [CrossRef]
- Geints, Y.; Zemlyanov, A.; Panina, E. Photonic nanojet calculations in layered radially inhomogeneous micrometer-sized spherical particles. J. Opt. Soc. Am. B 2011, 28, 1825–1830. [Google Scholar] [CrossRef]
- Liu, C. Superenhanced photonic nanojet by core-shell microcylinders. Phys. Lett. A 2012, 376, 1856–1860. [Google Scholar] [CrossRef]
- Shen, Y.; Wang, L.; Shen, J. Ultralong photonic nanojet formed by a two-layer dielectric microsphere. Opt. Lett. 2014, 39, 4120–4123. [Google Scholar] [CrossRef]
- Wu, P.; Li, J.; Wei, K.; Yue, W. Tunable and ultra-elongated photonic nanojet generated by a liquid-immersed core–shell dielectric microsphere. Appl. Phys. Express 2015, 8, 112001. [Google Scholar] [CrossRef]
- Minin, I.; Minin, O. Terahertz artificial dielectric cuboid lens on substrate for super-resolution images. Opt. Quant. Electron. 2017, 49, 326. [Google Scholar] [CrossRef]
- Xing, H.; Zhou, W.; Wu, Y. Side-lobes-controlled photonic nanojet with a horizontal graded-index microcylinder. Opt. Lett. 2018, 43, 4292–4295. [Google Scholar] [CrossRef] [PubMed]
- Liu, C.; Yen, T.; Minin, O.; Minin, I. Engineering photonic nanojet by a graded-index micro-cuboid. Phys. E 2018, 98, 105–110. [Google Scholar] [CrossRef]
- Geints, Y.; Zemlyanov, A.; Minin, O.; Minin, I. Systematic study and comparison of photonic nanojets produced by dielectric microparticles in 2D- and 3D-spatial configurations. J. Opt. 2018, 20, 065606. [Google Scholar] [CrossRef]
- Kotlyar, V.; Stafeev, S. Modeling the sharp focus of a radially polarized laser mode using a conical and a binary microaxicon. J. Opt. Soc. Am. B 2010, 27, 1991–1997. [Google Scholar] [CrossRef]
- Geints, Y.; Zemlyanov, A.; Panina, E. Microaxicon generated photonic nanojets. J. Opt. Soc. Am. B 2015, 32, 1570–1574. [Google Scholar] [CrossRef]
- Liu, C. Photonic jets produced by dielectric micro cuboids. Appl. Opt. 2015, 54, 8694–8699. [Google Scholar] [CrossRef]
- Yue, L.; Yan, B.; Wang, Z. Photonic nanojet of cylindrical metalens assembled by hexagonally arranged nanofibers for breaking the diffraction limit. Opt. Lett. 2016, 41, 1336–1339. [Google Scholar] [CrossRef]
- Yue, L.; Yan, B.; Monks, J.; Wang, Z.; Tung, N.; Lam, V.; Minin, O.; Minin, I. Production of photonic nanojets by using pupil-masked 3D dielectric cuboid. J. Phys. D: Appl. Phys. 2017, 50, 175102. [Google Scholar] [CrossRef]
- Pierron, R.; Zelgowski, J.; Pfeiffer, P.; Fontaine, J.; Lecler, S. Photonic jet: key role of injection for etchings with a shaped optical fiber tip. Opt. Lett. 2017, 42, 2707–2709. [Google Scholar] [CrossRef] [PubMed]
- Taflove, A.; Hagness, S. Computational Electrodynamics: The Finite Difference Time Domain Method; Artech House: Boston, MA, USA, 1998. [Google Scholar]
- Poco, J.; Hrubesh, L. Method of producing optical quality glass having a selected refractive index. U.S. Patent 6,158,244, 2008. [Google Scholar]
- Zhu, Q.; Fu, Y. Graded index photonic crystals: A review. Ann. Phys.-Berlin 2015, 527, 205–218. [Google Scholar] [CrossRef] [Green Version]
- Ruskuc, A.; Koehler, P.; Weber, M.; Andres-Arroyo, A.; Frosz, M.; Russell, P.; Euser, T. Excitation of higher-order modes in optofluidic photonic crystal fiber. Opt. Express 2018, 26, 30245–30254. [Google Scholar] [CrossRef] [PubMed]





© 2019 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Liu, C.-Y. Flexible Photonic Nanojet Formed by Cylindrical Graded-Index Lens. Crystals 2019, 9, 198. https://doi.org/10.3390/cryst9040198
Liu C-Y. Flexible Photonic Nanojet Formed by Cylindrical Graded-Index Lens. Crystals. 2019; 9(4):198. https://doi.org/10.3390/cryst9040198
Chicago/Turabian StyleLiu, Cheng-Yang. 2019. "Flexible Photonic Nanojet Formed by Cylindrical Graded-Index Lens" Crystals 9, no. 4: 198. https://doi.org/10.3390/cryst9040198
APA StyleLiu, C. -Y. (2019). Flexible Photonic Nanojet Formed by Cylindrical Graded-Index Lens. Crystals, 9(4), 198. https://doi.org/10.3390/cryst9040198




