Niobium Base Superalloys: Achievement of a Coherent Ordered Precipitate Structure in the Nb Solid-Solution
Abstract
:1. Introduction
- -
- (1) (planar) epitaxy occurs when a small quantity of atoms are disposed onto the surface of atoms having a different nature from the deposited one,
- -
- (2) the large number of atoms imposes their crystal structure to the small amount of atoms present on their surface (epitaxy),
- -
- (3) with the increase of the atom quantity, the atoms in contact with a surface, can adopt their own crystal structure (i.e., independently from the atoms they are in contact).
- -
- the order-hardening, is “related to the possible creation of a surface of antiphase boundary (APB) when a dislocation of the disordered matrix cuts across the precipitates” [4] (p. 2141),
- -
- the stacking-fault hardening, related to the “creation of a high energy surface” through the dissociation of perfect dislocations into two partials, which hinders dislocation climb and cross-slip mechanisms. In γ/γ’ alloys “calculations show that at room temperatures, the APB energy accounts for about 80% of the magnitude of the flow stress” [6] (p. 563).
- -
- alloys based on the Nb-Ti-Al system (for instance [12,13]). The idea behind the addition of Al and Ti is to increase to oxidation resistance and to get a low-density alloy: various amounts of Cr, V, Mo, Hf, W, Zr, and/or Si are added in order to increase the oxidation resistance and the mechanical properties [13].
- -
- -
2. Method: Alloy Design towards the Achievement of Coherency
2.1. Starting Aspects from the Paper Entitled “Potential Niobium Superalloys
2.2. Comments about the Nb-Ni System
2.3. In Search of Coherency for Nb Superalloy
- -
- the ‘affinity’ between Ni and the third element should be high, at least, higher than the one between Nb and Ni, so as to favour the formation of a phase with Ni. With this affinity condition, as Ni is essentially an element of the ordered precipitates, the third element should be within the precipitates and not within the Nb solid-solution,
- -
- the solubility of the third element in Nb must be very large in order, (1) to be statistically present everywhere within the Nb matrix and close by Ni and, (2) to avoid the formation of compounds with Nb. The second point leads to a weak ‘affinity’ between the third element and Nb.
2.4. The Nb-Hf-Ni System
2.5. Design of the Nb-Hf-Ni Ternary Alloy
- -
- the maximum Ni solubility in Nb is ~5 at% (at about 1290 °C),
- -
- the limit of the BCC crystal structure of Nb with Hf in solid-solution is ~10 at% Hf at 250 °C [47],
- -
- the solubility of Ni in Hf is lower than 1–2 at% Ni [49]: it was supposed that the addition of Hf to Nb alloy would reduce the Ni solubility,
- -
- the stoichiometry of the Ni-Hf ordered phase closest to the Hf rich side of the phase diagram is NiHf2: the Hf content is two times the Ni one.
- -
- any modifications induced by a chemical for the three binary systems were supposed to be kept on a linear basis for the ternary system. This assumption is questionable but due to the rather small additions of Ni and Hf, it can be considered for a first approach. This rule can be applied for an estimate of the reduction of Ni solubility in Nb with addition of Hf.
3. Materials and Experimental Methods
3.1. Specimen Preparation by Focussed Ion Beam (FIB) Milling
3.2. Atom Probe Tomography
3.3. Transmission Electron Microscopy
4. Experimental Results
4.1. Transmission Electron Microscopy Characterization
- -
- (a) relaxed dislocations pairs corresponding to the shearing of the matrix; there is not any APB formed as the matrix is a disordered solid-solution, the two dislocations of the pairs are rather far apart (relaxed),
- -
- (b) pinched regions, which are segments of strongly coupled dislocation pair, corresponding to the shearing of ordered coherent precipitates; this geometrical configuration reduces the size of the anti-phase domain boundary during shearing of the ordered precipitates [59] (p. 336). Between these pinched regions, the dislocation pair is relaxed.
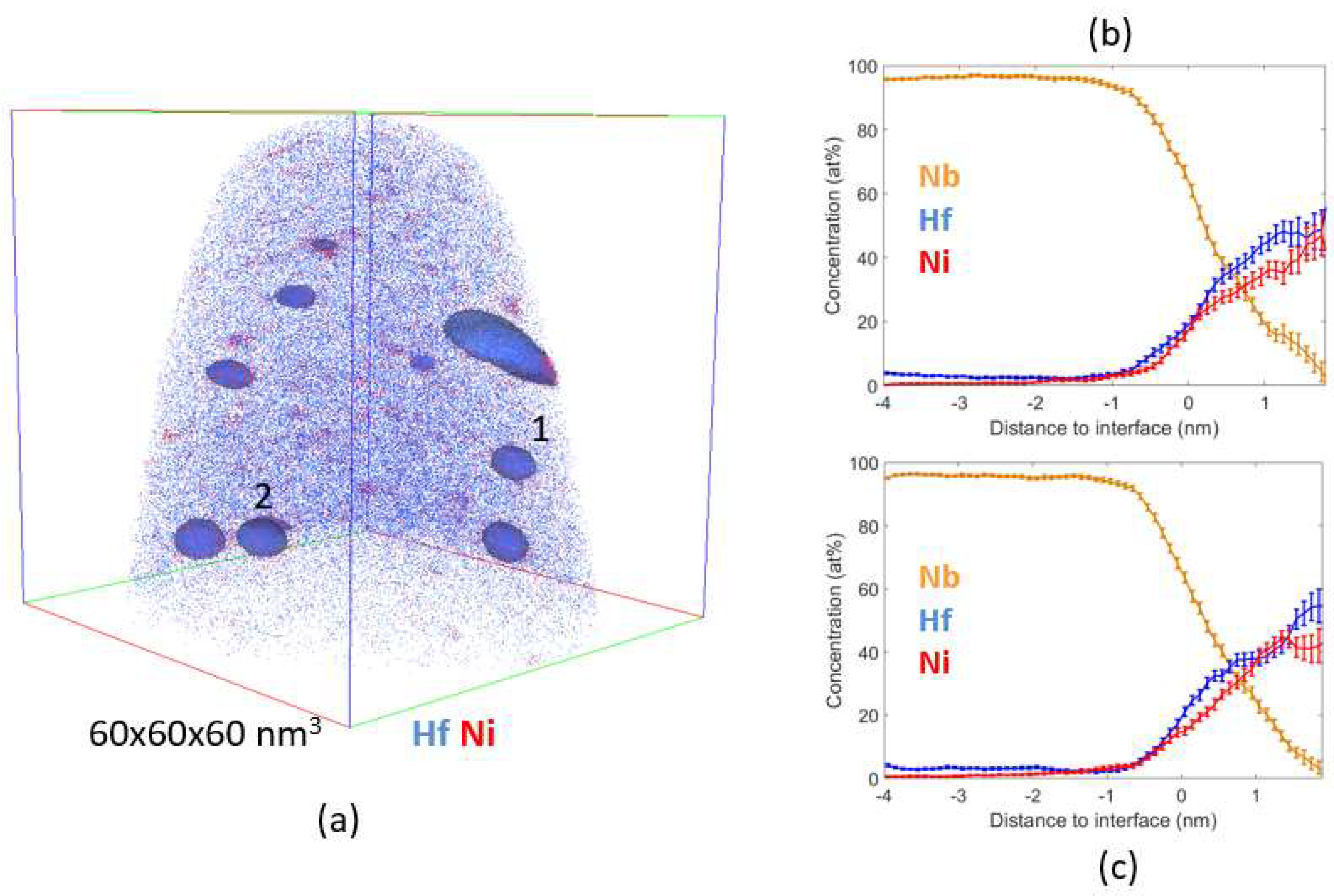
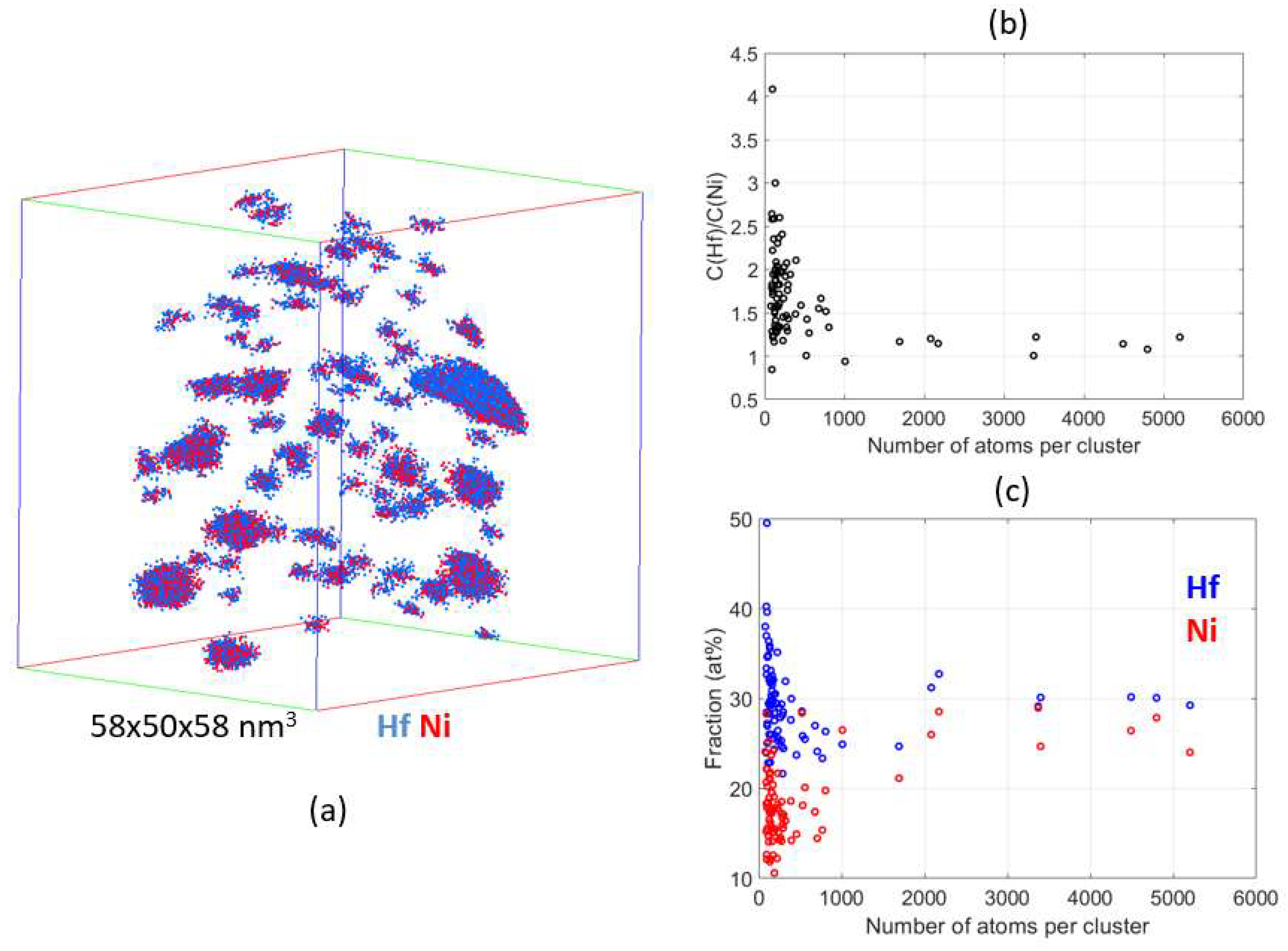
4.2. Atom Probe Tomography Characterization
5. Discussion
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Sims, C.T.; Stoloff, N.S.; Hagel, W.C. Superalloys II; John Wiley & Sons: Hoboken, NJ, USA, 1987. [Google Scholar]
- Reed, R.C. Superalloys: Fundamentals and Applications; Cambridge University Press: Cambridge, UK, 2006. [Google Scholar]
- Anton, D.L. Ni3Al in Nickel-based superalloys. In Intermetallic Compounds, Principles and Practice; Westbrook, J.H., Fleischer, R.L., Eds.; John Wiley & Sons: Hoboken, NJ, USA, 1995; Volume 2, pp. 3–15. [Google Scholar]
- Strudel, J.-L. Mechanical properties of multiphase alloys. In Physical Metallurgy, 4th ed; Cahn, R.W., Haasen, P., Eds.; North Holland: Amsterdam, The Netherlands, 1996; Volume 3, pp. 2015–2206. [Google Scholar]
- Martin, J.W. Micromechanisms in Particle-Hardened Alloys; Cambridge University Press: Cambridge, UK, 1980. [Google Scholar]
- Kear, B.H.; Pope, D.P. Role of refractory elements in strengthening of γ’ and γ’ precipitation hardened nickel base superalloys. In Superalloys, Supercomposites and Superceramics; Materials Science Series; Tien, J.K., Caulfield, T., Eds.; Academic Press: Boston, MA, USA, 1989; pp. 545–582. [Google Scholar]
- Saint-Antonin, F.; Strudel, J.-L. Stress relaxation in Ni base superalloy after low initial straining. In Proceedings of the 4th International Conference on Creep and Fracture of Engineering Materials and Structures, Swansea, UK, 1–6 April 1990; pp. 303–312. [Google Scholar]
- Saint-Antonin, F. Etude Microstructurale du Comportement en Relaxation d’un Superalliage Base Ni à 650°C. Ph.D. Thesis, Ecole des Mines de Paris, Paris, France, 8 February 1991. [Google Scholar]
- Loria, E.A. Niobium-base superalloys via powder metallurgy technology. J. Met. 1987, 39, 22–26. [Google Scholar] [CrossRef]
- Stephens, J.J.; Ahmad, I. High Temperature Niobium Alloys; TMS: Warrendale, PA, USA, 1991. [Google Scholar]
- Heisterkamp, F.; Carneiro, T. Niobium: Future possibilities-technology and the market place. In Proceedings of the International Symposium on Niobium Science & Technology, Orlando, FL, USA, 2–5 December 2001; pp. 1109–1159. [Google Scholar]
- Wheeler, R.; Perungulam, S.; Banerjee, S.; Hou, D.-H.; Grylls, R.J.; Fraser, H.L. Atomic structure and deformation of Nb-Ti-Al alloys. In Proceedings of the 2nd International Symposium on Structural Intermetallics, Champion, PA, USA, 21–25 September 1997; Nathal, M.V., Darolia, R., Liu, C.T., Martin, P.L., Miracle, D.B., Wagner, R., Yamaguchi, M., Eds.; TMS: Warrendale, PA, USA, 1997; pp. 851–858. [Google Scholar]
- Feng, W.; Xin, Z.; Run, B.; Xiaomei, C.; Xiaoming, Z.; Zhongkui, L. Characteristics of a Multicomponent and Low-Density Nb-Ti-Al Alloy. In Proceedings of the 18th Plansee Seminar, Reutte, Austria, 3–7 June 2013; pp. 691–696. [Google Scholar]
- Bewlay, B.P.; Jackson, M.R.; Lipsitt, H.A. The Balance of Mechanical and Environmental Properties of a Multi-element Niobium-Niobium Silicide-Based In-Situ Composite. Metall. Mater. Trans. A 1996, 27, 3801–3808. [Google Scholar] [CrossRef]
- Kasama, A.; Tanaka, H.; Tan, Y.; Ma, C.; Skamoto, K.; Tanahashi, H.; Fujikura, M.; Tanaka, R. Microstructure and mechanical properties of niobium-based refractory metals. In Proceedings of the Tantalum and Niobium Symposium, San Francisco, CA, USA, 22–25 October 2000; pp. 213–233. [Google Scholar]
- Kimura, Y.; Mishima, Y.; Yamaoka, H.; Sekido, N. Processing, microstructure, and mechanical properties of (Nb)/Nb5Si3 two-phase alloys. Metall. Mater. Trans. A 2005, 36, 483–488. [Google Scholar] [CrossRef]
- Drawin, S.; Monchoux, J.P.; Raviart, J.L.; Couret, A. Microstructural properties of Nb-Si based alloys manufactured by powder metallurgy. Adv. Mater. Res. 2011, 278, 533–538. [Google Scholar] [CrossRef]
- Su, L.; Jia, L.; Feng, Y.; Zhang, H.; Yuan, S.; Zhang, H. Microstructure and room-temperature fracture toughness of directionally solidified Nb-Si-Ti-Cr-Al-Hf alloy. Mater. Sci. Eng. A 2013, 560, 672–677. [Google Scholar] [CrossRef]
- Seemüller, C.; Heilmaier, M.; Hartwig, T.; Mulser, M.; Adkins, N.; Wickins, M. Influence of microstructure and processing on mechanical properties of advanced Nb-silicide alloys. Mater. Res. Soc. Symp. Proc. 2013, 1516, 317–322. [Google Scholar] [CrossRef]
- Tan, Y.; Ma, C.L.; Kasama, A.; Tanaka, R.; Yang, J.-M. High temperature mechanical behavior of Nb-Mo-ZrC. Mater. Sci. Eng. A 2003, 355, 260–266. [Google Scholar] [CrossRef]
- Shaboldo, O.P.; Vitorskii, Y.M.; Sagaradze, V.V.; Volkova, E.G. Effect of heat treatment on the fine structure and properties of a niobium-base superalloy. Phys. Met. Metall. 2016, 117, 1281–1287. [Google Scholar] [CrossRef]
- Fujikura, M.; Kasama, A.; Tanaka, R.; Hanada, S. Effect of alloy chemistry on the high temperature strengths and room temperature fracture toughness of advanced Nb-based alloys. Mater. Trans. 2004, 45, 493–501. [Google Scholar] [CrossRef]
- Tanaka, R.; Kasam, A.; Fujikura, M.; Iwanaga, I.; Tanaka, H.; Matsumura, Y. Newly developed niobium-base superalloys for elevated temperature application. In Proceedings of the International Symposium on Niobium for High Temperature Applications, Araxa, MG, Brazil, 1–3 December 2003; Kim, Y.-W., Carneiro, T., Eds.; TMS: Warrendale, PA, USA, 2004; pp. 89–98. [Google Scholar]
- Satya Prasad, V.V.; Baligidad, R.G.; Gokhale, A.A. Niobium and Other High Temperature Refractory Metals for Aerospace Applications. In Aerospace Materials and Material Technologies; Indian Institute of Metals Series; Prasad, N., Wanhill, R., Eds.; Springer: Singapore, 2017; pp. 267–288. [Google Scholar]
- Karpov, M.I. Niobium-base refractory alloys with silicide and carbide hardening current status and prospects. Met. Sci. Heat Treat. 2018, 60, 7–12. [Google Scholar] [CrossRef]
- Philibert, J. Atom Movements and Mass Transport in Solids; Monographie de Physique, Les Editions du CNRS: Paris, France, 1991. [Google Scholar]
- Hirth, J.P.; Lothe, J. Theory of Dislocations, 2nd ed.; John Wiley & Sons: Hoboken, NJ, USA, 1982. [Google Scholar]
- Umakoshi, Y. Deformation of intermetallic compounds, Chapter 6. In Plastic Deformation and Fracture of Materials; Materials Science and Technology: A Comprehensive Treatment Series; Cahn, R.W., Haasen, P., Kramer, E.J., Eds.; VCH Edition: Weinheim, Germany, 1993; Volume 6, pp. 251–310. [Google Scholar]
- Nash, P.; Nash, A. Nb-Ni (Niobium-Nickel). In Phase Diagrams of Binary Nickel Alloys; Nash, P., Ed.; ASM International: Materials Park, OH, USA, 1991; pp. 219–225, Reprinted from: Nash, P.; Nash, A. The Nb-Ni (Niobium-Nickel) system. Bull. Alloy Phase Diagr. 1986, 7, 124–130. [Google Scholar]
- Kejun, Z.; Xianzhang, Z.; Zhanpeng, J. A thermodynamic calculation of the Ni-Nb phase diagram. J. Alloys Compd. 1992, 179, 177–185. [Google Scholar] [CrossRef]
- Saint-Antonin, F.; Mitchell, A. Potential Nb base superalloys. High Temp. Mater. Process. 1994, 13, 159–171. [Google Scholar] [CrossRef]
- Saint-Antonin, F.; Mitchell, A. Corrigendum for the paper: F. Saint-Antonin, A. Mitchell, “Potential niobium base superalloys”. High Temp. Mater. Process. 2018, 37, 105. [Google Scholar] [CrossRef]
- Okamoto, H. Nb-Ni (Niobium-Nickel). J. Phase Equilibria 1992, 13, 444. [Google Scholar] [CrossRef]
- Bolcavage, A.; Kattner, U.R. A reassessment of the calculated Ni-Nb phase diagram. J. Phase Equilibria 1992, 17, 92–100. [Google Scholar] [CrossRef]
- Okamoto, H. Nb-Ni (Niobium-Nickel). J. Phase Equilibria 1998, 19, 289. [Google Scholar] [CrossRef]
- Joubert, J.-M.; Sundman, B.; Dupin, N. Assessment of the niobium-nickel system. Comput. Coupling Phase Diagr. Thermochem. 2004, 28, 299–306. [Google Scholar] [CrossRef]
- Chen, H.; Du, Y.; Xu, H.; Liu, Y.; Schuster, J.C. Experimental investigation of the Nb-Ni phase diagram. J. Mater. Sci. 2005, 40, 6019–6022. [Google Scholar] [CrossRef]
- Chen, H.; Du, Y. Refinement of the thermodynamic modelling of the Nb-Ni system. Comput. Coupling Phase Diagr. Thermochem. 2006, 30, 308–315. [Google Scholar] [CrossRef]
- Okamoto, H. Nb-Ni (Niobium-Nickel). J. Phase Equilibria Diffus. 2006, 27, 314. [Google Scholar] [CrossRef]
- Brown, E.E.; Muzyka, D.R. Nickel-Iron Alloys. In Superalloys II; Sims, C.T., Stoloff, N.S., Hagel, W.C., Eds.; John Wiley & Sons: Hoboken, NJ, USA, 1987; pp. 165–188. [Google Scholar]
- Chester, C.T. Prediction of phase composition. In Superalloys II; Sims, C.T., Stoloff, N.S., Hagel, W.C., Eds.; John Wiley & Sons: Hoboken, NJ, USA, 1987; pp. 217–240. [Google Scholar]
- Joubert, J.M.; Feutelais, Y. Contribution of the Rietveld method to non-stoichiometric phase modeling. Part II: γ-Tl5-Te3 and μ Nb-Ni as experimental examples. CALPHAD 2002, 26, 427–438. [Google Scholar] [CrossRef]
- Kripyakevich, P.I.; Pylaeva, E.N. Crystalline structures of some compounds in the Nb-Ni and Ta-Ni systems. Sov. Phys. Crystallogr. 1967, 12, 294–296. [Google Scholar]
- Villars, P.; Calvert, L.D. Pearson’s Handbook of Crystallographic Data for Intermetallic Phases; ASM: Metals Park, OH, USA, 1985. [Google Scholar]
- ICDD (03/2019). PDF-4+ 2019. International Centre for Diffraction Data, Newtown Square, PA, USA. ICDD. Available online: http://www.icdd.com (accessed on 30 June 2019).
- Pearson, W.B. The Crystal Chemistry and Physics of Metals and Alloys; Wiley: New York, NY, USA, 1972; pp. 68–69. [Google Scholar]
- Okamoto, H. Hf-Nb (Hafnium-Niobium). J. Phase Equilibria 1991, 12, 211–214. [Google Scholar] [CrossRef]
- Abriata, J.P.; Bolcich, J.C. Nb-Zr (Niobium-Zirconium). Bull. Alloy Phase Diagr. 1982, 3, 34–44. [Google Scholar] [CrossRef]
- Nash, P.; Nash, A. Hf-Ni (Hafnium-Nickel). Bull. Alloy Phase Diagr. 1983, 4, 250–253. [Google Scholar] [CrossRef]
- Okamoto, H. Hf-Ni (Hafnium-Nickel). J. Phase Equilibria 1991, 12, 393. Available online: https://link.springer.com/content/pdf/10.1007%2FBF02649937.pdf (accessed on 4 July 2019).
- Okamoto, H. Hf-Ni (Hafnium-Nickel). J. Phase Equilibria 1993, 14, 769. Available online: https://link.springer.com/content/pdf/10.1007%2FBF02667895.pdf (accessed on 4 July 2019). [CrossRef]
- Okamoto, H. Hf-Ni (Hafnium-Nickel). J. Phase Equilibria 2002, 23, 386. Available online: https://link.springer.com/content/pdf/10.1361%2F105497102770331677.pdf (accessed on 4 July 2019). [CrossRef]
- Nash, P.; Jayanth, C.S. Ni-Zr (Nickel-Zirconium). Bull. Alloy Phase Diagr. 1984, 5, 144–148. [Google Scholar] [CrossRef]
- Daams, J.L.C.; Villars, P.; van Vucht, J.H.N. Atlas of Crystal Structure Types for Intermetallic Phases; ASM International: Materials Park, OH, USA, 1991; Volume 4. [Google Scholar]
- Villars, P.; Prince, A.; Okamoto, H. Handbook of Ternary Alloy Phase Diagrams, Mg-Ni-Zr–Y-Zn-Zr; ASM: Materials Park, OH, USA, 1995; Volume 10, pp. 12812–12814. [Google Scholar]
- Pearson Symbol. Available online: https://en.wikipedia.org/wiki/Pearson_symbol (accessed on 30 march 2019).
- Villars, P. Factors governing crystal structures. In Intermetallic Compounds, Principles and Practice; Westbrook, J.H., Fleischer, R.L., Eds.; John Wiley & Sons: Hoboken, NJ, USA, 1995; Volume 1, pp. 227–275. [Google Scholar]
- Lefebvre-Ulrikson, W.; Vurpillot, F.; Sauvage, X. Atom Probe Tomography: Put Theory into Practice; Academic Press: New York, NY, USA, 2016. [Google Scholar]
- Reppich, B. Particle strengthening, Chapter 7. In Plastic Deformation and Fracture of Materials, Volume 6; Materials Science and Technology: A Comprehensive Treatment Series; Cahn, R.W., Haasen, P., Kramer, E.J., Eds.; VCH Edition: Weinheim, Germany, 1993. [Google Scholar]






| Microstructural Function | Nickel Base Superalloys | Niobium Base Superalloys |
|---|---|---|
| Elements necessary for phase precipitation in grain boundaries | C, B | Rare earth metals: Y, Er, … |
| Base element | Ni | Nb |
| Solid-solution strengtheners and oxidation resistant elements | Cr, Co, Fe, Mo, W, Re | Mo, W, Re, Al, Ta, Ti, V, Cr |
| Elements needed for the precipitate formation in the matrix | Al, Ti | Ni (Co) 1 |
| Elements for the strengthening of the precipitated phase in the matrix | Nb, Ta, V | Zr, Hf |
| Phase | Crystal Structure (Pearson Notation) |
|---|---|
| Nb | cI2 |
| Ni | cF4 |
| α-Hf | hP2 (below 1743 °C) |
| β-Hf | cI2 (above 1743 °C) |
| Ni6Nb7 (~49.6 to ~54.5 at% Nb) | hR13 |
| Nb5Ni (metastable?) (LC?) | cF96 |
| Ni2Nb (LC) | hP24, hP12, cF24 |
| Ni3Nb (LC) | oP8 |
| Ni8Nb (LC) | tI36 |
| Ni5Hf (LC) | cF24 |
| Ni7Hf2 (LC) | m** |
| α-Ni3Hf (LC) | hR12 |
| β-Ni3Hf (LC) | hP40 |
| Ni21Hf8 (LC) | aP29 |
| Ni7Hf3 (LC) | aP20 |
| Ni2Hf (LC) | cF24 |
| Ni10Hf7 (LC) | oC68 |
| Ni11Hf9 (LC) | tI* |
| NiHf (LC) | oC8 |
| NiHf2 (LC) | tI12 |
| NiHf3 (metastable) | oC16 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Saint-Antonin, F.; Lefebvre, W.; Blum, I. Niobium Base Superalloys: Achievement of a Coherent Ordered Precipitate Structure in the Nb Solid-Solution. Crystals 2019, 9, 345. https://doi.org/10.3390/cryst9070345
Saint-Antonin F, Lefebvre W, Blum I. Niobium Base Superalloys: Achievement of a Coherent Ordered Precipitate Structure in the Nb Solid-Solution. Crystals. 2019; 9(7):345. https://doi.org/10.3390/cryst9070345
Chicago/Turabian StyleSaint-Antonin, François, Williams Lefebvre, and Ivan Blum. 2019. "Niobium Base Superalloys: Achievement of a Coherent Ordered Precipitate Structure in the Nb Solid-Solution" Crystals 9, no. 7: 345. https://doi.org/10.3390/cryst9070345
APA StyleSaint-Antonin, F., Lefebvre, W., & Blum, I. (2019). Niobium Base Superalloys: Achievement of a Coherent Ordered Precipitate Structure in the Nb Solid-Solution. Crystals, 9(7), 345. https://doi.org/10.3390/cryst9070345




