Dissociation Behavior of Dislocations in Ice
Abstract
:1. Introduction
1.1. Burgers Vectors of Dislocations in Ice
1.2. Extended Dislocations in Ice
1.3. Basal Slip System in Ice
1.4. Equilibrium Widths of Extended Dislocations in Ice
2. Formation of a Glissile Extended Dislocation
2.1. Driving Force for Dissociation of Perfect Dislocation <a>
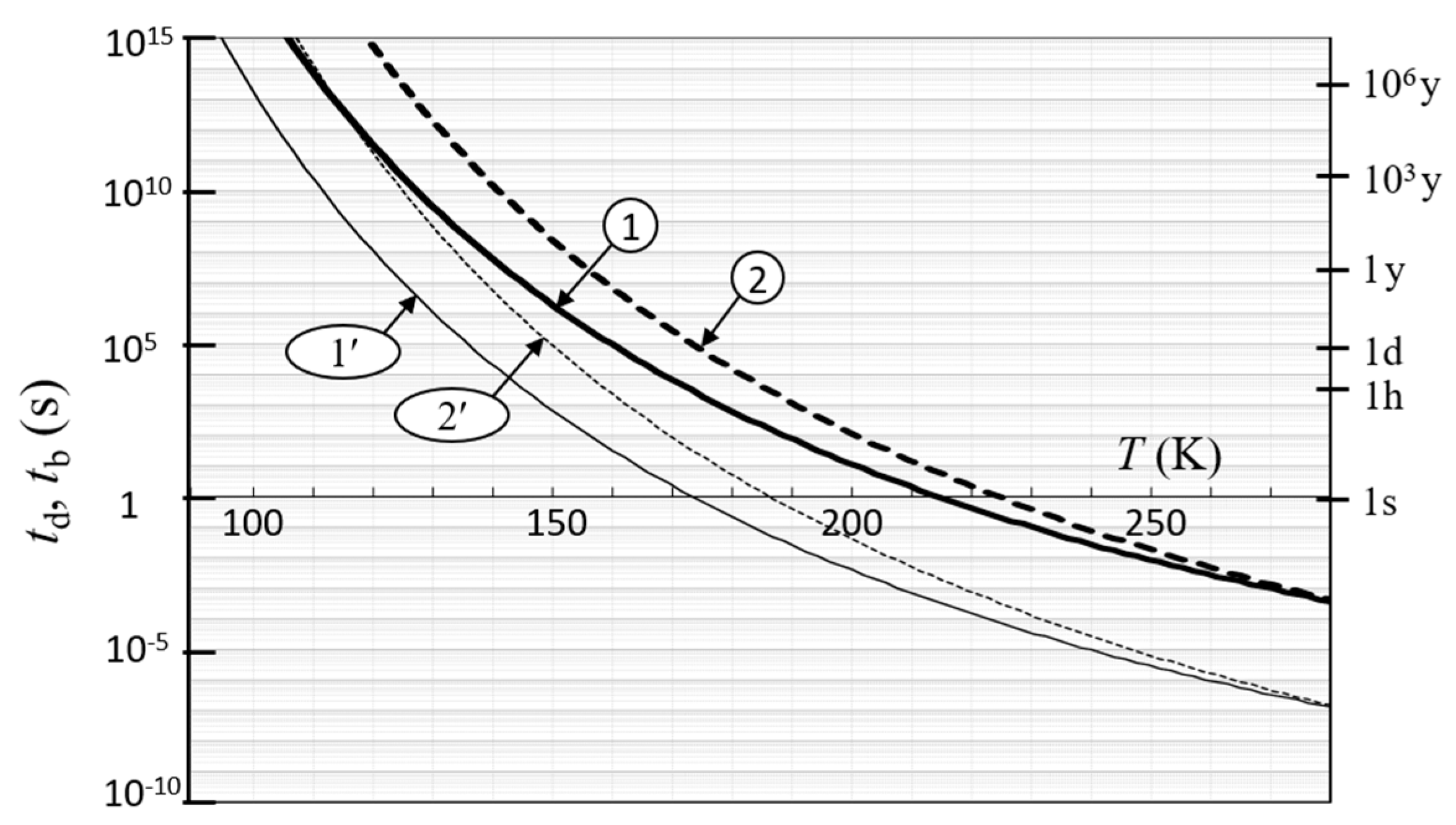
2.2. Dissociation-Completing Time
2.3. Dissociation-Beginning Time
2.4. Shuffle-Glide Transformation and Nucleation of Shockley Partials in Ice
2.5. Extended Width Changing under a Shear Stress
3. Formation of a Sessile Extended Dislocation
3.1. Driving Force for Dissociation of Perfect Dislocations <c> and <c + a>
3.2. Diffusive Flow of Self-Interstitials between Two Partial Dislocations
4. Summary
Funding
Conflicts of Interest
References
- Petrenko, V.F.; Whitworth, R.W. Physics of Ice; Oxford University Press: Oxford, UK, 1999. [Google Scholar]
- Hondoh, T. Nature and behavior of dislocations in ice. In Physics of Ice Core Records; Hondoh, T., Ed.; Hokkaido University Press: Sapporo, Japan, 2000; pp. 3–24. [Google Scholar]
- Hondoh, T. An overview of microphysical processes in ice sheets: Toward Nanoglaciology. Low Temp. Sci. 2009, 68, 1–23. [Google Scholar]
- Hondoh, T. Dislocation mechanism for transformation between cubic ice Ic and hexagonal ice Ih. Philos. Mag. 2015, 95, 3590–3620. [Google Scholar] [CrossRef]
- Fletcher, N.H. The Chemical Physics of Ice; Cambridge University Press: London, UK, 1970. [Google Scholar]
- Hobbs, P.V. Ice Physics; Oxford University Press: Oxford, UK, 1974. [Google Scholar]
- Kuhs, W.F.; Sippel, C.; Falenty, A.; Hansen, T.C. Extent and relevance of stacking disorder in “ice Ic”. Proc. Natl. Acad. Sci. USA 2012, 109, 21259–21264. [Google Scholar] [CrossRef]
- Fukuda, A.; Hondoh, T.; Higashi, A. Dislocation mechanisms of plastic deformation of ice. J. Phys. Paris 1987, 48, 163–173. [Google Scholar] [CrossRef]
- Hirth, J.P.; Lothe, J. Theory of Dislocations; McGraw-Hill book Inc.: New York, NY, USA, 1968. [Google Scholar]
- Anderson, P.M.; Hirth, J.P.; Lothe, J. Theory of Dislocations, 3rd ed.; Cambridge University Press: New York, NY, USA, 2017. [Google Scholar]
- Alexander, H. Dislocations in covalent crystals. In Dislocations in Solids; Nabarro, F.R.N., Ed.; Elsevier Science Publishers, B.V.: Amsterdam, The Netherlands, 1986; Volume 7, pp. 113–234. [Google Scholar]
- Holt, D.B.; Yacobi, B.G. Extended Defects in Semiconductors; Cambridge University Press: New York, NY, USA, 2007. [Google Scholar]
- Pizzagalli, L.; Beauchamp, P. Dislocation motion in silicon: The shuffle-glide controversy revisited. Philos. Mag. Lett. 2008, 88, 421–427. [Google Scholar] [CrossRef]
- Hondoh, T.; Itoh, T.; Amakai, S.; Goto, K.; Higashi, A. Formation and annihilation of stacking faults in pure ice. J. Phys. Chem. 1983, 87, 4040–4044. [Google Scholar] [CrossRef]
- Hudait, A.; Qiu, S.; Lupi, L.; Molinero, V. Free energy contributions and structural characterization of stacking disordered ices. Phys. Chem. Chem. Phys. 2016, 18, 9544–9553. [Google Scholar] [CrossRef]
- Lupi, L.; Hudait, A.; Peters, B.; Gründwald, M.; Mullen, R.G.; Nguyen, A.H.; Molinero, V. Role of stacking disorder in ice nucleation. Nature 2017, 551, 218–222. [Google Scholar] [CrossRef]
- Rӧttger, K.; Endriss, A.; Ihringer, J.; Doyle, S.; Kuhs, W.F. Lattice constants and thermal expansion of H2O and D2O ice Ih between 10 and 265 K. Addendum. Acta Cryst. 2012, B68, 91. [Google Scholar] [CrossRef]
- Gammon, P.H.; Kiefte, H.; Clouter, M.J. Elastic constants of ice samples by Brillouin spectroscopy. J. Phys. Chem. 1983, 87, 4025–4029. [Google Scholar] [CrossRef]
- Shearwood, C.; Whitworth, R.W. The velocity of dislocations in ice. Philos. Mag. 1991, A64, 289–302. [Google Scholar] [CrossRef]
- Okada, Y.; Hondoh, T.; Mae, S. Basal glide of dislocations in ice observed by synchrotron radiation topography. Philos. Mag. 1999, A79, 2853–2868. [Google Scholar] [CrossRef]
- Wessel, K.; Alexander, H. On the mobility of partial dislocations in silicon. Philos. Mag. 1977, 35, 1523–1536. [Google Scholar] [CrossRef]
- Silva Junior, D.L.; de Koning, M. Structure and energetics of extended defects in ice Ih. Phys. Rev. 2012, B85, 024119. [Google Scholar] [CrossRef]
- Schulson, E.M.; Duval, P. Creep and Fracture of Ice; Cambridge University Press: Cambridge, UK, 2009. [Google Scholar]
- Tan, J.J.; Li, Y. High-pressure phase transitions and thermodynamic behaviors of cadmium sulfide. Acta Phys. Pol. 2011, A120, 501–506. [Google Scholar] [CrossRef]
- Cullity, B.D. Elements of X-Ray Diffraction; Addison-Wesley Pub. Co. Inc.: Reading, MA, USA, 1956; (Japanese Edition). [Google Scholar]
- Hondoh, T.; Itoh, T.; Higashi, A. Formation of stacking faults in pure ice single crystals by cooling. Jpn. J. Appl. Phys. 1981, 20, L737–L740. [Google Scholar] [CrossRef]
- Higashi, A. (Ed.) Lattice Defects in Ice Crystals: X-Ray Topographic Observations; Hokkaido University Press: Sapporo, Japan, 1988. [Google Scholar]
- Goto, K.; Hondoh, T.; Higashi, A. Experimental determinations of the concentration and the mobility of interstitials in pure ice crystals. In Point Defects and Defect Interactions in Metals; Takamura, J., Doyama, M., Kiritani, M., Eds.; University of Tokyo Press: Tokyo, Japan, 1982; pp. 174–176. [Google Scholar]
- Goto, K.; Hondoh, T.; Higashi, A. Determination of diffusion coefficients of self-interstitials in ice with a new method of observing climb of dislocations by x-ray topography. Jpn. J. Appl. Phys. 1986, 25, 351–357. [Google Scholar] [CrossRef]
- Hondoh, T.; Hoshi, R.; Goto, A.; Yamagami, H. A new method using synchrotron-radiation topography for determining point-defect diffusivity under hydrostatic pressure. Philos. Mag. 1991, 63, 1–5. [Google Scholar] [CrossRef]
- Ramseier, R.O. Self-diffusion of tritium in natural and synthetic ice monocrystals. J. Appl. Phys. 1967, 38, 2553–2556. [Google Scholar] [CrossRef]
- Incropera, F.P.; Dewitt, D.P.; Bergman, T.L.; Lavine, A.S. Principles of Heat and Mass Transfer, 7th ed.; John Wiley & Sons: Singapore, 2003. [Google Scholar]
- Wei, Y.; Dempsey, J.P. The motion of non-basal dislocations in ice crystals. Philos. Mag. 1994, 69, 1–10. [Google Scholar] [CrossRef]
- Weikusat, I.; Kuiper, E.N.; Pennock, G.M.; Kipfstuhl, S.; Drury, M.R. EBSD analysis of subgrain boundaries and dislocation slip systems in Antarctic and Greenland ice. Solid Earth 2017, 8, 883–898. [Google Scholar] [CrossRef] [Green Version]






| Plane | Perfect Dislocation | Dissociation Reaction | Extended Width *1 we |
|---|---|---|---|
| (0001) | <a> | pj + (−pk) | 25 nm (<a>: screw) 49 nm (<a>: 60°) 57 nm (<a>: edge) |
| (0001) | <c> | c/2 + c/2 | 129 nm |
| (c/2 + pi) + (c/2 − pi) | 256 nm (<p>: screw) 193 nm (<p>: edge) | ||
| (0001) | <c + a> | (c/2 + pj) + (c/2 − pk) | 437 nm (<a>: screw) 501 nm (<a>: edge) |
| Case | Temperature | |||||
|---|---|---|---|---|---|---|
| 253 K (−20 °C) | 223 K (−50 °C) | 193 K (−80 °C) | 173 K (−100 °C) | 123 K (−150 °C) | ||
| td *1 | 1 | 5.8 × 10−3 s (5.8 ms) | 2.7 × 10−1 s (0.27 s) | 4.2 × 10 s (42 s) | 3.2 × 103 s (0.89 h) | 7.9 × 1010 s (2.5 Ky) |
| 2 | 1.2 × 10−2 s (12 ms) | 9.7 × 10−1 s (0.97 s) | 5.7 × 102 s (570 s) | 1.1 × 104 s (4 h) | 9.8 × 1013 s (3.1 My) | |
| tb *2 | 1′ | 2.0 × 10−6 s (2.0 μs) | 2.0 × 10−4 s (0.2 ms) | 1.5 × 10−2 s (15 ms) | 1.1 s (1.1 s) | 2.7 × 107 s (0.86 y) |
| 2′ | 4.1 × 10−6 s (4.1 μs) | 9.2 × 10−4 s (0.92 ms) | 0.20 s (0.20 s) | 3.8 × 101 s (38 s) | 3.4×1010 s (1.1 Ky) | |
| Material | Shear Modulus μ (GPa) *1 | Poisson’s Ratio ν *1 | Burgers Vector bp (nm) *2 | SF Energy γp (mJ/m2) *3 | Extended Width we (nm) | 2γp/bp (MPa) |
|---|---|---|---|---|---|---|
| Ice ( Ih ) | 3.55 | 0.325 | 0.261 | 0.62 | 25 | 4.8 |
| Si (diamond) | 68.1 | 0.218 | 0.222 | 55 | 4.2 | 500 |
| Ge (diamond) | 56.4 | 0.200 | 0.231 | 60 | 3.5 | 520 |
| CdS (wurzite) | 18.5 | 0.378 | 0.239 | 8.7 | 6.7 | 73 |
| Cu (fcc) | 54.6 | 0.324 | 0.148 | 45 | 1.6 | 610 |
| Zn (hcp) | 43.4 | 0.249 | 0.154 | 140 | 0.5 | 1800 |
| Cylinder Diameter d (nm) (=R0) | Final Distance R (nm) | Dissociation-Beginning and -Completing Times tb, td (s) | ||||
|---|---|---|---|---|---|---|
| T = 273 (K) (0 °C) | 253 (K) (−20 °C) | 223 (K) (−50 °C) | 183 (K) (−90 °C) | |||
| td | 2.94 (=4c) | 495 (=0.99we) *1 | 5.5 × 106 (64 d) | 1.3 × 108 (4.1 y) | 4.2 × 1010 (1.3 Ky) | 1.9 × 1015 (61 My) |
| 1.47 (=2c) | 6.2 × 106 (72 d) | 1.4 × 108 (4.6 y) | 4.8 × 1010 (1.5 Ky) | 2.2 × 1015 (68 My) | ||
| tb | 0.734 (=c) | 1.35 (=3a) | 0.15 | 3.0 | 720 | 1.7 × 107 (200 d) |
| 1.47 (=2c) | 2.25 (=5a) | 0.63 | 13.5 | 3840 | 1.3 × 108 (4.1 y) | |
© 2019 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Hondoh, T. Dissociation Behavior of Dislocations in Ice. Crystals 2019, 9, 386. https://doi.org/10.3390/cryst9080386
Hondoh T. Dissociation Behavior of Dislocations in Ice. Crystals. 2019; 9(8):386. https://doi.org/10.3390/cryst9080386
Chicago/Turabian StyleHondoh, Takeo. 2019. "Dissociation Behavior of Dislocations in Ice" Crystals 9, no. 8: 386. https://doi.org/10.3390/cryst9080386
APA StyleHondoh, T. (2019). Dissociation Behavior of Dislocations in Ice. Crystals, 9(8), 386. https://doi.org/10.3390/cryst9080386





