Monte Carlo Optical Simulations of a Small FoV Gamma Camera. Effect of Scintillator Thicknesses and Septa Materials
Abstract
:1. Introduction
- (a)
- Different thicknesses for the CsI:Na scintillating crystal,
- (b)
- Several types of material for the reflector and
- (c)
- Different colors of reflective material.
2. Materials and Methods
2.1. Standard Model Description and Validation
2.2. Implementation of the Optical Model in GATE
- A front-collimator aluminum layer, 0.5 mm thick;
- A parallel lead hole collimator, 27 mm thick, with a 1.2 mm diameter hexagonal holes and 0.15 mm septa;
- Two aluminum layers of 0.5 mm thickness, separated by an air layer of 0.1 mm;
- A front-crystals reflector layer made of dioxide titanium (TiO2), of 1 mm thickness;
- A 5 × 5 pixelated CsI:Na scintillator crystals array (1.45 mm × 1.45 mm × 5 mm), with TiO2 septa 0.25 mm thick; with external dimensions equal to (8.5 × 8.5 mm2).
- A glass layer of 2 mm thickness, for the detector coupling with PSPMTs.
2.3. Validation of the Optical Model
- (a)
- Using the physics of optical photons
- (b)
- Using the standard physics (no optical photons)
2.4. Optical Simulations
- The first configuration involved white TiO2 reflector material around each element and in front of the crystal surfaces;
- The second configuration consisted of white TiO2 in front of the crystal surface and black tape wrapping of the surrounding faces;
- The third configuration involved black TiO2 in front of the crystal surface and black tape wrapping of the surrounding crystal sides.
2.5. Performance Measurements
3. Results
3.1. Standard Model Validation
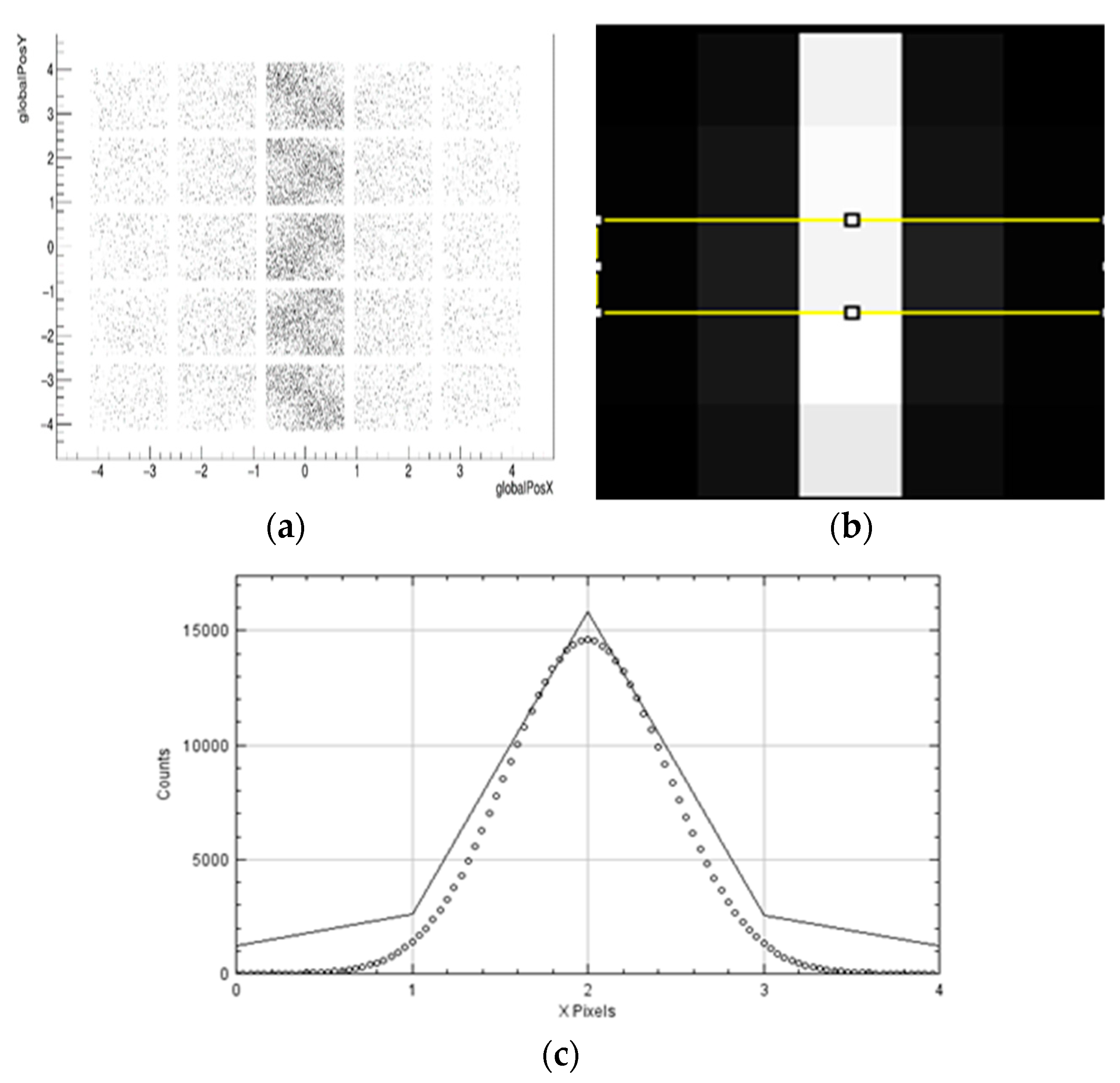
3.2. Optical Model Validation
3.3. Optical Simulations
4. Discussion
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Roncali, E.; Cherry, S.R. Simulation of light transport in scintillators based on 3D characterization of crystal surfaces. Phys. Med. Biol. 2013, 58, 2185–2198. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Stockhoff, M.; Jan, S.; Dubois, A.; Cherry, S.R.; Roncali, E. Advanced optical simulation of scintillation detectors in GATE V8.0: First implementation of a reflectance model based on measured data. Phys. Med. Biol. 2017, 62, L1. [Google Scholar] [CrossRef] [PubMed]
- Berg, E.; Roncali, E.; Cherry, S.R. Optimizing light transport in scintillation crystals for time-of-flight PET: An experimental and optical Monte Carlo simulation study. Biomed. Opt. Express 2015, 6, 2220–2230. [Google Scholar] [CrossRef] [PubMed]
- van der Laan, D.J.; Schaart, D.R.; Maas, M.C.; Beekman, F.J.; Bruyndonckx, P.; van Eijk, C.W.E. Optical simulation of monolithic scintillator detectors using GATE/GEANT4. Phys. Med. Biol. 2010, 55, 1659–1675. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Roncali, E.; Stockhoff, M.; Cherry, S.R. An integrated model of scintillator-reflector properties for advanced simulations of optical transport. Phys. Med. Biol. 2017, 62, 4811–4830. [Google Scholar] [CrossRef] [PubMed]
- Agostinelli, S.; Allisona, J.; Amako, K.; Apostolakis, J.; Araujo, H.; Arce, P.; Asai, M.; Axen, D.; Banerjee, S.; Barrand, G. GEANT4—A simulation toolkit. Nucl. Instrum. Methods A 2003, 506, 250–303. [Google Scholar] [CrossRef]
- Jan, S.; Allison, J.; Amako, K.; Apostolakis, J.; Araujo, H.; Arce, P.; Asai, M.; Axen, D.; Banerjee, S.; Barrand, G.; et al. GATE: A simulation toolkit for PET and SPECT. Phys. Med. Biol. 2004, 49, 4543–4561. [Google Scholar] [CrossRef] [PubMed]
- Janecek, M.; Moses, W. Simulating scintillator light collection using measured optical reflectance. IEEE Trans. Nucl. Sci. 2010, 57, 964–970. [Google Scholar] [CrossRef]
- Nayar, S.K.; Ikeuchi, K.; Kanade, T. Surface reflection: Physical and geometrical perspectives. IEEE Trans. Pattern Anal. Mach. Intell. 1991, 13, 611–634. [Google Scholar] [CrossRef]
- Nilsson, J.; Cuplov, V.; Isaksson, M. Identifying key surface parameters for optical photon transport in GEANT4/GATE simulations. Appl. Radiat. Isot. 2015, 103, 15–24. [Google Scholar] [CrossRef]
- Taherparvar, P.; Sadremomtaz, A. Development of GATE Monte Carlo simulation for a CsI pixelated gamma camera dedicated to high resolution animal SPECT. Phys. Eng. Sci. Med. 2018, 41, 31–39. [Google Scholar] [CrossRef]
- Ghabriala, A.; Franklin, D.; Zaidi, H. A Monte Carlo simulation study of the impact of novel scintillation crystals on performance characteristics of PET scanners. Phys. Med. Eur. J. Med Phys. 2018, 50, 37–45. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Ghazanfari, N.; Sarkar, S.; Loudos, G.; Ay, M.R. Quantitative assessment of crystal material and size on the performance of rotating dual head small animal PET scanners using Monte Carlo modeling. Hell. J. Nucl. Med. 2012, 15, 33–39. [Google Scholar] [PubMed]
- Inoue, T.; Oriuchi, N.; Koyama, K.; Ichikawa, A.; Tomiyoshi, K.; Sato, N.; Matsubara, K.; Suzuki, H.; Aoki, J.; Endo, K. Usefulness of dual-head coincidence gamma camera with thick NaI crystals for nuclear oncology: Comparison with dedicated PET camera and conventional gamma camera with thin NaI crystals. Ann. Nucl. Med. 2001, 15, 141–148. [Google Scholar] [CrossRef] [PubMed]
- Surti, S.; Werner, M.E.; Karp, J.S. Study of PET scanner designs using clinical metrics to optimize the scanner axial FOV and crystal thickness. Phys. Med. Biol. 2013, 58, 3995–4012. [Google Scholar] [CrossRef] [Green Version]
- Smith, T.; Jasani, B.M. Assessment of various reflectors used with rectangular scintillation detectors. J. Phys. E 1972, 5, 1083–1088. [Google Scholar] [CrossRef]
- McElroy, D.P.; Huang, S.C.; Hoffman, E.J. The Use of Retro-Reflective Tape for Improving Spatial Resolution of Scintillation Detectors. IEEE Trans. Nucl. Sci. 2002, 49, 165–171. [Google Scholar] [CrossRef]
- Bioemtech. Available online: http://bioemtech.com/γ-eye/ (accessed on 31 July 2019).
- Georgiou, M.; Fysikopoulos, E.; Mikropoulos, K.; Fragogeorgi, E.; Loudos, G. Characterization of “γ-Eye”: A Low-Cost Benchtop Mouse-Sized Gamma Camera for Dynamic and Static Imaging Studies. Mol. Imaging Biol. 2016, 19, 398–407. [Google Scholar] [CrossRef]
- Calvi, M.; Carniti, P.; Cassina, L.; Gotti, C.; Maino, M.; Matteuzzi, C.; Pessina, G. Characterization of the Hamamatsu H12700A-03 and R12699-03 multi-anode photomultiplier tubes. J. Instrum. 2015, 10, P09021. [Google Scholar] [CrossRef]
- Rakić, A.D. Algorithm for the determination of intrinsic optical constants of metal films: Application to aluminium. Appl. Opt. 1995, 34, 4755–4767. [Google Scholar] [CrossRef]
- Nelson, G.; Reilly, D. Gamma-Ray Interactions with Matter. In Passive Non-Destructive Analysis of Nuclear Materials; Los Alamos National Laboratory: Los Alamos, NM, USA, 1991; pp. 27–42. Available online: http://faculty.washington.edu/agarcia3/phys575/Week2/Gamma%20ray%20interactions.pdf (accessed on 31 July 2019).
- DeVore, J.R. Refractive index of Rutile and Sphalerite. J. Opt. Soc. Am. 1951, 41, 416–419. [Google Scholar] [CrossRef]
- Kim, S.Y. Simultaneous determination of refractive index, extinction coefficient, and void distribution of titanium dioxide thin film by optical methods. Appl. Opt. 1996, 35, 6703–6707. [Google Scholar] [CrossRef]
- Liu, T.; Henderson, C.L.; Samuels, R. Quantitative Characterization of the Optical Properties of Absorbing Polymer Films: Comparative Investigation of the Internal Reflection Intensity Analysis Method. J. Polym. Sci. Part B Polym. Phys. 2003, 41, 842–855. [Google Scholar] [CrossRef]
- SCHOTT. Optical glass Data Sheets. Available online: https://www.schott.com/advanced_optics (accessed on 31 July 2019).
- AMCRYS. Scintillation Material Data Sheet—Alkali Halide Scintillation Crystals. 2009. Available online: http://www.amcrys.com/pdf/4281_.pdf (accessed on 31 July 2019).
- NEMA. Standard Publication NU 1-2007 Performance Measurements of Gamma Cameras; National Electrical Manufacturers Association: Rosslyn, VA, USA, 2007. [Google Scholar]
- Sajedi, S.; Zeraatkar, N.; Moji, V.; Farahani, M.H.; Sarkar, S.; Arabi, H.; Teymoorian, B.; Ghafarian, P.; Rahmim, A.; Ay, R.M. Design and development of a high resolution animal SPECT scanner dedicated for rat and mouse imaging. Nucl. Instrum. Methods Phys. Res. Sect. A Accel. Spectrometers Detect. Assoc. Equip. 2014, 741, 169–176. [Google Scholar] [CrossRef]
- Bhatia, B.S.; Bugby, S.L.; Lees, J.E.; Perkins, A.C. A scheme for assessing the performance characteristics of small field-of-view gamma cameras. Phys. Med. 2015, 31, 98–103. [Google Scholar] [CrossRef]
- Loudos, G.; Majewski, S.; Wojcik, R.; Weisenberger, A.; Sakellios, N.; Nikita, K.; Uzunoglu, N.; Bouziotis, P.; Xanthopoulos, S.; Varvarigou, A. Performance evaluation of a dedicated camera suitable for dynamic radiopharmaceuticals evaluation in small animals. IEEE Trans. Nucl. Sci. 2007, 54, 454–460. [Google Scholar] [CrossRef]
- Bugby, S.L.; Lees, J.E.; Bhatia, B.S.; Perkins, C.A. Characterisation of a high resolution small field of view portable gamma camera. Phys. Med. 2014, 30, 331–339. [Google Scholar] [CrossRef]
- Moji, V.; Zeraatkar, N.; Farahani, M.H.; Aghamiri, M.R.; Sajedi, S.; Teimourian, B.; Ghafarian, P.; Sarkar, S.; Ay, M.R. A Performance evaluation of a newly developed high-resolution, dual-head animal SPECT system based on the NEMA NU1-2007 standard. J. Appl. Clin. Med Phys. 2014, 15, 267–278. [Google Scholar] [CrossRef]
- Abramoff, M.; Magalhaes, P.; Ram, S. Image processing with ImageJ. Biophotonics Int. 2004, 11, 36–42. [Google Scholar]
- Collins, T.J. ImageJ for microscopy. Biotechniques 2007, 43, 25–30. [Google Scholar] [CrossRef]







| Properties | γ-Eye |
|---|---|
| Useful Field of View (UFoV) | 48 mm × 98 mm |
| Sensitivity within ±20% energy window | 56 cps/MBq |
| Spatial resolution | 2.2 mm @ 0 mm |
| Energy resolution | 24.5% @ 140 keV |
| Material | Refractive Index (RI) | Energy Value (RI) [eV] | Absorption Length (AL) [m] | Energy Value (AL) [keV] |
|---|---|---|---|---|
| Aluminium | 1.1978 | 2.11 | 0.029288 0.030864 0.044052 | 100 200 500 |
| Lead | 3.637 | 1.95930 | 0.000154 0.000869 0.004672 | 100 200 500 |
| Air | 1.00027 1.00027 | 1.84 4.08 | 50 50 | 1.84 4.08 |
| TiO2 | 2.36 2.39 2.43 2.51 2.71 | 1.55 1.77 2.06 2.48 3.09 | 0.02 | 3.02 |
| Black Tape | 1.52 | 2.28332 | 0.0000036 | 2.28332 |
| Glass | 1.5140 | 1.85883 | 1000 | 1.23984 |
| Refractive Index | Absorption Length [m] | Scintillation Yield [photons/MeV] | Resolution Scale | Fast Time Constant [ns] | Yield Ratio | Fast Component |
|---|---|---|---|---|---|---|
| 1.84 (2.95 eV) | 0.02 (0.51 eV) 0.33 (3.99 eV) | 42000 | 5.25 | 630 | 1 | 1 (2.95 eV) |
| Parameters | Optical Simulation with Linear Source | Standard Simulation with Linear Source |
|---|---|---|
| Scintillator detector | 5 × 5 crystal array | 5 × 5 crystal Array |
| Reflector material | TiO2 | TiO2 |
| Source dimensions [mm] | Height: 8.7 Diameter: 0.6 | Height: 8.7 Diameter: 0.6 |
| Source activity [Bq] | 2000 | 6,216,000 |
| Source energy [keV] | 140 | 140 |
| Source distance from collimator [mm] | 0 | 0 |
| Simulation time [s] | 20,000 | 349 |
| Simulation | Energy Resolution [%] | Spatial Resolution [mm] |
|---|---|---|
| Optical simulation | 24.19 | 1.88 |
| Standard simulation | 25.35 | 1.98 |
| Crystals Thickness [mm] | Crystals Sides Reflector | Crystals Front Reflector | Sensitivity [cps/MBq] | Light Output | Spatial Resolution [mm] |
|---|---|---|---|---|---|
| 4 | White TiO2 | White TiO2 | 49.66 | 5381 | 1.75 ± 0.03 |
| 4 | Black Tape | White TiO2 | 45.18 | 5105 | 1.73 ± 0.02 |
| 4 | Black Tape | TiO2 as black surface | 45.15 | 4895 | 1.69 ± 0.05 |
| 4.5 | White TiO2 | White TiO2 | 55.28 | 4787 | 1.80 ± 0.04 |
| 4.5 | Black Tape | White TiO2 | 50.78 | 4552 | 1.77 ± 0.05 |
| 4.5 | Black Tape | TiO2 as black surface | 50.82 | 4397 | 1.72 ± 0.04 |
| “γ-eye” 5 | White TiO2 | White TiO2 | 62.00 | 4377 | 1.88 ± 0.03 |
| 5 | Black Tape | White TiO2 | 55.50 | 4215 | 1.83 ± 0.04 |
| 5 | Black Tape | TiO2 as black surface | 56.30 | 3919 | 1.79 ± 0.05 |
| 5.5 | White TiO2 | White TiO2 | 66.19 | 3991 | 1.92 ± 0.03 |
| 5.5 | Black Tape | White TiO2 | 62.08 | 3815 | 1.87 ± 0.02 |
| 5.5 | Black Tape | TiO2 as black surface | 60.88 | 3671 | 1.83 ± 0.05 |
| 6 | White TiO2 | White TiO2 | 71.00 | 3613 | 1.96 ± 0.04 |
| 6 | Black Tape | White TiO2 | 67.49 | 3461 | 1.91 ± 0.05 |
| 6 | Black Tape | TiO2 as black surface | 67.24 | 3326 | 1.88 ± 0.04 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ricci, R.; Kostou, T.; Chatzipapas, K.; Fysikopoulos, E.; Loudos, G.; Montalto, L.; Scalise, L.; Rinaldi, D.; David, S. Monte Carlo Optical Simulations of a Small FoV Gamma Camera. Effect of Scintillator Thicknesses and Septa Materials. Crystals 2019, 9, 398. https://doi.org/10.3390/cryst9080398
Ricci R, Kostou T, Chatzipapas K, Fysikopoulos E, Loudos G, Montalto L, Scalise L, Rinaldi D, David S. Monte Carlo Optical Simulations of a Small FoV Gamma Camera. Effect of Scintillator Thicknesses and Septa Materials. Crystals. 2019; 9(8):398. https://doi.org/10.3390/cryst9080398
Chicago/Turabian StyleRicci, Rita, Theodora Kostou, Konstantinos Chatzipapas, Eleftherios Fysikopoulos, George Loudos, Luigi Montalto, Lorenzo Scalise, Daniele Rinaldi, and Stratos David. 2019. "Monte Carlo Optical Simulations of a Small FoV Gamma Camera. Effect of Scintillator Thicknesses and Septa Materials" Crystals 9, no. 8: 398. https://doi.org/10.3390/cryst9080398
APA StyleRicci, R., Kostou, T., Chatzipapas, K., Fysikopoulos, E., Loudos, G., Montalto, L., Scalise, L., Rinaldi, D., & David, S. (2019). Monte Carlo Optical Simulations of a Small FoV Gamma Camera. Effect of Scintillator Thicknesses and Septa Materials. Crystals, 9(8), 398. https://doi.org/10.3390/cryst9080398










