Next Article in Journal
Quest for Compounds at the Verge of Charge Transfer Instabilities: The Case of Silver(II) Chloride †
Next Article in Special Issue
Creep of Heusler-Type Alloy Fe-25Al-25Co
Previous Article in Journal
Mechanism Design with Singularity Avoidance of Crystal-Inspired Deployable Structures
 
 
Search for Articles:
Title / Keyword
Author / Affiliation / Email
Journal
Article Type
 
 
Advanced Search
 
Section
Special Issue
Volume
Issue
Number
Page
 
Journals
Crystals
Volume 9
Issue 8
10.3390/cryst9080422
crystals-logo
Submit to this Journal Review for this Journal Propose a Special Issue
► Article Menu

Article Menu

share Share announcement Help format_quote Cite question_answer Discuss in SciProfiles thumb_up
...
Endorse textsms
...
Comment
first_page
settings
Order Article Reprints
Font Type:
Arial Georgia Verdana
Font Size:
Aa Aa Aa
Line Spacing:
Column Width:
Background:
Article

Theoretical Study of the Electronic and Magnetic Properties and Phase Stability of the Full Heusler Compound Pd2CoAl

by
Liyu Hao
1,†,
Jiaxue You
1,†,
Rabah Khenata
2,
Yanfeng Wang
3,
Xiaotian Wang
1 and
Tie Yang
1,*
1
School of Physical Science and Technology, Southwest University, Chongqing 400715, China
2
Laboratoire de Physique Quantique de la Matière et de Modélisation Mathématique, Université de Mascara, Mascara 29000, Algeria
3
College of Sciences, Hebei North University, Zhangjiakou 075000, China
*
Author to whom correspondence should be addressed.
†
Authors contributed equally.
Crystals 2019, 9(8), 422; https://doi.org/10.3390/cryst9080422
Submission received: 30 July 2019 / Revised: 9 August 2019 / Accepted: 13 August 2019 / Published: 14 August 2019
(This article belongs to the Special Issue Heusler Alloys)
Browse Figures
Versions Notes

Abstract

:
Based on first principles calculation, a systematical investigation has been performed to study the electronic, magnetic, dynamic, and mechanical properties of the full Heusler compound Pd2CoAl. It is found that the L21-type structure is energetically more stable than the XA-type due to the lower total energy. The obtained lattice constant in cubic ground state is 6.057 Å, which matches well with previous study. The calculated electronic band structure reveals the metallic nature of Pd2CoAl and its total magnetic moment of 1.78 μB is mainly contributed by Co atom from strong spin splitting effect, as indicated with the distinctive distributions of the density of states in two spin directions. Under uniform strains from −5% to +5%, the variation of total magnetic moment has been obtained and it is still caused by the much larger change from Co atom, compared with Pd and Al atoms. The tetragonal structure has further been analyzed and we found that there is possible martensitic phase transformation because the total energy can be further reduced when the cubic structure is varied into the tetragonal one. The large energy difference of 0.165 eV between the tetragonal and cubic phases is found at the c/a ratio of 1.30. The total density of states has been compared between the cubic and tetragonal phases for Pd2CoAl and results show tetragonal phase transformation could reduce the states at the Fermi energy level in both directions. In addition, the dynamic and mechanical stabilities have also been evaluated for Pd2CoAl in both cubic and tetragonal structures and results confirm that the tetragonal phase shows good stability against the cubic phase, which further verifies that the tetragonal phase transformation is highly expected. In the end, the strong elastic anisotropy in the tetragonal structure has been clearly shown with the calculated directional dependence of the Young’s modulus and shear modulus.

1. Introduction

The family of Heusler alloys has attracted much scientific attention and research interest during recent years, and their various and special functionalities have been extensively studied and explored in many different areas. The ferromagnetism was firstly observed in Heusler compounds with no ferromagnetic elements and, afterwards, many more new properties have been found, such as half metallicity [1,2,3,4,5,6,7,8,9,10], spin gapless semiconductivity [11,12,13,14,15,16,17], thermoelectricity [18,19,20,21,22,23], superconductivity [24,25,26], and topological insulativity [27,28]. Also, these properties can be easily tuned by simple element substitution within the periodic table. Therefore, ongoing investigations to enhance their performance or even search for new property are still very intense in the scientific community from both theoretical calculation and experimental synthesis. Most of the current applications for Heusler compound are related with the magnetic effect just in different forms, including mainly spintronics and magnetoelectronics.
Normally, Heusler compounds have highly ordered cubic crystal structures with different atomic ordering configurations. However, several recent studies have found many Heusler materials have tetragonal structure as the ground state, e.g., Felser et al. [29] found that Mn3-xFexGa and Mn3-xCoxGa have tetragonal structure over the whole range of compositions from experiment results, and then Faleev et al. [30,31] performed an extensive investigation on the origin of the tetragonal ground state for 286 Heusler compounds by theoretical calculation, which shows 62% have tetragonal structure. More recently, Han et al. [32,33] and Wu et al. [34] studied the phase competition between cubic and tetragonal structures in a series of conventional Heusler compounds Pd2YZ (Y = Co, Fe, Mn; Z = B, Al, Ga, In, Tl, Si, Ge, Sn, Pb, P, As, Sb) and all-d-metal Heusler compounds X2-xMn1+xV (X = Pd, Ni, Pt, Ag, Au, Ir, Co; x = 1, 0) and Zn2MMn (M = Ru, Rh, Pd, Os, Ir) and found that many of them also exhibit tetragonal phases, especially the most of Pd2Co-based Heusler alloys. Compared with the cubic structures, the tetragonal ones have several special properties, like large perpendicular magnetic anisotropy [35,36,37] and ferromagnetic shape memory behavior [38,39,40,41,42,43], which are very important for the development of spin-transfer torque magnetic random-access memory, ferromagnetic shape memory alloys and other spintronic applications [29,44,45,46].
In this work, a detailed study on the full Heusler compound Pd2CoAl has been carried out with first principles calculation. The electronic and magnetic properties have been calculated based on both cubic and tetragonal structures. Except the general total energy evaluation, the phase stability was further examined by means of both dynamic and mechanical manners and results show that the tetragonal structure has good stability against the cubic counterpart, which further confirms the possible tetragonal phase transformation could be highly expected in this material. Moreover, the elastic anisotropy in the tetragonal structure is revealed with the directional dependence of Young’s modulus and shear modulus. This study investigates the phase stability from several different perspectives and thus can give valuable information for the tetragonal state in the palladium-based full Heusler materials or even inspire other similar investigations.

2. Computational Methods and Details

The electronic, magnetic, and mechanical properties of the full Heusler compound Pd2CoAl have been investigated with the first principles calculations by applying the pseudopotential plane wave methods based on density functional theory [47], as implemented with the CASTEP codes [48]. The Perdew–Burke–Ernzerhof (PBE) 96 in the frame of the generalized gradient approximation (GGA) [49] was selected to describe the electronic exchange correlation energy. The ultrasoft pseudopotential [50] was used to treat the interactions between the valence electrons and the atomic core. The configurations of the valence electrons for Pd, Co, and Al are 4d10, 3d74s2, and 3s23p1, respectively. After an initial convergence test, a place wave cutoff energy of 500 eV has been used together with a k mesh of 12 × 12 × 12 Monkhorst–Pack grid for the Brillouin zone sampling. For the self-consistent field iteration convergence, the difference of the total energy was set to smaller than 1 × 10−6 eV/atom. For the phonon property, the finite displacement method within the density functional perturbation theory [51] has been used.

3. Results and Discussions

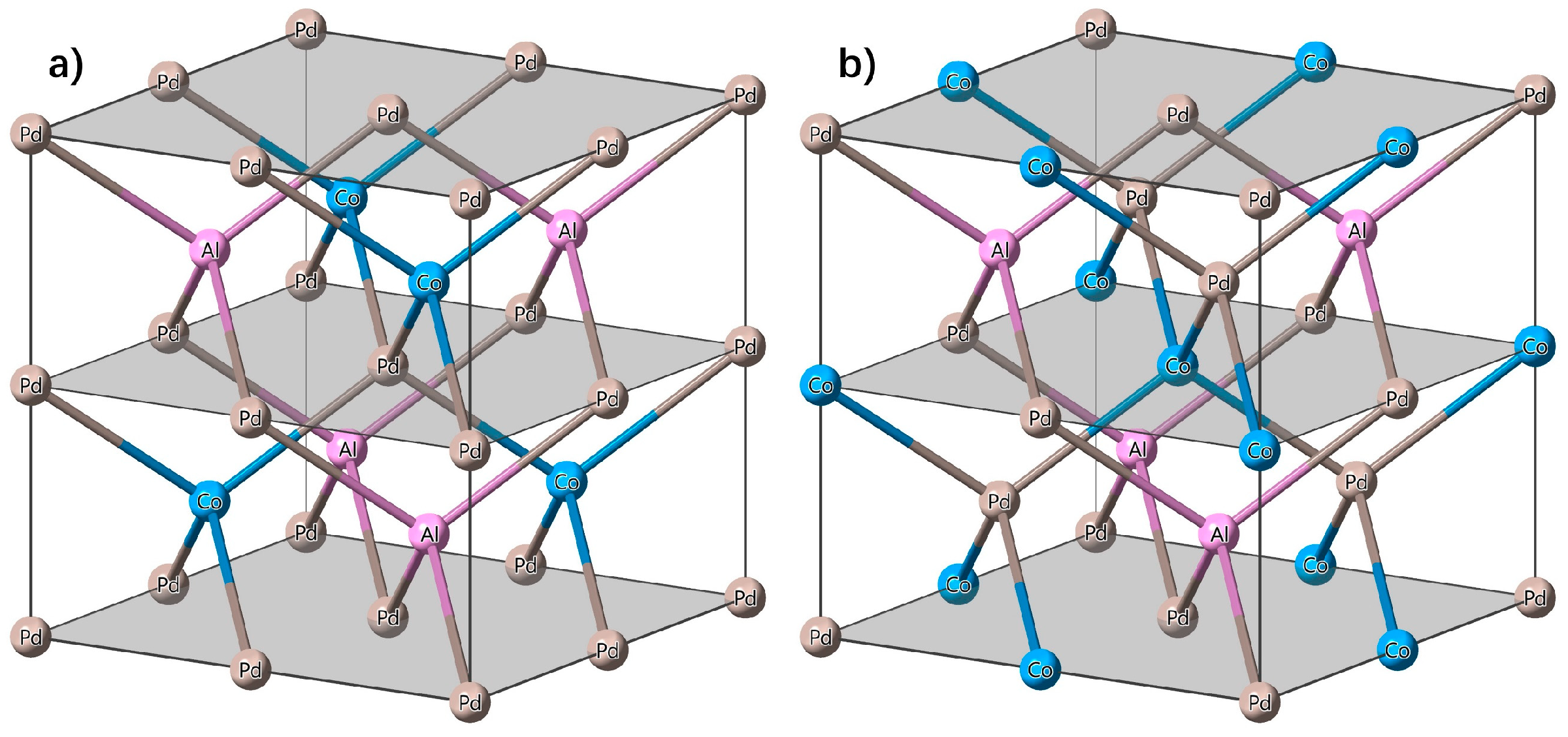
3.1. Crystal Structure and Equilibrium Lattice

The Heusler alloys generally have two variants of stoichiometric compositions: the half-Heusler compound with generic formula of XYZ [52,53,54,55,56,57] and the full Heusler compound X2YZ [5,58,59], where X and Y are from transition metal elements and Z from main group elements. In both half and full Heusler alloys, they normally crystalize in a cubic structure yet with different configurations [60]: non-centrosymmetric cubic structure C1b for half-Heusler; two different types for full Heusler: the Cu2MnAl structure with space group F m 3 ¯ m , also known as L21-type, and the Hg2CuTi structure with space ground F 4 ¯ 3 m , also known as “inverse structure” or XA-type. For the currently studied full Heusler compound Pd2CoAl, the two structural types have been taken into consideration and they are shown in Figure 1. It can been seen that the full Heusler Pd2CoAl has the general FCC-like symmetry with four interpenetrating sublattices defined by Wyckoff coordinates: A(0,0,0), B(0.25,0.25,0.25), C(0.5,0.5,0.5), and D(0.75,0.75,0.75). In L21-type structure, the two Pd atoms occupy the A and C sites, which are symmetrically identical, and the Co and Al atoms enter into the B and D sites, respectively; see Figure 1a. In XA-type structure, the two Pd atoms occupy the A and B sites with different surrounding environments, and the Co and Al atoms enter into the C and D sites; see Figure 1b.
In order to determine the ground state structural configuration and also obtain the equilibrium lattice constant, we have calculated the total energy of Pd2CoAl with different structures under different lattice constants. It should be noted that only the magnetic state is considered, as in the literature [34], since there is Co atom present. The obtained result is reported in Figure 2. It is found that the calculated total energy of Pd2CoAl in L21-type structure is always smaller than in XA-type structure throughout the whole lattice variation range, which means the L21-type structure is more energetically preferable and should be the ground state. This observation is in a good agreement with the general site preference rule found in other palladium-based Heusler compounds [32,34], i.e., since the Pd atom has more valence electrons than the Co atom, it is more electronegative and prefers the A and C sties. Thus, the L21-type structure is formed for Pd2CoAl. After the crystal structural configuration of Pd2CoAl has been determined, we further calculated its equilibrium lattice by polynomial fitting and minimization searching of the total energy and the derived equilibrium lattice is 6.057 Å, see Table 1, which coincides very well with previous study [30,34].

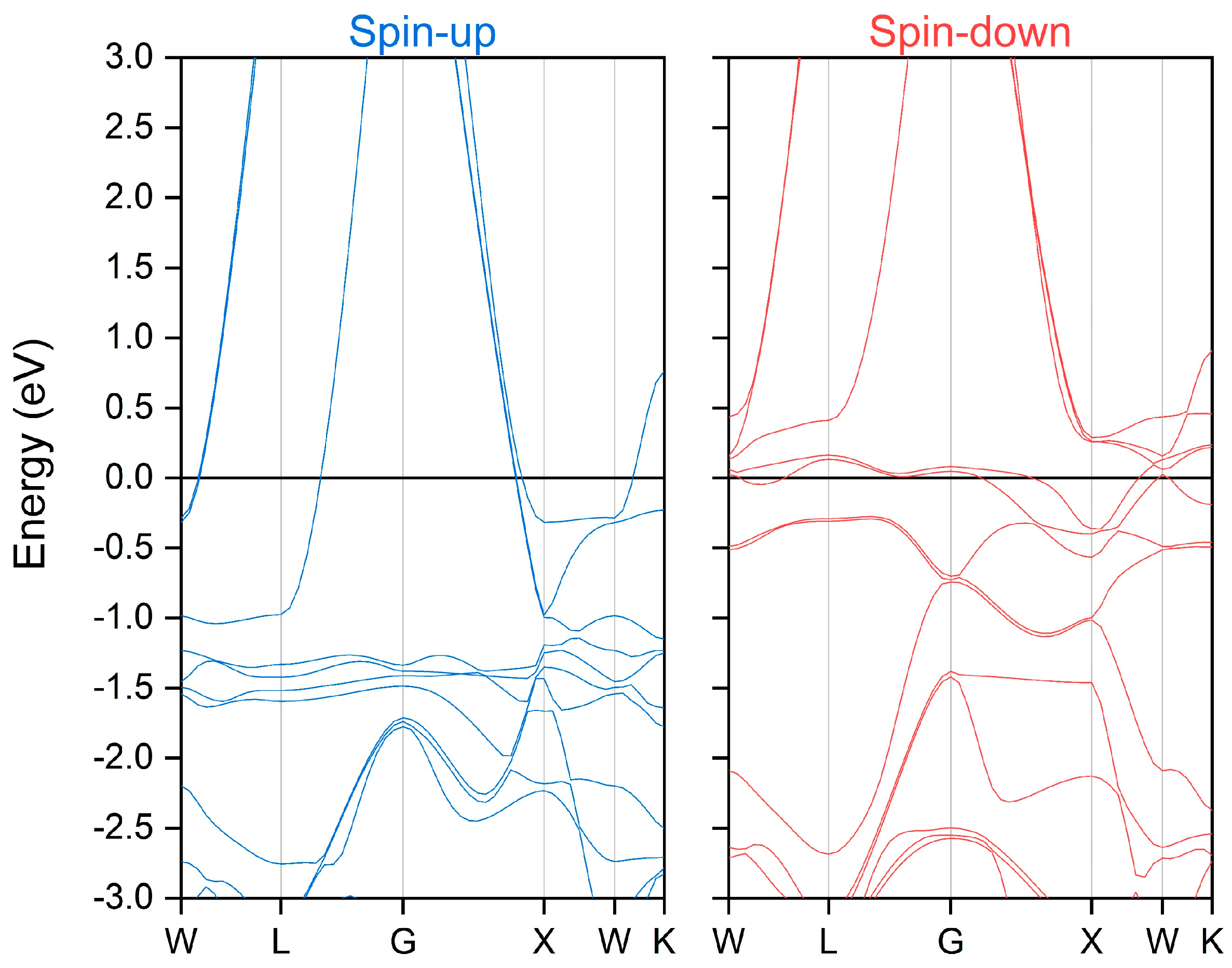
3.2. Electronic and Magnetic Properties

With the obtained equilibrium lattice constant, we can then investigate the corresponding electronic and magnetic properties of the full Heusler compound Pd2CoAl. Firstly, the spin-polarized electronic band structure has been calculated and it is shown in Figure 3. The Fermi energy is shifted to the zero energy level. It can be immediately observed that there are energy bands crossing the Fermi energy level in both spin directions, meaning that this Heusler compound behaves like metallic material at ground state.
In order to further elucidate the origin of the magnetism and also access the correlation states between different atoms in Pd2CoAl, the total and partial densities of states have been also computed and the result is shown in Figure 4. We can find that the main group element Al has negligible contribution and the total density of states is mainly contributed from the d states of the transition metal elements Pd and Co: a roughly symmetric distribution of states between the two spin directions around −5 to −2 eV from Pd and a strongly asymmetric distribution between the two spin directions around −2 to 1 eV from Co. In particular for the states near the Fermi energy level, they play a very important role in the determination of the electronic and magnetic properties for Heusler compounds. From the total density of states, there is a strong spin splitting effect in the two spin directions with a high peak below the Fermi level in the spin-up direction and a high peak just at the Fermi level in the spin-down direction. A closer look at the partial density of states reveals that this strong spin splitting is caused by the d-d hybridization between the Pd and Co atoms and the strong exchange splitting of the Co atom. The calculated magnetic moments are shown in Table 1, and it is found the total magnetic moment of Pd2CoAl is about 1.78 μB per formula unit and it is mainly from the Co atom. These results for the magnetic moments are consistent with the above analysis from electronic densities.
Furthermore, the electronic and magnetic properties of Pd2CoAl compound under uniform strains have been evaluated with lattice variation from −5% to +5% with respect to the equilibrium condition. The cubic L21-type structure for Pd2CoAl under different uniform strains is always maintained. The calculated band structures always exhibit overlaps with the Fermi energy level in both spin directions, indicating the metallic nature of Pd2CoAl is preserved under uniform strain at the studied range. The total and atom-resolved magnetic moments under uniform strains are displayed in Figure 5. It is found that the magnetic moment of Co atom has quite large variation while the moments of the Pd and Al atoms stay almost constant with strain applied. Note the different scale in different parts of the vertical axis. The total magnetic moment follows the trend of Co atom, which indicates that the strong exchange splitting remains under the studied whole uniform strain. With strain variation from 0% to −/+5% side, the lattice decreases/increases and the distance between every atom also decreases/increases. Thus, the interaction of the valence electrons from different atoms is decreased with lattice increase and they become more localized, which results in the partial regain of the spin moments from Co atom. It is worth mentioning that the magnetic moments of two Pd atoms are identical and overlap with each other through the whole uniform strain, which is because they have the same surrounding environments in L21-type structure

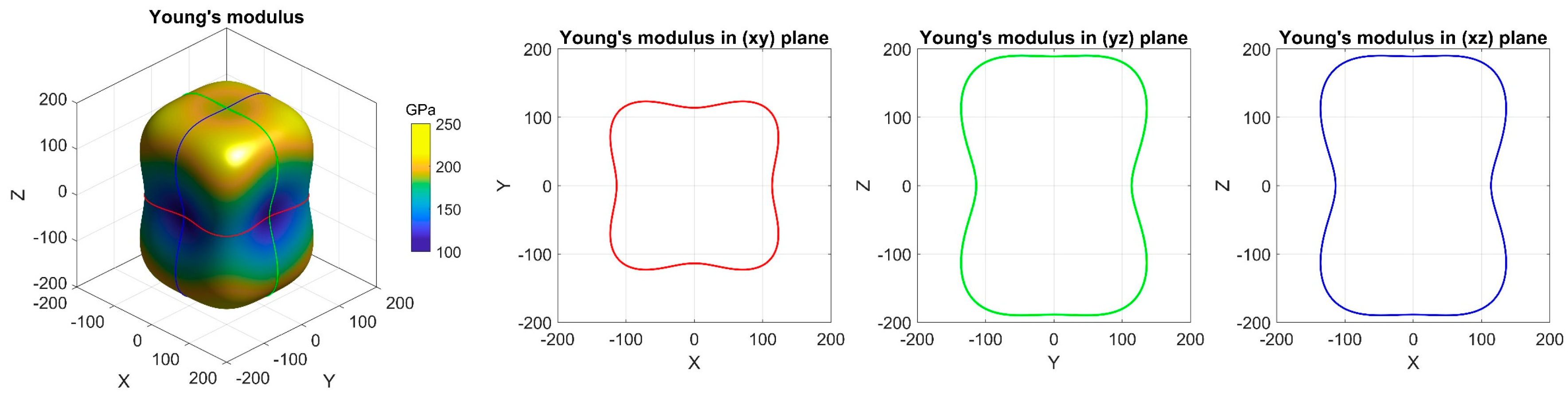
3.3. Tetragonal Structure and Phase Stability

In full Heusler compounds with possible phase transformation, the Bain paths have been widely utilized to study the reversible structural transformation between the austenitic and martensitic phases. A recent comprehensive theoretical study [30] of 286 full Heusler alloys from Faleev et al. has found that 62% have tetragonal ground states at zero temperature, including 15 Pd2-based full Heusler compounds. It is also well known that the physical properties of solid crystals are strongly related with the corresponding structures. To investigate the phase stability and also its effect in the full Heusler Pd2CoAl, we further calculate its electronic and magnetic properties under tetragonal structures, which is simply obtained by varying the lattice unproportionally; see Figure 6. Different tetragonal structures are formed by the different c/a ratios, yet the unit cell volume is kept constant, which is the same as the cubic structure. The total energies of the tetragonal phases for Pd2CoAl under different structure types have been calculated with different c/a ratios and the result is shown in Figure 6. It is seen that there is energy decrease when c/a is deviated from 1 for both structure types, that is, the tetragonal structure could further reduce the system energy and then lead to possible martensitic phase transformation. In comparison, the minimal total energy in the tetragonal XA-type structure is even higher than that in the cubic L21-type structure about 0.103 eV, meaning that the L21-type structure is energetically stable even under tetragonal structures. The energy minimum in tetragonal L21-type structure is found at c/a of 1.30 with energy difference of 0.165 eV relative to the cubic structure; see Figure 6. The energy difference between the cubic austenitic phase and the tetragonal martensitic phase and the c/a ratio at which the tetragonal structure reaches the minimum energy are commonly used to evaluate whether the phase transformation will occur or not in these Heusler compounds. The larger the energy difference is, the more probable the occurrence of the phase transformation is and the more stable the martensitic phase is. Some examples for the energy difference required for stable phase transformation are 0.14eV and 0.12 eV for Mn3Ga [61] and Mn2FeGa [29,31], respectively. The obtained value of 0.165 eV for Pd2CoAl is even bigger, which implies the stable tetragonal phase could be highly expected. As for the degree of shape memory, the c/a ratio can be used to access this effect and a larger value is preferred.
To examine the effect of phase transformation on the electronic properties, we calculate the electronic band structure of the tetragonal L21-type Pd2CoAl at c/a ratio of 1.30 and the result is reported in Figure 7. Note that the different high symmetry point path is adopted in the tetragonal structure from the cubic one. It is seen that the metallic feature maintains for the tetragonal structure because there are still bands crossing the Fermi energy level in both spin directions. Thus, the ferromagnetic metallic property of the full Heusler Pd2CoAl preserves even with the tetragonal phase.
To understand the possible reasons for this tetragonal phase stability, we explore the total densities of states in both cubic austenitic phase and tetragonal martensitic phase; see Figure 8. We can see there is strong spin splitting of the states in the two spin directions, especially around the Fermi energy level, indicating the ferromagnetic behavior for both phases. However, the two strong spin split distribution areas in the austenitic phase have been compressed into much wider and shallower ones in the martensitic phase, which means the strong d-d hybridization and exchange splitting in the cubic phase have been weakened in the tetragonal phase. As suggested by previous study [30], the density of states at the Fermi energy plays an important role in regulating the phase stability. Thus, we further provide the values of states in the two spin directions for both phases at the Fermi level, as shown in the right vertical axis in Figure 8. It is found that the values in the spin-up and spin-down channels have been reduced from 1.02 states/eV and 5.66 states/eV in the austenitic phase to 0.38 states/eV and 2.85 states/eV in the martensitic phase. According to the Jahn–Teller effect, this decreasing behavior of the density of states proves that the martensitic phase is more stable than the austenitic phase.
With different tetragonal structures, the total and partial magnetic moments have also been calculated and are displayed in Figure 9. Note the different scale in the two parts of the vertical axis. We can see that the magnetic moment of Co atom always decreases at both sides when c/a ratio is changed from 1, while the moments of Pd atoms decrease at first and then increase, leading to the switch from very weakly antiparallel to weakly parallel. In particular at c/a ratio of 1.30, the magnetic moments of Co and Pd atoms are 1.85 μB and 0.07 μB, respectively. The total magnetic moment is also increased from 1.78 μB in the cubic austenitic phase to 1.91 μB in the tetragonal martensitic phase.
For the full Heusler compound, the possible martensitic phase transformation can be examined not only with energetic perspective but also by the dynamic and mechanical stability. The phonon dispersion spectra along the high symmetry points in the Brillouin zone for L21-type Pd2CoAl in both cubic austenitic and tetragonal martensitic phases have been calculated with the finite displacement method and the results are plotted in Figure 10. It is clearly seen that there is a strong softening behavior present in the cubic structure with a lot of imaginary frequencies, suggesting the structural instability of the austenitic phase. Whereas, the phonon spectrum in the tetragonal structure exhibit no imaginary frequencies and, thus, the system is dynamically stable. This structural instability in the austenitic phase could lead to the martensitic phase transformation.
By employing the stress strain method [62,63], we also computed the various elastic constants for the full Heusler compound Pd2CoAl in both cubic and tetragonal structures. For a simple cubic structure, there are only three independent elastic constants, namely, C11, C12, and C14. For the tetragonal structure, there are six: C11, C12, C13, C33, C44, and C66. The derived values for all constants are summarized in Table 2. Based on the generalized Born–Huang elastic stability criteria [64], the mechanical stability of Pd2CoAl in cubic and tetragonal phases should fulfill the following two corresponding conditions:
C11 + 2C12 > 0, C11 − C12 > 0, C44 > 0
C 11 > | C 12 | ,   2 C 13 2 < C 33 ( C 11 + C 12 ) , C 44 > 0 ,   C 66 > 0
From these, we can derive that the cubic phase is not mechanically stable but the tetragonal phase is stable. In combination, the cubic phase Pd2CoAl is not stable from both the mechanical and dynamic point of view while the tetragonal phase shows good stability, which further elevates the martensitic phase transformation possibility.
Moreover, with the obtained elastic constants we can further evaluate the elastic anisotropy in the tetragonal L21-type Pd2CoAl compound. The calculated 3D directional dependence of the Young’s modulus and shear modulus with ELATE program [65] are plotted in Figure 11 and Figure 12, respectively. Besides this, the corresponding 2D projections in different planes are also provided together. We can clearly see that the tetragonal Pd2CoAl compound has strong elastic anisotropy. The maximum of the Young’s modulus and shear modulus are found in the [111] and [001] directions, respectively.

4. Conclusions

With first principles calculation, we have systematically investigated the electronic, magnetic, dynamic, and mechanical properties of the full Heusler compound Pd2CoAl and also examined its phase stability from different perspectives. Results show that the L21-type structure is energetically more preferable than the XA-type because of the lower total energy. The derived equilibrium lattice constant is 6.057 Å and it is in very good agreement with previous study. At ground state in cubic phase, Pd2CoAl behaves like ferromagnetic metal with total magnetic moment of 1.78 μB, which is mainly contributed by the Co atom from strong spin splitting effect of the density of states in two spin directions. Under uniform strains from −5% to +5%, the variation of total magnetic moments has been obtained and it is still caused by the much larger change from the Co atom, compared with Pd and Al atoms. The tetragonal structure has further been considered and it is found the total energy can be reduced when the cubic structure is varied into the tetragonal one, leading to the possible tetragonal martensitic phase transformation. The large energy difference of 0.165 eV between the tetragonal and cubic phases is found at the c/a ratio of 1.30. To evaluate the phase stability, the total density of states has been compared between the cubic and tetragonal phases for Pd2CoAl, and results show that the tetragonal phase transformation could reduce the states at the Fermi energy level in both directions and thus enhance the phase stability. In addition, the dynamic and mechanical stabilities have also been accessed for Pd2CoAl in both cubic and tetragonal structures and it is found that the tetragonal phase shows good stability against the cubic phase, which further confirms that the tetragonal phase transformation is highly expected. Lastly, the strong elastic anisotropy has been clearly shown with the 3D representation of the directional dependence of the Young’s modulus and shear modulus.

Author Contributions

T.Y. and X.W. conceived the work; L.H. and J.Y. performed the calculations and result analysis and wrote the paper; Y.W. and R.K. provided valuable comments on this work and the manuscript.

Funding

This research was supported by “Fundamental Research Funds for the Central Universities” grant number [XDJK2018C078] and “Doctoral Fund Project of Southwest University” grant number [SWU117037].

Acknowledgments

The authors thank the anonymous reviewers for their constructive suggestions.

Conflicts of Interest

The authors declare no conflict of interest.

References

  1. Abada, A.; Amara, K.; Hiadsi, S.; Amrani, B. First principles study of a new half-metallic ferrimagnets Mn2-based full Heusler compounds: Mn2ZrSi and Mn2ZrGe. J. Magn. Magn. Mater. 2015, 388, 59–67. [Google Scholar] [CrossRef]
  2. Babiker, S.; Gao, G.; Yao, K. Half-metallicity and magnetism of Heusler alloys Co2HfZ (Z = Al, Ga, Ge, Sn). J. Magn. Magn. Mater. 2017, 441, 356–360. [Google Scholar] [CrossRef]
  3. Bahramian, S.; Ahmadian, F. Half-metallicity and magnetism of quaternary Heusler compounds CoRuTiZ (Z=Si, Ge, and Sn). J. Magn. Magn. Mater. 2017, 424, 122–129. [Google Scholar] [CrossRef]
  4. Chen, Y.; Chen, S.; Wang, B.; Wu, B.; Huang, H.; Qin, X.; Li, D.; Yan, W. Half-Metallicity and Magnetism of the Quaternary Heusler Compound TiZrCoIn1−xGex from the First-Principles Calculations. Appl. Sci. 2019, 9, 620. [Google Scholar] [CrossRef]
  5. Galanakis, I.; Dederichs, P.H.; Papanikolaou, N. Slater-Pauling behavior and origin of the half-metallicity of the full-Heusler alloys. Phys. Rev. B 2002, 66, 174429. [Google Scholar] [CrossRef] [Green Version]
  6. Galanakis, I.; Mavropoulos, P. Spin-polarization and electronic properties of half-metallic Heusler alloys calculated from first principles. J. Phys. Condens. Matter 2007, 19, 315213. [Google Scholar] [CrossRef] [PubMed] [Green Version]
  7. Ganai, Z.S.; Yousuf, S.; Batoo, K.M.; Khan, M.; Gupta, D.C. Half-metallicity and onsite Hubbard interaction on d-electronic states: A case study of Fe2NiZ (Z = Al, Ga, Si, Ge) Heusler systems. Philos. Mag. 2019, 99, 1551–1562. [Google Scholar] [CrossRef]
  8. Gao, G.Y.; Yao, K.L.; Sasioglu, E.; Sandratskii, L.M.; Liu, Z.L.; Jiang, J.L. Half-metallic ferromagnetism in zinc-blende CaC, SrC, and BaC from first principles. Phys. Rev. B 2007, 75, 174442. [Google Scholar] [CrossRef]
  9. Wang, X.T.; Lin, T.T.; Rozale, H.; Dai, X.F.; Liu, G.D. Robust half-metallic properties in inverse Heusler alloys composed of 4d transition metal elements: Zr2RhZ (Z=Al, Ga, In). J. Magn. Magn. Mater. 2016, 402, 190–195. [Google Scholar] [CrossRef]
  10. Yang, T.; Cao, J.T.; Wang, X.T. Structural, Electronic, Magnetic, Mechanic and Thermodynamic Properties of the Inverse Heusler Alloy Ti2NiIn Under Pressure. Crystals 2018, 8, 429. [Google Scholar] [CrossRef]
  11. Bainsla, L.; Mallick, A.I.; Raja, M.M.; Coelho, A.A.; Nigam, A.K.; Johnson, D.D.; Alam, A.; Suresh, K.G. Origin of spin gapless semiconductor behavior in CoFeCrGa: Theory and Experiment. Phys. Rev. B 2015, 92, 045201. [Google Scholar] [CrossRef] [Green Version]
  12. Bainsla, L.; Mallick, A.I.; Raja, M.M.; Nigam, A.K.; Varaprasad, B.C.S.; Takahashi, Y.K.; Alam, A.; Suresh, K.G.; Hono, K. Spin gapless semiconducting behavior in equiatomic quaternary CoFeMnSi Heusler alloy. Phys. Rev. B 2015, 91, 104408. [Google Scholar] [CrossRef] [Green Version]
  13. Wang, X.L. Proposal for a new class of materials: Spin gapless semiconductors. Phys. Rev. Lett. 2008, 100, 156404. [Google Scholar] [CrossRef]
  14. Wang, X.T.; Cheng, Z.X.; Khenata, R.; Rozale, H.; Wang, J.L.; Wang, L.Y.; Guo, R.K.; Liu, G.D. A first-principle investigation of spin-gapless semiconductivity, half-metallicity, and fully-compensated ferrimagnetism property in Mn2ZnMg inverse Heusler compound. J. Magn. Magn. Mater. 2017, 423, 285–290. [Google Scholar] [CrossRef]
  15. Wang, X.T.; Cheng, Z.X.; Wang, J.L.; Wang, X.L.; Liu, G.D. Recent advances in the Heusler based spin-gapless semiconductors. J. Mater. Chem. C 2016, 4, 7176–7192. [Google Scholar] [CrossRef]
  16. Wang, X.T.; Li, T.Z.; Cheng, Z.X.; Wang, X.L.; Chen, H. Recent advances in Dirac spin-gapless semiconductors. Appl. Phys. Rev. 2018, 5, 041103. [Google Scholar] [CrossRef] [Green Version]
  17. Yang, T.; Hao, L.Y.; Khenata, R.; Wang, X.T. Strain Conditions for the Inverse Heusler Type Fully Compensated Spin-Gapless Semiconductor Ti2MnAl: A First-Principles Study. Materials 2018, 11, 2091. [Google Scholar] [CrossRef]
  18. Chen, X.; Huang, Y.; Yuan, H.; Liu, J.; Chen, H. Theoretical investigation on thermoelectric properties of spin gapless semiconductor Cr2ZnSi. Appl. Phys. A 2018, 124, 841. [Google Scholar] [CrossRef]
  19. Hamad, B. Ab initio investigations of the structural, electronic, and thermoelectric properties of Fe2NbAl-based alloys. J. Mater. Sci. 2016, 51, 10887–10896. [Google Scholar] [CrossRef]
  20. Hasan, R.; Ur, S.C. Thermoelectric and Transport Properties of FeV1−xTixSb Half-Heusler System Synthesized by Controlled Mechanical Alloying Process. Electron. Mater. Lett. 2018, 14, 725–732. [Google Scholar] [CrossRef]
  21. Kara, H.; Kahaly, M.U.; Ozdogan, K. Thermoelectric response of quaternary Heusler compound CrVNbZn. J. Alloy. Compd. 2018, 735, 950–958. [Google Scholar] [CrossRef]
  22. Lin, T.T.; Gao, Q.; Liu, G.D.; Dai, X.F.; Zhang, X.M.; Zhang, H.B. Dynamical stability, electronic and thermoelectric properties of quaternary ZnFeTiSi Heusler compound. Curr. Appl. Phys. 2019, 19, 721–727. [Google Scholar] [CrossRef]
  23. Patel, P.D.; Shinde, S.M.; Gupta, S.D.; Jha, P.K. A promising thermoelectric response of fully compensated ferrimagnetic spin gapless semiconducting Heusler alloy Zr2MnAl at high temperature: DFT study. Mater. Res. Express 2019, 6, 076307. [Google Scholar] [CrossRef]
  24. Shigeta, I.; Kubota, T.; Sakuraba, Y.; Kimura, S.; Awaji, S.; Takanashi, K.; Hiroi, M. Transport properties of epitaxial films for superconductor NbN and half-metallic Heusler alloy Co2MnSi under high magnetic fields. Phys. B Condens. Matter 2018, 536, 310–313. [Google Scholar] [CrossRef]
  25. Nakajima, Y.; Hu, R.; Kirshenbaum, K.; Hughes, A.; Syers, P.; Wang, X.; Wang, K.; Wang, R.; Saha, S.R.; Pratt, D.; et al. Topological RPdBi half-Heusler semimetals: A new family of noncentrosymmetric magnetic superconductors. Sci Adv. 2015, 1, e1500242. [Google Scholar] [CrossRef]
  26. Sprungmann, D.; Westerholt, K.; Zabel, H.; Weides, M.; Kohlstedt, H. Evidence for triplet superconductivity in Josephson junctions with barriers of the ferromagnetic Heusler alloy Cu2MnAl. Phys. Rev. B 2010, 82, 060505. [Google Scholar] [CrossRef]
  27. He, M.; Sun, H.; He, Q.L. Topological insulator: Spintronics and quantum computations. Front. Phys. 2019, 14, 43401. [Google Scholar] [CrossRef]
  28. Chadov, S.; Qi, X.; Kubler, J.; Fecher, G.H.; Felser, C.; Zhang, S.C. Tunable multifunctional topological insulators in ternary Heusler compounds. Nat. Mater. 2010, 9, 541–545. [Google Scholar] [CrossRef] [Green Version]
  29. Felser, C.; Alijani, V.; Winterlik, J.; Chadov, S.; Nayak, A.K. Tetragonal Heusler Compounds for Spintronics. IEEE Trans. Magn. 2013, 49, 682–685. [Google Scholar] [CrossRef]
  30. Faleev, S.V.; Ferrante, Y.; Jeong, J.; Samant, M.G.; Jones, B.; Parkin, S.S.P. Origin of the Tetragonal Ground State of Heusler Compounds. Phys. Rev. Appl. 2017, 7, 034022. [Google Scholar] [CrossRef] [Green Version]
  31. Faleev, S.V.; Ferrante, Y.; Jeong, J.; Samant, M.G.; Jones, B.; Parkin, S.S.P. Heusler compounds with perpendicular magnetic anisotropy and large tunneling magnetoresistance. Phys. Rev. Mater. 2017, 1, 024402. [Google Scholar] [CrossRef]
  32. Han, Y.; Wu, M.; Feng, Y.; Cheng, Z.; Lin, T.; Yang, T.; Khenata, R.; Wang, X. Competition between cubic and tetragonal phases in all-d-metal Heusler alloys, X2-xMn1+xV (X = Pd, Ni, Pt, Ag, Au, Ir, Co; x = 1, 0): A new potential direction of the Heusler family. IUCrJ 2019, 6, 465–472. [Google Scholar] [CrossRef]
  33. Han, Y.L.; Bouhemadou, A.; Khenata, R.; Cheng, Z.X.; Yang, T.; Wang, X.T. Prediction of possible martensitic transformations in all-d-metal Zinc-based Heusler alloys from first-principles. J. Magn. Magn. Mater. 2019, 471, 49–55. [Google Scholar] [CrossRef]
  34. Wu, M.; Han, Y.; Bouhemadou, A.; Cheng, Z.; Khenata, R.; Kuang, M.; Wang, X.; Yang, T.; Yuan, H.; Wang, X. Site preference and tetragonal distortion in palladium-rich Heusler alloys. IUCrJ 2019, 6, 218–225. [Google Scholar] [CrossRef]
  35. Wu, Y.; Xu, X.G.; Miao, J.; Jiang, Y. Perpendicular Magnetic Anisotropy in Co-Based Full Heusler Alloy Thin Films. Spin 2015, 05, 1540012. [Google Scholar] [CrossRef]
  36. Wang, W.H.; Przybylski, M.; Kuch, W.; Chelaru, L.I.; Wang, J.; Lu, Y.F.; Barthel, J.; Meyerheim, H.L.; Kirschner, J. Magnetic properties and spin polarization of Co2MnSi Heusler alloy thin films epitaxially grown on GaAs(001). Phys. Rev. B 2005, 71, 144416. [Google Scholar] [CrossRef]
  37. Huang, B.; Duan, Y.-H.; Hu, W.-C.; Sun, Y.; Chen, S. Structural, anisotropic elastic and thermal properties of MB (M=Ti, Zr and Hf) monoborides. Ceram. Int. 2015, 41, 6831–6843. [Google Scholar] [CrossRef]
  38. Fichtner, T.; Wang, C.; Levin, A.A.; Kreiner, G.; Mejia, C.S.; Fabbrici, S.; Albertini, F.; Felser, C. Effects of Annealing on the Martensitic Transformation of Ni-Based Ferromagnetic Shape Memory Heusler Alloys and Nanoparticles. Metals 2015, 5, 484–503. [Google Scholar] [CrossRef] [Green Version]
  39. Kainuma, R.; Imano, Y.; Ito, W.; Sutou, Y.; Morito, H.; Okamoto, S.; Kitakami, O.; Oikawa, K.; Fujita, A.; Kanomata, T.; et al. Magnetic-field-induced shape recovery by reverse phase transformation. Nature 2006, 439, 957–960. [Google Scholar] [CrossRef]
  40. Zhu, W.; Liu, E.K.; Feng, L.; Tang, X.D.; Chen, J.L.; Wu, G.H.; Liu, H.Y.; Meng, F.B.; Luo, H.Z. Magnetic-field-induced transformation in FeMnGa alloys. Appl. Phys. Lett. 2009, 95, 222512. [Google Scholar] [CrossRef]
  41. Planes, A.; Mañosa, L.; Acet, M. Magnetocaloric effect and its relation to shape-memory properties in ferromagnetic Heusler alloys. J. Phys. Condens. Matter 2009, 21, 233201. [Google Scholar] [CrossRef] [Green Version]
  42. Wei, Z.Y.; Liu, E.K.; Li, Y.; Han, X.L.; Du, Z.W.; Luo, H.Z.; Liu, G.D.; Xi, X.K.; Zhang, H.W.; Wang, W.H.; et al. Magnetostructural martensitic transformations with large volume changes and magneto-strains in all-d-metal Heusler alloys. Appl. Phys. Lett. 2016, 109, 071904. [Google Scholar] [CrossRef]
  43. Liu, K.; Ma, S.; Ma, C.; Han, X.; Yu, K.; Yang, S.; Zhang, Z.; Song, Y.; Luo, X.; Chen, C.; et al. Martensitic transformation and giant magneto-functional properties in all-d-metal Ni-Co-Mn-Ti alloy ribbons. J. Alloy. Compd. 2019, 790, 78–92. [Google Scholar] [CrossRef]
  44. Zutic, I.; Fabian, J.; Das Sarma, S. Spintronics: Fundamentals and applications. Rev. Mod. Phys. 2004, 76, 323–410. [Google Scholar] [CrossRef] [Green Version]
  45. Hirohata, A.; Sagar, J.; Fleet, L.R.; Endo, H. Polycrystalline co-based full-heusler-alloy films for spintronic devices. Spin 2014, 04, 1440021. [Google Scholar] [CrossRef]
  46. Yang, S.A. Dirac and Weyl Materials: Fundamental Aspects and Some Spintronics Applications. Spin 2016, 06, 1640003. [Google Scholar] [CrossRef]
  47. Payne, M.C.; Teter, M.P.; Allan, D.C.; Arias, T.A.; Joannopoulos, J.D. Iterative minimization techniques forab initiototal-energy calculations: Molecular dynamics and conjugate gradients. Rev. Mod. Phys. 1992, 64, 1045–1097. [Google Scholar] [CrossRef]
  48. Segall, M.D.; Lindan, P.J.D.; Probert, M.J.; Pickard, C.J.; Hasnip, P.J.; Clark, S.J.; Payne, M.C. First-principles simulation: Ideas, illustrations and the CASTEP code. J. Phys. Condens. Matter 2002, 14, 2717–2744. [Google Scholar] [CrossRef]
  49. Perdew, J.P.; Burke, K.; Ernzerhof, M. Generalized Gradient Approximation Made Simple. Phys. Rev. Lett. 1996, 77, 3865–3868. [Google Scholar] [CrossRef] [Green Version]
  50. Vanderbilt, D. Soft self-consistent pseudopotentials in a generalized eigenvalue formalism. Phys. Rev. B 1990, 41, 7892–7895. [Google Scholar] [CrossRef]
  51. Refson, K.; Tulip, P.R.; Clark, S.J. Variational density-functional perturbation theory for dielectrics and lattice dynamics. Phys. Rev. B 2006, 73, 155114. [Google Scholar] [CrossRef] [Green Version]
  52. Damewood, L.; Busemeyer, B.; Shaughnessy, M.; Fong, C.Y.; Yang, L.H.; Felser, C. Stabilizing and increasing the magnetic moment of half-metals: The role of Li in half-Heusler LiMnZ (Z=N,P,Si). Phys. Rev. B 2015, 91, 064409. [Google Scholar] [CrossRef]
  53. Gofryk, K.; Kaczorowski, D.; Plackowski, T.; Leithe-Jasper, A.; Grin, Y. Magnetic and transport properties of rare-earth-based half-Heusler phasesRPdBi: Prospective systems for topological quantum phenomena. Phys. Rev. B 2011, 84, 035208. [Google Scholar] [CrossRef]
  54. Karati, A.; Murty, B.S. Synthesis of nanocrystalline half-Heusler TiNiSn by mechanically activated annealing. Mater. Lett. 2017, 205, 114–117. [Google Scholar] [CrossRef]
  55. Kroder, J.; Manna, K.; Kriegner, D.; Sukhanov, A.S.; Liu, E.; Borrmann, H.; Hoser, A.; Gooth, J.; Schnelle, W.; Inosov, D.S.; et al. Spin glass behavior in the disordered half-Heusler compound IrMnGa. Phys. Rev. B 2019, 99, 174410. [Google Scholar] [CrossRef]
  56. Yin, M.; Nash, P. Standard enthalpies of formation of selected XYZ half-Heusler compounds. J. Chem. Thermodyn. 2015, 91, 1–7. [Google Scholar] [CrossRef]
  57. Zilber, T.; Cohen, S.; Fuks, D.; Gelbstein, Y. TiNiSn half-Heusler crystals grown from metallic flux for thermoelectric applications. J. Alloy. Compd. 2019, 781, 1132–1138. [Google Scholar] [CrossRef]
  58. Faleev, S.V.; Ferrante, Y.; Jeong, J.; Samant, M.G.; Jones, B.; Parkin, S.S.P. Unified explanation of chemical ordering, the Slater-Pauling rule, and half-metallicity in full Heusler compounds. Phys. Rev. B 2017, 95, 045140. [Google Scholar] [CrossRef] [Green Version]
  59. Graf, T.; Casper, F.; Winterlik, J.; Balke, B.; Fecher, G.H.; Felser, C. Crystal Structure of New Heusler Compounds. Z. Anorg. Allg. Chem. 2009, 635, 976–981. [Google Scholar] [CrossRef] [Green Version]
  60. Graf, T.; Felser, C.; Parkin, S.S.P. Simple rules for the understanding of Heusler compounds. Prog. Solid State Chem. 2011, 39, 1–50. [Google Scholar] [CrossRef]
  61. Liu, Z.H.; Tang, Z.J.; Tan, J.G.; Zhang, Y.J.; Wu, Z.G.; Wang, X.T.; Liu, G.D.; Ma, X.Q. Tailoring structural and magnetic properties of Mn3-xFexGa alloys towards multifunctional applications. IUCrJ 2018, 5, 794–800. [Google Scholar] [CrossRef]
  62. Wang, J.; Li, J.; Yip, S.; Phillpot, S.; Wolf, D. Mechanical instabilities of homogeneous crystals. Phys. Rev. B 1995, 52, 12627–12635. [Google Scholar] [CrossRef]
  63. Yip, S.; Li, J.; Tang, M.J.; Wang, J.G. Mechanistic aspects and atomic-level consequences of elastic instabilities in homogeneous crystals. Mater. Sci. Eng. A Struct. Mater. Prop. Microstruct. Process. 2001, 317, 236–240. [Google Scholar] [CrossRef]
  64. Mouhat, F.; Coudert, F.X. Necessary and sufficient elastic stability conditions in various crystal systems. Phys. Rev. B 2014, 90, 224104. [Google Scholar] [CrossRef]
  65. Gaillac, R.; Pullumbi, P.; Coudert, F.X. ELATE: An open-source online application for analysis and visualization of elastic tensors. J. Phys. Condens. Matter 2016, 28, 275201. [Google Scholar] [CrossRef]
Crystals 09 00422 g001 550
Figure 1. Schematic illustrations of the atomic configurations for the full Heusler compound Pd2CoAl in (a) L21-type and (b) XA-type structures.
Figure 1. Schematic illustrations of the atomic configurations for the full Heusler compound Pd2CoAl in (a) L21-type and (b) XA-type structures.
Crystals 09 00422 g001
Crystals 09 00422 g002 550
Figure 2. The calculated total energies of the full Heusler compound Pd2CoAl with different crystal structures under different lattice constants.
Figure 2. The calculated total energies of the full Heusler compound Pd2CoAl with different crystal structures under different lattice constants.
Crystals 09 00422 g002
Crystals 09 00422 g003 550
Figure 3. The calculated spin-polarized electronic band structures for the full Heusler compound Pd2CoAl in L21-type cubic structure at the equilibrium lattice constant.
Figure 3. The calculated spin-polarized electronic band structures for the full Heusler compound Pd2CoAl in L21-type cubic structure at the equilibrium lattice constant.
Crystals 09 00422 g003
Crystals 09 00422 g004 550
Figure 4. The calculated total and partial densities of states for the full Heusler compound Pd2CoAl in L21-type cubic structure at the equilibrium lattice constant.
Figure 4. The calculated total and partial densities of states for the full Heusler compound Pd2CoAl in L21-type cubic structure at the equilibrium lattice constant.
Crystals 09 00422 g004
Crystals 09 00422 g005 550
Figure 5. The calculated total and atom-resolved magnetic moments for the full Heusler compound Pd2CoAl in L21-type under different uniform strains. Note the different scale of the two parts in the vertical axis.
Figure 5. The calculated total and atom-resolved magnetic moments for the full Heusler compound Pd2CoAl in L21-type under different uniform strains. Note the different scale of the two parts in the vertical axis.
Crystals 09 00422 g005
Crystals 09 00422 g006 550
Figure 6. The tetragonal L21-type crystal structure for the full Heusler compound Pd2CoAl and the calculated total energies with two crystal structures under different tetragonal structures.
Figure 6. The tetragonal L21-type crystal structure for the full Heusler compound Pd2CoAl and the calculated total energies with two crystal structures under different tetragonal structures.
Crystals 09 00422 g006
Crystals 09 00422 g007 550
Figure 7. The calculated spin polarized electronic band structures for the full Heusler compound Pd2CoAl in L21-type tetragonal structure under c/a of 1.30.
Figure 7. The calculated spin polarized electronic band structures for the full Heusler compound Pd2CoAl in L21-type tetragonal structure under c/a of 1.30.
Crystals 09 00422 g007
Crystals 09 00422 g008 550
Figure 8. The calculated total densities of states for the full Heusler compound Pd2CoAl in L21-type cubic and tetragonal structures.
Figure 8. The calculated total densities of states for the full Heusler compound Pd2CoAl in L21-type cubic and tetragonal structures.
Crystals 09 00422 g008
Crystals 09 00422 g009 550
Figure 9. The calculated total and atom-resolved magnetic moments for the full Heusler compound Pd2CoAl in L21-type structure under different tetragonal strains. Note the different scale of the two parts in the vertical axis.
Figure 9. The calculated total and atom-resolved magnetic moments for the full Heusler compound Pd2CoAl in L21-type structure under different tetragonal strains. Note the different scale of the two parts in the vertical axis.
Crystals 09 00422 g009
Crystals 09 00422 g010 550
Figure 10. The calculated phonon dispersion spectrum along high symmetry points for the full Heusler compound Pd2CoAl in L21-type cubic and tetragonal structures.
Figure 10. The calculated phonon dispersion spectrum along high symmetry points for the full Heusler compound Pd2CoAl in L21-type cubic and tetragonal structures.
Crystals 09 00422 g010
Crystals 09 00422 g011 550
Figure 11. The calculated directional dependent Young’s modulus for the full Heusler compound Pd2CoAl in L21-type tetragonal structure.
Figure 11. The calculated directional dependent Young’s modulus for the full Heusler compound Pd2CoAl in L21-type tetragonal structure.
Crystals 09 00422 g011
Crystals 09 00422 g012 550
Figure 12. The calculated directional dependent shear modulus for the full Heusler compound Pd2CoAl in L21-type tetragonal structure.
Figure 12. The calculated directional dependent shear modulus for the full Heusler compound Pd2CoAl in L21-type tetragonal structure.
Crystals 09 00422 g012
Table
Table 1. The calculated equilibrium lattice constant, total and atom-resolved magnetic moment.
Table 1. The calculated equilibrium lattice constant, total and atom-resolved magnetic moment.
Compound Lattice (Å)Magnetic Moment (μB)
MTotal (μB)MPd(A)MPd(B)MCoMAl
Pd2CoAlCurrent6.0571.78−0.06−0.061.95−0.05
Ref [34]6.061.790.030.031.75−0.03
Table
Table 2. The calculated various elastic constants (Cij) for the full Heusler compound Pd2CoAl in both cubic and tetragonal structures.
Table 2. The calculated various elastic constants (Cij) for the full Heusler compound Pd2CoAl in both cubic and tetragonal structures.
CompoundStructureElastic Constants (GPa)
C11C12C13C14C33C44C66
Pd2CoAlCubic143.2167.4-100.2---
Tetragonal133.738.160.3-231.293.086.4

Share and Cite

MDPI and ACS Style

Hao, L.; You, J.; Khenata, R.; Wang, Y.; Wang, X.; Yang, T. Theoretical Study of the Electronic and Magnetic Properties and Phase Stability of the Full Heusler Compound Pd2CoAl. Crystals 2019, 9, 422. https://doi.org/10.3390/cryst9080422

AMA Style

Hao L, You J, Khenata R, Wang Y, Wang X, Yang T. Theoretical Study of the Electronic and Magnetic Properties and Phase Stability of the Full Heusler Compound Pd2CoAl. Crystals. 2019; 9(8):422. https://doi.org/10.3390/cryst9080422

Chicago/Turabian Style

Hao, Liyu, Jiaxue You, Rabah Khenata, Yanfeng Wang, Xiaotian Wang, and Tie Yang. 2019. "Theoretical Study of the Electronic and Magnetic Properties and Phase Stability of the Full Heusler Compound Pd2CoAl" Crystals 9, no. 8: 422. https://doi.org/10.3390/cryst9080422

APA Style

Hao, L., You, J., Khenata, R., Wang, Y., Wang, X., & Yang, T. (2019). Theoretical Study of the Electronic and Magnetic Properties and Phase Stability of the Full Heusler Compound Pd2CoAl. Crystals, 9(8), 422. https://doi.org/10.3390/cryst9080422

Note that from the first issue of 2016, this journal uses article numbers instead of page numbers. See further details here.

Article Metrics

Back to TopTop