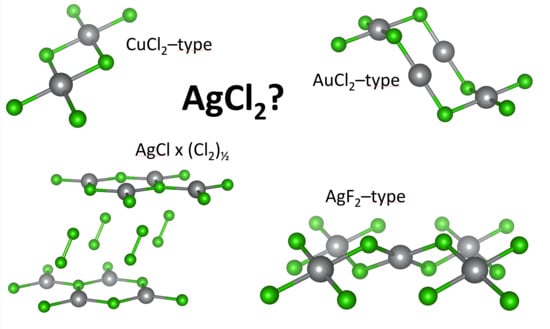
Quest for Compounds at the Verge of Charge Transfer Instabilities: The Case of Silver(II) Chloride †
Abstract
:1. Introduction
2. Methodology
3. Results
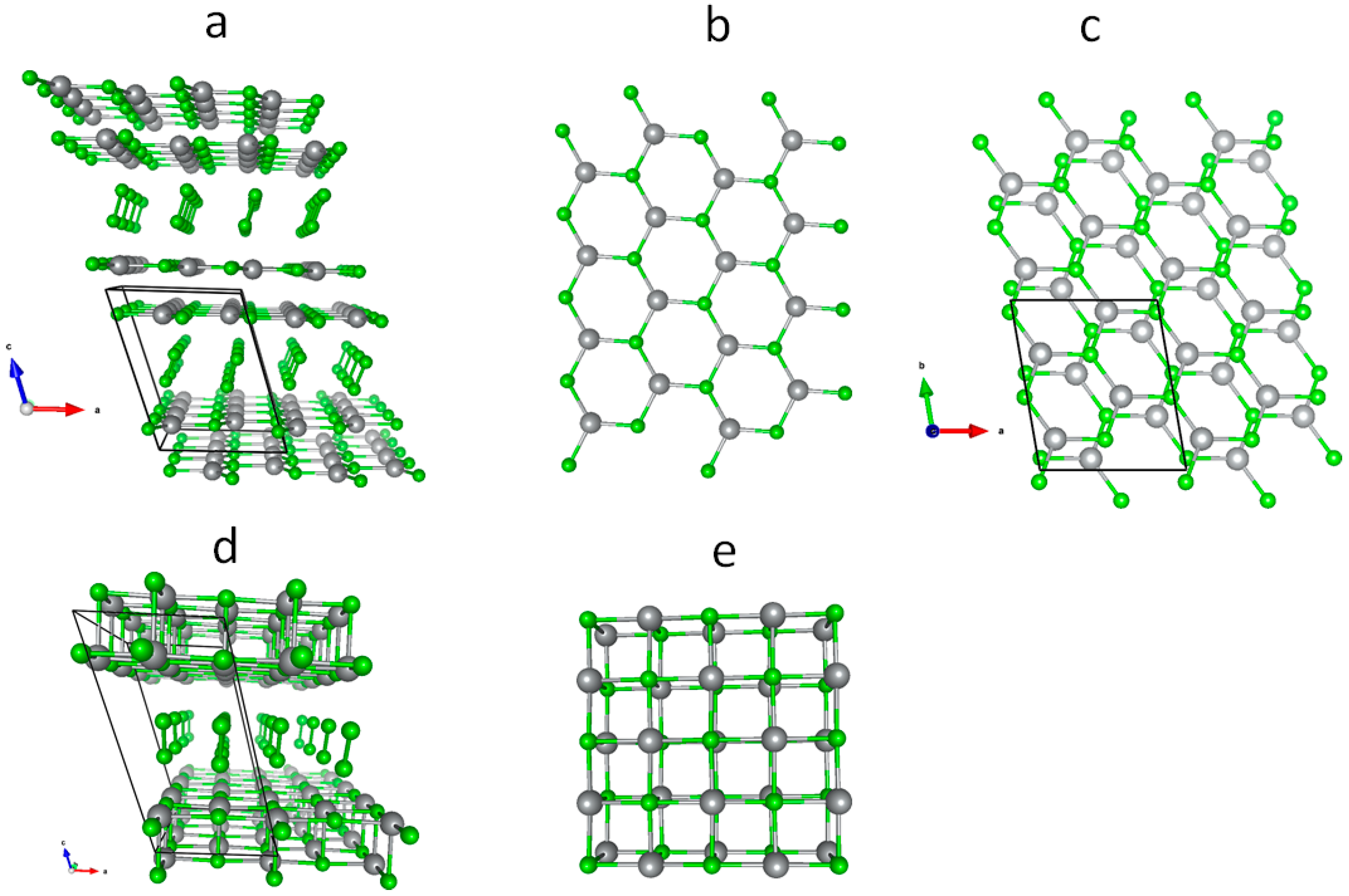
3.1. Scrutiny of Dynamically Stable Polymorphic forms of AgCl2 (Method of Following Imaginary Phonon Modes)
3.2. The Unusual Ag(I)Cl(Cl2)½ Polymorph
3.3. Relative and Absolute Energetic and Thermodynamic Stability of Several Important Polymorphic Forms of AgCl2
- While all forms of AgCl2 are stable with respect to elements, none of AgCl2 polymorphs is energetically stable at T → 0 K and p → 0 atm with respect to products from Equation (3), i.e., AgCl and ½ Cl2.
- The (relatively) most stable phase is that of Ag(I)[Cl(Cl2)½] (rocksalt AgCl layers), as it falls at circa 0.1 eV above AgCl + ½ Cl2.
- The ZPE correction changes very little the relative ranking of structures (it varies by no more than 12 meV for various phases), and for absolute stability of phases with respect to products (it destabilizes them by additional circa 42–53 meV), as could be expected for the system composed of rather heavy elements, Ag and Cl.
- While all forms of AgCl2 are stable with respect to elements, none of AgCl2 polymorphs is energetically stable at T → 0 K and p → 0 atm with respect to products from Equation (3), i.e., AgCl and ½ Cl2; thus, confirming the DFT + U + vdW (van der Waals correction) results.
- The (relatively) most stable phase is that of ribbon Ag(II)Cl2 form as it falls at a mere 52 meV above AgCl + ½ Cl2.
- HSE06 calculations predict the unit cell volumes of Ag, Cl2, and AgCl quite well. The large calculated volume of the ribbon polymorph should be taken with a grain of salt, and this structure is bound only by weak vdW inter-ribbon interactions. The layered AgF2-type structure is the only one for which the formation reaction volume is slightly negative.
3.4. Impact of Temperature and Pressure on Stability and Polymorphism of AgCl2
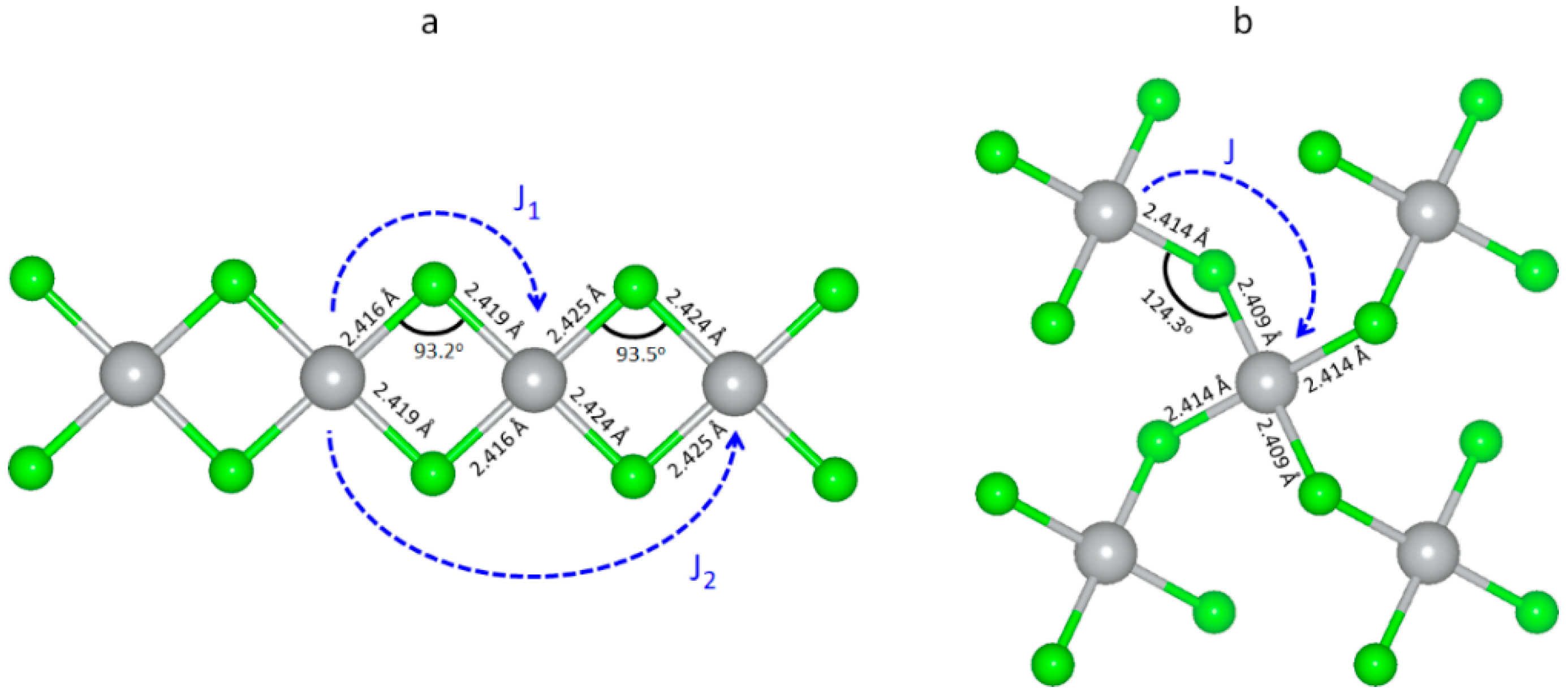
3.5. Magnetic Properties of Selected Polymorphic Forms of AgCl2
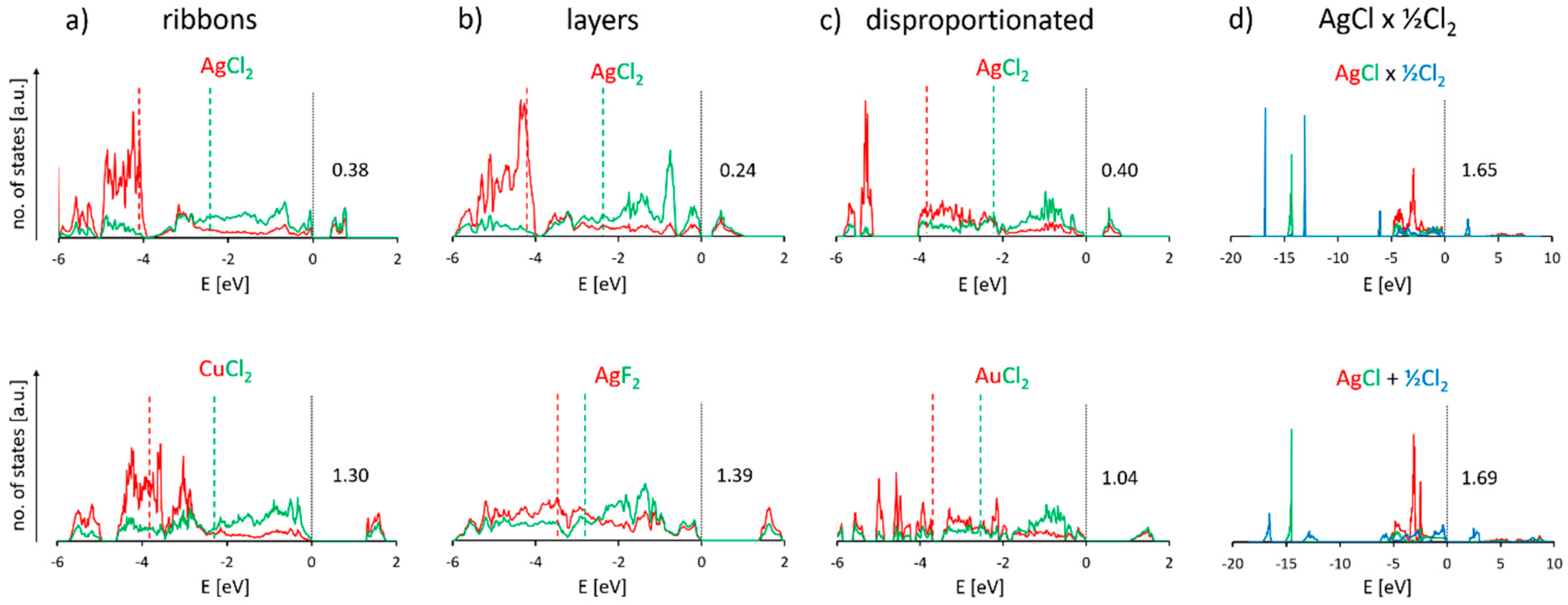
3.6. Electronic Properties of Selected Polymorphic Forms of AgCl2
4. Conclusions
Supplementary Materials
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Fajans, K. Electronic Structure of Some Molecules and Crystals. Ceramic Age 1949, 54, 288. [Google Scholar]
- Morris, D.F.C. The instability of some dihalides of copper and silver. J. Phys. Chem. Solids 1958, 7, 214–217. [Google Scholar] [CrossRef]
- Rossini, F.D.; Wagman, D.D.; Evans, W.H.; Levine, S.; Jaffe, I. Selected values of chemical thermodynamic properties. Circular of National Bureau of Standards No. 500. 1952. Available online: https://archive.org/details/circularofbureau500ross/page/n7 (accessed on 14 August 2019).
- Scatturin, V.; Bellon, P.L.; Zannetti, R. Planar coordination of the group IB elements: Crystal structure of Ag (II) oxide. J. Inorg. Nucl. Chem. 1958, 8, 462–467. [Google Scholar] [CrossRef]
- Yvon, K.; Bezinge, A.; Tissot, P.; Fischer, P. Structure and magnetic properties of tetragonal silver(I, III) oxide, AgO. J. Solid State Chem. 1986, 65, 225–230. [Google Scholar] [CrossRef]
- Hermann, A.; Derzsi, M.; Grochala, W.; Hoffmann, R. AuO: Evolving from dis- to comproportionation and back again. Inorg. Chem. 2016, 55, 1278–1286. [Google Scholar] [CrossRef] [PubMed]
- Gammons, C.H.; Yu, Y.; Williams-Jones, A.E. The disproportionation of gold(I) chloride complexes at 25 to 200 C. Geochim. Cosmochim. Acta 1997, 61, 1971–1983. [Google Scholar] [CrossRef]
- Malinowski, P.J.; Derzsi, M.; Gaweł, B.; Łasocha, W.; Jagličić, Z.; Mazej, Z.; Grochala, W. AgIISO4: A Genuine Sulfate of Divalent Silver with Anomalously Strong One-Dimensional Antiferromagnetic Interactions. Angew. Chem. Int. Ed. Engl. 2010, 49, 1683–1686. [Google Scholar] [CrossRef] [PubMed]
- Elder, S.H.; Lucier, G.M.; Hollander, F.J.; Bartlett, N. Synthesis of Au(II) fluoro complexes and their structural and magnetic properties. J. Am. Chem. Soc. 1997, 119, 1020–1026. [Google Scholar] [CrossRef]
- Derzsi, M.; Piekarz, P.; Grochala, W. Structures of late transition metal monoxides from Jahn-Teller instabilities in the rock salt lattice. Phys. Rev. Lett. 2014, 113, 025505. [Google Scholar] [CrossRef]
- Grzelak, A.; Gawraczyński, J.; Jaroń, T.; Sommayazulu, M.; Derzsi, M.; Struzhkin, V.V.; Grochala, W. Persistence of Mixed and Non-intermediate Valence in the High-Pressure Structure of Silver(I,III) Oxide, AgO: A Combined Raman, X-ray Diffraction (XRD), and Density Functional Theory (DFT) Study. Inorg. Chem. 2017, 56, 5804–5812. [Google Scholar] [CrossRef]
- Dell’amico, D.B.; Calderazzo, F.; Marchetti, F.; Merlino, S. Synthesis and molecular structure of [Au4Cl8], and the isolation of [Pt(CO)Cl5]− in thionyl chloride. J. Chem. Soc., Dalton Trans.: Inorg. Chem. 1982, 2257–2260. [Google Scholar] [CrossRef]
- Brückner, R.; Haller, H.; Steinhauer, S.; Müller, C.; Riedel, S. A 2D Polychloride Network Held Together by Halogen–Halogen Interactions. Angew. Chem. Int. Ed. Engl. 2015, 54, 15579–15583. [Google Scholar] [CrossRef] [PubMed]
- Taraba, J.; Zak, Z. Diphenyldichlorophosphonium Trichloride−Chlorine Solvate 1:1, [PPh2Cl2]+Cl3−·Cl2: An Ionic Form of Diphenyltrichlorophosphorane. Crystal Structures of [PPh2Cl2]+Cl3−·Cl2 and [(PPh2Cl2)+]2[InCl5]2−. Inorg. Chem. 2003, 42, 3591–3594. [Google Scholar] [CrossRef] [PubMed]
- Wickleder, M.S. AuSO4: A True Gold(II) Sulfate with an Au24+ Ion. Z. Anorg. Allg. Chem. 2001, 627, 2112–2114. [Google Scholar] [CrossRef]
- Derzsi, M.; Dymkowski, K.; Grochala, W. The Theoretical Quest for Sulfate of Ag2+: Genuine Ag(II)SO4, Diamagnetic Ag(I)2S2O8, or Rather Mixed-Valence Ag(I)[Ag(III)(SO4)2]? Inorg. Chem. 2010, 49, 2735–2742. [Google Scholar] [CrossRef] [PubMed]
- Kurzydłowski, D.; Grochala, W. Elusive AuF in the solid state as accessed via high pressure comproportionation. Chem. Commun. 2008, 1073–1075. [Google Scholar] [CrossRef] [PubMed]
- Kresse, G.; Hafner, J. Ab initio molecular dynamics for liquid metals. Phys. Rev. B: Condens. Matter Mater. Phys. 1993, 47, 558–561. [Google Scholar] [CrossRef] [PubMed]
- Kresse, G.; Hafner, J. Ab initio molecular-dynamics simulation of the liquid-metal–amorphous-semiconductor transition in germanium. Phys. Rev. B: Condens. Matter Mater. Phys. 1994, 49, 14251–14269. [Google Scholar] [CrossRef]
- Kresse, G.; Furthmüller, J. Efficiency of ab-initio total energy calculations for metals and semiconductors using a plane-wave basis set. Comput. Mater. Sci. 1996, 6, 15–50. [Google Scholar] [CrossRef]
- Kresse, G.; Furthmüller, J. Efficient iterative schemes for ab initio total-energy calculations using a plane-wave basis set. Phys. Rev. B: Condens. Matter Mater. Phys. 1996, 54, 11169–11186. [Google Scholar] [CrossRef]
- Kresse, G.; Joubert, D. From ultrasoft pseudopotentials to the projector augmented-wave method. Phys. Rev. B: Condens. Matter Mater. Phys. 1999, 59, 1758–1775. [Google Scholar] [CrossRef]
- Parlinski, K. PHONON Software. 2010. Available online: http://wolf.ifj.edu.pl/phonon/ (accessed on 2 January 2008).
- Zurek, E.; Grochala, W. Predicting crystal structures and properties of matter under extreme conditions via quantum mechanics: The pressure is on. Phys. Chem. Chem. Phys. 2015, 17, 2917–2934. [Google Scholar] [CrossRef] [PubMed]
- Lonie, D.C.; Zurek, E. XtalOpt: An open-source evolutionary algorithm for crystal structure prediction. Comput. Phys. Commun. 2011, 182, 372–387. [Google Scholar] [CrossRef]
- Zurek, E.; Hoffmann, R.; Ashcroft, N.W.; Oganov, A.; Lyakhov, A.O. A little bit of lithium does a lot for hydrogen. Proc. Nat. Acad. Sci. USA 2009, 106, 17640–17643. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Baettig, P.; Zurek, E. Pressure-Stabilized Sodium Polyhydrides: NaHn (n > 1). Phys. Rev. Lett. 2011, 106, 237002. [Google Scholar] [CrossRef]
- Hooper, J.; Zurek, E. Rubidium Polyhydrides Under Pressure: Emergence of the Linear H3− Species. Chem. Eur. J. 2012, 18, 5013–5021. [Google Scholar] [CrossRef]
- Liechtenstein, A.I.; Anisimov, V.I.; Zaane, J. Density-functional theory and strong interactions: Orbital ordering in Mott-Hubbard insulators. Phys. Rev. B 1995, 52, R5467. [Google Scholar] [CrossRef]
- Kasinathan, D.; Kyker, A.B.; Singh, D.J. Origin of ferromagnetism in Cs2AgF4: The importance of Ag–F covalency. Phys. Rev. B 2006, 73, 214420. [Google Scholar] [CrossRef]
- Grimme, S.; Antony, J.; Ehrlich, S.; Krieg, S. A consistent and accurate ab initio parametrization of density functional dispersion correction (DFT-D) for the 94 elements H-Pu. J. Chem. Phys. 2010, 132, 154104. [Google Scholar] [CrossRef]
- Grochala, W.; Hoffmann, R. Real and Hypothetical Intermediate-Valence AgII/AgIII and AgII/AgI Fluoride Systems as Potential Superconductors. Angew. Chem. Int. Ed. Engl. 2001, 40, 2742–2781. [Google Scholar] [CrossRef]
- Grzelak, A.; Gawraczyński, J.; Jaroń, T.; Kurzydłowski, D.; Mazej, Z.; Leszczyński, P.J.; Prakapenka, V.B.; Derzsi, M.; Struzhkin, V.V.; Grochala, W. Metal fluoride nanotubes featuring square-planar building blocks in a high-pressure polymorph of AgF2. Dalton Trans. 2017, 46, 14742–14745. [Google Scholar] [CrossRef] [PubMed]
- Park, S.; Choi, Y.J.; Zhang, C.L.; Cheong, S.W. Ferroelectricity in an S = ½ Chain Cuprate. Phys. Rev. Lett. 2007, 98, 057601. [Google Scholar] [CrossRef] [PubMed]
- Gibson, B.J.; Kremer, R.K.; Prokofiev, A.V.; Assmus, W.; McIntyre, G.J. Incommensurate antiferromagnetic order in the S = 12 quantum chain compound LiCuVO4. Physica B 2004, 350, e253. [Google Scholar] [CrossRef]
- Yahia, H.B.; Shikano, M.; Tabuchi, M.; Kobayashi, H.; Avdeev, M.; Tan, T.T.; Liu, S.; Ling, C.D. Synthesis and characterization of the crystal and magnetic structures and properties of the hydroxyfluorides Fe(OH)F and Co(OH)F. Inorg. Chem. 2014, 53, 365–374. [Google Scholar] [CrossRef] [PubMed]
- Hill, L.I.; Verbaere, A. On the structural defects in synthetic γ-MnO2s. J. Solid State Chem. 2004, 177, 4706–4723. [Google Scholar] [CrossRef]
- Evers, J.; Beck, W.; Göbel, M.; Jakob, S.; Mayer, P.; Oehlinger, G.; Rotter, M.; Klapötke, T. The Structures of δ-PdCl2 and γ-PdCl2: Phases with Negative Thermal Expansion in One Direction. Angew. Chem. Int. Ed. Engl. 2010, 49, 5677–5682. [Google Scholar] [CrossRef] [PubMed]
- Brückner, R.; Haller, H.; Ellwanger, M.; Riedel, S. Polychloride Monoanions from [Cl3]− to [Cl9]−: A Raman Spectroscopic and Quantum Chemical Investigation. Chem. Eur. J. 2012, 18, 5741–5747. [Google Scholar] [CrossRef]
- Riedel, E.F.; Willett, R.D. NQR study of the trichloride ion. Evidence for three-center four-electron bonding. J. Am. Chem. Soc. 1975, 97, 701–704. [Google Scholar] [CrossRef]
- Redeker, F.A.; Beckers, H.; Riedel, S. Matrix-isolation and comparative far-IR investigation of free linear [Cl3]− and a series of alkali trichlorides. Chem. Commun. 2017, 53, 12958–12961. [Google Scholar] [CrossRef]
- Hull, S.; Keen, D.A. Pressure-induced phase transitions in AgCl, AgBr, and AgI. Phys. Rev. B 1999, 59, 750–761. [Google Scholar] [CrossRef]
- Donohue, J.; Goodman, S.H. Interatomic distances in solid chlorine. Acta Cryst. 1965, 18, 568–569. [Google Scholar] [CrossRef]
- Jenkins, H.D.B.; Glasser, L. Volume-based thermodynamics: Estimations for 2:2 salts. Inorg. Chem. 2006, 45, 1754–1756. [Google Scholar] [CrossRef] [PubMed]
- NIST. gov chemistry webbook database 2019. Available online: https://webbook.nist.gov/chemistry/ (accessed on 2 July 2019).
- Horvath-Bordon, E.; Riedel, R.; Zerr, A.; McMillan, P.F.; Auffermann, G.; Prots, Y.; Bronger, W.; Kniep, R.; Kroll, P. High-pressure chemistry of nitride-based materials. Chem. Soc. Rev. 2006, 35, 987–1014. [Google Scholar] [CrossRef] [PubMed]
- Kurzydłowski, D. The Jahn-Teller distortion at high pressure: The case of copper difluoride. Crystals 2018, 8, 140. [Google Scholar]
- López-Moreno, S.; Romero, A.H.; Mejía-López, J.; Muñoz, A. First-principles study of pressure-induced structural phase transitions in MnF2. Phys. Chem. Chem. Phys. 2016, 18, 33250–33263. [Google Scholar] [CrossRef] [PubMed]
- Kurzydłowski, D.; Grochala, W. Prediction of extremely strong antiferromagnetic superexchange in silver (II) fluorides: Challenging the oxocuprates (II). Angew. Chem. Int. Ed. Engl. 2017, 56, 10114–10117. [Google Scholar] [CrossRef]
- Kurzydłowski, D.; Grochala, W. Large exchange anisotropy in quasi-one-dimensional spin-½ fluoride antiferromagnets with a d(z2)1 ground state. Phys. Rev. B 2017, 96, 155140. [Google Scholar] [CrossRef]
- Banks, M.G.; Kremer, R.K.; Hoch, C.; Simon, A.; Ouladdiaf, B.; Broto, J.-M.; Rakoto, H.; Lee, C.; Whangbo, M.-H. Magnetic ordering in the frustrated Heisenberg chain system cupric chloride CuCl2. Phys. Rev. B 2009, 80, 024404. [Google Scholar] [CrossRef]
- Aramburu, J.A.; Moreno, M. Bonding of Ag2+ in KCl lattice. Solid State Commun. 1986, 58, 305–309. [Google Scholar] [CrossRef]
- Gawraczyński, J.; Kurzydłowski, D.; Ewings, R.A.; Bandaru, S.; Gadomski, W.; Mazej, Z.; Ruani, G.; Bergenti, I.; Jaroń, T.; Ozarowski, A.; et al. Silver route to cuprate analogs. Proc. Nat. Acad. Sci. USA 2019, 116, 1495–1500. [Google Scholar] [CrossRef] [Green Version]
- Kurzydłowski, D.; Derzsi, M.; Barone, P.; Grzelak, A.; Struzhkin, V.V.; Lorenzana, J.; Grochala, W. Dramatic enhancement of spin–spin coupling and quenching of magnetic dimensionality in compressed silver difluoride. Chem. Commun. 2018, 54, 10252–10255. [Google Scholar] [CrossRef] [PubMed]
- Pyykkö, P. Theoretical chemistry of gold. Chem. Soc. Rev. 2008, 37, 1967–1997. [Google Scholar] [CrossRef] [PubMed]
- Pearson, R.G. Recent advances in the concept of hard and soft acids and bases. J. Chem. Educ. 1987, 64, 561–567. [Google Scholar] [CrossRef]
- Schwerdtfeger, P. Relativistic effects in properties of gold. Heteroatom Chem. 2002, 13, 578–584. [Google Scholar] [CrossRef]
- Grochala, W.; Mazej, Z. Unique silver (II) fluorides: The emerging electronic and magnetic materials. Phil. Trans. A 2015, 373, 20140179. [Google Scholar] [CrossRef] [PubMed]







| Phase | Z | V/FU (Å3) | E (eV/FU) | E1form/FU (eV) | E2form/FU (eV) | ZPE/FU (eV) | Vform/FU (Å3) |
|---|---|---|---|---|---|---|---|
| Ribbon AgCl2 (CdI2 related) | 4 | 65.7 | −7.683 | −0.840 | +0.136 | 0.080 | +3.6 |
| Layered AgCl2 (ramsdellite related) | 4 | 66.7 | −7.643 | −0.800 | +0.176 | 0.077 | +4.6 |
| Layered AgF2 type | 4 | 63.0 | −7.625 | −0.782 | +0.194 | 0.081 | +0.9 |
| Ag(I)[Cl(Cl2)½] (rocksalt AgCl layers) | 8 | 65.0 | −7.718 | −0.875 | +0.101 | 0.070 | +2.9 |
| Ag(I)[Cl(Cl2)½] (hex AgCl layers) | 8 | 77.2 * | −7.582 | −0.739 | +0.237 | 0.069 | +15.1 * |
| AgCl + ½ Cl2 | 62.1 | −7.819 | 0.027 | ||||
| Cl2 | 4 | 47.6 (58.1) | −4.288 | 0.029 | |||
| AgCl | 4 | 38.3 (42.7) | −5.675 | −0.976 | 0.021 | −1.0 | |
| Ag fcc | 4 | 15.5 (17.1) | −2.555 | 0.012 |
| Phase | Z | V/FU (Å3) | E (eV/FU) | E1form/FU (eV) | E2form/FU (eV) | ZPE/FU (eV) | Vform/FU (Å3) |
|---|---|---|---|---|---|---|---|
| Ribbon AgCl2 (CdI2 related) | 4 | 77.6 | −9.848 | −1.030 | +0.052 | ND | +8.1 |
| Layered AgF2 type | 4 | 68.7 | −9.727 | −0.909 | +0.173 | ND | −0.8 |
| Ag(I)[Cl(Cl2)½] (rocksalt AgCl layers) | 8 | 70.7 | −9.839 | −1.021 | +0.061 | ND | +1.2 |
| Ag(I)[Cl(Cl2)½] (hex AgCl layers) | 8 | 83.9 * | −9.837 | −1.019 | +0.063 | ND | +14.4 * |
| AuCl2-type (disproportionated) | 4 | 76.9 | −9.736 | −0.918 | +0.164 | ND | +8.2 |
| AgCl + ½ Cl2 | 69.5 | −9.900 | ND | ||||
| Cl2 | 4 | 56.8 (58.1) | −5.536 | ND | |||
| AgCl | 4 | 41.1 (42.7) | −7.132 | −1.082 | ND | −4.2 | |
| Ag fcc | 4 | 16.9 (17.1) | −3.282 | ND |
| Form | Ordering Pattern | E/FU (eV) | E_rel/FU (meV) | Ag (mB) | Cl(mB) |
|---|---|---|---|---|---|
| Ribbon polymorph | AFM1 (AABB) | −7.683 | 0 | ±0.31 | ±0.21 for F joining two like Ag spins ±0.00 between opposite Ag spins |
| AFM2 (ABAB) | −7.652 | 31 | ±0.31 | ±0.10 on all F | |
| FM (AAAA) | −7.640 | 43 | +0.35 | +0.26 on all F | |
| AgF2-type | AFM | −7.625 | 0 | ±0.24 | ±0.10 |
| FM | −7.549 | 76 | +0.35 | +0.26 |
| Metal | Cu | Ag | Au |
|---|---|---|---|
| MF2 | Stable Layered 2D AFM [47] | Stable Layered 2D AFM [53] | Unstable Phase separation |
| MCl2 | Stable Ribbon 1D complex [51] | Metastable Phase separation [this work] | Stable Disproportionated Diamagnetic [12] |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Derzsi, M.; Grzelak, A.; Kondratiuk, P.; Tokár, K.; Grochala, W. Quest for Compounds at the Verge of Charge Transfer Instabilities: The Case of Silver(II) Chloride †. Crystals 2019, 9, 423. https://doi.org/10.3390/cryst9080423
Derzsi M, Grzelak A, Kondratiuk P, Tokár K, Grochala W. Quest for Compounds at the Verge of Charge Transfer Instabilities: The Case of Silver(II) Chloride †. Crystals. 2019; 9(8):423. https://doi.org/10.3390/cryst9080423
Chicago/Turabian StyleDerzsi, Mariana, Adam Grzelak, Paweł Kondratiuk, Kamil Tokár, and Wojciech Grochala. 2019. "Quest for Compounds at the Verge of Charge Transfer Instabilities: The Case of Silver(II) Chloride †" Crystals 9, no. 8: 423. https://doi.org/10.3390/cryst9080423
APA StyleDerzsi, M., Grzelak, A., Kondratiuk, P., Tokár, K., & Grochala, W. (2019). Quest for Compounds at the Verge of Charge Transfer Instabilities: The Case of Silver(II) Chloride †. Crystals, 9(8), 423. https://doi.org/10.3390/cryst9080423