Quantitative Methodologies to Dissect Immune Cell Mechanobiology
Abstract
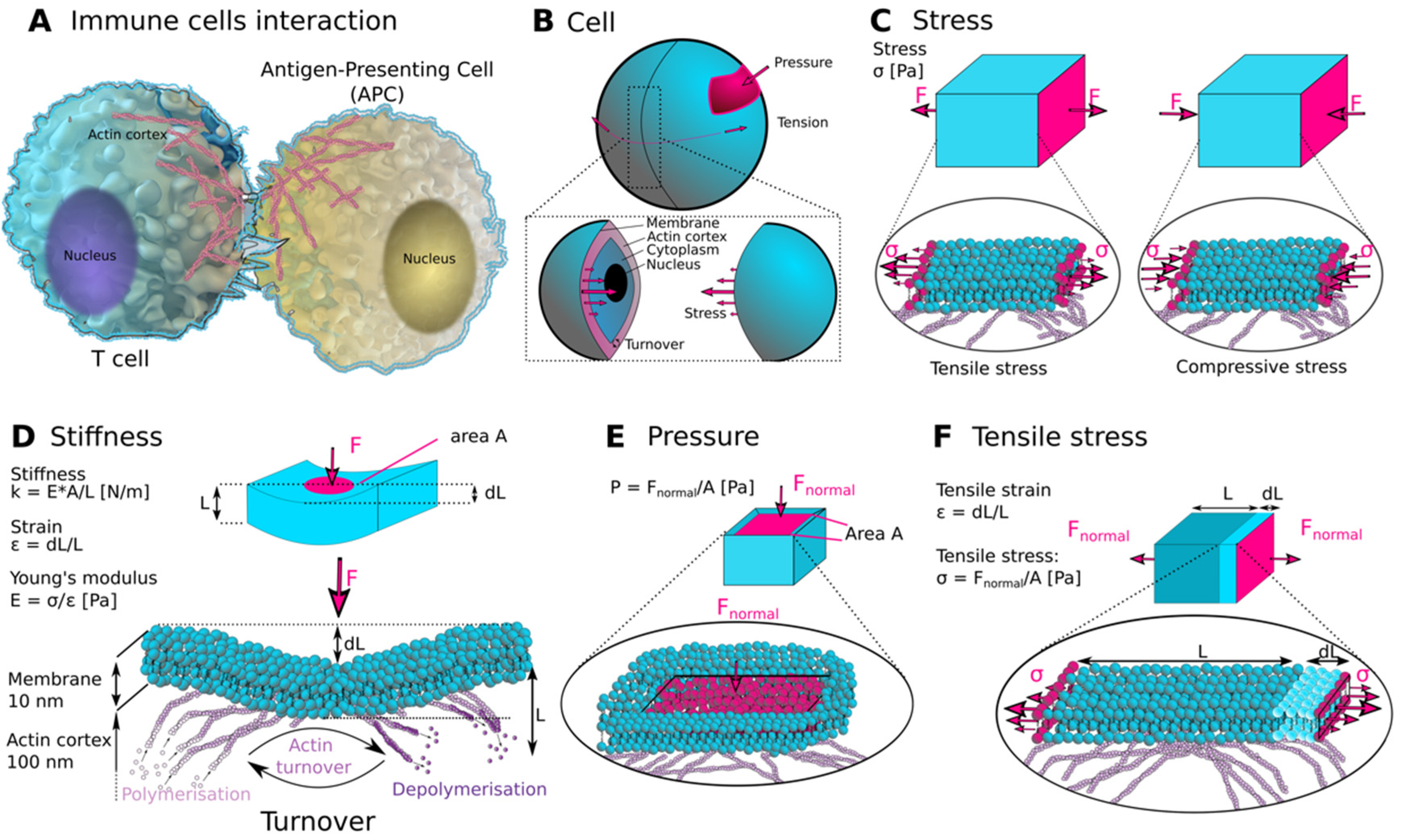
:1. Introduction
2. Mechanics of Immune Cells
| Technique | Measured Mechanical Parameter | Advantages | Disadvantages | Refs |
|---|---|---|---|---|
| Particle-tracking microrheology (PTM) | Viscoelastic material properties Force generation | Subcellular mechanical properties and force only Passive and active PTM | Invasive through injected particles | [34,36,41,57,58,59] |
| Fluorescence correlation spectroscopy (FCS) | Viscoelastic material properties | Very local measurement of intracellular molecules (nm) No addition of invasive particles required High time resolution (µs) | Only local information | [59,60] |
| Brillouin microscopy | Young’s modulus Stiffness Viscoelastic material properties | Only non-invasive contact-free method Very broad range of length and time scales (ns), from subcellular properties to entire organisms 3D method Label-free | Hard to compare to currently well-established techniques Complex data analysis | [62,63,64,65] |
| Environment-sensitive fluorescent dyes–functional probes | Membrane tension Viscosity | Subcellular properties Change fluorescent emission spectrum or fluorescent lifetime depending on their environment Can be easily combined with commercially available microscopes | Limited functional probes available for only particular mechanical parameters Some dyes have a very broad emission spectrum that makes it then hard to combine with the simultaneous quantification of labelled cellular structures | [6,66,67,68,75,76,77,79,80,83] |
3. Discussion and Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Paluch, E.K.; Nelson, C.M.; Biais, N.; Fabry, B.; Moeller, J.; Pruitt, B.L.; Wollnik, C.; Kudryasheva, G.; Rehfeldt, F.; Federle, W. Mechanotransduction: Use the force(s). BMC Biol. 2015, 13, 47. [Google Scholar] [CrossRef] [Green Version]
- Iskratsch, T.; Wolfenson, H.; Sheetz, M.P. Appreciating force and shape — the rise of mechanotransduction in cell biology. Nat. Rev. Mol. Cell Biol. 2014, 15, 825–833. [Google Scholar] [CrossRef]
- Fritzsche, M. Thinking multi-scale to advance mechanobiology. Commun. Biol. 2020, 3, 469. [Google Scholar] [CrossRef] [PubMed]
- Blanch-Mercader, C.; Guillamat, P.; Roux, A.; Kruse, K. Quantifying Material Properties of Cell Monolayers by Analyzing Integer Topological Defects. Phys. Rev. Lett. 2021, 126, 28101. [Google Scholar] [CrossRef]
- Limozin, L.; Puech, P.-H. Membrane Organization and Physical Regulation of Lymphocyte Antigen Receptors: A Biophysicist’s Perspective. J. Membr. Biol. 2019, 252, 397–412. [Google Scholar] [CrossRef] [PubMed]
- Schneider, F.; Colin-York, H.; Fritzsche, M. Quantitative Bio-Imaging Tools to Dissect the Interplay of Membrane and Cytoskeletal Actin Dynamics in Immune Cells. Front. Immunol. 2021, 11, 3377. [Google Scholar] [CrossRef] [PubMed]
- Guilak, F.; Butler, D.L.; Goldstein, S.A.; Baaijens, F.P.T. Biomechanics and mechanobiology in functional tissue engineering. J. Biomech. 2014, 47, 1933–1940. [Google Scholar] [CrossRef] [Green Version]
- Stoltz, J.-F.; Wang, X. From biomechanics to mechanobiology. Biorheology 2002, 39, 5–10. [Google Scholar]
- Discher, D.; Dong, C.; Fredberg, J.J.; Guilak, F.; Ingber, D.; Janmey, P.; Kamm, R.D.; Schmid-Schönbein, G.W.; Weinbaum, S. Biomechanics: Cell research and applications for the next decade. Ann. Biomed. Eng. 2009, 37, 847–859. [Google Scholar] [CrossRef] [Green Version]
- Fritzsche, M.; Erlenkämper, C.; Moeendarbary, E.; Charras, G.; Kruse, K. Actin kinetics shapes cortical network structure and mechanics. Sci. Adv. 2016, 2. [Google Scholar] [CrossRef] [Green Version]
- Levernier, N.; Kruse, K. Spontaneous formation of chaotic protrusions in a polymerizing active gel layer. New J. Phys. 2020, 22, 13003. [Google Scholar] [CrossRef]
- Kumari, A.; Pineau, J.; Sáez, P.J.; Maurin, M.; Lankar, D.; San Roman, M.; Hennig, K.; Boura, V.F.; Voituriez, R.; Karlsson, M.C.I.; et al. Actomyosin-driven force patterning controls endocytosis at the immune synapse. Nat. Commun. 2019, 10, 2870. [Google Scholar] [CrossRef] [Green Version]
- Liu, B.; Chen, W.; Evavold, B.D.; Zhu, C. Accumulation of dynamic catch bonds between TCR and agonist peptide-MHC triggers T cell signaling. Cell 2014, 157, 357–368. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Fritzsche, M.; Fernandes, R.A.; Chang, V.T.; Colin-York, H.; Clausen, M.P.; Felce, J.H.; Galiani, S.; Erlenkämper, C.; Santos, A.M.; Heddleston, J.M.; et al. Cytoskeletal actin dynamics shape a ramifying actin network underpinning immunological synapse formation. Sci. Adv. 2017, 3. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Kim, S.T.; Takeuchi, K.; Sun, Z.-Y.J.; Touma, M.; Castro, C.E.; Fahmy, A.; Lang, M.J.; Wagner, G.; Reinherz, E.L. The alphabeta T cell receptor is an anisotropic mechanosensor. J. Biol. Chem. 2009, 284, 31028–31037. [Google Scholar] [CrossRef] [Green Version]
- Reinherz, E.L. The structure of a T-cell mechanosensor. Nature 2019, 573, 502–504. [Google Scholar] [CrossRef] [Green Version]
- Wu, P.; Zhang, T.; Liu, B.; Fei, P.; Cui, L.; Qin, R.; Zhu, H.; Yao, D.; Martinez, R.J.; Hu, W.; et al. Mechano-regulation of Peptide-MHC Class I Conformations Determines TCR Antigen Recognition. Mol. Cell 2019, 73, 1015–1027.e7. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Zhu, C.; Bao, G.; Wang, N. Cell Mechanics: Mechanical Response, Cell Adhesion, and Molecular Deformation. Annu. Rev. Biomed. Eng. 2000, 2, 189–226. [Google Scholar] [CrossRef]
- Malissen, B.; Bongrand, P. Early T cell activation: Integrating biochemical, structural, and biophysical cues. Annu. Rev. Immunol. 2015, 33, 539–561. [Google Scholar] [CrossRef]
- Mohammed, D.; Versaevel, M.; Bruyère, C.; Alaimo, L.; Luciano, M.; Vercruysse, E.; Procès, A.; Gabriele, S. Innovative Tools for Mechanobiology: Unraveling Outside-In and Inside-Out Mechanotransduction. Front. Bioeng. Biotechnol. 2019, 7, 162. [Google Scholar] [CrossRef]
- Colin-York, H.; Javanmardi, Y.; Skamrahl, M.; Kumari, S.; Chang, V.T.; Khuon, S.; Taylor, A.; Chew, T.-L.; Betzig, E.; Moeendarbary, E.; et al. Cytoskeletal Control of Antigen-Dependent T Cell Activation. Cell Rep. 2019, 26, 3369–3379.e5. [Google Scholar] [CrossRef] [Green Version]
- Bálint, Š.; Müller, S.; Fischer, R.; Kessler, B.M.; Harkiolaki, M.; Valitutti, S.; Dustin, M.L. Supramolecular attack particles are autonomous killing entities released from cytotoxic T cells. Science 2020, 368, 897–901. [Google Scholar] [CrossRef]
- Judokusumo, E.; Tabdanov, E.; Kumari, S.; Dustin, M.L.; Kam, L.C. Mechanosensing in T lymphocyte activation. Biophys. J. 2012, 102, L5–L7. [Google Scholar] [CrossRef] [Green Version]
- O’Connor, R.S.; Hao, X.; Shen, K.; Bashour, K.; Akimova, T.; Hancock, W.W.; Kam, L.C.; Milone, M.C. Substrate rigidity regulates human T cell activation and proliferation. J. Immunol. 2012, 189, 1330–1339. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Barbieri, L.; Colin-York, H.; Korobchevskaya, K.; Li, D.; Wolfson, D.L.; Karedla, N.; Schneider, F.; Ahluwalia, B.S.; Seternes, T.; Dalmo, R.A.; et al. Two-dimensional TIRF-SIM—Traction Force Microscopy (2D TIRF-SIM-TFM). Accept. Nat. Commun. 2021. [Google Scholar] [CrossRef]
- Li, D.; Colin-York, H.; Barbieri, L.; Javanmardi, Y.; Guo, Y.; Korobchevskaya, K.; Moeendarbary, E.; Li, D.; Fritzsche, M. Astigmatic Traction Force Microscopy (a-TFM). Accept. Nat. Commun. 2021. [Google Scholar] [CrossRef]
- Majedi, F.S.; Hasani-Sadrabadi, M.M.; Thauland, T.J.; Li, S.; Bouchard, L.-S.; Butte, M.J. T-cell activation is modulated by the 3D mechanical microenvironment. Biomaterials 2020, 252, 120058. [Google Scholar] [CrossRef]
- Sibener, L.V.; Fernandes, R.A.; Kolawole, E.M.; Carbone, C.B.; Liu, F.; McAffee, D.; Birnbaum, M.E.; Yang, X.; Su, L.F.; Yu, W.; et al. Isolation of a Structural Mechanism for Uncoupling T Cell Receptor Signaling from Peptide-MHC Binding. Cell 2018, 174, 672–687.e27. [Google Scholar] [CrossRef] [PubMed]
- Fritzsche, M. What is the right mechanical readout for understanding the mechanobiology of the immune response? Front. Cell Dev. Biol. 2021. [Google Scholar] [CrossRef] [PubMed]
- Kasza, K.E.; Rowat, A.C.; Liu, J.; Angelini, T.E.; Brangwynne, C.P.; Koenderink, G.H.; Weitz, D.A. The cell as a material. Curr. Opin. Cell Biol. 2007, 19, 101–107. [Google Scholar] [CrossRef] [PubMed]
- Fletcher, D.A.; Geissler, P.L. Active Biological Materials. Annu. Rev. Phys. Chem. 2009, 60, 469–486. [Google Scholar] [CrossRef] [Green Version]
- Moeendarbary, E.; Valon, L.; Fritzsche, M.; Harris, A.R.; Moulding, D.A.; Thrasher, A.J.; Stride, E.; Mahadevan, L.; Charras, G.T. The cytoplasm of living cells behaves as a poroelastic material. Nat. Mater. 2013, 12, 253–261. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Banerjee, S.; Gardel, M.L.; Schwarz, U.S. The Actin Cytoskeleton as an Active Adaptive Material. Annu. Rev. Condens. Matter Phys. 2020, 11, 421–439. [Google Scholar] [CrossRef] [Green Version]
- Kollmannsberger, P.; Fabry, B. Linear and Nonlinear Rheology of Living Cells. Annu. Rev. Mater. Res. 2011, 41, 75–97. [Google Scholar] [CrossRef] [Green Version]
- Gardel, M.L.; Kasza, K.E.; Brangwynne, C.P.; Liu, J.; Weitz, D.A. Chapter 19: Mechanical response of cytoskeletal networks. Methods Cell Biol. 2008, 89, 487–519. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Moreno-Flores, S. Hallmarks of Life in Single Cell Contact Mechanics: Outstanding Challenges and Perspectives. Front. Mech. Eng. 2020, 6, 58. [Google Scholar] [CrossRef]
- Fritzsche, M.; Lewalle, A.; Duke, T.; Kruse, K.; Charras, G. Analysis of turnover dynamics of the submembranous actin cortex. Mol. Biol. Cell 2013, 24, 757–767. [Google Scholar] [CrossRef]
- Maninová, M.; Iwanicki, M.P.; Vomastek, T. Emerging role for nuclear rotation and orientation in cell migration. Cell Adh. Migr. 2014, 8, 42–48. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Almonacid, M.; Terret, M.-E.; Verlhac, M.-H. Nuclear positioning as an integrator of cell fate. Curr. Opin. Cell Biol. 2019, 56, 122–129. [Google Scholar] [CrossRef]
- Rossy, J.; Laufer, J.M.; Legler, D.F. Role of Mechanotransduction and Tension in T Cell Function. Front. Immunol. 2018, 9, 2638. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Moeendarbary, E.; Harris, A.R. Cell mechanics: Principles, practices, and prospects. Wiley Interdiscip. Rev. Syst. Biol. Med. 2014, 6, 371–388. [Google Scholar] [CrossRef]
- Wu, P.-H.; Aroush, D.R.-B.; Asnacios, A.; Chen, W.-C.; Dokukin, M.E.; Doss, B.L.; Durand-Smet, P.; Ekpenyong, A.; Guck, J.; Guz, N.V.; et al. A comparison of methods to assess cell mechanical properties. Nat. Methods 2018, 15, 491–498. [Google Scholar] [CrossRef]
- Nguyen, A.K.; Kilian, K.A. Physicochemical Tools for Visualizing and Quantifying Cell-Generated Forces. ACS Chem. Biol. 2020, 15, 1731–1746. [Google Scholar] [CrossRef]
- Li, Y.; Konstantopoulos, K.; Zhao, R.; Mori, Y.; Sun, S.X. The importance of water and hydraulic pressure in cell dynamics. J. Cell Sci. 2020, 133. [Google Scholar] [CrossRef]
- Chen, W.; Zhu, C. Mechanical regulation of T-cell functions. Immunol. Rev. 2013, 256, 160–176. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Diz-Muñoz, A.; Fletcher, D.A.; Weiner, O.D. Use the force: Membrane tension as an organizer of cell shape and motility. Trends Cell Biol. 2013, 23, 47–53. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Houk, A.R.; Jilkine, A.; Mejean, C.O.; Boltyanskiy, R.; Dufresne, E.R.; Angenent, S.B.; Altschuler, S.J.; Wu, L.F.; Weiner, O.D. Membrane tension maintains cell polarity by confining signals to the leading edge during neutrophil migration. Cell 2012, 148, 175–188. [Google Scholar] [CrossRef] [Green Version]
- Mueller, J.; Szep, G.; Nemethova, M.; de Vries, I.; Lieber, A.D.; Winkler, C.; Kruse, K.; Small, J.V.; Schmeiser, C.; Keren, K.; et al. Load Adaptation of Lamellipodial Actin Networks. Cell 2017, 171, 188–200.e16. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Rodriguez, M.L.; McGarry, P.J.; Sniadecki, N.J. Review on Cell Mechanics: Experimental and Modeling Approaches. Appl. Mech. Rev. 2013, 65. [Google Scholar] [CrossRef] [Green Version]
- Roca-Cusachs, P.; Conte, V.; Trepat, X. Quantifying forces in cell biology. Nat. Cell Biol. 2017, 19, 742–751. [Google Scholar] [CrossRef]
- Addae-Mensah, K.A.; Wikswo, J.P. Measurement Techniques for Cellular Biomechanics In Vitro. Exp. Biol. Med. 2008, 233, 792–809. [Google Scholar] [CrossRef] [Green Version]
- Polacheck, W.J.; Chen, C.S. Measuring cell-generated forces: A guide to the available tools. Nat. Methods 2016, 13, 415–423. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- González-Bermúdez, B.; Guinea, G.V.; Plaza, G.R. Advances in Micropipette Aspiration: Applications in Cell Biomechanics, Models, and Extended Studies. Biophys. J. 2019, 116, 587–594. [Google Scholar] [CrossRef] [Green Version]
- Turlier, H.; Fedosov, D.A.; Audoly, B.; Auth, T.; Gov, N.S.; Sykes, C.; Joanny, J.-F.; Gompper, G.; Betz, T. Equilibrium physics breakdown reveals the active nature of red blood cell flickering. Nat. Phys. 2016, 12, 513–519. [Google Scholar] [CrossRef] [Green Version]
- Janmey, P.A.; McCulloch, C.A. Cell mechanics: Integrating cell responses to mechanical stimuli. Annu. Rev. Biomed. Eng. 2007, 9, 1–34. [Google Scholar] [CrossRef] [Green Version]
- Mandriota, N.; Friedsam, C.; Jones-Molina, J.A.; Tatem, K.V.; Ingber, D.E.; Sahin, O. Cellular nanoscale stiffness patterns governed by intracellular forces. Nat. Mater. 2019, 18, 1071–1077. [Google Scholar] [CrossRef]
- Xia, Q.; Xiao, H.; Pan, Y.; Wang, L. Microrheology, advances in methods and insights. Adv. Colloid Interface Sci. 2018, 257, 71–85. [Google Scholar] [CrossRef] [PubMed]
- Laplaud, V.; Levernier, N.; Pineau, J.; Roman, M.S.; Barbier, L.; Saez, P.J.; Lennon, A.M.; Vargas, P.; Kruse, K.; du Roure, O.; et al. Pinching the cortex of live cells reveals thickness instabilities caused by Myosin II motors. bioRxiv 2020. [Google Scholar] [CrossRef]
- Kwapiszewska, K.; Szczepański, K.; Kalwarczyk, T.; Michalska, B.; Patalas-Krawczyk, P.; Szymański, J.; Andryszewski, T.; Iwan, M.; Duszyński, J.; Hołyst, R. Nanoscale Viscosity of Cytoplasm Is Conserved in Human Cell Lines. J. Phys. Chem. Lett. 2020, 11, 6914–6920. [Google Scholar] [CrossRef] [PubMed]
- Sezgin, E.; Schneider, F.; Galiani, S.; Urbančič, I.; Waithe, D.; Lagerholm, B.C.; Eggeling, C. Measuring nanoscale diffusion dynamics in cellular membranes with super-resolution STED–FCS. Nat. Protoc. 2019, 14, 1054–1083. [Google Scholar] [CrossRef] [PubMed]
- Caragine, C.M.; Haley, S.C.; Zidovska, A. Surface Fluctuations and Coalescence of Nucleolar Droplets in the Human Cell Nucleus. Phys. Rev. Lett. 2018, 121, 148101. [Google Scholar] [CrossRef] [Green Version]
- Antonacci, G.; Beck, T.; Bilenca, A.; Czarske, J.; Elsayad, K.; Guck, J.; Kim, K.; Krug, B.; Palombo, F.; Prevedel, R.; et al. Recent progress and current opinions in Brillouin microscopy for life science applications. Biophys. Rev. 2020, 12, 615–624. [Google Scholar] [CrossRef]
- Elsayad, K.; Polakova, S.; Gregan, J. Probing Mechanical Properties in Biology Using Brillouin Microscopy. Trends Cell Biol. 2019, 29, 608–611. [Google Scholar] [CrossRef]
- Scarcelli, G.; Polacheck, W.J.; Nia, H.T.; Patel, K.; Grodzinsky, A.J.; Kamm, R.D.; Yun, S.H. Noncontact three-dimensional mapping of intracellular hydromechanical properties by Brillouin microscopy. Nat. Methods 2015, 12, 1132–1134. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Elsayad, K.; Werner, S.; Gallemí, M.; Kong, J.; Sánchez Guajardo, E.R.; Zhang, L.; Jaillais, Y.; Greb, T.; Belkhadir, Y. Mapping the subcellular mechanical properties of live cells in tissues with fluorescence emission-Brillouin imaging. Sci. Signal. 2016, 9, rs5. [Google Scholar] [CrossRef]
- Miao, W.; Yu, C.; Hao, E.; Jiao, L. Functionalized BODIPYs as Fluorescent Molecular Rotors for Viscosity Detection. Front. Chem. 2019, 7, 825. [Google Scholar] [CrossRef] [Green Version]
- Ma, C.; Sun, W.; Xu, L.; Qian, Y.; Dai, J.; Zhong, G.; Hou, Y.; Liu, J.; Shen, B. A minireview of viscosity-sensitive fluorescent probes: Design and biological applications. J. Mater. Chem. B 2020, 8, 9642–9651. [Google Scholar] [CrossRef] [PubMed]
- Colom, A.; Derivery, E.; Soleimanpour, S.; Tomba, C.; Molin, M.D.; Sakai, N.; González-Gaitán, M.; Matile, S.; Roux, A. A fluorescent membrane tension probe. Nat. Chem. 2018, 10, 1118–1125. [Google Scholar] [CrossRef] [PubMed]
- Colin-York, H.; Fritzsche, M. The future of traction force microscopy. Curr. Opin. Biomed. Eng. 2018, 5, 1–5. [Google Scholar] [CrossRef]
- Plotnikov, S.V.; Sabass, B.; Schwarz, U.S.; Waterman, C.M. High-resolution traction force microscopy. Methods Cell Biol. 2014, 123, 367–394. [Google Scholar] [CrossRef] [Green Version]
- Legant, W.R.; Choi, C.K.; Miller, J.S.; Shao, L.; Gao, L.; Betzig, E.; Chen, C.S. Multidimensional traction force microscopy reveals out-of-plane rotational moments about focal adhesions. Proc. Natl. Acad. Sci. USA 2013, 110, 881–886. [Google Scholar] [CrossRef] [Green Version]
- Colin-York, H.; Javanmardi, Y.; Barbieri, L.; Li, D.; Korobchevskaya, K.; Guo, Y.; Hall, C.; Taylor, A.; Khuon, S.; Sheridan, G.K.; et al. Spatiotemporally Super-Resolved Volumetric Traction Force Microscopy. Nano Lett. 2019, 19, 4427–4434. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Legant, W.R.; Miller, J.S.; Blakely, B.L.; Cohen, D.M.; Genin, G.M.; Chen, C.S. Measurement of mechanical tractions exerted by cells in three-dimensional matrices. Nat. Methods 2010, 7, 969–971. [Google Scholar] [CrossRef] [PubMed]
- Aramesh, M.; Mergenthal, S.; Issler, M.; Plochberger, B.; Weber, F.; Qin, X.-H.; Liska, R.; Duda, G.N.; Huppa, J.B.; Ries, J.; et al. Functionalized Bead Assay to Measure Three-dimensional Traction Forces during T-cell Activation. Nano Lett. 2021, 21, 507–514. [Google Scholar] [CrossRef]
- Meng, F.; Suchyna, T.M.; Sachs, F. A fluorescence energy transfer-based mechanical stress sensor for specific proteins in situ. FEBS J. 2008, 275, 3072–3087. [Google Scholar] [CrossRef] [Green Version]
- Meng, F.; Sachs, F. Visualizing dynamic cytoplasmic forces with a compliance-matched FRET sensor. J. Cell Sci. 2011, 124, 261–269. [Google Scholar] [CrossRef] [Green Version]
- Zhang, Y.; Ge, C.; Zhu, C.; Salaita, K. DNA-based digital tension probes reveal integrin forces during early cell adhesion. Nat. Commun. 2014, 5, 5167. [Google Scholar] [CrossRef]
- Hong, J.; Ge, C.; Jothikumar, P.; Yuan, Z.; Liu, B.; Bai, K.; Li, K.; Rittase, W.; Shinzawa, M.; Zhang, Y.; et al. A TCR mechanotransduction signaling loop induces negative selection in the thymus. Nat. Immunol. 2018, 19, 1379–1390. [Google Scholar] [CrossRef]
- Glazier, R.; Brockman, J.M.; Bartle, E.; Mattheyses, A.L.; Destaing, O.; Salaita, K. DNA mechanotechnology reveals that integrin receptors apply pN forces in podosomes on fluid substrates. Nat. Commun. 2019, 10, 4507. [Google Scholar] [CrossRef] [Green Version]
- Blanchard, A.T.; Salaita, K. Emerging uses of DNA mechanical devices. Science 2019, 365, 1080–1081. [Google Scholar] [CrossRef] [PubMed]
- Zhu, C.; Chen, W.; Lou, J.; Rittase, W.; Li, K. Mechanosensing through immunoreceptors. Nat. Immunol. 2019, 20, 1269–1278. [Google Scholar] [CrossRef]
- Hwang, W.; Mallis, R.J.; Lang, M.J.; Reinherz, E.L. The αβTCR mechanosensor exploits dynamic ectodomain allostery to optimize its ligand recognition site. Proc. Natl. Acad. Sci. USA 2020, 117, 21336–21345. [Google Scholar] [CrossRef]
- Liu, Y.; Blanchfield, L.; Ma, V.P.-Y.; Andargachew, R.; Galior, K.; Liu, Z.; Evavold, B.; Salaita, K. DNA-based nanoparticle tension sensors reveal that T-cell receptors transmit defined pN forces to their antigens for enhanced fidelity. Proc. Natl. Acad. Sci. USA 2016, 113, 5610–5615. [Google Scholar] [CrossRef] [Green Version]
- Wang, N.; Tytell, J.D.; Ingber, D.E. Mechanotransduction at a distance: Mechanically coupling the extracellular matrix with the nucleus. Nat. Rev. Mol. Cell Biol. 2009, 10, 75–82. [Google Scholar] [CrossRef]
- Matthews, B.D.; Overby, D.R.; Mannix, R.; Ingber, D.E. Cellular adaptation to mechanical stress: Role of integrins, Rho, cytoskeletal tension and mechanosensitive ion channels. J. Cell Sci. 2006, 119, 508–518. [Google Scholar] [CrossRef] [Green Version]
- Kruse, K.; Joanny, J.F.; Jülicher, F.; Prost, J.; Sekimoto, K. Generic theory of active polar gels: A paradigm for cytoskeletal dynamics. Eur. Phys. J. E 2005, 16, 5–16. [Google Scholar] [CrossRef]
- Schierbaum, N.; Rheinlaender, J.; Schäffer, T.E. Combined atomic force microscopy (AFM) and traction force microscopy (TFM) reveals a correlation between viscoelastic material properties and contractile prestress of living cells. Soft Matter 2019, 15, 1721–1729. [Google Scholar] [CrossRef]
- Gossett, D.R.; Tse, H.T.K.; Lee, S.A.; Ying, Y.; Lindgren, A.G.; Yang, O.O.; Rao, J.; Clark, A.T.; Di Carlo, D. Hydrodynamic stretching of single cells for large population mechanical phenotyping. Proc. Natl. Acad. Sci. USA 2012, 109, 7630–7635. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Mietke, A.; Otto, O.; Girardo, S.; Rosendahl, P.; Taubenberger, A.; Golfier, S.; Ulbricht, E.; Aland, S.; Guck, J.; Fischer-Friedrich, E. Extracting Cell Stiffness from Real-Time Deformability Cytometry: Theory and Experiment. Biophys. J. 2015, 109, 2023–2036. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Beicker, K.; O’Brien, E.T.; Falvo, M.R.; Superfine, R. Vertical Light Sheet Enhanced Side-View Imaging for AFM Cell Mechanics Studies. Sci. Rep. 2018, 8, 1504. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Skamrahl, M.; Colin-York, H.; Barbieri, L.; Fritzsche, M. Simultaneous Quantification of the Interplay Between Molecular Turnover and Cell Mechanics by AFM–FRAP. Small 2019, 15, 1902202. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Nelsen, E.; Hobson, C.M.; Kern, M.E.; Hsiao, J.P.; O’Brien, E.T., III; Watanabe, T.; Condon, B.M.; Boyce, M.; Grinstein, S.; Hahn, K.M.; et al. Combined Atomic Force Microscope and Volumetric Light Sheet System for Correlative Force and Fluorescence Mechanobiology Studies. Sci. Rep. 2020, 10, 8133. [Google Scholar] [CrossRef] [PubMed]
- Hobson, C.M.; Kern, M.; O’Brien, E.T.; Stephens, A.D.; Falvo, M.R.; Superfine, R. Correlating nuclear morphology and external force with combined atomic force microscopy and light sheet imaging separates roles of chromatin and lamin A/C in nuclear mechanics. Mol. Biol. Cell 2020, 31, 1788–1801. [Google Scholar] [CrossRef] [PubMed]
| Technique | Measured Mechanical Parameter | Advantages | Disadvantages | Refs |
|---|---|---|---|---|
| Atomic force microscope (AFM) | Young’s modulus Stiffness Viscoelastic material properties Membrane/cortex tension Force generation | Static and dynamic measurements Broad range of length and time scales, from single-molecule interactions to whole-cell deformations measured from ms to hrs Cellular and subcellular properties Well suited for studying molecular interactions with cells Piconewton resolution | Direct mechanical interaction with cells Complex analysis since the overlay of mechanical responses from various cellular components is measured | [32,36,41,42,49,50,51,52] |
| Optical and magnetic tweezers (OT and MT) | Young’s modulus Stiffness Viscoelastic material properties Membrane/cortex tension Force generation | Static and dynamic measurements Molecular to cellular interactions Possible stretching and twisting Piconewton range | Sample heating (OT) Need for magnetic particles (MT) | [36,41,42,49,51,54] |
| Micropipette aspiration/Biomembrane force probe | Young’s modulus Stiffness Viscoelastic material properties Membrane/cortex tension Pressure Force generation | Local and global cell mechanical properties Piconewton resolution Low cost | Most set ups have a low throughput Limited spatial resolution to the micron scale Direct mechanical interaction with cells Possible cell damage | [13,36,49,51,53] |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Pfannenstill, V.; Barbotin, A.; Colin-York, H.; Fritzsche, M. Quantitative Methodologies to Dissect Immune Cell Mechanobiology. Cells 2021, 10, 851. https://doi.org/10.3390/cells10040851
Pfannenstill V, Barbotin A, Colin-York H, Fritzsche M. Quantitative Methodologies to Dissect Immune Cell Mechanobiology. Cells. 2021; 10(4):851. https://doi.org/10.3390/cells10040851
Chicago/Turabian StylePfannenstill, Veronika, Aurélien Barbotin, Huw Colin-York, and Marco Fritzsche. 2021. "Quantitative Methodologies to Dissect Immune Cell Mechanobiology" Cells 10, no. 4: 851. https://doi.org/10.3390/cells10040851
APA StylePfannenstill, V., Barbotin, A., Colin-York, H., & Fritzsche, M. (2021). Quantitative Methodologies to Dissect Immune Cell Mechanobiology. Cells, 10(4), 851. https://doi.org/10.3390/cells10040851






