Optimization of Mechanosensitive Cross-Talk between Matrix Stiffness and Protein Density: Independent Matrix Properties Regulate Spreading Dynamics of Myocytes
Abstract
:1. Introduction
2. Materials and Methods
2.1. Glass Preparation
2.2. Hydrogel Preparation
2.3. Mechanical Testing
2.4. Height Determination
2.5. Surface Functionalization
2.6. Cell Culture
2.7. Image and Time-Lapse Acquisition
2.8. Fluorescence Staining
2.9. Lifeact Transfection
2.10. Image Acquisition of Fluorescent Cells
2.11. Actin Quantification Analysis (AQuA)
3. Results
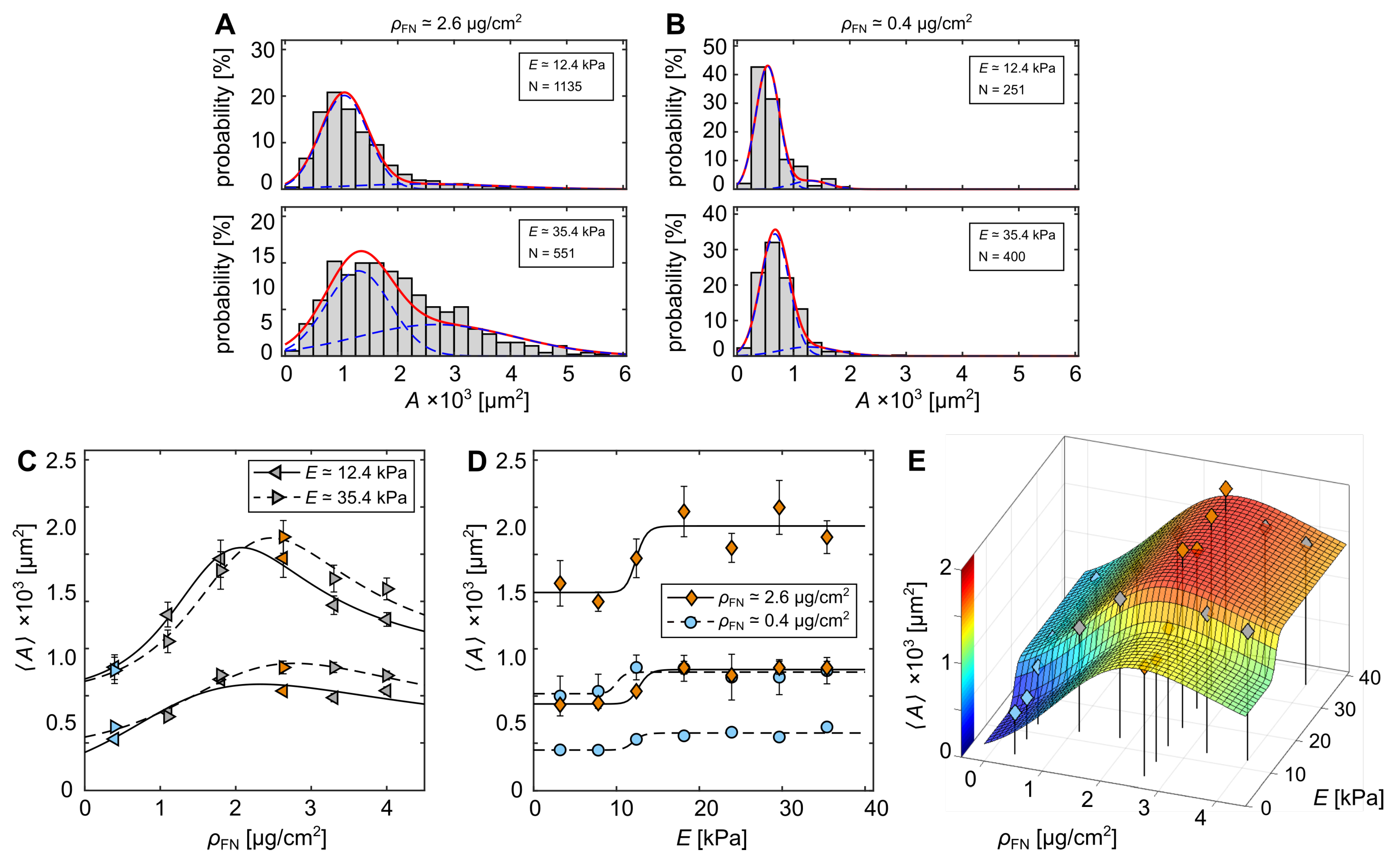
3.1. Cell-Morphological Response to Substrate Properties
3.2. Cytoskeletal Actin Response to Substrate Properties
3.3. Quantification of Proliferation Dynamics
4. Discussion and Conclusions
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| FN | fibronectin |
| RT | room temperature |
| ECM | extracellular matrix |
| AQuA | actin quantification analysis |
| DMEM | Dulbecco’s modified Eagle’s medium |
| eLoG | elongated Laplace of Gaussian |
| PED | protein equilibrium distance |
References
- Urbanczyk, M.; Layland, S.L.; Schenke-Layland, K. The Role of Extracellular Matrix in Biomechanics and Its Impact on Bioengineering of Cells and 3D Tissues. Matrix Biol. 2020, 85–86, 1–14. [Google Scholar] [CrossRef] [PubMed]
- Hörning, M.; Kidoaki, S.; Kawano, T.; Yoshikawa, K. Rigidity Matching between Cells and the Extracellular Matrix Leads to the Stabilization of Cardiac Conduction. Biophys. J. 2012, 102, 379–387. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Hörning, M.; Nakahata, M.; Linke, P.; Yamamoto, A.; Veschgini, M.; Kaufmann, S.; Takashima, Y.; Harada, A.; Tanaka, M. Dynamic Mechano-Regulation of Myoblast Cells on Supramolecular Hydrogels Cross-Linked by Reversible Host-Guest Interactions. Sci. Rep. 2017, 7, 7660. [Google Scholar] [CrossRef] [PubMed]
- Yin, L.; Bien, H.; Entcheva, E. Scaffold Topography Alters Intracellular Calcium Dynamics in Cultured Cardiomyocyte Networks. Am. J.-Physiol.-Heart Circ. Physiol. 2004, 287, H1276–H1285. [Google Scholar] [CrossRef]
- Erben, A.; Hörning, M.; Hartmann, B.; Becke, T.; Eisler, S.A.; Southan, A.; Cranz, S.; Hayden, O.; Kneidinger, N.; Königshoff, M.; et al. Precision 3D-Printed Cell Scaffolds Mimicking Native Tissue Composition and Mechanics. Adv. Healthc. Mater. 2020, 9, 2000918. [Google Scholar] [CrossRef]
- Harburger, D.S.; Calderwood, D.A. Integrin Signalling at a Glance. J. Cell Sci. 2009, 122, 159–163. [Google Scholar] [CrossRef] [Green Version]
- Takagi, Y.; Homsher, E.E.; Goldman, Y.E.; Shuman, H. Force Generation in Single Conventional Actomyosin Complexes under High Dynamic Load. Biophys. J. 2006, 90, 1295–1307. [Google Scholar] [CrossRef] [Green Version]
- Lo, C.W. Role of Gap Junctions in Cardiac Conduction and Development. Circ. Res. 2000, 87, 346–348. [Google Scholar] [CrossRef] [Green Version]
- Miura, K.; Siegert, F. Light Affects cAMP Signaling and Cell Movement Activity in Dictyostelium Discoideum. Proc. Natl. Acad. Sci. USA 2000, 97, 2111–2116. [Google Scholar] [CrossRef] [Green Version]
- Ali-Murthy, Z.; Kornberg, T.B. Bicoid Gradient Formation and Function in the Drosophila Pre-Syncytial Blastoderm. eLife 2016, 5, e13222. [Google Scholar] [CrossRef]
- Zhang, Z.; Zwick, S.; Loew, E.; Grimley, J.S.; Ramanathan, S. Mouse Embryo Geometry Drives Formation of Robust Signaling Gradients through Receptor Localization. Nat. Commun. 2019, 10, 4516. [Google Scholar] [CrossRef] [PubMed]
- Capron, A.; Chatfield, S.; Provart, N.; Berleth, T. Embryogenesis: Pattern Formation from a Single Cell. Arab. Book/Am. Soc. Plant Biol. 2009, 7, e0126. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Engler, A.J.; Sen, S.; Sweeney, H.L.; Discher, D.E. Matrix Elasticity Directs Stem Cell Lineage Specification. Cell 2006, 126, 677–689. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Engler, A.J.; Griffin, M.A.; Sen, S.; Bönnemann, C.G.; Sweeney, H.L.; Discher, D.E. Myotubes Differentiate Optimally on Substrates with Tissue-like Stiffness: Pathological Implications for Soft or Stiff Microenvironments. J. Cell Biol. 2004, 166, 877–887. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Engler, A.J.; Carag-Krieger, C.; Johnson, C.P.; Raab, M.; Tang, H.Y.; Speicher, D.W.; Sanger, J.W.; Sanger, J.M.; Discher, D.E. Embryonic Cardiomyocytes Beat Best on a Matrix with Heart-like Elasticity: Scar-like Rigidity Inhibits Beating. J. Cell Sci. 2008, 121, 3794–3802. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Zemel, A.; Rehfeldt, F.; Brown, A.E.X.; Discher, D.E.; Safran, S.A. Optimal Matrix Rigidity for Stress Fiber Polarization in Stem Cells. Nat. Phys. 2010, 6, 468–473. [Google Scholar] [CrossRef]
- Engler, A.; Bacakova, L.; Newman, C.; Hategan, A.; Griffin, M.; Discher, D. Substrate Compliance versus Ligand Density in Cell on Gel Responses. Biophys. J. 2004, 86, 617–628. [Google Scholar] [CrossRef] [Green Version]
- Schreiber, C.; Amiri, B.; Heyn, J.C.J.; Rädler, J.O.; Falcke, M. On the Adhesion–Velocity Relation and Length Adaptation of Motile Cells on Stepped Fibronectin Lanes. Proc. Natl. Acad. Sci. USA 2021, 118, e2009959118. [Google Scholar] [CrossRef]
- Yoshikawa, H.Y.; Rossetti, F.F.; Kaufmann, S.; Kaindl, T.; Madsen, J.; Engel, U.; Lewis, A.L.; Armes, S.P.; Tanaka, M. Quantitative Evaluation of Mechanosensing of Cells on Dynamically Tunable Hydrogels. J. Am. Chem. Soc. 2011, 133, 1367–1374. [Google Scholar] [CrossRef]
- Li, J.; Zhang, L.; Yu, L.; Minami, I.; Miyagawa, S.; Hörning, M.; Dong, J.; Qiao, J.; Qu, X.; Hua, Y.; et al. Circulating Re-Entrant Waves Promote Maturation of hiPSC-derived Cardiomyocytes in Self-Organized Tissue Ring. Commun. Biol. 2020, 3, 1–12. [Google Scholar] [CrossRef] [Green Version]
- Trappmann, B.; Gautrot, J.E.; Connelly, J.T.; Strange, D.G.T.; Li, Y.; Oyen, M.L.; Stuart, M.A.C.; Boehm, H.; Li, B.; Vogel, V.; et al. Extracellular-Matrix Tethering Regulates Stem-Cell Fate. Nat. Mater. 2012, 11, 642–649. [Google Scholar] [CrossRef] [PubMed]
- Kern, W.; Puotinen, D. Cleaning Solutions Based on Hydrogen Peroxide for Use in Silicon Semiconductor Technology. RCA Rev. 1970, 31, 187–206. [Google Scholar]
- Kidoaki, S.; Matsuda, T. Microelastic Gradient Gelatinous Gels to Induce Cellular Mechanotaxis. J. Biotechnol. 2008, 133, 225–230. [Google Scholar] [CrossRef] [PubMed]
- Buxboim, A.; Rajagopal, K.; Brown, A.E.X.; Discher, D.E. How Deeply Cells Feel: Methods for Thin Gels. J. Phys. Condens. Matter 2010, 22, 194116. [Google Scholar] [CrossRef] [Green Version]
- Butt, H.J.; Cappella, B.; Kappl, M. Force Measurements with the Atomic Force Microscope: Technique, Interpretation and Applications. Surf. Sci. Rep. 2005, 59, 1–152. [Google Scholar] [CrossRef] [Green Version]
- Sneddon, I.N. The Relation between Load and Penetration in the Axisymmetric Boussinesq Problem for a Punch of Arbitrary Profile. Int. J. Eng. Sci. 1965, 3, 47–57. [Google Scholar] [CrossRef]
- Domke, J.; Radmacher, M. Measuring the Elastic Properties of Thin Polymer Films with the Atomic Force Microscope. Langmuir 1998, 14, 3320–3325. [Google Scholar] [CrossRef]
- Lin, D.C.; Dimitriadis, E.K.; Horkay, F. Robust Strategies for Automated AFM Force Curve Analysis—I. Non-adhesive Indentation of Soft, Inhomogeneous Materials. J. Biomech. Eng. 2006, 129, 430–440. [Google Scholar] [CrossRef] [Green Version]
- Wouters, O.Y.; Ploeger, D.T.; van Putten, S.M.; Bank, R.A. 3,4-Dihydroxy-L-Phenylalanine as a Novel Covalent Linker of Extracellular Matrix Proteins to Polyacrylamide Hydrogels with a Tunable Stiffness. Tissue Eng. Part C Methods 2016, 22, 91–101. [Google Scholar] [CrossRef] [Green Version]
- García, A.J.; Vega, M.D.; Boettiger, D. Modulation of Cell Proliferation and Differentiation through Substrate-dependent Changes in Fibronectin Conformation. Mol. Biol. Cell 1999, 10, 785–798. [Google Scholar] [CrossRef] [Green Version]
- Inoue, S.; Frank, V.; Hörning, M.; Kaufmann, S.; Yoshikawa, H.Y.; Madsen, J.P.; Lewis, A.L.; Armes, S.P.; Tanaka, M. Live Cell Tracking of Symmetry Break in Actin Cytoskeleton Triggered by Abrupt Changes in Micromechanical Environments. Biomater. Sci. 2015, 3, 1539–1544. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Otsu, N. A Threshold Selection Method from Gray-Level Histograms. IEEE Trans. Syst. Man Cybern. 1979, 9, 62–66. [Google Scholar] [CrossRef] [Green Version]
- Matson, J.P.; Cook, J.G. Cell Cycle Proliferation Decisions: The Impact of Single Cell Analyses. Febs J. 2017, 284, 362–375. [Google Scholar] [CrossRef] [Green Version]
- Lira, L.M.; Martins, K.A.; de Torresi, S.I.C. Structural Parameters of Polyacrylamide Hydrogels Obtained by the Equilibrium Swelling Theory. Eur. Polym. J. 2009, 45, 1232–1238. [Google Scholar] [CrossRef]
- Oyen, M.L. Mechanical Characterisation of Hydrogel Materials. Int. Mater. Rev. 2014, 59, 44–59. [Google Scholar] [CrossRef]
- Righetti, P.G.; Brost, B.C.W.; Snyder, R.S. On the Limiting Pore Size of Hydrophilic Gels for Electrophoresis and Isoelectric Focussing. J. Biochem. Biophys. Methods 1981, 4, 347–363. [Google Scholar] [CrossRef]
- Bian, W.; Bursac, N. Engineered Skeletal Muscle Tissue Networks with Controllable Architecture. Biomaterials 2009, 30, 1401–1412. [Google Scholar] [CrossRef] [Green Version]
- Finney, D.J. On the Distribution of a Variate Whose Logarithm Is Normally Distributed. Suppl. J. R. Stat. Soc. 1941, 7, 155–161. [Google Scholar] [CrossRef]
- Kanchanawong, P.; Shtengel, G.; Pasapera, A.M.; Ramko, E.B.; Davidson, M.W.; Hess, H.F.; Waterman, C.M. Nanoscale Architecture of Integrin-Based Cell Adhesions. Nature 2010, 468, 580–584. [Google Scholar] [CrossRef] [Green Version]
- Rajagopalan, P.; Marganski, W.A.; Brown, X.Q.; Wong, J.Y. Direct Comparison of the Spread Area, Contractility, and Migration of Balb/c 3T3 Fibroblasts Adhered to Fibronectin- and RGD-Modified Substrata. Biophys. J. 2004, 87, 2818–2827. [Google Scholar] [CrossRef] [Green Version]
- Sunyer, R.; Jin, A.J.; Nossal, R.; Sackett, D.L. Fabrication of Hydrogels with Steep Stiffness Gradients for Studying Cell Mechanical Response. PLoS ONE 2012, 7, e46107. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Lovett, D.B.; Shekhar, N.; Nickerson, J.A.; Roux, K.J.; Lele, T.P. Modulation of Nuclear Shape by Substrate Rigidity. Cell. Mol. Bioeng. 2013, 6, 230–238. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Gong, Z.; Szczesny, S.E.; Caliari, S.R.; Charrier, E.E.; Chaudhuri, O.; Cao, X.; Lin, Y.; Mauck, R.L.; Janmey, P.A.; Burdick, J.A.; et al. Matching Material and Cellular Timescales Maximizes Cell Spreading on Viscoelastic Substrates. Proc. Natl. Acad. Sci. USA 2018, 115, E2686–E2695. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Chaudhuri, O.; Gu, L.; Darnell, M.; Klumpers, D.; Bencherif, S.A.; Weaver, J.C.; Huebsch, N.; Mooney, D.J. Substrate Stress Relaxation Regulates Cell Spreading. Nat. Commun. 2015, 6, 6365. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Dupont, S.; Morsut, L.; Aragona, M.; Enzo, E.; Giulitti, S.; Cordenonsi, M.; Zanconato, F.; Le Digabel, J.; Forcato, M.; Bicciato, S.; et al. Role of YAP/TAZ in Mechanotransduction. Nature 2011, 474, 179–183. [Google Scholar] [CrossRef] [PubMed]
- Yamazaki, M.; Kidoaki, S.; Fujie, H.; Miyoshi, H. Designing Elastic Modulus of Cell Culture Substrate to Regulate YAP and RUNX2 Localization for Controlling Differentiation of Human Mesenchymal Stem Cells. Anal. Sci. 2021, 37, 447–453. [Google Scholar] [CrossRef] [PubMed]
- Panciera, T.; Azzolin, L.; Cordenonsi, M.; Piccolo, S. Mechanobiology of YAP and TAZ in Physiology and Disease. Nat. Rev. Mol. Cell Biol. 2017, 18, 758–770. [Google Scholar] [CrossRef]
- Morikawa, Y.; Zhang, M.; Heallen, T.; Leach, J.; Tao, G.; Xiao, Y.; Bai, Y.; Li, W.; Willerson, J.T.; Martin, J.F. Actin Cytoskeletal Remodeling with Protrusion Formation Is Essential for Heart Regeneration in Hippo-deficient Mice. Sci. Signal. 2015, 8, ra41. [Google Scholar] [CrossRef] [Green Version]
- Xin, M.; Kim, Y.; Sutherland, L.B.; Murakami, M.; Qi, X.; McAnally, J.; Porrello, E.R.; Mahmoud, A.I.; Tan, W.; Shelton, J.M.; et al. Hippo Pathway Effector Yap Promotes Cardiac Regeneration. Proc. Natl. Acad. Sci. USA 2013, 110, 13839–13844. [Google Scholar] [CrossRef] [Green Version]
- Aratyn-Schaus, Y.; Oakes, P.W.; Stricker, J.; Winter, S.P.; Gardel, M.L. Preparation of Complaint Matrices for Quantifying Cellular Contraction. J. Vis. Exp. JoVE 2010, 14, 2173. [Google Scholar] [CrossRef] [Green Version]
- Tse, J.R.; Engler, A.J. Preparation of Hydrogel Substrates with Tunable Mechanical Properties. Curr. Protoc. Cell Biol. 2010, 10. [Google Scholar] [CrossRef] [PubMed]
- Hörning, M.; Blanchard, F.; Isomura, A.; Yoshikawa, K. Dynamics of Spatiotemporal Line Defects and Chaos Control in Complex Excitable Systems. Sci. Rep. 2017, 7, 7757. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Loppini, A.; Erhardt, J.; Fenton, F.H.; Filippi, S.; Hörning, M.; Gizzi, A. Optical Ultrastructure of Large Mammalian Hearts Recovers Discordant Alternans by In Silico Data Assimilation. Front. Netw. Physiol. 2022, 2. [Google Scholar] [CrossRef]






| Total Monomer Concentration, | HO | AAm | bAAm |
|---|---|---|---|
| (mol·kg) | (L) | (L) | (L) |
| 0.60 | 780.2 | 104.5 | 92.5 |
| 0.80 | 714.5 | 139.3 | 123.3 |
| 1.00 | 648.9 | 174.2 | 154.2 |
| 1.25 | 566.8 | 217.7 | 192.7 |
| 1.50 | 484.7 | 261.2 | 231.3 |
| 1.75 | 402.6 | 304.8 | 269.8 |
| 2.00 | 320.6 | 348.3 | 308.3 |
| FN Coating Density, | Volume on Gel | FN Concentration | FN Coating Density | Protein Equilibrium Distance |
|---|---|---|---|---|
| (g/cm) | (L) | (g/mL) | () | (nm) |
| 0.4 | 300 | 5.00 | 1456 | 17.2 |
| 1.1 | 250 | 16.72 | 4005 | 10.4 |
| 1.8 | 250 | 27.36 | 6554 | 8.1 |
| 2.6 | 250 | 40.00 | 9467 | 6.8 |
| 3.3 | 250 | 50.16 | 12,016 | 6.0 |
| 4.0 | 250 | 60.80 | 14,565 | 5.5 |
| Total Monomer Concentration, | Young’s Modulus, E (Measured via AFM) | Young’s Modulus, E (Linear Fit) |
|---|---|---|
| (mol·kg) | (kPa) | (kPa) |
| 0.60 | 3.3 ± 0.2 | 3.2 |
| 0.80 | 7.2 ± 0.2 | 7.8 |
| 1.00 | 12.3 ± 1.1 | 12.4 |
| 1.25 | 19.9 ± 1.8 | 18.2 |
| 1.50 | 23.4 ± 1.5 | 23.9 |
| 1.75 | 30.3 ± 2.5 | 29.7 |
| 2.00 | 34.8 ± 3.7 | 35.4 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Brock, J.; Erhardt, J.; Eisler, S.A.; Hörning, M. Optimization of Mechanosensitive Cross-Talk between Matrix Stiffness and Protein Density: Independent Matrix Properties Regulate Spreading Dynamics of Myocytes. Cells 2022, 11, 2122. https://doi.org/10.3390/cells11132122
Brock J, Erhardt J, Eisler SA, Hörning M. Optimization of Mechanosensitive Cross-Talk between Matrix Stiffness and Protein Density: Independent Matrix Properties Regulate Spreading Dynamics of Myocytes. Cells. 2022; 11(13):2122. https://doi.org/10.3390/cells11132122
Chicago/Turabian StyleBrock, Judith, Julia Erhardt, Stephan A. Eisler, and Marcel Hörning. 2022. "Optimization of Mechanosensitive Cross-Talk between Matrix Stiffness and Protein Density: Independent Matrix Properties Regulate Spreading Dynamics of Myocytes" Cells 11, no. 13: 2122. https://doi.org/10.3390/cells11132122
APA StyleBrock, J., Erhardt, J., Eisler, S. A., & Hörning, M. (2022). Optimization of Mechanosensitive Cross-Talk between Matrix Stiffness and Protein Density: Independent Matrix Properties Regulate Spreading Dynamics of Myocytes. Cells, 11(13), 2122. https://doi.org/10.3390/cells11132122






