Spatiotemporal Coordination of Rac1 and Cdc42 at the Whole Cell Level during Cell Ruffling
Abstract
1. Introduction
2. Results
2.1. Coupling Reaction-Diffusion Models of GTPase Regulation and Cell Morphodynamics
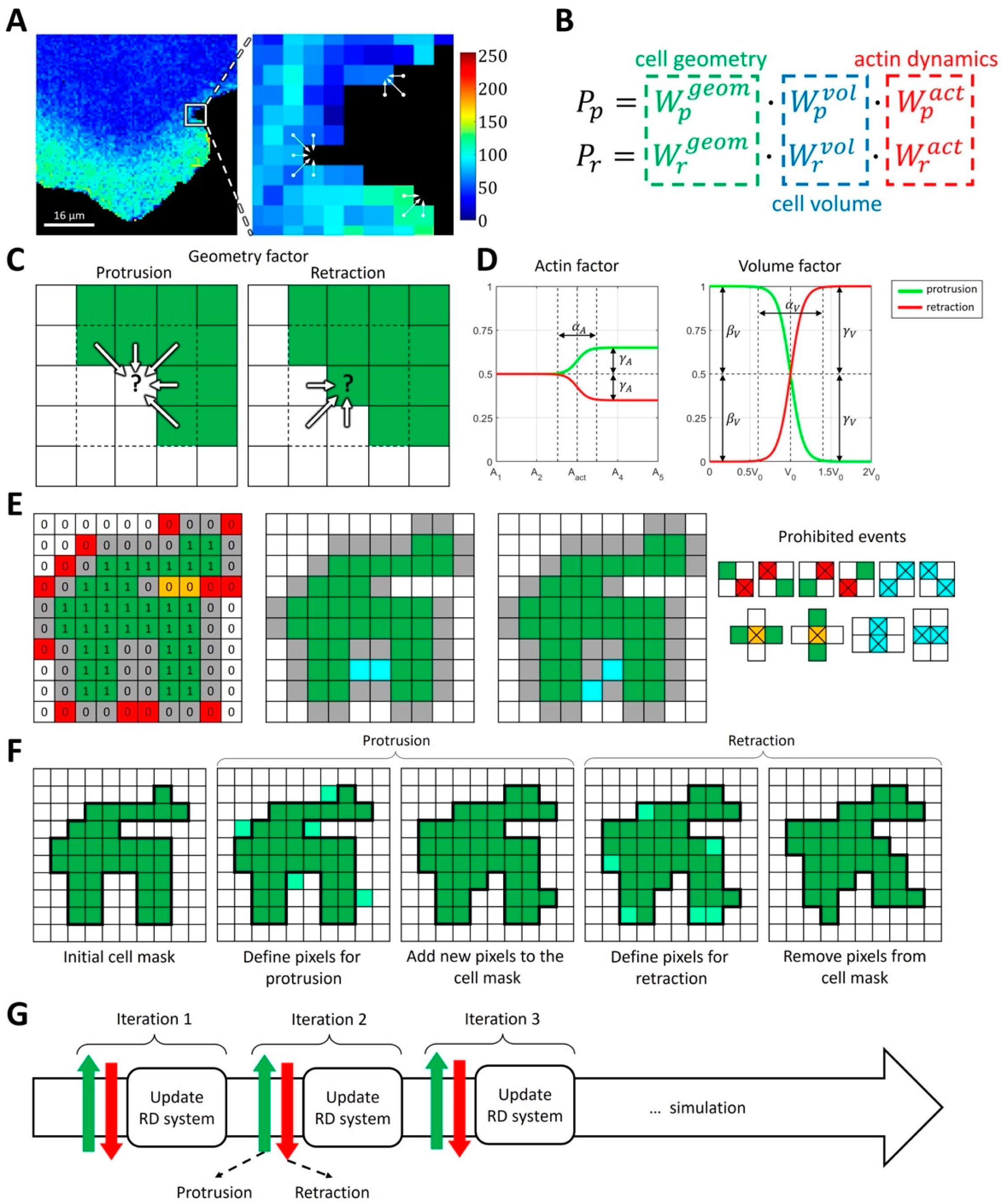
2.1.1. Modeling Cell Morphodynamics
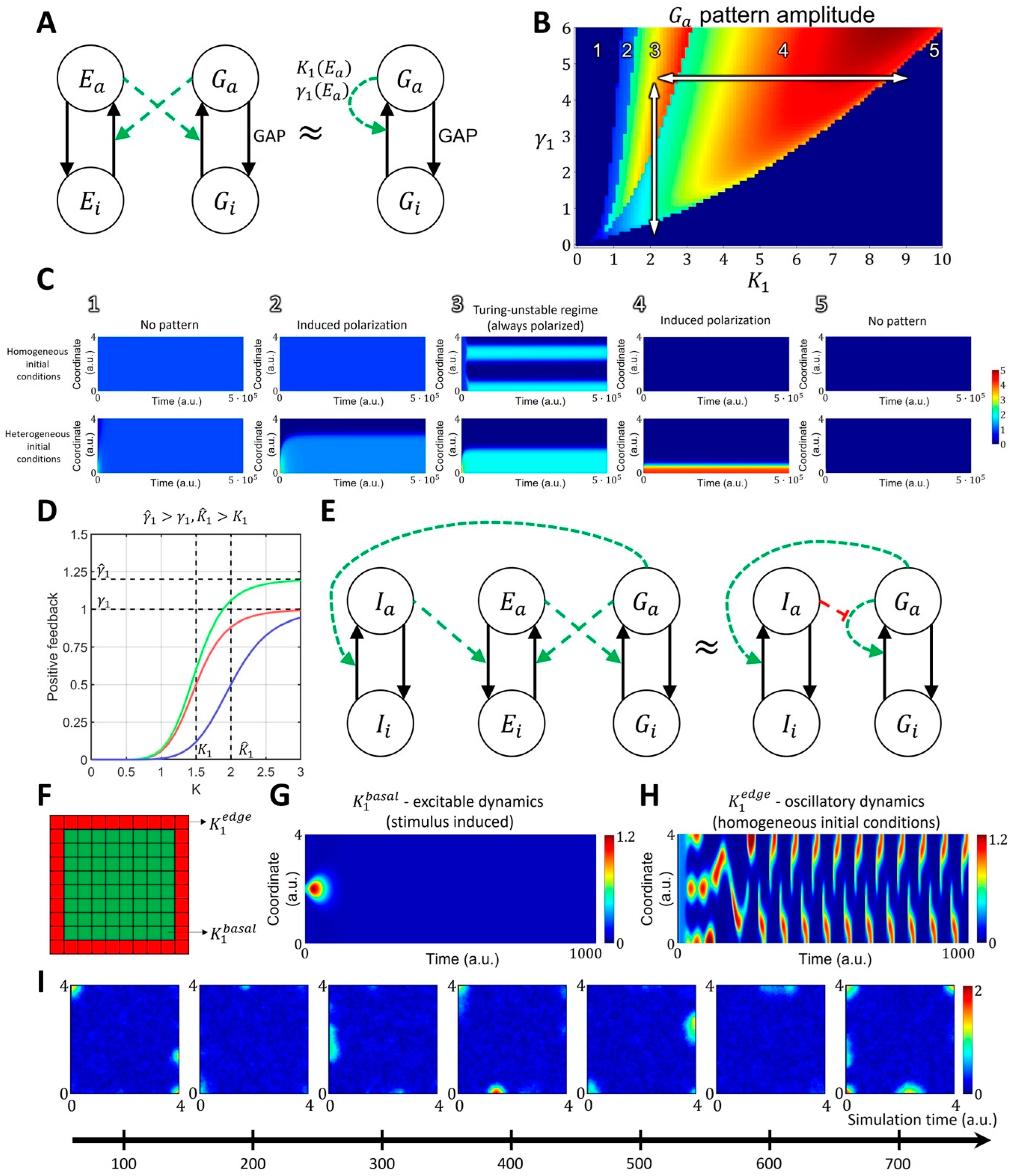
2.1.2. Spatiotemporal Model of GTPase Activity during Cell Ruffling
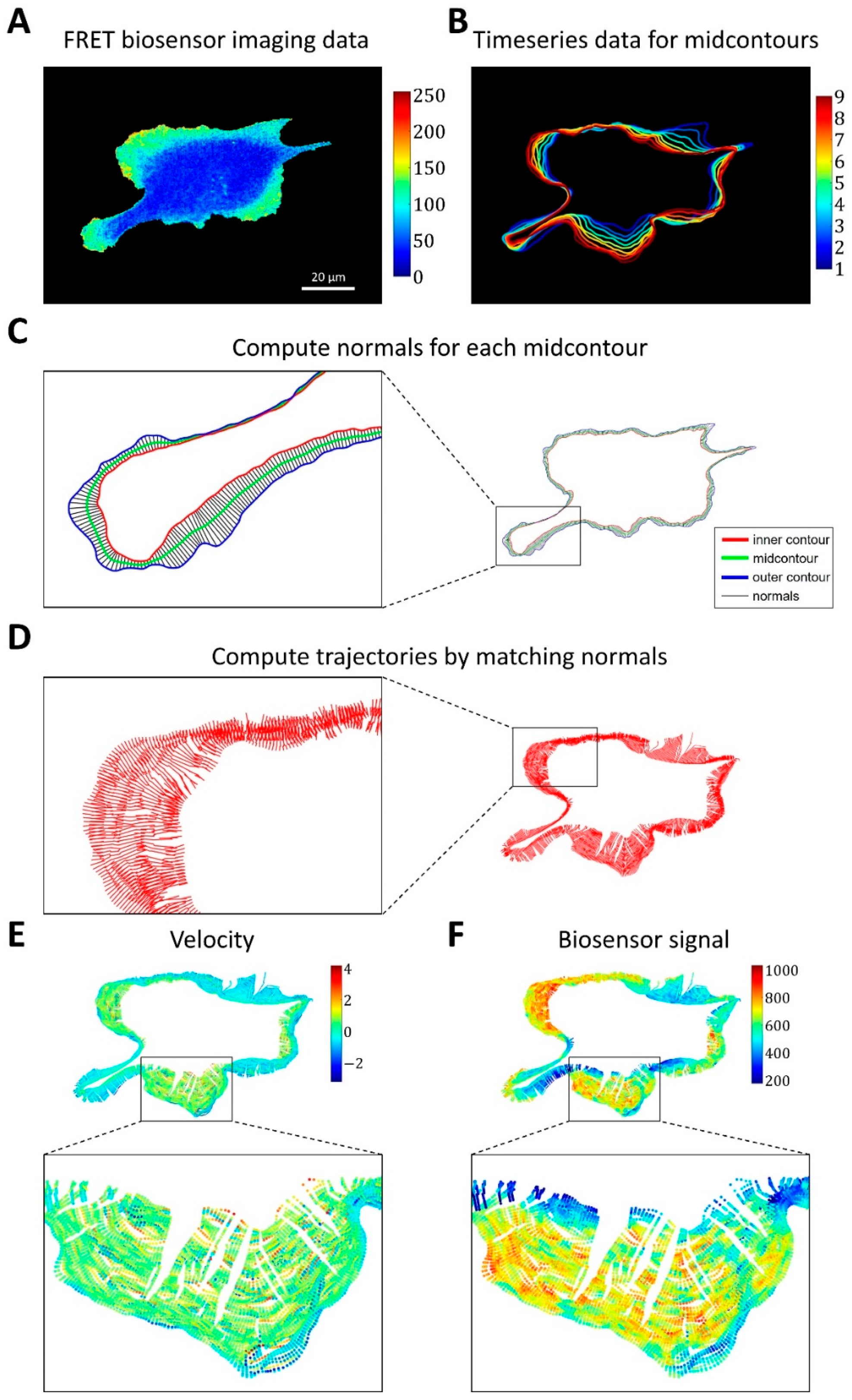
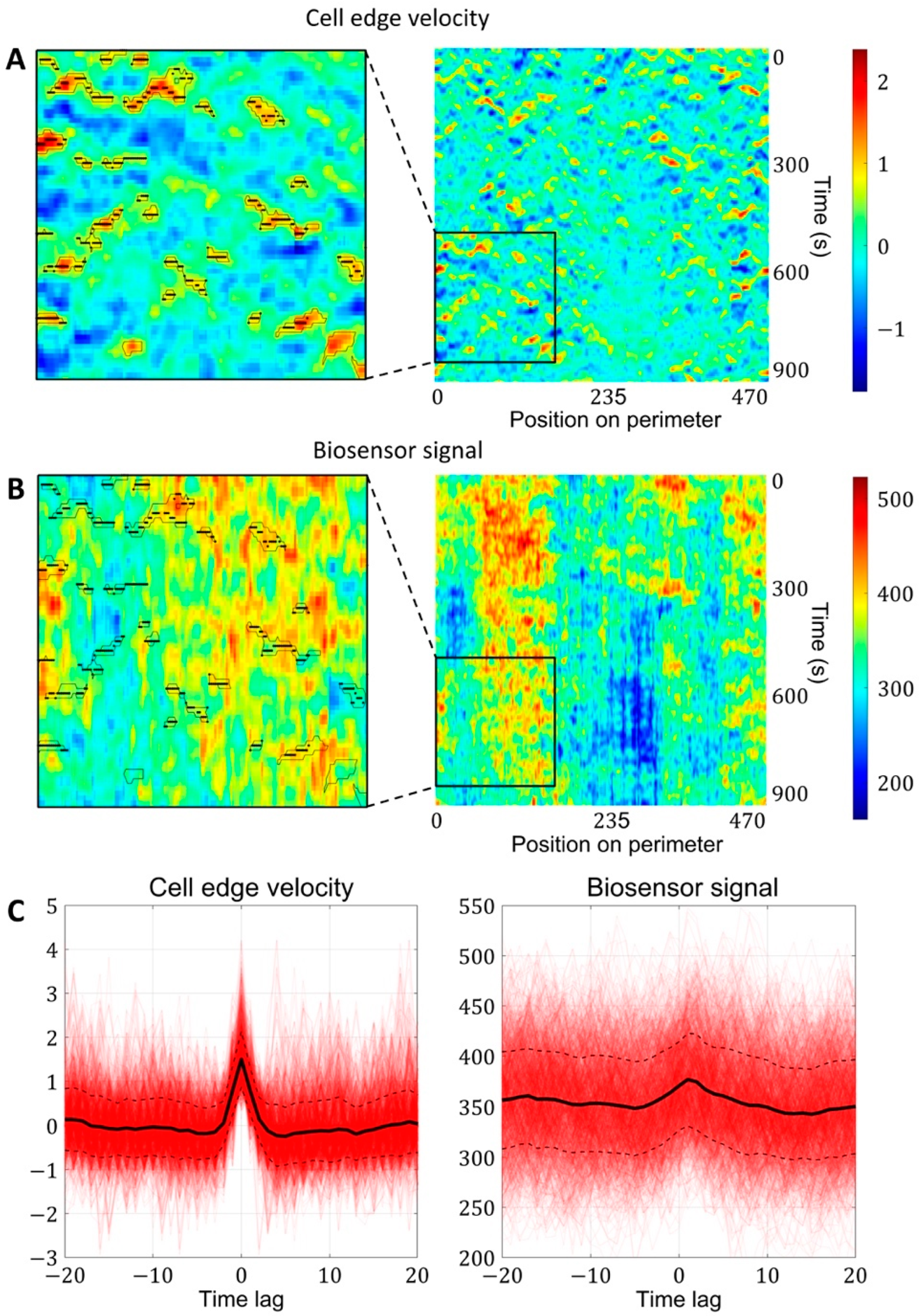
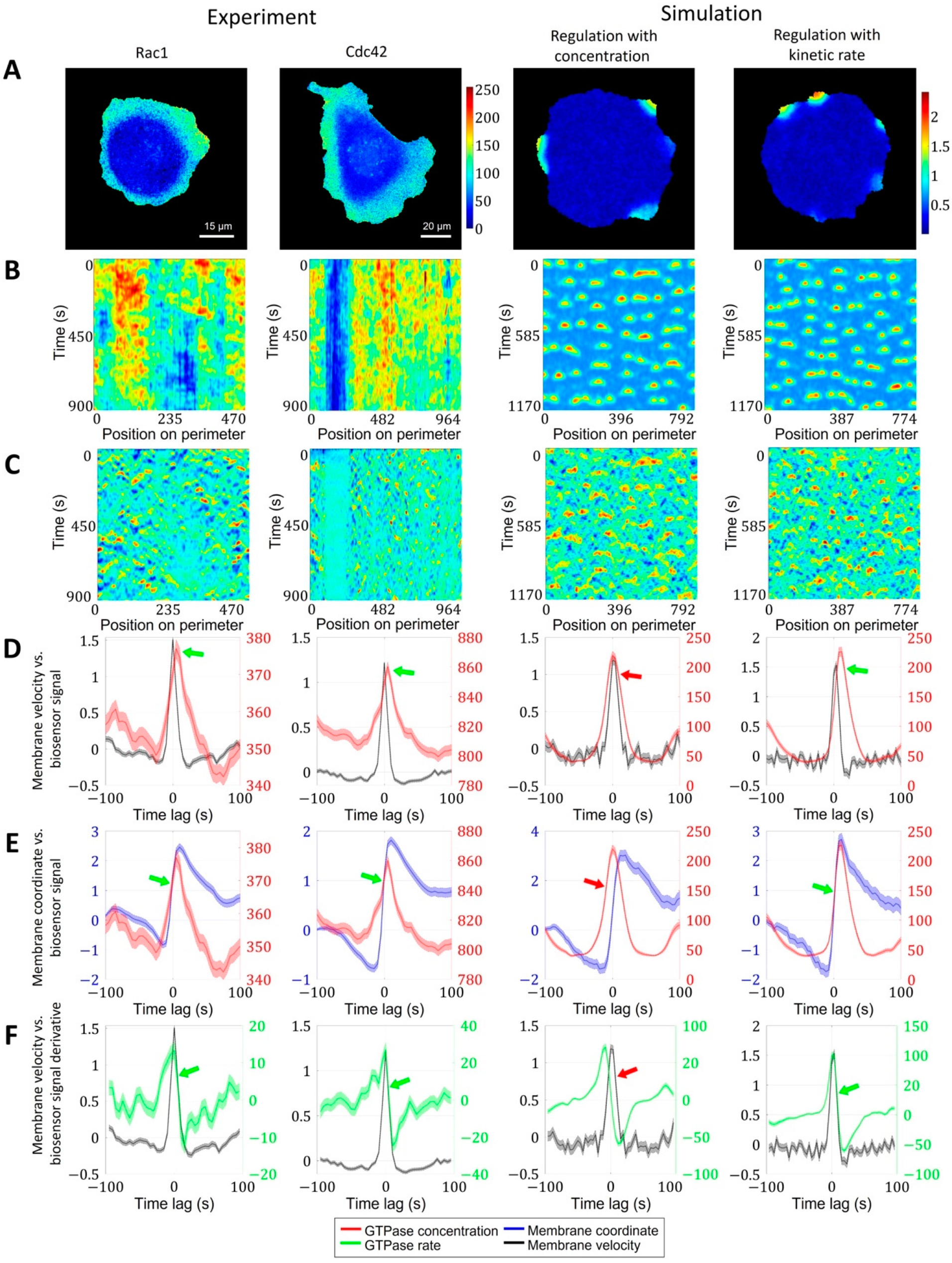
2.1.3. A Pipeline for the Analysis of Cell Edge Velocity and GTPase Activity in Experiments and Simulations
2.2. Cell Edge Velocity Is Regulated by the GTPase’s Rate of Activation Rather than Its Concentration Value
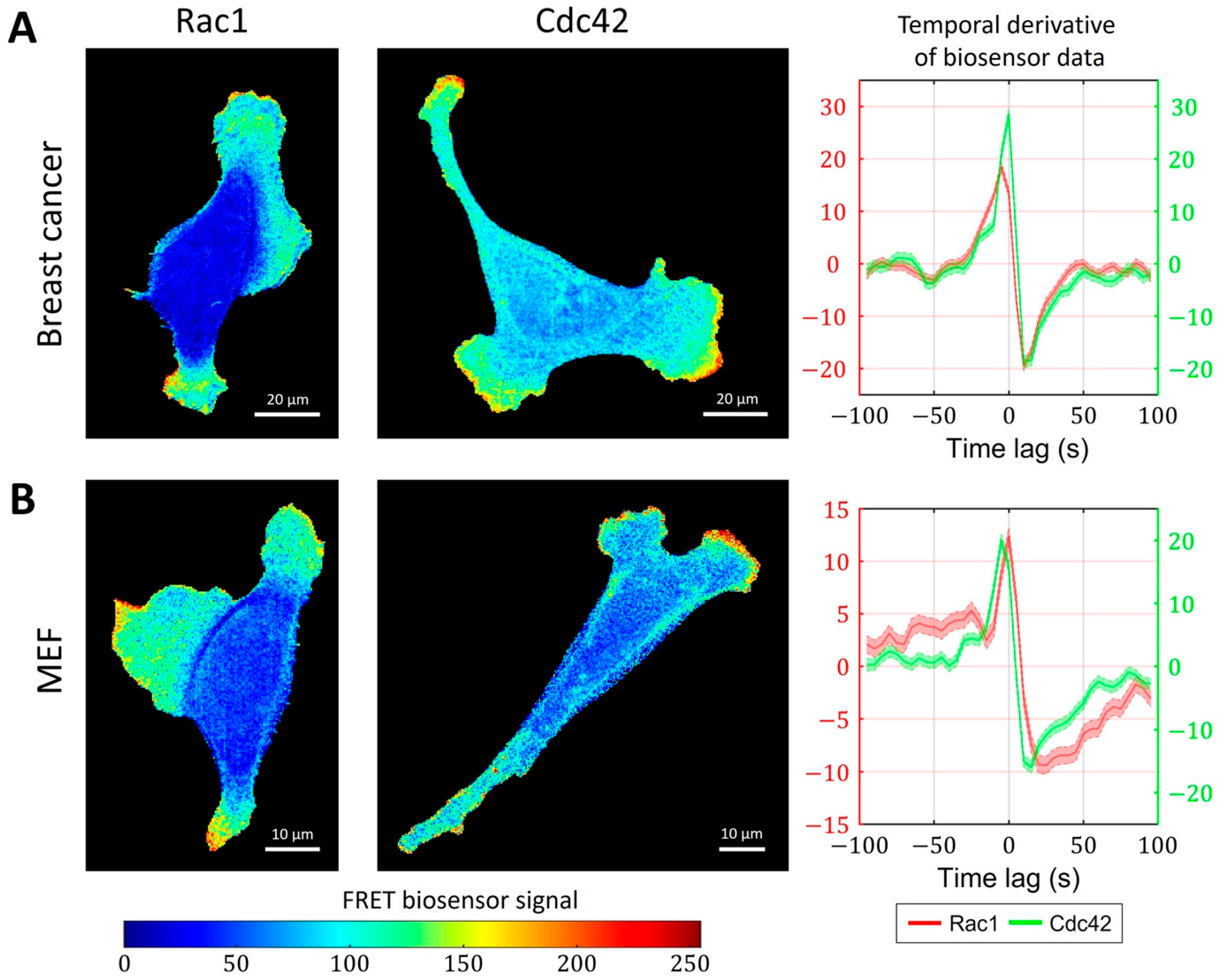
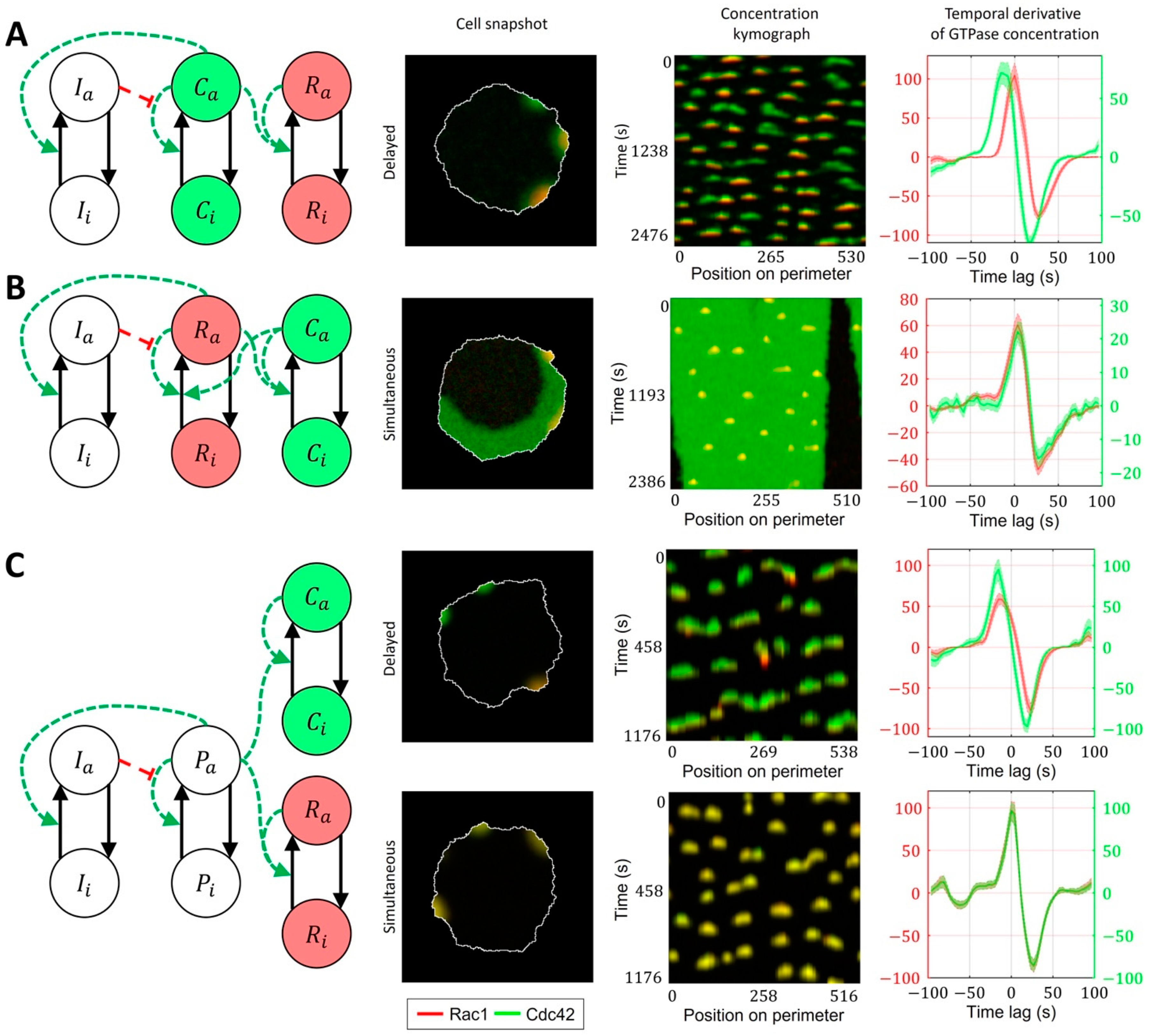
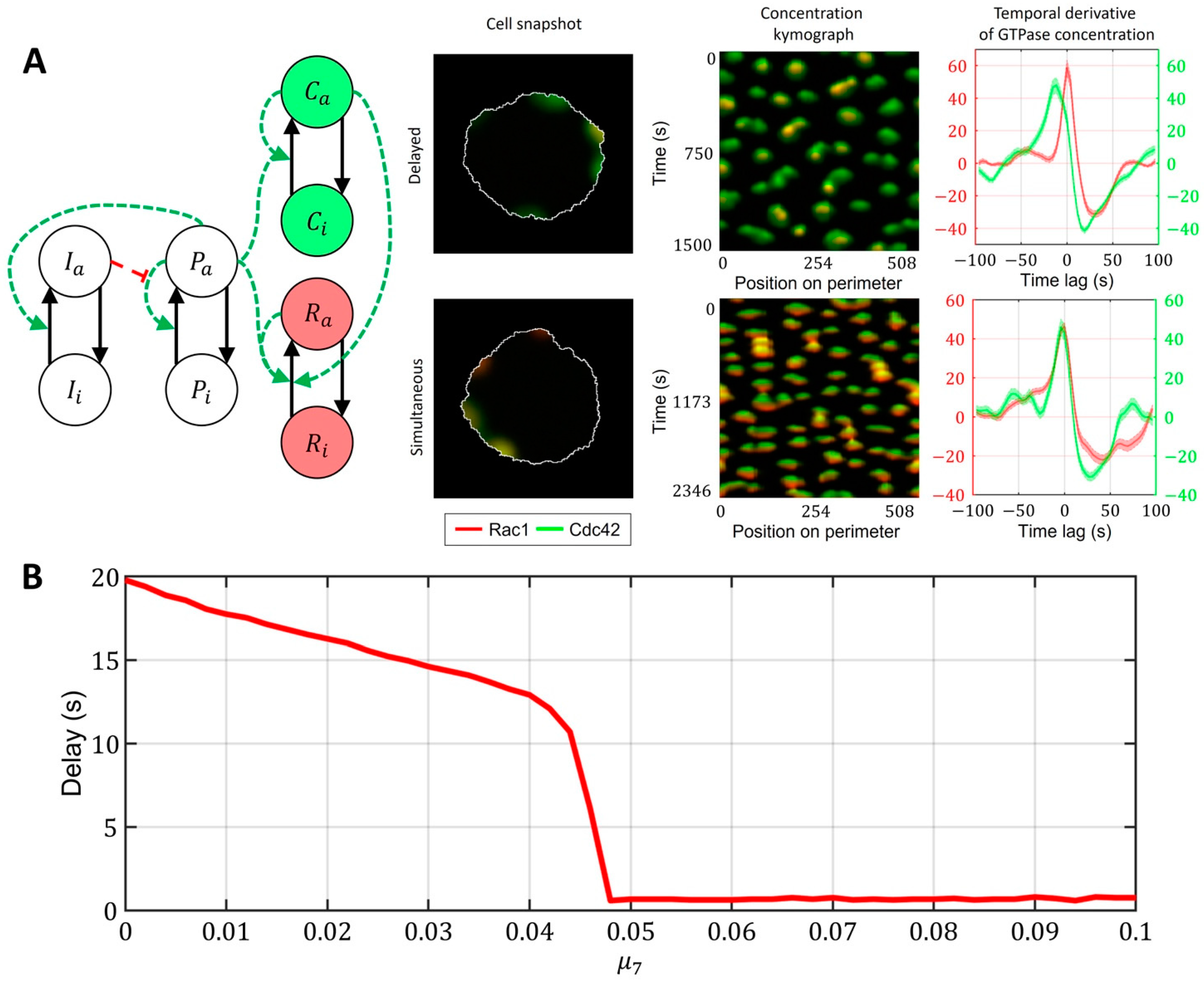
2.3. Cell-Type Specific Relationship between Peaks of Rac1 and Cdc42 Activity Can Be Reproduced with a Unified Model Operating in Different Dynamic Regimes
3. Discussion
4. Materials and Methods
4.1. Reaction-Diffusion Models of GTPase Signaling
4.2. Four-Component Model of GTPase Activity during Cell Ruffling
- Model of Cdc42 Induced Activation of Rac1
- Model of Bidirectionally Coupled Cdc42 and Rac1 Activity
- Model of Cdc42 and Rac1 Activity Regulated by the Upstream Effector
- Model of Cdc42 and Rac1 Activity Regulated by the Upstream Effector and the Feedback from Cdc42 to Rac1
4.3. Computational Method for Coupling Reaction-Diffusion Equations with Cellular Morphodynamics
4.4. Image Analysis Pipeline for Coupled Analysis of Cell Edge Velocity and Biosensor Signaling
5. Conclusions
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Etienne-Manneville, S.; Hall, A. Rho GTPases in cell biology. Nature 2002, 420, 629–635. [Google Scholar] [CrossRef]
- Hodge, R.G.; Ridley, A.J. Regulating Rho GTPases and their regulators. Nat. Rev. Mol. Cell Biol. 2016, 17, 496–510. [Google Scholar] [CrossRef] [PubMed]
- Lawson, C.D.; Ridley, A.J. Rho GTPase signaling complexes in cell migration and invasion. J. Cell Biol. 2018, 217, 447–457. [Google Scholar] [CrossRef] [PubMed]
- Hall, A. Rho GTPases and the actin cytoskeleton. Science 1998, 279, 509–514. [Google Scholar] [CrossRef]
- Haga, R.B.; Ridley, A.J. Rho GTPases: Regulation and roles in cancer cell biology. Small GTPases 2016, 7, 207–221. [Google Scholar] [CrossRef]
- Lee, K.; Elliott, H.L.; Oak, Y.; Zee, C.T.; Groisman, A.; Tytell, J.D.; Danuser, G. Functional hierarchy of redundant actin assembly factors revealed by fine-grained registration of intrinsic image fluctuations. Cell Syst. 2015, 1, 37–50. [Google Scholar] [CrossRef]
- Guilluy, C.; Garcia-Mata, R.; Burridge, K. Rho protein crosstalk: Another social network? Trends. Cell Biol. 2011, 21, 718–726. [Google Scholar] [CrossRef]
- Cherfils, J.; Zeghouf, M. Regulation of small GTPases by GEFs, GAPs, and GDIs. Physiol. Rev. 2013, 93, 269–309. [Google Scholar] [CrossRef]
- Zegers, M.M.; Friedl, P. Rho GTPases in collective cell migration. Small GTPases 2014, 5, e28997. [Google Scholar] [CrossRef]
- Maldonado, M.D.M.; Medina, J.I.; Velazquez, L.; Dharmawardhane, S. Targeting Rac and Cdc42 GEFs in Metastatic Cancer. Front. Cell. Dev. Biol. 2020, 8, 201. [Google Scholar] [CrossRef]
- Mosaddeghzadeh, N.; Ahmadian, M.R. The RHO Family GTPases: Mechanisms of Regulation and Signaling. Cells 2021, 10, 1831. [Google Scholar] [CrossRef]
- Simon, C.M.; Vaughan, E.M.; Bement, W.M.; Edelstein-Keshet, L. Pattern formation of Rho GTPases in single cell wound healing. Mol. Biol. Cell. 2013, 24, 421–432. [Google Scholar] [CrossRef]
- Jiang, H.; Deng, R.; Yang, X.; Shang, J.; Lu, S.; Zhao, Y.; Song, K.; Liu, X.; Zhang, Q.; Chen, Y.; et al. Peptidomimetic inhibitors of APC-Asef interaction block colorectal cancer migration. Nat. Chem. Biol. 2017, 13, 994–1001. [Google Scholar] [CrossRef] [PubMed]
- Pertz, O. Spatio-temporal Rho GTPase signaling—Where are we now? J. Cell Sci. 2010, 123, 1841–1850. [Google Scholar] [CrossRef]
- de Beco, S.; Vaidziulyte, K.; Manzi, J.; Dalier, F.; di Federico, F.; Cornilleau, G.; Dahan, M.; Coppey, M. Optogenetic dissection of Rac1 and Cdc42 gradient shaping. Nat. Commun. 2018, 9, 4816. [Google Scholar] [CrossRef]
- Campa, C.C.; Ciraolo, E.; Ghigo, A.; Germena, G.; Hirsch, E. Crossroads of PI3K and Rac pathways. Small GTPases 2015, 6, 71–80. [Google Scholar] [CrossRef]
- Zhan, H.; Bhattacharya, S.; Cai, H.; Iglesias, P.A.; Huang, C.H.; Devreotes, P.N. An Excitable Ras/PI3K/ERK Signaling Network Controls Migration and Oncogenic Transformation in Epithelial Cells. Dev. Cell 2020, 54, 608–623.e605. [Google Scholar] [CrossRef]
- Miao, Y.; Bhattacharya, S.; Banerjee, T.; Abubaker-Sharif, B.; Long, Y.; Inoue, T.; Iglesias, P.A.; Devreotes, P.N. Wave patterns organize cellular protrusions and control cortical dynamics. Mol. Syst. Biol. 2019, 15, e8585. [Google Scholar] [CrossRef]
- Wu, M.; Wu, X.; De Camilli, P. Calcium oscillations-coupled conversion of actin travelling waves to standing oscillations. Proc. Natl. Acad. Sci. USA 2013, 110, 1339–1344. [Google Scholar] [CrossRef]
- Marston, D.J.; Vilela, M.; Huh, J.; Ren, J.; Azoitei, M.L.; Glekas, G.; Danuser, G.; Sondek, J.; Hahn, K.M. Multiplexed GTPase and GEF biosensor imaging enables network connectivity analysis. Nat. Chem. Biol. 2020, 16, 826–833. [Google Scholar] [CrossRef]
- Machacek, M.; Hodgson, L.; Welch, C.; Elliott, H.; Pertz, O.; Nalbant, P.; Abell, A.; Johnson, G.L.; Hahn, K.M.; Danuser, G. Coordination of Rho GTPase activities during cell protrusion. Nature 2009, 461, 99–103. [Google Scholar] [CrossRef]
- Machacek, M.; Danuser, G. Morphodynamic profiling of protrusion phenotypes. Biophys. J. 2006, 90, 1439–1452. [Google Scholar] [CrossRef]
- Kunida, K.; Matsuda, M.; Aoki, K. FRET imaging and statistical signal processing reveal positive and negative feedback loops regulating the morphology of randomly migrating HT-1080 cells. J. Cell Sci. 2012, 125, 2381–2392. [Google Scholar] [CrossRef] [PubMed]
- Yamao, M.; Naoki, H.; Kunida, K.; Aoki, K.; Matsuda, M.; Ishii, S. Distinct predictive performance of Rac1 and Cdc42 in cell migration. Sci. Rep. 2015, 5, 17527. [Google Scholar] [CrossRef] [PubMed]
- Beckers, C.M.; van Hinsbergh, V.W.; van Nieuw Amerongen, G.P. Driving Rho GTPase activity in endothelial cells regulates barrier integrity. Thromb. Haemost. 2010, 103, 40–55. [Google Scholar] [CrossRef]
- Hoppe, A.D.; Swanson, J.A. Cdc42, Rac1, and Rac2 display distinct patterns of activation during phagocytosis. Mol. Biol. Cell 2004, 15, 3509–3519. [Google Scholar] [CrossRef]
- Meinhardt, H.; Gierer, A. Pattern formation by local self-activation and lateral inhibition. Bioessays 2000, 22, 753–760. [Google Scholar] [CrossRef]
- Meinhardt, H. Turing’s theory of morphogenesis of 1952 and the subsequent discovery of the crucial role of local self-enhancement and long-range inhibition. Interface Focus 2012, 2, 407–416. [Google Scholar] [CrossRef]
- Kondo, S.; Miura, T. Reaction-diffusion model as a framework for understanding biological pattern formation. Science 2010, 329, 1616–1620. [Google Scholar] [CrossRef]
- Halatek, J.; Brauns, F.; Frey, E. Self-organization principles of intracellular pattern formation. Philos. Trans. R. Soc. Lond. B Biol. Sci. 2018, 373, 20170107. [Google Scholar] [CrossRef]
- Turing, A.M. The Chemical Basis of Morphogenesis. Philos. T. Roy Soc. B 1952, 237, 37–72. [Google Scholar] [CrossRef]
- Meinhardt, H. Models of biological pattern formation: From elementary steps to the organization of embryonic axes. Curr. Top. Dev. Biol. 2008, 81, 1–63. [Google Scholar] [CrossRef]
- Gierer, A.; Meinhardt, H. A theory of biological pattern formation. Kybernetik 1972, 12, 30–39. [Google Scholar] [CrossRef] [PubMed]
- Iglesias, P.A.; Devreotes, P.N. Navigating through models of chemotaxis. Curr. Opin. Cell Biol. 2008, 20, 35–40. [Google Scholar] [CrossRef]
- Subramanian, K.K.; Narang, A. A mechanistic model for eukaryotic gradient sensing: Spontaneous and induced phosphoinositide polarization. J. Theor. Biol. 2004, 231, 49–67. [Google Scholar] [CrossRef]
- Symons, M. Rac1 activation comes full circle. EMBO J. 2011, 30, 3875–3877. [Google Scholar] [CrossRef]
- Mogilner, A.; Allard, J.; Wollman, R. Cell polarity: Quantitative modeling as a tool in cell biology. Science 2012, 336, 175–179. [Google Scholar] [CrossRef]
- Iglesias, P.A.; Devreotes, P.N. Biased excitable networks: How cells direct motion in response to gradients. Curr. Opin. Cell Biol. 2012, 24, 245–253. [Google Scholar] [CrossRef]
- Goryachev, A.B.; Leda, M. Many roads to symmetry breaking: Molecular mechanisms and theoretical models of yeast cell polarity. Mol. Biol. Cell 2017, 28, 370–380. [Google Scholar] [CrossRef]
- Liu, Y.; Rens, E.G.; Edelstein-Keshet, L. Spots, stripes, and spiral waves in models for static and motile cells: GTPase patterns in cells. J. Math. Biol. 2021, 82, 28. [Google Scholar] [CrossRef]
- Yang, J.M.; Bhattacharya, S.; West-Foyle, H.; Hung, C.F.; Wu, T.C.; Iglesias, P.A.; Huang, C.H. Integrating chemical and mechanical signals through dynamic coupling between cellular protrusions and pulsed ERK activation. Nat. Commun. 2018, 9, 4673. [Google Scholar] [CrossRef]
- Brauns, F.; Halatek, J.; Frey, E. Phase-Space Geometry of Mass-Conserving Reaction-Diffusion Dynamics. Phys. Rev. X 2020, 10, 041036. [Google Scholar] [CrossRef]
- Wigbers, M.C.; Brauns, F.; Hermann, T.; Frey, E. Pattern localization to a domain edge. Phys. Rev. E 2020, 101, 022414. [Google Scholar] [CrossRef] [PubMed]
- Chiou, J.G.; Ramirez, S.A.; Elston, T.C.; Witelski, T.P.; Schaeffer, D.G.; Lew, D.J. Principles that govern competition or co-existence in Rho-GTPase driven polarization. PLoS Comput. Biol. 2018, 14, e1006095. [Google Scholar] [CrossRef] [PubMed]
- Goryachev, A.B.; Pokhilko, A.V. Dynamics of Cdc42 network embodies a Turing-type mechanism of yeast cell polarity. FEBS Lett. 2008, 582, 1437–1443. [Google Scholar] [CrossRef]
- Edelstein-Keshet, L.; Holmes, W.R.; Zajac, M.; Dutot, M. From simple to detailed models for cell polarization. Philos. Trans. R. Soc. Lond. B Biol. Sci. 2013, 368, 20130003. [Google Scholar] [CrossRef]
- Hladyshau, S.; Kho, M.; Nie, S.; Tsygankov, D. Spatiotemporal development of coexisting wave domains of Rho activity in the cell cortex. Sci. Rep. 2021, 11, 19512. [Google Scholar] [CrossRef]
- Bolado-Carrancio, A.; Rukhlenko, O.S.; Nikonova, E.; Tsyganov, M.A.; Wheeler, A.; Garcia-Munoz, A.; Kolch, W.; von Kriegsheim, A.; Kholodenko, B.N. Periodic propagating waves coordinate RhoGTPase network dynamics at the leading and trailing edges during cell migration. Elife 2020, 9, e58165. [Google Scholar] [CrossRef]
- Kholodenko, B.N.; Rauch, N.; Kolch, W.; Rukhlenko, O.S. A systematic analysis of signaling reactivation and drug resistance. Cell Rep. 2021, 35, 109157. [Google Scholar] [CrossRef]
- Mahankali, M.; Peng, H.J.; Cox, D.; Gomez-Cambronero, J. The mechanism of cell membrane ruffling relies on a phospholipase D2 (PLD2), Grb2 and Rac2 association. Cell Signal 2011, 23, 1291–1298. [Google Scholar] [CrossRef]
- Pittman, M.; Iu, E.; Li, K.; Wang, M.J.; Chen, J.J.; Taneja, N.; Jo, M.H.; Park, S.; Jung, W.H.; Liang, L.; et al. Membrane ruffling is a mechanosensor of extracellular fluid viscosity. Nat. Phys. 2022, 18, 1112–1121. [Google Scholar] [CrossRef] [PubMed]
- MacNevin, C.J.; Toutchkine, A.; Marston, D.J.; Hsu, C.W.; Tsygankov, D.; Li, L.; Liu, B.; Qi, T.; Nguyen, D.V.; Hahn, K.M. Ratiometric Imaging Using a Single Dye Enables Simultaneous Visualization of Rac1 and Cdc42 Activation. J. Am. Chem. Soc. 2016, 138, 2571–2575. [Google Scholar] [CrossRef] [PubMed]
- Chen, N.; Glazier, J.A.; Izaguirre, J.A.; Alber, M.S. A parallel implementation of the Cellular Potts Model for simulation of cell-based morphogenesis. Comput. Phys. Commun. 2007, 176, 670–681. [Google Scholar] [CrossRef]
- Marston, D.J.; Slattery, S.D.; Hahn, K.M.; Tsygankov, D. Correcting Artifacts in Ratiometric Biosensor Imaging; an Improved Approach for Dividing Noisy Signals. Front. Cell. Dev. Biol. 2021, 9, 685825. [Google Scholar] [CrossRef]
- de Kreuk, B.J.; Hordijk, P.L. Control of Rho GTPase function by BAR-domains. Small GTPases 2012, 3, 45–52. [Google Scholar] [CrossRef]
- Zhao, H.; Pykalainen, A.; Lappalainen, P. I-BAR domain proteins: Linking actin and plasma membrane dynamics. Curr. Opin. Cell Biol. 2011, 23, 14–21. [Google Scholar] [CrossRef]
- Connolly, B.A.; Rice, J.; Feig, L.A.; Buchsbaum, R.J. Tiam1-IRSp53 complex formation directs specificity of rac-mediated actin cytoskeleton regulation. Mol. Cell Biol. 2005, 25, 4602–4614. [Google Scholar] [CrossRef]
- Nishimura, T.; Yamaguchi, T.; Kato, K.; Yoshizawa, M.; Nabeshima, Y.; Ohno, S.; Hoshino, M.; Kaibuchi, K. PAR-6-PAR-3 mediates Cdc42-induced Rac activation through the Rac GEFs STEF/Tiam1. Nat. Cell Biol. 2005, 7, 270–277. [Google Scholar] [CrossRef]
- Yang, X.; Cruz, M.I.; Nguyen, E.V.; Huang, C.; Schittenhelm, R.B.; Luu, J.; Cowley, K.J.; Shin, S.Y.; Nguyen, L.K.; Lim Kam Sian, T.C.C.; et al. The pseudokinase NRBP1 activates Rac1/Cdc42 via P-Rex1 to drive oncogenic signalling in triple-negative breast cancer. Oncogene 2023, 42, 833–847. [Google Scholar] [CrossRef] [PubMed]
- Murphy, N.P.; Binti Ahmad Mokhtar, A.M.; Mott, H.R.; Owen, D. Molecular subversion of Cdc42 signalling in cancer. Biochem. Soc. Trans. 2021, 49, 1425–1442. [Google Scholar] [CrossRef]
- Etienne-Manneville, S. Cdc42—The centre of polarity. J. Cell Sci. 2004, 117, 1291–1300. [Google Scholar] [CrossRef] [PubMed]
- Wittmann, T.; Bokoch, G.M.; Waterman-Storer, C.M. Regulation of leading edge microtubule and actin dynamics downstream of Rac1. J. Cell Biol. 2003, 161, 845–851. [Google Scholar] [CrossRef]
- Aspenstrom, P. The Intrinsic GDP/GTP Exchange Activities of Cdc42 and Rac1 Are Critical Determinants for Their Specific Effects on Mobilization of the Actin Filament System. Cells 2019, 8, 759. [Google Scholar] [CrossRef]
- Singh, A.; Karnoub, A.E.; Palmby, T.R.; Lengyel, E.; Sondek, J.; Der, C.J. Rac1b, a tumor associated, constitutively active Rac1 splice variant, promotes cellular transformation. Oncogene 2004, 23, 9369–9380. [Google Scholar] [CrossRef]
- Panopoulos, A.; Howell, M.; Fotedar, R.; Margolis, R.L. Glioblastoma motility occurs in the absence of actin polymer. Mol. Biol. Cell 2011, 22, 2212–2220. [Google Scholar] [CrossRef]
- Kozma, R.; Ahmed, S.; Best, A.; Lim, L. The Ras-related protein Cdc42Hs and bradykinin promote formation of peripheral actin microspikes and filopodia in Swiss 3T3 fibroblasts. Mol. Cell Biol. 1995, 15, 1942–1952. [Google Scholar] [CrossRef]
- Holmes, W.R.; Carlsson, A.E.; Edelstein-Keshet, L. Regimes of wave type patterning driven by refractory actin feedback: Transition from static polarization to dynamic wave behaviour. Phys. Biol. 2012, 9, 046005. [Google Scholar] [CrossRef]
- Mori, Y.; Jilkine, A.; Edelstein-Keshet, L. Wave-pinning and cell polarity from a bistable reaction-diffusion system. Biophys. J. 2008, 94, 3684–3697. [Google Scholar] [CrossRef]
- Smith, C.A.; Yates, C.A. Incorporating domain growth into hybrid methods for reaction-diffusion systems. J. R. Soc. Interface 2021, 18, 20201047. [Google Scholar] [CrossRef] [PubMed]
| Model | |||
|---|---|---|---|
| GTPase activity in cell ruffling (regulation by absolute concentration value) | 30 | 0.7 | 0.1 |
| GTPase activity in cell ruffling (regulation by activation rate) | 50 | 0.1 | 0.2 |
| Rac1 activation by Cdc42 | 50 | 0.3 | 0.2 |
| Coupled model with bidirectional feedback between Rac1 and Cdc42 | 50 | 0.2 | 0.35 |
| Rac1 and Cdc42 activation by the upstream regulator (simultaneous activation) | 100 | 0.1 | 0.1 |
| Rac1 and Cdc42 activation by the upstream regulator (delayed activation) | 30 | 0.5 | 0.1 |
| Rac1 and Cdc42 activation by the upstream regulator with feedback between Cdc42 and Rac1 (simultaneous and delayed activation) | 30 | 0.3 | 0.1 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Hladyshau, S.; Stoop, J.P.; Kamada, K.; Nie, S.; Tsygankov, D. Spatiotemporal Coordination of Rac1 and Cdc42 at the Whole Cell Level during Cell Ruffling. Cells 2023, 12, 1638. https://doi.org/10.3390/cells12121638
Hladyshau S, Stoop JP, Kamada K, Nie S, Tsygankov D. Spatiotemporal Coordination of Rac1 and Cdc42 at the Whole Cell Level during Cell Ruffling. Cells. 2023; 12(12):1638. https://doi.org/10.3390/cells12121638
Chicago/Turabian StyleHladyshau, Siarhei, Jorik P. Stoop, Kosei Kamada, Shuyi Nie, and Denis Tsygankov. 2023. "Spatiotemporal Coordination of Rac1 and Cdc42 at the Whole Cell Level during Cell Ruffling" Cells 12, no. 12: 1638. https://doi.org/10.3390/cells12121638
APA StyleHladyshau, S., Stoop, J. P., Kamada, K., Nie, S., & Tsygankov, D. (2023). Spatiotemporal Coordination of Rac1 and Cdc42 at the Whole Cell Level during Cell Ruffling. Cells, 12(12), 1638. https://doi.org/10.3390/cells12121638







