Exploring the Interactions of Oncolytic Viral Therapy and Immunotherapy of Anti-CTLA-4 for Malignant Melanoma Mice Model
Abstract
1. Introduction
2. Model Construction and Parameterization
2.1. Model Development
- Equation (1) models the uninfected tumor cell population. We assume susceptible tumor cells grow in a logistic fashion with an intrinsic growth rate and carrying capacity for all tumor cells. We choose logistic growth model for the susceptible tumor population because evidence shows that the growth of tumor is slower when the tumor becomes larger [15,26]. The term is the viral infection rate of uninfected tumor cells with the maximum rate , which turns a susceptible tumor cell into an infected tumor cell. The saturated form of the tumor–virus interaction is considered according to [26]. The killings of tumor cells are modeled by the terms and due to CD8+ T cells and cytokines, respectively. They represent susceptible tumor population killed directly by the effector CD8+ T cells and indirectly by CD4+ T cells through cytokines at a rate of and , respectively. The Michaelis–Menten kinetics form of the tumor and the tumor-specific immune cell interaction is adopted according to [15] and [27]. The saturated form shows the limited property of effector cells and cytokines abilities to lyse tumor cells. NK cells are able to recognize tumor antigens and indiscriminately kill tumor cells. The term is used to model the tumor killing by NK cells at a rate .
- Equation (2) models the population of infected tumor cells. Similar to susceptible tumor cells, we assume infected tumor cells grow in a logistic fashion with an intrinsic growth rate and carrying capacity for all tumor cells. Susceptible tumor cells infected by oncolytic virus at a rate result in the increase of the infected tumor cells. This cell population dies at a rate . Since T cells kill not only virus-free tumor cells but also virus-infected tumor cells, the infected tumor cells are lysed via anti-tumor adaptive immune cells CD8+ T cells (directly killing) with and by CD4+ T cells (indirectly killing through cytokines) with . The killing due to anti-viral adaptive immune cells is modeled by the term at a rate [15]. The term is used to address the killing by NK cells on infected tumor cells at a constant rate .
- Equation (3) models the virus population. New virus particles are produced upon clearance of an infected cancer cell. The parameter is the burst size of viruses released from an infected tumor cell. is the viral lysis by anti-viral immune cells. The virus decays at a rate and s represents the dose of OV. NK cells not only directly recognize and kill viral-infected cells through their receptors but also provide an antigen-specific adaptive response to viral infections, which represents the first line of defense and a rapid immune response against viral infections [28]. The term models virus killing of free OV by NK cells at a rate .
- Equation (4) models tumor-specific CD8+ T cells related adaptive immune responses. The term models proliferation of CD8+ T cells. Here, a Michaelis–Menten term is used to denote that the anti-tumor immune response is induced by tumor antigens presented on both uninfected and infected tumor cells [15], where is the half-saturation constant and is the proliferation rate of anti-tumor adaptive immune cells. Since anti-tumor immune response is activated by oncolytic viruses to fight tumor cells, the term denotes the rate for which T cells are recruited by immune cells through the interactions with viruses at a rate . This addresses the T cell activation following encounter with the viruses, rather than by encountering with infected cells [29]. is the natural death rate of anti-tumor T cells.
- Equation (5) models tumor-specific CD4+ T cells related adaptive immune responses (e.g., cytokine related immune responses). The evolution of CD4+ T cells takes similar proliferation formation as that of Equation (4) but with different half-saturation constant . Since CD4+ T cells are released mainly by IFN- and anti-CTLA-4 amplifies CD4+ T cell activation [27], the proliferation of CD4+ T is modeled in the form of , where is the proliferation rate of Th cells. The inhibition of CTLA-4 on CD4+ T cells is modeled by the term with a measure of inhibition . Parameter is the apoptosis rate of Th cells.
- Equation (6) models the time evolution of major cytokine IFN-. T cells and NK cells produce several cytokines and chemokines that coordinate various immune responses and are the major source of IFN-. The terms , , and represent that IFN- is activated by both susceptible and infected tumor cells, and secreted by activated CD8+ T [20,30], CD4+ T cells [20,25], and NK cells [31] at a constant rate , , and , respectively. The terms , , and model CTLA-4 engagement that prevents cytokine production and the fact that anti-CTLA-4 therapy results a significant amount of IFN- [25,32]. The parameter is the natural degradation rate of IFN-.
- Equation (7) models soluble proteins CTLA-4. The CTLA-4 molecules are expressed on activated T cells such as effector T cells and regulatory T cells and can out-compete CD28 for binding to B7 and thus dampen the co-stimulatory signals. The CTLA-4 expression rate on a single CD4+ T cell is assumed a constant and is denoted by the parameter . Evidence has shown that CTLA-4 is also expressed on CD8+ T cells [20]. The CTLA-4 expression rate on a single CD8+ T cell is denoted by the parameter . The natural lost rate of CTLA-4 is denoted by . The blockade rate of immune checkpoint CTLA-4 is presented by the parameter u.
- Equation (8) models the virus-specific immune response. The equation describes immune responses to viral infection. The parameter is the virus-specific proliferate rate of anti-viral immune cells which become activated due to debris or viral antigens on infected cells [15]. The natural death rate of anti-viral immune cells is denoted by .
- Equation (9) models natural killer (NK) cells. NK cells are known to be non-specific and attack “non-self” cells, but NK cells can be specific or non-specific during oncolytic virotherapy [17]. There is a pre-existing NK cell population () within the tumor vicinity and is recruited to the TME and mediates initial OV clearance [17]. In this study, we assume activation of NK cells is dependent on the contact with OV infected tumor cells, as experimentally observed in Leung et al. [33]. The second term, , represents the stimulation and recruitment of NK cells. A saturation term is used to describe the limited effects of NK response by infected tumor cells. We also assume that NK cell response is further enhanced by lysis, which induces immunogenic cell death (ICD) of infected tumor cells at the rate until it attains the maximum capacity . Parameter is the recruitment/proliferation of NK cells in response to danger signals (such as DAMPs and PAMPs) released during ICD of OV-infected tumor cells. Parameter represents the half-saturation constant of NK cells that supports the maximum killing of tumor cells by NK cells. Proliferation of NK cells is also stimulated by IFN- [34]. Parameter is used to indicate the saturated effects of immune response, and parameter is the stimulation and recruitment of NK cells by IFN-. The interactions of NK cells with tumor cells can lead to inactivation of NK cells at a constant rate, that is proportional to their interaction term. In fact, denotes the inactivation of NK cells upon their interactions with tumor cells at the rate . Finally, the last term, , denotes the natural death rate of NK cells. The formulation of equation of NK cells is derived from [17,34].
2.2. Parameter Estimation
3. Numerical Simulations
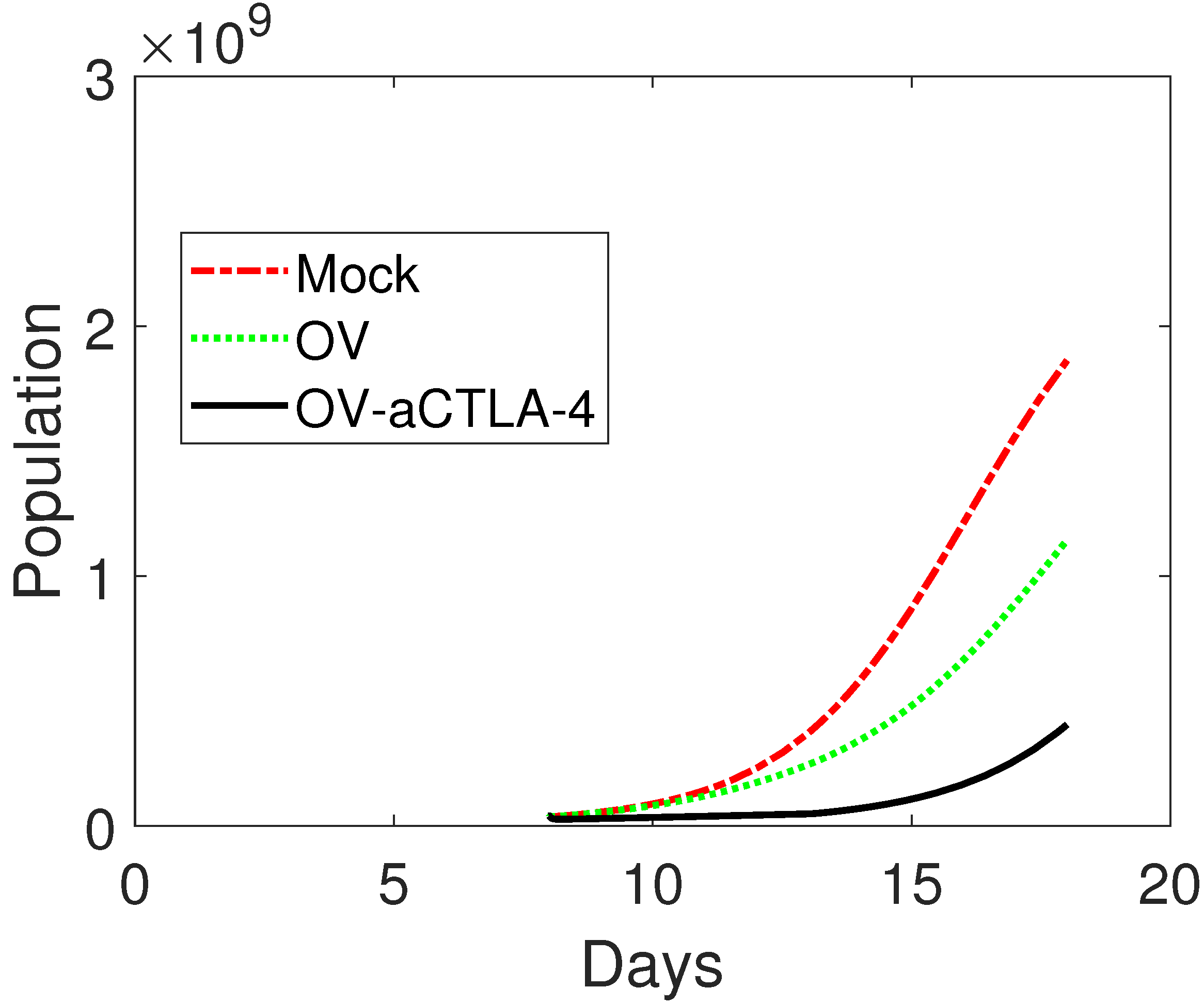
3.1. Model Validation
3.2. Treatment Protocol for Improved Therapeutic Outcomes
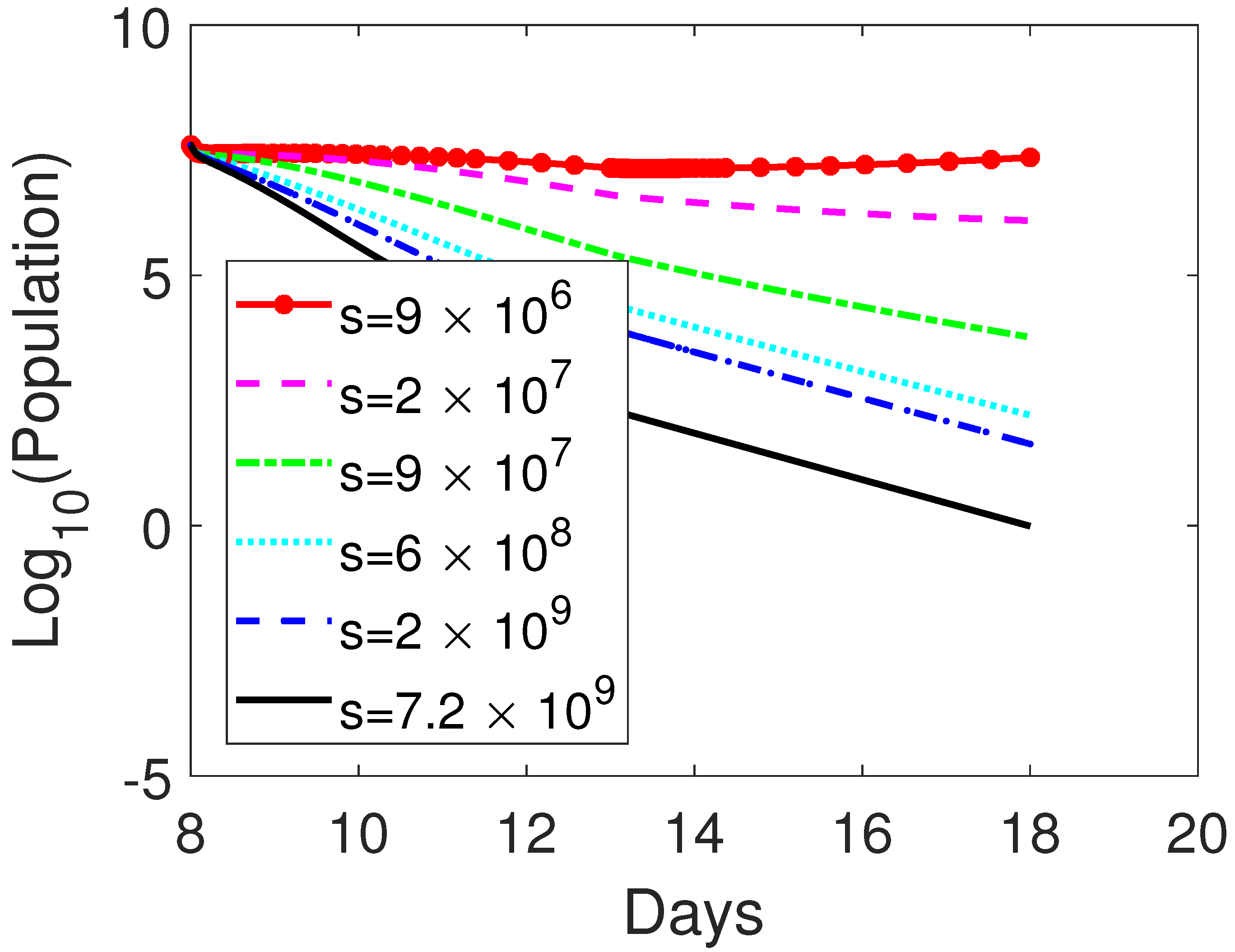
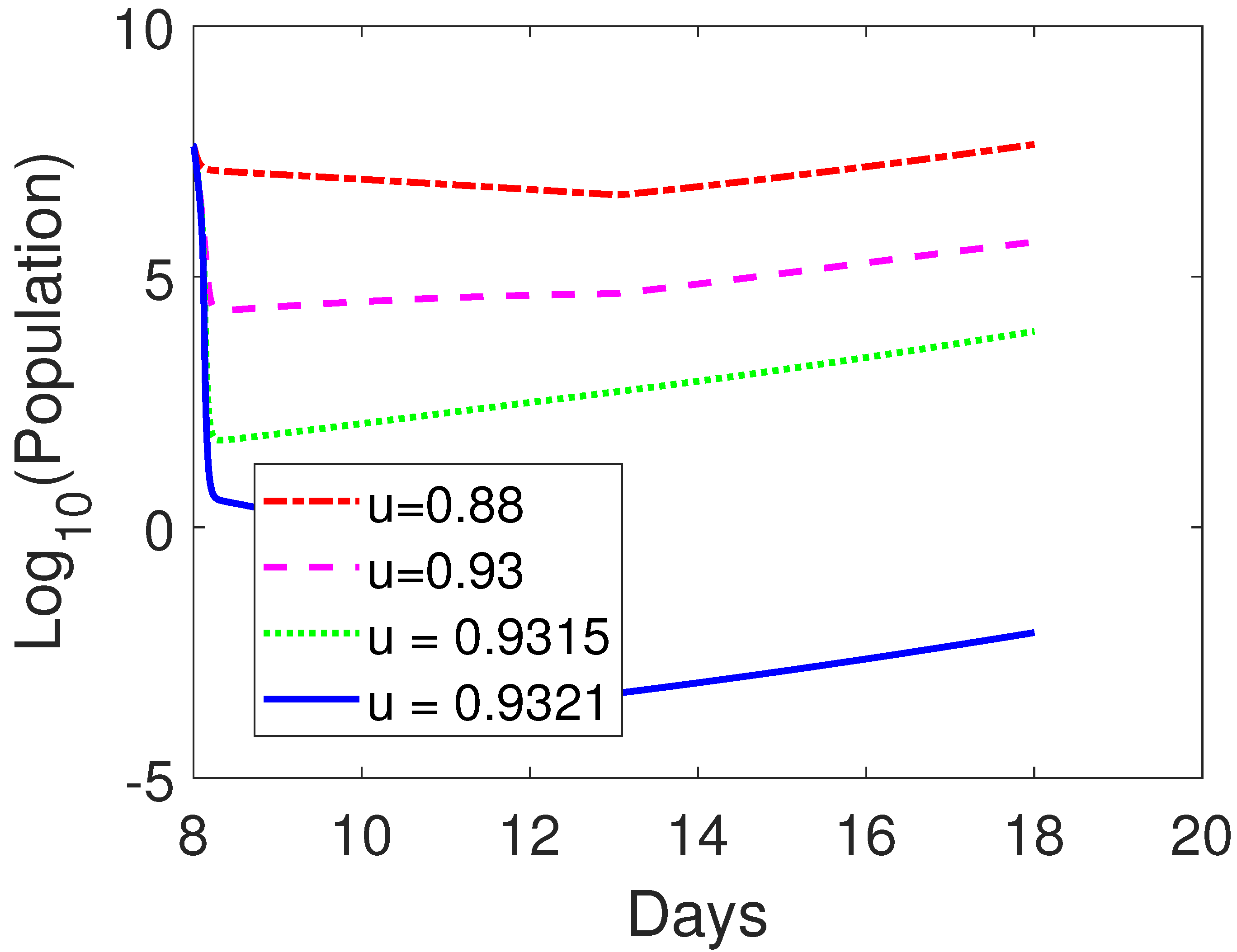
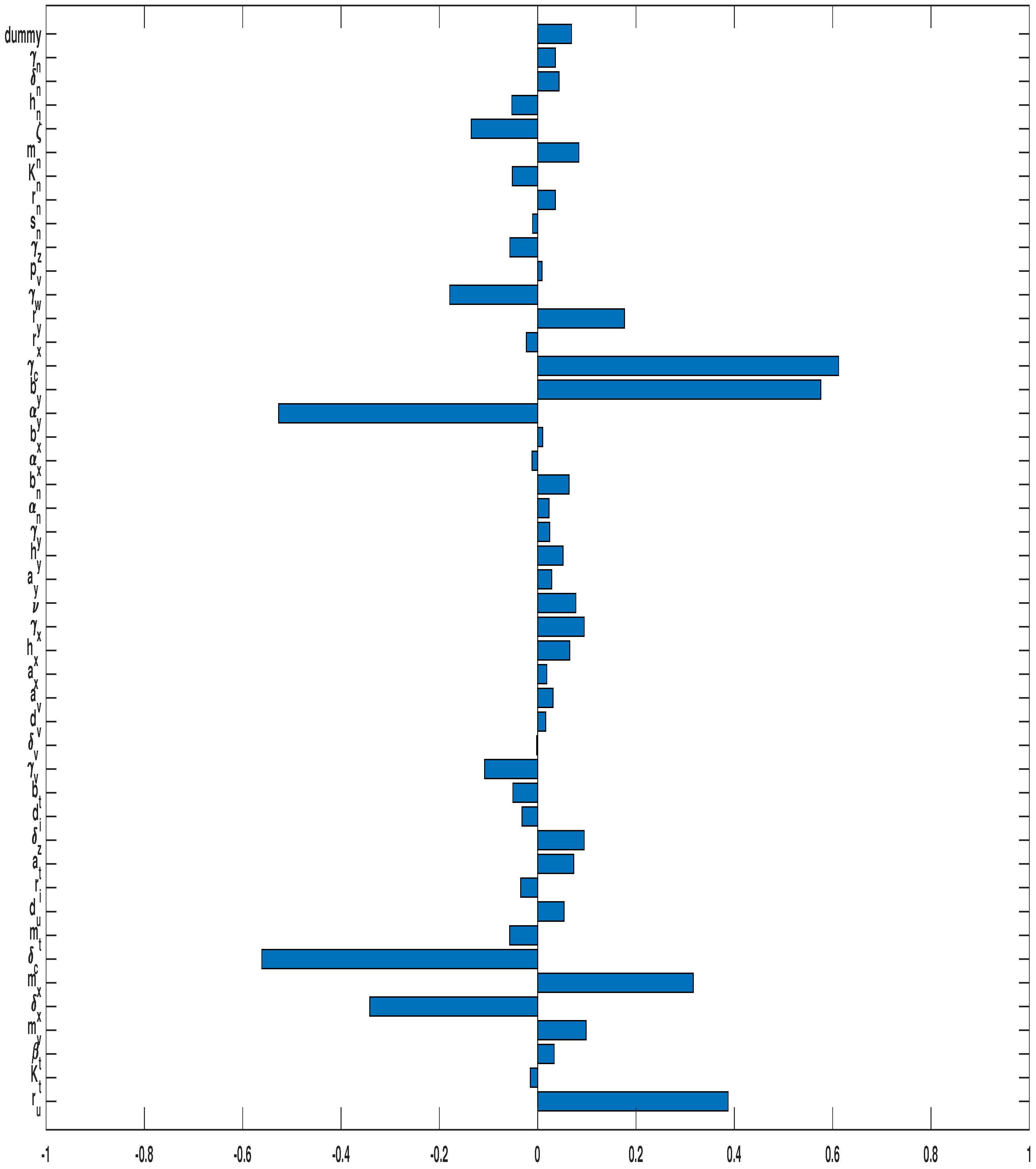
3.3. Parameter Sensitivity Analysis
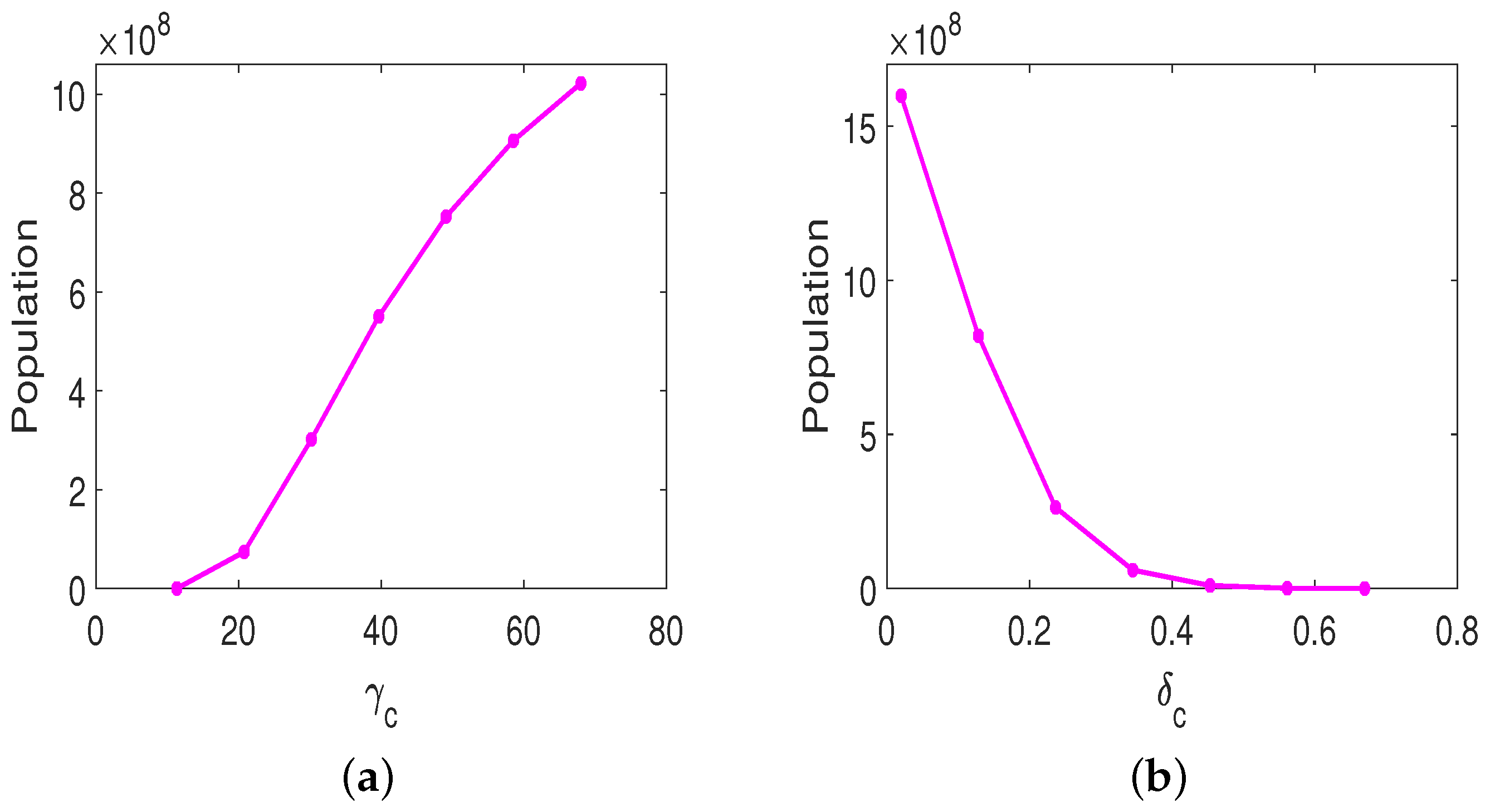
3.3.1. Monotherapy of Oncolytic Virus
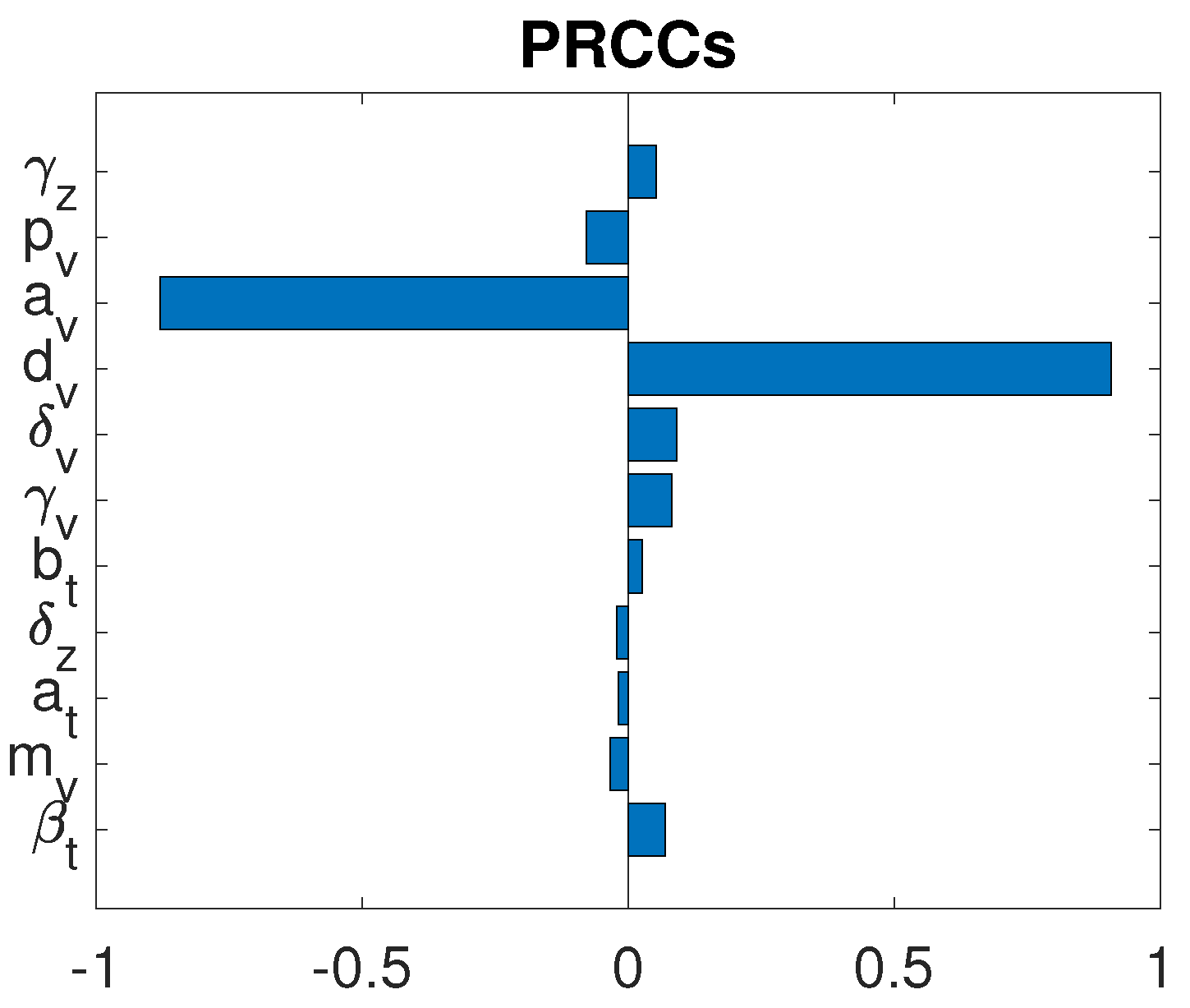
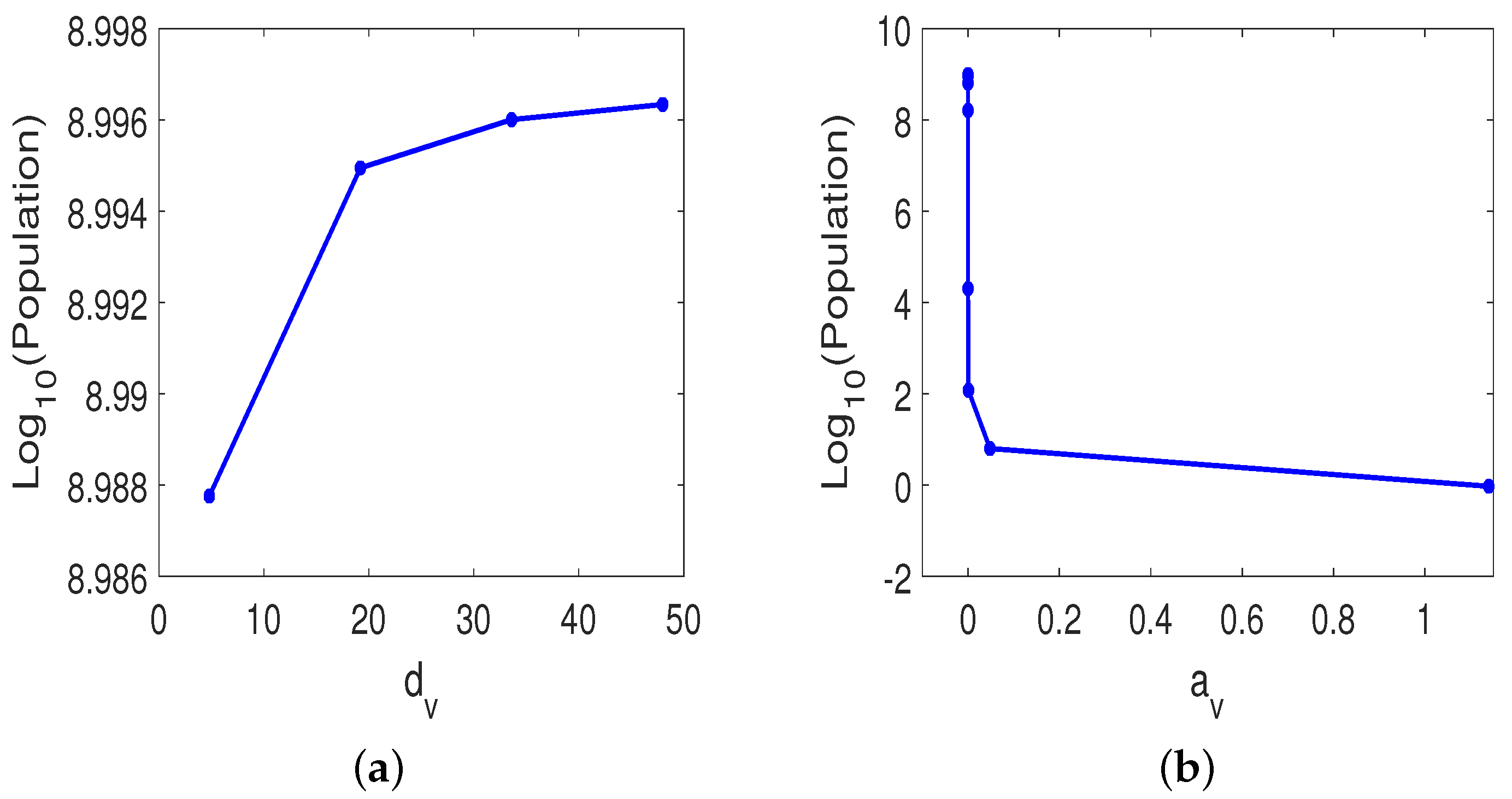
3.3.2. Combined OVT with Anti-CTLA4
4. Discussion
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Appendix A
References
- Aurelian, L. Oncolytic virotherapy: The questions and the promise. Oncolytic Virother. 2013, 2, 19–29. [Google Scholar] [CrossRef]
- Seymour, L.W.; Fisher, K.D. Oncolytic viruses: Finally delivering. Br. J. Cancer 2016, 114, 357–361. [Google Scholar] [CrossRef]
- Chiocca, E.A.; Rabkin, S.D. Oncolytic viruses and their application to cancer immunotherapy. Cancer Immunol. Res. 2014, 2, 295–300. [Google Scholar] [CrossRef]
- Dias, J.D.; Hemminki, O.; Diaconu, I.; Hirvinen, M.; Bonetti, A.; Guse, K. Targeted cancer immunotherapy with oncolytic adenovirus coding for a fully human monoclonal antibody specific for CTLA-4. Gene Ther. 2012, 19, 988–998. [Google Scholar] [CrossRef]
- Engeland, C.E.; Grossardt, C.; Veinalde, R.; Bossow, S.; Lutz, D.; Kaufmann, J.K.; Shevchenko, I.; Umansky, V.; Nettelbeck, D.M.; Weichert, W.; et al. CTLA-4 and PD-L1 Checkpoint Blockade Enhances Oncolytic Measles Virus Therapy. Mol. Ther. 2014, 22, 1949–1959. [Google Scholar] [CrossRef]
- Hemminki, O.; Manuel dos Santos, J.; Hemminki, A. Oncolytic viruses for cancer immunotherapy. J. Hematol. Oncol. 2020, 13, 84. [Google Scholar] [CrossRef]
- Buchbinder, E.I.; Desai, A. CTLA-4 and PD-1 Pathways Similarities, Differences, and Implications of Their Inhibition. Am. J. Clin. Oncol. 2016, 39, 98–106. [Google Scholar] [CrossRef]
- CTLA-4. Available online: https://en.wikipedia.org/wiki/CTLA-4 (accessed on 1 March 2022).
- Ipilimumab. Available online: https://en.wikipedia.org/wiki/Ipilimumab (accessed on 1 March 2022).
- Pollack, A. Approval for Drug That Treats Melanoma. The New York Times, 27 March 2011. [Google Scholar]
- Ribas, A. Tumor immunotherapy directed at PD-1. N. Engl. J. Med. 2012, 366, 2517–2519. [Google Scholar] [CrossRef]
- Tarhini, A.A.; Iqbal, F. CTLA-4 blockade: Therapeutic potential in cancer treatments. Onco Targets Ther. 2010, 3, 15–25. [Google Scholar] [CrossRef]
- Quezada, S.A.; Peggs, K.S. Exploiting CTLA-4, PD-1 and PD-L1 to reactivate the host immune response against cancer. Br. J. Cancer 2013, 108, 1560–1565. [Google Scholar] [CrossRef]
- Shi, T.; Song, X.; Wang, Y.; Liu, F.; Wei, J. Combining Oncolytic Viruses With Cancer Immunotherapy: Establishing a New Generation of Cancer Treatment. Front. Immunol. 2020, 11, 683. [Google Scholar] [CrossRef] [PubMed]
- Mahasa, K.J.; Eladdadi, A.; de Pillis, L.; Ouifki, R. Oncolytic potency and reduced virus tumor specificity in oncolytic virotherapy. A mathematical modelling approach. PLoS ONE 2017, 12, e0184347. [Google Scholar] [CrossRef] [PubMed]
- Eftimie, R.; Dushoff, J.; Bridle, B.W.; Bramson, J.L.; Earn, D.J.D. Multi-stability and multi-instability phenomena in a mathematical model of tumor-immune-virus interactions. Bull. Math. Biol. 2011, 73, 2932–2961. [Google Scholar] [CrossRef] [PubMed]
- Senekal, N.S.; Mahasa, K.J.; Eladdadi, A.; de Pillis, L.; Ouifki, R. Natural Killer Cells Recruitment in Oncolytic Virotherapy: A Mathematical Model. Bull. Math. Biol. 2021, 83, 75. [Google Scholar] [CrossRef]
- Storey, K.M.; Jackson, T.L. An Agent-Based Model of Combination Oncolytic Viral Therapy and Anti-PD-1 Immunotherapy Reveals the Importance of Spatial Location When Treating Glioblastoma. Cancers 2021, 13, 5314. [Google Scholar] [CrossRef]
- Wodarz, D.; Sierro, S.; Klenerman, P. Dynamics of killer T cell inflation in viral infections. J. R. Soc. Interface 2007, 4, 533–543. [Google Scholar] [CrossRef]
- Chan, D.V.; Gibson, H.M.; Aufiero, B.M.; Wilson, A.J.; Hafner, M.S.; Mi, Q.-S.; Wong, H.K. Differential CTLA-4 expression in human CD4+ versus CD8+ T cells is associated with increased NFAT1 and inhibition of CD4+ proliferation. Genes Immun. 2014, 15, 25–32. [Google Scholar] [CrossRef]
- Anderson, L.; Jang, S.; Yu, J.-L. Qualitative behavior of systems of tumor–CD4+–cytokine interactions with treatments. Math. Methods Appl. Sci. 2015, 38, 4330–4344. [Google Scholar] [CrossRef]
- Mattes, J.; Hulett, M.; Xie, W.; Hogan, S.; Rothenberg, M.E.; Foster, P.; Parish, C. Immunotherapy of cytotoxic T cell-resistant tumors by T helper 2 cells: An eotaxin and STAT6-dependent process. J. Exp. Med. 2003, 197, 387–393. [Google Scholar] [CrossRef]
- Perez-Diez, A.; Joncker, N.T.; Choi, K.; William, F.N.C.; Anderson, C.C.; Olivier, L.; Matzinger, P. CD4 cells can be more efficient at tumor rejection than CD8 cells. Blood 2007, 109, 5346–5354. [Google Scholar] [CrossRef]
- Zhang, S.; Bernard, D.; Khan, W.I.; Kaplan, M.H.; Bramson, J.L.; Wan, Y. CD4 T-cell-mediated anti-tumor immunity can be uncoupled from autoimmunity via the STAT4/STAT6 signaling axis. Eur. J. Immunol. 2009, 39, 1252–1259. [Google Scholar] [CrossRef] [PubMed]
- Quezada, S.A.; Simpson, T.R.; Peggs, K.S.; Merghoub, T.; Vider, J.; Fan, X.; Blasberg, R.; Yagita, H.; Muranski, P.; Antony, P.A.; et al. Tumor-reactive CD4(+) T cells develop cytotoxic activity and eradicate large established melanoma after transfer into lymphopenic hosts. J. Exp. Med. 2010, 207, 637–650. [Google Scholar] [CrossRef] [PubMed]
- Macnamara, C.; Eftimie, R. Memory versus effector immune responses in oncolytic virotherapies. J. Theor. Biol. 2015, 377, 1–9. [Google Scholar] [CrossRef] [PubMed]
- Yu, J.-L.; Jang, S.R.-J. A mathematical model of tumor-immune interactions with an immune checkpoint inhibitor. Appl. Math. Comput. 2019, 362, 124523. [Google Scholar] [CrossRef]
- Ma, Y.; Li, X.; Kuang, E. Viral Evasion of Natural Killer Cell Activation. Viruses 2016, 8, 95. [Google Scholar] [CrossRef]
- Storey, K.M.; Sean, E.L.; Jackson, T.L. Modeling Oncolytic Viral Therapy, Immune Checkpoint Inhibition, and the Complex Dynamics of Innate and Adaptive Immunity in Glioblastoma Treatment. Front. Physiol. 2020, 11, 151. [Google Scholar] [CrossRef]
- Mohr, E.; Cunningham, A.F.; Toellner, K.-M.; Bobat, S.; Coughlan, R.E.; Bird, R.A.; MacLennan, I.C.M.; Serre, K. IFN-γ produced by CD8 T cells induces T-bet–dependent and –independent class switching in B cells in responses to alum-precipitated protein vaccine. Proc. Natl. Acad. Sci. USA 2010, 107, 17292–17297. [Google Scholar] [CrossRef]
- Mah, A.Y.; Cooper, M.A. Metabolic Regulation of Natural Killer Cell IFN-γ Production. Crit. Rev. Immunol. 2016, 36, 131–147. [Google Scholar] [CrossRef]
- Hurwitz, A.A.; Sullivan, T.J.; Raymond, R.A.; Allison, J.P. Cytotoxic T lymphocyte antigen-4 (CTLA-4) limits the expansion of encephalitogenic T cells in experimental autoimmune encephalomyelitis (EAE)-resistant BALB/c mice. Proc. Natl. Acad. Sci. USA 2002, 99, 3013–3017. [Google Scholar] [CrossRef]
- Leung, E.Y.; Ennis, D.P.; Kennedy, P.R.; Hansell, C.; Dowson, S.; Farquharson, M.; McNeish, I.A. NK cells augment oncolytic adenovirus cytotoxicity in ovarian cancer. Mol. Ther. Oncolytics 2020, 16, 289–301. [Google Scholar] [CrossRef]
- Li, X.; Xu, J.-X. A mathematical prognosis model for pancreatic cancer patients receiving immunotherapy. J. Theor. Biol. 2016, 406, 42–51. [Google Scholar] [CrossRef] [PubMed]
- Eftimie, R.; Eftimie, G. Tumour-associated macrophages and oncolytic virotherapies: A mathematical investigation into a complex dynamics. Lett. Biomath. 2018, 5, S6–S35. [Google Scholar] [CrossRef]
- Eftimie, R.; Bramson, J.L.; Earn, D.J.D. Modeling anti-tumor Th1 and Th2 immunity in the rejection of melanoma. J. Theor. Biol. 2010, 265, 467–480. [Google Scholar] [CrossRef] [PubMed]
- Bajzer, Z.; Carr, T.; Josić, K.; Russell, S.J.; Dingli, D. Modeling of cancer virotherapy with recombinant measles viruses. J. Theor. Biol. 2008, 252, 109–122. [Google Scholar] [CrossRef] [PubMed]
- Dingli, D.; Offord, C.; Myers, R.; Peng, K.W.; Carr, T.W.; Josic, K.; Bajzer, Z. Dynamics of multiple myeloma tumor therapy with a recombinant measles virus. Cancer Gene Ther. 2009, 16, 873. [Google Scholar] [CrossRef]
- Texeira, L.K.; Fonseca, B.P.F.; Vieira-de-Abreu, A.; Barboza, B.A.; Robbs, B.K.; Bozza, P.T.; Viola, J.P.B. IFN-γ Production by CD8+ T Cells Depends on NFAT1 Transcription Factor and Regulates Th Differentiation. J. Immunol. 2005, 175, 5931–5939. [Google Scholar] [CrossRef]
- Yu, J.-L.; Wei, H.-C.; Jang, S.R.-J. A model of tumor-immune system interactions with healthy cells and immunotherapies. Math. Methods Appl. Sci. 2022, 45, 2852–2870. [Google Scholar] [CrossRef]
- Jaffe, J.B. Characterizing and Modulating the Canine T-Cell Costimulatory Molecules CTLA-4 and CD28. Master’s Thesis, University of Washington, Washington, DC, USA, 2016. [Google Scholar]
- De Pillis, L.G.; Fister, K.R.; Gu, W.; Head, T.; Maples, K.; Neal, T.; Kozai, K. Optimal control of mixed immunotherapy and chemotherapy of tumors. J. Biol. Syst. 2008, 16, 51–80. [Google Scholar] [CrossRef]
- Eftimie, R.; Eftimie, G. Investigating Macrophages Plasticity Following Tumour–Immune Interactions During Oncolytic Therapies. Acta Biotheor. 2019, 67, 321–359. [Google Scholar] [CrossRef]
- Dai, Q.; Rong, M.; Zhang, R. Bifurcations and multistability in a virotherapy model with two time delays. Math. Comput. Simul. 2022, 198, 289–311. [Google Scholar] [CrossRef]
- Komarova, N.L.; Wodarz, D. Targeted Cancer Treatment in Silico: Small Molecule Inhibitors and Oncolytic Viruses (Modeling and Simulation in Science, Engineering and Technology); Birkhäuser: Basel, Switzerland, 2014. [Google Scholar]
- Monte, U.D. Does the cell number 10(9) still really fit one gram of tumor tissue? Cell Cycle 2009, 8, 505–506. [Google Scholar] [CrossRef]
- Marino, S.; Ian, B.; Hogue, I.B.; Christian, J.; Ray, C.J.; Kirschner, D.E. A Methodology For Performing Global Uncertainty In addition, Sensitivity Analysis In Systems Biology. J. Theor. Biol. 2008, 254, 178–196. [Google Scholar] [CrossRef] [PubMed]
- McKay, M.D.; Beckman, R.J.; Conover, W.J. A Comparison of Three Methods for Selecting Values of Input Variables in the Analysis of Output from a Computer Code. Technometrics 1979, 21, 239–245. [Google Scholar] [CrossRef]
- Ben-Shmuel, A.; Biber, G.; Barda-Saad, M. Unleashing natural killer cells in the tumor microenvironment-the next generation of immunotherapy? Front. Immunol. 2020, 11, 275. [Google Scholar] [CrossRef] [PubMed]
- Gesundheit, B.; Ben-David, E.; Posen, Y.; Ellis, R.; Wollmann, G.; Schneider, E.M.; Thaller, A. Effective treatment of glioblastoma multiforme with oncolytic virotherapy: A case-series. Front. Oncol. 2020, 10, 702. [Google Scholar] [CrossRef]
- Kim, Y.; Yoo, J.Y.; Lee, T.J.; Liu, J.; Yu, J.; Caligiuri, M.A.; Friedman, A. Complex role of NK cells in regulation of oncolytic virus-bortezomib therapy. Proc. Natl. Acad. Sci. USA 2018, 115, 4927–4932. [Google Scholar] [CrossRef]
- Schmidt, C. Awaiting a moment of truth for oncolytic viruses. J. Natl. Cancer Inst. 2013, 105, 675–676. [Google Scholar] [CrossRef]
- Glasner, A.; Levi, A.; Enk, J.; Isaacson, B.; Viukov, S.; Orlanski, S.; Melboim, O. NKp46 Receptor-Mediated Interferon-γ Production by Natural Killer Cells Increases Fibronectin 1 to Alter Tumor Architecture and Control Metastasis. Immunity 2018, 48, 107–119.e4. [Google Scholar] [CrossRef]
- Salerno, F.; Guislain, A.; Cansever, D.; Wolkers, M.C. TLR-Mediated Innate Production of IFN-γ by CD8+ T Cells Is Independent of Glycolysis. J. Immunol. 2016, 196, 3695–3705. [Google Scholar] [CrossRef]
- Blank, C.U.; Haining, W.N.; Held, W.; Hogan, P.G.; Kallies, A.; Lugli, E.; Zehn, D. Defining ‘T cell exhaustion’. Nat. Rev. Immunol. 2019, 19, 665–674. [Google Scholar] [CrossRef]


| Variable | Description |
|---|---|
| total number of susceptible (uninfected) tumor cell population | |
| total number of infected tumor cell population | |
| total number of oncolytic virions | |
| total number of anti-tumor immune cells (CD8+ T cells) | |
| total number of anti-tumor immune cells (CD4+ T cells) | |
| concentration of IFN- (pg/mL) | |
| total number of CLTA-4 protein population | |
| total number of anti-viral immune cells | |
| total number of natural killer cells |
| Parameter | Description |
|---|---|
| Uninfected tumor growth rate | |
| Tumor carrying capacity | |
| Infection rate of tumor cells by the oncolytic virus | |
| Half-saturation constant for the tumor cells infection | |
| Tumor killing rate by cytokines | |
| Half-saturation constant for the tumor cells killed by the immune cells and cytokines | |
| Lysis rate of tumor cells (infected and uninfected) by immune cells | |
| Half-saturation constant of cytotoxic killing rate by immune cells | |
| Death rate of infected tumor cells | |
| Lysis rate of the infected tumor cells by virus-specific immune cells | |
| Viral clearance rate | |
| Burst size from infected tumor cells lysed by the oncolytic virus | |
| Virus killing rate by anti-viral immune cells | |
| T cells recruited rate in response to immune cells through interactions with the virus | |
| Anti-tumor adaptive immune cells proliferation rate | |
| Half-saturation constant of tumor cells due to tumor antigens | |
| Death rate of effector cells | |
| The measure of CTLA-4 blocking rate on CD4+ T cells | |
| Half-saturation constant for tumor cell population detected by T cells | |
| Proliferation rate of Th cells | |
| Apoptosis rate of Th cells | |
| IFN- proliferation rate by CD8+ T cells | |
| IFN- proliferation rate by CD4+ T cells | |
| The measure of CTLA-4-mediated inhibition on IFN- produced by NK cells | |
| The measure of CTLA-4-mediated inhibition on IFN- produced by CD8+ T cells | |
| The measure of CTLA-4-mediated inhibition on IFN- produced by CD4+ T cells | |
| Natural degradation rate of tumor-suppressing cytokines | |
| Death rate of CTLA-4 | |
| Proliferation rate of virus-specific immune cells in response to antigens | |
| Decay rate of the anti-viral immune cells | |
| Constant influx of NK cells | |
| Recruitment rate of NK cells via ICD by infected cells | |
| Maximum capacity for NK cell production | |
| Half-saturation constant of infected tumor cells | |
| Stimulation and recruitment rate of NK cells by IFN | |
| Half-saturation constant for NK cell population activated by cytokines | |
| Inactivation rate of NK cells by tumor cells | |
| Decay rate of NK cells | |
| The growth rate of infected tumor cells. | |
| Killing rate of uninfected tumor cells by NK cells | |
| Killing rate of infected tumor cells by NK cells | |
| Killing rate of virions by innate immune cells | |
| IFN- proliferation rate by NK cells | |
| CTLA-4-expressing rate on a single CD8+ T cell | |
| CTLA-4-expressing rate on a single CD4+ T cell |
| Parameter | Baseline | Range | Units | Reference |
|---|---|---|---|---|
| [0.12–1.2] | day | [29,35] | ||
| – | cells | [35,43] | ||
| (cells)(PFU)(day) | [26] | |||
| 1 | 1 | cells | [26] | |
| (cell)(day)(pg/mL) | [36] | |||
| cells | [36] | |||
| 2 | [0.0096–4.8] | day | [26,29] | |
| cells | [26] | |||
| (day)(cells) | [15,17] | |||
| [0.12–1.2] | day | [44] or [45] | ||
| 1 | [0.5–2.6667] | (cell)(day) | [15,16,29] | |
| 1 | [0.0096–4.8] | (cell)(day) | [15] | |
| (day)(cells) | [15,17] | |||
| 1949 | [10–1949] | (PFU)(cell) | [37] | |
| [0.024–24] | (day) | [29,38] | ||
| – | (cell)(day) | [29] | ||
| [0.024–48] | (cell)(day) | [29] | ||
| (PFU)(day) | Estimated | |||
| – | (cell)(day) | [15,29] | ||
| 40 | [40– | cells | [15,29] | |
| day | [26] | |||
| molecule | [27] | |||
| – | (cells)(days)(pg/mL) | [27,29] | ||
| – | cells | [27,29] | ||
| day | [27] | |||
| (pg/mL)(day)(cell)(cell) | Estimated | |||
| molecule | Estimated | |||
| 9 | 9 | (pg/mL)(day)(cell)(cells) | [27,40] | |
| molecule | [27,40] | |||
| 9 | 9 | (pg/mL)(day)(cell)(cell) | [27,40] | |
| molecule | [27,40] | |||
| 34 | 34 | day | [27,40] | |
| 800 | – | (molecules)(day)(cell) | Estimated | |
| 5000 | – | (molecules)(day)(cell) | [27] | |
| day | [27] | |||
| – | day | [15,16] | ||
| day | [15] | |||
| – | (cells)(day) | [17] | ||
| day | [17] | |||
| cells | [17] | |||
| cells | [17,29] | |||
| (cell)(day) | [15,17] | |||
| day | [42] | |||
| (pg/mL) | [34] | |||
| day | [17] |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yu, J.-L.; Jang, S.R.-J.; Liu, K.-Y. Exploring the Interactions of Oncolytic Viral Therapy and Immunotherapy of Anti-CTLA-4 for Malignant Melanoma Mice Model. Cells 2023, 12, 507. https://doi.org/10.3390/cells12030507
Yu J-L, Jang SR-J, Liu K-Y. Exploring the Interactions of Oncolytic Viral Therapy and Immunotherapy of Anti-CTLA-4 for Malignant Melanoma Mice Model. Cells. 2023; 12(3):507. https://doi.org/10.3390/cells12030507
Chicago/Turabian StyleYu, Jui-Ling, Sophia R.-J. Jang, and Kwei-Yan Liu. 2023. "Exploring the Interactions of Oncolytic Viral Therapy and Immunotherapy of Anti-CTLA-4 for Malignant Melanoma Mice Model" Cells 12, no. 3: 507. https://doi.org/10.3390/cells12030507
APA StyleYu, J.-L., Jang, S. R.-J., & Liu, K.-Y. (2023). Exploring the Interactions of Oncolytic Viral Therapy and Immunotherapy of Anti-CTLA-4 for Malignant Melanoma Mice Model. Cells, 12(3), 507. https://doi.org/10.3390/cells12030507







