Optical Tweezers in Studies of Red Blood Cells
Abstract
:1. Introduction
2. Working Principles
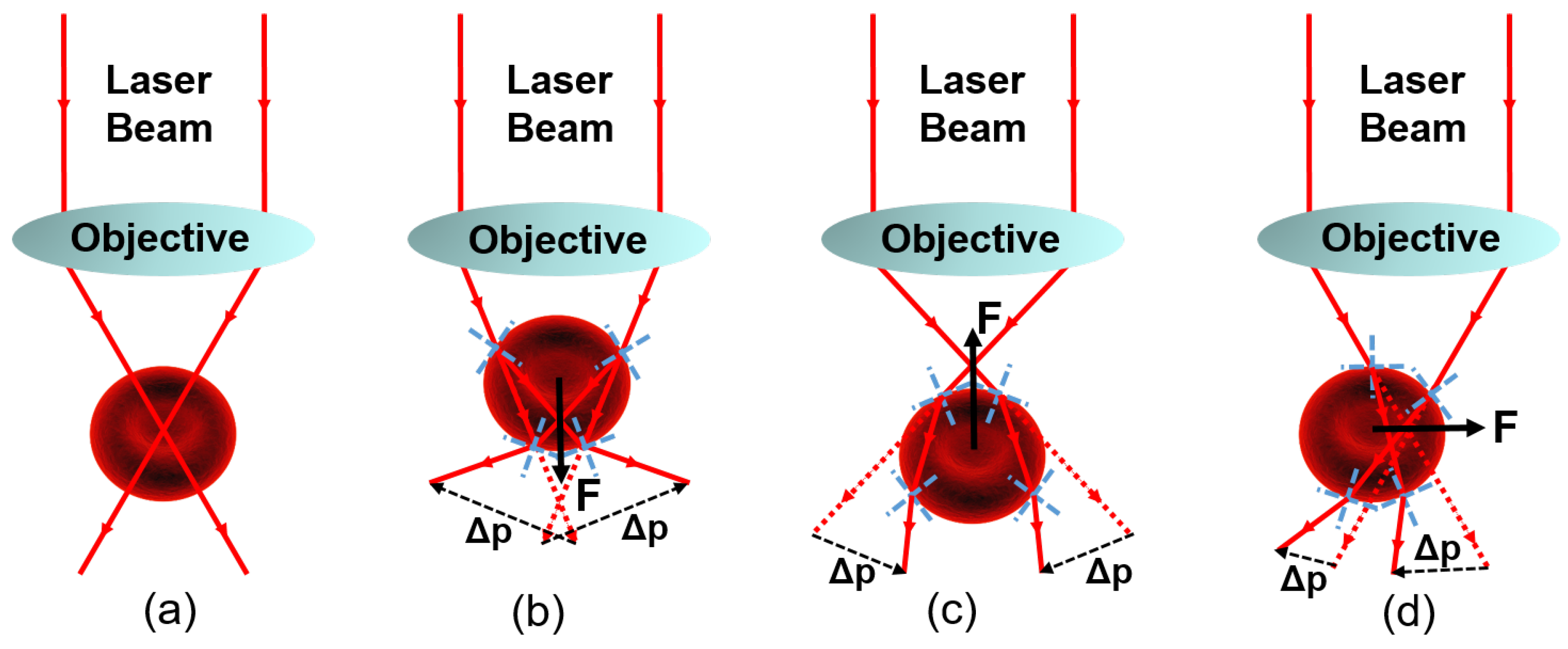
2.1. Physical Interpretation of Optical Trapping
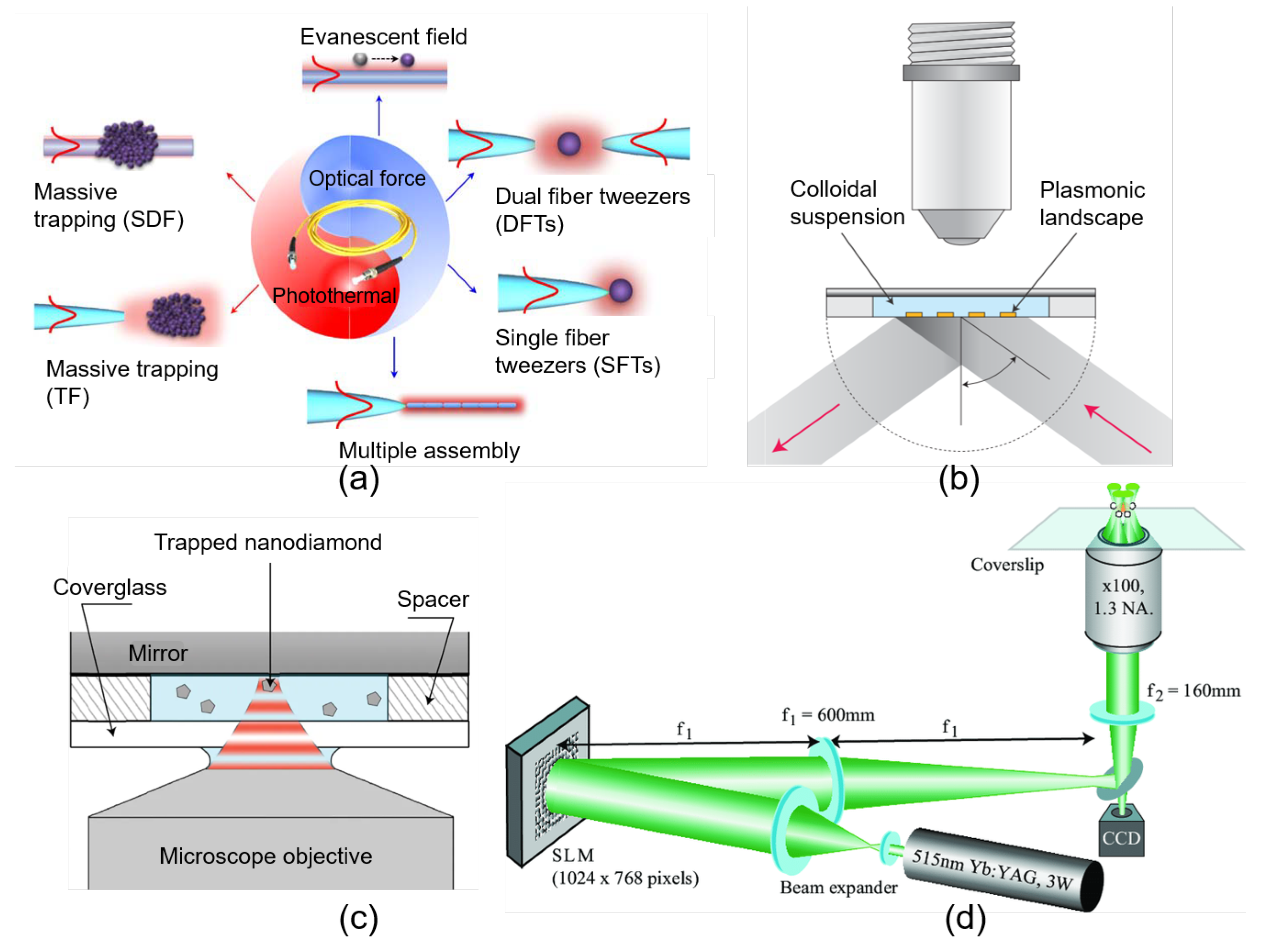
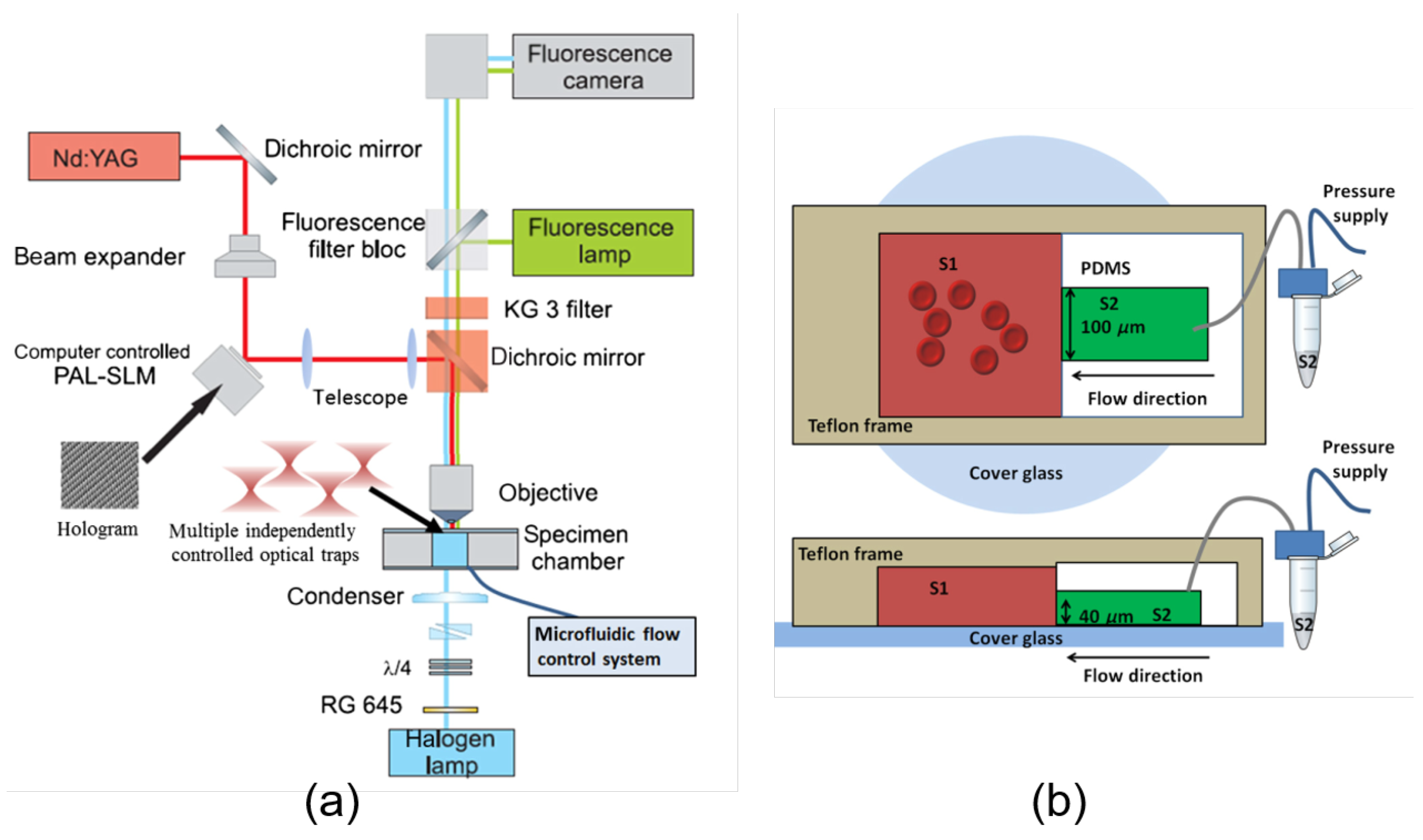
2.2. Implementation
2.3. Trapping Force Calibration
2.4. Thermal and Nonthermal Damage to Biological Objects by Optical Trapping
3. Studies of Human RBCs by OTs
3.1. RBC Preparation and Trapping
3.2. Evaluation of RBCs Developing and Functioning
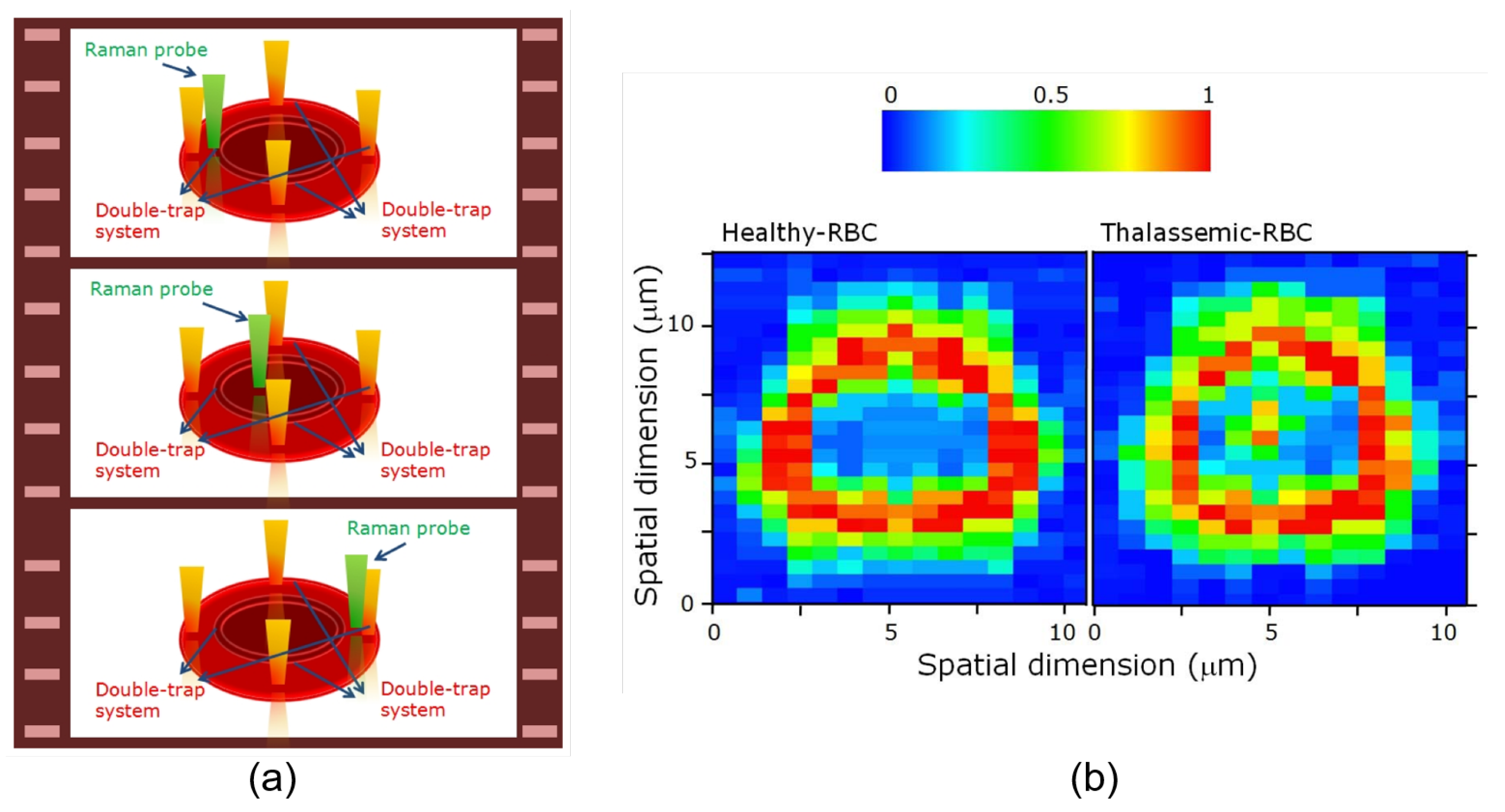
3.2.1. Applications of Raman Tweezers
3.2.2. Applications of Conventional and Polarized OTs
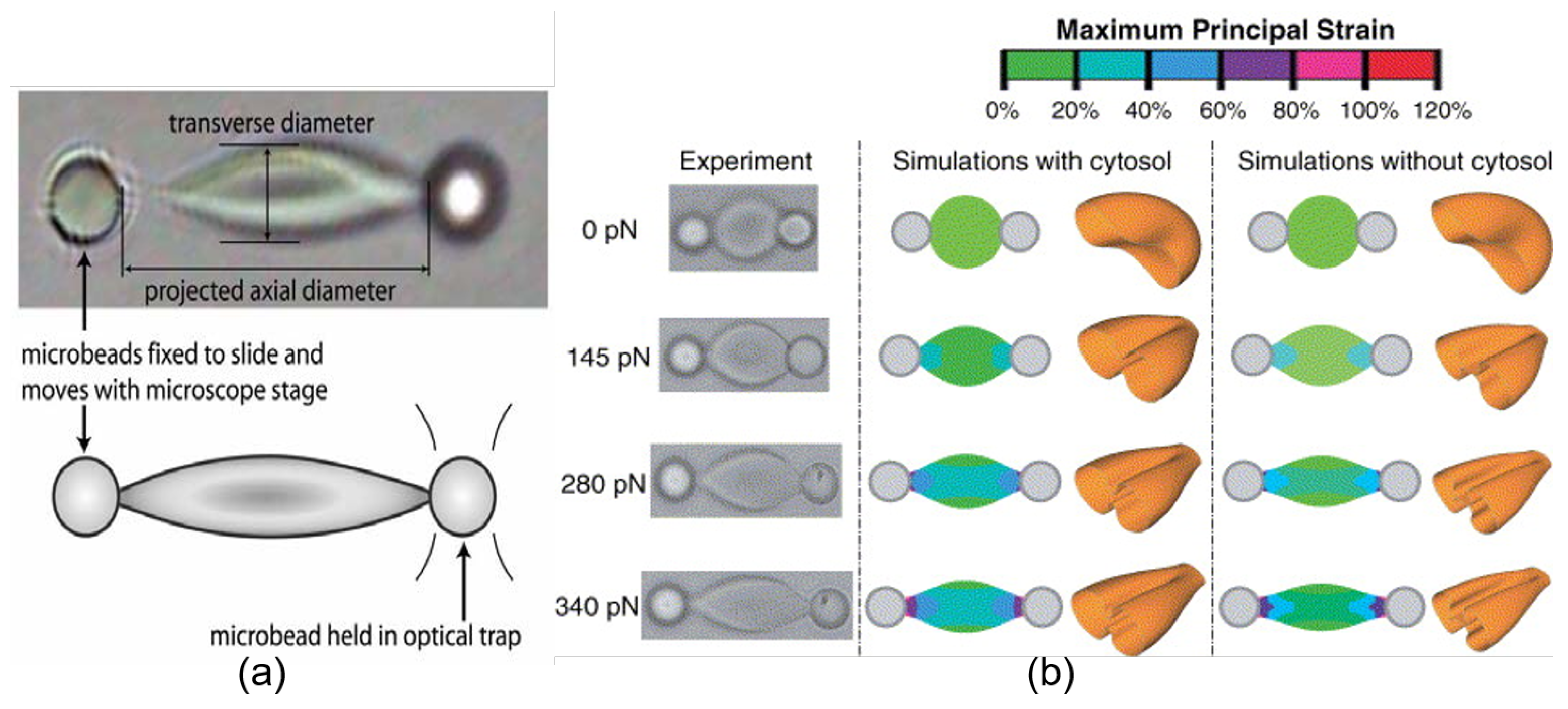
3.3. Evaluation of RBC Membrane Deformation
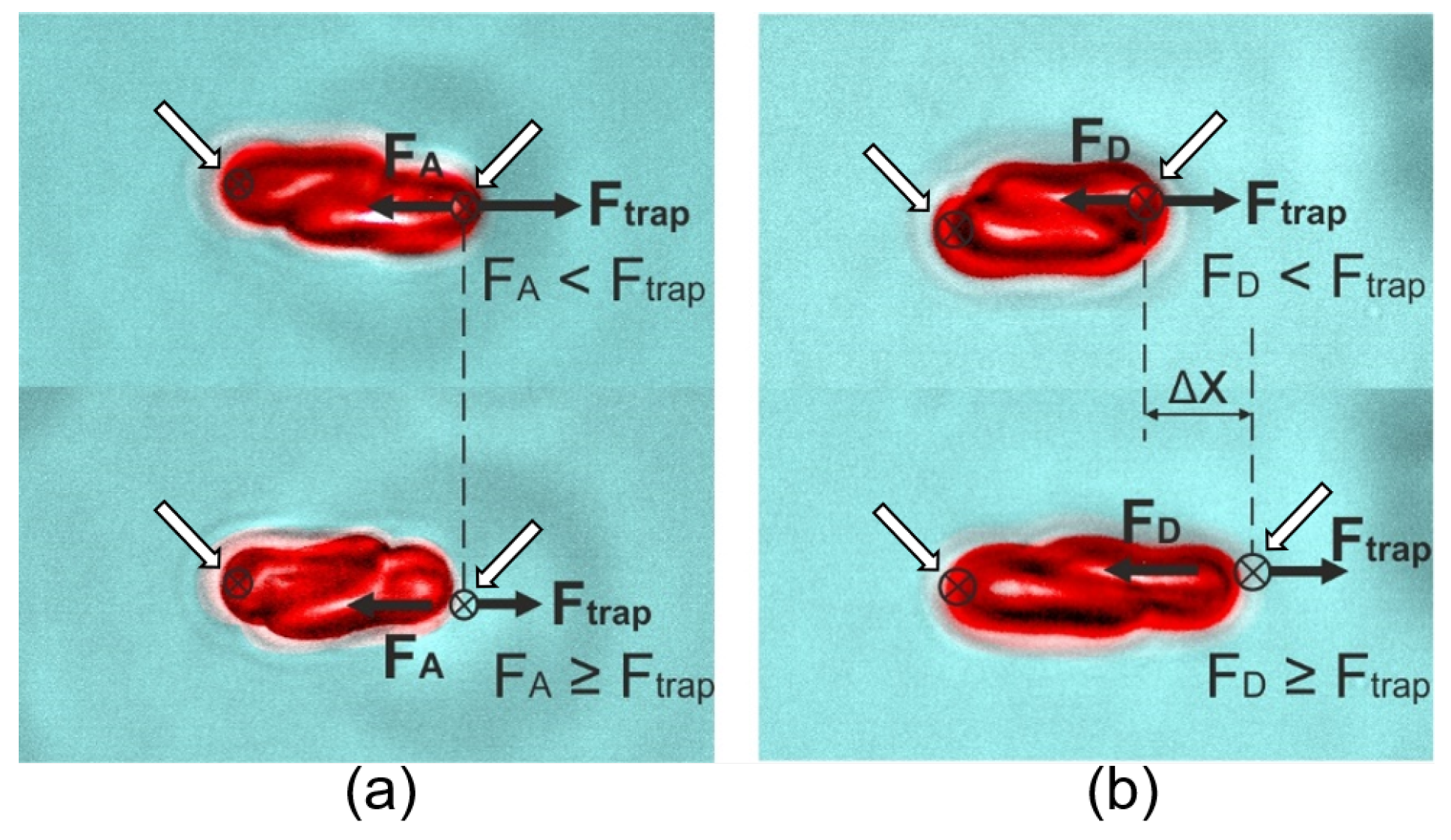
3.4. Evaluation of Dynamic Cell-Cell Interaction between RBCs
4. Evaluation of RBCs Electrical Properties
5. Cell Trapping and Manipulation In Vivo
6. Conclusions and Prospects
Author Contributions
Funding
Conflicts of Interest
References
- Ashkin, A. Acceleration and trapping of particles by radiation pressure. Phys. Rev. Lett. 1970, 24, 156. [Google Scholar] [CrossRef] [Green Version]
- Polimeno, P.; Magazzù, A.; Iatì, M.; Patti, F.; Saija, R.; Esposti Boschi, C.; Donato, M.; Gucciardi, P.; Jones, P.; Volpe, G.; et al. Optical tweezers and their applications. J. Quant. Spectrosc. Radiat. Transf. 2018, 218, 131–150. [Google Scholar] [CrossRef] [Green Version]
- Gao, D.; Ding, W.; Nieto-Vesperinas, M.; Ding, X.; Rahman, M.; Zhang, T.; Lim, C.; Qiu, C.W. Optical manipulation from the microscale to the nanoscale: Fundamentals, advances and prospects. Light Sci. Appl. 2017, 6, e17039. [Google Scholar] [CrossRef] [PubMed]
- Capitanio, M.; Pavone, F. Interrogating biology with force: Single molecule high-resolution measurements with optical tweezers. Biophys. J. 2013, 105, 1293–1303. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Ashkin, A. History of optical trapping and manipulation of small-neutral particle, atoms, and molecules. IEEE J. Sel. Top. Quantum Electron. 2000, 6, 841–856. [Google Scholar] [CrossRef]
- Ashkin, A.; Dziedzic, J.; Bjorkholm, J.; Chu, S. Observation of a single-beam gradient force optical trap for dielectric particles. Opt. Lett. 1986, 11, 288–290. [Google Scholar] [CrossRef] [Green Version]
- Ashkin, A.; Dziedzic, J. Optical trapping and manipulation of viruses and bacteria. Science 1987, 235, 1517–1520. [Google Scholar] [CrossRef]
- Pool, R. Trapping with optical tweezers. Science 1988, 241, 1042–1043. [Google Scholar] [CrossRef]
- Ashkin, A.; Dziedzic, J. Internal cell manipulation using infrared laser traps. Proc. Natl. Acad. Sci. USA 1989, 86, 7914–7918. [Google Scholar] [CrossRef] [Green Version]
- Block, S.; Goldstein, L.; Schnapp, B. Bead movement by single kinesin molecules studied with optical tweezers. Nature 1990, 348, 348. [Google Scholar] [CrossRef]
- Steubing, R.; Cheng, S.; Wright, W.; Numajiri, Y.; Berns, M. Laser induced cell fusion in combination with optical tweezers: The laser cell fusion trap. Cytometry 1991, 12, 505–510. [Google Scholar] [CrossRef] [PubMed]
- Wang, M.; Yin, H.; Landick, R.; Gelles, J.; Block, S. Stretching DNA with optical tweezers. Biophys. J. 1997, 72, 1335–1346. [Google Scholar] [CrossRef] [Green Version]
- Curtis, J.; Koss, B.; Grier, D. Dynamic holographic optical tweezers. Opt. Commun. 2002, 207, 169–175. [Google Scholar] [CrossRef]
- Liu, Y.; Cheng, D.; Sonek, G.; Berns, M.; Chapman, C.; Tromberg, B. Evidence for localized cell heating induced by infrared optical tweezers. Biophys. J. 1995, 68, 2137–2144. [Google Scholar] [CrossRef] [Green Version]
- Liu, Y.; Sonek, G.; Berns, M.; Tromberg, B. Physiological monitoring of optically trapped cells: Assessing the effects of confinement by 1064-nm laser tweezers using microfluorometry. Biophys. J. 1996, 71, 2158–2167. [Google Scholar] [CrossRef] [Green Version]
- Blázquez-Castro, A. Optical tweezers: Phototoxicity and thermal stress in cells and biomolecules. Micromachines 2019, 10, 507. [Google Scholar] [CrossRef] [Green Version]
- Kuo, S.; Sheetz, M. Optical tweezers in cell biology. Trends Cell Biol. 1992, 2, 116–118. [Google Scholar] [CrossRef]
- Svoboda, K.; Block, S. Biological applications of optical forces. Annu. Rev. Biophys. Biomol. Struct. 1994, 23, 247–285. [Google Scholar] [CrossRef]
- Mehta, A.; Rief, M.; Spudich, J.; Smith, D.; Simmons, R. Single-molecule biomechanics with optical methods. Science 1999, 283, 1689–1695. [Google Scholar] [CrossRef] [Green Version]
- Dholakia, K.; Spalding, G.; MacDonald, M. Optical tweezers: The next generation. Phys. World 2002, 15, 31. [Google Scholar] [CrossRef]
- Grier, D. A revolution in optical manipulation. Nature 2003, 424, 810. [Google Scholar] [CrossRef] [PubMed]
- MacDonald, M.; Spalding, G.; Dholakia, K. Microfluidic sorting in an optical lattice. Nature 2003, 426, 421. [Google Scholar] [CrossRef] [PubMed]
- Ericsson, M.; Hanstorp, D.; Hagberg, P.; Enger, J.; Nystrom, T. Sorting out bacterial viability with optical tweezers. J. Bacteriol. 2000, 182, 5551–5555. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Agayan, R.; Gittes, F.; Kopelman, R.; Schmidt, C. Optical trapping near resonance absorption. Appl. Opt. 2002, 41, 2318–2327. [Google Scholar] [CrossRef]
- Preece, D.; Warren, R.; Evans, R.; Gibson, G.; Padgett, M.; Cooper, J.; Tassieri, M. Optical tweezers: Wideband microrheology. J. Opt. 2011, 13, 044022. [Google Scholar] [CrossRef] [Green Version]
- Ashok, P.; Dholakia, K. Optical trapping for analytical biotechnology. Curr. Opin. Biotechnol. 2012, 23, 16–21. [Google Scholar] [CrossRef]
- Nussenzveig, H. Cell membrane biophysics with optical tweezers. Eur. Biophys. J. 2018, 47, 499–514. [Google Scholar] [CrossRef]
- Greulich, K. Selected applications of laser scissors and tweezers and new applications in heart research. Methods Cell Biol. 2007, 82, 59–80. [Google Scholar]
- Johansen, P.; Fenaroli, F.; Evensen, L.; Griffiths, G.; Koster, G. Optical micromanipulation of nanoparticles and cells inside living zebrafish. Nat. Commun. 2016, 7, 10974. [Google Scholar] [CrossRef] [Green Version]
- Favre-Bulle, I.; Stilgoe, A.; Scott, E. Optical trapping in vivo: Theory, practice, and applications. Nanophotonics 2019, 8, 1023–1040. [Google Scholar] [CrossRef] [Green Version]
- Guo, F.; French, J.; Li, P.; Zhao, H.; Chan, C.; Fick, J.; Benkovic, S.; Huang, T. Probing cell–cell communication with microfluidic devices. Lab Chip 2013, 13, 3152–3162. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Moffitt, J.; Chemla, Y.; Smith, S.; Bustamante, C. Recent advances in optical tweezers. Annu. Rev. Biochem. 2008, 77, 205–228. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Zhang, H.; Liu, K. Optical tweezers for single cells. J. R. Soc. Interface 2008, 5, 671–690. [Google Scholar] [CrossRef] [Green Version]
- Bunea, A.; Glückstad, J. Strategies for optical trapping in biological samples: Aiming at microrobotic surgeons. Laser Photon. Rev. 2019, 13, 1800227. [Google Scholar] [CrossRef] [Green Version]
- Tassieri, M.; Evans, R.; Warren, R.; Bailey, N.; Cooper, J. Microrheology with optical tweezers: Data analysis. New J. Phys. 2012, 14, 115032. [Google Scholar] [CrossRef]
- Neuman, K.; Nagy, A. Single-molecule force spectroscopy: Optical tweezers, magnetic tweezers and atomic force microscopy. Nat. Methods 2008, 5, 491. [Google Scholar] [CrossRef]
- Fazal, F.; Block, S. Optical tweezers study life under tension. Nat. Photonics 2011, 5, 318. [Google Scholar] [CrossRef]
- Maragò, O.; Jones, P.; Gucciardi, P.; Volpe, G.; Ferrari, A. Optical trapping and manipulation of nanostructures. Nat. Nanotechnol. 2013, 8, 807. [Google Scholar] [CrossRef] [Green Version]
- Čižmár, T.; Romero, L.; Dholakia, K.; Andrews, D. Multiple optical trapping and binding: New routes to self-assembly. J. Phys. B At. Mol. Opt. Phys. 2010, 43, 102001. [Google Scholar] [CrossRef]
- Bowman, R.; Padgett, M. Optical trapping and binding. Rep. Prog. Phys. 2013, 76, 026401. [Google Scholar] [CrossRef]
- Adamo, L.; Naveiras, O.; Wenzel, P.; McKinney-Freeman, S.; Mack, P.; Gracia-Sancho, J.; Suchy-Dicey, A.; Yoshimoto, M.; Lensch, M.; Yoder, M.; et al. Biomechanical forces promote embryonic haematopoiesis. Nature 2009, 459, 1131. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Nieminen, T.; Knöner, G.; Heckenberg, N.; Rubinsztein-Dunlop, H. Physics of optical tweezers. Methods Cell Biol. 2007, 82, 207–236. [Google Scholar] [PubMed]
- Ashkin, A.; Dziedzic, J. Optical trapping and manipulation of single living cells using infra-red laser beams. Berichte der Bunsengesellschaft für physikalische Chemie 1989, 93, 254–260. [Google Scholar] [CrossRef]
- Ashkin, A. Forces of a single-beam gradient laser trap on a dielectric sphere in the ray optics regime. Biophys. J. 1992, 61, 569–582. [Google Scholar] [CrossRef] [Green Version]
- Harada, Y.; Asakura, T. Radiation forces on a dielectric sphere in the Rayleigh scattering regime. Opt. Commun. 1996, 124, 529–541. [Google Scholar] [CrossRef]
- Cox, A.; DeWeerd, A.; Linden, J. An experiment to measure Mie and Rayleigh total scattering cross sections. Am. J. Phys. 2002, 70, 620–625. [Google Scholar] [CrossRef]
- Nieminen, T.; du Preez-Wilkinson, N.; Stilgoe, A.; Loke, V.; Bui, A.; Rubinsztein-Dunlop, H. Optical tweezers: Theory and modelling. J. Quant. Spectrosc. Radiat. Transf. 2014, 146, 59–80. [Google Scholar] [CrossRef]
- Du, J.; Yuen, C.H.; Li, X.; Ding, K.; Du, G.; Lin, Z.; Chan, C.; Ng, J. Tailoring optical gradient force and optical scattering and absorption force. Sci. Rep. 2017, 7, 18042. [Google Scholar] [CrossRef] [Green Version]
- Patti, F.; Saija, R.; Denti, P.; Pellegrini, G.; Biagioni, P.; Iatì, M.; Maragò, O. Chiral optical tweezers for optically active particles in the T-matrix formalism. Sci. Rep. 2019, 9, 29. [Google Scholar] [CrossRef] [Green Version]
- Visscher, K.; Gross, S.; Block, S. Construction of multiple-beam optical traps with nanometer-resolution position sensing. IEEE J. Sel. Top. Quantum Electron. 1996, 2, 1066–1076. [Google Scholar] [CrossRef] [Green Version]
- Dufresne, E.; Grier, D. Optical tweezer arrays and optical substrates created with diffractive optics. Rev. Sci. Instrum. 1998, 69, 1974–1977. [Google Scholar] [CrossRef]
- Constable, A.; Kim, J.; Mervis, J.; Zarinetchi, F.; Prentiss, M. Demonstration of a fiber-optical light-force trap. Opt. Lett. 1993, 18, 1867–1869. [Google Scholar] [CrossRef] [PubMed]
- Juan, M.; Righini, M.; Quidant, R. Plasmon nano-optical tweezers. Nat. Photonics 2011, 5, 349. [Google Scholar] [CrossRef]
- Juan, M.; Bradac, C.; Besga, B.; Johnsson, M.; Brennen, G.; Molina-Terriza, G.; Volz, T. Cooperatively enhanced dipole forces from artificial atoms in trapped nanodiamonds. Nat. Phys. 2017, 13, 241. [Google Scholar] [CrossRef] [Green Version]
- Whyte, G.; Gibson, G.; Leach, J.; Padgett, M.; Robert, D.; Miles, M. An optical trapped microhand for manipulating micron-sized objects. Opt. Express 2006, 14, 12497–12502. [Google Scholar] [CrossRef] [PubMed]
- Chiou, A.; Wang, W.; Sonek, G.; Hong, J.; Berns, M. Interferometric optical tweezers. Opt. Commun. 1997, 133, 7–10. [Google Scholar] [CrossRef] [Green Version]
- Casaburi, A.; Pesce, G.; Zemánek, P.; Sasso, A. Two-and three-beam interferometric optical tweezers. Opt. Commun. 2005, 251, 393–404. [Google Scholar] [CrossRef]
- Demergis, V.; Florin, E.L. High precision and continuous optical transport using a standing wave optical line trap. Opt. Express 2011, 19, 20833–20848. [Google Scholar] [CrossRef] [Green Version]
- Kotsifaki, D.; Kandyla, M.; Lagoudakis, P. Plasmon enhanced optical tweezers with gold-coated black silicon. Sci. Rep. 2016, 6, 26275. [Google Scholar] [CrossRef]
- Huang, J.; Yang, Y. Origin and future of plasmonic optical tweezers. Nanomaterials 2015, 5, 1048–1065. [Google Scholar] [CrossRef] [Green Version]
- Afanasiev, K.; Korobtsov, A.; Kotova, S.; Losevsky, N.; Mayorova, A.; Patlan, V.; Volostnikov, V. Further development of the laser tweezers technique for biomedical applications. J. Phys. Conf. Ser. 2013, 414, 012017. [Google Scholar] [CrossRef]
- Korda, P.; Spalding, G.; Dufresne, E.; Grier, D. Nanofabrication with holographic optical tweezers. Rev. Sci. Instrum. 2002, 73, 1956–1957. [Google Scholar] [CrossRef] [Green Version]
- Bhebhe, N.; Williams, P.; Rosales-Guzmán, C.; Rodriguez-Fajardo, V.; Forbes, A. A vector holographic optical trap. Sci. Rep. 2018, 8, 1–9. [Google Scholar] [CrossRef] [PubMed]
- Grier, D.; Roichman, Y. Holographic optical trapping. Appl. Opt. 2006, 45, 880–887. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Arlt, J.; Garcés-Chávez, V.; Sibbett, W.; Dholakia, K. Optical micromanipulation using a Bessel light beam. Opt. Commun. 2001, 197, 239–245. [Google Scholar] [CrossRef]
- Simpson, N.; Dholakia, K.; Allen, L.; Padgett, M. Mechanical equivalence of spin and orbital angular momentum of light: An optical spanner. Opt. Lett. 1997, 22, 52–54. [Google Scholar] [CrossRef]
- Abramochkin, E.G.; Kotova, S.P.; Korobtsov, A.V.; Losevsky, N.N.; Mayorova, A.M.; Rakhmatulin, M.A.; Volostnikov, V.G. Microobject manipulations using laser beams with nonzero orbital angular momentum. Laser Phys. 2006, 16, 842–848. [Google Scholar] [CrossRef]
- Curtis, J.; Grier, D. Structure of optical vortices. Phys. Rev. Lett. 2003, 90, 133901. [Google Scholar] [CrossRef] [Green Version]
- Padgett, M.; Bowman, R. Tweezers with a twist. Nat. Photonics 2011, 5, 343. [Google Scholar] [CrossRef]
- Smith, S.; Bhalotra, S.; Brody, A.; Brown, B.; Boyda, E.; Prentiss, M. Inexpensive optical tweezers for undergraduate laboratories. Am. J. Phys. 1999, 67, 26–35. [Google Scholar] [CrossRef] [Green Version]
- Bechhoefer, J.; Wilson, S. Faster, cheaper, safer optical tweezers for the undergraduate laboratory. Am. J. Phys. 2002, 70, 393–400. [Google Scholar] [CrossRef]
- Pesce, G.; Volpe, G.; Maragó, O.; Jones, P.; Gigan, S.; Sasso, A.; Volpe, G. Step-by-step guide to the realization of advanced optical tweezers. JOSA B 2015, 32, B84–B98. [Google Scholar] [CrossRef] [Green Version]
- Zhu, R.; Avsievich, T.; Popov, A.; Meglinski, I. Influence of interaction time on the red blood cell (dis) aggregation dynamics in vitro studied by optical tweezers. In European Conference on Biomedical Optics; Optical Society of America: Washington, DC, USA, 2019; p. 11075_12. [Google Scholar]
- Xin, H.; Li, B. Fiber-based optical trapping and manipulation. Front. Optoelectron. 2019, 12, 97–110. [Google Scholar] [CrossRef]
- Simmons, R.; Finer, J.; Chu, S. Quantitative measurements of force and displacement using an optical trap. Biophys. J. 1996, 70, 1813–1822. [Google Scholar] [CrossRef] [Green Version]
- Tolić-Nørrelykke, S.; Schäffer, E.; Howard, J.; Pavone, F.; Jülicher, F.; Flyvbjerg, H. Calibration of optical tweezers with positional detection in the back focal plane. Rev. Sci. Instrum. 2006, 77, 103101. [Google Scholar] [CrossRef] [Green Version]
- Berg-Sørensen, K.; Flyvbjerg, H. Power spectrum analysis for optical tweezers. Rev. Sci. Instrum. 2004, 75, 594–612. [Google Scholar] [CrossRef] [Green Version]
- Lee, K.; Wagner, C.; Priezzhev, A.V. Assessment of the “cross-bridge“-induced interaction of red blood cells by optical trapping combined with microfluidics. J. Biomed. Opt. 2017, 22, 091516. [Google Scholar] [CrossRef]
- Bui, A.; Kashchuk, A.V.; Balanant, M.; Nieminen, T.; Rubinsztein-Dunlop, H.; Stilgoe, A. Calibration of force detection for arbitrarily shaped particles in optical tweezers. Sci. Rep. 2018, 8, 10798. [Google Scholar] [CrossRef] [Green Version]
- Nieminen, T.; Rubinsztein-Dunlop, H.; Heckenberg, N. Calculation and optical measurement of laser trapping forces on non-spherical particles. J. Quant. Spectrosc. Radiat. Transf. 2001, 70, 627–637. [Google Scholar] [CrossRef] [Green Version]
- Peterman, E.; Gittes, F.; Schmidt, C. Laser-induced heating in optical traps. Biophys. J. 2003, 84, 1308–1316. [Google Scholar] [CrossRef] [Green Version]
- Kumari, P.; Dharmadhikari, J.; Dharmadhikari, A.; Basu, H.; Sharma, S.; Mathur, D. Optical trapping in an absorbing medium: From optical tweezing to thermal tweezing. Opt. Express 2012, 20, 4645–4652. [Google Scholar] [CrossRef] [PubMed]
- Berns, M. Optical tweezers: Tethers, wavelengths, and heat. Methods Cell Biol. 2007, 82, 455–466. [Google Scholar]
- Maklygin, A.; Priezzhev, A.; Karmenian, A.; Nikitin, S.; Obolenskii, I.; Lugovtsov, A.; Li, K. Measurement of interaction forces between red blood cells in aggregates by optical tweezers. Quantum Electron. 2012, 42, 500. [Google Scholar] [CrossRef]
- Wurlitzer, S.; Lautz, C.; Liley, M.; Duschl, C.; Fischer, T. Micromanipulation of Langmuir-monolayers with optical tweezers. J. Phys. Chem. B 2001, 105, 182–187. [Google Scholar] [CrossRef]
- Schönle, A.; Hell, S.W. Heating by absorption in the focus of an objective lens. Opt. Lett. 1998, 23, 325–327. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- König, K.; Tadir, Y.; Patrizio, P.; Berns, M.; Tromberg, B. Andrology: Effects of ultraviolet exposure and near infrared laser tweezers on human spermatozoa. Hum. Reprod. 1996, 11, 2162–2164. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Ahlawat, S.; Kumar, N.; Dasgupta, R.; Shanker Verma, R.; Uppal, A.; Kumar Gupta, P. Raman spectroscopic investigations on optical trap induced deoxygenation of red blood cells. Appl. Phys. Lett. 2013, 103, 183704. [Google Scholar] [CrossRef]
- Chowdhury, A.; Waghmare, D.; Dasgupta, R.; Majumder, S. Red blood cell membrane damage by light-induced thermal gradient under optical trap. J. Biophotonics 2018, 11, e201700222. [Google Scholar] [CrossRef]
- Kelley, M.; Cooper, J.; Devito, D.; Mushi, R.; Aguinaga, M.d.P.; Erenso, D. Laser trap ionization for identification of human erythrocytes with variable hemoglobin quantitation. J. Biomed. Opt. 2018, 23, 055005. [Google Scholar] [CrossRef] [Green Version]
- Kelley, M.; Gao, Y.; Erenso, D. Single cell ionization by a laser trap: A preliminary study in measuring radiation dose and charge in BT20 breast carcinoma cells. Biomed. Opt. Express 2016, 7, 3438–3448. [Google Scholar] [CrossRef] [Green Version]
- Greulich, K. Practical aspects of working with laser microbeams and optical tweezers: Data and equations. Methods Cell Biol. 2007, 82, 735–743. [Google Scholar] [PubMed]
- Suresh, S. Mechanical response of human red blood cells in health and disease: Some structure-property- function relationships. J. Mater. Res. 2006, 21, 1871–1877. [Google Scholar] [CrossRef]
- Lee, K.; Kinnunen, M.; Khokhlova, M.; Lyubin, E.V.; Priezzhev, A.V.; Meglinski, I.; Fedyanin, A. Optical tweezers study of red blood cell aggregation and disaggregation in plasma and protein solutions. J. Biomed. Opt. 2016, 21, 035001. [Google Scholar] [CrossRef] [PubMed]
- Van Vliet, K.; Bao, G.; Suresh, S. The biomechanics toolbox: Experimental approaches for living cells and biomolecules. Acta Mater. 2003, 51, 5881–5905. [Google Scholar] [CrossRef]
- Dao, M.; Lim, C.; Suresh, S. Mechanics of the human red blood cell deformed by optical tweezers. J. Mech. Phys. Solids 2003, 51, 2259–2280. [Google Scholar] [CrossRef]
- Fontes, A.; Fernandes, H.; de Thomaz, A.; Barbosa, L.; Barjas-Castro, M.; Cesar, C. Measuring electrical and mechanical properties of red blood cells with double optical tweezers. J. Biomed. Opt. 2008, 13, 014001. [Google Scholar] [CrossRef] [Green Version]
- Khokhlova, M.; Lyubin, E.; Zhdanov, A.; Fedyanin, A.; Rykova, S.; Sokolova, I. Normal and system lupus erythematosus red blood cell interactions studied by double trap optical tweezers: Direct measurements of aggregation forces. J. Biomed. Opt. 2012, 17, 025001. [Google Scholar] [CrossRef] [Green Version]
- Baskurt, O.; Meiselman, H. Erythrocyte aggregation: Basic aspects and clinical importance. Clin. Hemorheol. Microcirc. 2013, 53, 23–37. [Google Scholar] [CrossRef] [Green Version]
- Kwon, S.; Lee, D.; Han, S.; Yang, W.; Quan, F.; Kim, K. Biomechanical properties of red blood cells infected by Plasmodium berghei ANKA. J. Cell. Physiol. 2019, 234, 20546–20553. [Google Scholar] [CrossRef]
- Agrawal, R.; Smart, T.; Nobre-Cardoso, J.; Richards, C.; Bhatnagar, R.; Tufail, A.; Shima, D.; Jones, P.H.; Pavesio, C. Assessment of red blood cell deformability in type 2 diabetes mellitus and diabetic retinopathy by dual optical tweezers stretching technique. Sci. Rep. 2016, 6, 15873. [Google Scholar] [CrossRef]
- Zhu, R.; Avsievich, T.; Bykov, A.; Popov, A.; Meglinski, I. Influence of pulsed He–Ne Laser irradiation on the red blood cell interaction studied by optical tweezers. Micromachines 2019, 10, 853. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Waugh, R.; Mantalaris, A.; Bauserman, R.; Hwang, W.; Wu, J. Membrane instability in late-stage erythropoiesis. Blood 2001, 97, 1869–1875. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Henon, S.; Lenormand, G.; Richert, A.; Gallet, F. A new determination of the shear modulus of the human erythrocyte membrane using optical tweezers. Biophys. J. 1999, 76, 1145–1151. [Google Scholar] [CrossRef] [Green Version]
- Lenormand, G.; Hénon, S.; Richert, A.; Siméon, J.; Gallet, F. Direct measurement of the area expansion and shear moduli of the human red blood cell membrane skeleton. Biophys. J. 2001, 81, 43–56. [Google Scholar] [CrossRef] [Green Version]
- Mohanty, S.; Mohanty, K.; Gupta, P. Dynamics of Interaction of RBC with optical tweezers. Opt. Express 2005, 13, 4745–4751. [Google Scholar] [CrossRef]
- Paul, A.; Padmapriya, P.; Natarajan, V. Diagnosis of malarial infection using change in properties of optically trapped red blood cells. Biomed. J. 2017, 40, 101–105. [Google Scholar] [CrossRef]
- Guzniczak, E.; Mohammad Zadeh, M.; Dempsey, F.; Jimenez, M.; Bock, H.; Whyte, G.; Willoughby, N.; Bridle, H. High-throughput assessment of mechanical properties of stem cell derived red blood cells, toward cellular downstream processing. Sci. Rep. 2017, 7, 14457. [Google Scholar] [CrossRef] [Green Version]
- Mairbäurl, H. Red blood cell function in hypoxia at altitude and exercise. Int. J. Sports Med. 1994, 15, 51–63. [Google Scholar] [CrossRef]
- Schrier, S. Pathophysiology of thalassemia. Curr. Opin. Hematol. 2002, 9, 123–126. [Google Scholar] [CrossRef]
- Rivella, S. Ineffective erythropoiesis and thalassemias. Curr. Opin. Hematol. 2009, 16, 187. [Google Scholar] [CrossRef] [Green Version]
- Chen, K.; Qin, Y.; Zheng, F.; Sun, M.; Shi, D. Diagnosis of colorectal cancer using Raman spectroscopy of laser-trapped single living epithelial cells. Opt. Lett. 2006, 31, 2015–2017. [Google Scholar] [CrossRef] [PubMed]
- Rusciano, G.; De Luca, A.; Pesce, G.; Sasso, A. Raman tweezers as a diagnostic tool of hemoglobin-related blood disorders. Sensors 2008, 8, 7818–7832. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Wang, G.; Yao, H.; Huang, S.; Chen, P.; Li, Y. Vibartional Spectroscopic Identification of α-and β-thalassemia with single-cell Raman tweezers. In Biomedical Topical Meeting; Optical Society of America: Washington, DC, USA, 2006; p. ME77. [Google Scholar]
- Lin, J.; Shao, L.; Qiu, S.; Huang, X.; Liu, M.; Zheng, Z.; Lin, D.; Xu, Y.; Li, Z.; Lin, Y.; et al. Application of a near-infrared laser tweezers Raman spectroscopy system for label-free analysis and differentiation of diabetic red blood cells. Biomed. Opt. Express 2018, 9, 984–993. [Google Scholar] [CrossRef] [PubMed]
- Liu, R.; Mao, Z.; Matthews, D.; Li, C.; Chan, J.; Satake, N. Novel single-cell functional analysis of red blood cells using laser tweezers Raman spectroscopy: Application for sickle cell disease. Exp. Hematol. 2013, 41, 656–661. [Google Scholar] [CrossRef] [PubMed]
- Raj, S.; Marro, M.; Wojdyla, M.; Petrov, D. Mechanochemistry of single red blood cells monitored using Raman tweezers. Biomed. Opt. Express 2012, 3, 753–763. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Zachariah, E.; Bankapur, A.; Santhosh, C.; Valiathan, M.; Mathur, D. Probing oxidative stress in single erythrocytes with Raman Tweezers. J. Photoch. Photobio. B 2010, 100, 113–116. [Google Scholar] [CrossRef]
- Lin, D.; Zheng, Z.; Wang, Q.; Huang, H.; Huang, Z.; Yu, Y.; Qiu, S.; Wen, C.; Cheng, M.; Feng, S. Label-free optical sensor based on red blood cells laser tweezers Raman spectroscopy analysis for ABO blood typing. Opt. Express 2016, 24, 24750–24759. [Google Scholar] [CrossRef]
- Dasgupta, R.; Shanker Verma, R.; Ahlawat, S.; Uppal, A.; Kumar Gupta, P. Studies on erythrocytes in malaria infected blood sample with Raman optical tweezers. J. Biomed. Opt. 2011, 16, 077009. [Google Scholar] [CrossRef] [Green Version]
- Chan, J.; Taylor, D.; Zwerdling, T.; Lane, S.; Ihara, K.; Huser, T. Micro-Raman spectroscopy detects individual neoplastic and normal hematopoietic cells. Biophys. J. 2006, 90, 648–656. [Google Scholar] [CrossRef] [Green Version]
- Brandao, M.; Fontes, A.; Barjas-Castro, M.; Barbosa, L.; Costa, F.; Cesar, C.; Saad, S. Optical tweezers for measuring red blood cell elasticity: Application to the study of drug response in sickle cell disease. Eur. J. Haematol. 2003, 70, 207–211. [Google Scholar] [CrossRef]
- Brandao, M.; Saad, S.; Cezar, C.; Fontes, A.; Costa, F.; Barjas-Castro, M. Elastic properties of stored red blood cells from sickle trait donor units. Vox Sang 2003, 85, 213–215. [Google Scholar] [CrossRef] [PubMed]
- Pellizzaro, A.; Welker, G.; Scott, D.; Solomon, R.; Cooper, J.; Farone, A.; Farone, M.; Mushi, R.; Aguinaga, M.d.P.; Erenso, D. Direct laser trapping for measuring the behavior of transfused erythrocytes in a sickle cell anemia patient. Biomed. Opt. Express 2012, 3, 2190–2199. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Sheikh-Hasani, V.; Babaei, M.; Azadbakht, A.; Pazoki-Toroudi, H.; Mashaghi, A.; Moosavi-Movahedi, A.; Reihani, S. Atorvastatin treatment softens human red blood cells: An optical tweezers study. Biomed. Opt. Express 2018, 9, 1256–1261. [Google Scholar] [CrossRef] [Green Version]
- Liu, J.; Zhang, F.; Zhu, L.; Chu, D.; Qu, X. Mechanical properties of RBCs under oxidative stress measured by optical tweezers. Opt. Commun. 2019, 442, 56–59. [Google Scholar] [CrossRef]
- Avsievich, T.; Popov, A.; Bykov, A.; Meglinski, I. Mutual interaction of red blood cells influenced by nanoparticles. Sci. Rep. 2019, 9, 5147. [Google Scholar] [CrossRef] [PubMed]
- Dharmadhikari, J.; Roy, S.; Dharmadhikari, A.; Sharma, S.; Mathur, D. Torque-generating malaria-infected red blood cells in an optical trap. Opt. Express 2004, 12, 1179–1184. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Paul, A.; Ramdani, G.; Tatu, U.; Langsley, G.; Natarajan, V. Studying the rigidity of red blood cells induced by Plasmodium falciparum infection. Sci. Rep. 2019, 9, 6336. [Google Scholar] [CrossRef]
- Smith, J. Erythrocyte membrane: Structure, function, and pathophysiology. Vet. Pathol. 1987, 24, 471–476. [Google Scholar] [CrossRef] [Green Version]
- Kim, J.; Lee, H.; Shin, S. Advances in the measurement of red blood cell deformability: A brief review. J. Cell. Biotechnol. 2015, 1, 63–79. [Google Scholar] [CrossRef] [Green Version]
- Dupire, J.; Abkarian, M.; Viallat, A. A simple model to understand the effect of membrane shear elasticity and stress-free shape on the motion of red blood cells in shear flow. Soft Matter 2015, 11, 8372–8382. [Google Scholar] [CrossRef]
- Rancourt-Grenier, S.; Wei, M.T.; Bai, J.J.; Chiou, A.; Bareil, P.; Duval, P.L.; Sheng, Y. Dynamic deformation of red blood cell in dual-trap optical tweezers. Opt. Express 2010, 18, 10462–10472. [Google Scholar] [CrossRef] [PubMed]
- Liao, G.B.; Bareil, P.; Sheng, Y.; Chiou, A. One-dimensional jumping optical tweezers for optical stretching of bi-concave human red blood cells. Opt. Express 2008, 16, 1996–2004. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Mills, J.; Qie, L.; Dao, M.; Lim, C.; Suresh, S. Nonlinear elastic and viscoelastic deformation of the human red blood cell with optical tweezers. Mech. Chem. Biosyst. 2004, 1, 169–180. [Google Scholar] [PubMed]
- Lim, C.; Dao, M.; Suresh, S.; Sow, C.; Chew, K. Large deformation of living cells using laser traps. Acta Mater. 2004, 52, 1837–1845. [Google Scholar] [CrossRef]
- Czerwinska, J.; Wolf, S.; Mohammadi, H.; Jeney, S. Red blood cell aging during storage, studied using optical tweezers experiment. Cell. Mol. Bioeng. 2015, 8, 258–266. [Google Scholar] [CrossRef]
- Silva, D.; Jovino, C.; Silva, C.; Fernandes, H.; Filho, M.; Lucena, S.; Costa, A.; Cesar, C.; Barjas-Castro, M.; Santos, B.; et al. Optical tweezers as a new biomedical tool to measure zeta potential of stored red blood cells. PloS ONE 2012, 7, e31778. [Google Scholar] [CrossRef] [Green Version]
- Xu, Z.; Zheng, Y.; Wang, X.; Shehata, N.; Wang, C.; Sun, Y. Stiffness increase of red blood cells during storage. Microsyst. Nanoeng. 2018, 4, 17103. [Google Scholar] [CrossRef] [Green Version]
- Fernandes, H.; Fontes, A.; Thomaz, A.; Castro, V.; Cesar, C.; Barjas-Castro, M. Measuring red blood cell aggregation forces using double optical tweezers. Scand. J. Clin. Lab. Invest. 2013, 73, 262–264. [Google Scholar] [CrossRef]
- Rampling, M.; Meiselman, H.; Neu, B.; Baskurt, O. Influence of cell-specific factors on red blood cell aggregation. Biorheology 2004, 41, 91–112. [Google Scholar]
- Yang, B.W.; Li, Z. Measuring micro-interactions between coagulating red blood cells using optical tweezers. Biomed. Opt. Express 2010, 1, 1217–1224. [Google Scholar] [CrossRef] [Green Version]
- Armstrong, J.; Wenby, R.; Meiselman, H.; Fisher, T. The hydrodynamic radii of macromolecules and their effect on red blood cell aggregation. Biophys. J. 2004, 87, 4259–4270. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Neu, B.; Meiselman, H. Depletion-mediated red blood cell aggregation in polymer solutions. Biophys. J. 2002, 83, 2482–2490. [Google Scholar] [CrossRef] [Green Version]
- Tozeren, A.; Sung, K. Theoretical and experimental studies on cross-bridge migration during cell disaggregation. Biophys. J. 1989, 55, 479–487. [Google Scholar] [CrossRef] [Green Version]
- Lee, K.; Danilina, A.V.; Kinnunen, M.; Priezzhev, A.V.; Meglinski, I. Probing the red blood cells aggregating force with optical tweezers. IEEE J. Sel. Top. Quantum Electron. 2015, 22, 365–370. [Google Scholar] [CrossRef]
- Semenov, A.; Lugovtsov, A.; Shin, S.; Barshtein, G.; Priezzhev, A.V. Red blood cells interaction mediated by dextran macromolecules: In vitro study using diffuse light scattering technique and optical tweezers. In Saratov Fall Meeting 2018: Optical and Nano-Technologies for Biology and Medicine; SPIE: Belingham, WA, USA, 2019; Volume 11065, p. 110651X. [Google Scholar]
- Lee, K.; Kinnunen, M.; Danilina, A.V.; Ustinov, V.; Shin, S.; Meglinski, I.; Priezzhev, A.V. Characterization at the individual cell level and in whole blood samples of shear stress preventing red blood cells aggregation. J. Biomech. 2016, 49, 1021–1026. [Google Scholar] [CrossRef]
- Lee, K.; Priezzhev, A.; Shin, S.; Yaya, F.; Meglinski, I. Characterization of shear stress preventing red blood cells aggregation at the individual cell level: The temperature dependence. Clin. Hemorheol. Microcirc. 2016, 64, 853–857. [Google Scholar] [CrossRef]
- Lee, K.; Shirshin, E.; Rovnyagina, N.; Yaya, F.; Boujja, Z.; Priezzhev, A.; Wagner, C. Dextran adsorption onto red blood cells revisited: Single cell quantification by laser tweezers combined with microfluidics. Biomed. Opt. Express 2018, 9, 2755–2764. [Google Scholar] [CrossRef]
- Avsievich, T.; Popov, A.; Bykov, A.; Meglinski, I. Mutual interaction of red blood cells assessed by optical tweezers and scanning electron microscopy imaging. Opt. Lett. 2018, 43, 3921–3924. [Google Scholar] [CrossRef]
- Avsievich, T.; Tarakanchikova, Y.; Zhu, R.; Popov, A.; Bykov, A.; Skovorodkin, I.; Vainio, S.; Meglinski, I. Impact of nanocapsules on red blood cells interplay jointly assessed by optical tweezers and microscopy. Micromachines 2020, 11, 19. [Google Scholar] [CrossRef] [Green Version]
- Zhong, M.C.; Wei, X.B.; Zhou, J.H.; Wang, Z.Q.; Li, Y.M. Trapping red blood cells in living animals using optical tweezers. Nat. Commun. 2013, 4, 1768. [Google Scholar] [CrossRef] [Green Version]
- Hörner, F.; Meissner, R.; Polali, S.; Pfeiffer, J.; Betz, T.; Denz, C.; Raz, E. Holographic optical tweezers-based in vivo manipulations in zebrafish embryos. J. Biophotonics 2017, 10, 1492–1501. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Meissner, R.; Sugden, W.; Siekmann, A.; Denz, C. Multimodal in vivo blood flow sensing combining particle image velocimetry and optical tweezers-based blood steering. In Diagnostic and Therapeutic Applications of Light in Cardiology 2018; SPIE: Belingham, WA, USA, 2018; Volume 10471, p. 1047110. [Google Scholar]
- Ng, A.; Alexander, W. Haematopoietic stem cells: Past, present and future. Cell Death Discov. 2017, 3, 17002. [Google Scholar] [CrossRef] [PubMed]
- Turcotte, R.; Alt, C.; Runnels, J.; Ito, K.; Wu, J.; Zaher, W.; Mortensen, L.; Silberstein, L.; Côté, D.; Kung, A.; et al. Image-guided transplantation of single cells in the bone marrow of live animals. Sci. Rep. 2017, 7, 3875. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Arbore, C.; Perego, L.; Sergides, M.; Capitanio, M. Probing force in living cells with optical tweezers: From single-molecule mechanics to cell mechanotransduction. In Biophysical Review; Springer: Amsterdam, The Netherlands, 2019; pp. 1–18. [Google Scholar]
- Lensch, M.; Daley, G. Origins of mammalian hematopoiesis: In vivo paradigms and in vitro models. In Current Topics in Developmental Biology; Elsevier: Amsterdam, The Netherlands, 2004; Volume 60, pp. 127–196. [Google Scholar]
- Korobtsov, A.; Kotova, S.; Losevsky, N.; Mayorova, A.; Patlan, V.; Timchenko, E.; Lysov, N.; Zarubina, E. Optical tweezers technique for the study of red blood cells deformation ability. Laser Phys. 2012, 22, 1265–1270. [Google Scholar] [CrossRef]








© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhu, R.; Avsievich, T.; Popov, A.; Meglinski, I. Optical Tweezers in Studies of Red Blood Cells. Cells 2020, 9, 545. https://doi.org/10.3390/cells9030545
Zhu R, Avsievich T, Popov A, Meglinski I. Optical Tweezers in Studies of Red Blood Cells. Cells. 2020; 9(3):545. https://doi.org/10.3390/cells9030545
Chicago/Turabian StyleZhu, Ruixue, Tatiana Avsievich, Alexey Popov, and Igor Meglinski. 2020. "Optical Tweezers in Studies of Red Blood Cells" Cells 9, no. 3: 545. https://doi.org/10.3390/cells9030545
APA StyleZhu, R., Avsievich, T., Popov, A., & Meglinski, I. (2020). Optical Tweezers in Studies of Red Blood Cells. Cells, 9(3), 545. https://doi.org/10.3390/cells9030545






