Sparsity-Penalized Stacked Denoising Autoencoders for Imputing Single-Cell RNA-seq Data
Abstract
:1. Introduction
2. Materials and Methods
2.1. Data Collection and Pre-Processing
2.2. scSDAE Model Structure and Training Procedure
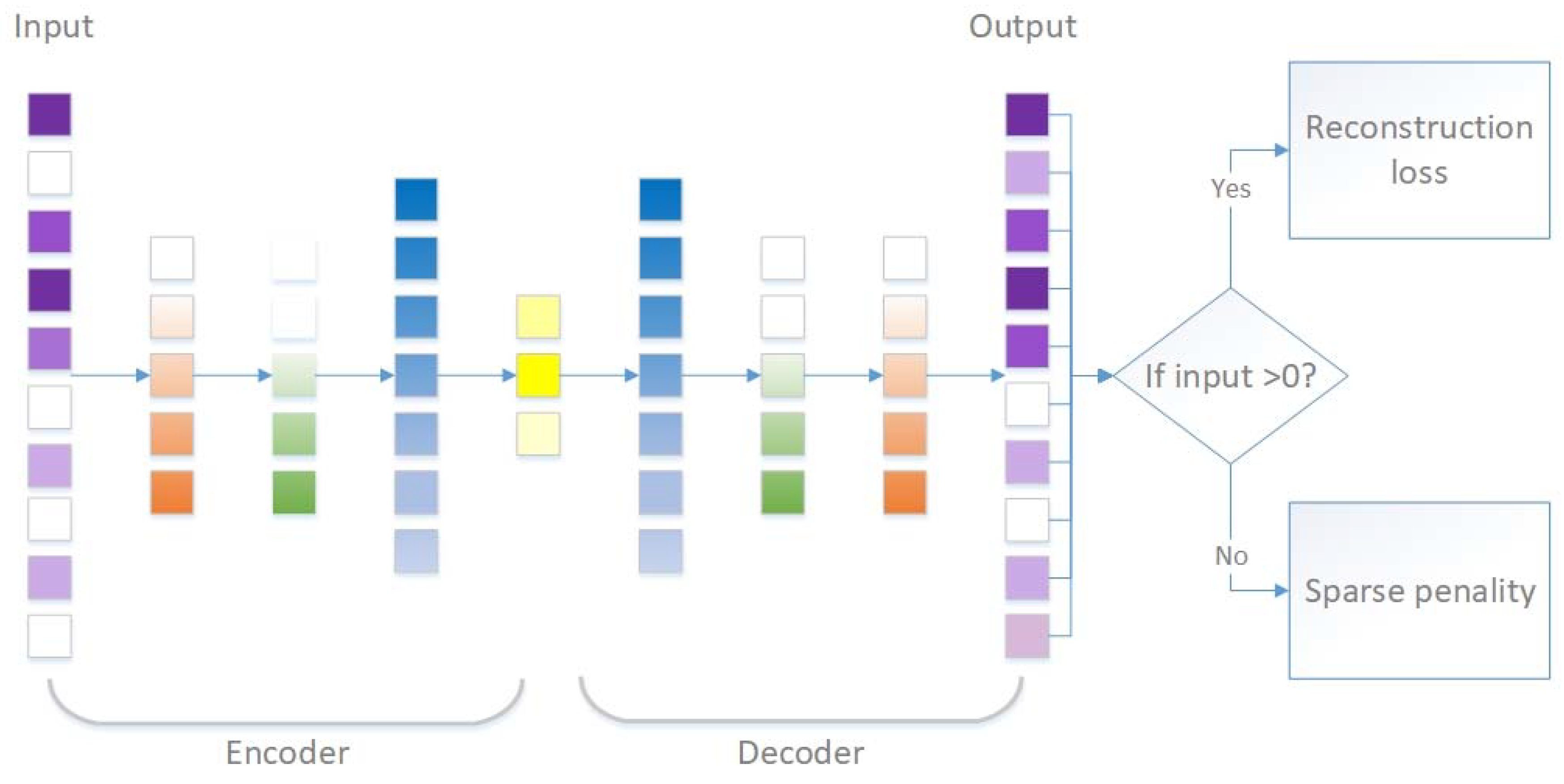
2.2.1. Autoencoders
2.2.2. Denoising Autoencoders (DAE)
2.2.3. Sparsity-Penalized Stacked Denoising Autoencoders (scSDAEs)
| Algorithm 1. Sparsity penalized stacked denoising autoencoders for single cell RNA-seq data (scSDAE). |
| Input: normalized expression vector , network layer width vector with denoted the bottleneck layer width |
| Output: imputed expression vector |
| for in do |
| if do |
| corrupt into with noise, build neural network : and train to minimize ; predict |
| else do |
| corrupt into with noise, build neural network : and train to minimize formula |
| ifdo |
| predict |
| end for |
| build neural network : and train to minimize |
| predict |
| calculate the mask vector : ( is the indicator function.) |
| calculate the output ( denotes element-wise multiplication.) |
2.3. Parameter Setting and Implementation
3. Results
3.1. scSDAE Recovers Gene Expression Affected by Simulated Missing Values
3.2. Assessing the False Signals Induced by Different Imputation Methods
3.3. scSDAE Increases the Within-Group Similarity in RNA Mixture Dataset
3.4. scSDAE Accurately Recovers Spike-in RNA Concentrations Affected by Technical Zeros
3.5. scSDAE Improves the Consistency of RNA and Protein Levels in CITE-seq Data
3.6. scSDAE Can Help Improve Clustering Accuracy
4. Discussion
5. Conclusions
Supplementary Materials
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Appendix A
References
- Tang, F.; Barbacioru, C.; Wang, Y.; Nordman, E.; Lee, C.; Xu, N. mRNA-Seq whole-transcriptome analysis of a single cell. Nat. Methods 2009, 6, 377–382. [Google Scholar] [CrossRef] [PubMed]
- Usoskin, D.; Furlan, A.; Islam, S.; Abdo, H.; Lönnerberg, P.; Lou, D. Unbiased classification of sensory neuron types by large-scale single-cell RNA sequencing. Nat. Neurosci. 2015, 18, 145–153. [Google Scholar] [CrossRef] [PubMed]
- Chen, H.; Ye, F.; Guo, G. Revolutionizing immunology with single-cell RNA sequencing. Cell Mol. Immunol. 2019, 16, 242–249. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Wagner, J.; Rapsomaniki, M.A.; Chevrier, S.; Anzeneder, T.; Langwieder, C.; Dykgers, A. A Single-Cell Atlas of the Tumor and Immune Ecosystem of Human Breast Cancer. Cell 2019, 177, 1330.e18–1345.e18. [Google Scholar] [CrossRef] [Green Version]
- Regev, A.; Teichmann, S.A.; Lander, E.S.; Amit, I.; Benoist, C.; Birney, E. The Human Cell Atlas. Elife 2017, 6. [Google Scholar] [CrossRef]
- Han, X.; Wang, R.; Zhou, Y.; Fei, L.; Sun, H.; Lai, S. Mapping the Mouse Cell Atlas by Microwell-Seq. Cell 2018, 172, 1091.e17–1107.e17. [Google Scholar] [CrossRef] [Green Version]
- Schaum, N.; Karkanias, J.; Neff, N.F. Single-cell transcriptomics of 20 mouse organs creates a Tabula Muris. Nature 2018, 562, 367–372. [Google Scholar] [CrossRef]
- Haque, A.; Engel, J.; Teichmann, S.A.; Lönnberg, T. A practical guide to single-cell RNA-sequencing for biomedical research and clinical applications. Genome Med. 2017, 9, 75. [Google Scholar] [CrossRef]
- Bacher, R.; Kendziorski, C. Design and computational analysis of single-cell RNA-sequencing experiments. Genome Biol. 2016, 17, 63. [Google Scholar] [CrossRef] [Green Version]
- Van Dijk, D.; Sharma, R.; Nainys, J.; Wolf, G.; Krishnaswamy, S.; Pe’er Correspondence, D. Recovering Gene Interactions from Single-Cell Data Using Data Diffusion In Brief Population Analysis Archetypal Analysis Gene Interactions. Cell 2018, 174, 716.e27–729.e27. [Google Scholar] [CrossRef] [Green Version]
- Li, W.V.; Li, J.J. An accurate and robust imputation method scImpute for single-cell RNA-seq data. Nat. Commun. 2018, 9, 997. [Google Scholar] [CrossRef] [Green Version]
- Huang, M.; Wang, J.; Torre, E.; Dueck, H.; Shaffer, S.; Bonasio, R. SAVER: Gene expression recovery for single-cell RNA sequencing. Nat. Methods 2018, 15, 539–542. [Google Scholar] [CrossRef] [PubMed]
- Islam, S.; Zeisel, A.; Joost, S.; La Manno, G.; Zajac, P.; Kasper, M. Quantitative single-cell RNA-seq with unique molecular identifiers. Nat. Methods 2014, 11, 163–166. [Google Scholar] [CrossRef] [PubMed]
- Linderman, G.C.; Zhao, J.; Kluger, Y. Zero-preserving imputation of scRNA-seq data using low-rank approximation. bioRxiv 2018, 397588. [Google Scholar] [CrossRef]
- Chen, C.; Wu, C.J.; Wu, L.J.; Wang, X.C.; Deng, M.H.; Xi, R.B. scRMD: Imputation for single cell RNA-seq data via robust matrix decomposition. Bioinformatics 2020, btaa139. [Google Scholar] [CrossRef]
- Amodio, M.; van Dijk, D.; Srinivasan, K.; Chen, W.S.; Mohsen, H.; Moon, K.R. Exploring single-cell data with deep multitasking neural networks. Nat. Methods 2019, 16, 1139–1145. [Google Scholar] [CrossRef] [PubMed]
- Talwar, D.; Mongia, A.; Sengupta, D.; Majumdar, A. AutoImpute: Autoencoder based imputation of single-cell RNA-seq data. Sci. Rep. 2018, 8, 16329. [Google Scholar] [CrossRef] [Green Version]
- Badsha, M.B.; Li, R.; Liu, B.; Li, Y.I.; Xian, M.; Banovich, N.E. Imputation of single-cell gene expression with an autoencoder neural network. bioRxiv 2019, 504977. [Google Scholar] [CrossRef] [Green Version]
- Eraslan, G.; Simon, L.M.; Mircea, M.; Mueller, N.S.; Theis, F.J. Single-cell RNA-seq denoising using a deep count autoencoder. Nat. Commun. 2019, 10, 390. [Google Scholar] [CrossRef] [Green Version]
- Lopez, R.; Regier, J.; Cole, M.B.; Jordan, M.I.; Yosef, N. Deep generative modeling for single-cell transcriptomics. Nat. Methods 2018, 15, 1053–1058. [Google Scholar] [CrossRef]
- Kingma, D.P.; Welling, M. Auto-Encoding Variational Bayes. Available online: Https://arxiv.org/pdf/1312.6114.pdf (accessed on 14 August 2019).
- Arisdakessian, C.; Poirion, O.; Yunits, B.; Zhu, X.; Garmire, L.X. DeepImpute: An accurate, fast and scalable deep neural network method to impute single-cell RNA-Seq data. Genome Biol. 2019, 20, 211. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Rao, J.; Zhou, X.; Lu, Y.; Zhao, H.; Yang, Y. Imputing Single-cell RNA-seq data by combining Graph Convolution and Autoencoder Neural Networks. Biorxiv 2020, 935296. [Google Scholar] [CrossRef] [Green Version]
- Vincent Pascalvincent, P.; Larochelle Larocheh, H. Stacked Denoising Autoencoders: Learning Useful Representations in a Deep Network with a Local Denoising Criterion Pierre-Antoine Manzagol. J. Mach. Learn Res. 2010, 11, 3371–3408. Available online: Http://www.jmlr.org/papers/volume11/vincent10a/vincent10a.pdf (accessed on 29 April 2018).
- Mongia, A.; Sengupta, D.; Majumdar, A. deepMc: Deep Matrix Completion for imputation of single cell RNA-seq data. bioRxiv 2018, 387621. [Google Scholar] [CrossRef]
- Hsu, D.; Kakade, S.M.; Zhang, T. Robust Matrix Decomposition with Sparse Corruptions. IEEE Trans. Inf. Theory 2011, 57, 7221–7234. [Google Scholar] [CrossRef] [Green Version]
- Pierson, E.; Yau, C. ZIFA: Dimensionality reduction for zero-inflated single-cell gene expression analysis. Genome Biol. 2015, 16, 241. [Google Scholar] [CrossRef] [Green Version]
- Jia, C.; Hu, Y.; Kelly, D.; Kim, J.; Li, M.; Zhang, N.R. Accounting for technical noise in differential expression analysis of single-cell RNA sequencing data. Nucleic Acids Res. 2017, 45, 10978–10988. [Google Scholar] [CrossRef] [Green Version]
- Kingma, D.P.; Ba, J. Adam: A Method for Stochastic Optimization. 2014. Available online: Http://arxiv.org/abs/1412.6980 (accessed on 23 July 2019).
- Francesconi, M.; Lehner, B. The effects of genetic variation on gene expression dynamics during development. Nature 2013, 505, 208–211. [Google Scholar] [CrossRef]
- Herdin, M.; Czink, N.; Özcelik, H.; Bonek, E. Correlation matrix distance, a meaningful measure for evaluation of non-stationary MIMO channels. In Proceedings of the IEEE Vehicular Technology Conference, Stockholm, Sweden, 30 May–1 June 2005; pp. 136–140. [Google Scholar]
- Andrews, T.S.; Hemberg, M.; Tiberi, S.; Fan, J.; Miescher Charlotte Soneson, F.; Hopkins Stephanie Hicks, J. Open Peer Review False signals induced by single-cell imputation [version 2; peer review: 4 approved]. F1000Research 2019, 7, 1740. [Google Scholar] [CrossRef]
- Zappia, L.; Phipson, B.; Oshlack, A. Splatter: Simulation of single-cell RNA sequencing data. Genome Biol. 2017, 18, 174. [Google Scholar] [CrossRef]
- Kruskal, W.H.; Wallis, W.A. Use of Ranks in One-Criterion Variance Analysis. J. Am. Stat. Assoc. 1952, 47, 583–621. [Google Scholar] [CrossRef]
- Tian, L.; Dong, X.; Freytag, S.; Lê Cao, K.-A.; Su, S.; JalalAbadi, A. Benchmarking single cell RNA-sequencing analysis pipelines using mixture control experiments. Nat. Methods 2019, 16, 479–487. [Google Scholar] [CrossRef] [PubMed]
- Robinson, M.D.; Oshlack, A. A scaling normalization method for differential expression analysis of RNA-seq data. Genome Biol. 2010, 11, R25. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Love, M.I.; Huber, W.; Anders, S. Moderated estimation of fold change and dispersion for RNA-seq data with DESeq2. Genome Biol. 2014, 15, 550. [Google Scholar] [CrossRef] [Green Version]
- Cole, M.B.; Risso, D.; Wagner, A.; DeTomaso, D.; Ngai, J.; Purdom, E. Performance Assessment and Selection of Normalization Procedures for Single-Cell RNA-Seq. Cell Syst. 2019, 8, 315.e8–328.e8. [Google Scholar] [CrossRef]
- Yip, S.H.; Wang, P.; Kocher, J.-P.A.; Sham, P.C.; Wang, J. Linnorm: Improved statistical analysis for single cell RNA-seq expression data. Nucleic Acids Res. 2017, 45, e179. [Google Scholar] [CrossRef]
- Lun, A.T.L.; Bach, K.; Marioni, J.C. Pooling across cells to normalize single-cell RNA sequencing data with many zero counts. Genome Biol. 2016, 17, 75. [Google Scholar] [CrossRef]
- Ziegenhain, C.; Vieth, B.; Parekh, S.; Reinius, B.; Guillaumet-Adkins, A.; Smets, M. Comparative Analysis of Single-Cell RNA Sequencing Methods. Mol. Cell. 2017, 65, 631.e4–643.e4. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Jiang, L.; Schlesinger, F.; Davis, C.A.; Zhang, Y.; Li, R.; Salit, M. Synthetic spike-in standards for RNA-seq experiments. Genome Res. 2011, 21, 1543–1551. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Stoeckius, M.; Hafemeister, C.; Stephenson, W.; Houck-Loomis, B.; Chattopadhyay, P.K.; Swerdlow, H. Simultaneous epitope and transcriptome measurement in single cells. Nat. Methods 2017, 14, 865–868. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Stuart, T.; Butler, A.; Hoffman, P.; Hafemeister, C.; Papalexi, E.; Mauck, W.M. Comprehensive Integration of Single-Cell Data. Cell 2019, 177, 1888.e21–1902.e21. [Google Scholar] [CrossRef] [PubMed]
- Van Der Maaten, L.J.P.; Hinton, G.E. Visualizing high-dimensional data using t-sne. J. Mach. Learn. Res. 2008, 9, 2579–2605. [Google Scholar] [CrossRef]
- Kim, J.K.; Kolodziejczyk, A.A.; Illicic, T.; Teichmann, S.A.; Marioni, J.C. Characterizing noise structure in single-cell RNA-seq distinguishes genuine from technical stochastic allelic expression. Nat. Commun. 2015, 6, 8687. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Pollen, A.A.; Nowakowski, T.J.; Shuga, J.; Wang, X.; Leyrat, A.A.; Lui, J.H. Low-coverage single-cell mRNA sequencing reveals cellular heterogeneity and activated signaling pathways in developing cerebral cortex. Nat. Biotechnol. 2014, 32, 1053–1058. [Google Scholar] [CrossRef] [Green Version]
- Zeisel, A.; Muñoz-Manchado, A.B.; Codeluppi, S.; Lönnerberg, P.; La Manno, G.; Juréus, A. Brain structure. Cell types in the mouse cortex and hippocampus revealed by single-cell RNA-seq. Science 2015, 347, 1138–1142. [Google Scholar] [CrossRef]
- Lake, B.B.; Ai, R.; Kaeser, G.E.; Salathia, N.S.; Yung, Y.C.; Liu, R. Neuronal subtypes and diversity revealed by single-nucleus RNA sequencing of the human brain. Science 2016, 352, 1586–1590. [Google Scholar] [CrossRef] [Green Version]
- Patel, A.P.; Tirosh, I.; Trombetta, J.J.; Shalek, A.K.; Gillespie, S.M.; Wakimoto, H. Single-cell RNA-seq highlights intratumoral heterogeneity in primary glioblastoma. Science 2014, 344, 1396–1401. [Google Scholar] [CrossRef] [Green Version]
- Hubert, L.; Arabie, P. Comparing partitions. J. Classif. 1985, 2, 193–218. [Google Scholar] [CrossRef]
- Mcinnes, L.; Healy, J.; Melville, J. UMAP: Uniform Manifold Approximation and Projection for Dimension Reduction. 2018. Available online: Https://arxiv.org/pdf/1802.03426.pdf (accessed on 12 April 2019).






| Zero Rate | Dropout | scSDAE | scImpute | MAGIC | DCA | SAUCIE |
|---|---|---|---|---|---|---|
| 50% | 0.295 | 0.094 | 0.604 | 0.430 | 0.546 | 0.298 |
| (0.003) | (0.023) | (0.027) | (0.006) | (0.173) | (0.016) | |
| 60% | 0.318 | 0.101 | 0.796 | 0.447 | 0.642 | 0.305 |
| (0.004) | (0.013) | (0.009) | (0.004) | (0.235) | (0.018) | |
| 70% | 0.360 | 0.109 | 0.847 | 0.849 | 0.685 | 0.300 |
| (0.005) | (0.021) | (0.024) | (0.013) | (0.285) | (0.013) | |
| 80% | 0.503 | 0.136 | 0.830 | 0.990 | 0.790 | 0.325 |
| (0.009) | (0.019) | (0.020) | (0.000) | (0.244) | (0.037) | |
| 90% | 0.717 | 0.193 | 0.932 | 0.991 | 0.991 | 0.516 |
| (0.009) | (0.039) | (0.007) | (0.000) | (0.000) | (0.039) |
| Dataset | Raw | scSDAE | scImpute | MAGIC | SDAE0 | SDAE | DCA |
|---|---|---|---|---|---|---|---|
| Kolodziejczyk | 0.368 | 0.831 | 0.668 | 0.525 | 0.413 | 0.552 | 0.008 |
| Pollen | 0.829 | 0.932 | 0.824 | 0.657 | 0.635 | 0.824 | 0.411 |
| Zeisel | 0.747 | 0.794 | 0.776 | 0.696 | 0.736 | 0.764 | 0.702 |
| Lake | 0.591 | 0.687 | 0.446 | 0.556 | 0.301 | 0.491 | 0.017 |
| Patel | 0.857 | 0.864 | 0.663 | 0.848 | 0.857 | 0.857 | 0.084 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Chi, W.; Deng, M. Sparsity-Penalized Stacked Denoising Autoencoders for Imputing Single-Cell RNA-seq Data. Genes 2020, 11, 532. https://doi.org/10.3390/genes11050532
Chi W, Deng M. Sparsity-Penalized Stacked Denoising Autoencoders for Imputing Single-Cell RNA-seq Data. Genes. 2020; 11(5):532. https://doi.org/10.3390/genes11050532
Chicago/Turabian StyleChi, Weilai, and Minghua Deng. 2020. "Sparsity-Penalized Stacked Denoising Autoencoders for Imputing Single-Cell RNA-seq Data" Genes 11, no. 5: 532. https://doi.org/10.3390/genes11050532
APA StyleChi, W., & Deng, M. (2020). Sparsity-Penalized Stacked Denoising Autoencoders for Imputing Single-Cell RNA-seq Data. Genes, 11(5), 532. https://doi.org/10.3390/genes11050532





